1 - Institut d'Astrophysique, Université de Liège, Avenue de Cointe 5, 4000 Liège, Belgium
2 - Astronomical Observatory of Kyiv University, Observatorna St. 3, UA- 04053 Kyiv, Ukraine

Abstract
We use the Véron-Cetty & Véron (2000) catalog (VV) of 13 213 quasars to investigate their possible physical grouping over angular scales $10\hbox{$^{\prime\prime}$ }\leq\Delta\theta\leq 1000\hbox{$^{\prime\prime}$ }$ . We first estimate the number of quasar pairs that would be expected in VV assuming a random distribution for the quasar positions and taking into account observational selection effects affecting heterogeneous catalogs. We find in VV a statistically significant (>3 $\sigma$ ) excess of pairs of quasars with similar redshifts ( $\Delta z\leq 0.01$ ) and angular separations in the $50\hbox {$^{\prime \prime }$ }{-}100\hbox {$^{\prime \prime }$ }$ range, corresponding to projected linear separations $(0.2{-}0.5)~{\rm Mpc}/h_{75} (\Omega_{\rm M}=1, \Omega_\Lambda=0)$ or $(0.4{-}0.7)~{\rm Mpc}/h_{75} (\Omega_{\rm M}=0.3, \Omega_\Lambda = 0.7)$ . There is also some excess in the $100\hbox{$^{\prime\prime}$ }{-}600\hbox{$^{\prime\prime}$ }$ range corresponding to (1-5) Mpc in projected linear separations. If most of these quasar pairs do indeed belong to large physical entities, these separations must represent the inner scales of huge mass concentrations (cf. galaxy clusters or superclusters) at high redshifts; but it is not excluded that some of the pairs may actually consist of multiple quasar images produced by gravitational lensing. Of course, a fraction of these pairs could also arise due to random projections of quasars on the sky. The list of 11 pairs of quasars with redshift differences $\Delta z \leq 0.02$ and angular separations $50\hbox{$^{\prime\prime}$ }\leq \Delta\theta\leq 100\hbox{$^{\prime\prime}$ }$ is presented in order to stimulate further observational studies and to better understand the astrophysical and cosmological significance of these interesting objects.

Close pairs of quasars with small angular separations (typically $\Delta\theta\leq10\hbox{$^{\prime\prime}$ }$ ) and small redshift differences ( $\Delta z\leq 0.01$ ) have attracted much attention in recent years because of their possible relevance to a number of challenging astrophysical and cosmological problems (e.g. Kochanek et al. 1999). Identification of multiply imaged quasars in optical and radio surveys has frequently been used to set interesting constraints on cosmological parameters, including the Hubble constant (cf. the recent review by Claeskens & Surdej 2001). However, little is known about the statistics of physical pairs of quasars or of multiply imaged lensed quasars with angular separations $\Delta\theta > 10 \hbox{$^{\prime\prime}$ }$ , which would probe lensing masses over scales of galaxy clusters, or even superclusters. Maoz et al. (1997) have carried out a survey with HST for very large image separation lensed quasars, but they failed to detect any secondary image near each of their 76 primarily selected quasars with separations in the 7 $\hbox{$^{\prime\prime}$ }$ -50 $\hbox{$^{\prime\prime}$ }$ range. On the other hand, Shaver (1984) has pointed out an excess of quasar pairs over several Mpc linear scales, based upon an original statistical analysis of the Véron-Cetty & Véron (1984) catalog, which included at that time 2251 quasars. This has been later confirmed by correlation function analysis with smaller but homogeneous datasets (Andreani & Cristiani 1992; Mo & Fang 1993; Croom & Shanks 1996).

It is obvious that alike for the case of close pairs of quasars, the identification of very large separation ones (with $\Delta \theta \in [10\hbox{$^{\prime\prime}$ }{-}1000\hbox{$^{\prime\prime}$ }]$ ) would have very challenging astrophysical and cosmological implications. Indeed, such physical pairs of quasars could be associated with high redshift galaxy clusters and provide interesting clues on the origin and early evolution of clusters, dark matter, etc. Similarly, setting more stringent observational limits on the frequency of gravitational lensing at very large angular scales would enable us to rule out the existence of galaxy clusters with very large M/L ratio, to set upper limits on the central density of clusters and superclusters, to reject certain proposed cosmogonic models and to set an independent upper limit on the cosmological constant (Kochanek 1995; Wambsganss et al. 1995).

In the present paper, we show that in the recent version of the Véron-Cetty & Véron catalog (2000, hereafter VV) the number $N_{\rm p}$ of quasar pairs with similar redshift ( $\Delta z\leq 0.01$ ) deviates significantly, within certain specific angular separation intervals, from the number $N_{\rm exp}$ that would be expected assuming a random distribution of quasars over the sky. Therefore, in these intervals, there is an excess $N_{\rm PP}=N_{\rm p}-N_{\rm exp}$ of pairs that may either be caused by statistical fluctuations or consist of very interesting genuine physical pairs of quasars, or, possibly, doubly imaged quasars.

Because the VV catalog is heterogeneous, it is important to obtain a reliable estimate of $N_{\rm exp}$ in spite of the various unphysical selection effects (cf. different survey areas, limiting magnitudes, ...) that may accordingly affect the two-point correlation function. Shaver (1984) has proposed to take into account such selection effects by using information from the distribution of quasar pairs with different, but nevertheless close redshifts, that may only arise due to random coincidences. In our case, thanks to the very large number of entries available in VV, it is possible to supplement Shaver's method with estimates of $N_{\rm exp}$ and their dispersions. We have applied this improved method to VV and report here on some interesting results in the $50\hbox{$^{\prime\prime}$ }{-} 600\hbox{$^{\prime\prime}$ }$ angular separation interval.

2 Number estimates of quasar pairs

2.1 Basic assumptions and conventions

In order to study the physical pairing of quasars, Shaver (1984) has considered, for given angular separation intervals, the ratio of the number of quasar pairs having nearly the same redshifts (e.g. $\Delta z\leq 0.01$ , which may include physical pairs) to that with different, but nevertheless close redshifts (e.g. $0.03\leq \Delta z\leq 0.2$ ) that may only arise due to random coincidences.

Because several tens of multiply imaged quasars have been reported with angular separations $\Delta \theta < 10\hbox {$^{\prime \prime }$ }$ (Claeskens & Surdej 2001) and since our search in the VV catalog has not revealed any single pair with $10\hbox{$^{\prime\prime}$ }\leq\Delta \theta\leq 50\hbox{$^{\prime\prime}$ }$ and $\Delta z \leq 0.02$ , we restrict hereafter our study of physical pairs of quasars to those with angular separations $50\hbox{$^{\prime\prime}$ }\leq\Delta \theta\leq 1000\hbox{$^{\prime\prime}$ }$ .

Given that any apparent excess of quasar pairs could possibly result from large statistical fluctuations in the random projections of quasars, combined with the inherent observational selection effects in VV, a correct investigation of this problem requires to justify the validity of extrapolating the relations for the expected number $N_{\rm exp}$ from large angular separations to smaller ones. Similarly, a realistic estimate of the dispersion $\sigma(N_{\rm exp})$ is necessary to check for possible deviations from Poisson statistics, which could arise from hidden selection effects. Estimates of $N_{\rm exp}$ and $\sigma(N_{\rm exp})$ are made possible thanks to the very large number of entries available in VV. We do this by considering the pairs of quasars with small but definite redshift differences from 10 selected comparison bins (i.e. $\Delta z \in [0.03,0.04], ..., [0.12,0.13]$ ) and the pairs of quasars with $\Delta z\leq 0.01$ and angular separations $\Delta \theta > 5000\hbox{$^{\prime\prime}$ }$ (our investigation for $\Delta \theta > 1000\hbox{$^{\prime\prime}$ }$ yields similar results). For both these sets of quasar pairs, no physical grouping is expected between the quasars (cf. Andreani & Cristiani 1992; Mo & Fang 1993; Croom & Shanks 1996) and we may then use this information to estimate $N_{\rm exp}$ and $\sigma(N_{\rm exp})$ for $\Delta z\leq 0.01$ and $\Delta \theta \leq 1000\hbox{$^{\prime\prime}$ }$ .

The results are presented in terms of the pair numbers $N(\theta,\xi)$ having an angular separation $\theta \leq \Delta\theta < \theta+\delta$ , $\delta$ representing the width of the ring with angular radius $\theta$ , and a redshift difference $\xi \leq \Delta z < \xi +\zeta$ . In the remainder, we use the normalized pair numbers defined per unit interval of $\zeta$ and per unit area of the ring

Our choice to discretize the redshifts in bins having a width $\Delta z=0.01$ prevents us to deal with the problem of redshift measurement errors, roundoffs in VV or peculiar velocities which are always smaller than 0.01.

We define the normalized number of quasar pairs from VV with approximately similar redshifts as $n_{\rm p}=n(\theta,0)$ , adopting $\zeta =0.01$ . We assume that PP may contribute to $n_{\rm p}$ up to $5000\hbox{$^{\prime\prime}$ }$ , at maximum, but that they do not contribute to $n_{\rm r}=n(\theta,\xi\geq 0.03)$ , neither to $n_{\rm p}$ for $\Delta\theta\in [5000\hbox{$^{\prime\prime}$ },20\,000\hbox{$^{\prime\prime}$ }]$ . Accordingly, we denote $n_{\rm exp}$ the expected value of $n(\theta,0)$ that would be in VV, provided PP were absent. Following Shaver (1984), we also assume that for small values of $\xi$ , the distribution of $n_{\rm r}$ must bear the same imprint of non physical effects as $n_{\rm p}$ . It should be noted that the values of $n_{\rm exp}$ , $n_{\rm r}$ and their dispersions need not necessarily be the same (though they appear to be rather close) because of the very irregular dependence of the number counts of quasars with redshift, but their dependence upon angular separations must be similar. Thus, if there were no physical pairs or lensed quasar images in VV, we should have for small values of $\xi$ (typically $\xi \in [0.03,0.13]$ ) a behaviour for $n_{\rm r}$ as a function of $\theta$ that is similar to that of $n_{\rm p}$ . But, as we shall see below, this is just not the case.

2.2 Permutated catalogs and estimates of n $_{\mathsf {exp}}$

The artificial catalogs have been created from VV as follows. We have taken the list of quasars from the original VV with their positions unchanged, but their redshifts have been randomly rearranged without changing their values. Thus, we obtain new "permutated'' catalogs having the same positional inhomogeneities and the same global redshift distribution. However, all possible correlations existing between position and redshift due to observational selection effects in VV should have been washed out. We have generated 2500 such rearranged catalogs to derive average data for comparison with VV and calculated the functions $n_{\rm p}^{*}$ , $n_{\rm r}^{*}$ and $n_{\rm a}^{*}$ , marked with an asterisk, by averaging the corresponding functions $n_{\rm p}$ , $n_{\rm r}$ and $n_{\rm a}$ over the artificial catalogs. Obviously, these averaged dependences are smoother than the original $n_{\rm p}$ , $n_{\rm r}$ and $n_{\rm a}$ from VV (see, e.g., Fig. 1 for $n_{\rm p}^{*}$ and $n_{\rm a}^{*}$ ), thus increasing the quality of the extrapolations.

$\begin{figure} \par\includegraphics[width=7cm,clip]{H2506F1.ps}\end{figure}$

Figure 1: The functions $n_{\rm p}^*(\theta )$ (thick line) and $n_{\rm a}^*(\theta )$ (thin line) in the $50\hbox {$^{\prime \prime }$ }{-}20\,000\hbox {$^{\prime \prime }$ }$ angular separation interval resulting from averages over 2500 "permutated'' catalogs. The dots represent the $n_{\rm a}$ data from VV for $\delta = 50\hbox {$^{\prime \prime }$ }$ and $\zeta =0.01$ . Here and in the other figures, $\theta$ represents the angle defined in Eq. (1).

Open with DEXTER

We present in Figs. 2, 3 the values of $\rho_{\rm p} = n_{\rm p}/n_{\rm p}^{*}$ and $\rho_{\rm a} = n_{\rm a}/n_{\rm a}^{*}$ as a function of $\theta$ for $\delta = 50\hbox {$^{\prime \prime }$ }$ .

$\begin{figure} \par\includegraphics[width=7cm,clip]{H2506F2.ps} \end{figure}$

Figure 2: Ratios $\rho _{\rm p}(\theta )$ and $\rho _{\rm a}(\theta )$ of quasar pair numbers from VV to average values from 2500 rearranged catalogs against $\theta$ (crosses for $\rho _{\rm p}$ and dots for $\rho _{\rm a}$ ; $\delta = 50\hbox {$^{\prime \prime }$ }$ and $\zeta =0.01$ ). The error bars represent rms deviations of $\rho _{\rm r}$ from $\rho _{\rm a}$ . The $\rho _{\rm p}$ value for $\Delta \theta < 50\hbox {$^{\prime \prime }$ }$ is far too high to be shown in this figure due to the large number of pairs, especially gravitational lenses, with $\Delta \theta < 10\hbox {$^{\prime \prime }$ }$ ; note that there are no quasar pairs present in VV in the $10\hbox {$^{\prime \prime }$ }{-}50\hbox {$^{\prime \prime }$ }$ interval.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=7cm,clip]{H2506F3.ps} \end{figure}$	Figure 3: The same as in Fig. 2 over the $50\hbox {$^{\prime \prime }$ }{-}20\,000\hbox {$^{\prime \prime }$ }$ angular separation interval. Note the very slight increase of $\rho _{\rm a}$ as a function of $\theta$ for which the dependence can be easily modeled.
Open with DEXTER

The main result apparent from these figures is that the values of $\rho_{\rm a} = n_{\rm a}/n_{\rm a}^{*}$ vary slowly up to $20\,000\hbox{$^{\prime\prime}$ }$ angular separations; the deviations from a linear (even nearly constant) behavior can be neglected in comparison with the considerable scatter of $\rho_{\rm r}=n_{\rm r}/n_{\rm r}^{*}$ and the large excess of $\rho _{\rm p}$ present within certain angular separation bins. We conclude on the basis of the $\rho _{\rm a}$ dependence that the selection effects do not produce any significant changes of $\rho _{\rm r}$ when we pass from large angular separations (up to $20\,000\hbox{$^{\prime\prime}$ }$ ) to smaller ones ( $50\hbox{$^{\prime\prime}$ }{-}1000\hbox{$^{\prime\prime}$ }$ ). The weak variation of $\rho _{\rm a}$ , and therefore, of the expected value $n_{\rm exp}/n_{\rm p}^{*}$ , makes extrapolations from large $\Delta \theta$ very simple to estimate $n_{\rm exp}$ at small angular separations. This allows us to use the $n_{\rm p}$ data from the $\Delta \theta > 5000\hbox{$^{\prime\prime}$ }$ range to estimate the expected number of quasar pairs $n_{\rm exp}$ and its dispersion at smaller angular separations.

The similar behaviour of $n_{\rm a}$ and $n_{\rm a}^{*}$ may be interpreted as reflecting the absence of any significant angle-redshift correlations in VV due to unphysical selection effects over several degrees; at least they are not important for our particular problem. Thus, the permutated catalogs appear to provide a very useful tool for studying the selection effects in the VV catalog, because they retain all of them except those due to position-redshift correlations. In particular, the positional effects reveal themselves in the $n_{\rm p}^{*}$ and $n_{\rm a}^{*}$ dependences showing a similar behavior (Fig. 1). The latter would have been constant if positional inhomogeneities were absent.

It should be noted that an excess of $\rho_{\rm p}(50\hbox{$^{\prime\prime}$ })$ (i.e. in the $50\hbox {$^{\prime \prime }$ }{-}100\hbox {$^{\prime \prime }$ }$ range), and therefore $n_{\rm p}(50\hbox{$^{\prime\prime}$ })$ , is clearly seen from the figures; however it must be complemented with dispersion estimates. Some additional excess of quasar pairs is possibly present in the $100\hbox{$^{\prime\prime}$ }{-}600\hbox{$^{\prime\prime}$ }$ range. If there were only RP in the VV catalog, the behaviour of $\rho _{\rm p}$ should be much the same as that of $\rho _{\rm a}$ .

Now it is easy to calculate $n_{\rm exp}$ in the $0\hbox{$^{\prime\prime}$ }{-}1000\hbox{$^{\prime\prime}$ }$ angular separation interval. Extrapolating from the $5000\hbox{$^{\prime\prime}$ }{-}20\,000\hbox{$^{\prime\prime}$ }$ range, we obtain the expected values of $\rho _{\rm p}$ in case of RP, and using the known $n_{\rm p}^{*}$ dependence (see Fig. 1), we derive $n_{\rm exp}$ in the desired interval. The results are shown in Fig. 4 with the dispersion estimates calculated here under the assumption of Poisson statistics that will be justified in the next subsection. From the observed $n_{\rm p}(\theta)$ data in Fig. 4, we directly see that a significant excess of pairs of quasars is detected in the $\Delta \theta \in [50\hbox{$^{\prime\prime}$ },100\hbox{$^{\prime\prime}$ }]$ ring and this appears to be well beyond the $3\sigma$ limit.

$\begin{figure} \par\includegraphics[width=7cm,clip]{H2506F4.ps} \end{figure}$	Figure 4: Normalized numbers $n_{\rm p}$ (crosses) of quasar pairs from VV as a function of $\theta$ for $\delta = 50\hbox {$^{\prime \prime }$ }$ and $\zeta =0.01$ . The continuous line represents the expected value $n_{\rm exp}$ for the case of random projections of quasars over the sky. The dashed line corresponds to the upper 3 $\sigma$ limits for $n_{\rm exp}$ .
Open with DEXTER

In the $50\hbox {$^{\prime \prime }$ }{-}100\hbox {$^{\prime \prime }$ }$ interval for $\Delta z\leq 0.01$ , the expected data $n_{\rm exp}$ correspond to $N_{\rm exp}=2.2$ pairs. In reality, there are 9 quasar pairs in this interval present in the VV catalog.

Additional excess of quasar pairs with separations in the 100 $\hbox{$^{\prime\prime}$ }{-} 600\hbox{$^{\prime\prime}$ }$ range also seems to be present but it is just very near the $3\sigma$ limit (see Fig. 4). Nevertheless, it is evident that the data for $n_{\rm p}$ in this range are systematically higher than $n_{\rm exp}$ . The cumulative number of quasar pairs with $\Delta z\leq 0.01$ in the whole $100\hbox{$^{\prime\prime}$ }{-}600\hbox{$^{\prime\prime}$ }$ interval is 133 against 86 expected; that is $N_{\rm PP}=47\pm 9$ . This excess of pairs of quasars in VV is thus found to be highly statistically significant by more than $5\sigma$ .

The results for the expected number of quasar pairs are robust: $n_{\rm exp}$ appears to be approximately the same for the extrapolation versions with $\delta = 25\hbox{$^{\prime\prime}$ }$ or $\delta = 100\hbox{$^{\prime\prime}$ }$ , and for a comparison bin size $\zeta=0.02$ and $\xi$ in the [0.03,0.23] interval. Similar estimates are obtained using extrapolations from the $1000\hbox{$^{\prime\prime}$ }{-}10\,000\hbox{$^{\prime\prime}$ }$ interval.

2.3 Dispersion estimates

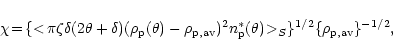
An analogous procedure has been applied to the $n_{\rm r}$ data from the comparison bins. The value of $\chi$ estimated for $n_{\rm r}$ is $0.96\pm0.04$ . These estimates change insignificantly if we take into account the small trend in the $\rho _{\rm p}$ and $\rho _{\rm r}$ data. All these estimates are compatible with Poisson statistics.

It is now important to check the dispersions over those angular separation intervals where we have an excess of $n_{\rm p}$ . For this, we use the dispersions from the comparison bins that are in fact even somewhat overestimated: they have been computed using deviations from the average $n_{\rm a}$ , but there are some additional systematic variations with $\Delta z$ between different bins that are not due to variations with $\theta$ . The results are shown in Fig. 5; we see that the data from the comparison bins agree very well with those obtained according to Eq. (2) from the extrapolated data. This convinces us that, at least for our particular problem, there is no violation of the Poisson statistics due to the selection effects.

$\begin{figure} \par\includegraphics[width=7cm,clip]{H2506F5.ps} \end{figure}$	Figure 5: Dispersions of the normalized pair numbers $n_{\rm r}$ from the comparison bins against $\theta$ ; $\delta = 50\hbox {$^{\prime \prime }$ }$ (rhombs for the data from the comparison bins in VV, continuous line for the estimated dispersions in accordance with Eq. (2)).
Open with DEXTER

2.4 Distribution in projected linear separations

The results obtained in this section may be used to study the correlation functions of the quasar distribution. In particular, the ratio $n_{\rm p}/n_{\rm exp}$ is directly related to the two-point angular correlation function (Peebles 1980).

$\begin{figure} \par\includegraphics[width=7cm,clip]{H2506F6.ps} \end{figure}$	Figure 6: Normalized numbers $n_{\rm p}$ (crosses) of quasar pairs from VV as a function of their projected linear separations for $\delta=0.1~{\rm Mpc}$ and $\zeta =0.01$ ; $\Omega _{\Lambda }=0$ . The continuous line represents the expected value, the dashed line corresponds to its upper 3 $\sigma$ limits.
Open with DEXTER

Table 1: Cumulative number $N_{\rm PP}=N_{\rm p}-N_{\rm exp}$ of physical pairs of quasars within certain projected separation intervals S; $\sigma$ is the dispersion estimate; $\Omega _{\rm M}+\Omega _{\Lambda }=1$ . The last column lists the fraction of PP in VV for the above intervals.
$\Omega_{\Lambda}$ S $N_{\rm PP}$ $\sigma$ $N_{\rm PP}/N_{\rm p}$

$({\rm Mpc}/h_{75})$

0 0.2-0.5 7.15 1.4 79%

1.0-5.0 69 13 28%

0.7 0.4-0.7 7.5 1.4 84%

1.0-5.0 57 10 38%

**Table 1:** Cumulative number $N_{\rm PP}=N_{\rm p}-N_{\rm exp}$ of physical pairs of quasars within certain projected separation intervals S; $\sigma$ is the dispersion estimate; $\Omega _{\rm M}+\Omega _{\Lambda }=1$ . The last column lists the fraction of PP in VV for the above intervals.
$\Omega_{\Lambda}$	S	$N_{\rm PP}$	$\sigma$	$N_{\rm PP}/N_{\rm p}$
	$({\rm Mpc}/h_{75})$
0	0.2-0.5	7.15	1.4	79%
	1.0-5.0	69	13	28%
0.7	0.4-0.7	7.5	1.4	84%
	1.0-5.0	57	10	38%

3 Discussion

We have estimated the number of quasar pairs expected in VV for the case of random quasar positions and have compared this to the actual number of pairs in this catalog. The results of the comparison are presented in Fig. 4 in terms of the angular separation $\theta$ and in Figs. 6, 7 as a function of the projected linear separation for two popular cosmological models. These figures along with Table 1 show that there is a considerable excess of quasar pairs in VV over the expected value within certain separation intervals. In particular, there are 9 pairs of quasars in VV against two expected ones with redshift differences $\Delta z\leq 0.01$ and angular separations $\Delta \theta$ in the $50\hbox {$^{\prime \prime }$ }{-}100\hbox {$^{\prime \prime }$ }$ range (see Table 2, 9 first pairs). Therefore, this excess of pairs of quasars - probably consisting of genuine physical pairs or doubly imaged quasars - is highly statistically significant by more than 3 $\sigma$ . If we extend $\Delta z$ to 0.02, two additional pairs of quasars must be included in the above list (Table 2, two last pairs). We also find that there is a highly statistically significant excess of close redshift pairs ( $\Delta z\leq 0.01$ ) in the $100\hbox{$^{\prime\prime}$ }{-}600\hbox{$^{\prime\prime}$ }$ range by more than 5 $\sigma$ . In terms of projected linear separations, we have an analogous excess near 0.5 Mpc. There does also appear to be a significant excess of pairs of quasars in the $(1{-}5)~{\rm Mpc}$ projected linear separation range. If PP consist of genuine physical pairs of quasars, these ranges correspond to some inner scales of huge mass concentrations at high redshifts.

It should be noted that any amplification bias due to enhanced convergence, induced by some hypothetical foreground smooth structures, is easily ruled out from our treatment. It would actually change the brightness of all the quasars with different z, and this would equivalently affect both the numbers $n_{\rm r}$ and $n_{\rm p}$ of quasar pairs.

Table 2: Quasar pairs in VV with redshift differences $\Delta z \leq 0.02$ and angular separations in the $50\hbox {$^{\prime \prime }$ }{-}100\hbox {$^{\prime \prime }$ }$ range. The names and the data are according to VV. Here $z_{\rm s}$ represents the source redshift, $\Delta \theta$ the angular separation, S the projected linear separation between the two quasars that corresponds to a cosmological model with flat space, H₀=75 km s^-1/Mpc) and $\Omega _{\Lambda }=0$ , S' represents the same for $\Omega _{\Lambda }= 0.7$ . The last column (R) lists relevant references: (1) Iovino et al. (1996), data from VV; (2) Surdej et al. (1986), Chaffee et al. (1991), Gosset et al. (1997); Dinshaw et al. (1997); (3) Maza et al. (1995); (4) Windhorst et al. (1995); (5) McHardy et al. (1998); (6) Crampton et al. (1990); (7) Hawkins (2000), Hawkins & Véron (1995); (8) Morris et al. (1991), Véron & Hawkins (1995); (9) Boyle et al. (1990); (10) Crampton et al. (1988); (11) Borra et al. (1996).
Name $z_{\rm s}$ $\Delta \theta$ S S' R

$(\hbox{$^{\prime\prime}$ })$ (Mpc) (Mpc)

Q 0053-3342A 2.00 83.7 0.46 0.65 1

Q 0053-3342B 2.00

Q 0107-0235 0.958 77.5 0.44 0.57 2

PB 6291 0.956

CTS H26.12 2.33 58.9 0.31 0.45 3

CTS H26.13 2.33

Q 1310+4254A 2.561 91.4 0.47 0.69 4

Q 1310+4254B 2.561

1WGA 1.89 82.2 0.46 0.65 5

J1334.7+3757

1WGA 1.89

J1334.8+3757

1333.2+2604 1.182 68.3 0.39 0.53 6

1333.2+2603 1.179

Q 2121-4642 1.347 82.8 0.46 0.65 7

Q 2121-4641 1.352

Q 2139-4433 3.22 62.6 0.29 0.44 8

Q 2139-4434 3.230

QSM1:35 1.123 70.1 0.40 0.54 9

QSM1:25 1.128

1336.5+2804 1.31 94.7 0.54 0.74 10

1336.6+2803 1.325

Q 23540+1839 1.666 96.2 0.54 0.76 11

Q 23541+1840 1.680

**Table 2:** Quasar pairs in VV with redshift differences $\Delta z \leq 0.02$ and angular separations in the $50\hbox {$^{\prime \prime }$ }{-}100\hbox {$^{\prime \prime }$ }$ range. The names and the data are according to VV. Here $z_{\rm s}$ represents the source redshift, $\Delta \theta$ the angular separation, S the projected linear separation between the two quasars that corresponds to a cosmological model with flat space, H₀=75 km s^-1/Mpc) and $\Omega _{\Lambda }=0$ , S' represents the same for $\Omega _{\Lambda }= 0.7$ . The last column (R) lists relevant references: (1) Iovino et al. (1996), data from VV; (2) Surdej et al. (1986), Chaffee et al. (1991), Gosset et al. (1997); Dinshaw et al. (1997); (3) Maza et al. (1995); (4) Windhorst et al. (1995); (5) McHardy et al. (1998); (6) Crampton et al. (1990); (7) Hawkins (2000), Hawkins & Véron (1995); (8) Morris et al. (1991), Véron & Hawkins (1995); (9) Boyle et al. (1990); (10) Crampton et al. (1988); (11) Borra et al. (1996).
Name	$z_{\rm s}$	$\Delta \theta$	S	S'	R
		$(\hbox{$^{\prime\prime}$ })$	(Mpc)	(Mpc)
Q 0053-3342A	2.00	83.7	0.46	0.65	1
Q 0053-3342B	2.00
Q 0107-0235	0.958	77.5	0.44	0.57	2
PB 6291	0.956
CTS H26.12	2.33	58.9	0.31	0.45	3
CTS H26.13	2.33
Q 1310+4254A	2.561	91.4	0.47	0.69	4
Q 1310+4254B	2.561
1WGA	1.89	82.2	0.46	0.65	5
J1334.7+3757
1WGA	1.89
J1334.8+3757
1333.2+2604	1.182	68.3	0.39	0.53	6
1333.2+2603	1.179
Q 2121-4642	1.347	82.8	0.46	0.65	7
Q 2121-4641	1.352
Q 2139-4433	3.22	62.6	0.29	0.44	8
Q 2139-4434	3.230
QSM1:35	1.123	70.1	0.40	0.54	9
QSM1:25	1.128

1336.5+2804	1.31	94.7	0.54	0.74	10
1336.6+2803	1.325
Q 23540+1839	1.666	96.2	0.54	0.76	11
Q 23541+1840	1.680

Unfortunately, the present data concerning most pairs from Table 2 do not enable us to distinguish between genuine physical pairs and doubly imaged quasars (cf. Kochanek et al. 1999; Mortlock et al. 1999). However, the lensing scenario would require a rather large lens mass. Adopting for instance a spherically symmetric mass distribution that is sufficiently compact located on the sky between the putative lensed quasar images, we do find a lens redshift $z_{\rm d}$ in the range [0.1-0.3]for the 11 listed pairs of quasars, assuming a deflector mass $M_{\rm d} = 10^{14}~M_{\odot}$ and making use of the magnitude difference from the VV data. For any reasonable value of the M/L ratio, a $10^{14}~M_{\odot}$ lens should have been detected at such low redshifts. For smaller masses, the redshift $z_{\rm d}$ scales almost linearly with $M_{\rm d}$ and an analogous situation naturally arises. It is therefore more likely that, if they exist at all, the putative lenses have a mass $M_{\rm d} > 10^{14}~M_{\odot}$ and are located at higher redshifts.

A search for weak lensing effects (see, e.g., Bartelmann & Schneider 1999) around the 11 pairs of quasars would be extremely helpful in order to test the lensing hypothesis. One could also look for some possible stretching of the quasar host images, which in case of the lensing scenario should reveal preferential tangential elongations due to the lens shear. Furthermore, each of the 11 pairs of quasars should be further investigated in the various regions of the electromagnetic spectrum. In particular, one could investigate the distribution of narrow absorption lines in the spectra of quasar pairs, which correspond to a region with characteristic timescales >>100 yrs, in order to exclude any possible effect due to time delays in case of the lens scenario. These same observations could be used to improve the values of the emission redshift of the individual quasars forming a pair.

On the other hand, the pairs of quasars in question may represent some of the most high redshift clusters ever identified which are expected to contain a population of early-type galaxies detectable, e.g. in the near-infrared, or hot intergalactic gas emitting in the X-rays. Such proposed observations are being planned.

But, no matter to which group they belong, these objects consist of very interesting targets for further studies. We expect that forthcoming homogeneous surveys such as 2dF and SDSS will independently confirm the physical grouping of QSOs with arcminute angular separations.

Quasar pairs with arcminute angular separations

1 Introduction