A&A 372, L9-L12 (2001)
DOI: 10.1051/0004-6361:20010539
A. Maeder - V. Desjacques
Geneva Observatory, 1290 Sauverny, Switzerland
Received 19 December 2000 / Accepted 11 April 2001
Abstract
Stellar winds emitted by
rotating massive stars may show two main components:
firstly bipolar lobes with low density
and fast wind, produced by the higher
![]() and
gravity at the poles ("
and
gravity at the poles ("
![]() -effect''); secondly,
an equatorial disc with a slow dense wind,
produced by the stronger opacities at the equator ("
-effect''); secondly,
an equatorial disc with a slow dense wind,
produced by the stronger opacities at the equator ("![]() -effect'').
To see the possible role of this anisotropic wind
on the shape of LBV nebulae,
we calculate the distribution of the ejected matter in 2 simplified cases:
1) A brief shell ejection. We find that prolate and
peanut-shaped hollow nebulae naturally form due to the
-effect'').
To see the possible role of this anisotropic wind
on the shape of LBV nebulae,
we calculate the distribution of the ejected matter in 2 simplified cases:
1) A brief shell ejection. We find that prolate and
peanut-shaped hollow nebulae naturally form due to the
![]() -effect in rotating stars.
2) A constant wind for a long time.
This produces prolate filled nebulae, with a
possible strong disc when a bi-stability limit
is crossed in the equatorial region.
Thus, many features of the
-effect in rotating stars.
2) A constant wind for a long time.
This produces prolate filled nebulae, with a
possible strong disc when a bi-stability limit
is crossed in the equatorial region.
Thus, many features of the ![]() Carinae and
LBV nebulae are accounted for by the anisotropic
ejection from rotating stars.
Carinae and
LBV nebulae are accounted for by the anisotropic
ejection from rotating stars.
Key words: ![]() Carinae - massive stars - LBV stars - mass loss
Carinae - massive stars - LBV stars - mass loss
The HST picture of the ![]() Carinae nebula (J. Morse and
K. Davidson, STScI PRC96-23a) shows two big
symmetrical lobes and a disk-shaped skirt around the star
(Davidson & Humphreys 1997; Davidson et al. 1997). These authors find that the lobes
were created during the "Great Eruption''of 1843,
during which
Carinae nebula (J. Morse and
K. Davidson, STScI PRC96-23a) shows two big
symmetrical lobes and a disk-shaped skirt around the star
(Davidson & Humphreys 1997; Davidson et al. 1997). These authors find that the lobes
were created during the "Great Eruption''of 1843,
during which ![]() 1 to 3
1 to 3
![]() were ejected forming the Homunculus Nebula, with a total energy of
were ejected forming the Homunculus Nebula, with a total energy of ![]() 1049.5 ergs
(Humphreys 1999).
The kinematics confirms that it is a bipolar
outflow (Nota 1999), and the
study of their limb darkening shows that the lobes are hollow
(Davidson et al. 1997).
The mass in the skirt
amounts to 0.1 to 0.2
1049.5 ergs
(Humphreys 1999).
The kinematics confirms that it is a bipolar
outflow (Nota 1999), and the
study of their limb darkening shows that the lobes are hollow
(Davidson et al. 1997).
The mass in the skirt
amounts to 0.1 to 0.2
![]() ,
it is still unclear
whether it is resulting from the 1843 or later events.
A massive cold torus of about 15
,
it is still unclear
whether it is resulting from the 1843 or later events.
A massive cold torus of about 15
![]() has been found out in the equatorial plane (Morris et al. 1999).
Peanut-shaped nebulae and lobes are present around several
other LBV stars (Nota 1999).
has been found out in the equatorial plane (Morris et al. 1999).
Peanut-shaped nebulae and lobes are present around several
other LBV stars (Nota 1999).
Spectral variations
with a period of 5.5 yr have led to the suggestion that ![]() Carinae
is a binary system (Damineli 1996;
Lamers et al. 1998; Damineli et al. 2000).
However, the periodicity is not as strict as
claimed, with shifts of 3 monthes between two
successive cycles, which casts some doubt
on the binary hypothesis (Smith et al. 2000)
Numerous models for the
Carinae
is a binary system (Damineli 1996;
Lamers et al. 1998; Damineli et al. 2000).
However, the periodicity is not as strict as
claimed, with shifts of 3 monthes between two
successive cycles, which casts some doubt
on the binary hypothesis (Smith et al. 2000)
Numerous models for the ![]() Carinae nebula
have been proposed
(e.g. see Schulte-Ladbeck 1997;
Hillier 1997). Several ones invoke
collisions of winds emitted
at various evolutionary stages, such as
the interaction of an isotropic fast wind with a previous slow
equatorially enhanced wind (Kwok et al.
1978; Frank et al. 1995).
The opposite scenario of an aspherical
fast wind, expanding into a previously deposited slow spherical
wind has been studied by Frank et al.
(1998). This model recovers several features,
but not the equatorial skirt.
Langer (1998), Langer & Heger (1998)
consider that the LBV outbursts occur
when the outwards centrifugal and radiation forces
cancel gravity at the equator.
Langer et al. (1999) develop a model where a slow, dense,
equatorial wind is followed by a fast and almost spherical wind
and this leads to very representative
simulations of the Homunculus Nebula.
The models are using the wind compressed disc model
of Bjorkman & Cassinelli (1993).
Carinae nebula
have been proposed
(e.g. see Schulte-Ladbeck 1997;
Hillier 1997). Several ones invoke
collisions of winds emitted
at various evolutionary stages, such as
the interaction of an isotropic fast wind with a previous slow
equatorially enhanced wind (Kwok et al.
1978; Frank et al. 1995).
The opposite scenario of an aspherical
fast wind, expanding into a previously deposited slow spherical
wind has been studied by Frank et al.
(1998). This model recovers several features,
but not the equatorial skirt.
Langer (1998), Langer & Heger (1998)
consider that the LBV outbursts occur
when the outwards centrifugal and radiation forces
cancel gravity at the equator.
Langer et al. (1999) develop a model where a slow, dense,
equatorial wind is followed by a fast and almost spherical wind
and this leads to very representative
simulations of the Homunculus Nebula.
The models are using the wind compressed disc model
of Bjorkman & Cassinelli (1993).
Owocki et al. (1993) have emphasized
that the account of the von Zeipel theorem (1924)
drastically modifies the wind distribution around a rotating star.
The properties of stellar winds ejected by rotating stars
have been studied (Maeder 1999; Maeder & Meynet
2000), in particular the changes of the mass loss rates
by rotation and the latitudinal distribution
of the mass loss.
Here, we examine the distribution of the anisotropic wind
around rotating star models corresponding to ![]() Carinae.
The noticeable result is that
there are bi-polar components and a disc naturally
arising in the wind.
Interactions
of the lobes and discs emitted at various phases during
the back and forth motions of an LBV in the HR diagram
may further shape the nebulae (cf. Langer et al.
1999).
Carinae.
The noticeable result is that
there are bi-polar components and a disc naturally
arising in the wind.
Interactions
of the lobes and discs emitted at various phases during
the back and forth motions of an LBV in the HR diagram
may further shape the nebulae (cf. Langer et al.
1999).
![\begin{figure}
\par\includegraphics[width=5cm,clip]{Cm191_f1.eps}\end{figure}](/articles/aa/full/2001/22/aacm191/Timg11.gif) |
Figure 1:
The mass fluxes around a rotating star like |
| Open with DEXTER | |
In rotating stars with high radiation
pressure, the surface shape is also described by the Roche model.
The total gravity is the sum of the gravitational, centrifugal and radiative accelerations:
![]() .
The local flux at colatitude
.
The local flux at colatitude ![]() is proportional
to the effective gravity
is proportional
to the effective gravity
![]() according to the von Zeipel theorem
according to the von Zeipel theorem
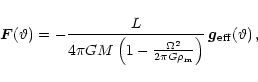 |
(1) |
where we ignore a small term (![]() 1%) due to differential
rotation. The correct
Eddington factor
1%) due to differential
rotation. The correct
Eddington factor
![]() in a rotating star depends on rotation (Maeder & Meynet
2000).
in a rotating star depends on rotation (Maeder & Meynet
2000).
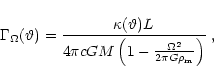 |
(2) |
where
![]() is the local opacity.
One has
is the local opacity.
One has
![\begin{displaymath}\vec{g}_{{\rm tot}} = \vec{g}_{{\rm eff}}
\left[ 1 - \Gamma_{\Omega}(\vartheta) \right] \; .
\end{displaymath}](/articles/aa/full/2001/22/aacm191/img19.gif) |
(3) |
The relation
![]() gives the critical velocity.
The expression
gives the critical velocity.
The expression
![]() often used
for massive stars only applies
if the star is uniformly bright. If not, Eq. (3) has
two roots which need to be discussed (Maeder & Meynet 2000).
The result is that, due to the von Zeipel theorem,
often used
for massive stars only applies
if the star is uniformly bright. If not, Eq. (3) has
two roots which need to be discussed (Maeder & Meynet 2000).
The result is that, due to the von Zeipel theorem,
![]() only
slowly tends towards zero for high Eddington factor.
only
slowly tends towards zero for high Eddington factor.
The distribution of the mass loss by unit surface
at colatitude ![]() over the surface of a rotating
star is
over the surface of a rotating
star is
![$\displaystyle \frac{\Delta\dot{M}(\vartheta)}{\Delta \sigma}
\simeq A \left[\fr...
...1}{\alpha}} \frac{g_{\rm eff}}
{[1 - \Gamma_{\Omega}]^{\frac{1}{\alpha}-1}} \;,$](/articles/aa/full/2001/22/aacm191/img23.gif) |
(4) |
where
![]() is given by Eq. (2) for
electron scattering opacity. We have
is given by Eq. (2) for
electron scattering opacity. We have
![]() .
The parameter
.
The parameter ![]() is a so-called force multiplier,
which characterizes the intensities and distribution of the strengths
of the spectral lines.
At some
is a so-called force multiplier,
which characterizes the intensities and distribution of the strengths
of the spectral lines.
At some
![]() ,
the ionisation equilibrium of the stellar
wind is changing rather abruptly and so does the opacity of the
plasma. Consequently,
the values of the force multipliers undergo rapid transitions,
e.g.
,
the ionisation equilibrium of the stellar
wind is changing rather abruptly and so does the opacity of the
plasma. Consequently,
the values of the force multipliers undergo rapid transitions,
e.g.
![]() for log
for log
![]()
![]() ,
,
![]() for log
for log
![]() between 4.342 and 4.00 and
between 4.342 and 4.00 and
![]() for
log
for
log
![]()
![]() (Lamers et al. 1995; Lamers 1997; see also Kudritzki & Puls 2000). Such
transitions of the wind properties, which
still have some uncertainties, are called bi-stability limits.
Since
(Lamers et al. 1995; Lamers 1997; see also Kudritzki & Puls 2000). Such
transitions of the wind properties, which
still have some uncertainties, are called bi-stability limits.
Since
![]() is
decreasing from pole to equator, one has the corresponding
variations of the force multipliers and thus of
the mass loss fluxes from pole to equator.
is
decreasing from pole to equator, one has the corresponding
variations of the force multipliers and thus of
the mass loss fluxes from pole to equator.
Equation (4) shows that two main effects may
enhance the mass ejection. The first one is
the higher gravity at the pole which makes it hotter, this is
the "
![]() -effect''. The second is
the "
-effect''. The second is
the "![]() -effect'', it is due to
the rapid growth of the opacity below a
bi-stability limit. The result is a lower value
of
-effect'', it is due to
the rapid growth of the opacity below a
bi-stability limit. The result is a lower value
of ![]() in
the equatorial regions, if they become cool
enough; this favours strong equatorial ejections.
in
the equatorial regions, if they become cool
enough; this favours strong equatorial ejections.
We consider the case of
![]() Carinae, with a mass of
Carinae, with a mass of ![]() 100
100 ![]() ,
a luminosity of
,
a luminosity of ![]() 106.5
106.5
![]() ,
an Eddington factor
,
an Eddington factor ![]() = 0.823 for electron scattering opacity,
and a
= 0.823 for electron scattering opacity,
and a
![]() 30000 K
or a few thousands degrees less at minimum
(Humphreys 1988;
Davidson et al. 1997). Rotation is defined by
30000 K
or a few thousands degrees less at minimum
(Humphreys 1988;
Davidson et al. 1997). Rotation is defined by
![]() ,
the fraction of
the angular velocity at break-up, i.e.
,
the fraction of
the angular velocity at break-up, i.e.
![]() .
Figure 1 shows the distribution of the
mass fluxes for
.
Figure 1 shows the distribution of the
mass fluxes for
![]() and a reference polar
and a reference polar
![]() K.
We notice the prolate distribution with a peanut-shape,
which results from the
K.
We notice the prolate distribution with a peanut-shape,
which results from the
![]() -effect. For higher values of
-effect. For higher values of ![]() ,
the
peanut-shape is more and more pronounced, while for lower
,
the
peanut-shape is more and more pronounced, while for lower ![]() we have a prolate spheroid.
we have a prolate spheroid.
When a bi-stability limit is crossed at some latitude
on the rotating star, the ![]() -rates are strongly enhanced
at lower latitudes by the
-rates are strongly enhanced
at lower latitudes by the
![]() -effect. A crossing of the bi-stability limit
is favoured by fast rotation and a lower choice of the
reference
-effect. A crossing of the bi-stability limit
is favoured by fast rotation and a lower choice of the
reference
![]() .
Figure 2 shows, as an example, the mass flux
for
.
Figure 2 shows, as an example, the mass flux
for
![]() as in Fig. 1, but for
as in Fig. 1, but for
![]() = 25000 K. We notice the presence of a strong
equatorial ejection. The wider the latitude range with
= 25000 K. We notice the presence of a strong
equatorial ejection. The wider the latitude range with
![]() below the bistability limit, the thicker the disk.
below the bistability limit, the thicker the disk.
The shape of the nebulae is given by the distribution of matter at some time around the ejecting star. For purpose of simplicity, we consider here two simplified cases: a) a short time ejection, b) a continuous ejection.
We assume that the geometry
![]() at time tof the shell ejected at t0 is determined
by the coasting velocity,
while Eq. (4) determines the
amount of matter at a given position in the shell. Thus, one has
(cf. Maeder 1999)
at time tof the shell ejected at t0 is determined
by the coasting velocity,
while Eq. (4) determines the
amount of matter at a given position in the shell. Thus, one has
(cf. Maeder 1999)
| (5) | |||
| (6) |
Figure 3 shows the distribution of matter for a short time ejection
for a case with
![]() .
If there is no bi-stability limit
crossed, this shape is the same for all kinds of stars
with a given
.
If there is no bi-stability limit
crossed, this shape is the same for all kinds of stars
with a given ![]() (cf. Eq. (6)).
The nebula is hollow and shows a
peanut shape with an equatorial pinch.
For lower
values of
(cf. Eq. (6)).
The nebula is hollow and shows a
peanut shape with an equatorial pinch.
For lower
values of ![]() ,
the shape is a prolate spheroid; for higher
,
the shape is a prolate spheroid; for higher
![]() ,
the equatorial pinch is even more marked.
At a given
,
the equatorial pinch is even more marked.
At a given ![]() ,
the peanut shape is more pronounced for the
,
the peanut shape is more pronounced for the ![]() distribution
than for the
distribution
than for the
![]() distribution, since the first one depends
on
distribution, since the first one depends
on
![]() ,
while the second one depends on
,
while the second one depends on
![]() .
Such a
shape well corresponds to that of many LBV nebulae (Nota
1999).
.
Such a
shape well corresponds to that of many LBV nebulae (Nota
1999).
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{Cm191_f2.eps}\end{figure}](/articles/aa/full/2001/22/aacm191/Timg45.gif) |
Figure 2:
The mass flux around a rotating star with the mass
and luminosity of |
| Open with DEXTER | |
We may also assume the wind to be constant in time,
and for a long time. On each radial line,
the density decreases like r-2. Thus, the lines
![]() of constant densities are given by
of constant densities are given by
![$\displaystyle r(\vartheta) = \left[\frac{\rho(r_{0},\vartheta)}
{\rho(r,\vartheta)} \right]^{\frac{1}{2}} r_{0}(\vartheta)
\quad {\rm with}$](/articles/aa/full/2001/22/aacm191/img47.gif) |
(7) | ||
![$\displaystyle \rho(r_{0},\vartheta) \simeq
\left(1-\alpha\right)^{\frac{1}{\alp...
...eta)^{\frac{1}{2}}
[1 - \Gamma_{\Omega}]^{\frac{1}{\alpha}-\frac{1}{2} }} \cdot$](/articles/aa/full/2001/22/aacm191/img48.gif) |
(8) |
This model gives centrally filled nebulae. Figure 4 illustrates
the iso-density lines in the case corresponding to Fig. 1.
Since, the iso-density lines behave like
![]() ,
the variations of
,
the variations of
![]() have smaller effects and
the peanut shape is absent. We notice a
strong equatorial enhancement due to the
lower
have smaller effects and
the peanut shape is absent. We notice a
strong equatorial enhancement due to the
lower ![]() in these regions.
In real cases, if a sudden ejection is superposed on a more
continuous wind, we may have some compound of
the hollow peanut shell as in Fig. 3 and of the filled nebula
with a disc as in Fig. 4, well corresponding to
the various possible shapes of the LBV
nebulae and
in these regions.
In real cases, if a sudden ejection is superposed on a more
continuous wind, we may have some compound of
the hollow peanut shell as in Fig. 3 and of the filled nebula
with a disc as in Fig. 4, well corresponding to
the various possible shapes of the LBV
nebulae and ![]() Carinae.
Interestingly enough, the group of the
B[e] stars (Zickgraf 1999) shows a two-component
stellar wind with a hot, highly ionized, fast wind at the poles
and a slow dense disk-like wind at the equator.
Carinae.
Interestingly enough, the group of the
B[e] stars (Zickgraf 1999) shows a two-component
stellar wind with a hot, highly ionized, fast wind at the poles
and a slow dense disk-like wind at the equator.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{Cm191_f3.eps}
\end{figure}](/articles/aa/full/2001/22/aacm191/Timg50.gif) |
Figure 3:
Spatial distribution of the matter for a short ejection
around a star with |
| Open with DEXTER | |
Figures 3 and 4 only give two schematic
examples of nebulae. Certainly, a kind of catalogue is to
be made of all possible sorts of nebulae arising from
Eq. (4). This is a problem with many parameters:
- Stellar rotation given by ![]() ;
;
- Reference polar
![]() of the star;
of the star;
- Eddington factor ![]() ;
;
- Opacities, bi-stability limits, opacity peaks, etc.;
- Particular history of mass ejection
![]() ;
;
- Wind-wind interaction (cf. Langer et al. 1999).
Certainly many interesting situations may occur. For example,
a B-star with a polar
![]() not so much above
the bi-stability limit could give rise to a substantial
equatorial ejection and a disc formation, even if
the star is not at break-up!
not so much above
the bi-stability limit could give rise to a substantial
equatorial ejection and a disc formation, even if
the star is not at break-up!
Finally, we may wonder whether LBV stars have fast rotation
velocities. We see
two possibilities. a) If due to a small
magnetic field rotation keeps solid body
(Langer 1998), for most non-zero initial velocities
the star may reach the break-up
velocity near the end of the MS. b) Models with
differential rotation also show that very massive stars may reach the
so-called
![]() -limit, i.e the break-limit function
of rotation and of the Eddington factor (Maeder & Meynet 2000).
In particular, after the end of the MS
phase, the stars do a bluewards hook in the HR diagram;
also after an outburst, they may
reach fast velocities as a result of the contraction of the outer layers.
-limit, i.e the break-limit function
of rotation and of the Eddington factor (Maeder & Meynet 2000).
In particular, after the end of the MS
phase, the stars do a bluewards hook in the HR diagram;
also after an outburst, they may
reach fast velocities as a result of the contraction of the outer layers.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{Cm191_f4.eps}\end{figure}](/articles/aa/full/2001/22/aacm191/Timg53.gif) |
Figure 4:
Iso-density lines for a continuous ejection
around a star with |
| Open with DEXTER | |
Rotation produces
strongly anisotropic mass loss
in massive stars.
Two schematic cases of winds have been considered.
The occurence of a
peanut-shaped nebula with bi-polar lobes
and an equatorial disc may
naturally result from
the
![]() and
and ![]() -effects.
Without particular wind interactions and collisions,
the wind distribution
already possesses several important features of
-effects.
Without particular wind interactions and collisions,
the wind distribution
already possesses several important features of ![]() Carinae
and of other LBV stars.
Carinae
and of other LBV stars.
The critical question is whether the polar lobes and the skirt
in ![]() Carinae result directly
from the anisotropic mass ejection (cf. Figs. 3 and 4)
or whether they result from the interaction
of the successive anisotropic winds.
Whatever the answer, the anisotropic ejection with polar lobes and
an equatorial disc, as shown here,
is an essential part of the game.
Carinae result directly
from the anisotropic mass ejection (cf. Figs. 3 and 4)
or whether they result from the interaction
of the successive anisotropic winds.
Whatever the answer, the anisotropic ejection with polar lobes and
an equatorial disc, as shown here,
is an essential part of the game.
Acknowledgements
A. M. expresses his best thanks to Dr. Norbert Langer and to Dr. Georges Meynet for their very helpful and constructive comments, and to Raoul Behrend for his help in numerical modelling.