A&A 372, 71-84 (2001)
DOI: 10.1051/0004-6361:20010305

Multicolour CCD photometry of old open clusters:

King 5 and Be 20[*]

A. K. Durgapal - A. K. Pandey - V. Mohan

State Observatory, Manora Peak, Naini Tal - 263 129, India

Received 11 May 2000 / Accepted 6 February 2001

Abstract
We present multicolour CCD photometry for two poorly studied open clusters (King 5 and Be 20). Photometry for a field near King 5 was also carried out to estimate the contamination by field stars. The colour magnitude diagrams (CMD) of the clusters show a well defined main sequence extending to the limit of the photometry, $V \approx20$ mag. The reddening for King 5, estimated from the colour-colour diagram, is $\sim$0.82, whereas that for Be 20 as estimated by comparing theoretical main-sequence (MS) with the observed MS is 0.10. The morphology of the CMDs indicates that these clusters are old. The CMD of Be 20 shows a globular cluster-like horizontal branch. In case of King 5 the comparison of observational CMDs with the standard isochrones of VandenBerg (1985) indicates an apparent discrepancy between the shape of the turnoff and isochrones. The CMDs of King 5 seem to be better understood in terms of stellar models with convective overshoot. The comparison of the CMDs with the stellar models by Bertelli et al. (1994) with convective overshoot produces a good fit for a metallicity Z = 0.008 and an age = 1 Gyr for King 5 and 5 Gyr for Be 20. An apparent distance modulus (m-M) = 14.0 and 15.1 has been estimated for King 5 and Be 20 respectively. They correspond to a distance of $1900 \pm100$ pc and 9026 $\pm$ 480 pc, respectively. The radial density distribution in King 5 indicates that there is an excess of low mass stars in the outer region of the cluster, whereas the density distribution in Be 20 shows a good fit with the empirical King (1962) model. For both clusters, observations have also been carried out to search for variable stars.

Key words: Hertzsprung-Russel (HR) diagram - open clusters - individual: King 5; Be 20


1 Introduction

Open clusters have long been recognized as important tools in the study of the Galactic Disk. Within the large population of known open clusters, old ones are an interesting minority.

The system of galactic open clusters, in particular the oldest members, serve as excellent probes of the structure and evolution of the Galactic Disk; (Janes & Phelps 1994; Carraro & Chiosi 1994; Friel & Janes 1993). In addition, the intermediate-age open clusters are well suited to study the issue of convective overshooting (Barbaro & Pigatto 1984; Bertelli et al. 1985; Mazzei & Pigatto 1988). These clusters have turnoff masses near the critical value separating the domain of core He flash from that of mild He-ignition. A comparison of the HR diagram of the observed clusters with the evolutionary models of the same chemical composition can be used to test overshooting and classical stellar models. Spatial and age distribution of clusters provide insight into the processes of cluster formation and destruction that have allowed a substantial number of old open clusters to survive.

 

 
Table 1: Log of observations.

Date		 Field Filter Exp.(sec)
 

      
King 5:      

18 Nov.-93

 Cluster U $4\times300$
  Region    
,, ,, B $4\times90$
,, ,, V $2\times600$
      $2\times180$
      $4\times30$
,, ,, R $2\times300 $
,, ,,   $2\times60$
,, ,,   $4\times5$
,, ,, I $2\times300 $
,, ,,   $2\times60$
,, ,,   $4\times5$
19 Nov.-93  ,, U $3\times1800$
      $3\times600$
,, ,, B $3\times900$
      $4\times100$
,, ,, V $4\times30$
,, ,, R $3\times50$
      $5\times10$
,, ,, I $3\times5$
      $5\times10$
16 Dec.-93 Nearby B $2\times600$
  (east)    
,, ,, V $2\times300 $
,, ,, R $2\times100$
,, ,, I $1\times 150$
      $1\times 100$
       

Be 20:

      

14 Nov.-96

 Cluster B $3\times1800$
  Region    
,, ,, V $3\times900$
,, ,, R $3\times300$
,, ,, I $3\times300$
15 Nov.-96   B $6\times900$
      $2\times300 $
,, ,, V $6\times300$
      $2\times100$
,, ,, R $6\times100$
      $2\times30$
,, ,, I $6\times100$
      $2\times30$


Recently, much interest has been shown by various groups in determining accurate ages for intermediate and old open clusters (see e.g. Kaluzny 1990, 1994; Janes & Phelps 1990; Twarog et al. 1993; Phelps et al. 1994; Carraro & Chiosi 1994) with the aim of setting a lower limit to the age of the Galactic Disk. The understanding of their properties (age, metallicity and kinematics) is mandatory for many studies, such as the history of star formation in the Galactic Disk, the structure of the disk etc. Continuing the series of papers on the photometric study of intermediate/old-age open clusters, we present here photometric data for two old open clusters, namely King 5 (C0311+525, $l=143\hbox{$.\!\!^\circ$ }75$, $b=-4\hbox{$.\!\!^\circ$ }27$) and Be 20 (C0530+001, $l= 203\hbox{$.\!\!^\circ$ }50$, $b= -17\hbox{$.\!\!^\circ$ }28$). The aim of the present work is to study the structure of the clusters and to compare the observed CMD with the theoretical one.

The paper is divided into eleven sections: in Sect. 2 we deal with previous studies performed for these clusters; in Sect. 3 we describe the observations and discuss the data reduction procedure; Sect. 4 deals with the photometric errors and the comparison of the present photometry with previous photometries. The determination of the cluster age with the help of a morphological age parameter method is given in Sect. 5. Section 6 contains comments on the spatial distribution of the stars in the clusters and on the possible existence of a corona in the cluster King 5. In Sect. 7 morphological features of CMD are discussed. Section 8 deals with determination of interstellar extinction in the clusters. In Sect. 9, the comparison of the CMDs with theoretical isochrones and distance of the clusters are given. Section 10 deals with the binary content and variable stars in the clusters; finally, Sect. 11 summarizes the main results and conclusions of our work.

2 Previous studies

2.1 King 5

Previous studies for this cluster include a preliminary investigation by Phelps et al. (1994) who obtained VI photometry for about 1300 stars in a region of $11' \times 11'$ and near IR (J & K bands) photometry by Carraro et al. (2000). Both studies show that the cluster is of the Hyades generation ($\sim$1 Gyr old). Carraro et al. (2000) estimate the distance of King 5 as 1.9 Kpc from the Sun. Durgapal et al. (1998) have reported preliminary results on this cluster. Spectroscopic studies for 24 stars were also conducted by Scott et al. (1995). From this analysis King 5 seems to be a member of the old thin disk population. A study of metal abundance was made by Friel et al. (1995) using medium resolution spectroscopy of twelve giant stars. They get ${\rm [Fe/H]}\approx -0.38 \pm 0.20$.
  \begin{figure} \par\includegraphics[width=9cm,clip]{ms9902f1.eps}\end{figure} Figure 1: The internal error of the stars in King 5 and Be 20 given by DAOPHOT as a function of V magnitude.
Open with DEXTER

2.2 Be 20

Macminn et al. (1994) reported CCD VI photometric data and derived an age of 6 Gyr, metallicity ${\rm [Fe/H]} \approx -0.23$, E(V-I)= 0.16 and a distance of 8.4 kpc. They mention that its great distance below the galactic plane poses difficult questions for any picture of disk formation and structure. In their study several good candidates for blue straggler stars have also been predicted. Using medium resolution spectroscopy of five stars, Friel et al. (1995) obtained ${\rm [Fe/H]} = -0.75$.

3 Observations and reductions

The observations of the cluster King 5 in UBVRI and Be 20 in BVRI passbands were carried out using the photometric CCD system at f/13 Cassegrain focus of the 104-cm reflector of the State Observatory, Naini Tal. In this set-up, each pixel of 24 $\mu$ of $1024\times 1024$ size CCD corresponds to 0.37'' and the entire chip covers a field of $\sim$6.0  $\times 6.0$ arcmin. In order to improve the S/N ratio, the observations were taken in the binning mode of $2 \times 2$ pixels. Multiple exposures were taken with exposure time ranging from 5 s to 1800 s, depending upon the presence of bright stars and filter in use. The frames were co-added in order to achieve a total integration time of 90 min in U, 45 min in B, 20 min in V and 10 min in R and I passbands for King 5 and 90 min in B, 45 min in V and 15 min in R and I passbands for Be 20. One field region located at $\sim$$30^\prime$ towards east of the King 5 cluster region was also observed to estimate the field star contamination in King 5.

A number of bias and twilight flat-field frames were also taken during the observing runs. The frames were cleaned employing the standard procedures using ESO- MIDAS software running on the computer systems of the Observatory. The photometry of co-added frames was carried out using DAOPHOT package by Stetson (1987). The PSF was obtained for each frame using several uncontaminated stars and the PSF magnitudes were suitably tied to aperture photometry magnitudes. One star of the cluster field was taken as the comparison star and differential magnitude and colours of each star were obtained. The differential magnitudes were then standardized using Landolt (1983) stars. The transformation equations used for the CCD system are:

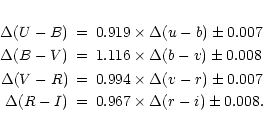
\begin{eqnarray*}\Delta(U-B) &=& 0.919 \times\Delta(u-b)\pm 0.007\\ \Delta(B-V)... ...r)\pm 0.007\\ \Delta(R-I) &=& 0.967 \times\Delta(r-i)\pm 0.008. \end{eqnarray*}


The probable errors in zero point are of the order of 0.02 in V, 0.04 in (U-B), 0.01 in (B-V), 0.02 in (V-R) and (V-I). The log of observations for both the clusters is given in Table 1. Observations to check variability were also carried out on one night for both the clusters.


  \begin{figure} \par\includegraphics[width=9cm,clip]{ms9902f2.eps}\end{figure} Figure 2: Comparison of present photometry for King 5 and Be 20 with the previous photometries.
Open with DEXTER

4 Photometric errors and comparison with previous photometry

The errors affecting photometric data of stars in a crowded field have been discussed by many authors (see, e.g., Mateo & Hodge 1986; Stetson 1987; Chiosi et al. 1989; Aparicio et al. 1990). To a first approximation, the photometric errors should be related to the signal-to-noise ratio. The errors given by ALLSTAR are calculated as the mean square root of the residuals of the fitting of the PSF to the profile of the central part of each star.

Plots of the photometric errors in different passbands, for both the clusters as given by the DAOPHOT package, are shown in Fig. 1 as a function of V magnitude. The average value of $\sigma$ for stars having $V\leq 18.0$ mag in the King 5 region is 0.03 in U and 0.01 in B,V,R and I bands, whereas the average value of $\sigma$ for stars having $V\leq 18.0$ mag in the region of Be 20 is 0.02, 0.01, 0.01 and 0.02 in B,V,R and I respectively, where $\sigma$ is the estimated standard error of the star's magnitude given by ALLSTAR. The X and Y coordinates as well as the photometric data of the stars measured in the cluster King 5, the surrounding region of King 5 and in Be 20 are given in Tables 2-4 respectively. They are available only in electronic form at the CDS.

We compared our data on King 5 in V and I passbands with those by Phelps et al. (1994). The difference Delta (present data - Phelps et al. data) as a function of V magnitude is shown in Fig. 2. In general the two sets of observations are in good agreement.

A comparison of present photometry in V and I passbands for Be 20 with the previously published photometry by Macminn et al. (1994) indicates that both the photometries are in good agreement. The difference Delta (present data - Macminn et al. data) as a function of V magnitude is also shown in Fig. 2. The results of the comparison for both the clusters are given in Table 5.


 

 
Table 5: Comparison of present photometries for King 5 and Be 20 with previous photometry.

Magnitude		 $\triangle V$   $\triangle(V-I)$  
Range $Mean\pm\sigma$ N $Mean\pm\sigma$ N
 

       
King 5:        

$V\leq$ 15.0

 $-0.028\pm0.021$ 20 $-0.028\pm0.024$ 19
$15.0<V\leq16.0$ $-0.019\pm0.023$ 34 $-0.022\pm0.024$ 20
$16.0<V\leq17.0$ $-0.024\pm0.020$ 21 $-0.021\pm0.020$ 20
$17.0<V\leq18.0$ $-0.025\pm0.019$ 28 $-0.019\pm0.022$ 28
$18.0<V\leq19.0$ $-0.023\pm0.023$ 31 $-0.016\pm0.023$ 31
$19.0<V\leq20.0$    $0.029\pm0.025$ 33 $-0.028\pm0.024$ 33
         
Be 20:        

$V\leq17.0$

 $-0.007\pm0.017$ 16 $-0.033\pm0.026$ 16
$17.0<V\leq18.0$ $-0.009\pm0.021$ 14 $-0.035\pm0.023$ 14
$18.0<V\leq19.0$ $-0.004\pm0.021$ 42 $-0.040\pm0.027$ 42
$19.0<V\leq20.0$ $-0.002\pm0.037$ 40 $-0.028\pm0.037$ 40
$20.0<V\leq21.0$    $0.000\pm0.040$ 18 $-0.030\pm0.034$ 18



  \begin{figure} \par\includegraphics[width=9cm,clip]{ms9902f3.eps}\end{figure} Figure 3: Projected stellar density distributions in the region of King 5. Solid curves represent King profiles (for details see text).
Open with DEXTER

5 Morphological age of the clusters

The morphology of the CMDs of star clusters of different ages has been used to estimate the age of the two clusters in question. This method does not require information on cluster metallicity and reddening. Morphological ages for various clusters have been obtained by Carraro & Chiosi (1994) and Phelps et al. (1994). We have derived morphological ages of the cluster using the $\Delta_{B-V}$ parameter which is a difference in (B-V) colour index of the base of red giant branch (BRGB) and the blue turnoff point (BTO)

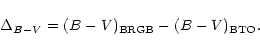\begin{displaymath}\Delta_{B-V}= (B-V)_{\rm BRGB} -(B-V)_{\rm BTO}.\\ \end{displaymath} (1)

This parameter is useful for the clusters which have no noticeable red giant clump. Pandey et al. (1997) have derived $\Delta_{B-V}$ as a function of age using the model of VandenBerg (1985) and the convective overshoot model of Bertelli et al. (1994). Although $\Delta_{B-V}$ of a cluster slightly depends on the metallicity, the ages obtained from the two stellar models are almost the same. The BTO and BRGB for both the clusters are obtained in Sect. 7 and are marked in Figs. 5 and 7.

For the cluster King 5, $\Delta_{B-V}$ is $\sim$0.57, which corresponds to an age range of $\sim$1.2-1.6 Gyr for different values of the metallicity. For the cluster Be 20, $\Delta_{B-V}$ is estimated to be $\sim$0.35, which corresponds to an age $\sim$5 Gyr for models with convective overshoot and $\sim$ 3.4 Gyr for a classical model. However, we have to keep in mind that estimation of age from the morphology of the CMDs of the cluster is just a first approximation.

6 Stellar density profiles

6.1 King 5

Since it is difficult to estimate the cluster center from our observations because of the small area coverage, we determined the cluster center with the help of data by Phelps et al. (1994). The image coordinates of the center were estimated by convolving a Gaussian kernel with the star distribution and taking the center to be the point of maximum density. This is performed for both the axes. In this way, we get the center coordinates for the data by Phelps et al. (1994), at (450, 670) pixels. We used this center to determine the center in our observations: it corresponds to (227, 205) pixels. In order to study the stellar distribution we computed the radial density profile by counting all stars lying in concentric rings at increasing distances from the cluster center. The star counts have been normalized to the area of each ring.

  \begin{figure} \par\includegraphics[width=11.8cm,clip]{ms9902f4.eps}\end{figure} Figure 4: Projected stellar density distribution in the region of Be 20. The solid line represents the King profile (see text).
Open with DEXTER

We used all the stars to determine the stellar density without applying any correction for photometric incompleteness. Figure 3 shows the stellar surface density in stars/arcmin2 as a function of distance from the cluster center, where the error bars were calculated assuming that the number of stars in a bin was governed by Poisson statistics. We tried to fit the empirical model of King (1962) to the projected stellar density distribution of King 5.

\begin{displaymath}f(r) = k\left[ \frac{1}{[1 + (r/r_{\rm c})^2]^{1/2}} -\frac{1}{[1 + (r_{\rm t}/r_{\rm c})^2]^{1/2}} \right]^2 \end{displaymath} (2)


\begin{displaymath}f_0 = k\left[1-\frac{1}{[1 + (r_{\rm t}/r_{\rm c})^2]^{1/2}} \right]^2, \\ \end{displaymath} (3)

where k is a constant related to the central surface density (f0) by Eq. (3).
  \begin{figure} \par\includegraphics[width=10cm,clip]{ms9902f5.eps}\end{figure} Figure 5: The CMDs for the stellar content of King 5 and its surrounding region. Field star corrected CMDs for the cluster King 5 (lower panel). The location of BTO (shown by dotted line) and BRGB are marked in the (V,B-V) CMD (lower panel).
Open with DEXTER

In the above equations f(r) is the projected number density as a function of the radius r, $r_{\rm c}$ is core radius and $r_{\rm t}$ is tidal radius. The above formula is commonly used to fit the projected density distribution of open clusters, globulars and dwarf spheroidal galaxies. We generated a King profile for k= 35, $r_{\rm c} = 32$ and $r_{\rm t}= 145$ and compared it visually with the stellar density profiles obtained from the present data and those of Phelps et al. (1994), (see Figs. 3a and 3b). The comparison indicates an increase in stellar density in $80''< {\rm rad} <160''$. In Figs 3c and 3d, density profiles for $V\leq16$ and V > 16 have been plotted. The density profile for $V\leq16$ shows a systematic variation with radial distance obeying the King profile whereas an excess of stars is seen in the outer region of the cluster in the density profile for stars with V > 16. This indicates that there is an excess of faint (i.e. low mass) stars in the outer region of the cluster. The excess of low mass stars in the extended regions of open clusters, commonly known as the corona, has been discussed by several authors (see e.g. Kaluzny 1994). Density profiles for the stars lying in the eastern and western parts of the cluster are also shown in Figs. 3e and 3f, which indicate that the profiles in both portions are nearly the same.
  \begin{figure} \par\includegraphics[width=9cm,clip]{ms9902f6.eps}\end{figure} Figure 6: CMDs of the cluster King 5 for three subfields having $r \leq 80''$ (upper panel); $80''<r\leq 170''$ (middle panel) and r >170'' (lower panel).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=11cm,clip]{ms9902f7.eps}\end{figure} Figure 7: The CMDs for the stellar content of Be 20. The location of BTO (shown by dotted line) and BRGB are also marked in the (V,B-V) CMD.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=9cm,clip]{ms9902f8.eps}\end{figure} Figure 8: CMDs of the cluster Be 20 for three subfields having $r \leq 40''$ (upper panel); $40''<r\leq 150''$ (middle panel) and r >150'' (lower panel). The solid line represents isochrones by Bertelli et al. (1994) (for details see Sect. 9.2).
Open with DEXTER

To constrain the various parameters, the tidal radius in particular, we need a high S/N ratio in the star counts. Kaluzny (1992) has already shown that it is not possible to get conclusive estimates of tidal radius of the clusters using the whole set of parameters and imposed a fit, f(r), using only two free parameters. The model is

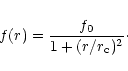\begin{displaymath}f(r) = {\frac{f_0}{1+(r/r_{\rm c})^2}}\cdot \end{displaymath} (4)

We used this equation to get a best-fit density profile for the stars having $V\leq$ 16. The result for $f{_0} = 12.1 \pm 1.4$ and $r_{\rm c} = 45.1''\pm 8.6$, is shown in Fig. 3c.

6.2 Be 20

The cluster center is estimated at (224, 220) pixels. The radial density profiles for the cluster are shown in Fig. 4. The radial density profile hints at the radial extension of Be 20 at $r \approx 150''$. The best fit of Eq. (4) gives the following parameters, $f{_0} = 80\pm 2.1$, $r_{\rm c} = 35.2''\pm 1.4$ for all the stars in the cluster and $f{_0} = 50.1\pm 2.0$, $r_{\rm c} = 47.6''\pm 2.7$ for the stars having $V \geq 17$ respectively. The solid lines in Fig. 4 represent curves obtained from Eq. (4).

7 Colour-magnitude diagrams

In this section we present the CMDs for the clusters King 5 and Be 20. The CMDs of both the clusters show a well defined, broad main sequence (MS). The broadness of the MS may be due to various causes, among which are the photometric error, the presence of unresolved binary stars, possible internal reddening and a spread in metallicity.

7.1 King 5

The CMDs in the (V,B-V), (V,V-R), (V,V-I) planes for all the stars are shown in the upper panel of Fig. 5, whereas those of the field region situated $\sim$30$^{\prime}$ east are shown in middle panel of the same figure. The comparison of the CMDs of the cluster region and the nearby region indicates that the sample of red giants is not contaminated by the field stars. In order to minimize contamination due to field stars, we statistically removed them using the following procedure. For each star in the V, (V-I) CMD of the field region, the nearest star in the cluster region within $V\pm 0.25$, $(V-I)\pm 0.10$ of the field star, was removed. The resulting CMDs are shown in Fig. 5 (lower panel). The BTO is at V= 15.5, (B-V)= 1.00, (V-I) = 1.3 and (V-R)= 0.6. A clump of red giants appears at V $\sim 14.1$, $(B-V)\sim 1.85$. The BRGB is estimated at $V\sim$15.2, $(B-V) \sim$ 1.57, $(V-R) \sim$ 0.9 and $(V-I) \sim~1.8$.

In order to estimate the contamination due to field stars, we have counted the MS stars in the uncleaned (V, V-I) CMDs of cluster and nearby regions. The width of the MS is taken to be $\sim$0.25 mag. The counts are given in Table 6.

(V, B-V), (V, V-R) and (V, V-I) CMDs for three subfields having $r \leq 80''$, $80''<r\leq 170''$ and r >170'' are shown in Fig. 6. The CMDs of the central region ( $r \leq 80''$) and in the ring $80''<r\leq 170''$ are rather similar, whereas the CMDs in the region having $r \geq 170''$ are most similar to the CMDs of the field region. The stellar density in this outermost region is 8.71 stars/(arcmin)2 which is close to the field star density as seen from the stellar density profile (Fig. 3a). This indicates that this region contains mainly field stars.

7.2 Be 20

The (V, B-V), (V, V-R) and (V, V-I) CMDs are shown in Fig. 7. The BTO appears at $V \approx$ 18.2, $(B-V) \approx 0.55$, $(V-R) \approx 0.4$ and $(V-I) \approx 0.7$. The BRGB is estimated at $V\sim$ 18.2, $(B-V) \sim 0.9$, $(V-R) \sim 0.55$ and $(V-I) \sim 1.05$. We note the presence of a small number of stars populating the lower right part of the CMD. These stars are likely to be foreground stars and their small number suggests that the contamination by field stars is not very large.

CMDs for three subfields having $r \leq 40''$, $40''<r\leq 150''$ and r >150'' are shown in Fig. 8. CMDs for the innermost cluster region ($r \leq 40''$) show a horizontal branch which resembles the horizontal branch of globular clusters. A similar feature has also been found in other old open clusters (e.g. M 67, NGC 6791, Be 18 and AM-2). CMDs for the region $40''<r\leq 150''$ are shown in the middle panel of Fig. 8. Here we can see that the MS is contaminated by field stars. The lower panel of Fig. 8 shows CMDs for the stars lying outside radius r =150''. From the density profile of the cluster, we can conclude that the cluster extends up to $r \approx 150''$(see Fig. 4). Therefore, the stars appearing in this diagram are mostly field stars. The counts of the MS stars obtained from (V,V-I) CMD for the cluster and field region (r >150'') are given in Table 6. The area of the outer region is normalized to the area of the cluster.

8 Interstellar extinction

8.1 King 5

To estimate the interstellar extinction in the cluster, we use the (U-B, B-V) diagram. Since the cluster field has a significant amount of contamination due to field stars, the distribution of stars in colour-colour diagram will be a combination of field stars and cluster stars. Using the Zero-age MS given by Cameron (1985) for Z =0.006 and a slope E(U-B)/E(B-V)= 0.72 (Johnson & Morgan 1953) we find a good fit for E(B-V) =0.82, whereas with the ZAMS by Schmidt-Kaler (1982) for Z =0.02 we get E(B-V) =0.78. We prefer E(B-V) = 0.82, as Friel et al. (1995) estimated ${\rm [Fe/H]} = -0.385\pm 0.20$ for this cluster, which corresponds to $Z \approx 0.008$. The colour-colour diagram (U-B, B-V) is shown in Fig. 9.

8.2 Be 20

Reddening E(B-V) in the cluster is generally determined with the help of colour-colour diagram (U-B, B-V). In the absence of U band observations in the cluster, we used MS fitting to estimate the colour excess. By comparing the observed CMDs with the theoretical isochrones by Bertelli et al. (1994) and VandenBerg (1985), we estimate $E(B-V) \sim$ 0.10. E(V-I) and E(V-R) are obtained by using the relation E(V-I) = 1.25 $\times E(B-V)$ and E(V-R) = 0.6 $\times E(B-V)$ (Dean et al. 1978). However for the stellar models by VandenBerg, the ratio E(V-I)/E(B-V) comes out to be 1.15. The E(V-I) value determined by us (0.13) is in close agreement with the value E(V-I) = 0.16 obtained by Macminn et al. (1994).


 

 
Table 6: Distribution of main sequence stars in the cluster and nearby field region.

V		 No.  of  stars No.  of  stars
Magnitude interval Cluster  region Nearby  region
     
King 5:    

15.0 - 16.0

 37 2
16.0 - 17.0 27 2
17.0 - 18.0 36 12
18.0 - 19.0 68 13
19.0 - 20.0 54 35
     

Be 20:		    

18.5 - 19.0

 32 6
19.0 - 19.5 27 6
19.5 - 20.0 33 6
20.0 - 20.5 33 8
20.5 - 21.0 15 2


9 Comparison of the CMDs with theoretical isochrones

9.1 King 5

In this section our aim is to compare the observed CMDs with theoretical isochrones computed with and without considering convective core overshooting during the phases of nuclear burning. The quality of fit to the observed CMDs will provide clues to decide whether the overshooting approach should be preferred or not.

The clean CMDs of King 5 after removing the contribution of probable foreground/background stars have been used to perform such a comparison. The best comparison with the classical evolutionary models by VandenBerg (1985) for Z = 0.01, age = 1 Gyr is shown in Fig. 10 (upper panel). There seems to be an apparent discrepancy between the shape of turnoff and the isochrones. This discrepancy has already been noted by several authors (Anthony-Twarog et al. 1991; Alfaro et al. 1992; Pandey et al. 1997) and can be explained as a failure of the standard isochrones. However, to discriminate between different evolutionary scenerios, photometry with membership determination is required.

Theoretical isochrones with convective overshoot by Bertelli et al. (1994) have also been compared with the CMDs of King 5 (Fig. 10, lower panel). From the figure, it seems that these isochrones are better fitted to the data. The best fit is obtained for Z = 0.008, age = 1 Gyr and apparent distance modulus (m-M) = 14.0 which indicates that the cluster is situated at $1.9 \pm 0.1$ Kpc from Sun. The errors in distance estimates result from errors in the interstellar extinction and by uncertainty in the eye fit of isochrones with the data.

9.2 Be 20

The best comparison of the CMDs with the classical models by VandenBerg (1985) shown in Fig. 11 (upper panel) gives an age of 5 Gyr for Z = 0.0169. Similarly, the comparison of the CMDs of Be 20 with the convective core overshooting models by Bertelli et al. (1994), also shown in Fig. 11 (lower panel), yields an age $\sim$5 Gyr for Z = 0.008. For Be 20 Macminn et al. (1994) have reported the metallicity ${\rm [Fe/H]} \approx -0.23$ which corresponds to Z = 0.01. Friel et al. (1995) have obtained ${\rm [Fe/H]} = -0.75$ which corresponds to Z = 0.0034. We also compared the models of Bertelli et al. (1994) for Z = 0.004 but in this case were unable to fit the data. To discriminate better we used the sample for $r \leq 40''$. The best fits are shown in Fig. 8. All the morphological features are well explained by the models of Bertelli et al. (1994) with convective overshoot. Macminn et al. (1994) have estimated an age of $\sim$6 Gyr, using the theoretical evolutionary track given by VandenBerg (1985). The fit with the models with convective overshooting gives an apparent distance modulus (m-M) = 15.1 which corresponds to a distance of 9026 $\pm$ 480 pc.
  \begin{figure} \par\includegraphics[width=7cm,clip]{ms9902f9.eps}\end{figure} Figure 9: The colour-colour diagram for the stars in the cluster King 5. The ZAMS given by Cameron (1985) for Z = 0.006 has been adjusted for E(B-V) = 0.82 mag.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=9cm,clip]{ms9902f10.eps}\end{figure} Figure 10: The comparison of evolutionary model by VandenBerg (1985) (upper panel) and convective core overshooting model by Bertelli et al. (1994) (lower panel) with the observed CMDs of King 5. The dotted curve shows the isochrone brightened by 0.75 mag. Probable variable stars and blue stragglers are shown by filled triangles.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=9cm,clip]{ms9902f11.eps}\end{figure} Figure 11: Same as Fig. 10 but for Be 20.
Open with DEXTER

10 Binary sequence and variable stars/Blue stragglers in the clusters

As discussed in Sect. 7, the unresolved binaries may be one of the causes of broadening of the CMDs. In order to quantitatively investigate the effect of binary stars, we calculate $\Delta(B-V) = (B-V)_{*} - (B-V)_{\rm MS}$ in three subregions of the observed field, where (B-V)* is the (B-V) colour of the star and $(B-V)_{\rm MS}$ is the corresponding (B-V) colour of the MS. The frequency distribution of $\Delta (B-V)$ in the three regions is shown in Figs. 12 and 13 for King 5 and Be 20 respectively, where a prominent peak at $\Delta (B-V)\sim 0.0$ is due to the single stars. In the central regions of both the clusters (Figs. 12b and 13b) where field star contamination can be considered as negligible, a peak, although less prominent, can be noticed towards the red side of the MS. This peak can be attributed to binary stars. The separation in (B-V) between MS and binary stars peaks is $\sim$0.18 mag and 0.12 mag for King 5 and Be 20 respectively. The brightening of MS by 0.75 reddens the MS by $\sim$0.2 mag in (B-V) colour. Figures 12c,d and 13c,d show the frequency distribution of $\Delta (B-V)$ in the outer region of the clusters and in the field regions respectively. In the case of King 5, the binary peak is separated from the MS peak by $\sim$0.24 mag in (B-V). Whereas, in the case of Be 20, we can see three peaks separated by $(B-V) \sim 0.12$, 0.22 and 0.34 mag from the MS peak. The number of stars contributing to the above mentioned peaks can give idea about the number of binaries present in the clusters. The frequency distribution of $\Delta (B-V)$ in the field region of both the clusters (Figs. 12d and 13d) does not show any systematic variation. From Figs. 12 and 13 we can estimate the fraction of binaries among MS stars. For the central and extended region of King 5, the binary fraction is estimated to be $\sim$7$\%$ and $\sim$9$\%$ respectively, whereas for Be 20 this fraction is about 20$\%$ and 17$\%$. Doing so, we do not consider the third peak, which may be due to field star contamination.
  \begin{figure} \par\includegraphics[width=7.6cm,clip]{ms9902f12.eps}\end{figure} Figure 12: Frequency distribution $\Delta (B-V)$ for MS of King 5. The distribution of $\Delta (B-V)$ in the cluster regions can be represented by a Gaussian curve (shown qualitatively), whereas in the field region, distribution of $\Delta (B-V)$ does not show any systematic variation.
Open with DEXTER

One night of monitoring in both clusters reveals a few variable stars. The nature of their variability will be discussed in a forthcoming paper. The variable stars are shown by filled triangles in CMDs (Figs. 10b and 11b).

Stars numbered [99, 414] of King 5 and [161, 222] of Be 20, which are found on the prolongation of the main sequence, can be good candidates for blue stragglers (Ahumada & Lapasset 1995). These stars are also shown by filled triangles in the CMDs (Figs. 10b and 11b). Light curves for probable variable stars in King 5 and Be 20 are shown in Figs. 14 and 15 respectively. Data for these stars are given in Table 7.


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{ms9902f13.eps}\end{figure} Figure 13: Same as Fig. 12 but for Be 20.
Open with DEXTER

11 Conclusions


 

 
Table 7: List of variable stars in the clusters King 5 and Be 20 with their distance from the cluster center.

Star No.		 V (V-I) Distance
      (In  arcsec)
 

     
King 5:      

394

 15.573   1.346 121
259 14.319   1.078 128
13 14.852   1.194 160
192 15.023   1.307 150
71 15.167   1.287 106
185 14.841   1.253 79
42 16.074   0.982 131
       
Be 20:      

247

 18.380 0.765 41
215 18.845 0.716 23
51 18.674 0.806 92
222 18.001 0.588 84
210 18.408 0.812 176
161 17.365 0.613 7
41 18.617 0.753 216



  \begin{figure} \par\includegraphics[height=11cm,width=10cm,clip]{ms9902f14.eps}\end{figure} Figure 14: Light curves of the probable variable stars in the field of King 5. Difference of two comparisons (s2-s1), where s1 and s2 are star Nos. 201 and 217, is also shown in the figure by cross ($\times $).
Open with DEXTER


  \includegraphics[height=11cm,width=10cm,clip]{ms9902f15.eps} Figure 15: Same as Fig. 14 but for Be 20. Here s1 and s2 are star Nos. 257 and 263.
Open with DEXTER

1.
The stellar density profile of King 5 indicates the possibility of an excess of low mass stars in the corona of the cluster. The stellar density profile for Be 20 matches very well the King (1962) model;

2.
The reddening is E(B-V)= 0.82 and 0.10 mag for King 5 and Be 20 respectively;

3.
The age of King 5 is found to be $\sim$1 Gyr, whereas that of Be 20 is about 5 Gyr for Z = 0.008;

4.
The morphological features of the CMDs of King 5 can be better explained in terms of models with convective overshooting;

5.
The cluster distance is $1900 \pm100$ pc and $9026 \pm 480$ pc for King 5 and Be 20 respectively. The galactocentric distance for Be 20 is estimated to be 17.1 kpc. This is one of the outermost objects observed in the Galaxy;

6.
The vertical distance above the Galactic plane for Be 20 is 2.7 kpc, which locates this cluster farthest from the galactic plane. This large z distance indicates that this cluster may be part of the thick disk;
7.
The CMDs of the clusters suggest the existence of many binary stars;

8.
Observations for variability in both clusters show that a few stars of the main sequence and sub giant branch are variable stars. We estimate that about 10% and 20% of the MS stars in King 5 and Be 20 respectively, may be binary stars. In both clusters the existence of some blue stragglers cannot be excluded.

Acknowledgements
Thanks are due to Prof. K. A. Janes for providing CCD data of the clusters King 5 and Be 20. The authors are grateful to Prof. Ram Sagar for useful discussions. We gratefully acknowledge the valuable suggestions given by the anonymous referee, which improved the contents of the paper.

References

 

Copyright ESO 2001