A&A 372, 173-194 (2001)
DOI: 10.1051/0004-6361:20010474
S. Bontemps1,2 - P. André3 - A. A. Kaas4,2 - L. Nordh2 - G. Olofsson2 - M. Huldtgren2 - A. Abergel5 - J. Blommaert6 - F. Boulanger5 - M. Burgdorf6 - C. J. Cesarsky3 - D. Cesarsky5 - E. Copet7 - J. Davies8 - E. Falgarone9 - G. Lagache5 - T. Montmerle3 - M. Pérault9 - P. Persi10 - T. Prusti6 - J. L. Puget5 - F. Sibille11
1 - Observatoire de Bordeaux, BP 89, 33270 Floirac, France
2 -
Stockholm Observatory, 133 36 Saltsjöbaden, Sweden
3 -
Service d'Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette, France
4 -
ESA/ESTEC, Astrophysics Division, The Netherlands
5 -
IAS, Université Paris XI, 91405 Orsay, France
6 -
ISO/SOC, Astrophysics Division of ESA, Villafranca, Spain
7 -
DESPA, Obs. Paris-Meudon, 5 Pl. J. Janssen, 92195 Meudon, France
8 -
JAC, 660 N. A'Ohoku Place, University Park, Hilo, HI 96720, USA
9 -
ENS Radioastronomie, 24 rue Lhomond, 75231 Paris, France
10 -
IAS, CNR, Area di Ricerca Tor Vergata, 00133 Roma, Italy
11 -
Observatoire de Lyon, 69230 Saint Genis Laval, France
Received 9 May 2000 / Accepted 07 March 2001
Abstract
We present the results of the first extensive
mid-infrared (IR) imaging survey
of the ![]() Ophiuchi embedded cluster, performed
with the ISOCAM camera on board the ISO satellite.
The main
Ophiuchi embedded cluster, performed
with the ISOCAM camera on board the ISO satellite.
The main
![]() molecular cloud L1688, as well as the two
secondary clouds L1689N and L1689S, have been completely surveyed
for point sources at 6.7
molecular cloud L1688, as well as the two
secondary clouds L1689N and L1689S, have been completely surveyed
for point sources at 6.7 ![]() m and 14.3
m and 14.3 ![]() m.
A total of 425 sources are detected in
m.
A total of 425 sources are detected in ![]() 0.7 deg2, including
16 Class I, 123 Class II, and 77 Class III young stellar objects (YSOs).
Essentially all of the mid-IR sources coincide with near-IR
sources, but a large proportion of them are recognized for the first
time as YSOs. Our dual-wavelength survey allows us to identify essentially
all the YSOs with IR excess in the
embedded cluster down to
0.7 deg2, including
16 Class I, 123 Class II, and 77 Class III young stellar objects (YSOs).
Essentially all of the mid-IR sources coincide with near-IR
sources, but a large proportion of them are recognized for the first
time as YSOs. Our dual-wavelength survey allows us to identify essentially
all the YSOs with IR excess in the
embedded cluster down to ![]()
![]() 10-15 mJy.
It more than doubles the known population of Class II YSOs
and represents the most complete census to date of
newly formed stars in the
10-15 mJy.
It more than doubles the known population of Class II YSOs
and represents the most complete census to date of
newly formed stars in the ![]() Ophiuchi central region.
There are, however, reasons to believe that several tens of
Class III YSOs remain to be identified below
Ophiuchi central region.
There are, however, reasons to believe that several tens of
Class III YSOs remain to be identified below
![]() .
The mid-IR luminosities of most (
.
The mid-IR luminosities of most (![]() 65%) Class II objects are
consistent with emission from purely passive circumstellar disks.
The stellar luminosity function of the complete sample of Class II
YSOs is derived with good accuracy down to
65%) Class II objects are
consistent with emission from purely passive circumstellar disks.
The stellar luminosity function of the complete sample of Class II
YSOs is derived with good accuracy down to
![]() .
It is basically flat (in logarithmic units)
below
.
It is basically flat (in logarithmic units)
below
![]() ,
exhibits a possible local maximum at
,
exhibits a possible local maximum at
![]() ,
and sharply falls off at higher luminosities.
A modeling of the luminosity function, using
available pre-main sequence tracks and plausible star formation histories,
allows us to derive the mass distribution of the Class II YSOs
which arguably reflects the initial mass function (IMF) of the
embedded cluster. After correction for the presence of unresolved binary systems,
we estimate that the IMF in
,
and sharply falls off at higher luminosities.
A modeling of the luminosity function, using
available pre-main sequence tracks and plausible star formation histories,
allows us to derive the mass distribution of the Class II YSOs
which arguably reflects the initial mass function (IMF) of the
embedded cluster. After correction for the presence of unresolved binary systems,
we estimate that the IMF in
![]() is well described by a two-component
power law with a low-mass index of
is well described by a two-component
power law with a low-mass index of
![]() ,
a high-mass index of -1.7(to be compared with the Salpeter value of -1.35), and a break
occurring at
,
a high-mass index of -1.7(to be compared with the Salpeter value of -1.35), and a break
occurring at
![]() .
This IMF is flat with
no evidence for a low-mass cutoff down to at least
.
This IMF is flat with
no evidence for a low-mass cutoff down to at least ![]()
![]() .
.
Key words: stars: formation -
stars: low-mass, brown dwarfs -
stars: luminosity function, mass function -
stars: pre-main sequence -
ISM: individual objects: ![]() Ophiuchi cloud
Ophiuchi cloud
Recent observations suggest that most stars in our Galaxy and other galaxies form in compact clusters. In particular, near-IR imaging surveys of nearby molecular cloud complexes have shown that the star formation activity is typically concentrated within a few rich clusters associated with massive dense cores which constitute only a small fraction of the total gas mass available (e.g. Lada et al. 1993; Zinnecker et al. 1993). These embedded clusters comprise various types of young stellar objects (YSOs) - from still collapsing protostars to young main sequence stars - but are usually dominated in number by low-mass pre-main sequence (PMS) stars, i.e., T Tauri stars. Young clusters provide excellent laboratories for studying the formation and early evolution of stars through the observational analysis of large, genetically homogeneous samples of embedded YSOs. Two key characteristics of these young stellar populations are their luminosity distribution and their mass spectrum, which give important observational constraints on the stellar initial mass function (IMF) in the Galaxy. Observations of young embedded clusters can also help us understand possible links between parent cloud properties and the resulting stellar masses. They are however hampered by: (1) dust extinction from the parent cloud which hides most of the newly formed stars at optical wavelengths, (2) the difficulty to recognize the nature of individual sources (e.g. protostars, T Tauri stars, or background sources), (3) the youth (and thus poorly known intrinsic properties) of most cluster members.
Owing to these difficulties, the census of embedded YSOs provided by IRAS and near-IR studies is far from complete even in the nearest clouds (e.g. Wilking et al. 1989 - hereafter WLY89). Thanks to its high sensitivity and good spatial resolution in the mid-IR, the ISOCAM camera on board ISO (Cesarsky et al. 1996; Kessler et al. 1996) was a powerful tool to achieve more complete surveys for YSOs in all major nearby star-forming regions (see Nordh et al. 1996, 1998; Olofsson et al. 1999; Persi et al. 2000).
The nearby
![]() cloud is one of the most actively studied sites of
low-mass star formation. Its central region harbors
a rich embedded cluster with about 100 members recognized prior
to the present work
(e.g. WLY89, Casanova et al. 1995).
While a dispersed population of optically visible young stars,
associated with the Upper-Scorpius OB association, has a typical age of
several million years (Myr) (e.g. Preibisch & Zinnecker 1999), the central embedded
cluster is recognized as one of the youngest clusters known with
an estimated age on the order of
cloud is one of the most actively studied sites of
low-mass star formation. Its central region harbors
a rich embedded cluster with about 100 members recognized prior
to the present work
(e.g. WLY89, Casanova et al. 1995).
While a dispersed population of optically visible young stars,
associated with the Upper-Scorpius OB association, has a typical age of
several million years (Myr) (e.g. Preibisch & Zinnecker 1999), the central embedded
cluster is recognized as one of the youngest clusters known with
an estimated age on the order of ![]() 0.3-1 Myr (e.g. WLY89,
Greene & Meyer 1995; Luhman & Rieke 1999).
This young cluster has been extensively studied at
wavelengths ranging from the X-ray to the radio band.
The satellites Einstein and ROSAT have revealed
0.3-1 Myr (e.g. WLY89,
Greene & Meyer 1995; Luhman & Rieke 1999).
This young cluster has been extensively studied at
wavelengths ranging from the X-ray to the radio band.
The satellites Einstein and ROSAT have revealed ![]() 70
highly variable X-ray sources associated with magnetically-active young stars,
including deeply embedded protostellar sources
(Montmerle et al. 1983; Casanova et al. 1995;
Grosso et al. 2000).
In the near-IR, the cloud has been deeply
surveyed from the ground using large-format arrays (Greene & Young
1992; Comerón et al. 1993; Strom et al. 1995; Barsony et al. 1997).
Unfortunately, due to difficulties in discriminating between background sources
and embedded YSOs without performing time-consuming mid-IR photometry (e.g.
Greene et al. 1994) or near-IR spectroscopy
(e.g. Greene & Lada 1996; Luhman & Rieke 1999),
these recent near-IR surveys have only partially
increased the number of classified, recognized members.
Finally, while only relatively poor angular resolution IRAS data are
available so far in the far-IR (e.g. WLY89), deep imaging surveys
at an angular resolution of
70
highly variable X-ray sources associated with magnetically-active young stars,
including deeply embedded protostellar sources
(Montmerle et al. 1983; Casanova et al. 1995;
Grosso et al. 2000).
In the near-IR, the cloud has been deeply
surveyed from the ground using large-format arrays (Greene & Young
1992; Comerón et al. 1993; Strom et al. 1995; Barsony et al. 1997).
Unfortunately, due to difficulties in discriminating between background sources
and embedded YSOs without performing time-consuming mid-IR photometry (e.g.
Greene et al. 1994) or near-IR spectroscopy
(e.g. Greene & Lada 1996; Luhman & Rieke 1999),
these recent near-IR surveys have only partially
increased the number of classified, recognized members.
Finally, while only relatively poor angular resolution IRAS data are
available so far in the far-IR (e.g. WLY89), deep imaging surveys
at an angular resolution of
![]() or better exist at (sub)millimeter
wavelengths (e.g., Motte et al. 1998 - hereafter MAN98 -
Wilson et al. 1999).
or better exist at (sub)millimeter
wavelengths (e.g., Motte et al. 1998 - hereafter MAN98 -
Wilson et al. 1999).
It is thanks to the illuminating
example of the
![]() embedded cluster that the now
widely used empirical classification of YSOs was originally introduced.
Three IR classes were initially distinguished based on the shapes of
the observed spectral energy distributions (SEDs) between
embedded cluster that the now
widely used empirical classification of YSOs was originally introduced.
Three IR classes were initially distinguished based on the shapes of
the observed spectral energy distributions (SEDs) between ![]() 2
2 ![]() m
and
m
and ![]() 25-100
25-100 ![]() m (Lada & Wilking 1984, WLY89).
Objects with rising SEDs in this wavelength range were classified as Class I,
sources with SEDs broader than blackbodies but decreasing longward of
m (Lada & Wilking 1984, WLY89).
Objects with rising SEDs in this wavelength range were classified as Class I,
sources with SEDs broader than blackbodies but decreasing longward of
![]() 2
2 ![]() m as Class II, and sources with SEDs consistent with
(or only slightly broader than) reddened stellar blackbodies
as Class III.
These morphological SED classes are interpreted in terms of an
evolutionary sequence
from (evolved) protostars (Class I), to T Tauri stars with optically thick
IR circumstellar disks (Class II), to weak T Tauri stars with at
most optically thin disks (Class III)
(Lada 1987; Adams et al. 1987;
André & Montmerle 1994 - hereafter AM94).
A fourth class (Class 0) was subsequently introduced by
André et al. (1993)
to accommodate the discovery in the radio range
of cold sources with large submillimeter to
bolometric luminosity ratios
and powerful jet-like outflows, such as
VLA 1623 in
m as Class II, and sources with SEDs consistent with
(or only slightly broader than) reddened stellar blackbodies
as Class III.
These morphological SED classes are interpreted in terms of an
evolutionary sequence
from (evolved) protostars (Class I), to T Tauri stars with optically thick
IR circumstellar disks (Class II), to weak T Tauri stars with at
most optically thin disks (Class III)
(Lada 1987; Adams et al. 1987;
André & Montmerle 1994 - hereafter AM94).
A fourth class (Class 0) was subsequently introduced by
André et al. (1993)
to accommodate the discovery in the radio range
of cold sources with large submillimeter to
bolometric luminosity ratios
and powerful jet-like outflows, such as
VLA 1623 in ![]() Oph A (e.g. André et al. 1990; Bontemps
et al. 1996).
Class 0 objects,
which have measured circumstellar envelope masses larger than their inferred
central stellar masses,
are interpreted as young protostars at the beginning of the main
accretion phase
(e.g. André et al. 2000).
The fact that the
Oph A (e.g. André et al. 1990; Bontemps
et al. 1996).
Class 0 objects,
which have measured circumstellar envelope masses larger than their inferred
central stellar masses,
are interpreted as young protostars at the beginning of the main
accretion phase
(e.g. André et al. 2000).
The fact that the
![]() central region contains at least two Class 0
protostars (André et al. 1993),
as well as numerous (
central region contains at least two Class 0
protostars (André et al. 1993),
as well as numerous (
![]() 60) pre-stellar condensations
(MAN98), demonstrates that it is still actively forming stars at the present
time.
The distance to the
60) pre-stellar condensations
(MAN98), demonstrates that it is still actively forming stars at the present
time.
The distance to the
![]() cloud is somewhat uncertain.
Usually, a value of 160 pc is adopted (e.g. Chini 1981).
However, recent Hipparcos results on the Upper-Scorpius OB
association (de Zeeuw et al. 1999)
provide a reasonably accurate estimate of
cloud is somewhat uncertain.
Usually, a value of 160 pc is adopted (e.g. Chini 1981).
However, recent Hipparcos results on the Upper-Scorpius OB
association (de Zeeuw et al. 1999)
provide a reasonably accurate estimate of ![]() pc for the average
distance to the stars of the OB association. The
embedded cluster is located at the inner edge of the molecular
complex on the outskirts of the OB association (e.g. de Geus 1989),
and not very far, in projection, from the association
center (less than
pc for the average
distance to the stars of the OB association. The
embedded cluster is located at the inner edge of the molecular
complex on the outskirts of the OB association (e.g. de Geus 1989),
and not very far, in projection, from the association
center (less than
![]() apart which corresponds to
apart which corresponds to ![]() 10 pc;
see Fig. 9 of de Zeeuw et al. 1999).
In this paper, we therefore
adopt a distance of
10 pc;
see Fig. 9 of de Zeeuw et al. 1999).
In this paper, we therefore
adopt a distance of
![]() pc
for the
pc
for the
![]() IR cluster which corresponds to a distance modulus
IR cluster which corresponds to a distance modulus
![]() .
.
The layout of the paper is as follows.
Section 2 gives observational details (Sect. 2.2)
and describes the way the data have been reduced to obtain mid-IR
images and extract point-sources (Sect. 2.3) along with the photometric uncertainties
and the sensitivity levels (Sect. 2.4). In Sect. 3, the identification of
detected sources is discussed (Sect. 3.1) and the selection of a new population
of 123 Class II YSOs, as well as 16 Class I and 77 Class III YSOs,
is described (Sects. 3.2-3.5). We then derive
luminosities for these YSOs and build the corresponding
luminosity functions in Sect. 4.
In Sect. 5, we model the
luminosity functions for Class II and Class III YSOs in terms of the underlying
mass function and star formation history.
In Sect. 6, we discuss the resulting
constraints on the IMF of the
![]() cloud down to
cloud down to ![]()
![]() ,
(Sects. 6.1-6.2)
as well as related implications (Sects. 6.3-6.5).
,
(Sects. 6.1-6.2)
as well as related implications (Sects. 6.3-6.5).
![\begin{figure}
\includegraphics[height=17.8cm,angle=-90,clip]{ms9901f1.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg41.gif) |
Figure 1:
Sky map of the
|
| Open with DEXTER | |
The survey encompasses
the ![]() Ophiuchi central region associated with the
prominent dark cloud L1688, as well as
the two subsidiary sites L1689N and L1689S.
The L1688 field is a
Ophiuchi central region associated with the
prominent dark cloud L1688, as well as
the two subsidiary sites L1689N and L1689S.
The L1688 field is a ![]()
![]() square,
while the L1689N and L1689S fields each cover an area of
square,
while the L1689N and L1689S fields each cover an area of
![]() (see Fig. 1).
Most previously known members of the
(see Fig. 1).
Most previously known members of the ![]() Ophiuchi cluster lie within
these fields. In particular, this is the case for
94 of a total of 113 recognized
members from WLY89, AM94,
Greene et al. (1994), and MAN98.
The known young stars which lie outside the boundaries of our survey
are mostly optically visible, weak-line or post T Tauri stars (belonging to
Class III) spread over a large area on the outskirts of the
molecular complex (e.g. Martín et al. 1998).
Ophiuchi cluster lie within
these fields. In particular, this is the case for
94 of a total of 113 recognized
members from WLY89, AM94,
Greene et al. (1994), and MAN98.
The known young stars which lie outside the boundaries of our survey
are mostly optically visible, weak-line or post T Tauri stars (belonging to
Class III) spread over a large area on the outskirts of the
molecular complex (e.g. Martín et al. 1998).
The mapping was performed in the raster mode of ISOCAM in which
the mid-IR
![]() pixel array
imaged the sky at consecutive positions along
a series of scans parallel to the right-ascension axis.
The offset between consecutive array positions along each scan
(
pixel array
imaged the sky at consecutive positions along
a series of scans parallel to the right-ascension axis.
The offset between consecutive array positions along each scan
(
![]() )
was 15 pixels, while the offset between
two scans (
)
was 15 pixels, while the offset between
two scans (
![]() )
was 26 pixels.
Each set of scans was then co-added and combined into a single raster image.
The final image of the L1688 field (Fig. 1 and Abergel et al. 1996)
actually results from the combination of six separate rasters.
A pixel field of view of 6
)
was 26 pixels.
Each set of scans was then co-added and combined into a single raster image.
The final image of the L1688 field (Fig. 1 and Abergel et al. 1996)
actually results from the combination of six separate rasters.
A pixel field of view of 6
![]() was used for four of these rasters,
but smaller 3
was used for four of these rasters,
but smaller 3
![]() pixels were employed for the other two rasters in order
to avoid saturating the array on the brightest sources of the
cluster.
The L1689N and L1689S fields were imaged with one raster each
using 6
pixels were employed for the other two rasters in order
to avoid saturating the array on the brightest sources of the
cluster.
The L1689N and L1689S fields were imaged with one raster each
using 6
![]() pixels.
pixels.
In order to avoid saturation, the individual readout time for the L1688
rasters was set to
![]() s. About 55 of these readouts
(i.e. an integration time of
s. About 55 of these readouts
(i.e. an integration time of ![]()
![]() s) were performed
per sky position. Thanks to the half-frame overlap between subsequent
individual images, each sky position was observed twice,
yielding an effective total integration time of
s) were performed
per sky position. Thanks to the half-frame overlap between subsequent
individual images, each sky position was observed twice,
yielding an effective total integration time of ![]()
![]() s.
For L1689N and L1689S it was possible to use
s.
For L1689N and L1689S it was possible to use
![]() s, and about 15
readouts were performed per sky position with the same half-frame overlap,
giving an integration time per sky position of
s, and about 15
readouts were performed per sky position with the same half-frame overlap,
giving an integration time per sky position of ![]()
![]() s.
A total of 1104 individual images were necessary
to mosaic the L1688 field, and an additional 60 images each were used to map
L1689N and L1689S.
All three fields were mapped in two broad-band filters of
ISOCAM: LW2 (5-8.5
s.
A total of 1104 individual images were necessary
to mosaic the L1688 field, and an additional 60 images each were used to map
L1689N and L1689S.
All three fields were mapped in two broad-band filters of
ISOCAM: LW2 (5-8.5![]() m) and LW3 (12-18
m) and LW3 (12-18![]() m).
These filters are approximately centered on two minima of the interstellar
extinction curve and are situated apart from the silicate absorption
bands (at roughly 10 and 18
m).
These filters are approximately centered on two minima of the interstellar
extinction curve and are situated apart from the silicate absorption
bands (at roughly 10 and 18 ![]() m).
However, they include most of the Unidentified Infrared Bands
(UIBs, likely due to PAH-like molecules)
which constitute a major source of background emission toward
star-forming clouds (e.g. Bernard et al. 1993;
Boulanger et al. 1996).
The ISOCAM central wavelengths adopted here for LW2 and LW3 are
6.7
m).
However, they include most of the Unidentified Infrared Bands
(UIBs, likely due to PAH-like molecules)
which constitute a major source of background emission toward
star-forming clouds (e.g. Bernard et al. 1993;
Boulanger et al. 1996).
The ISOCAM central wavelengths adopted here for LW2 and LW3 are
6.7 ![]() m and 14.3
m and 14.3 ![]() m respectively.
m respectively.
Each raster consists of a temporal series of individual integration
frames (i.e. of
![]() pixel images) which was reduced using
the CAM Interactive Analysis software (CIA)
pixel images) which was reduced using
the CAM Interactive Analysis software (CIA)![]() .
We have subtracted the best dark current from the ISOCAM calibration
library, and as a second step we improved it with a second order correction
using a FFT thresholding method (Starck et al. 1999).
Cosmic-ray hits were detected and masked using the
multi-resolution median transform algorithm (Starck et al. 1996).
The transients in the time history of each pixel due to detector
memory effects were corrected with the inversion method described
in Abergel et al. (1996).
The images were then flat-fielded with a flat image obtained from
the observations themselves.
Since these various corrections applied to the images are not
perfect, the extraction of faint sources from the images is
a difficult task. We have developed an interactive IDL
point-source detection and photometry program for raster observations
which works in the CIA environment. This program helps to discriminate between
astronomical sources and remaining low-level glitches
or ghosts due to strong transients (see also Nordh et al. 1996;
Kaas et al. 2001).
The fluxes of the detected sources were estimated from the series of
flux measurements made in the individual images (usually 2 to 4 individual images cover each source)
which were obtained from classical aperture
photometry. The emission was integrated in a sky aperture,
the background emission subtracted, and finally an appropriate
aperture correction was applied
based on observed point-spread functions available in the
ISOCAM calibration library.
In practice, the radius of the aperture used was 9
.
We have subtracted the best dark current from the ISOCAM calibration
library, and as a second step we improved it with a second order correction
using a FFT thresholding method (Starck et al. 1999).
Cosmic-ray hits were detected and masked using the
multi-resolution median transform algorithm (Starck et al. 1996).
The transients in the time history of each pixel due to detector
memory effects were corrected with the inversion method described
in Abergel et al. (1996).
The images were then flat-fielded with a flat image obtained from
the observations themselves.
Since these various corrections applied to the images are not
perfect, the extraction of faint sources from the images is
a difficult task. We have developed an interactive IDL
point-source detection and photometry program for raster observations
which works in the CIA environment. This program helps to discriminate between
astronomical sources and remaining low-level glitches
or ghosts due to strong transients (see also Nordh et al. 1996;
Kaas et al. 2001).
The fluxes of the detected sources were estimated from the series of
flux measurements made in the individual images (usually 2 to 4 individual images cover each source)
which were obtained from classical aperture
photometry. The emission was integrated in a sky aperture,
the background emission subtracted, and finally an appropriate
aperture correction was applied
based on observed point-spread functions available in the
ISOCAM calibration library.
In practice, the radius of the aperture used was 9
![]() (i.e., 3 and 1.5 pixels for a pixel size of
(i.e., 3 and 1.5 pixels for a pixel size of
![]() and
6
and
6
![]() ,
respectively). For the weakest sources, however, we reduced
the aperture radius to 4.5
,
respectively). For the weakest sources, however, we reduced
the aperture radius to 4.5
![]() (i.e. 1.5 pixels for a pixel size of
(i.e. 1.5 pixels for a pixel size of
![]() ), in order to improve the
signal-to-noise ratio.
Finally, we applied the following conversion factors:
2.33 and
1.97 ADU/gain/s/mJy for LW2 and LW3 respectively (from
in-orbit latest calibration-Blommaert 1998). These
calibration factors are strictly valid only for sources
with a flat SED (
), in order to improve the
signal-to-noise ratio.
Finally, we applied the following conversion factors:
2.33 and
1.97 ADU/gain/s/mJy for LW2 and LW3 respectively (from
in-orbit latest calibration-Blommaert 1998). These
calibration factors are strictly valid only for sources
with a flat SED (
![]() ).
Here, a small but significant (
).
Here, a small but significant (
![]() 1%) color correction needs to be
applied to the bluest sources, recognized
as Class III YSOs in Sect. 3 below. For these sources,
the conversion factors quoted above were divided by 1.05 for LW2
and 1.02 for LW3 to account for the color effect.
The 212 ISOCAM sources recognized as cluster members (see Sect. 3 below)
are listed in Table 1 (available only in electronic form at
http://cdsweb.u-strasbg.fr/cgi-bin/qcat?/A+A/372/173) with their J2000 coordinates, their flux
densities and associated rms uncertainties (see Sect. 2.4), as well as
the corresponding near-IR identifications.
1%) color correction needs to be
applied to the bluest sources, recognized
as Class III YSOs in Sect. 3 below. For these sources,
the conversion factors quoted above were divided by 1.05 for LW2
and 1.02 for LW3 to account for the color effect.
The 212 ISOCAM sources recognized as cluster members (see Sect. 3 below)
are listed in Table 1 (available only in electronic form at
http://cdsweb.u-strasbg.fr/cgi-bin/qcat?/A+A/372/173) with their J2000 coordinates, their flux
densities and associated rms uncertainties (see Sect. 2.4), as well as
the corresponding near-IR identifications.
The uncertainties on the final photometric measurements result from
systematic errors due to uncertainties in the
absolute calibration and the aperture correction factors, and
from random errors associated with the flat-fielding noise, the statistical
noise in the raw data, the noise due to remaining low-level glitches,
and the imperfect correction for the transient behavior of the detectors.
The in-orbit absolute calibration has been verified to be
correct to within 5% (Blommaert 1998), and we estimate that
the maximum systematic error on the aperture correction is
![]() 10% (by comparing theoretical and observed point-spread functions). The
maximum systematic error on our photometry is thus
10% (by comparing theoretical and observed point-spread functions). The
maximum systematic error on our photometry is thus ![]() 15%.
The magnitudes of the random errors were directly estimated from the
data by measuring both a "temporal'' noise (noise in the temporal
sequence of individual integrations) and a "spatial'' noise (due to
imperfect flat-fielding and/or spatial structures in the local
mid-IR background emission) for each source in the automatic
detection procedure.
The temporal noise was computed as the
standard deviation of the individual aperture measurements divided by the
square root of the number of measurements.
The spatial noise was estimated
as the standard deviation around the mean background
(linear combination of the median and the mean
of the pixels optimized for the source flux estimates)
in the immediate vicinity of each source.
15%.
The magnitudes of the random errors were directly estimated from the
data by measuring both a "temporal'' noise (noise in the temporal
sequence of individual integrations) and a "spatial'' noise (due to
imperfect flat-fielding and/or spatial structures in the local
mid-IR background emission) for each source in the automatic
detection procedure.
The temporal noise was computed as the
standard deviation of the individual aperture measurements divided by the
square root of the number of measurements.
The spatial noise was estimated
as the standard deviation around the mean background
(linear combination of the median and the mean
of the pixels optimized for the source flux estimates)
in the immediate vicinity of each source.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{ms9901f2.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg56.gif) |
Figure 2:
a) Distribution of the
|
| Open with DEXTER | |
The sensitivity limit of the survey was estimated by
calculating the average value of the quadratic sum of
the temporal and spatial noises measured on the weakest detected sources.
The total rms flux uncertainty found in this way,
![]() ,
is
,
is
![]() mJy at 6.7
mJy at 6.7 ![]() m
and
m
and
![]() mJy at 14.3
mJy at 14.3 ![]() m,
m,
![]() 75% of which is due to the spatial noise component.
The large contribution
of the spatial noise originates in the highly structured
diffuse mid-IR emission from the ambient molecular cloud itself
(see Abergel et al. 1996).
Figure 2 displays the distributions of fluxes at 6.7
75% of which is due to the spatial noise component.
The large contribution
of the spatial noise originates in the highly structured
diffuse mid-IR emission from the ambient molecular cloud itself
(see Abergel et al. 1996).
Figure 2 displays the distributions of fluxes at 6.7 ![]() m and 14.3
m and 14.3 ![]() m
for all the detected ISOCAM sources. We used the Wainscoat et al.
(1992)
Galactic model of the mid-IR point source sky to estimate the expected
number of foreground and background sources up to a distance of 20
m
for all the detected ISOCAM sources. We used the Wainscoat et al.
(1992)
Galactic model of the mid-IR point source sky to estimate the expected
number of foreground and background sources up to a distance of 20![]() kpc.
The model predictions are shown by solid and dashed curves in Fig. 2
for cloud extinctions of AV = 0 and AV = 10, respectively
(see Kaas et al. 2001 for more details).
It can be seen that the flux histograms of the ISOCAM sources
not associated with YSOs (light shading in Fig. 2) are remarkably
similar in shape to the model distributions down to
kpc.
The model predictions are shown by solid and dashed curves in Fig. 2
for cloud extinctions of AV = 0 and AV = 10, respectively
(see Kaas et al. 2001 for more details).
It can be seen that the flux histograms of the ISOCAM sources
not associated with YSOs (light shading in Fig. 2) are remarkably
similar in shape to the model distributions down to ![]() 6 mJy at 6.7
6 mJy at 6.7 ![]() m
and
m
and ![]() 10 mJy at 14.3
10 mJy at 14.3 ![]() m. These flux densities can be used to
estimate the completeness level of our observations which is not uniform
over the spatial extent of the survey.
The histograms with light (grey) shading in Fig. 2
are dominated by background sources preferentially located in
low-noise regions (i.e., outside the crowded central part of L1688), where
the total rms flux uncertainty
is
m. These flux densities can be used to
estimate the completeness level of our observations which is not uniform
over the spatial extent of the survey.
The histograms with light (grey) shading in Fig. 2
are dominated by background sources preferentially located in
low-noise regions (i.e., outside the crowded central part of L1688), where
the total rms flux uncertainty
is ![]() 2.0 mJy at 6.7
2.0 mJy at 6.7 ![]() m and
m and ![]() 3.5 mJy at 14.3
3.5 mJy at 14.3 ![]() m.
The effective completeness level in these regions
is thus
m.
The effective completeness level in these regions
is thus ![]()
![]() ,
where
,
where
![]() is the total
is the total![]() flux uncertainty (see above).
However, most of the YSOs are located in regions where the noise is
somewhat larger. The largest rms noise is reached in the Oph A core area
(see Fig. 1), where
flux uncertainty (see above).
However, most of the YSOs are located in regions where the noise is
somewhat larger. The largest rms noise is reached in the Oph A core area
(see Fig. 1), where
![]() mJy at 6.7
mJy at 6.7 ![]() m and
m and
![]() mJy at 14.3
mJy at 14.3 ![]() m.
Therefore, we conservatively estimate the completeness levels of
the global ISOCAM survey to be
m.
Therefore, we conservatively estimate the completeness levels of
the global ISOCAM survey to be ![]() 10 mJy at 6.7
10 mJy at 6.7 ![]() m and
m and
![]() 15 mJy at 14.3
15 mJy at 14.3 ![]() m.
m.
Finally, we note that the AV = 10 model curve in Fig. 2b
accounts for essentially all the "blue'' sources detected
at 14.3 ![]() m and not associated with known YSOs. At 6.7
m and not associated with known YSOs. At 6.7 ![]() m,
the predictions of the Wainscoat et al. model suggest that there
might still be a slight excess of
m,
the predictions of the Wainscoat et al. model suggest that there
might still be a slight excess of ![]() 30 unidentified
sources belonging to the cloud (Fig. 2a).
30 unidentified
sources belonging to the cloud (Fig. 2a).
Within the ![]() 0.7 square degree imaged by ISOCAM,
a total of 425 sources has been identified, among which 211 are seen at both
6.7
0.7 square degree imaged by ISOCAM,
a total of 425 sources has been identified, among which 211 are seen at both
6.7 ![]() m and 14.3
m and 14.3 ![]() m. The spatial distribution of the
sources is shown in Fig. 1,
where the "red'' sources
[those with log10(
m. The spatial distribution of the
sources is shown in Fig. 1,
where the "red'' sources
[those with log10(
![]() ,
see below]
are indicated as filled circles.
These "red'' sources appear to be clustered into four main groupings: three
sub-clusters in L1688, i.e., Oph A (West), Oph B (North-East),
Oph EF (South) (see also Strom et al. 1995),
as well as a new sub-cluster in L1689S.
,
see below]
are indicated as filled circles.
These "red'' sources appear to be clustered into four main groupings: three
sub-clusters in L1688, i.e., Oph A (West), Oph B (North-East),
Oph EF (South) (see also Strom et al. 1995),
as well as a new sub-cluster in L1689S.
Four bright embedded stars (S1, SR3, WL16, WL22) are spatially resolved by
ISOCAM in both filters.
Their extended mid-IR emission is most likely due to
PAH-like molecules excited by relatively strong far-ultraviolet (FUV)
radiation fields![]() .
These bright sources are displayed as open star symbols in Fig. 1
(SR3, S1, WL22, WL16 from right to left).
.
These bright sources are displayed as open star symbols in Fig. 1
(SR3, S1, WL22, WL16 from right to left).
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{ms9901f3.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg71.gif) |
Figure 3:
a) Logarithmic ratio of the ISOCAM fluxes, log10(
|
| Open with DEXTER | |
A total of 89 previously classified YSOs lie within the area of the
present survey:
2 Class 0, 69 Class I/II, and 18 Class III YSOs.
ISOCAM detected 84 of these 89 YSOs (94%):
97% of the Class I/IIs, 94% of the Class IIIs,
and none of the Class 0s.
The two undetected Class I/IIs (GY256, GY257), and the undetected
Class III (IRS50), are located very close (![]() 10
10
![]() -15
-15
![]() )
to bright sources (WL6 and IRS48, respectively), which
may account for their non-detection.
The two Class 0 objects (VLA 1623 and IRAS 16293-2422) are
deeply embedded within massive, cold circumstellar envelopes
which are probably opaque at
6.7
)
to bright sources (WL6 and IRS48, respectively), which
may account for their non-detection.
The two Class 0 objects (VLA 1623 and IRAS 16293-2422) are
deeply embedded within massive, cold circumstellar envelopes
which are probably opaque at
6.7 ![]() m and 14.3
m and 14.3 ![]() m (see André et al. 1993)
and too weak to be detected by ISOCAM.
m (see André et al. 1993)
and too weak to be detected by ISOCAM.
As can be seen in Fig. 3, the mid-IR regime is ideal to detect and
characterize the excess emission due to circumstellar
disks around young stars.
In Fig. 3a,
the 207 sources detected at
6.7 ![]() m and 14.3
m and 14.3 ![]() m (excluding S1, SR3, WL16, WL22) are shown
in a diagram
which displays the logarithmic flux ratio log10(
m (excluding S1, SR3, WL16, WL22) are shown
in a diagram
which displays the logarithmic flux ratio log10(
![]() )
against the mid-IR flux
)
against the mid-IR flux
![]() .
On the right axis of the diagram,
the flux ratio
.
On the right axis of the diagram,
the flux ratio
![]() has been
converted into a classical IR spectral index,
has been
converted into a classical IR spectral index,
![]() d
d
![]() d
d
![]() (e.g. WLY89),
calculated between 6.7
(e.g. WLY89),
calculated between 6.7 ![]() m and 14.3
m and 14.3 ![]() m, i.e.,
m, i.e.,
![]() .
In this diagram, two groups of sources can clearly be distinguished.
The lower ratio group has log10(
.
In this diagram, two groups of sources can clearly be distinguished.
The lower ratio group has log10(
![]() ,
i.e.,
a spectral index on the order of
,
i.e.,
a spectral index on the order of
![]() ,
which is the
value expected for simple photospheric blackbody emission in
the Rayleigh-Jeans regime.
The dispersion around
,
which is the
value expected for simple photospheric blackbody emission in
the Rayleigh-Jeans regime.
The dispersion around
![]() is obviously larger for
weaker sources. This is mainly due to increasing photometric uncertainty
with decreasing flux.
The higher ratio group consists of "red'' sources
defined by log10(
is obviously larger for
weaker sources. This is mainly due to increasing photometric uncertainty
with decreasing flux.
The higher ratio group consists of "red'' sources
defined by log10(
![]() ) > -0.2 (cf. Nordh et al. 1996).
Most of these actually have
) > -0.2 (cf. Nordh et al. 1996).
Most of these actually have ![]() log10(
log10(
![]() ,
i.e.,
,
i.e.,
![]() ,
which is typical of
classical T Tauri stars (hereafter CTTS). This range of
,
which is typical of
classical T Tauri stars (hereafter CTTS). This range of
![]() roughly delineates the domain of Class II YSOs
(e.g. Adams et al. 1987, AM94; Greene et al. 1994), and
is usually interpreted in terms of
optically thick circumstellar disk emission (e.g. Lada & Adams 1992).
In Fig. 3, the new ISOCAM sources are distinguished from
the previously known cluster members by different symbols.
One can see in Fig. 3a that all the previously known
Class II sources but one lie above the dividing line for red sources,
while all the previously known Class III sources but two lie below it.
roughly delineates the domain of Class II YSOs
(e.g. Adams et al. 1987, AM94; Greene et al. 1994), and
is usually interpreted in terms of
optically thick circumstellar disk emission (e.g. Lada & Adams 1992).
In Fig. 3, the new ISOCAM sources are distinguished from
the previously known cluster members by different symbols.
One can see in Fig. 3a that all the previously known
Class II sources but one lie above the dividing line for red sources,
while all the previously known Class III sources but two lie below it.
| ISO | Identification |
|
|
| #a | [ |
||
| 182 | IRS54/GY378 | 1.76 | 6.6 |
| 143 | IRS44/GY269 | 1.57 | 8.7 |
| 137 | CRBR85 | 1.48 | 0.36 |
| 99 | LFAM26/GY197 | 1.25 | 0.064 |
| 29 | GSS30/GY6 | 1.20 | 21. |
| 31 | LFAM1 | 1.08 | 0.13 |
| 65 | WL12/GY111 | 1.04 | 2.6 |
| 108 | EL29/GY214 | 0.98 | 26. |
| 141 | IRS43/GY265 | 0.98 | 6.7 |
| 145 | IRS46/GY274 | 0.94 | 0.62 |
| 21 | CRBR12 | 0.91 | 0.42 |
| 209 | IRS67/L1689-IRS6 | 0.74 | 1.5 |
| 54 | GY91/CRBR42 | 0.70 | 0.17 |
| 134 | WL6/GY254 | 0.59 | 1.7 |
| 159 | IRS48/GY304c | 0.18 | 7.4 |
| 167 | IRS51/GY315c | -0.04 | 1.1 |
| a
The ISO number refers to the numbering of Table 1 (available
only in electronic form at http://cdsweb.u-strasbg.fr/).
b c Although ISO159 |
The object WL19, classified as a Class I YSO by WLY89 and as a
reddened Class II by AM94 (see also Lada & Wilking 1984),
is here found to be a "blue'' source in the mid-IR range
(
![]() ). This object may
correspond to a luminous Class III star
located behind the cloud (see also Comerón et al. 1993).
Although GY12 formally has a "red'' mid-IR spectral
index (
). This object may
correspond to a luminous Class III star
located behind the cloud (see also Comerón et al. 1993).
Although GY12 formally has a "red'' mid-IR spectral
index (
![]() )
here,
we still consider it as a Class III object (cf. Greene et al. 1994).
(The mid-IR color is highly uncertain since GY12
is only marginaly resolved at 14.3
)
here,
we still consider it as a Class III object (cf. Greene et al. 1994).
(The mid-IR color is highly uncertain since GY12
is only marginaly resolved at 14.3 ![]() m
from its bright Class I neighbor GSS30.)
Finally the Class III source DoAr21 has a borderline mid-IR
spectral index (
m
from its bright Class I neighbor GSS30.)
Finally the Class III source DoAr21 has a borderline mid-IR
spectral index (
![]() )
but is kept as a
Class III object since its color between 2.2
)
but is kept as a
Class III object since its color between 2.2 ![]() m and
14.3
m and
14.3 ![]() m corresponds to
m corresponds to
![]() .
.
A total of 71 sources are identified for the first time as mid-IR excess
objects in Fig. 3a.
These new "red'' sources are most likely
all embedded YSOs, i.e., members of the
![]() cluster.
Since dust extinction is roughly the same at
6.7
cluster.
Since dust extinction is roughly the same at
6.7 ![]() m and 14.3
m and 14.3 ![]() m (Rieke & lebofsky 1985;
Lutz 1999), any background source should be
intrinsically red in order to contaminate the sample of red YSOs.
Based on the Galactic model by Wainscoat et al. (1992),
the vast majority
of background objects should appear "blue'' (cf. Fig. 2).
Seven background giant stars (GY45, GY65, VSSG6, GY232, GY351,
GY411, and GY453 - cf. Luhman & Rieke 1999),
and a known foreground dwarf (HD 148352 - Garrison 1967)
are detected, which all have
blue mid-IR colors (
m (Rieke & lebofsky 1985;
Lutz 1999), any background source should be
intrinsically red in order to contaminate the sample of red YSOs.
Based on the Galactic model by Wainscoat et al. (1992),
the vast majority
of background objects should appear "blue'' (cf. Fig. 2).
Seven background giant stars (GY45, GY65, VSSG6, GY232, GY351,
GY411, and GY453 - cf. Luhman & Rieke 1999),
and a known foreground dwarf (HD 148352 - Garrison 1967)
are detected, which all have
blue mid-IR colors (
![]() ,
and -3.1, respectively).
,
and -3.1, respectively).
| ISO | Identification |
|
MJ | MH |
|
|
|
| #a | [mag] | [mag] | [mag] | [ |
[ |
||
| 170 | B162741-244645 | 0.51 | - | 6.1 | 24.9 | 0.018 | 0.047 |
| 103 | WL17/GY205 | 0.42 | 5.2 | - | 22.5 | 0.12 | 0.76 |
| 124 | IRS37/GY244 | 0.35 | - | 2.4 | 36.9 | 0.99 | 0.50 |
| 112 | GY224 | 0.34 | - | 2.4 | 36.2 | 1.1 | 0.56 |
| 118 | IRS33/GY236 | 0.32 | - | 3.6 | 38.3 | 0.28 | 0.15 |
| 33 | GY11 | 0.31 | 10.1 | - | 2.7 | 0.001 | 0.010 |
| 119 | IRS35/GY238 | 0.30 | - | 3.4 | 45.7 | 0.34 | 0.11 |
| 129 | WL3/GY249 | 0.23 | - | 2.2 | 42.2 | 1.3 | 0.34 |
| 75 | GY144 | 0.20 | - | 5.9 | 26.8 | 0.023 | 0.030 |
| 147 | IRS47/GY279 | 0.17 | 2.6 | - | 26.8 | 1.9 | 1.8 |
| 46 | VSSG27/GY51 | 0.17 | 5.2 | - | 21.6 | 0.11 | 0.30 |
| 127 | GY245 | 0.17 | 6.7b | - | 24.7 | 0.023 | 0.11 |
| 161 | GY301 | 0.12 | - | 2.1 | 44.9 | 1.5 | 0.25 |
| 132 | IRS42/GY252 | 0.08 | 2.1 | - | 27.7 | 3.1 | 2.5 |
| 77 | GY152 | 0.05 | - | - | - | 0.037c | 0.015 |
| 70 | WL2/GY128 | 0.05 | - | 2.3 | 38.6 | 1.1 | 0.27 |
| 165 | GY312 | 0.03 | 6.6 | - | 14.8 | 0.027 | 0.064 |
| 85 | CRBR51 | 0.03 | - | - | - | 0.025c | 0.010 |
| 175 | GY344 | 0.02 | 6.5 | - | 17.4 | 0.030 | 0.074 |
| 26 | CRBR15 | 0.01 | 6.7 | - | 14.6 | 0.022 | 0.061 |
| 139 | GY260 | -0.03 | - | 3.7 | 40.3 | 0.24 | 0.058 |
| 37 | LFAM3/GY21 | -0.06 | 4.5 | - | 14.5 | 0.25 | 0.33 |
| 121 | WL20/GY240 | -0.07 | 3.3 | - | 16.5 | 0.86 | 0.67 |
| 51 | B162636-241554 | -0.09 | 4.4 | - | 7.6 | 0.28 | 0.43 |
| 95 | WL1/GY192 | -0.11 | 4.9 | - | 20.9 | 0.15 | 0.16 |
| 122 | IRS36/GY241 | -0.11 | - | 4.9 | 34.3 | 0.066 | 0.025 |
| 171 | GY323 | -0.12 | - | 4.0 | 30.9 | 0.19 | 0.070 |
| 107 | GY213 | -0.15 | 5.6 | - | 19.4 | 0.075 | 0.089 |
| 76 | GY146 | -0.16 | - | 4.1 | 43.5 | 0.17 | 0.025 |
| 120 | IRS34/GY239 | -0.23 | - | 2.4 | 34.8 | 1.1 | 0.19 |
| 144 | IRS45/GY273 | -0.24 | 3.6 | - | 19.5 | 0.66 | 0.45 |
| 204 | L1689-IRS5d | -0.25 | 2.6 | - | 12.8 | 1.9 | 1.4 |
| 17 | GSS26 | -0.30 | 3.2 | - | 22.6 | 0.95 | 0.43 |
| 93 | GY188 | -0.36 | 6.3 | - | 20.5 | 0.034 | 0.020 |
| 98 | GY195 | -0.36 | 5.5 | - | 20.6 | 0.087 | 0.063 |
| 53 | GY84 | -0.39 | 5.8 | - | 14.1 | 0.060 | 0.037 |
| 190 | GY450 | -0.39 | 9.2 | - | 8.6 | 0.002 | 0.008 |
| 23 | SKS1-10 | -0.41 | 7.2 | - | 8.2 | 0.013 | 0.018 |
| 13 | B162607-242725 | -0.41 | 4.6 | - | 19.5 | 0.22 | 0.12 |
| 117 | GY235 | -0.43 | 4.9 | - | 9.9 | 0.16 | 0.12 |
| 212 | L1689-IRS7d | -0.44 | 2.6 | - | 14.7 | 1.8 | 0.64 |
| 79 | GY154 | -0.44 | - | 5.5 | 24.3 | 0.033 | 0.013 |
| 24 | VSSG1 | -0.49 | 3.2 | - | 17.1 | 0.97 | 0.49 |
| 3 | IRS3 | -0.50 | 4.3 | - | 4.6 | 0.31 | 0.28 |
| 39 | S2/GY23 | -0.51 | 2.0 | - | 11.8 | 3.7 | 1.6 |
| 140 | GY262 | -0.52 | 3.5 | - | 23.7 | 0.71 | 0.20 |
| 40 | EL24 | -0.54 | 1.8 | - | 10.0 | 4.5 | 2.1 |
| 52 | VSSG4/GY81 | -0.54 | 5.2 | - | 17.6 | 0.11 | 0.058 |
| 154 | GY291 | -0.60 | 4.3 | - | 23.0 | 0.29 | 0.058 |
| 94 | B162703-242007 | -0.61 | - | 6.6 | 16.6 | 0.010 | 0.006 |
| 128 | WL4/GY247 | -0.67 | 3.2 | - | 19.5 | 1.1 | 0.24 |
| 59 | WL7/GY98 | -0.69 | 4.1 | - | 27.2 | 0.37 | 0.061 |
| 84 | WL21/GY164 | -0.70 | 7.8 | - | 14.2 | 0.007 | 0.008 |
| 67 | GSS39/GY116 | -0.72 | 3.1 | - | 16.3 | 1.1 | 0.25 |
| 41 | GY29 | -0.73 | 5.1 | - | 19.1 | 0.13 | 0.043 |
| 88 | SR24N/GY168 | -0.74 | 2.5 | - | 7.7 | 2.1 | 0.76 |
| 35 | GY15 | -0.75 | 6.2 | - | 11.5 | 0.040 | 0.019 |
| 164 | GY310 | -0.75 | 6.4 | - | 4.0 | 0.032 | 0.024 |
| 63 | GY109 | -0.77 | 5.8 | - | 14.6 | 0.064 | 0.022 |
| 151 | GY284 | -0.77 | 4.9 | - | 7.6 | 0.15 | 0.065 |
| 43 | GY33 | -0.78 | 4.2 | - | 15.5 | 0.36 | 0.092 |
| 138 | B162726-241925 | -0.78 | 7.9 | - | 11.2 | 0.006 | 0.004 |
| 36 | GSS31/GY20 | -0.79 | 1.5 | - | 6.1 | 5.9 | 1.6 |
| 177 | GY352 | -0.79 | 5.2 | - | 17.7 | 0.11 | 0.031 |
| 197 | B162821-244246 | -0.81 | 6.0 | - | 20.3 | 0.050 | 0.009 |
| 110 | SR21/VSSG23 | -0.81 | 1.9 | - | 3.5 | 4.0 | 1.7 |
| 166 | GY314 | -0.83 | 3.4 | - | 6.4 | 0.80 | 0.26 |
| 9 | SKS1-4 | -0.85 | 6.0 | - | 9.5 | 0.051 | 0.022 |
| 12 | B162604-241753 | -0.86 | 6.6 | - | 13.4 | 0.027 | 0.009 |
| 155 | GY292 | -0.90 | 2.7 | - | 10.8 | 1.6 | 0.37 |
| ISO | Identification |
|
MJ | MH |
|
|
|
| #a | [mag] | [mag] | [mag] | [ |
[ |
||
| 88 | SR24S/GY167 | -0.91 | 2.5 | - | 5.9 | 2.2 | 0.72 |
| 19 | GSS29 | -0.91 | 2.9 | - | 9.4 | 1.4 | 0.28 |
| 115 | WL11/GY229 | -0.92 | 6.3 | - | 13.8 | 0.037 | 0.015 |
| 196 | WSB60e | -0.92 | 4.9 | - | 2.8 | 0.16 | 0.075 |
| 30 | GY5 | -0.92 | 6.3 | - | 2.5 | 0.036 | 0.019 |
| 176 | GY350 | -0.94 | 6.4 | - | 6.4 | 0.033 | 0.014 |
| 72 | WL18/GY129 | -0.94 | 4.7 | - | 10.4 | 0.19 | 0.061 |
| 163 | IRS49/GY309 | -0.96 | 3.1 | - | 10.1 | 1.1 | 0.23 |
| 193 | B162812-241138 | -0.99 | 6.2 | - | 6.2 | 0.039 | 0.016 |
| 2 | B162538-242238 | -1.00 | 4.6 | - | 10.9 | 0.22 | 0.063 |
| 78 | VSSG5/GY153 | -1.02 | 3.8 | - | 19.7 | 0.55 | 0.056 |
| 86 | IRS26/GY171 | -1.04 | 5.2 | - | 19.9 | 0.12 | 0.015 |
| 105 | WL10/GY211 | -1.05 | 3.4 | - | 12.5 | 0.78 | 0.12 |
| 87 | B162658-241836 | -1.06 | 6.0 | - | 14.2 | 0.050 | 0.011 |
| 160 | B162737-241756 | -1.08 | 7.2 | - | 4.5 | 0.014 | 0.006 |
| 83 | B162656-241353 | -1.08 | 4.2 | - | 11.1 | 0.33 | 0.058 |
| 32 | GY3 | -1.09 | 6.5 | - | 0.4 | 0.029 | 0.015 |
| 1 | IRS2 | -1.09 | 3.4 | - | 4.9 | 0.79 | 0.15 |
| 185 | GY397 | -1.10 | 6.1 | - | 4.1 | 0.045 | 0.016 |
| 6 | SR4/IRS12 | -1.12 | 2.8 | - | 1.9 | 1.5 | 0.37 |
| 142 | VSSG25/GY267 | -1.13 | 4.0 | - | 9.8 | 0.42 | 0.065 |
| 20 | DoAr24/GSS28 | -1.14 | 3.5 | - | 1.8 | 0.72 | 0.16 |
| 178 | GY371 | -1.16 | 5.2 | - | 7.1 | 0.11 | 0.026 |
| 62 | GSS37/GY110 | -1.19 | 2.7 | - | 8.5 | 1.6 | 0.18 |
| 89 | WL14/GY172 | -1.24 | 5.8 | - | 17.2 | 0.059 | 0.006 |
| 194 | B162813-243249 | -1.24 | 5.2 | - | 5.9 | 0.12 | 0.024 |
| 116 | B162713-241818 | -1.27 | 3.7 | - | 10.7 | 0.57 | 0.046 |
| 106 | B162708-241204 | -1.33 | 4.5 | - | 8.0 | 0.24 | 0.027 |
| 102 | GY204 | -1.33 | 6.2 | - | 1.5 | 0.039 | 0.011 |
| 168 | SR9/IRS52 | -1.35 | 2.7 | - | -0.7 | 1.6 | 0.23 |
| 199 | SR13 | -1.37 | 3.4 | - | -0.9 | 0.78 | 0.12 |
| 187 | SR10/GY400 | -1.39 | 4.1 | - | -3.2 | 0.38 | 0.052 |
| 68 | VSS27 | -1.53 | 2.6 | - | 5.6 | 1.9 | 0.13 |
| 172 | GY326 | -1.56 | 5.3 | - | 8.5 | 0.11 | 0.008 |
| 56 | WSB37/GY93 | -1.58 | 4.7 | - | 1.2 | 0.20 | 0.024 |
| 38 | DoAr25/GY17 | -1.58 | 3.4 | - | 0.7 | 0.83 | 0.11 |
| - | GY256 | - | - | 4.5 | 34.5 | 0.11 | - |
| - | GY257 | - | - | 4.1 | 33.2 | 0.17 | - |
| 90 | WL22/GY174 | - | - | - | - | 29.f | - |
| 92 | WL16/GY182 | - | - | - | - | 44.f | - |
| 207 | IRAS16289-2457 | - | - | - | - | 1.3c | 0.51 |
| 123 | Newg | - | - | - | - | 0.077c | 0.031 |
| 150 | Newg | - | - | - | - | 0.21c | 0.083 |
| 195 | Newg | - | - | - | - | 0.14c | 0.058 |
| 200 | Newg | - | - | - | - | 0.95c | 0.38 |
| 201 | Newg | - | - | - | - | 0.025c | 0.010 |
| 202 | Newg | - | - | - | - | 0.024c | 0.010 |
| 203 | Newg | - | - | - | - | 0.71c | 0.28 |
| 205 | Newg | - | - | - | - | 0.17c | 0.067 |
| 206 | Newg | - | - | - | - | 0.099c | 0.040 |
| 208 | Newg | - | - | - | - | 0.058c | 0.023 |
| 210 | Newg | - | - | - | - | 0.067c | 0.027 |
| 211 | Newg | - | - | - | - | 0.068c | 0.027 |
The newly identified cloud members nicely extend the previously
known Class I/II population toward low IR fluxes.
While previous studies could only identify sources with
![]() mJy,
the present census is complete for objects down
to
mJy,
the present census is complete for objects down
to
![]() mJy.
Altogether, a sample of 139 Class I/Class II YSOs
is identified, of which 71 are new members.
The present survey has thus allowed us
to more than double the number of recognized YSOs with
circumstellar IR excess in the
mJy.
Altogether, a sample of 139 Class I/Class II YSOs
is identified, of which 71 are new members.
The present survey has thus allowed us
to more than double the number of recognized YSOs with
circumstellar IR excess in the
![]() cloud.
cloud.
The 139 red YSOs are listed in Table 2 (Class I YSOs)
and Table 3 (Class II YSOs) by decreasing order of
![]() .
Twelve of them (last entries of Table 3) are completely new sources
with respect to published IR surveys.
.
Twelve of them (last entries of Table 3) are completely new sources
with respect to published IR surveys.
In Fig. 3,
the YSOs classified as Class I and Class II by AM94
and Greene et al. (1994) are shown as filled stars and filled
circles, respectively.
In the log10(
![]() /
/
![]() )
versus
)
versus
![]() diagram, there is no
clear color gap between the two classes of objects,
even though the Class I YSOs tend to lie in the upper part
of the "red'' group (see Fig. 3a).
Since extinction has a negligible effect on the mid-IR ratio
diagram, there is no
clear color gap between the two classes of objects,
even though the Class I YSOs tend to lie in the upper part
of the "red'' group (see Fig. 3a).
Since extinction has a negligible effect on the mid-IR ratio
![]() /
/
![]() ,
this suggests that Class I and Class II objects have fairly similar
intrinsic colors between 6.7
,
this suggests that Class I and Class II objects have fairly similar
intrinsic colors between 6.7 ![]() m and 14.3
m and 14.3 ![]() m.
m.
The classical IR spectral index
calculated from 2 ![]() m to 10
m to 10 ![]() m (or 25
m (or 25 ![]() m)
(e.g. Lada & Wilking 1984 and WLY89) appears to provide a better way of
discriminating between envelope-dominated Class I YSOs
and disk-dominated Class II sources (see Fig. 3b).
In particular, millimeter continuum mapping of optically thin circumstellar
dust emission confirms that, apart from a few important
exceptions (e.g., WL22, WL16, WL17, IRS37, IRS47),
the
m)
(e.g. Lada & Wilking 1984 and WLY89) appears to provide a better way of
discriminating between envelope-dominated Class I YSOs
and disk-dominated Class II sources (see Fig. 3b).
In particular, millimeter continuum mapping of optically thin circumstellar
dust emission confirms that, apart from a few important
exceptions (e.g., WL22, WL16, WL17, IRS37, IRS47),
the
![]() objects selected on the basis of
objects selected on the basis of
![]() are indeed Class I protostars surrounded by spheroidal
envelopes (AM94, MAN98).
are indeed Class I protostars surrounded by spheroidal
envelopes (AM94, MAN98).
As expected, the previously known Class I YSOs are
well concentrated in the upper-right part of the
![]() versus
versus
![]() diagram of Fig. 3b (where
diagram of Fig. 3b (where
![]() and
and
![]() are close to the
are close to the
![]() index used in previous studies -
e.g., AM94 and Greene et al. 1994).
There is also a hint of two gaps in this diagram
at
index used in previous studies -
e.g., AM94 and Greene et al. 1994).
There is also a hint of two gaps in this diagram
at
![]() and
and
![]() ,
which roughly bracket the regime of flat-spectrum sources as defined by
Greene et al. (1994).
These may represent a distinct population of
transition objects between Class I and Class II
(e.g. Calvet et al. 1994).
,
which roughly bracket the regime of flat-spectrum sources as defined by
Greene et al. (1994).
These may represent a distinct population of
transition objects between Class I and Class II
(e.g. Calvet et al. 1994).
Here, we thus consider sources with
![]() as Class I YSOs
(Table 2), sources with
as Class I YSOs
(Table 2), sources with
![]() as candidate
flat-spectrum objects (see Table 3), and sources with
as candidate
flat-spectrum objects (see Table 3), and sources with
![]() as Class II YSOs (Table 3).
These limiting indices are displayed in Fig. 3b. In the
following, the candidate flat-spectrum sources will be treated as
Class II YSOs.
as Class II YSOs (Table 3).
These limiting indices are displayed in Fig. 3b. In the
following, the candidate flat-spectrum sources will be treated as
Class II YSOs.
Most of the ISOCAM sources (e.g. 90% of the Class II sources) were also detected in the near-IR (JHK) survey of Barsony et al. (1997). Comparison between Figs. 3b and 3c illustrates the advantage of mid-IR measurements for selecting sources with intrinsic circumstellar IR excesses. While the red and blue groups of Fig. 3a are well separated in the mid-IR diagram of Fig. 3b, they blend together in the near-IR diagram of Fig. 3c.
Figure 3c also shows that most of the ISOCAM-selected YSOs lie within the reddening band associated with the intrinsic locus of CTTSs as derived by Meyer et al. (1997) in Taurus. The few exceptions, which lie to the right of the reddening band, correspond to Class I and flat-spectrum YSOs.
While Class I/II YSOs are easily recognized in the mid-IR
range thanks to their strong IR excesses, Class III objects are difficult
to identify without
deep X-ray and/or radio centimeter continuum observations.
We have used the ROSAT X-ray surveys of Casanova et al. (1995) and
Grosso et al. (2000), along with the VLA radio surveys by, e.g.,
André et al. (1987) and Stine et al.
(1988)
to build up a sample of bona-fide Class III YSOs covered by the present
survey. With the additional Class III candidate WL19 (see Sect. 3.2 above),
there are 38 such YSOs which are listed in order of decreasing
![]() in Table 4.
in Table 4.
| ISO | Identification |
|
MJ | MH |
|
|
| #a | (
|
[mag] | [mag] | [mag] | [ |
|
| 114 | WL19/GY227b | -0.05 | - | -1.0 | 73.4 | 52. |
| 125 | WL5/GY246b | -1.02 | - | -0.7 | 59.8 | 39. |
| 34 | GY12b | -1.06 | 3.3 | - | 19.5 | 0.89 |
| 58 | WL8/GY96b | -1.11 | 1.9 | - | 35.5 | 4.2 |
| 152 | GY289b | -1.33 | 3.3 | - | 27.5 | 0.90 |
| 198 | SR20 | -1.65 | 1.9 | - | 4.0 | 4.0 |
| 133 | GY253b | -1.73 | 3.3 | - | 31.2 | 0.85 |
| 45 | LFAM8/SKS1-19b | -1.82 | 4.2 | - | 25.2 | 0.34 |
| 80 | GY156b | -2.00 | 3.4 | - | 22.5 | 0.84 |
| 10 | DoAr21/GSS23b | -2.00 | 0.7 | - | 6.0 | 15. |
| 27 | WSB28 | -2.06 | 4.1 | - | 4.3 | 0.36 |
| 149 | B162730-244726 | -2.20 | 3.7 | - | 10.3 | 0.61 |
| 135 | VSSG22 | -2.23 | 3.0 | - | 17.1 | 1.2 |
| 64 | VSSG11b | -2.24 | 3.4 | - | 15.2 | 0.83 |
| 73 | VSSG3/GY135 | -2.26 | 2.3 | - | 15.7 | 2.8 |
| 180 | VSSG14/GY372 | -2.51 | 2.2 | - | 5.5 | 3.0 |
| 184 | IRS55/GY380 | -2.65 | 2.6 | - | 6.0 | 1.8 |
| 11 | VSSG19b | -2.75 | 3.8 | - | 3.9 | 0.50 |
| 7 | GSS20 | -2.84 | 3.1 | - | 4.7 | 1.1 |
| 60 | GY101b | ( 0.00) | - | 2.0 | 55.5 | 2.0 |
| 61 | GY103b | (-0.45) | - | 2.6 | 48.5 | 1.1 |
| 126 | GY248b | (-0.82) | 4.2 | - | 25.5 | 0.36 |
| 101 | IRS30/GY203b | (-0.99) | - | 2.2 | 36.5 | 1.6 |
| 14 | B162607-242742 | (-1.43) | 3.5 | - | 20.6 | 0.70 |
| 8 | B162601-242945 | (-1.96) | 3.9 | - | 8.1 | 0.47 |
| 183 | GY377b | (-1.98) | 4.0 | - | 16.0 | 0.40 |
| 157 | GY296b | (-2.02) | 5.5 | - | 5.1 | 0.081 |
| 4 | B162541-242138 | (-2.05) | 5.8 | - | 6.7 | 0.060 |
| 69 | GY122 | (-2.17) | 5.5 | - | 2.7 | 0.080 |
| 96 | GY193 | (-2.24) | 4.2 | - | 7.4 | 0.34 |
| 97 | GY194 | (-2.35) | 4.1 | - | 9.1 | 0.40 |
| 188 | GY410 | (-2.36) | 4.0 | - | 10.2 | 0.43 |
| 66 | GY112 | (-2.42) | 4.2 | - | 3.6 | 0.35 |
| 130 | SR12/GY250b | (-2.48) | 3.4 | - | 1.2 | 0.83 |
| 5 | IRS10 | (-2.78) | 2.7 | - | 5.4 | 1.7 |
| - | IRS50/GY306 | - | 3.7 | - | 11.5 | 0.60 |
| 16 | SR3/GSS25 | - | - | - | - | 100.c |
| 48 | S1/GY70b | - | - | - | - | 1100.c |
| a
The ISO number refers to the numbering in Table 1 (available
only in electronic form at http://cdsweb.u-strasbg.fr/).
b Class III YSOs located inside the CS contours of Fig. 1 (see Sects. 3.5 and 4.4). c For the two B stars ISO16 |
This Class III sample is unfortunately not as complete as the Class I
and Class II samples discussed above.
According to Grosso et al. (2000), the number of Class IIIs
may be roughly as large as the number of Class IIs: above their typical X-ray
detection limit of
![]() ergs-1
(corresponding to
ergs-1
(corresponding to
![]() - see Fig. 7 of Grosso et al.),
they found a Class III/Class II number ratio
of 19/22 in the ROSAT-HRI/ISO-ISOCAM overlapping survey area.
If this ratio is representative of the
complete population of young stars in
- see Fig. 7 of Grosso et al.),
they found a Class III/Class II number ratio
of 19/22 in the ROSAT-HRI/ISO-ISOCAM overlapping survey area.
If this ratio is representative of the
complete population of young stars in
![]() ,
the total number of Class IIs
found here (123 objects) suggests that as many as 106 Class IIIs may be
present in the cluster down to
,
the total number of Class IIs
found here (123 objects) suggests that as many as 106 Class IIIs may be
present in the cluster down to
![]() (our completeness level
for Class IIs, see Sect. 4.4).
A total of 38 Class IIIs are already known within the ISOCAM
survey area, so that
(our completeness level
for Class IIs, see Sect. 4.4).
A total of 38 Class IIIs are already known within the ISOCAM
survey area, so that ![]() 68
unknown Class IIIs may remain to be found.
Since it was noted in Sect. 2.4 that
68
unknown Class IIIs may remain to be found.
Since it was noted in Sect. 2.4 that
![]() 30 sources detected at 6.7
30 sources detected at 6.7 ![]() m
might be unidentified cluster members,
about half of the missing Class IIIs
may have been actually seen by ISOCAM.
m
might be unidentified cluster members,
about half of the missing Class IIIs
may have been actually seen by ISOCAM.
We also note that a large proportion (80/123) of the Class II sources
are closely associated with the densest part of L1688 (see Fig. 1).
Assuming the same proportion applies to Class IIIs, we would
expect ![]() 44 unknown Class III sources to be located within
the CS contours of Fig. 1. A total of
39 unclassified ISOCAM sources (also detected by Barsony et al. 1997)
lie within these CS contours where the number
of detected background stars should be small due to high cloud extinction.
Most of these 39 sources might thus be yet unidentified
Class III YSOs. These candidate Class III sources are listed in order of
decreasing
44 unknown Class III sources to be located within
the CS contours of Fig. 1. A total of
39 unclassified ISOCAM sources (also detected by Barsony et al. 1997)
lie within these CS contours where the number
of detected background stars should be small due to high cloud extinction.
Most of these 39 sources might thus be yet unidentified
Class III YSOs. These candidate Class III sources are listed in order of
decreasing
![]() in Table 5.
in Table 5.
| ISO | Identification |
|
MJ | MH |
|
|
| #a | (
|
[mag] | [mag] | [mag] | [ |
|
| 191 | GY463 | -1.46 | 4.4 | - | 25.2 | 0.28 |
| 44 | B162628-241543 | -1.63 | 3.9 | - | 21.7 | 0.45 |
| 81 | VSSG7/GY157 | -2.13 | 2.1 | - | 29.8 | 3.4 |
| 91 | VSSG8/GY181 | -2.20 | 2.4 | - | 22.9 | 2.4 |
| 28 | B162621-241544 | -2.23 | 2.9 | - | 15.5 | 1.4 |
| 18 | SKS1-7 | -2.38 | 3.6 | - | 17.4 | 0.64 |
| 25 | CRBR17 | ( 0.68) | 8.3 | - | 10.1 | 0.004 |
| 153 | GY290 | ( 0.41) | - | 3.7 | 41.5 | 0.31 |
| 100 | B162705-244013b | ( 0.12) | - | - | - | - |
| 109 | GY215b | ( 0.05) | - | - | - | - |
| 104 | GY207 | (-0.31) | - | 4.6 | 39.5 | 0.11 |
| 49 | B162636-241811b | (-0.36) | - | - | - | - |
| 15 | CRBR4 | (-0.41) | - | 1.9 | 58.9 | 2.2 |
| 146 | GY278 | (-0.58) | - | 2.4 | 47.8 | 1.3 |
| 136 | GY258 | (-0.72) | 8.2 | - | 10.8 | 0.004 |
| 55 | IRS16/GY92 | (-0.80) | - | 5.0 | 29.1 | 0.079 |
| 173 | IRS53/GY334 | (-0.81) | - | 2.0 | 40.2 | 2.1 |
| 71 | GY130 | (-0.87) | - | 3.7 | 38.8 | 0.31 |
| 162 | GY309 | (-1.01) | - | 3.3 | 42.5 | 0.47 |
| 50 | B162636-241902 | (-1.06) | 6.6 | - | 14.0 | 0.025 |
| 57 | B162641-241801 | (-1.22) | - | 3.1 | 32.3 | 0.58 |
| 111 | WL9/GY220 | (-1.27) | 5.5 | - | 21.6 | 0.086 |
| 22 | B162618-241712 | (-1.50) | 4.2 | - | 26.8 | 0.34 |
| 113 | IRS32/GY228 | (-1.52) | 3.6 | - | 18.5 | 0.62 |
| 82 | GY163 | (-1.53) | - | 4.1 | 32.8 | 0.19 |
| 131 | GY255 | (-1.57) | 4.2 | - | 21.6 | 0.35 |
| 169 | GY322 | (-1.59) | 4.0 | - | 16.3 | 0.43 |
| 47 | IRS14/GY54 | (-1.85) | 4.7 | - | 16.6 | 0.21 |
| 189 | GY412 | (-1.90) | 5.2 | - | 17.6 | 0.12 |
| 181 | GY373 | (-1.91) | 6.4 | - | 7.7 | 0.032 |
| 174 | GY346 | (-1.93) | 5.6 | - | 19.5 | 0.075 |
| 74 | IRS20/GY143 | (-1.97) | 3.8 | - | 16.0 | 0.50 |
| 179 | GY370 | (-1.99) | 5.4 | - | 10.0 | 0.094 |
| 148 | GY283 | (-2.09) | 4.3 | - | 13.1 | 0.32 |
| 42 | VSSG29/GY37 | (-2.14) | 6.8 | - | 6.5 | 0.021 |
| 192 | GY472 | (-2.14) | 5.9 | - | 20.1 | 0.054 |
| 186 | GY398 | (-2.20) | 5.2 | - | 5.2 | 0.11 |
| 158 | GY297 | (-2.22) | 6.0 | - | 0.7 | 0.047 |
| 156 | GY295 | (-2.52) | 4.3 | - | 4.8 | 0.32 |
Most of the new YSOs identified by ISOCAM
are weak IR sources which were not detected by IRAS
and were not observed in previous ground-based
mid-IR surveys (dedicated to bright near-IR sources).
They likely correspond to low-luminosity, low-mass young stars.
In Sect. 4.1 below, we derive stellar luminosity estimates
for Class II and Class III objects
using published near-IR photometry from Barsony et al. (1997).
In Sect. 4.2, we provide mid-IR estimates of the disk luminosities,
![]() ,
for Class II YSOs.
Finally, calorimetric estimates of the bolometric
luminosities,
,
for Class II YSOs.
Finally, calorimetric estimates of the bolometric
luminosities,
![]() ,
for Class I YSOs are calculated in Sect. 4.3.
The luminosity function
of the
,
for Class I YSOs are calculated in Sect. 4.3.
The luminosity function
of the
![]() embedded cluster is then assembled in Sect. 4.4.
embedded cluster is then assembled in Sect. 4.4.
The J-band flux provides a good tracer of the stellar luminosity
for late-type PMS stars (i.e., T Tauri stars) because the J-band is
close to the maximum of the photospheric energy distribution
for such cool stars. It is also a good compromise between bands too much affected by
interstellar extinction at short wavelengths
(very few
![]() YSOs have been detected in the V, R, or I bands),
and the H, K and mid-IR bands which are contaminated by
intrinsic excesses.
Greene et al. (1994) showed that there is a good
correlation between the dereddened J-band flux and the stellar luminosity
derived by other methods. They pointed out that in
YSOs have been detected in the V, R, or I bands),
and the H, K and mid-IR bands which are contaminated by
intrinsic excesses.
Greene et al. (1994) showed that there is a good
correlation between the dereddened J-band flux and the stellar luminosity
derived by other methods. They pointed out that in
![]() this correlation is roughly consistent with a more theoretically
based correlation expected for 1-Myr old PMS stars following the
D'Antona & Mazzitelli (1994) evolutionary tracks.
More recently, Strom et al. (1995) and Kenyon & Hartmann (1995)
used the same model PMS tracks to directly convert dereddened
J-band fluxes into stellar masses. We adopt a similar approach here.
this correlation is roughly consistent with a more theoretically
based correlation expected for 1-Myr old PMS stars following the
D'Antona & Mazzitelli (1994) evolutionary tracks.
More recently, Strom et al. (1995) and Kenyon & Hartmann (1995)
used the same model PMS tracks to directly convert dereddened
J-band fluxes into stellar masses. We adopt a similar approach here.
The main difficulty and source of uncertainty with this method is due to the foreground extinction affecting the J-band fluxes. One must estimate the interstellar extinction toward each source in order to correct the observed J-band fluxes. We have used the observed near-IR colors to estimate the J-band extinction. The (J-H) color excess is most suitable for this purpose (e.g. Greene et al. 1994) since the dispersion in the intrinsic (J-H) colors of CTTSs is small and observationally well determined (cf. Strom et al. 1989; Meyer et al. 1997).
The reddening law quoted by Cohen et al. (1981),
which is determined for the standard CIT system, should be applicable
to the JHK photometry of Barsony et al. (1997).
We have thus used:
![\begin{displaymath}A_V = 9.09\times [(J-H)-(J-H)_0]
\end{displaymath}](/articles/aa/full/2001/22/aa9901/img111.gif) |
(1) |
![\begin{displaymath}A_V = 15.4\times [(H-K)-(H-K)_0]
\end{displaymath}](/articles/aa/full/2001/22/aa9901/img112.gif) |
(2) |
The uncertainties on MJ and MH result from
the typical uncertainties on the J, H, Kmagnitudes and on the intrinsic
colors (J-H)0 and (H-K)0. With
![]() ,
,
![]() (Barsony et al. 1997), and
(Barsony et al. 1997), and
![]() ( (J-H)0)
( (J-H)0)![]() ,
,
![]() ( (H-K)0)
( (H-K)0)![]() (Meyer et al. 1997),
we obtain the following typical uncertainties:
(Meyer et al. 1997),
we obtain the following typical uncertainties:
![]() ( MJ) = 0.39 mag, and
( MJ) = 0.39 mag, and
![]() ( MH) = 0.60 mag. In addition, the uncertainty on the
cluster distance (
( MH) = 0.60 mag. In addition, the uncertainty on the
cluster distance (
![]() pc) induces a maximum systematic error
of
pc) induces a maximum systematic error
of ![]() mag on MJ and MH.
mag on MJ and MH.
The absolute J-band magnitude MJ can be directly converted into a stellar
luminosity
![]() if the effective stellar temperature
if the effective stellar temperature
![]() is known:
is known:
![]() ,
where BCJ
is the bolometric correction for the J band depending only on
,
where BCJ
is the bolometric correction for the J band depending only on
![]() .
Pre-main sequence objects in the mass range
.
Pre-main sequence objects in the mass range
![]() are cool sub-giant stars with typical photospheric temperatures
are cool sub-giant stars with typical photospheric temperatures
![]() 2500-5500 K (e.g. Greene & Meyer 1995;
D'Antona & Mazzitelli 1994).
In this temperature range (0.34 dex wide),
the photospheric blackbody peaks close
to the J band (1.2
2500-5500 K (e.g. Greene & Meyer 1995;
D'Antona & Mazzitelli 1994).
In this temperature range (0.34 dex wide),
the photospheric blackbody peaks close
to the J band (1.2 ![]() m), so that the J-band bolometric correction
spans only a limited range,
m), so that the J-band bolometric correction
spans only a limited range,
![]() ,
corresponding
to a total shift in luminosity of only 0.4 dex.
Therefore, if we use a (geometrical) average value for the
effective temperature,
,
corresponding
to a total shift in luminosity of only 0.4 dex.
Therefore, if we use a (geometrical) average value for the
effective temperature,
![]() K,
we should not make an error larger than
K,
we should not make an error larger than
![]() dex on
dex on
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{ms9901f4.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg133.gif) |
Figure 4:
MJ - log10(
|
| Open with DEXTER | |
Furthermore, since
bright MJ sources tend to be of earlier spectral type than faint sources,
we can in fact achieve more accurate luminosity estimates.
Indeed, PMS stars are predicted to lie
within a well-defined strip of the HR diagram. This
is illustrated in Fig. 4 which displays
model evolutionary tracks and isochrones from D'Antona & Mazzitelli
(1998)
on a MJ-log
![]() diagram
for PMS stars with ages between
diagram
for PMS stars with ages between ![]() Myr and
Myr and ![]() Myr.
We have used the compilations of
Hartigan et al. (1994), Kenyon & Hartmann (1995),
and Wilking et al. (1999) to derive an approximate linear
interpolation for BCJ:
Myr.
We have used the compilations of
Hartigan et al. (1994), Kenyon & Hartmann (1995),
and Wilking et al. (1999) to derive an approximate linear
interpolation for BCJ:
![]() log10(
log10(
![]() ).
Figure 4 shows that, for a given observed value of MJ, the possible
range of log10(
).
Figure 4 shows that, for a given observed value of MJ, the possible
range of log10(
![]() )
is reduced to less than
)
is reduced to less than ![]() 0.15 dex, inducing a
maximum error of
0.15 dex, inducing a
maximum error of ![]() % (
% (![]() dex) on
dex) on
![]() .
Based on Fig. 4, we have adopted a linear
relationship between MJ and
.
Based on Fig. 4, we have adopted a linear
relationship between MJ and
![]() :
log
:
log
![]() (see the heavy dashed line in Fig. 4).
This leads to the following
(see the heavy dashed line in Fig. 4).
This leads to the following
![]() conversion:
conversion:
The
![]() conversion described above cannot be applied
to sources undetected in the J band. Instead, we use the H-band magnitude,
along with the extinction estimate derived from the (H-K) color, but with
the additional complication that the circumstellar (disk) emission
cannot be neglected.
Meyer et al. (1997) found that the H-band circumstellar excess
is on the order of 20% of the stellar flux, on average, for the
Taurus CTTS sample of Strom et al. (1989)
(for a
conversion described above cannot be applied
to sources undetected in the J band. Instead, we use the H-band magnitude,
along with the extinction estimate derived from the (H-K) color, but with
the additional complication that the circumstellar (disk) emission
cannot be neglected.
Meyer et al. (1997) found that the H-band circumstellar excess
is on the order of 20% of the stellar flux, on average, for the
Taurus CTTS sample of Strom et al. (1989)
(for a
![]() sample, see Greene & Lada 1996).
This excess, expressed as a veiling index
sample, see Greene & Lada 1996).
This excess, expressed as a veiling index
![]() (e.g.
Greene & Meyer 1995), is equal to
(e.g.
Greene & Meyer 1995), is equal to ![]() 0.2.
Accordingly, we have applied a systematic correction
0.2.
Accordingly, we have applied a systematic correction
![]() H
H
![]() mag.
The
mag.
The
![]() relationship obtained in a way similar to the
J-band relation is then:
relationship obtained in a way similar to the
J-band relation is then:
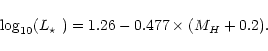 |
(4) |
This method can also be applied to Class III YSOs, using different values
for (J-H)0 and (H-K)0.
We have derived
![]() for all Class III YSOs
using the following relationships:
for all Class III YSOs
using the following relationships:
![]() ,
or
,
or
![]() ;
and
log
;
and
log
![]() ,
or
log
,
or
log
![]() (the H-band IR excess for Class III YSOs is negligible).
(the H-band IR excess for Class III YSOs is negligible).
The resulting
MJ, MH, AV, and
![]() estimates are listed in
Table 3 for Class II YSOs, and in Tables 4 and 5 for Class III YSOs.
estimates are listed in
Table 3 for Class II YSOs, and in Tables 4 and 5 for Class III YSOs.
Since the SED of an embedded Class II YSO peaks in the mid-IR
range,
the ISOCAM fluxes should be approximately valid tracers of the total,
bolometric luminosities (
![]() ).
To estimate
).
To estimate
![]() for weak Class II sources, an empirical approach
thus consists in using this
for weak Class II sources, an empirical approach
thus consists in using this
![]() -
-
![]() relationship
after proper calibration on a sub-sample of (brighter) objects for which the
luminosity can be derived by a more direct method.
This approach has been adopted by, e.g., Olofsson et al. (1999).
Here, we have used the
relationship
after proper calibration on a sub-sample of (brighter) objects for which the
luminosity can be derived by a more direct method.
This approach has been adopted by, e.g., Olofsson et al. (1999).
Here, we have used the
![]() estimates of Sect. 4.1 to check that
a correlation is actually present between
estimates of Sect. 4.1 to check that
a correlation is actually present between
![]() and the mid-IR
fluxes. Figure 5 displays
and the mid-IR
fluxes. Figure 5 displays
![]() (corrected for extinction)
as a function of
(corrected for extinction)
as a function of
![]() for the 104 Class II sources detected both in the near-IR and in the mid-IR range.
for the 104 Class II sources detected both in the near-IR and in the mid-IR range.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms9901f5new.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg158.gif) |
Figure 5:
Correlation between
|
| Open with DEXTER | |
A correlation is found, showing that, despite some scatter, the ISOCAM fluxes can be used to give rough estimates of the stellar luminosities of Class II YSOs. This is useful for the few ISOCAM sources of our sample which have not been detected at near-IR wavelengths.
The mid-IR emission of Class II YSOs is usually interpreted as
arising from warm dust in an optically thick circumstellar disk.
Using a simplified disk model (e.g. Beckwith et al. 1990),
it is easy to show that any observed monochromatic flux in
the optically thick, power-law range of the disk SED
is simply proportional to the total disk luminosity
![]() divided by the projection factor cos(i), where i is the
disk inclination angle to the line of sight.
In the Beckwith et al. (1990) model, the disk is parameterized by a power-law
temperature profile with three free parameters, T0, r0, and q,
such that:
divided by the projection factor cos(i), where i is the
disk inclination angle to the line of sight.
In the Beckwith et al. (1990) model, the disk is parameterized by a power-law
temperature profile with three free parameters, T0, r0, and q,
such that:
![]() .
Here, we have adopted
T0 = 1500 K, meaning that the disk inner radius
is at the dust sublimation temperature, and q=2/3, corresponding
to an IR spectral index
.
Here, we have adopted
T0 = 1500 K, meaning that the disk inner radius
is at the dust sublimation temperature, and q=2/3, corresponding
to an IR spectral index
![]() typical of CTTS spectra.
typical of CTTS spectra.
We must, however, account for the fact that the stellar emission
itself is not completely negligible
in the mid-IR bands, especially at 6.7 ![]() m.
A simple blackbody emission at
m.
A simple blackbody emission at
![]() K
gives
K
gives
| (5) | |||
| (6) |
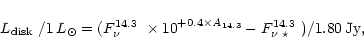 |
(7) |
According to this model, the mid-IR flux is a direct tracer of the
disk luminosity, and the
![]() correlation
of Fig. 5 simply expresses that
correlation
of Fig. 5 simply expresses that
![]() correlates with
correlates with
![]() .
The origin of
.
The origin of
![]() is either the release of gravitational
energy by accretion in the disk,
or the absorption/reprocessing of stellar photons by the dusty disk.
In the latter case,
is either the release of gravitational
energy by accretion in the disk,
or the absorption/reprocessing of stellar photons by the dusty disk.
In the latter case,
![]() is naturally proportional to
is naturally proportional to
![]() .
The fraction
.
The fraction
![]() of stellar luminosity reprocessed by the disk
depends on the spatial distribution of dust.
In the ideal case of an infinite, spatially flat
disk, this fraction is 0.25 (Adams & Shu 1986). If the disk is
flared,
of stellar luminosity reprocessed by the disk
depends on the spatial distribution of dust.
In the ideal case of an infinite, spatially flat
disk, this fraction is 0.25 (Adams & Shu 1986). If the disk is
flared,
![]() is larger, while it is smaller if the disk has a inner hole.
The theoretical
is larger, while it is smaller if the disk has a inner hole.
The theoretical
![]() correlations
plotted in Fig. 5 correspond to
correlations
plotted in Fig. 5 correspond to
![]() and to three
representative inclination angles.
The fact that this simple
model accounts for the
observed correlation quite well,
suggests that the disks of most
and to three
representative inclination angles.
The fact that this simple
model accounts for the
observed correlation quite well,
suggests that the disks of most
![]() Class II YSOs are passive disks
dominated by reprocessing.
This is consistent with recent estimates of the disk accretion level
in Taurus CTTSs (e.g. Gullbring et al. 1998).
The typical disk accretion rate of a CTTS is estimated to be
Class II YSOs are passive disks
dominated by reprocessing.
This is consistent with recent estimates of the disk accretion level
in Taurus CTTSs (e.g. Gullbring et al. 1998).
The typical disk accretion rate of a CTTS is estimated to be
![]() yr, corresponding to an accretion luminosity
yr, corresponding to an accretion luminosity
![]() for
for
![]() and
and
![]() (i.e.,
(i.e.,
![]() at 1
at 1![]() Myr).
In this case, the luminosity due to reprocessing is
Myr).
In this case, the luminosity due to reprocessing is ![]() 5 times
larger than the accretion luminosity in the disk.
5 times
larger than the accretion luminosity in the disk.
On the other hand, 37 sources (among a total of 104) are located
above the passive disk model lines in Fig. 5.
These are good candidates for having an active disk with an accretion
rate typically larger than
![]() yr.
yr.
Overall, we find that the median
![]() ratio is 0.41 for the
93 Class II sources detected in the near-IR and
with
ratio is 0.41 for the
93 Class II sources detected in the near-IR and
with
![]() mJy (i.e. the completeness level derived in
Sect. 2.4).
Using this ratio, we have derived rough estimates of the
stellar luminosities of the 15 Class II YSOs which have no
near-IR photometry (see Table 3) as follows:
mJy (i.e. the completeness level derived in
Sect. 2.4).
Using this ratio, we have derived rough estimates of the
stellar luminosities of the 15 Class II YSOs which have no
near-IR photometry (see Table 3) as follows:
| (8) |
The most direct method of estimating the total
luminosities
![]() of embedded YSOs consists in integrating the
observed SEDs (cf. WLY89).
However, since most of the
of embedded YSOs consists in integrating the
observed SEDs (cf. WLY89).
However, since most of the ![]() Ophiuchi Class II and Class III YSOs
are deeply embedded within the cloud (
Ophiuchi Class II and Class III YSOs
are deeply embedded within the cloud (
![]() ), only
a negligible fraction of their bolometric luminosity can be recovered
by finite-beam IR observations (e.g. Comerón et al. 1993).
We thus do not attempt to derive calorimetric estimates of
), only
a negligible fraction of their bolometric luminosity can be recovered
by finite-beam IR observations (e.g. Comerón et al. 1993).
We thus do not attempt to derive calorimetric estimates of
![]() for these sources.
In contrast, the calorimetric method is believed to be appropriate
for Class I YSOs since these are self-embedded in substantial
amounts of circumstellar material which re-radiate locally
the absorbed luminosity (cf. WLY89 and AM94).
Using our new mid-IR measurements, we have evaluated
the calorimetric luminosities (
for these sources.
In contrast, the calorimetric method is believed to be appropriate
for Class I YSOs since these are self-embedded in substantial
amounts of circumstellar material which re-radiate locally
the absorbed luminosity (cf. WLY89 and AM94).
Using our new mid-IR measurements, we have evaluated
the calorimetric luminosities (
![]() )
of the 16 Class I YSOs
observed in our survey.
Only 7 of them have reliable IRAS fluxes
up to 60 or 100
)
of the 16 Class I YSOs
observed in our survey.
Only 7 of them have reliable IRAS fluxes
up to 60 or 100 ![]() m (IRS54, IRS44, GSS30, IRS43, EL29, IRS48,
IRS51). For these, the median of the ratio of
m (IRS54, IRS44, GSS30, IRS43, EL29, IRS48,
IRS51). For these, the median of the ratio of
![]() (6.7-14.3
(6.7-14.3 ![]() m)
to
m)
to
![]() is found to be 9.8, suggesting that the typical fraction of a
Class I source's luminosity radiated between 6.7
and 14.3
is found to be 9.8, suggesting that the typical fraction of a
Class I source's luminosity radiated between 6.7
and 14.3 ![]() m is
m is ![]() 10%.
Assuming that this ratio is representative of all Class I YSOs,
we have derived estimates of
10%.
Assuming that this ratio is representative of all Class I YSOs,
we have derived estimates of
![]() for the
remaining 9 weaker Class I sources (i.e., CRBR85, LFAM26, LFAM1, WL12, IRS46,
CRBR12, IRS67, CRBR42, WL6). These luminosities are listed in Table 2.
for the
remaining 9 weaker Class I sources (i.e., CRBR85, LFAM26, LFAM1, WL12, IRS46,
CRBR12, IRS67, CRBR42, WL6). These luminosities are listed in Table 2.
Combining the
![]() luminosities determined in Sect. 4.1 for the
sources detected in the near-IR with the
luminosities determined in Sect. 4.1 for the
sources detected in the near-IR with the
![]() estimates from
estimates from
![]() for the sources without near-IR measurements (Sect. 4.2),
we have built a luminosity function for Class II YSOs which represents
a major improvement over previous studies (see Fig. 6a).
In terms of
for the sources without near-IR measurements (Sect. 4.2),
we have built a luminosity function for Class II YSOs which represents
a major improvement over previous studies (see Fig. 6a).
In terms of
![]() ,
the completeness level for this population
can be estimated from the
,
the completeness level for this population
can be estimated from the
![]() completeness limit
derived in Sect. 2.4 (
completeness limit
derived in Sect. 2.4 (
![]() mJy)
using Eq. (8):
mJy)
using Eq. (8):
![]() .
While the luminosity function previously published by
Greene et al. (1994) included only 33 (bright) Class II sources
and suffered from severe incompleteness below
.
While the luminosity function previously published by
Greene et al. (1994) included only 33 (bright) Class II sources
and suffered from severe incompleteness below
![]() ,
our present completeness level
is a factor
,
our present completeness level
is a factor ![]() 30-50 lower.
The new luminosity function shows a marked flattening
in logarithmic units at
30-50 lower.
The new luminosity function shows a marked flattening
in logarithmic units at
![]() ,
well above our completeness limit.
This important new feature is discussed in Sect. 5 below.
,
well above our completeness limit.
This important new feature is discussed in Sect. 5 below.
![\begin{figure}
\mbox{\includegraphics[width=8.9cm,clip]{ms9901f6a.eps}\includegraphics[width=5.8cm]{ms9901f6b.eps} }\end{figure}](/articles/aa/full/2001/22/aa9901/Timg187.gif) |
Figure 6:
Luminosity functions (LF) a) for the 123 Class II YSOs
(continuous histogram with statistical
error bars).
The function corresponding to a similar histogram
shifted by half the 0.2 dex bin size
is shown as a thin curve to illustrate the level of
statistical fluctuations due to binning.
The LF of 33 Class II sources from Greene et al. (1994)
is displayed as a darker histogram
(rebinned to 0.2 dex bins, and rescaled to d=140 pc
for better comparison with the new LF).
The typical
|
| Open with DEXTER | |
Based on the
![]() estimates of Sect. 4.3,
a new bolometric luminosity function for the
16 Class I YSOs of
estimates of Sect. 4.3,
a new bolometric luminosity function for the
16 Class I YSOs of
![]() is displayed in Fig. 6b.
The associated completeness level is
derived from
is displayed in Fig. 6b.
The associated completeness level is
derived from
![]() mJy and
mJy and
![]() mJy (Sect. 2.4)
using
mJy (Sect. 2.4)
using
![]() (6.7-14.3
(6.7-14.3 ![]() m)
m)
![]() (Sect. 4.3):
(Sect. 4.3):
![]() .
The median
.
The median
![]() for Class I YSOs
is
for Class I YSOs
is
![]() ,
which is
,
which is ![]() 8 times larger
than the median
8 times larger
than the median
![]() of Class II YSOs (
of Class II YSOs (
![]() ).
The luminosities of Class I YSOs span a range of two orders of magnitude
between
).
The luminosities of Class I YSOs span a range of two orders of magnitude
between ![]() 0.1
0.1![]() and
and ![]() 10
10![]() ,
which is roughly as wide as
the luminosity range spanned by Class II YSOs.
The comparatively large value of
,
which is roughly as wide as
the luminosity range spanned by Class II YSOs.
The comparatively large value of
![]() for Class I YSOs is probably
due to a dominant contribution of accretion luminosity
as expected in the case of protostars.
for Class I YSOs is probably
due to a dominant contribution of accretion luminosity
as expected in the case of protostars.
In Fig. 6c, we plot the luminosity function of
the 55 Class III sources that are located within the CS contours
of Fig. 1 and for which we have enough near-IR data
to derive
![]() according to the procedure described in Sect. 4.1.
This sample comprises 19 confirmed Class IIIs from Table 4 together
with 36 candidate Class III sources from Table 5.
It might be contaminated by a few background/foreground sources but
is characterized by a relatively well defined completeness luminosity.
From the completeness level
according to the procedure described in Sect. 4.1.
This sample comprises 19 confirmed Class IIIs from Table 4 together
with 36 candidate Class III sources from Table 5.
It might be contaminated by a few background/foreground sources but
is characterized by a relatively well defined completeness luminosity.
From the completeness level
![]() mJy
and using Eq. (5) with an average extinction
correction corresponding to AV = 17 mag, we get
mJy
and using Eq. (5) with an average extinction
correction corresponding to AV = 17 mag, we get
![]() ,
which is
,
which is ![]() 6 times higher than
6 times higher than
![]() .
Deep X-ray observations with XMM
should improve the completeness luminosity for Class III YSOs
by an order of magnitude in the near future (cf. discussion by Grosso et al. 2000
in a companion paper).
.
Deep X-ray observations with XMM
should improve the completeness luminosity for Class III YSOs
by an order of magnitude in the near future (cf. discussion by Grosso et al. 2000
in a companion paper).
If the mass-luminosity relationship of PMS stars were a simple,
fixed power-law function, the shape of the luminosity function
would directly reflect the underlying mass function.
Unfortunately, the mass-luminosity relation
is a complex function with inflexion points and is strongly
age-dependent. Deriving the mass function from the luminosity function
thus requires knowledge of the stellar age distribution.
The
![]() embedded cluster is believed to be
younger than most known star clusters (e.g. Luhman & Rieke 1999),
with a typical age on the order of, or less than, 1 Myr
(e.g. WLY89, Greene & Meyer 1995).
embedded cluster is believed to be
younger than most known star clusters (e.g. Luhman & Rieke 1999),
with a typical age on the order of, or less than, 1 Myr
(e.g. WLY89, Greene & Meyer 1995).
The 123 Class II sources identified with ISOCAM are presently
the most complete sample of young stars available in
the cluster.
The corresponding mass function is estimated down to
![]() in Sect. 5.1.
We investigate
the effect of including Class III YSOs by modeling the luminosity function of
the 135 Class II and Class III objects located inside the CS contours
of Fig. 1 (Sect. 5.3).
in Sect. 5.1.
We investigate
the effect of including Class III YSOs by modeling the luminosity function of
the 135 Class II and Class III objects located inside the CS contours
of Fig. 1 (Sect. 5.3).
![\begin{figure}
\par\includegraphics[width=13cm,clip]{ms9901f7.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg198.gif) |
Figure 7: Best model fits (heavy curves) to the luminosity function of Class II sources obtained for a stellar age distribution corresponding to a constant formation rate over a) 0.5 Myr, b) 1 Myr, and c) 2 Myr (the first 0.2 Myr have been avoided in the PMS tracks to account for a typical protostellar timescale). In d), similar best fits are shown for the combined luminosity function of 135 Class II and Class III sources inside the CS contours of Fig. 1. The vertical dashed lines show the completeness levels of the respective luminosity functions (see Fig. 6). |
| Open with DEXTER | |
We have modeled the observed luminosity function using a two-segment
power-law mass function with two free parameters,
![]() and
and ![]() :
dN/d
:
dN/d![]() log
log
![]() for
for
![]() ,
and dN/d
,
and dN/d![]() log
log
![]() for
for
![]() .
The high-mass range (for
.
The high-mass range (for
![]() )
is simply taken to be a power-law with index
-1.7 (whereas the Salpeter index would be -1.35), in agreement with
the IMFs favored by Kroupa et al. (1993) and Scalo (1998).
We assume that the cluster forms stars with a fixed IMF, independent of
time. The evolutionary tracks of D'Antona & Mazzitelli
(1998)
)
is simply taken to be a power-law with index
-1.7 (whereas the Salpeter index would be -1.35), in agreement with
the IMFs favored by Kroupa et al. (1993) and Scalo (1998).
We assume that the cluster forms stars with a fixed IMF, independent of
time. The evolutionary tracks of D'Antona & Mazzitelli
(1998)![]() are used to derive a set of mass-luminosity relations adapted to the
are used to derive a set of mass-luminosity relations adapted to the
![]() PMS population, under the following three hypotheses about the star
formation history:
Constant star formation rate over a) 0.5 Myr (Fig. 7a),
b) 1 Myr (Fig. 7b), and c) 2 Myr (Fig. 7c).
Cases b) and c) correspond to the simplest scenarios consistent with
current observational constraints (e.g. WLY89). Case a) mimics a recent
"burst'' of star formation suggested by recent
studies (e.g. Greene & Meyer 1995; Luhman & Rieke 1999).
These three scenarios are roughly representative of our current (imperfect)
knowledge of the stellar age distribution in the cluster.
PMS population, under the following three hypotheses about the star
formation history:
Constant star formation rate over a) 0.5 Myr (Fig. 7a),
b) 1 Myr (Fig. 7b), and c) 2 Myr (Fig. 7c).
Cases b) and c) correspond to the simplest scenarios consistent with
current observational constraints (e.g. WLY89). Case a) mimics a recent
"burst'' of star formation suggested by recent
studies (e.g. Greene & Meyer 1995; Luhman & Rieke 1999).
These three scenarios are roughly representative of our current (imperfect)
knowledge of the stellar age distribution in the cluster.
The fitting analysis is performed on the 12 (logarithmic) luminosity bins
above the completeness level of 0.032![]() and below
and below
![]() by varying
by varying ![]() and
and
![]() .
Due to the age ambiguity for a
particular (
.
Due to the age ambiguity for a
particular (
![]() ,
,
![]() )
in the PMS tracks for
)
in the PMS tracks for
![]() and
and
![]() Myr as a result of
the transition from convective to radiative interiors (e.g.
Fig. 4), our simplified modeling is not valid for
Myr as a result of
the transition from convective to radiative interiors (e.g.
Fig. 4), our simplified modeling is not valid for
![]() .
The best fit is shown as a heavy curve
for each of the three assumed age distributions (Figs. 7a-c).
The flattening of the luminosity function below
.
The best fit is shown as a heavy curve
for each of the three assumed age distributions (Figs. 7a-c).
The flattening of the luminosity function below
![]() is well
reproduced in all three cases.
The best-fit model in the 1 Myr case (Fig. 7b) is however not quite as
good as the two others since it predicts a peak at
is well
reproduced in all three cases.
The best-fit model in the 1 Myr case (Fig. 7b) is however not quite as
good as the two others since it predicts a peak at
![]() where the data show a dip. This is reflected
by the largest value 1.41 for the reduced
where the data show a dip. This is reflected
by the largest value 1.41 for the reduced
![]() (with N=12 fitted data points and
n=2 free parameters).
The model of Fig. 7c reproduces the data somewhat better
(
(with N=12 fitted data points and
n=2 free parameters).
The model of Fig. 7c reproduces the data somewhat better
(
![]() )
as the predicted peak luminosity
moves down to
)
as the predicted peak luminosity
moves down to
![]() .
A marginally better fit is obtained with the 0.5 Myr model
(Fig. 7a,
.
A marginally better fit is obtained with the 0.5 Myr model
(Fig. 7a,
![]() ).
In this case, the model luminosity function has a local maximum
at
).
In this case, the model luminosity function has a local maximum
at
![]() as observed and the flattening for
as observed and the flattening for
![]() is particulary well reproduced.
is particulary well reproduced.
The best-fit values of
![]() along with the formal
along with the formal ![]() errors resulting from the fitting procedure are as follows:
errors resulting from the fitting procedure are as follows:
![]() ,
,
![]() ,
and
,
and
![]() for Figs. 7a-c, respectively.
These
for Figs. 7a-c, respectively.
These
![]() values follow the expected trend that the older the stars,
the higher the derived masses for the same luminosities.
The final error on the determination of
values follow the expected trend that the older the stars,
the higher the derived masses for the same luminosities.
The final error on the determination of
![]() is clearly dominated by the
uncertainties on the stellar age distribution.
We adopt the following average value:
is clearly dominated by the
uncertainties on the stellar age distribution.
We adopt the following average value:
![]() .
The best-fit values for
.
The best-fit values for ![]() are
are
![]() ,
,
![]() ,
and
,
and
![]() ,
respectively. There is no correlation with age in this
case. We conservatively adopt
,
respectively. There is no correlation with age in this
case. We conservatively adopt
![]() .
These constraints on the mass function are valid for
.
These constraints on the mass function are valid for
![]() ,
which approximately corresponds to
,
which approximately corresponds to
![]() .
.
Under the same three assumptions about the stellar age distribution as
above, we have also derived a range of stellar masses directly from the
MJ magnitude for each of the 123 Class II YSOs. We display the results
as a mass function in Fig. 8, where the vertical error bars reflect the
uncertainties induced by the various age assumptions rather than the
statistical errors.
The best two-component power-law mass function derived above
is superposed as a heavy curve.
The error bars are particulary large for the two mass bins close to 1
![]() ,
i.e., just above
,
i.e., just above
![]() .
This is due to a shift of a large number of stars beyond
.
This is due to a shift of a large number of stars beyond
![]() when the stellar ages are varied upward.
The global shape of the mass function is however fairly
well determined: It is basically flat (in logarithmic units)
at low masses down to 0.055
when the stellar ages are varied upward.
The global shape of the mass function is however fairly
well determined: It is basically flat (in logarithmic units)
at low masses down to 0.055
![]() and shows a steep decline beyond
and shows a steep decline beyond
![]() 0.5
0.5
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.0cm,clip]{ms9901f8.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg229.gif) |
Figure 8:
Mass function of the 123 Class II YSOs.
The range of possible age distributions
(see Sect. 5.1) induces a range of masses for each star and thus
an uncertainty on the derived histogram displayed as vertical
error bars. The best two-segment power-law mass function of
Sect. 5.1 (heavy solid curve), and the effect of
binarity as a function of the binary fraction from 50% to 100%
(light curves - see Sect. 6.2) are shown.
The vertical dashed line marks the completeness level of
|
| Open with DEXTER | |
Some of the features (peaks and dips) apparent in the observed
luminosity function might be real as they are also predicted by the models
(see Fig. 7).
The feature expected in the luminosity function
of young stars as a result of
deuterium burning during PMS contraction is particularly interesting
since its location is age-dependent
(e.g. Zinnecker et al. 1993).
As already noted, the model fit obtained under the 0.5 Myr scenario
is particularly good
as it predicts a peak at
![]() ,
consistent with the
observations (see Fig. 7a).
In the model, this
,
consistent with the
observations (see Fig. 7a).
In the model, this
![]() peak corresponds to an inflexion point in
the mass-luminosity relation due to deuterium
burning in
peak corresponds to an inflexion point in
the mass-luminosity relation due to deuterium
burning in ![]() 0.4-Myr old stars with
0.4-Myr old stars with
![]() .
If this peak in the luminosity function is confirmed,
it will provide strong evidence that the population of Class II YSOs
is particularly young in
.
If this peak in the luminosity function is confirmed,
it will provide strong evidence that the population of Class II YSOs
is particularly young in
![]() .
.
There is most probably a significant population of Class III objects
embedded in the cloud (e.g. Sect. 3.5). To evaluate how the
presence of this population may affect our conclusions
on the IMF of the cluster (see Sect. 6 below), we
here consider the luminosity function of a combined sample of Class II
and Class III sources. The sample comprises the 80 Class II and 55 Class III
YSOs located inside the CS contours of Fig. 1. It should be complete
down to ![]() 0.2
0.2![]() .
(Note, however,
that only 19 of the 55 Class III sources of this sample
are confirmed YSOs at this stage - see Sect. 4.4.)
The associated luminosity function, displayed in Fig. 7d,
is very similar to the luminosity function of Class II YSOs.
In particular, it exhibits a flattening below
.
(Note, however,
that only 19 of the 55 Class III sources of this sample
are confirmed YSOs at this stage - see Sect. 4.4.)
The associated luminosity function, displayed in Fig. 7d,
is very similar to the luminosity function of Class II YSOs.
In particular, it exhibits a flattening below ![]()
![]() .
.
The results of a modeling similar to that of Sect. 5.1, but performed
on only 8 luminosity bins between 0.2 and 10![]() ,
are
shown in Fig. 7d. The best fits found under the same three star
formation scenarios as in Sect. 5.1 are good (with
,
are
shown in Fig. 7d. The best fits found under the same three star
formation scenarios as in Sect. 5.1 are good (with
![]() ,
0.94,
and 1.15, respectively).
The best-fit values for the parameters
,
0.94,
and 1.15, respectively).
The best-fit values for the parameters
![]() and
and ![]() of the mass function are as follows:
of the mass function are as follows:
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() ,
,
![]() ,
,
![]() for star formation durations of 0.5, 1, and 2 Myr,
respectively. Combining these results, we obtain
for star formation durations of 0.5, 1, and 2 Myr,
respectively. Combining these results, we obtain
![]() and
and
![]() .
Within the uncertainties these values are essentially identical to those found
in Sect. 5.1 for the sample of Class II YSOs, although they apply to a more
limited mass range, approximately
.
Within the uncertainties these values are essentially identical to those found
in Sect. 5.1 for the sample of Class II YSOs, although they apply to a more
limited mass range, approximately
![]() .
.
In contrast to the Class II case, the luminosity function of the
Class II-Class III combined sample does not show a peak at
![]() (cf. Fig. 7d).
This may be understood if the average stellar age of the combined population
is somewhat larger than that of the population of Class II sources
(as is expected).
(cf. Fig. 7d).
This may be understood if the average stellar age of the combined population
is somewhat larger than that of the population of Class II sources
(as is expected).
Since the
![]() molecular cloud is still actively forming stars,
the final IMF of the cluster cannot be directly measured.
The masses of the stars already formed
in the cluster
provide only a "snapshot'' of the local IMF (cf. Meyer et al.
2000).
However, assuming that the mass distribution of formed stars does not
change significantly with time during the cluster's history
(an assumption made in the models of Sect. 5.1), any
snapshot of the mass distribution taken on a large, complete population of
PMS objects should accurately reflect the end-product IMF.
molecular cloud is still actively forming stars,
the final IMF of the cluster cannot be directly measured.
The masses of the stars already formed
in the cluster
provide only a "snapshot'' of the local IMF (cf. Meyer et al.
2000).
However, assuming that the mass distribution of formed stars does not
change significantly with time during the cluster's history
(an assumption made in the models of Sect. 5.1), any
snapshot of the mass distribution taken on a large, complete population of
PMS objects should accurately reflect the end-product IMF.
Compared to previous investigations of the IMF
in the
![]() cloud based exclusively on
near-IR data (e.g. Comerón et al. 1993;
Strom et al. 1995; Williams et al. 1995;
Luhman & Rieke 1999),
the use of mid-IR photometry
has allowed us to consider a much larger sample of young stars
(see, e.g., Fig. 6).
Since our sub-sample of Class II YSOs is fairly large (123 objects)
and complete
down to low luminosities, it provides an excellent opportunity to derive
improved constraints on the
cloud based exclusively on
near-IR data (e.g. Comerón et al. 1993;
Strom et al. 1995; Williams et al. 1995;
Luhman & Rieke 1999),
the use of mid-IR photometry
has allowed us to consider a much larger sample of young stars
(see, e.g., Fig. 6).
Since our sub-sample of Class II YSOs is fairly large (123 objects)
and complete
down to low luminosities, it provides an excellent opportunity to derive
improved constraints on the
![]() IMF down to low masses.
IMF down to low masses.
In a statistical sense at least,
Class II YSOs are believed to represent a specific
phase of PMS evolution which follows the (Class 0 and Class I)
protostellar phases, and precedes the Class III phase (see
Sect. 1). Due to their short lifetime (
![]()
![]() yr), protostars make up
only a small fraction of a young cluster's population
(cf. Fletcher & Stahler 1994), and can be neglected in the global
mass function. Furthermore, in contrast to PMS stars, protostars
have not yet reached their final stellar masses.
yr), protostars make up
only a small fraction of a young cluster's population
(cf. Fletcher & Stahler 1994), and can be neglected in the global
mass function. Furthermore, in contrast to PMS stars, protostars
have not yet reached their final stellar masses.
Class III objects are more numerous and should thus contribute significantly
to the global mass distribution. Furthermore, it has been suggested that
some YSOs evolve quickly to the Class III stage, perhaps as early as the
"birthline'' for PMS stars (e.g. Stahler & Walter 1993),
and spend virtually no time in the Class II phase
(cf. André et al. 1992; Greene & Meyer 1995). Since such objects cannot be
identified through IR observations, their exact number and mass distribution
will not be known until the results of deep X-ray (and follow-up) surveys are
available (see Sect. 3.5).
However, providing the (range of) evolutionary timescale(s)
from Class II to Class III is independent of mass, both
classes of PMS objects should have identical mass functions.
The results of Sect. 5.3 do seem to support this view, as they suggest
that the mass functions of the Class II and Class III samples
do not differ down to
![]() .
.
We therefore conclude (and will assume in the following)
that the mass distribution of Class II YSOs
determined in Sect. 5.1 and shown in Fig. 8 currently represents our best
estimate of the IMF in the
![]() embedded cluster down to
embedded cluster down to
![]() .
As discussed in Sect. 6.2 below, this mass
function applies to stellar systems rather than single stars.
.
As discussed in Sect. 6.2 below, this mass
function applies to stellar systems rather than single stars.
A large proportion (
![]() 50%) of field stars are in fact multiple
(e.g. binary) systems (e.g. Duquennoy & Mayor 1991).
This is also true for young PMS stars, and there is a growing body
of evidence that the binary fraction is even larger in a young PMS cluster
like
50%) of field stars are in fact multiple
(e.g. binary) systems (e.g. Duquennoy & Mayor 1991).
This is also true for young PMS stars, and there is a growing body
of evidence that the binary fraction is even larger in a young PMS cluster
like
![]() than for main sequence stars in the field
(e.g. Leinert et al. 1993; Simon et al. 1995).
Since the present study is based on ISOCAM/near-IR observations which
do not have enough angular resolution to separate most of the expected
binaries, a significant population of low-mass stellar companions
are presumably missing from the mass function derived above.
These low-mass companions are hidden by the corresponding primaries.
than for main sequence stars in the field
(e.g. Leinert et al. 1993; Simon et al. 1995).
Since the present study is based on ISOCAM/near-IR observations which
do not have enough angular resolution to separate most of the expected
binaries, a significant population of low-mass stellar companions
are presumably missing from the mass function derived above.
These low-mass companions are hidden by the corresponding primaries.
To estimate the magnitude of this binary effect, we show three simple
models in Fig. 8 which assume a population of hidden secondaries
corresponding to a
binary fraction f of 50%, 75%, and 100%, respectively.
In each case, we start from a primary mass function
with the two-segment power law form
derived in Sect. 5.1. We then add a population
of secondaries with
masses distributed uniformly (in logarithmic units) between a minimum mass
of
![]() and the mass of the primary.
We thus assume that the
component masses are uncorrelated and drawn from essentially the same
mass function (cf. Kroupa et al. 1993).
and the mass of the primary.
We thus assume that the
component masses are uncorrelated and drawn from essentially the same
mass function (cf. Kroupa et al. 1993).
The global mass functions resulting from addition of companions to
the primary mass function are shown in Fig. 8.
It can be seen that the global mass functions are similar
in form to the original primary mass function.
Neither the position of the break point (
![]() )
nor the slope in the
high-mass range are affected by the addition of companions.
However, the slope in the low-mass range (
)
nor the slope in the
high-mass range are affected by the addition of companions.
However, the slope in the low-mass range (![]() )
steepens as the
binary fraction increases. Indeed, the power-law index between
)
steepens as the
binary fraction increases. Indeed, the power-law index between
![]() and
and
![]() changes from
changes from
![]() to
to
![]() for
for ![]() ,
,
![]() for
for ![]() ,
and
,
and
![]() for
for ![]() .
.
In summary, if we account for uncertainties in
the binary fraction (
![]() ), our
best estimate of the single-star mass function in
), our
best estimate of the single-star mass function in
![]() is
well described by a two-segment power-law with a
low-mass index
is
well described by a two-segment power-law with a
low-mass index
![]() down to
down to
![]() ,
a high-mass index
,
a high-mass index
![]() ,
and a
break (flattening) occurring at
,
and a
break (flattening) occurring at
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9901f9.eps}
\par\end{figure}](/articles/aa/full/2001/22/aa9901/Timg262.gif) |
Figure 9: Individual luminosity functions for the four sub-clusters associated with the dense cores Oph A, Oph B, Oph EF, and L1689S (see Fig. 1). These are displayed with 0.4 dex bins and scaled by a factor 1/2 for direct comparison with the 0.2 dex bin total luminosity function (light grey histogram in the background). The light solid curves correspond to the model of Fig. 7a scaled to the number of stars in each sub-cluster. |
| Open with DEXTER | |
Our sample of Class II YSOs is large enough
that we can study the properties of the four sub-clusters
associated with the dense cores Oph A, Oph B, Oph EF,
and L1689S (see Fig. 1). All 123 Class II sources but 5 belong to
these 4 sub-clusters.
The luminosity functions of Class II objects in the individual sub-clusters
are displayed in Fig. 9 along with the "best-fit'' model of Sect. 5.1
(solid curve). They all agree reasonably well in shape with both the total luminosity
function and the model: all four luminosity functions are essentially flat
over two orders of magnitude in luminosity and appear to have a peak at
![]() .
The agreement is particularly good for the sub-cluster with the largest
number of stars, Oph A (see Fig. 9a), but even the smallest sub-cluster,
L1689S, tends to reproduce the shape of the global luminosity function
on a smaller scale (Fig. 9d).
In contrast, for instance,
the luminosity function derived for the Chamaeleon I cloud based on
ISOCAM data (Persi et al. 2000) differs markedly from
the
.
The agreement is particularly good for the sub-cluster with the largest
number of stars, Oph A (see Fig. 9a), but even the smallest sub-cluster,
L1689S, tends to reproduce the shape of the global luminosity function
on a smaller scale (Fig. 9d).
In contrast, for instance,
the luminosity function derived for the Chamaeleon I cloud based on
ISOCAM data (Persi et al. 2000) differs markedly from
the
![]() luminosity functions. It does not exhibit any peak
at 1.5
luminosity functions. It does not exhibit any peak
at 1.5![]() and is consistent with an older (
and is consistent with an older (![]() 3 Myr)
PMS population having a similar underlying mass function (see
Kaas & Bontemps 2001).
3 Myr)
PMS population having a similar underlying mass function (see
Kaas & Bontemps 2001).
The similarity of the individual luminosity functions suggests similar distributions of stellar ages and stellar masses in each of the four sub-clusters.
After correction for unresolved binaries (assuming a binary
fraction ![]() ), the total number of Class II sources (including
companions) down to 0.055
), the total number of Class II sources (including
companions) down to 0.055
![]() is
is ![]() 145.
Assuming a Class III to Class II number ratio of 19/22 as found by X-ray
surveys (Grosso et al. 2000
- see Sect. 3.5), we infer the presence of
145.
Assuming a Class III to Class II number ratio of 19/22 as found by X-ray
surveys (Grosso et al. 2000
- see Sect. 3.5), we infer the presence of ![]() 125 Class III stars
(including associated companions) in the
same mass range.
The typical number ratio of Class Is (plus Class 0s) to Class IIs is
18/123 suggesting an additional
125 Class III stars
(including associated companions) in the
same mass range.
The typical number ratio of Class Is (plus Class 0s) to Class IIs is
18/123 suggesting an additional ![]() 21 embedded YSOs.
Altogether, we therefore estimate that there are currently
21 embedded YSOs.
Altogether, we therefore estimate that there are currently
![]() YSOs
down to
YSOs
down to ![]()
![]() including
including ![]() 19% of brown dwarfs.
The average and median masses of these objects are
19% of brown dwarfs.
The average and median masses of these objects are ![]()
![]() and
and ![]()
![]() respectively.
The total mass of condensed objects (including brown dwarfs) in
the cluster is thus estimated to be
respectively.
The total mass of condensed objects (including brown dwarfs) in
the cluster is thus estimated to be
![]() .
(The brown dwarfs with
.
(The brown dwarfs with
![]() contribute only
contribute only
![]()
![]() of this mass.)
Restricting ourselves to L1688 (thus subtracting the
of this mass.)
Restricting ourselves to L1688 (thus subtracting the
![]()
![]() contribution from L1689) whose average radius is approximately
0.4 pc (cf. CS contours in Fig. 1), we find
contribution from L1689) whose average radius is approximately
0.4 pc (cf. CS contours in Fig. 1), we find
![]() ,
,
![]() ,
,
![]() stars/pc3, and
stars/pc3, and
![]() /pc3, where
/pc3, where ![]() and
and
![]() are the stellar number density and stellar mass (volume) density
of the cluster, respectively.
are the stellar number density and stellar mass (volume) density
of the cluster, respectively.
Adopting a conservative value of 2 Myr for the cluster age, the total
mass of
![]() translates into
an average star formation rate of
translates into
an average star formation rate of
![]() yr, corresponding to
one new YSO (of typical mass 0.20
yr, corresponding to
one new YSO (of typical mass 0.20
![]() )
every
)
every ![]() 4000 yr.
Lastly, we can derive the star formation efficiency (SFE)
in L1688, defined as SFE
4000 yr.
Lastly, we can derive the star formation efficiency (SFE)
in L1688, defined as SFE
![]() .
The total molecular gas
mass,
.
The total molecular gas
mass,
![]() ,
of L1688 has been estimated to range between
,
of L1688 has been estimated to range between
![]() (from C18O measurements - Wilking & Lada 1983) and
(from C18O measurements - Wilking & Lada 1983) and
![]() (from CS(2-1) data - Liseau et al. 1995).
Using
(from CS(2-1) data - Liseau et al. 1995).
Using
![]() ,
we thus get
SFE
,
we thus get
SFE
![]() %, which is somewhat lower than
previous estimates (
%, which is somewhat lower than
previous estimates (![]()
![]() - WLY89).
Note, however, that active star formation in L1688 appears to be limited to
the three sub-clusters/dense cores Oph A, Oph EF, and Oph B (see Fig. 1 and
Loren et al. 1990), where the local star formation efficiency
is significantly higher:
- WLY89).
Note, however, that active star formation in L1688 appears to be limited to
the three sub-clusters/dense cores Oph A, Oph EF, and Oph B (see Fig. 1 and
Loren et al. 1990), where the local star formation efficiency
is significantly higher:
![]() ,
using a total core mass of
,
using a total core mass of
![]() (Loren et al. 1990).
(Loren et al. 1990).
![\begin{figure}
\par\includegraphics[width=8.0cm,clip]{ms9901f10.eps}
\end{figure}](/articles/aa/full/2001/22/aa9901/Timg288.gif) |
Figure 10: Comparison of the pre-stellar mass spectrum measured by MAN98 for 58 protocluster condensations (dark histogram with statistical error bars) with the YSO mass function derived in Sect. 5.1 for 123 Class II systems (light histogram with error bars accounting for both statistical and age uncertainties). |
| Open with DEXTER | |
In an extensive 1.3![]() mm dust continuum imaging survey of L1688
with the IRAM 30 m
telescope (11
mm dust continuum imaging survey of L1688
with the IRAM 30 m
telescope (11
![]() resolution),
MAN98 could identify 58
compact starless condensations.
Molecular line observations (e.g. Belloche et al. 2001) indicate that the condensations are
gravitationally bound and thus likely pre-stellar in nature.
MAN98 noted a remarkable similarity between the mass spectrum of these
pre-stellar condensations and the IMF of Miller & Scalo (1979).
resolution),
MAN98 could identify 58
compact starless condensations.
Molecular line observations (e.g. Belloche et al. 2001) indicate that the condensations are
gravitationally bound and thus likely pre-stellar in nature.
MAN98 noted a remarkable similarity between the mass spectrum of these
pre-stellar condensations and the IMF of Miller & Scalo (1979).
In Fig. 10, we compare the pre-stellar mass spectrum determined
by MAN98 with the mass distribution of Class II YSOs
derived in Sect. 5.1. (As such, both distributions are uncorrected for the
presence of close binary systems.)
It can be seen that there is a good agreement
in shape between the two mass spectra.
A Kolmogorov-Smirnov test performed on the corresponding
cumulative distributions confirms that they are statistically
indistinguishable at the 95% confidence level.
This supports the suggestion of MAN98 that the IMF of
embedded clusters is primarily determined by cloud fragmentation at the
pre-stellar stage of star formation.
The fact that both the pre-stellar and the YSO spectrum
of Fig. 10 present a break at roughly the same mass ![]()
![]() is quite remarkable. A small, global shift of the masses by only
is quite remarkable. A small, global shift of the masses by only
![]() 30% upward or downward in one of the spectra would make
them differ at the 2
30% upward or downward in one of the spectra would make
them differ at the 2![]() statistical level. Although in absolute
terms, both sets of masses are probably uncertain by a factor of
statistical level. Although in absolute
terms, both sets of masses are probably uncertain by a factor of ![]() 2
(due to uncertainties in the 1.3
2
(due to uncertainties in the 1.3![]() mm dust opacity and in the cluster
age, respectively), this suggests that the protocluster
condensations identified at 1.3
mm dust opacity and in the cluster
age, respectively), this suggests that the protocluster
condensations identified at 1.3![]() mm may form stars/systems with an
efficiency larger than
mm may form stars/systems with an
efficiency larger than ![]() 50-70%.
50-70%.
We have used ISOCAM to survey the
![]() main cloud for embedded YSOs
down to a completeness level of
main cloud for embedded YSOs
down to a completeness level of ![]() 10-15 mJy at 6.7
10-15 mJy at 6.7![]() m
and 14.3
m
and 14.3![]() m. Our main findings are as follows:
m. Our main findings are as follows:
Acknowledgements
S.B. was supported by an ESA Research Fellowship during his stay at the Stockholm Observatory. The authors thank the referee, Andrea Moneti, for constructive criticisms.