

Up: Measurement of several transition
4 Results and conclusions
Once an Aki-value has been obtained for each line and at
each instant where this line was measured, plots representing all
these values along the plasma life have been made. One of them,
showing the measured transitions probabilities for the KrII
459.28 and 555.299 nm is shown in Fig. 6. As can be seen,
no systematic trends are observed in any of the lines. The random
distribution around the mean value is a typical behaviour in
these measurements. From now on, we will assign the mean value as
the Aki-value and the standard deviation as a quality
indicator of the mean value. In this sense, it is significant
that 28 of the 35 measured KrII lines have uncertainties lower
than 15% and only the 7 weakest lines show greater uncertainties.
This result shows the quality of the measurements performed.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig6.eps} \end{figure}](/articles/aa/full/2001/22/aa1051/Timg23.gif) |
Figure 6:
Two examples of the evolution of the measured transition
probabilities measured in this work along the plasma life. No
systematic trends are detected. |
In Table 2, all measured transitions have been indicated.
They have been ordered by increasing wavelength (first column).
The second and third columns indicate the transition array and
multiplet respectively, in all cases according to the notation
suggested by Striganov & Sventitskii (1968). The fourth
and fifth columns contain all the experimental works considered,
indicating in the case of data coming from this work the
calculated standard deviation (in percentage) in parentheses. It
is important to remark that, in the case of the work from Miller
et al. (1972), this work offers relative transition
probabilities but, since the value for
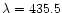 nm is
coincident with that recommended by Fuhr & Wiese (1998),
both sets of data are comparable between them and of course, with
our data. The sixth and seventh columns contain the
Aki-values obtained from theoretical calculations.
nm is
coincident with that recommended by Fuhr & Wiese (1998),
both sets of data are comparable between them and of course, with
our data. The sixth and seventh columns contain the
Aki-values obtained from theoretical calculations.
When taking a look at the comparisons among data in Table 2, the first noticeable point is the great scatter in the
data. This is a very old problem in KrII transition
probabilities, with two different aspects: the absolute scale of
the Aki-values compared and the quality of the relative
ones. In this work, as explained in Sect. 3.3, the
scale selected by us to transform our relative measurements to
absolute ones corresponds to that of Castro et al. (2001),
which is really the same as that of Fuhr & Wiese (1998).
In this last publication, the authors maintain as a reference the
same data published by NIST from 1978 (Wiese & Martin
1978, 1980; Fuhr & Wiese 1990,
1996). If we re-examine Fig. 4, we see the nice
linear behaviour of the KrII excited states population, a
situation always present with our plasma source (e.g. Gigosos et al. 1994; Aparicio et al. 1997; del Val et al.
2000; Mar et al. 2000) and a first result can be
guessed. The data from Castro et al. (2001), from Fuhr &
Wiese (1998) and therefore, from ourselves, might not be
a good absolute scale, but at least does seem to represent a good
relative one. Small differences between the data from Castro et al. (2001) and ours, corresponding to measurements
performed in the same plasma source, arise from the uncertainty in
intensity measurements and statistical deviations of the fits in
the Boltzmann plots.
If we compare our data with other experimental ones, we find a
curious agreement with those from Brandt et al. (1982) and
Keil (1973). Both works correspond to measurements
performed in wall-stabilized arcs at atmospheric pressure by
assuming total LTE. Although there are only three data points to
compare with Brandt et al. (1982), the mean ratio between
our data and theirs is 0.91 with only 2% statistical deviation.
The arc at atmospheric pressure is probably one of the plasma
sources closest to LTE and the two-wavelength interferometry
technique employed by them in  diagnostics is one of the
most accurate ones used to determine this parameter. The plasma
generated in our work has been demonstrated to be well described
by a pLTE model and other plasmas generated by this source have
been shown to be very close to LTE (Aparicio et al.
1999). As a conclusion, we can say that the scale from
Brandt et al. (1982) is probably near to the absolute
scale. In relation to data from Miller et al. (1972), very
frequently considered as a good reference in a relative scale, we
do not find good coincidence with our data. In fact, even
assuming that
diagnostics is one of the
most accurate ones used to determine this parameter. The plasma
generated in our work has been demonstrated to be well described
by a pLTE model and other plasmas generated by this source have
been shown to be very close to LTE (Aparicio et al.
1999). As a conclusion, we can say that the scale from
Brandt et al. (1982) is probably near to the absolute
scale. In relation to data from Miller et al. (1972), very
frequently considered as a good reference in a relative scale, we
do not find good coincidence with our data. In fact, even
assuming that
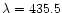 nm is not a good line to use as the
reference to rescale their work (this is one of the most
prominent lines in KrII visible spectra and is very sensitive to
self-absorption), we find that the ratio between their data and
ours is
nm is not a good line to use as the
reference to rescale their work (this is one of the most
prominent lines in KrII visible spectra and is very sensitive to
self-absorption), we find that the ratio between their data and
ours is
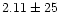 %. We can conclude that data from Miller et al. (1972) must be taken with care as a relative scale of
KrII transition probabilities. These comparisons can be shown in
Fig. 7. If we try comparisons with Bertuccelli & Di Rocco
(1991), the mean ratio between their data and ours is
%. We can conclude that data from Miller et al. (1972) must be taken with care as a relative scale of
KrII transition probabilities. These comparisons can be shown in
Fig. 7. If we try comparisons with Bertuccelli & Di Rocco
(1991), the mean ratio between their data and ours is
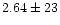 %. Comparisons with other experimental works reveal
greater differences between their relative scales and ours.
%. Comparisons with other experimental works reveal
greater differences between their relative scales and ours.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig7.eps} \end{figure}](/articles/aa/full/2001/22/aa1051/Timg27.gif) |
Figure 7:
Comparisons between the ratios of data taken from the
bibliography (bib) and ours (Tw). Data taken from Table 1
correspond with those labelled with an asterisk there, that is
to say, those employed in the Boltzmann plots. For the ratios
with these data, 15% error bars have been considered for our
results. |
Relative to theoretical works, comparisons with data from
Koozekanani & Trusty (1969), based on intermediate
coupling calculations with the absolute values obtained from
Hartree-Fock functions, are very poor. Their data are on average
1.87 times greater than ours, with a deviation around 49%.
Discrepancies are even greater when compared to calculations from
El Sherbini (1976). However, we note the very good
coincidence between the conclusions extracted by Brandt et al.
(1982) and ours in relation to calculations performed by
Spector & Garpman (1977), on the basis of intermediate
coupling coefficients with the radial integral obtained from
relativistic self-consistent-field wavefunctions. They found a
mean ratio between their data and those from this theoretical
reference of around
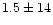 %. Certainly, the present work
contains only three lines measured by Brandt et al.
(1982) as stated before, and four other ones not measured
by them but calculated by Spector & Garpman (1977), but
curiously the mean ratio between this theoretical work and our
data is
%. Certainly, the present work
contains only three lines measured by Brandt et al.
(1982) as stated before, and four other ones not measured
by them but calculated by Spector & Garpman (1977), but
curiously the mean ratio between this theoretical work and our
data is
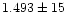 %, almost the same as that found by Brandt et al. (1982) with a systematic but reasonable deviation. We
think this result reinforces the idea of a good placing of our
data in a relative scale and is probably not far from an absolute
one.
%, almost the same as that found by Brandt et al. (1982) with a systematic but reasonable deviation. We
think this result reinforces the idea of a good placing of our
data in a relative scale and is probably not far from an absolute
one.
As a final conclusion, this work offers transition probabilities
of a set of 35 KrII lines in the spectral region from 450 to 580 nm. For 20 of them, there are no previous data. We can estimate an
error of 15% for more than 80% of them and 40% for the rest,
always on a relative scale. Many of them will be useful in
refining new calculation models. Furthermore, this work sheds some
light what are probably the most significant theoretical and
experimental works, those of Spector & Garpman (1977) and
Brandt et al. (1982) respectively. However, new and more
precise calculations and measurements are still required in order
to clarify the uncertainties remaining in KrII transition
probabilities.
Acknowledgements
The authors thank S. González for his collaboration in the
experimental arrangement, and the Spanish Dirección General de
Investigación Científica y Técnica (Ministerio de
Educación y Ciencia) and the Consejería de Educación y
Cultura de Castilla y León for their financial support under
contracts No. PB98-0356 and VA23-99 respectively. Dr. J. A.
Aparicio wants to express his personal acknowledgement to the
Organización Nacional de Ciegos de España (ONCE) for help.


Up: Measurement of several transition
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig6.eps} \end{figure}](/articles/aa/full/2001/22/aa1051/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig7.eps} \end{figure}](/articles/aa/full/2001/22/aa1051/Timg27.gif)