A&A 372, 105-116 (2001)
DOI: 10.1051/0004-6361:20010477

The mean surface density of companions in a stellar-dynamical context

R. S. Klessen1,2,3 - P. Kroupa4


1 - UCO/Lick Observatory, University of California, 499 Kerr Hall, Santa Cruz, CA 95064, USA
2 - Otto Hahn Fellow, Max-Planck-Institut für Astronomie, Königstuhl 17, 69917 Heidelberg, Germany
3 - Sterrewacht Leiden, Postbus 9513, 2300-RA Leiden, The Netherlands
4 - Institut für Theoretische Physik und Astrophysik, Universität Kiel, 24098 Kiel, Germany

Received 11 July 2000 / Accepted 26 March 2001

Abstract
Applying the mean surface density of companions, $\Sigma (r)$, to the dynamical evolution of star clusters is an interesting approach to quantifying structural changes in a cluster. It has the advantage that the entire density structure, ranging from the closest binary separations, over the core-halo structure through to the density distribution in moving groups that originate from clusters, can be analysed coherently as one function of the stellar separation r. This contribution assesses the evolution of $\Sigma (r)$ for clusters with different initial densities and binary populations. The changes in the binary, cluster and halo branches as the clusters evolve are documented using direct N-body calculations, and are correlated with the cluster core and half-mass radius. The location of breaks in the slope of $\Sigma (r)$ and the possible occurrence of a binary gap can be used to infer dynamical cluster properties.

Key words: stars: binaries: general - open clusters and associations: general - stars: formation - stellar dynamics


   
1 Introduction

Studying the clustering properties of stars in star-forming regions is a necessary input towards understanding the formation and evolution of young stellar clusters (Elmegreen & Efremov 1997). Using two-point angular correlation functions to analyse the spatial distribution of stars, Gomez et al. (1993) showed that young stars in the Taurus-Auriga molecular cloud form in small associations containing of the order of ten stellar systems. Larson (1995) extended this investigation by taking into account the results from different searches for binary companions to the pre-main sequence stars in the Taurus-Auriga region. He computed the mean surface density of companions, $\Sigma(\theta)$, per star as a function of angular separation $\theta$. This statistical measure is closely related to the two-point correlation function but does not require normalisation. As two different power laws are necessary to fit the data, with a slope $\approx$-2 for separations below $\approx$$0.04\,$pc and with a slope $\approx$-0.6 above, Larson concluded that there are two distinct clustering regimes. At small separations, the derived companion density is determined by binaries and higher-order multiple systems, whereas at large separations the overall spatial structure of the stellar cluster is observed. Larson interpreted the observed non-integer slope in the clustering regime as evidence for fractal structure of the cluster. In addition, Larson noted that the break of the distribution occurs in Taurus-Auriga at length scales which are equivalent to the typical Jeans length in molecular clouds, corresponding to a Jeans mass of $\approx$ $1~M_{\odot}$. He speculated that stellar systems with smaller separations form from the fragmentation of single collapsing proto-stellar cores, whereas the spatial distribution on larger scales is due to the hierarchical structure of the parent molecular cloud.

These results prompted the reanalysis of the Taurus-Auriga data by other authors (Simon 1997; Bate et al. 1998; Gladwin et al. 1999), as well as the subsequent investigation of additional star-forming regions. Mean surface densities of companions as a function of angular separation have been derived for Orion (Simon 1997; Bate et al. 1998; Nakajima et al. 1998), for the $\rho$-Ophiuchus cloud (Simon 1997; Bate et al. 1998; Nakajima et al. 1998; Gladwin et al. 1999), and for the star-forming regions in Chamaeleon, Vela and Lupus (Nakajima et al. 1998). Common to all studies is that the companion surface density is best described as a double power-law, with slopes of $\approx$-2 in the binary branch and slopes between -0.9 and -0.1 in the large-scale clustering regime. However, the length scales where the break of the distribution is found to vary considerably, from $\approx$$400\,$AU in the Trapezium cluster in Orion, over $\approx$$5000\,$AU in Ophiuchus and $\approx$$8000\,$AU in Taurus, to $30\,000\,$AU for the Orion OB region. This fact raises considerable doubts about the interpretation of the break location as being determined by the Jeans condition in the cloud. This would imply quite different Jeans masses which in turn should lead to deviations of the initial mass function, which have not been observed.

A thorough theoretical evaluation of the mean surface density of companions, $\Sigma(\theta)$, and a discussion of viable interpretations can be found in Bate et al. (1998). Altogether the following picture emerges: at small separations, $\Sigma(\theta)$traces the separations of binary stars and higher-order multiple stellar systems. The slope $\approx$-2 results from the frequency distribution of binary separations being roughly uniform in logarithm (Duquennoy & Mayor 1991, for main sequence stars). The break occurs at the "crowding'' limit, i.e. at separations where wide binaries blend into the "background'' density of the cluster. At larger separations, $\Sigma(\theta)$ simply reflects the large-scale spatial structure of the stellar cluster. Bate et al. (1998) pointed out that $\Sigma(\theta)$ can be strongly affected by boundary effects and that a non-integer power-law slope in the cluster branch does not necessarily imply fractal structure. They showed that a simple core-halo structure, as is typical for evolved stellar clusters, will result in a non-integer slope for separations larger than the core radius. They also speculated about possible effects of dynamical cluster evolution on the properties of $\Sigma(\theta)$.

It is the aim of the present paper to investigate, for the first time, evolutionary effects on $\Sigma(\theta)$ as derived from realistic N-body computations. We use models studied by Kroupa (1995a,b,c, 1998, hereinafter K1-K4) for a comparison with a "standard'' dynamical analysis, where the binary population is analysed separately from the bulk cluster properties. For comparison, the mean surface density of companions for models of protostellar clusters that form and evolve through turbulent molecular cloud fragmentation is discussed in Klessen & Burkert (2000, 2001).

The structure of the paper is as follows. In the next section (Sect. 2) we mathematically define the mean surface density of companions, $\Sigma (r)$, and briefly discuss its limitations. In Sect. 3 we describe the star cluster models and their properties. In Sect. 4, we investigate the influence of cluster evolution on $\Sigma (r)$ and in particular discuss wide-binary depletion. The effects of averaging and projection are analysed in Sect. 5, and a possible observational bias is discussed in Sect. 6. Section 7 discusses features in $\Sigma(\theta)$ and their relation to cluster morphology. Finally, our results are summarised in Sect. 8.


 

 
Table 1: Properties of the model clusters. All clusters have N=400 stars with a mean stellar mass of $0.32~M_{\odot}$, n lists the number of different realizations of the model, and f gives the starting binary fraction. Initially, the density profile of all clusters follows a Plummer law with half-mass radius $r_{\rm h}$, leading to a half-mass diameter crossing time $\tau _{\rm h}$, and to central and central surface densities $\rho _0$ and $\Sigma _0$, respectively. The times, when we analyse the clusters, are indicated in the last four lines.
    Model $\cal A$ Model $\cal B$ Model ${\cal C}$ Model $\cal D$ Model $\cal E$ Model $\cal F$
n   5 5 5 5 3 3
f   1 1 1 1 0 0
$r_{\rm h}$ (pc) 0.08 0.25 0.8 2.5 0.08 0.25
$\tau _{\rm h}$ ($10^6\,$yr) 0.094 0.54 3.0 17 0.094 0.54
log $_{10}\,\rho_0$ (stars/pc3) 5.6 4.1 2.7 1.1 5.6 4.1
log $_{10}\,\Sigma_0$ (stars/pc2) 4.3 3.3 2.3 1.2 4.3 3.3
$t=t_{\rm init}$ ($10^6\,$yr) 0.0 0.0 0.0 0.0 0.0 0.0
$t=12.5\,\tau _{\rm h}$ ($10^6\,$yr) 1.19 6.67 37.5 211 1.19 6.68
$t=125\,\tau _{\rm h}$ ($10^6\,$yr) 11.9 66.7 -- -- 11.9 66.8
$t=t_{\rm end}$ ($10^6\,$yr) 297 300 300 296 297 300


   
2 Mean surface density of companions

The mean surface density of companions, $\Sigma(\theta)$, specifies the average number of neighbours per square degree on the sky at an angular separation $\theta$ for each cluster star. Knowing the distance of the cluster, the angular separation $\theta$ between two stars in the cluster translates into an absolute distance r. In the numerical models we have full access to all phase space coordinates and we define, in what follows, the mean surface density of companions $\Sigma (r)$ as the number of stars per pc2 as a function of the projected distance r (in pc). In Sect. 5.2 we show that the results are invariant to which plane is used for projection. We calculate for each star i in the system the projected distance rij to all other stars $j \ne i$. The separations rij are sorted into annuli with radii r and width $\delta r$, where we use logarithmic binning such that each decade in separation is partitioned into 10 logarithmically equidistant bins ( $\log_{10} \delta r = 0.1$). To obtain the function $\Sigma (r)$, we divide the number $\delta\;N(r)$ of stellar pairs per annulus rby the surface area $2\pi r\delta r$ and average by dividing by the total number N of stars in the cluster. The mean surface density of companions as a function of separation r then follows as

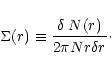\begin{displaymath}\Sigma(r) \equiv \frac{\delta\;N(r)}{2\pi N r\delta r}\cdot \end{displaymath} (1)

The function $\Sigma (r)$ is related to the two-point correlation function, $\xi(r)$, by $\xi(r) = \left(\Sigma(r) /\langle \Sigma \rangle \right)-1$, where $\langle \Sigma \rangle$ is the mean stellar surface density in the considered area (Peebles 1993). Because the normalisation $\langle \Sigma \rangle$ is often difficult to determine, it is preferable to use the function $\Sigma (r)$.

Stellar surveys have finite area and boundary effects may occur. For stars closer than a distance $r_{\rm b}$ to the boundary all annuli with $r>r_{\rm b}$ extend beyond the limits of the survey and companion stars may be missed. This has little effect when considering small separations r as only a small fraction of all stars is affected, however, when r becomes close to the survey size the missing companions result in a steep decline of $\Sigma (r)$. Several methods have been proposed to correct for that effect (Bate et al. 1998, and references therein), where either the accepted range of r is reduced to separations much smaller than the survey size, or additional assumptions about the background density of stars are made. Neither approach is completely satisfactory.

In the present study we do not attempt to adopt any of the correction methods for the following reasons. First, in the numerical simulations all information about the system is accessible. There are no observational constraints and we always consider all stars in the cluster. The survey area can be arbitrary large and is chosen such that it includes the complete cluster. Second, although the considered clusters are subject to the tidal field of the Galaxy we do not include Galactic-field stars in consideration. Hence, there is no confusion limit, where contamination with foreground or background stars becomes important.

   
3 Star cluster models

A range of star-cluster models are constructed, and their dynamical evolution is calculated using NBODY5 (Aarseth 1999), which includes a standard Galactic tidal field (Terlevich 1987). The cluster models have been discussed extensively in K1-K4, so that only a short outline is provided here.

The stellar systems initially follow a Plummer density distribution (Aarseth et al. 1974) with half-mass radius $r_{\rm h}$, and the average stellar mass is independent of the radial distance, r, from the cluster centre.

Stellar masses are distributed according to the solar-neighbourhood IMF (Kroupa et al. 1993) with $0.1\le m\le 1.1~M_{\rm\odot}$. Larger masses are omitted so as to avoid complications arising from stellar evolution. Binaries are created by pairing the stars randomly, giving a birth binary proportion $f=N_{\rm bin}/(N_{\rm sing}+N_{\rm bin})$, where $N_{\rm sing}$ and $N_{\rm bin}$ are the number of single-star and binary systems, respectively. The initial mean system mass is $2\langle m \rangle$, with $\langle m \rangle =0.32~M_{\rm\odot}$ being the average stellar mass. This results in an approximately flat mass-ratio distribution at birth (Fig. 12 in K2). Periods and eccentricities are distributed following K1. The initial periods range from 103 to 107.5 days, and the eccentricity distribution is thermal, i.e. the relative number of binaries increases linearly with eccentricity being consistent with observational constraints.

The parameters are listed in Table 1. Four clusters with f=1 are constructed spanning a wide range of central densities, from log $_{10}\rho_0=1.1$ to 5.6 [stars/pc3]. Each model contains N=400 stars and has a mass $M_{\rm cl}=128~M_\odot$. The initial tidal radius in all cases is $r_{\rm t}\approx8$ pc. All stars are kept in the calculation to facilitate binary-star analysis, but those with $r\gg r_{\rm t}$ experience unphysical accelerations in the linearised local tidal field and rotating coordinate system (Terlevich 1987), so that the density distribution of stellar systems at large radii does not reflect the true distribution in the moving group. Five different renditions are calculated for each model to increase the statistical significance of our results. In addition, two clusters with f=0 are constructed for comparison with the binary-rich cases. The evolution of these models is calculated for three cluster realisations each. The computations cover $3\times 10^8\,$years, but we consider only a sub-set of all possible snap-shots in the current analysis.


  \begin{figure} \par\includegraphics[width=15.8cm,clip]{MS10093-figure01.ps} \end{figure} Figure 1: The mean surface density of companions, $\Sigma (r)$, as a function of separation r for star clusters $\cal A$ to $\cal D$ with an initial binary fraction of 100% at different states of the dynamical evolution: initially (t=0.0, left column), at $t=12.5\,\tau _{\rm h}$ and $t=125\,\tau _{\rm h}$ (2. and 3. column) and at $t=t_{\rm end}$ (right column). The corresponding time in units of $10^6\,$years is indicated in the upper right corner of each plot. $\Sigma (r)$ is obtained as an average over n=5 different cluster realizations for each model as a projection into the xy-plane. The error bars indicate Poisson errors.
Open with DEXTER

   
4 Evolutionary effects

In this section, we discuss the influence of the dynamical cluster evolution on the resulting mean surface density of companions $\Sigma (r)$. For each star cluster, $\Sigma (r)$ is calculated as an average over the set of n individual model realisations, and we restrict ourselves to discussing the projection into the xy-plane. The influence of averaging and projection is discussed in Sect. 5.

   
4.1 The global evolution of stellar clusters

The evolutionary sequence of $\Sigma (r)$ for models $\cal A$ to $\cal D$ is illustrated in Fig. 1. Its first column denotes the initial state of each system at t = 0, the second and third columns depict the function $\Sigma (r)$ taken at $t=12.5\,\tau _{\rm h}$ and $t=125\,\tau _{\rm h}$, where $\tau _{\rm h}$ is the initial half-mass diameter crossing time (Table 1). As $\tau _{\rm h}$increases with increasing $r_{\rm h}$, these equivalent stages of cluster evolution correspond to different absolute times as indicated in the figure. The final state of the systems, at roughly $t\approx 3\times 10^8\,$yr, is given in the last column. For models ${\cal C}$ and $\cal D$, $125\,\tau_{\rm h} > t_{\rm end}$, so that the third column in Fig. 1 contains no entry.
  \begin{figure} \par\includegraphics[width=15.8cm,clip]{MS10093-figure02.ps} \end{figure} Figure 2: The mean surface density of companions, $\Sigma (r)$, as a function of separation r for star clusters $\cal E$ and $\cal F$. These models are equivalent to $\cal A$ and $\cal B$, respectively, but initially contain no binary stars. The figure is analogous to Fig. 1, except that n=3 different realizations of each model are used in the averaging process.
Open with DEXTER

At any time and for all models, the mean surface density of companions exhibits, at low separations r, a well defined power-law behaviour $\Sigma(r) \propto 1/r^2$. It implies an approximate uniform distribution of binary separations in $\log r$ (Bate et al. 1998). For larger r, the binary branch blends into the plateau of constant companion density corresponding to the core of the star cluster. This first break of the distribution occurs at separations r1where the number of chance projections of cluster members becomes equal to the number of binaries in that separation bin. At larger rchance projections completely dominate $\Sigma (r)$, and wide binaries, if in fact present, can no longer be identified as such. The location of the first break therefore depends on the binary fraction and on the central density of the cluster. On larger scales the stellar clusters follow a Plummer radial density profile with half-mass radius $r_{\rm h}$. Therefore, a second break occurs at r2 and $\Sigma (r)$declines sharply for separations $r \:\lower0.6ex\hbox{$\stackrel{\textstyle >}{\sim}$ }\:r_{\rm h}\approx r_{2}$ (see Sect. 7).

As the dynamical evolution progresses, the clusters expand and the density declines. Hence, the projected mean surface density of companions decreases as well. While many of the binaries with separations comparable to the mean distance of stellar systems in the cluster core become disrupted, some new binaries may form by capture. Usually these are higher-order multiples (K2) with separations close to the first break or smaller. As the cluster expands, the binary branch becomes less affected by crowding and the first break in $\Sigma (r)$ shifts to greater separations. This behaviour is clearly visible in Fig. 1. For all models the core plateau in $\Sigma (r)$ "decreases in height'' and "moves'' to larger separations as time progresses. At late stages of the evolution the entire binary branch is uncovered and a few long-period orbits appear through capture. This is also documented in Figs. 3 and 4 in K4.

The clusters develop core-halo structures through energy equipartition. Low-mass stars gain kinetic energy through encounters with more massive stars. The low-mass stars move away from the cluster centre, forming the halo, whereas the more massive stars sink towards the centre. The trajectories of halo stars that trespass beyond the tidal radius of the cluster are dominated by the Galactic tidal field, and most become unbound. Hence, the clusters expand until they fill their tidal radii. When this stage is reached (roughly after $t>1\times 10^8\,$years), the different clusters evolve identically (see also Fig. 1 in K3), mostly loosing stars through their first and second Lagrange points (Terlevich 1987; Portegies Zwart et al. 2001). As a result, $\Sigma (r)$ extends beyond the second break to increasingly larger separations with an increasingly shallower slope, which we identify as the halo branch in $\Sigma (r)$. Near the tidal radius $r_{\rm t}$, a third break occurs, as stars with $r>r_{\rm t}$ become unbound. The trajectories of stars belonging to these unbound moving groups are not followed with sufficient resolution (see Sect. 3). Also, these stars are likely to be severely contaminated by field stars in the Galaxy, and we refrain from a further discussion of this outermost branch in $\Sigma (r)$.

As can be seen from Fig. 1, knowledge of the initial global properties of the system is effectively erased through the dynamical evolution. The cluster and halo branches in $\Sigma (r)$look quite indistinguishable in the final frames. The situation changes, however, when considering the binary branch, as discussed in Sect. 4.2. The f=1 versus f=0experiments demonstrate that there is no significant difference in bulk cluster evolution between clusters containing a large primordial binary proportion and no binaries (K3). This is also evident by studying $\Sigma (r)$; concentrating only on the cluster and halo branches, the upper two final panels in Figs. 1 and 2 are indistinguishable.


  \begin{figure} \par\includegraphics[width=15.8cm,clip]{MS10093-figure03.ps} \end{figure} Figure 3: The function $r^2\,\Sigma (r)$ for models $\cal A$ to $\cal D$. The depicted times, averaging and projection are analogous to Fig. 1. The plots concentrate on the properties of the binary branch, where the horizontal dashed lines indicate its initial slope. The depletion of the distribution at late stages in the interval $10^{-4}\,$pc $\,<\,r\,<\,0.1\,$pc is the result of wide-binary disruption. The rising part of $r^2\,\Sigma (r)$ at separations greater than the first break corresponds to the cluster core, and the following decline for $r>r_{\rm h}$ is the contribution from the cluster halo. To demonstrate the effects of dynamical evolution, the dotted lines for t>0.0 indicate the initial distribution.
Open with DEXTER

   
4.2 Binary stars

Binary systems and wide hierarchical systems form through capture during the evolution of the clusters, as seen in Fig. 2. These systems result from triple or higher-order stellar encounters, and are consequently very rare. The periods of these systems range from 107 to $10^{11}\,$days (Fig. 10 in K2), and a well distinguished binary branch with slope $\approx$-2develops, extending to radii well beyond the initial position of the first break.

However, as the clusters evolve, binaries are not only created but also destroyed. Due to their smaller binding energies, wide binaries are more vulnerable to dynamical processes than close ones. If the initial binary fraction is high, then the destruction processes dominate over binary formation, and cluster evolution leads to a depletion of wide binaries. As a result, $\Sigma (r)$ steepens on the large-separation side of the binary branch. In extreme cases, some annuli r of $\Sigma (r)$ may become completely depopulated, and consequently a gap between the binary and the cluster branches opens up, as is noticeable in Fig. 1.

The efficiency of binary disruption depends strongly on the initial density of the cluster. For high stellar densities, the typical impact parameters of stellar encounters are small. Hence, there is a relatively high frequency of encounters for which the energy exchange exceeds the binding energy of typical binary systems, which subsequently dissolve. In our suite of models, the effect of binary depletion is largest in $\cal A$, which has the highest central density $\rho _0$, and decreases with increasing half-mass radius $r_{\rm h}$ as $\rho _0$ becomes smaller.

This is demonstrated in Fig. 3. Unlike the previous figures it shows a reduced range of separations, concentrating on the binary branch, and it plots $r^2\,\Sigma (r)$ to make it easier to determine the power-law slope and deviations from it. At t=0.0, for all models $r^2\,\Sigma (r)$ is constant in the binary branch. This reflects the initial distribution of the binary separations, which is uniform in the logarithm within the range $10^{-5}\,$pc to $10^{-2}\,$pc. Values $r<10^{-5}\,$pc come from the projection of the 3-dimensional distribution into the xy-plane. For model $\cal D$the complete binary branch is visible and fully segregated from the cluster branch (which corresponds to the rising part of the plot). This is because the half-mass radius of the cluster is large enough that the projected mean separation between cluster members exceeds the separation of the widest binary system. As both branches are clearly separated initially, dynamical evolution does not alter the binary distribution significantly. There is little sign of wide binary depletion, even at $t=t_{\rm end}$.


  \begin{figure} \par\includegraphics[width=12.2cm,clip]{MS10093-figure04.ps} \end{figure} Figure 4: Mean surface density of companions, $\Sigma (r)$, of cluster $\cal A$ at time $t=125\,\tau _{\rm h}$ for the projection into the xy-plane. The figure illustrates the effect of the averaging process. The small plots show $\Sigma (r)$ for the five different realizations ${\cal A}1$ to ${\cal A}5$of model $\cal A$, whereas the large plot gives the resulting averaged function.
Open with DEXTER

In the other models, the typical separations in the cluster core are smaller than $10^{-2}\,$pc, and binary and cluster branches overlap in the beginning. This is most significant for model $\cal A$, where the initial central density is highest. Consequently a large number of wide binaries are disrupted during the dynamical evolution of the system, and $r^2\,\Sigma (r)$ drops considerably below its initial value (indicated by the dashed line) in the range $10^{-4}\,$pc $\,<\,r\,<\,10^{-1}\,$pc. Because the size of this gap depends on the age and the initial central concentration of the cluster, analysing the signatures in $\Sigma (r)$ could be used to constrain the initial state of observed stellar clusters. This fact, namely that the binary population retains a memory of its past dynamical environment, is also used in K1 to infer the typical structures in which most Galactic-field stars form, by studying the shape of the binary period distribution ("inverse dynamical population synthesis'').

   
5 Statistical effects

In the previous section we analysed the mean surface density of companions averaged over several model realisations seen in one projection (into the xy-plane). Both, the effect of averaging and the effect of projection shall be discussed here.
  \begin{figure} \par\includegraphics[width=13.5cm,clip]{MS10093-figure05.ps} \end{figure} Figure 5: Illustration of the effect of projection. Mean surface density of companions $\Sigma (r)$ for cluster realization ${\cal A}1$ at time $t=125\,\tau _{\rm h}$ for three different projections. The upper panel shows the stellar distribution within $\pm 2\,$pc of the cluster centre and the lower panels show the resulting $\Sigma (r)$. The global features of $\Sigma (r)$ are independent of projection.
Open with DEXTER

   
5.1 Cluster to cluster variations

To estimate the effect of statistical variations between different model realisations, Fig. 4 plots $\Sigma_i(r)$constructed for each of the n=5 individual cluster rendition of model $\cal A$ at $t=125\,\tau _{\rm h}$. This model is chosen, because it has the smallest initial crossing time, hence, our simulations span the largest evolutionary interval. After the system has evolved for $125\,\tau_{\rm h}$, differences become noticeable at separations where the number of neighbours is small. This is the case at very large separations, where the stellar density rapidly decreases, and deviations may also occur at the extreme ends of the binary branch. At the smallest separations, $\Sigma (r)$ is determined by only one or two very close binary systems, and near the first break of the distribution, the depletion of wide binary systems becomes noticeable and a gap may open up. As can be seen in Fig. 4, the exact location and number of depleted separation bins slightly varies between different model realizations. Therefore, the wide binary gap appears wider and more noticeable for individual realisations compared to the ensemble average.

   
5.2 Different projections

Clusters of young stars are seen on the sky in only one projection. Inferring the full 3-dimensional structure of the cluster is therefore in principle impossible without additional information or assumptions. In the previous sections, we concentrated on the projection into the xy-plane when plotting $\Sigma (r)$. For the spherical clusters considered in the current analysis the different projections are equivalent, and each gives a fair representation of the complete system. Only at distances comparable to the tidal radius does the flattening through the Galactic tidal field of the cluster become significant (Terlevich 1987).

The invariance to changes in projection is demonstrated in Fig. 5, which shows cluster ${\cal A}1$ again at $t=125\,\tau _{\rm h}$. The function $\Sigma (r)$ is essentially independent of the projection, and slight differences occur only where there are smaller numbers of stars. Analogue to the variations between different model realisations discussed above, this is the case at very large and very small r, and at separations where wide-binary depletion occurs. At large separations, the tidal field breaks the symmetry. For small r and at the binary gap, it depends on the projection which separation bin stays populated and which may become empty. However, besides these details the overall structure of $\Sigma (r)$ is projection invariant.


  \begin{figure} \par\includegraphics[width=15.8cm,clip]{MS10093-figure06.ps} \end{figure} Figure 6: Mean surface density of companions, $\Sigma (r)$, of cluster $\cal A$ for different observational minimum mass limits $m_{\rm min}$. First row of panels: all stars in the cluster are considered (analogue to top row in Fig. 1). Second row: only stars with $m>0.25~M_\odot$contribute to $\Sigma (r)$. Third row: $m_{\rm min}=0.50~M_\odot$. Fourth row: $m_{\rm min}=0.75~M_\odot$, and lowest row: $m_{\rm min}=1.00~M_\odot$. Times and averaging procedure are equivalent to Figs. 1 to 3. There are 400 stars in each cluster realization in the mass range $0.1~M_\odot$ to $1.1~M_\odot$ following the Kroupa et al. (1993) IMF. The fraction of cluster stars considered in each panel is 100%, 51%, 17%, 6%, and 1%, respectively.
Open with DEXTER

   
6 Observational bias

The most likely observational bias in surveys of stellar clusters results from the unavoidable detection flux limit, which corresponds to a stellar mass limit $m_{\rm min}$ such that stars with $m<m_{\rm min}$ are not detected simply because they are too faint. This effect influences the derived mean surface density of companions, as illustrated in Fig. 6, where we again concentrate on cluster model $\cal A$. As in the previous figures, we plot $\Sigma (r)$ at four different stages of the cluster evolution, however, we now "observe'' the cluster at various distances, i.e. we introduce different detection limits $m_{\rm min}$ for the mass. We consider $m_{\rm min}$ in the range $0.25~M_\odot$ to $1~M_{\odot}$.

With increasing $m_{\rm min}$, the total number of detected stars decreases, and as a result $\Sigma (r)$ is reduced. Also the shape of $\Sigma (r)$ changes. This effect is small for low detection thresholds ( $m\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...), as the overall star distribution in the cluster is still well sampled. However, it becomes significant at large cluster distances when only the brightest stars can be detected. The binary branch becomes severely under-sampled, and wide gaps open up. For $m_{\rm min}=1~M_\odot$ the binary branch disappears in all models.

The inferred cluster core radius also depends quite sensitively on the completeness of the stellar sample. As the clusters evolve dynamically, high-mass stars sink towards the cluster centre due to mass segregation, whereas low-mass stars move outwards, building up the extended halo (Fig. 2 in K3). Sub-populations of higher-mass stars therefore exhibit smaller core radii as time progresses relative to the low-mass population.

This trend is clearly seen in Fig. 6, where the second break moves to smaller separations as $m_{\rm min}$ increases. At very late stages of the dynamical evolution and for very large cut-off masses, the core radius may become too small, so that the second break is no longer noticeable. For example, the function $\Sigma (r)$ follows an almost perfect r-2-power-law for $m_{\rm min}=0.75~M_\odot$ at $t_{\rm end}$, exhibiting a smooth transition from the binary regime to the halo regime without any sign of the cluster core, which is present when taking all stars into account. When considering only stars with $m>1~M_{\odot}$, then the signature of the cluster core disappears at all times. This bias needs be taken into account when interpreting observational data on star clusters.

 

 
Table 2: Morphologically important length scales. The table lists the separations r1 and r2, where the first and second break of the distribution $\Sigma (r)$ occur in all model clusters. The values for r1 and r2 are obtained at the intersection of the power-law fits to the binary branch and the central flat plateau, and the plateau and the halo distribution of cluster stars out to the tidal radius, respectively. These separations are compared to the core radius $r_{\rm c}$ and the half-mass radius $r_{\rm h}$ at the different times in Fig. 7.
Model time t $(10^6\,$yr) r1 (pc) r2 (pc) $r_{\rm c}$ (pc) $r_{\rm h}$ (pc) $r_{\rm t}$ (pc)
Model $\cal A$ $t=t_{\rm init}$ 0.0 0.0014 0.079 0.03 0.08 8.0
  $t=12.5 \tau_{\rm h}$ 1.19 0.0018 0.16 0.04 0.1 8.0
  $t=125 \tau_{\rm h}$ 11.9 0.0035 0.32 0.08 0.4 8.0
  $t=t_{\rm end}$ 300 0.011 1.0 0.5 2.1 6.0
Model $\cal B$ $t=t_{\rm init}$ 0.0 0.005 0.20 0.08 0.25 8.0
  $t=12.5 \tau_{\rm h}$ 6.67 0.004 0.32 0.09 0.4 8.0
  $t=125 \tau_{\rm h}$ 66.7 0.01 0.63 0.25 1.2 7.5
  $t=t_{\rm end}$ 300 0.022 1.6 0.7 2.6 6.2
Model ${\cal C}$ $t=t_{\rm init}$ 0.0 0.016 0.79 0.32 0.8 8.0
  $t=12.5 \tau_{\rm h}$ 37.5 0.016 1.26 0.26 1.0 8.0
  $t=t_{\rm end}$ 300 0.035 2.0 0.75 2.6 6.7
Model $\cal D$ $t=t_{\rm init}$ 0.0 0.032 2.0 1.1 2.5 8.0
  $t=12.5 \tau_{\rm h}$ 211 0.05 1.9 1.0 2.5 7.2
  $t=t_{\rm end}$ 296 0.05 2.0 0.83 2.5 6.7
Model $\cal E$ $t=t_{\rm init}$ 0.0 -- 0.12 0.03 0.08 8.0
  $t=12.5 \tau_{\rm h}$ 1.19 -- 0.11 0.03 0.1 8.0
  $t=125 \tau_{\rm h}$ 11.9 0.0028 0.34 0.05 0.3 8.0
  $t=t_{\rm end}$ 297 0.022 1.6 0.28 2.0 6.4
Model $\cal F$ $t=t_{\rm init}$ 0.0 -- 0.31 0.07 0.25 8.0
  $t=12.5 \tau_{\rm h}$ 6.67 -- 0.44 0.07 0.3 8.0
  $t=125 \tau_{\rm h}$ 66.7 0.0025 1.1 0.14 0.9 7.8
  $t=t_{\rm end}$ 300 0.022 2.0 0.63 2.2 6.9


   
7 Cluster morphology

As has been elucidated above, the mean surface density of companions shows distinct branches, the extend of which appear to couple with the dynamical state of the cluster. In this section we consider this in more detail.

Simple bulk cluster properties that can be used to describe the dynamical state of a cluster are the core radius, $r_{\rm c}$, the half-mass radius, $r_{\rm h}$, and the tidal radius, $r_{\rm t}$. The core radius is approximated by calculating the density-weighted radius $r_{\rm c}$ (Heggie & Aarseth 1992),

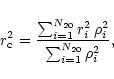\begin{displaymath}r_{\rm c}^2 = {\sum_{i=1}^{N_{20}} r_i^2\,\rho_i^2 \over \sum_{i=1}^{N_{20}} \rho_i^2}, \end{displaymath} (2)

where $\rho_i= 3\,m_{i,5}/(4\pi\,d_{i,5}^3)$ is the density around star i estimated within the closest distance di,5 from star i containing n=5 additional stars with combined mass mi,5, and ri is the distance of star i from the density centre of the cluster. The summation extends only over the innermost 20% of all stars in the cluster, N20, since this is sufficient to ensure convergence. The approximate tidal radius (Binney & Tremaine 1987),

 \begin{displaymath}r_{\rm t}(t) = \left({M_{\rm st}(t)\over3\,M_{\rm gal}}\right)^{1\over3}\, r_{\rm GC}, \end{displaymath} (3)

with $M_{\rm gal}=5~10^{10}\,M_\odot$ being approximately the Galactic mass enclosed within the distance of the Sun to the Galactic centre, $r_{\rm GC}=8.5$ kpc. To estimate $r_{\rm t}(t)$, $M_{\rm st}(t)$ is calculated by summing only those stars which have $r(t)\le 2\,r_{\rm t}(t-\delta t_{\rm op})$, where the data output time interval $\delta t_{\rm op} \ll t_{\rm relax}(t)$. The quantities $r_{\rm c}$, $r_{\rm h}$ and $r_{\rm t}$ are averages of n models per time-snap (Table 1).

We define two breaks in $\Sigma (r)$, r1 and r2, by fitting power laws to the three distinct branches of $\Sigma (r)$ (the binary branch, the flat central plateau, and the cluster halo out to the tidal radius $r_{\rm t}$) and determining the separation at the intersection of the fits. These values are listed in Table 2, and plots of $r_{\rm c}$ vs. r1 and $r_{\rm h}$ vs. r2 are presented in Fig. 7.


  \begin{figure} \par\includegraphics[width=14.8cm,clip]{MS10093-figure07.ps} \end{figure} Figure 7: Correlation between the first break radius r1 and cluster core radius $r_{\rm c}$(left panel), and the radius r2 of the second break and the half mass radius $r_{\rm h}$ (right panel).
Open with DEXTER

The figure shows that the quantities are well correlated. Specifically, we find (the uncertainties are mean absolute deviations)

 \begin{displaymath}\langle r_{\rm c}/r_1 \rangle = 20.5 \pm 9.7 \end{displaymath} (4)

and

 \begin{displaymath}\langle r_{\rm h}/r_2 \rangle = 1.14 \pm 0.29. \end{displaymath} (5)

This suggests that the break points in $\Sigma (r)$ can be used to infer the core radius and half-mass radius of a cluster. We also find good correlations between $r_{\rm h}$ and $r_{\rm c}$ ( $\langle r_{\rm h}/r_{\rm c} \rangle = 3.86 \pm 1.04$) and between the break points in $\Sigma (r)$ ( $r_2/r_1 = 74.3 \pm 44.4$).

The above scaling relations apply for the specific low-mass cluster models that we investigate. These models do not suffer significant core collapse, which is partly given by the relatively fast evaporation time ($\approx$0.5-1 Gyr, K3), and the ubiquitous binary stars which oppose core collapse. More massive clusters are likely to show different correlations, notably between $r_{\rm h}$ and $r_{\rm c}$, and between r1 and r2, since core collapse leads to the contraction of $r_{\rm c}$ but an expansion of $r_{\rm h}$ (Giersz & Spurzem 2000). Analysis of more massive clusters using $\Sigma (r)$ is a future goal, and it will be interesting to see if correlations 4 and 5 remain valid.

   
8 Summary

In this paper, we investigate how dynamical cluster evolution is manifest in the mean surface density of companions, $\Sigma (r)$, as a function of separation r. We find that throughout all evolutionary phases, $\Sigma (r)$ can be subdivided into four distinct branches, each following approximately a power-law behaviour:

1.
At small separations, and throughout all evolutionary phases of the star cluster, $\Sigma (r)$ traces binary stars and higher-order multiple systems. In the binary branch the slope of the companion density is approximately -2;
The binary population keeps a memory of the dynamical evolution of star clusters. The depletion of the binary population at large separations leads to a steepening of $\Sigma (r)$ in the wide-binary branch. In extreme cases, it may become completely depopulated and a gap between binaries and the cluster branch opens up. The gap increases with cluster age and with increasing initial density. For the binary branch, $\Sigma (r)$ is sensitive to the initial properties of the system, so that analysing $\Sigma (r)$ for a cluster can constrain its birth configuration;

2.
The well-defined binary branch blends into a plateau of constant companion density which corresponds to the main body of the stellar cluster, and which we refer to as the cluster branch in $\Sigma (r)$. The transition occurs at separations when chance projections of cluster members begin to outnumber the contribution of binary stars in that separation bin. The location of this first break at r1depends on the binary fraction and the central stellar density of the cluster, and thus on $r_{\rm c}$. As the cluster expands, the density decreases and the core radius increases with $r_{\rm c}\approx 21\,r_1$ for the set of models studied here. As a consequence, the binary branch becomes less affected by crowding and the first break in $\Sigma (r)$ shifts to greater separations. Generally, as the cluster evolves, the plateau "decreases in height'' and "moves'' to larger separations. Larger parts of the binary branch are "uncovered'' as a result of the expansion and the formation of wide hierarchical systems through capture;
3.
Relaxed Galactic clusters exhibit a core/halo structure. This becomes apparent in $\Sigma (r)$ through the existence of a second break at r2, which is approximately located at the half-mass radius, $r_{\rm h}\approx r_2$, beyond which $\Sigma (r)$ decreases again. The slope of this halo branch depends sensitively on the evolutionary state of the cluster. If the cluster is still sufficiently young so that most of it is confined well inside its tidal radius, then $\Sigma (r)$ decreases rapidly. However, relaxed clusters that fill their tidal radii have a halo branch with a slope of approximately -2;
4.
Beyond the tidal radius, the density of unbound stars decreases gradually, which is reflected in a fourth branch in $\Sigma (r)$. It is a measure of the density distribution of the moving group relative to the centre of its origin, which is the star cluster. The decay of $\Sigma (r)$ is steeper here because the stars are finally removed from the vicinity of the cluster within an orbital period about the Galaxy (Terlevich 1987);

5.
The mean surface density of companions closely reflects morphological properties of stellar clusters. The break points in $\Sigma (r)$, r1 and r2, therefore can be used to infer the core radius $r_{\rm c}$ and half-mass radius $r_{\rm h}$ of a cluster. These quantities are well correlated, and we find $\langle r_{\rm c}/r_1 \rangle = 20.5 \pm 9.7$ and $\langle r_{\rm h}/r_2 \rangle = 1.14 \pm 0.29$, respectively.
Altogether, $\Sigma (r)$ contains valuable information on the dynamical state of a star cluster, and allows an assessment of cluster properties such as the core and half-mass radii. As the location of the first break in $\Sigma (r)$ (or the possible occurrence of a gap between binary and cluster branch) depends on the binary fraction and on the initial central density, these parameters can in principle be inferred from analysing $\Sigma (r)$.

Our study confirms that different projections of the same data do not change $\Sigma (r)$ significantly during the evolution of initially spherical clusters in the Galactic tidal field. Also, different numerical renditions of the same models lead to indistinguishable results. Hence, they can be combined to improve the statistical significance of the ensemble average $\Sigma (r)$.

To allow for a proper assessment of stellar cluster properties using $\Sigma (r)$, it is important to consider as complete a census of cluster stars as possible. Observational bias (i.e. non-detection of faint stars) may complicate the interpretation of $\Sigma (r)$ and limit its applicability for inferring the initial stage of the cluster under study (see also Bate et al. 1998). Our tests show, however, that $\Sigma (r)$ remains a useful quantity even when stars with $m\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ... are not detected. We also find that mass segregation is evident in $\Sigma (r)$ through the location of the second break in dependence of the mass-range used to construct $\Sigma (r)$.

Future analysis of numerical models of rich clusters, for which mass segregation and possibly core collapse play important roles in the late phases of the dynamical evolution, will be performed to deepen the issues raised in this pilot study.

Acknowledgements
We thank Sverre Aarseth for distributing NBODY5 freely. RSK acknowledges support by a Otto-Hahn-Stipendium from the Max-Planck-Gesellschaft and partial support through a NASA astrophysics theory program at the joint Center for Star Formation Studies at NASA-Ames Research Center, UC Berkeley, and UC Santa Cruz. PK acknowledges support from DFG grant KR1635.

References

 

Copyright ESO 2001