A&A 371, 1035-1047 (2001)
DOI: 10.1051/0004-6361:20010456

Line-profile variations of the double-lined spectroscopic binary $\mathsf{\kappa}$ Scorpii

K. Uytterhoeven¹ - C. Aerts¹ - P. De Cat¹ - K. De Mey¹ - J. H. Telting² - C. Schrijvers³ - J. De Ridder¹ -
K. Daems¹ - G. Meeus¹ - C. Waelkens¹

1 - Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200 B, 3001 Leuven, Belgium
2 - Netherlands Organisation for Scientific Research, Isaac Newton Group of Telescopes, Apartado 321,
38700 Santa Cruz de La Palma, Spain
3 - Astronomical Institute Anton Pannekoek, University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam,
The Netherlands

Received 9 February 2001 / Accepted 22 March 2001

Abstract
We present a total time series of high signal-to-noise, high-resolution spectra of the SiIII $\lambda 4552.6$, $\lambda 4567.8$ and $\lambda 4574.8$ Å lines of the fast-rotating, spectroscopic binary and $\beta$ Cephei star $\kappa$ Scorpii. Among this data set is a sample of 422 spectra of intensive monitoring during eight subsequent nights in July 1997. We find variability of the line profiles on two time-scales: a variation of several months as a result of the orbital motion and rapid variations of a few hours, which are explained in terms of non-radial pulsation modes. From the total dataset, covering a time span of 9 years, we derive for the first time the orbital parameters of $\kappa$ Scorpii and find an orbital period of 195 days. The complex patterns on the grayscale representations of the residual SiIII $\lambda 4552.6$ Å profiles with respect to the average profile point towards more than one (non-axisymmetric) pulsation mode. A frequency analysis of the three normalised velocity moments confirms the main period of 4.80 hours and the second period of 4.93 hours, which were previously derived from photometric data. We attempt an identification of the pulsation modes by means of the moment method and line-profile fitting and find that $\kappa$ Scorpii pulsates in a main prograde sectoral mode of degree 1 or 2 and in an additional tesseral mode for which l = 5, m = 1 are the most likely wavenumbers. In the variations of the line profiles we find indications for the presence of additional pulsation modes.

Key words: stars: binaries: spectroscopic - stars : oscillations - line: profiles - stars: individual: $\kappa$ Scorpii

1 Introduction

Many $\beta$ Cephei stars are found to vary multi-periodically. The variability of these stars can be explained by non radial pulsation (NRP), which manifests itself in line-profile variations (LPVs). Higher-degree modes with l > 4 lead to features moving from blue to red or vice versa through the line profile. In cases of fast-rotating stars, the profiles are broadened mostly due to rotation. The effects of rotation on the excitation of pulsation modes is not understood. Because the LPVs hold information on the pulsation modes, one hopes to visualize the impact of the rotation on the modes by studying the LPVs.

A detailed knowledge of the pulsation of the star may also lead to mapping of the stellar interior. This branch of astronomy, so called asteroseismology, has gained a lot of interest the last few years, mainly thanks to the large progress made in the study of the solar interior (helioseismology) from SOHO data. A prime step towards asteroseismology is a correct identification of the excited modes. Therefore, an identification of the pulsation parameters by means of a detailed study of the line-profile variability is very useful, particularly when only a limited number of $\kappa$-driven modes are excited.

The multi-periodic variations in line profiles, due to NRP, detected in fast-rotating spectroscopic binary $\beta$ Cephei stars, seem to be similar to each other (see e.g. $\alpha$ Vir, Smith 1985; $\lambda$ Sco, De Mey et al. 1997; $\omega ^1$ Sco, Telting & Schrijvers 1998; $\epsilon$ Per, De Cat et al. 2000; $\nu$ Cen, Schrijvers 1999). They all exhibit bumps moving through the profiles.

Here, we present a study of a new dataset of LPVs of the rapidly rotating $\beta$ Cephei star $\kappa$ Scorpii (HD 160578, m_V = 2.41, SpT B1.5III), which is a spectroscopic binary. On the base of a photometric study, Shobbrook & Lomb (1972) and Lomb & Shobbrook (1975) classified $\kappa$ Scorpii as a variable star, - and more specifically as a $\beta$ Cephei variable -, in a binary system. The binarity was also confirmed by means of spectroscopic data by Heasley et al. (1982). From the peculiar shapes of the HeI-profile they suggested that this star may be a double-lined spectroscopic binary. Aerts et al. (1989), on the other hand, noticed the line-profile variability for the first time.

The intrinsic variability was interpreted by Shobbrook & Lomb (1972) and Lomb & Shobbrook (1975). A period-analysis performed on photometric data covering the time span 1969-1973 led to the detection of one frequency $f_{1} = 5.0042461 \pm 0 .0000010$ cd^-1. The presence of a second frequency $f_{2} = 4.8678381 \pm 0.0000025$ cd^-1 was suspected from a longer (beat) periodicity of about 7 days in the data.

The aim of our study is to clarify both the binary and the pulsational nature of $\kappa$ Scorpii in full detail. Hereto, we made use of a series of 422 high-resolution ( $55\,000 \leq R \leq 60\,000$), high signal-to-noise spectroscopic observations gathered during 8 subsequent nights in July 1997, in addition to other spectroscopic data, covering a total time span of 9 years.

The paper is organised as follows. Initially we give a description of the observations. In Sect. 3, we study the orbital motion from the data. Section 4 presents an analysis of the intrinsic pulsation. A study of the grayscale representations, a frequency analysis and a mode identification is given. The latter is based on a confrontation between the moment method and the method of line-profile fitting. In Sect. 5 we give an estimation of the physical parameters of the binary components. We end the paper with a discussion of the results in Sect. 6.

2 The observations

During the period 1988-1997 high-resolution and high-S/N spectra of $\kappa$Scorpii were obtained at ESO, La Silla, with the CAT telescope and the CES spectrograph. The observations made in 1988 were realised by means of a Reticon detector, contrary to all other observations which were made by a CCD.

In order to allow an in-depth investigation of the line-profile variability of $\kappa$ Scorpii high-spatial and -temporal resolution ( $55\,000 \leq R \leq 60\,000$) spectroscopic observations were made during 8 subsequent nights in July 1997. These spectra were obtained by means of CCD#38, a Loral/Lesser $2688 \times 512$ pixel CCD with a pixel size of $15 \times 15\ \mu$m² in the Long Camera mode, and the observed spectral domain was the one centered on the SiIII triplet at $\lambda 4552.6$ Å, $\lambda 4567.8$ Å and $\lambda 4574.8$ Å. The integration time of the spectra varied from two to six minutes, which is less than 1.5% of the photometric frequency f₁.

Besides these 422 high-signal-to-noise (S/N > 400) spectra, additional observations were gathered with the same instruments and focussed on the same wavelength region by several observers during nights in the period 1988-1997. These were used to study both the orbital motion and the line-profile variability. A logbook of the observations is given in Table 1.

 

 

Table 1: Logbook of the observations of $\kappa$ Scorpii. $\Delta T$ stands for the total time span of the individual observation run (days), N denotes the number of spectra obtained during the given campaign. S/N stands for the signal-to-noise ratio

date	observer	$\Delta T$	N	S/N
May 1988	C. Waelkens	5	46	400-600
June 1995	C. Aerts	4	187	350
September 1995	J. Telting	2	12	500-600
March 1996	C. Aerts	7	13	350
April 1996	G. Meeus	6	14	350
April 1996	C. Schrijvers	5	5	400
May 1996	G. Meeus	1	2	350
June 1996	K. Daems	1	9	150-200
July 1996	C. Aerts	5	12	300-450
February 1997	C. Aerts	6	9	400-500
March 1997	P. De Cat	3	4	450-550
May 1997	J. De Ridder	6	5	500
July 1997	P. De Cat	2	8	250-500
July 1997	K. De Mey	8	422	400-750
October 1997	P. De Cat	5	4	200-350

2.1 Reduction of the data

The obtained spectra were reduced using the ESO-MIDAS software package. Firstly the spectra were adjusted for the background radiation by subtracting a mean bias-value. After flatfielding by means of spectra of a quartz flatfield lamp to remove the pixel-to-pixel sensitivity variations inherent to the detector, we used the spectra of a thorium hollow cathode lamp to provide the wavelength calibration. Then the rebinned spectrum was divided by the response curve for its continuum, which was obtained by a spline function. The results were normalised spectra with continuum at unity. Finally a barycentric and heliocentric correction was carried out. We rebinned all spectra such that $\Delta \lambda = 0.02$ Å.

We ran up against some difficulties in normalising the spectrum. In most cases the broadening of the line of the secondary component extends into the continuum. Also the presence of "moving-bumps'' through the line-wings made the tracing of the continuum more complicated than usual. Third, a weak absorption line at $\lambda 4558$ Å caused confusion with the continuum. The presence of this line reduced the continuum between the SiIII lines at $\lambda 4552.6$ Å and $\lambda 4567.8$ Å to only a few Ångström. All these effects put a limitation on the accuracy of the spline-approximation of the response curve of the continuum.

2.2 The reduced spectra

	Figure 1: Left panel a) A random chosen set of SiIII line profiles from the eight subsequent nights in July 1997, showing the variation in the profiles. Right panel b) The average spectra of the observations made in (from bottom to top) March 1997, July 1997 and October 1997 at $\lambda 4552.6$ Å. The movement of the line of the component through the profile of the primary is visible
Open with DEXTER

Figure 1a shows a random chosen set of line profiles of the SiIII triplet, taken during the eight subsequent nights of July 1997 (20-28 July). The lines are broadened and we can see wiggles in them. They prograde from blue to red through the profile (see left-hand panel of Fig. 3). In the red wing of each of the spectra the broadened line due to the component can be seen. The component stays almost at the same position in the profile during the eight nights.

Figure 1b shows the average spectra of the observations made in March 1997, July 1997 and October 1997 at $\lambda 4552.6$ Å. The broad lines of the component are clearly visible and appear subsequently in the red and blue wing of the profile of the primary. From this we estimate an orbital period of several months.

3 Determination of the orbital parameters

A preceding study of the binary character of $\kappa$ Scorpii was made by De Mey (1997) as part of her Ph.D. Thesis. She used all spectra which were obtained before July 1997 to determine the orbital elements. She found an orbital period of $195\hbox{$.\!\!^{\rm d}$ }8 \pm 0\hbox{$.\!\!^{\rm d}$ }4$. De Mey also made an analysis of line-profile variations from the restricted number of data of June 1995. Because of the small frequency resolution, she only found one frequency f = 4.97 cd^-1, which is in between the two frequencies earlier found in photometry (Lomb & Shobbrook 1975).

In order to determine the orbital parameters of $\kappa$ Scorpii with higher precision, we derived the radial velocities (RVs) from all the spectra listed in Table 1. Because of the distortion of the line profiles we prefered to use the first moment of the lines instead of a determination of RVs by means of Gaussian fits. The first moment was calculated for both the first ( $\lambda 4552.6$ Å) and the second ( $\lambda 4567.8$ Å) line of the SiIII triplet. We note that, as a result of a loss of information of the $\lambda 4552.6$ Å line due to vignetting, we only could use the $\lambda 4567.8$ Å line of the data of 7 June 1995. In order to increase the accuracy of the RVs, we used the average value of the first moment, obtained from the $\lambda 4552.6$ Å and the $\lambda 4567.8$ Å line.

The orbital parameters of $\kappa$ Scorpii we derived from the RVs by means of the Léhmann-Filhés method (1894), are listed in Table 2. The orbital period associated with the best fit is 195.65 days. The orbit has a large eccentricity of 0.49.

A phase diagram of this solution is presented as the full line in Fig. 2. We note that the data of 7 June 1995 lie slightly above the calculated theoretical curve. This is due to the loss of information of the $\lambda 4552.6$ Å line mentioned above, in combination with the result that the RVs of the second SiIII line appear always to be larger than those determined from the first SiIII line. We note that the determination of the RVs from different SiIII lines also led to different values for the binary line-profile variable $\epsilon$ Per (De Cat et al. 2000). We also note that the descending branch of the fitted curve contains just a few points. Consequently, they could have an influence on the determination of the orbital parameters. We calculated also the orbital parameters based upon the RVs calculated from the first ( $\lambda 4552.6$ Å) line of the SiIII triplet, and find slightly different values for the estimated eccentricity ( $e = 0.435 \pm 0.006$) and $\omega$ ( $\omega = 97.7^{\circ} \pm 1.0 ^{\circ}$).

 

 

Table 2: The orbital parameters of $\kappa$ Scorpii derived from all the data listed in Table 1

Orbital parameter	estimate
$P_{\rm orb}$ (days)	195.65
$v_{\gamma}$ (km s-1)	0.2 $\pm$ 0.1
K (km s-1)	48.0 $\pm$ 0.3
E0 (HJD)	2449983.9 $\pm$ 0.3
e	0.488 $\pm$ 0.005
$a\sin{i}$ (A. U.)	0.75
$\omega$ (degrees)	92.7 $\pm$ 0.5
f(M) ($M_{\odot}$)	1.49

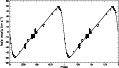	Figure 2: The radial velocity curve associated with the velocities which were calculated from the first moment of the $\lambda 4552.6$ Å line. The full line represents the best fitting orbit. This orbit has an orbital period $P_{\rm orb} = 195\hbox{$.\!\!^{\rm d}$ }65$
Open with DEXTER

4 Analysis of the intrinsic pulsation of $\mathsf{\kappa}$ Scorpii

To perform an analysis of the intrinsic pulsation of $\kappa$ Scorpii, we prewhitened all the data with the orbital solution presented in Fig. 2. For the analysis we used the 422 observations gathered during eight nights in July 1997, which were obtained specifically for this aim.

4.1 Study of the grayscale representations

Firstly, we studied the grayscale representation of the residual SiIII $\lambda 4552.6$ Å profiles with respect to the average profile. The grayscale plots display the variations in time within the line profiles. For each individual observation the residual flux is reflected in a shade of gray: light gray to white indicates a positive and dark gray to black represents a negative flux with respect to the mean. The grayscale plots are shown in the left-hand panel of Fig. 3. Each plot shows a different complex pattern, which points towards a non strict repetitive nature of the line-profile variations from one night to the other. A possible cause could be the presence of more than one pulsation mode. We see a continuation of black and white bands, whose shapes point towards (a) non axisymmetric mode(s).

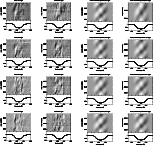Figure 3: Left: grayscale representations of the eight subsequent nights 20-28 of July 1997. Top of each figure: grayscale representations of the residual SiIII $\lambda 4552.6$ Å profile with respect to the average profile of the eight nights. Bottom: the average profile of the eight nights. Right: grayscale representations of the calculated theoretical profiles, corresponding with the observed profiles of the eight subsequent nights of July 1997. The pulsation parameters of the computed profiles are: $i = 40^{\circ }$, $v \sin i = 115$ kms-1, $\sigma = 22$ kms-1, and modes (2, -2) and (5, 1), with pulsation amplitude, resp. 8 and 12 kms-1. Top of each figure: grayscale representations of the residual SiIII $\lambda 4552.6$ Å profile with respect to the average profile. Bottom: the average profile

Open with DEXTER

4.2 Frequency analysis

In order to study more thoroughly the intrinsic variation, we performed a frequency analysis of the three normalised velocity moments ( <v>, <v²> and <v³>). The three velocity moments of the profiles are related to the radial velocity, the line width and the skewness of the profiles. The normalised velocity moments are obtained by normalising the moments by the equivalent width. For a desciption of the velocity moments, we refer to Aerts et al. (1992). We used different analysis-methods: Stellingwerf's (1978) Phase Dispersion Minimisation (hereafter referred to as PDM) and two methods based on Fourier techniques, particularly the Lomb-Scargle (Scargle 1982) method and the CLEAN-algorithm (Roberts et al. 1987). We searched for frequencies in the 0.001-10.000 cycles/day (cd^-1) interval, with frequency steps of 10^-3 cd^-1. In case of the PDM-method, we used the combinations 5 bins and 2 covers and 10 bins and 3 covers. The half width at half maximum of the highest peak of the window function gave us an indication for the frequency resolution; it turned out to be 0.07 cd^-1.

A downward trend in the first normalised moment <v> (shown in Fig. 4) caused a deformation of the phase diagrams associated with the first moment. This trend cannot be explained by a periodic phenomenon with a period shorter than 15 days. It could be due to a long beat-period, but our data have insufficient time spread to draw this conclusion. Most probably, the downward trend is simply a consequence of the relatively inaccurate orbit determination (see Fig. 2). We cancelled out the phenomenon by assuming a linear trend and removing it from <v> and subsequently also from <v²> and <v³>.

In order not to exclude the possibility of the downward trend resulting from a beat, we compare the results of our frequency analyses performed on the non-corrected and the corrected moments (referred to as the first and the second analysis).

As well the first analysis as the second yielded the same result with respect to the determination of the most significant frequency in the different moments. In all the data we find a frequency compatible with the first frequency f₁, suggested by Lomb & Shobbrook (1975) on the basis of a photometric study. Using the different methods, for each of <v>, <v²> and <v³> we find frequencies that differ less than 0.07 cd^-1 from f₁. Phase plots of the velocity moments, corrected for the trend, are given in Fig. 5. According to the definition of the moments (see Aerts et al. 1992), <v> varies with f₁, <v²> with f₁ and 2f₁, and the variation of <v³> depends on f₁, 2f₁ and 3f₁. These three fits, taking respectively f₁; f₁ and 2f₁; f₁, 2f₁ and 3f₁ into account, reduce the variability with $73 \%$, $56 \%$ and $51 \%$ in respectively <v>, <v²> and <v³>.

The results of a search for a second frequency turned out to be more ambiguous. We prewhitened the original and trend-corrected <v>, <v²> and <v³> with the first (photometric) frequency f₁ and performed successively the first and the second analysis.

The first analysis of the different velocity moments identified frequencies which can be related to the second frequency f₂, found by means of an analysis of photometric data (Lomb & Shobbrook 1975), in terms of alias frequencies. The second analysis , on the other hand, found, mainly in the <v> data, the second photometric frequency itself.

We used the SAS statistical package to calculate the best fitting values of the amplitudes associated with the sinusoidal variation in the trend-corrected moments. We calculated the amplitudes of the monoperiodic (f₁) and the biperiodic (f₁ and f₂) model. The results are listed in Table 3, which also presents the contributions of f₁ and f₂ in the variations of the normalised trend-corrected moments <v>, <v²> and <v³>. In the higher-order moments, we also took the beat frequencies, which appear as a result of the interaction of the different pulsation modes, into account (see Mathias et al. 1994). We note from Table 3 that the addition of f₂ does not result in a large enhancement of the variance reduction.

 

 

Table 3: The contributions of f₁and f₂ and their sum- and beat frequenties in the variations of the trend-corrected normalised moments <v>, <v²> and <v³>. For every frequency, the corresponding amplitude with its standard error (s. e.) is given. The last column denotes the total variance reduction (f. v.: fraction of the variance)

normalised moment	frequency	ampl $\pm$ s. e.	f. v.
<v> (km s-1)	f1	2.250 $\pm$ 0.061
	f2	0.633 $\pm$ 0.060	77.9%
<v2> (km s-1)2	f1	135.3 $\pm$ 6.2
	2f1	61.6 $\pm$ 6.3
	f2	24.3 $\pm$ 6.4
	2f2	12.1 $\pm$ 6.2
	f1 + f2	14.7 $\pm$ 6.3
	f1 - f2	26.9 $\pm$ 6.3	60.1%
<v3> (km s-1)3	f1	11392 $\pm$ 480
	2f1	685 $\pm$ 493
	3f1	596 $\pm$ 491
	f2	3383 $\pm$ 487
	2f2	535 $\pm$ 481
	3f2	461 $\pm$ 487
	f1 + f2	1402 $\pm$ 481
	f1 - f2	4990 $\pm$ 502
	2f1 + f2	516 $\pm$ 475
	2f1 - f2	2143 $\pm$ 491
	2f2 + f1	497 $\pm$ 478
	2f2 - f1	2785 $\pm$ 481	59.6%

	Figure 4: The downward trend in the first normalised moment <v>
Open with DEXTER

We also performed a two dimensional analysis of the variable signal in the spectra, for the Fourier and PDM methods. For every wavelength bin ( $\Delta \lambda = 0.02$ Å), we computed first of all the Fourier component for the frequencies between 0 and 16 cd^-1, with a frequency spacing of 0.001 cd^-1. We used the CLEAN parameters $N_{\rm it} = 400$ and a gain of 0.2 and 0.5. The power spectrum across the SiIII Å line profile (gain = 0.2) is plotted in Fig. 6.

The variational power is mainly found at the first photometric frequency f₁. We note that a gap appears in the power at the center of the line profile. The greater part of the gap can be filled by the one-day alias frequencies of f₁. The use of a larger gain factor (gain = 0.5) did not result in a better filling of the gap. The second frequency f₂ can not be found in the frequency spectrum. Nevertheless, evidence for the presence of f₂ can be found in the smaller peaks at some beat frequencies. The power is strong at 2f₂ - f₁, and its one-day alias frequencies (2f₂ - f₁) + 1 cd^-1 and (2f₂ - f₁) + 2 cd^-1. A weak peak at 2(f₁ - f₂) cd^-1 can also be detected. These four peaks and the frequencies f₂ and f₂/2 are indicated as dashed lines in Fig. 6. Other non-identified frequencies seem to appear as well (e.g. 3.52 cd^-1 and 1.55 cd^-1).

A two dimensional PDM analysis resulted in the power spectrum, which is plotted in Fig. 7. We used several combinations of PDM bins and covers, wich led to comparable results. The mean peak is also situated at f₁, but we are not able to find any evidence for the presence of the second photometric frequency. The strongest peaks are situated at frequencies which are connected with f₁: f₁ + i, f₁/i (full lines). We note that the gap in the f₁power also is visible in the PDM power spectrum.

The fragmentation of the power peak at f₁ into peaks at one-day alias frequencies of f₁ and the strong power at some beat frequencies in the two dimensional plots can be attributed to the complexity of the line-profile variations of $\kappa$ Scorpii.

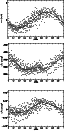	Figure 5: The first three normalised moments of the SiIII  $\lambda 4552.6$ Å line of $\kappa$ Scorpii after removing the unexplained trend shown in Fig. 4. <v> is folded with f1; <v2> with f1 and 2f1; <v3> with f1, 2f1 and 3f1
Open with DEXTER

Figure 6: Power spectrum across the line profile of the SiIII line at $\lambda 4552.6$ Å of $\kappa$ Scorpii, obtained by a two dimensional CLEAN analysis ( $N_{\rm it} = 400$ and a gain of 0.2). For each wavelength bin the power as a function of frequency is plotted as a gray value. The main peak occurs at the frequency f1. The frequencies f1, f1 + n (full lines); f2 and some beat frequencies (dashed lines) are indicated with an arrow. Many other frequencies appear in the power spectrum, which cannot be explained by f1, f2, a combination of f1 and f2 or one of their aliases

Open with DEXTER

	Figure 7: Power spectrum across the line profile of the SiIII line at $\lambda 4552.6$ Å associated with the PDM analysis (5 bins, 3 covers). For each wavelength bin, ( $1 - \theta$) is plotted as a gray value. The power of the first frequency f1 and its one-day aliasses is very strong (full lines). We find no evidence for the presence of the second frequency f2 (dashed lines)
Open with DEXTER

We conclude that the observed line-profile variations in $\kappa$ Scorpii are due to a dominant pulsation mode with pulsation frequency f₁ and a second mode with pulsation frequency f₂. Both frequencies were suggested from the photometric study and it is the first time that a frequency analysis of the (three normalised velocity moments of the) line profiles confirms the presence of both frequencies in the spectroscopic variability of the star. The power spectrum shown in Fig. 6 indicates the presence of other modes, but the candidate frequencies occur with an amplitude at the level of the detection treshold. Therefore we can only suggest the existence of other modes from our data set.

4.3 Mode identification

Various methods to retrieve the pulsation parameters are developed during the past years. We will use the method of line-profile fitting (Smith 1977, 1986) based on the results obtained with the moment method (Balona 1986; Aerts et al. 1992; Aerts 1996).

4.3.1 The moment method

The moment method, suggested by Balona (1986) and refined by Aerts et al. (1992) and by Aerts (1996), is based on the variations of the first three velocity moments of the line profile. This method enables an identification of the wavenumbers (l, m) by the so called discriminant ( $\gamma ^m_l$), which is a function of the observed and theoretically calculated amplitudes of the moments. The smaller $\gamma ^m_l$, the better the agreement between observed and theoretical amplitudes of the moments. Also an estimation of the amplitude of the pulsation, the rotational velocity and inclination of the star and the width of the intrinsic profile is derived. For a full description of the discriminant, we refer to Aerts (1996).

We transferred the code presented by Aerts (1996) that determines the discriminant into a user-friendly FORTRAN code, which is available upon request. Given the limb-darkening coefficient, the frequency(ies), the associated K-value(s) (i.e. the ratio of horizontal to vertical pulsation amplitude), and the observed amplitudes of the moments, the algorithm calculates for a given range of modes and a given grid of velocity parameters the discriminant values and selects the pulsation parameters of the lowest values of the discriminant. In case of a multiperiodic pulsation model, the program calculates the discriminant for each mode separately.

   

Table 4: The results of the moment method for the identification of the pulsation parameters of $\kappa$ Scorpii associated with the first frequency f₁ (top) and second frequency f₂ (bottom), using a biperiodic model. The input parameters are given in the text. $\gamma ^m_l$, $v_{\rm p}$, $v \sin i$ and $\sigma$ are expressed in kms^-1

l	|m|	$\gamma ^m_l$	$v_{\rm p}$	i	$v \sin i$	$\sigma$
2	1	1.02	6	$60^{\circ}$	100	13
1	1	1.36	4	$40^{\circ}$	110	15
2	2	1.37	8	$20^{\circ}$	110	15
4	2	1.38	12	$50^{\circ}$	105	10
3	3	1.45	4	$60^{\circ}$	120	10

f₂

l	|m|	$\gamma ^m_l$	$v_{\rm p}$	i	$v \sin i$	$\sigma$
4	1	0.48	6	$70^{\circ}$	100	11
5	1	0.58	10	$10^{\circ}$	105	14
6	5	0.78	16	$50^{\circ}$	120	15
6	4	0.81	26	$30^{\circ}$	105	11
5	3	0.88	18	$80^{\circ}$	100	10

We ran the FORTRAN program with the following grid of parameters: inclination (i): from 0$^{\circ}$-90$^{\circ}$, with step 10$^{\circ}$; amplitude of the pulsation ($v_{\rm p}$): from 4-26 kms^-1, with step = 2 km s^-1; projected rotation velocity ($v \sin i$): from 100-130 km·s^-1, with step = 5 kms^-1; intrinsic width of the profile ($\sigma$): from 10-15km s^-1, with step = 1 kms^-1. We searched for the minimum value of the discriminant for all candidate modes in the range of l-values 0-6 for f₁. In the case of the pulsation parameters, associated with the second frequency f₂, we tested all ($l,\,m$) combinations with $l \leq 9$. The observed amplitudes of the moments we used, are listed in Table 3.

The results of the discriminant for the biperiodic model are listed in Table 4 for the five best solutions in the parameter space. The identification results in the presence of a low degree ($l \leq 4$) tesseral or sectoral mode and a tesseral mode of higher degree ( $4 \leq l \leq 6$). The best solutions derived from Table 4 are of such a nature that they lead to complex velocity structures at the stellar surface. Due to this complexity, it is very likely that several combinations from Table 4 lead to almost the same line-profile variability, such that one unique identification based on the discriminant alone is difficult. We investigate this in the following part.

4.3.2 Line-profile fitting

Line-profile fitting is the numerical fitting of observed line-profile variations with the simulated line-profile variations from numerical models describing the surface-velocity fields related to NRP (Smith 1977, 1986).

We used a FORTRAN code to generate theoretical profiles, given the limb-darkening coefficient, the pulsation frequenties and the associated K-value and the parameters of pulsation. For a given set of observed profiles, covering the whole phase of pulsation, we then compare the theoretical profiles with the observed ones, after adapting the phase of the generated profiles to the one of the observed profiles. We devided the phase interval [0,1], associated with the frequency f₁, into 20 phase bins of 0.05 and chose at random from the 422 profiles obtained in July 1997 a representative profile for each bin. We focus on the SiIII profile at $\lambda 4552.6$ Å. We based the pulsation parameters, required for the input of the FORTRAN code, on the results of the moment method. On the basis of the lowest pixel-to-pixel deviation between the observed and the theoretically calculated profile, measured by the value of $\Sigma \equiv \sqrt{\frac{1}{20} \sum_{N = 1}^{20} \sigma _N ^2}$, with $\sigma _N ^2 = \frac{1}{n} \sum_{i = 1}^{n} (I_{i,{\rm obs}} - I_{i,{\rm theo}})^2$, with n the number of wavelength pixels in the profile and N the number of spectra, between the generated and the observed profiles, the best sets of pulsation parameters is chosen (i.e. the ones with the smallest values of $\Sigma$). Thus, $\Sigma$ denotes the average standard deviation between the flux of the observed and the generated profiles. The final choice of the overal best set still requires visual inspection of the comparison between observed and theoretically calculated profiles for the lowest $\Sigma$ values.

Mode identification from direct line-profile fitting can be done on the basis of $\Sigma$ nowadays, if one is dealing with a monoperiodic pulsation. As soon as more than one mode is present, the number of free parameters is too large to calculate theoretical profiles for a sufficiently fine grid. For this reason, we do not perform "fitting'' in the strict sense, but calculate $\Sigma$ for all possible combinations of modes, given in Table 4.

The best fitting pulsation mode, associated with the dominant frequency, turned out to be a low degree prograde sectoral mode. The lowest value of the deviation $\Sigma$ was obtained by the combination (1,-1) and (5,1). Table 5 gives the five best solutions from the tested set of parameters. The result of the line-profile fitting with pulsation modes (1, -1) and (5, 1) is shown in Fig. 8. We note that the theoretical profiles do not explain sufficiently the bumps, moving through the individual profiles. The l-value of the prime mode is in any case too low to account for the shape of the bumps.

To investigate the character of the bumps, we determined from the July 1997 data for each phase bin of width 0.05 a mean profile. This mean is based on typically 20 profiles. As suspected, the irregular bumps, which are visible in the individual profiles, are wiped out in the mean profiles. In the latter, only a weak global bump is visible. In order to avoid coming up with a solution dependent on the randomly chosen profiles (with randomly appearing bumps), we performed the same profile-fitting on the new set of mean profiles. This analysis resulted in a even stronger preference for the combination (1, -1) and (5, 1).

We next tried to find the best fitting combination of pulsation parameters associated with this combination of modes, by rerunning the profile-fitting FORTRAN program with the following much more detailed grid of parameters other than the degrees and azimuthal orders: inclination (i): from 0$^{\circ}$-90$^{\circ}$, with step 10$^{\circ}$; amplitude of the pulsation ($v_{\rm p}$): from 4-26 kms^-1, with step = 2: kms^-1; projected rotation velocity ($v \sin i$): from 100-130 kms^-1, with step = 5 kms^-1; intrinsic width of the profile ($\sigma$): from 10-25 kms^-1, with step = 1 kms^-1. The lowest value of the testparameter $\Sigma$ ( $\Sigma = 1.265E-3$) was obtained for an inclination of $30^{\circ}$, $v \sin i = 115$ km s^-1, an intrinsic width of the profile of 23 km s^-1 and pulsation amplitudes of resp. 9 and 18 km s^-1 (shown in Fig. 9). A list of the five best combinations is given in Table 6.

We note that the selected value of the intrinsic width $\sigma = 23$ km s^-1is higher than the value $\sigma = 15$ kms^-1 we obtained from the moment method, which was also the highest tested value in that case. So, we ran the program of the moment method with the same grid as mentioned in the previous section, but with values of the intrinsic width from 15-25 kms^-1, with step = 1 kms^-1. This test resulted again in a preference for $\sigma = 15$km s^-1, although line-profile fitting signs up for a higher value. An explanation could be the following: the parameter $\sigma$ appears only in the terms varying with frequencies f₁ and f₂ in <v³>. Estimating $\sigma$through the discriminant is therefore mainly based on <v³>, for which our biperiodic fit explains only 60% of the observed variability. As already mentioned, we found indications for the presence of additional low-amplitude modes, which are not taken into account in deriving the amplitudes listed in Table 3. The broadening parameters $\sigma$ and $v \sin i$derived from the moments do not take the broadening due to the low amplitude features into account, while they are "forced'' to have a higher value in fitting since the total broadening of the profile needs to meet the observed broadening with that method.

 

 

Table 5: The five best results of the line-profile fitting on a random chosen set of 20 profiles, each representing a phase bin of length 0.05 associated with the frequency f₁. The tested combinations of pulsation parameters are based on the results of the moment method. $v \sin i$, $\sigma$ and $v_{\rm p}$ are expressed in kms^-1

(l,m)	$\Sigma$	i	$v \sin i$	$\sigma$	$v_{\rm p}$
(1, -1)	1.928E-3	40$^{\circ}$	110	15	6
(5, 1)					10
(1, -1)	1.984E-3	40$^{\circ}$	110	15	4
(4, 1)					6
(2, -2)	1.989E-3	20$^{\circ}$	110	15	8
(5, 1)					6
(1, -1)	2.015E-3	40$^{\circ}$	110	15	4
(3, 1)					6
(2, -2)	2.018E-3	20$^{\circ}$	110	15	8
(4, 1)					4

 

 

Table 6: The five parameter combinations with the lowest value of the testparameter $\Sigma$ associated with the modes (1, -1) and (5, 1), obtained by line-profile fitting of the mean profiles of each phase bin. The input parameters of the tested grid are given in the text. $v \sin i$, $\sigma$, $v_{\rm p_1}$ and $v_{\rm p_2}$ are expressed in kms^-1

$\Sigma$	i	$v \sin i$	$\sigma$	$v_{\rm p_1}$	$v_{\rm p_2}$
1.2651E-3	30$^{\circ}$	115	23	9	18
1.2653E-3	40$^{\circ}$	115	23	9	18
1.2657E-3	30$^{\circ}$	115	22	9	17
1.2659E-3	30$^{\circ}$	115	23	10	17
1.2663E-3	30$^{\circ}$	115	24	10	18

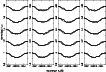Figure 8: For each phase bin of length 0.05, associated with the frequency f1, a SiIII $\lambda$ 4552.6 Å profile (full line), randomly chosen from the July 1997 data, is plotted, folded with a theoretically generated profile (dashed-dot line). The pulsation parameters of the computed profiles are: $i = 30^{\circ }$, $v \sin i = 115$ kms-1, $\sigma = 23$ kms-1, and modes (1, -1) and (5, 1), with pulsation amplitude, resp. 9 and 18 kms-1. The value of the testparameter associated with this model is $\Sigma = 1.923E-3$. The pulsation cycle related to f1 starts bottom left and ends top right

Open with DEXTER

Figure 9: The mean profile at SiIII $\lambda$ 4552.6 Å (full line), computed from the July 1997 data, for each phase bin of length 0.05, associated with the frequency f1, folded with a theoretically generated profile (dashed-dot line). The pulsation parameters of the computed profiles are: $i = 30^{\circ }$, $v \sin i = 115$ kms-1, $\sigma = 23$ kms-1, and modes (1, -1) and (5, 1), with pulsation amplitude, resp. 9 and 18 kms-1. The value of the testparameter associated with this model is $\Sigma = 1.265E-3$. The pulsation cycle related to f1 starts bottom left and ends top right

Open with DEXTER

As can be seen in Fig. 9, our pulsation model is still not sufficient enough to explain all the variability in the profiles. The insufficiency also becomes clear when we compare the grayscale representations of the theoretical simulated SiIII $\lambda 4552.6$ Å profiles, with the corresponding grayscale representations of the observed profiles, given in the left-hand panel of Fig. 3. The grayscale representations of the third and fourth night of the calculated theoretical profiles are shown in Fig. 10.

In order to explain the grayscale plots in more detail, we reconsidered the combinations listed in Table 4. Though pulsation models with modes (2, -2) and (5, 1) result in higher values of the testparameter $\Sigma$(e.g. $\Sigma = 1.277E-3$), the grayscale figures seem to match the observed grayscales in a better way than the profiles calculated with (1, -1) and (5, 1) modes. A comparative study between observed and theoretical calculated grayscale representations, led to a preference for the following pulsation model: $i = 40^{\circ }$, $v \sin i = 115$ kms^-1, $\sigma = 22$ kms^-1, and modes (2, -2) and (5, 1), with pulsation amplitude, resp. 8 and 12 kms^-1. The results are shown in the right-hand panel of Fig. 3. We come to the following conclusion regarding the mode identification. Using the moment method and line-profile fitting we tried to find a pulsation model which accounts for both the LPVs visible in the grayscale representations of the observed profiles and their moment variations. The relative small velocity changes of about 1 kms^-1 in the LPVs made it not easy to determine the pulsation parameters. The pulsation model, shown in the right panel of Fig. 3, seems to reconstruct the variations in the observed profiles approximately and occurred among the best solutions from the discriminant. Part of the variations cannot be explained by our model, though.

Figure 10: Grayscale representations of the calculated theoretical profiles, corresponding with the observed profiles of the third and fourth night of July 1997. The pulsation parameters of the computed profiles are: $i = 30^{\circ }$, $v \sin i = 115$ kms-1, $\sigma = 23$ kms-1, and modes (1, -1) and (5, 1), with pulsation amplitude, resp. 9 and 18 kms-1. Top of each figure: grayscale representations of the residual SiIII $\lambda 4552.6$ Å profile with respect to the average profile. Bottom: the average profile

Open with DEXTER

4.4 Additional investigations of the results

In order to find a periodicity in the appearance of the bands in the grayscale plots, we focus on the black bands pendulating through the grayscale figures of the observations, which display the line-profile variations in time (see the left panel of Fig. 3). Additionally we investigate two alternative biperiodic models.

We tried to understand the brightest bands by determing the time on which the bump (dis)appears (expressed by $\Delta$), the wavelength range the bump has travelled before disappearing ( $\Delta \lambda$) and the slope of the band. The results of the investigation are given in Table 7. The frequencies we found in the fifth and the sixth night (resp. 6.51 cd^-1 and 6.73 cd^-1) can be linked with the frequency (2f₂ - f₁) + 2 cd^-1= 6.7314 cd^-1, which also has a strong power in the plot of the two dimensional CLEAN analysis (Fig. 6).

 

 

Table 7: An overview of the mapping of the brightest black bands which appear in the eight grayscale plots that display the variations in time within the line profiles of the data of July 1997 (see left panel of Fig. 3). The time span of the travelling bump ($\Delta$ expressed in days) with the associated frequency given in cd^-1, the velocity range the bump has travelled before disappearing (expressed in kms^-1) and the slope of the band (kms^-2) are tabulated

Night	$\Delta$	frequency	$\Delta \lambda$	slope
3	0.107	9.36	46	0.147
5	0.154	6.51	26	0.348
6	0.149	6.73	18	0.378
7	0.106	9.47	36	0.182

Based on the strong presence of the frequency 2f₂ - f₁ and its one-day aliases in the results of the two dimensional CLEAN analysis (Fig. 6) and the appearance of (2f₂ -f₁) + 2 in the periodicity of the black bands in the grayscale representations of the line-profile variability in time, we investigated if two alternative biperiodic models could better explain the moment and line-profile variability: f₁ and f₂' = 2f₂ - f₁, and the model f₁ and f₂'' = 4.68 cd^-1, which is the frequency selected by the two dimensional CLEAN analysis. We did not find evidence to prefer the alternative models to the "classical'' model with f₁ and f₂.

5 Physical parameters of the binary components

In this section we give an estimation of the masses and radii of the two components of the binary system.

From an estimation (upper limit) of the equivalent width of the SiIII $\lambda$4552.6 Å line profile of the first and the secondary binary component (respectively 196 mÅ and 92 mÅ, the latter value is obtained by extrapolating the line of the component, shown in the middle panel of the right Fig. 1, assuming a Gaussian profile), we determined the effective temperature associated with a fixed value of $\log g$, the logarithm of the number density of silicon $\log \epsilon _{\rm Si}$ and the velocity of turbulence $v_{\rm turb}$ (Becker & Butler 1990). Using for both components the same values: $\log \epsilon_{\rm Si} = -4.45$ (the solar abundance of SiIII), $v_{\rm turb} = 6.0$ kms^-1 and $\log g = 3.4$ (a mean value from Strömgren and Geneva photometry, Heynderickx et al. 1994), we find for respectively the secondary and the first component $T_{\rm eff} = 18\,000$ K and $T_{\rm eff} = 22\,000$ K. The latter is consistent with the mean value of $T_{\rm eff} = 22\,361$ K found in the literature (Gulati et al. 1989; Heynderickx et al. 1994; Sokolov 1995; Berghöfer et al. 1996). Using the relation between the mass and luminosity given by Balona (1984), $\log M/M_{\odot} = -0.156 + 0.300 \log L/L_{\odot}$, the equation (Heynderickx 1991), $\log g = \log M/M_{\odot} - \log L/L_{\odot} + 4 \log T_{\rm eff} - 10.606$, and the relation between luminosity and $T_{\rm eff}$, $L = 4 \pi R^2 \sigma T_{\rm eff}^4,$ we find the following estimation of masses and radii: $M_1 = 17~M_{\odot}$ and $R_1 = 6.8~R_{\odot}$; $M_2 = 12~M_{\odot}$ and $R_2 = 5.8~R_{\odot}$. We checked the consistency of the assumption that $\log g_1 = \log g_2$, and find $\log g_1 = 4.01$ and $\log g_2 = 4.00$. Using these new values of $\log g_1$ and $\log g_2$, instead of $\log g = 3.4$, we find from Becker & Butler (1990) for respectively the first and the secondary component $T_{\rm eff} = 23\,400$ K and $T_{\rm eff} = 18\,800$ K, which we adopt as the final estimates of the effective temperature of both components.

In order to check the validity of the masses of both components of $\kappa$Scorpii we re-consider the mass function $f(M) = 1.49~M_{\odot}$ (see Table 2). From it, and from the masses of both components, we derive an orbital inclination of $50^{\circ} < i < 60^{\circ}$, which is not too different from our estimate $i = 40^{\circ }$ of the inclination angle of the rotation axis of the primary from the mode identification. Our mass estimates from the EW of the Si III lines are therefore compatible with the mass function.

From the estimate of $v \sin i = 115$ kms^-1 for the primary, we derive a rotational period of 1.90 days. If we accept our mode identification, then this leads to frequencies of 3.96 and 5.48 cd^-1 in the co-rotating frame for respectively the first and the second mode. Such frequencies are compatible with the excitation models based on the $\kappa$ mechanism. From these values we also derive that the period of the first and second mode are respectively 13% and 10% of the rotation period of the star, which is considerable for $\beta\,$Cep stars but still sufficiently low to allow a neglect of the toroidal correction terms in the pulsational velocity field.

The rotation period of the secondary cannot be derived very accurately. If we assume that this star does not pulsate, then half the width of the $\lambda 4552.6$ Å line profile at the continuum can be regarded as an upper limit for its $v \sin i$. Using the orbital inclination as a good approximation of the inclination angle of the component thus leads to a rotational period of about 1.14 days.

6 Discussion

In this paper, we have presented an extensive study of the orbital motion and of the line-profile variability of the double-lined spectroscopic binary $\kappa$Scorpii. The system consists of two rapidly-rotating B-type stars in an eccentric orbit with an orbital period of some 196 days.

The primary is clearly a line-profile variable with at least two pulsation modes. The model we obtained from the fitting of the profiles has led to the following parameters: $i = 40^{\circ }$, $v \sin i = 115$ kms^-1, $\sigma = 22$ kms^-1, and modes (2, -2) and (5, 1), with pulsation amplitudes of respectively 8 and 12 kms^-1. Of all the considered combinations, this set of parameters globally fits the profile variations best. However, this pulsation model is not able to explain all the complex variations in the line profiles. The same situation occurs for all the $\beta\,$Cep stars with a rotational velocity above 100 kms^-1 for which line-profile studies were performed very recently (see the introduction of our paper for the references). Since the number of targets with such behaviour is increasing steadily, this systematic detection of complex patterns of wiggles in the line profiles definitely seems to suggest that rotation affects significantly the pulsational behaviour of the stars.

For $\kappa$ Scorpii we clearly find indications that many more frequencies occur in the line-profile variations, besides the two modes that we tried to model in this work. Their amplitude, however, is too low to accept them, since their occurrence is usually limited to one specific part of the line profile. Data with a much higher quality, i.e. with a much larger resolving power and better signal-to-noise during a long time-base, are needed to confirm the presence of these frequency peaks and to derive their origin. In view of this additional variability it is no surprise that our best guess for a biperiodic pulsation model is not able to explain the variations in full detail. There is no sign whatsoever of these additional frequencies in the ground-based photometry of the star. We regard our study as an indication that many modes are probably excited in $\kappa$ Scorpii, as probably in most of the other rapid rotators as well.

A confirmation of the presence of a large number of pulsation modes in $\beta$ Cep stars is quite important for the evaluation of massive pulsators as good potential asteroseismic targets. The previous photometric studies of $\kappa$ Scorpii clearly point out that only data from space will have sufficient quality to discuss this issue. We therefore suggest that these stars be included in the programmes of the future seismological space missions such as MOST, MONS and COROT.

References

 

• Aerts, C., Balona, L. A., & Waelkens, C. 1989, in Confrontation between Stellar Pulsation and Evolution, ed. C. Cacciari, & G. Clementini, Astron. Soc. Pac. Conf. Ser., 11, 290 In the text  
• Aerts, C., De Pauw, M., & Waelkens, C. 1992, A&A, 266, 294 In the text NASA ADS  
• Aerts, C. 1996, A&A, 314, 115 In the text NASA ADS  
• Balona, L. A. 1984, MNRAS, 211, 973 In the text NASA ADS  
• Balona, L. A. 1986a, MNRAS, 219, 111 In the text NASA ADS  
• Balona, L. A. 1986b, MNRAS, 220, 647 NASA ADS  
• Becker, S. R., & Butler, K. 1990, A&AS, 84, 95 In the text NASA ADS  
• Berghöfer, T. W., Schmitt, J. H., & Cassinelli, J. P. 1996, A&AS, 118, 481 In the text NASA ADS  
• De Cat, P., Telting, J., Aerts, C., & Mathias, P. 2000, A&A, 359, 539 In the text NASA ADS  
• De Mey, K. 1997, Ph.D. Thesis, Katholieke Universiteit Leuven, Belgium In the text  
• De Mey, K., Aerts, C., Waelkens, C., et al. 1997, A&A, 324, 1096 In the text NASA ADS  
• Gulati, R. K., Malagnini, M. L., & Morossi, C. 1989, A&AS, 80, 73 In the text NASA ADS  
• Heasley, J. N., Wolff, S. C., & Timothy, J. G. 1982, ApJ, 262, 663 In the text NASA ADS  
• Heynderickx, D. 1991, Ph.D. Thesis, Katholieke Universiteit Leuven, Belgium  
• Heynderickx, D., Waelkens, C., & Smeyers, P. 1994, A&AS, 105, 447 In the text NASA ADS  
• Lomb, N. R., & Shobbrook, R. R. 1975, MNRAS, 173, 709 In the text NASA ADS  
• Léhmann-Filhés, R. 1894, Astr. Nach., 136, 17 In the text  
• Mathias, P., Aerts, C., Gillet, D., & Waelkens, C. 1994, A&A, 289, 875 In the text NASA ADS  
• Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 In the text NASA ADS  
• Scargle, J. D. 1982, ApJ, 263, 835 In the text NASA ADS  
• Schrijvers, C. 1999, Ph.D. Thesis, Universiteit van Amsterdam, The Netherlands In the text  
• Shobbrook, R., & Lomb, N. R. 1972, MNRAS, 156, 181 In the text NASA ADS  
• Sokolov, N. A. 1995, A&AS, 110, 553 In the text NASA ADS  
• Smith, M. A. 1977, ApJ, 215, 574 In the text NASA ADS  
• Smith, M. A. 1985, ApJ, 297, 206 In the text NASA ADS  
• Smith, M. A. 1986, ApJ, 304, 728 In the text NASA ADS  
• Stellingwerf, R. F. 1978, ApJ, 224, 953 In the text NASA ADS  
• Telting, J. H., & Schrijvers, C. 1998, A&A, 339, 150 In the text NASA ADS