A&A 371, 921-931 (2001)
DOI: 10.1051/0004-6361:20010388
On the white dwarf distances to galactic globular clusters
M. Salaris1,2 -
S. Cassisi3,2 -
E. García-Berro4,6 -
J. Isern5,6 -
S. Torres4
1 - Astrophysics Research Institute, Liverpool John Moores
University, Twelve Quays House, Egerton Wharf, Birkenhead
CH41 1LD, UK
2 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Straße 1, 85741 Garching, Germany
3 -
Osservatorio Astronomico di Collurania, via M. Maggini,
64100 Teramo, Italy
4 -
Departament de Física Aplicada, Universitat Politècnica
de Catalunya, c/Jordi Girona Salgado s/n, Módul B-4,
Campus Nord, 08034 Barcelona, Spain
5 -
Institut de Ciències de l'Espai (CSIC), Edifici Nexus, Gran
Capitá 2-4, 08034 Barcelona, Spain
6 -
Institut d'Estudis Espacials de Catalunya
Received 11 January 2001 / Accepted 9 March 2001
Abstract
We analyze in detail various possible sources of systematic errors on
the distances of globular clusters derived by fitting a local template
DA white dwarf sequence to the cluster counterpart (the so-called
WD-fitting technique). We find that the unknown thickness of the
hydrogen layer of white dwarfs in clusters plays a non negligible role.
For reasonable assumptions - supported by the few sparse available
observational constraints - about the unknown mass and thickness of
the hydrogen layer for the cluster white dwarfs, a realistic estimate of
the systematic error on the distance is within 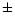 0.10 mag. However,
particular combinations of white dwarf masses and envelope thicknesses
- which at present cannot be excluded a priori - could produce
larger errors. Contamination of the cluster DA sequence by non-DA
white dwarfs introduces a very small systematic error of about -0.03mag in the
MV/(V-I) plane, but in the
MV/(B-V) plane
the systematic error amounts to
0.10 mag. However,
particular combinations of white dwarf masses and envelope thicknesses
- which at present cannot be excluded a priori - could produce
larger errors. Contamination of the cluster DA sequence by non-DA
white dwarfs introduces a very small systematic error of about -0.03mag in the
MV/(V-I) plane, but in the
MV/(B-V) plane
the systematic error amounts to 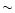 +0.20 mag. Contamination by
white dwarfs with helium cores should not influence appreciably the
WD-fitting distances. Finally, we obtain a derivative
+0.20 mag. Contamination by
white dwarfs with helium cores should not influence appreciably the
WD-fitting distances. Finally, we obtain a derivative
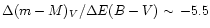 for the WD-fitting distances,
which is very similar to the dependence found when using the Main
Sequence fitting technique.
for the WD-fitting distances,
which is very similar to the dependence found when using the Main
Sequence fitting technique.
Key words: distance scale - globular clusters: general - stars: white
dwarfs
Globular cluster stars are possibly the most suitable objects to be used
in order to constrain the age of the universe. Since stars in a given
globular cluster are coeval and share the same initial chemical
composition, the turn-off brightness derived from the globular cluster
colour-magnitude diagram (CMD) provides straightforwardly the cluster
age: if the cluster distance is known, one only has to compare the
observed cluster turn-off brightness with the correspondent quantity
predicted by theoretical isochrones with the appropriate chemical
composition in order to derive a firm estimate of its age.
The globular cluster distance scale is however still the subject of an
intense debate. Main Sequence (MS) fitting distances using metal poor
Hipparcos subdwarfs with well determined parallaxes provide long
distances implying globular cluster ages of the order of 12 Gyr (see,
e.g., Gratton et al. 1997). The same long distances are derived by
Salaris & Weiss (1997, 1998), Mazzitelli et al. (1995),
Cassisi et al. (1999) when using as standard candles theoretical Zero
Age Horizontal Branch (ZAHB) models, while shorter distances are
obtained from the ZAHB models of Vandenberg et al. (2000). On the other
hand, the calibration of the RR Lyrae stars absolute brightness using
the statistical parallax methods (see, for instance, Fernley et al. 1998
and Luri et al. 1998) provides consistently much shorter distances and
therefore higher globular cluster ages. Taking these results at face
value, the uncertainty of the globular cluster distance scale appears to
be still of the order of 0.25-0.30 mag, which translates into an
indetermination on the globular cluster age of about 20% - see the
discussion in Renzini et al. (1996).
An alternative empirical method to derive globular cluster distances has
been recently applied to the galactic globular cluster NGC 6752 (Renzini
et al. 1996). The distance indicator is in this case a template local
sequence of white dwarf stars with effective temperature (
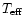 )
ranging between 10000 and 20000 K, and precise parallax
measurements, which is fitted to the dereddened cluster white dwarf
sequence. The vertical shift applied to the local template sequence in
order to fit the sequence of the cluster provides its distance modulus.
We shall refer to this technique as the WD-fitting technique, because
of its close analogy with the MS-fitting technique.
)
ranging between 10000 and 20000 K, and precise parallax
measurements, which is fitted to the dereddened cluster white dwarf
sequence. The vertical shift applied to the local template sequence in
order to fit the sequence of the cluster provides its distance modulus.
We shall refer to this technique as the WD-fitting technique, because
of its close analogy with the MS-fitting technique.
A key assumption of this method is that the white dwarfs of the local
template sequence - which, in the case of the paper by Renzini et al.
(1996), have an estimated average mass
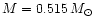 - are
totally equivalent to the white dwarfs of the cluster. If this is the
case, the main advantage of the WD-fitting technique over the
MS-fitting one is that it is in principle independent of the knowledge
of the initial chemical composition of the globular cluster, since all
white dwarfs have virtually metal free atmospheres, and therefore it
avoids the uncertainties introduced in the MS-fitting method by the
colour corrections that have to be necessarily applied to the local
subdwarfs in order to precisely match the metallicity of the globular
cluster under scrutiny.
- are
totally equivalent to the white dwarfs of the cluster. If this is the
case, the main advantage of the WD-fitting technique over the
MS-fitting one is that it is in principle independent of the knowledge
of the initial chemical composition of the globular cluster, since all
white dwarfs have virtually metal free atmospheres, and therefore it
avoids the uncertainties introduced in the MS-fitting method by the
colour corrections that have to be necessarily applied to the local
subdwarfs in order to precisely match the metallicity of the globular
cluster under scrutiny.
Another potential advantage of the WD-fitting method with respect to
the MS-fitting technique is, according to Renzini et al. (1996), that
local white dwarfs are more abundant than metal poor subdwarfs, and
therefore it is possible in principle to have a larger sample of local
calibrators. However, since white dwarfs are much dimmer than the
subdwarfs used in the MS-fitting technique, up to now it is possible to
apply the WD-fitting technique only through HST observations of
relatively close globular clusters.
Finally it should be mentioned as well that in the
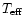 range
considered by Renzini et al. (1996), local white dwarfs appear in two
types, either as the so-called DA spectral type, which are
characterized by an envelope made up of pure H (on top of a He layer),
or as the non-DA type, which is characterized by an almost pure He
envelope and possibly, at least for 20% of them, traces of H with
abundances of the order of 10-4 by number, or even less - see the
review by Koester & Chanmugam (1990), and references therein. For
local white dwarfs the number ratio of DA versus non-DA is of the order
of 4:1 in this temperature range. Thus, the heterogeneity of the local
sample of white dwarfs could potentially have undesired effects on the
determinations of the ages and distances of globular clusters using the
WD-fitting method.
range
considered by Renzini et al. (1996), local white dwarfs appear in two
types, either as the so-called DA spectral type, which are
characterized by an envelope made up of pure H (on top of a He layer),
or as the non-DA type, which is characterized by an almost pure He
envelope and possibly, at least for 20% of them, traces of H with
abundances of the order of 10-4 by number, or even less - see the
review by Koester & Chanmugam (1990), and references therein. For
local white dwarfs the number ratio of DA versus non-DA is of the order
of 4:1 in this temperature range. Thus, the heterogeneity of the local
sample of white dwarfs could potentially have undesired effects on the
determinations of the ages and distances of globular clusters using the
WD-fitting method.
Because of the potential advantages offered by the WD-fitting method,
we analyze in detail the possible systematic uncertainties involved in
this technique due to the poor knowledge of parameters affecting the CMD
location of the template and globular cluster white dwarfs, expanding
upon the discussion by Renzini et al. (1996). We pay particular
attention to the role played by differences in the thickness of the
surface H and He layers on the final distance determination - which
has not yet been explored -, to the possible differences between white
dwarfs in clusters with predominantly blue or red Horizontal Branches
(HB), and also to the differences obtained when using DA or non-DA
model atmospheres, or evolutionary models of white dwarfs with He cores.
All along our analysis we use evolutionary white dwarf models in a
purely differential way.
The paper is organized as follows. In Sect. 2 we briefly describe the
theoretical models, while in Sect. 3 the influence of the various
parameters affecting the CMD of white dwarfs is assessed. An exhaustive
estimate of the systematic errors involved in the WD-fitting technique
is derived in Sect. 4, which is followed by Sect. 5 were we draw our
conclusions.
The stellar evolution computations have been performed using the same
code and the same input physics described in Salaris et al. (2000). We
just recall here that in the temperature range we are dealing with
(
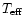 well above 6000 K) the OPAL radiative opacities
(Iglesias & Rogers 1993) with Z=0 are used, together with the
conductive opacities by Itoh et al. (1983) supplemented by the Hubbard
& Lampe (1969) ones; the boundary conditions for the integration of the
stellar structure have been derived in this case from a grey
well above 6000 K) the OPAL radiative opacities
(Iglesias & Rogers 1993) with Z=0 are used, together with the
conductive opacities by Itoh et al. (1983) supplemented by the Hubbard
& Lampe (1969) ones; the boundary conditions for the integration of the
stellar structure have been derived in this case from a grey 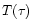 relationship, which is completely adequate at these temperatures -
see, for instance, Hansen (1999) and Salaris et al. (2000). The
equation of state for the H and He envelopes is that of Saumon et al. (1995), while the equation of state for the carbon-oxygen
(CO) core is from Segretain et al. (1994); neutrino energy losses have
been taken from Itoh et al. (1996). Bolometric luminosities and
effective temperatures have been transformed into V magnitudes and
colours using the relationships by Bergeron et al. (1995).
relationship, which is completely adequate at these temperatures -
see, for instance, Hansen (1999) and Salaris et al. (2000). The
equation of state for the H and He envelopes is that of Saumon et al. (1995), while the equation of state for the carbon-oxygen
(CO) core is from Segretain et al. (1994); neutrino energy losses have
been taken from Itoh et al. (1996). Bolometric luminosities and
effective temperatures have been transformed into V magnitudes and
colours using the relationships by Bergeron et al. (1995).
We have computed white dwarf model sequences for several masses, CO
stratifications - unless stated otherwise our reference CO
stratification is that from Salaris et al. (1997) - and various H
and/or He envelope thicknesses, which will be described in the following
section. For all the computations an initial model with the selected CO
profile and envelope structure was converged at
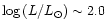 and evolved down to sufficiently low temperatures.
and evolved down to sufficiently low temperatures.
As already mentioned in Sect. 1, the WD-fitting method is based on the
fitting of a template white dwarf sequence to the correspondent globular
cluster one. The key ingredient to derive reliable distances (and hence
ages) is to ensure that the local white dwarfs included in the template
sequence are homogeneous with the globular cluster ones.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{H2635f1.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg19.gif) |
Figure 1:
Colour magnitude diagram of two cluster white dwarf cooling
sequences with ages t=10 (solid line) and 12 Gyr (dotted line), and
solar metallicity, for the white dwarf progenitors from Salaris et al. (2000). The
horizontal dashed lines mark the region with
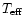 between 20000 and 10000 K
between 20000 and 10000 K |
| Open with DEXTER |
All stars in a globular cluster are coeval; therefore, the luminosity
(and, thus,
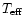 )
of a white dwarf of a given mass is
constrained by the fact that the sum of its cooling age (
)
of a white dwarf of a given mass is
constrained by the fact that the sum of its cooling age (
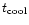 )
plus the evolutionary time of its progenitor (
)
plus the evolutionary time of its progenitor (
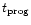 )
- which,
to a good approximation, is equal to its main sequence lifetime, since
subsequent evolutionary phases are much shorter - must be equal to the
globular cluster age (
)
- which,
to a good approximation, is equal to its main sequence lifetime, since
subsequent evolutionary phases are much shorter - must be equal to the
globular cluster age (
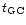 ). It is immediately clear that one
also has to assume an initial-final mass relationship, that is, a
relation between the white dwarf mass and the initial mass of its
progenitor. In Fig. 1 we show, as an example, the location of the
white dwarfs of an old cluster of initial solar metallicity and ages of 10 and 12 Gyr, respectively, in the
MV/(B-V) plane, as
predicted by the theoretical models (Salaris et al. 2000). The
horizontal lines mark the region where white dwarfs have effective
temperatures between 10000 and 20000 K, which is the temperature
range of the template field white dwarfs used by Renzini et al. (1996)
to derive the distance to NGC 6752.
). It is immediately clear that one
also has to assume an initial-final mass relationship, that is, a
relation between the white dwarf mass and the initial mass of its
progenitor. In Fig. 1 we show, as an example, the location of the
white dwarfs of an old cluster of initial solar metallicity and ages of 10 and 12 Gyr, respectively, in the
MV/(B-V) plane, as
predicted by the theoretical models (Salaris et al. 2000). The
horizontal lines mark the region where white dwarfs have effective
temperatures between 10000 and 20000 K, which is the temperature
range of the template field white dwarfs used by Renzini et al. (1996)
to derive the distance to NGC 6752.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f2.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg23.gif) |
Figure 2:
Progenitor mass (upper panel) and white dwarf mass (lower
panel) as a function of MV for the cluster cooling sequences
displayed in Fig. 1. As in the previous figure the vertical dashed
lines mark the region with
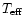 between 20000 and 10000 K
between 20000 and 10000 K |
| Open with DEXTER |
The initial-final mass relationship has been derived considering the CO
core masses after the first thermal pulse from the evolutionary models
of Salaris et al. (1997). This initial-final mass relationship
provides white dwarf masses nearly constant and equal to 0.54 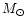 for progenitor masses up to
for progenitor masses up to 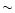
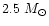 ,
and then
increasing up to 1.0
,
and then
increasing up to 1.0 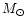 when the progenitor mass reaches
when the progenitor mass reaches
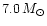 .
It can be easily seen in Fig. 1 that the cluster
white dwarf sequences show a pronounced turn to the blue at their dimmer
end which, as the age of the cluster increases, is located at
increasingly larger magnitudes. Until this blue-turn the white dwarf
sequence is almost coincident with the cooling track of the
.
It can be easily seen in Fig. 1 that the cluster
white dwarf sequences show a pronounced turn to the blue at their dimmer
end which, as the age of the cluster increases, is located at
increasingly larger magnitudes. Until this blue-turn the white dwarf
sequence is almost coincident with the cooling track of the 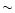
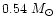 ,
while the blue-turn is due to the contribution of
more massive white dwarfs. It is easy to understand this behaviour by
recalling that at each brightness along the cooling sequence the
constraint
,
while the blue-turn is due to the contribution of
more massive white dwarfs. It is easy to understand this behaviour by
recalling that at each brightness along the cooling sequence the
constraint
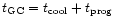 has to be valid.
Since
has to be valid.
Since
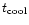 is very short at the bright end of the cooling
sequence, and practically negligible with respect to
is very short at the bright end of the cooling
sequence, and practically negligible with respect to
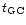 ,
,
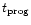 and, hence, the progenitor mass has to be, to a very good
approximation, constant for a large magnitude range, and very close to
the turn-off mass. On the contrary, towards the dim end of the cooling
sequence
and, hence, the progenitor mass has to be, to a very good
approximation, constant for a large magnitude range, and very close to
the turn-off mass. On the contrary, towards the dim end of the cooling
sequence
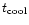 becomes a sizeable fraction of
becomes a sizeable fraction of
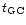 and,
thus, the contribution of the white dwarfs coming from higher mass
progenitors (and, consequently, with smaller
and,
thus, the contribution of the white dwarfs coming from higher mass
progenitors (and, consequently, with smaller
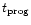 )
is quite
apparent. A similar feature is expected for the halo white dwarf
population (Isern et al. 1998).
)
is quite
apparent. A similar feature is expected for the halo white dwarf
population (Isern et al. 1998).
This feature can also be seen in Fig. 2 (upper panel) where we show
the run of the initial masses as a function of the MV magnitude
along the cluster white dwarf sequences shown in Fig. 1. In the
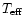 range we are dealing with (marked, as in Fig. 1, by vertical
dashed lines), the initial mass is almost constant - as well as, due
to our selected initial-final mass relationship, the actual white dwarf
mass shown in the lower panel. It is remarkable that even two
magnitudes below the lower limit of this effective temperature range the
initial mass of white dwarf progenitors is still constant. This result
(the constancy of the progenitor mass of white dwarfs contributing to
the effective temperature range, not its actual value) is completely
general, that is, independent of the adopted initial-final mass
relationship, since for all possible white dwarf masses the evolutionary
times are very fast at these high temperatures; moreover, this result is
also independent of the initial metallicity of the white dwarf
progenitors and therefore valid also in the case of white dwarf
progenitors with lower metallicities, typical of galactic globular
clusters.
range we are dealing with (marked, as in Fig. 1, by vertical
dashed lines), the initial mass is almost constant - as well as, due
to our selected initial-final mass relationship, the actual white dwarf
mass shown in the lower panel. It is remarkable that even two
magnitudes below the lower limit of this effective temperature range the
initial mass of white dwarf progenitors is still constant. This result
(the constancy of the progenitor mass of white dwarfs contributing to
the effective temperature range, not its actual value) is completely
general, that is, independent of the adopted initial-final mass
relationship, since for all possible white dwarf masses the evolutionary
times are very fast at these high temperatures; moreover, this result is
also independent of the initial metallicity of the white dwarf
progenitors and therefore valid also in the case of white dwarf
progenitors with lower metallicities, typical of galactic globular
clusters.
Since the progenitor mass is constant, one can then reasonably expect
that, even in the case of a completely different initial-final mass
relationship, the mean white dwarf mass and the spread around this value
is constant, and equal to the values attained at the beginning of the
cooling sequence. This behaviour is very different from what happens in
field disk white dwarfs. In this case, because of the ongoing star
formation processes, very different white dwarf masses can populate the
same
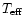 range, depending on the age of their progenitors.
range, depending on the age of their progenitors.
There are in principle four quantities which can introduce a systematic
error in the white dwarf distance determination to globular clusters,
provided that there are significant differences between the properties
of the local template white dwarf sequence and the globular cluster one,
namely:
- i)
- The mass of the white dwarf cooling sequence;
- ii)
- The chemical composition of the envelope (DA, non-DA);
- iii)
- The thickness (in mass) of the envelope;
- iv)
- The chemical stratification of the core (different CO
profiles or, even, He-core white dwarfs).
In the following we are going to discuss the influence of these four
parameters on the CMD location of white dwarf cooling sequences in the
M V/(B-V) (hereinafter BV) and
MV/(V-I) (hereinafter
VI) planes, which are actually the most popular CMDs employed for
studying cluster white dwarfs - see, e.g., Renzini et al. (1996);
Richer et al. (1997); and Von Hippel et al. (2000). We consider as a
reference the
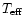 range between 10000 and 20000 K, already
selected by Renzini et al. (1996) for their distance determination. In
this temperature range the white dwarf sequence is sufficiently
populated and bright enough to be detected with a reasonable photometric
error in close globular clusters, using the HST or giant ground based
telescopes.
range between 10000 and 20000 K, already
selected by Renzini et al. (1996) for their distance determination. In
this temperature range the white dwarf sequence is sufficiently
populated and bright enough to be detected with a reasonable photometric
error in close globular clusters, using the HST or giant ground based
telescopes.
Stars in a globular cluster lose their mass along the Red Giant Branch
(RGB) due to stellar winds. The amount of mass lost during this phase
is not the same for each red giant star, and this, in turn, is the
origin of the extended horizontal branches (HB) observed in Galactic
globular clusters; this also means that the mass evolving along the RGB
(which at the beginning of the red giant phase is almost equal to the
mass of the star at the cluster turn-off) can give birth to HB stars
with different values of the total mass, but with the same initial He
core mass. These different HB stars will all end up as white dwarfs
with a mass range which is constrained mainly by the size of the helium
core at the beginning of the He-burning phase and by the mass loss
processes along the subsequent Asymptotic Giant Branch (AGB) phase.
Renzini et al. (1996) summarize the results about the few semiempirical
determinations of white dwarf masses in galactic globular clusters,
providing a very narrow range of values, namely
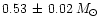 .
This range of values nicely overlaps with current
determinations of the CO core mass at the first thermal pulse derived
from stellar evolutionary models - see, e.g., Wagenhuber (1996) and
Salaris et al. (1997) - for initial masses of about
.
This range of values nicely overlaps with current
determinations of the CO core mass at the first thermal pulse derived
from stellar evolutionary models - see, e.g., Wagenhuber (1996) and
Salaris et al. (1997) - for initial masses of about
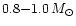 .
Moreover, it is also in agreement with determinations of
the mass distribution of nearby field white dwarfs, which peaks at about
.
Moreover, it is also in agreement with determinations of
the mass distribution of nearby field white dwarfs, which peaks at about
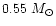 (Bragaglia et al. 1995; Reid 1996). However,
regarding this last result, the reader should keep also in mind the
recent results of Bergeron et al. (2000), who find a mean mass
of field white dwarfs about
(Bragaglia et al. 1995; Reid 1996). However,
regarding this last result, the reader should keep also in mind the
recent results of Bergeron et al. (2000), who find a mean mass
of field white dwarfs about
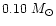 higher at lower
higher at lower
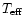 values.
values.
Very recently however, Alves et al. (2000) derived
semiempirically the mass of the central star in a planetary nebula of
the globular cluster M 15, obtaining a value
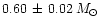 .
It is not clear yet if this result is an indication of a
globular cluster initial-final mass relationship with a larger
dispersion than that derived by Renzini et al. (1996), or it is due (as
discussed by the authors) to an increment of the mass through an
interaction in a close binary system. We just recall here that there is
also another possible indication of a large dispersion for
the initial-final mass relationship in the results obtained by Reid (1996)
when considering the white dwarf population of the Hyades open cluster.
.
It is not clear yet if this result is an indication of a
globular cluster initial-final mass relationship with a larger
dispersion than that derived by Renzini et al. (1996), or it is due (as
discussed by the authors) to an increment of the mass through an
interaction in a close binary system. We just recall here that there is
also another possible indication of a large dispersion for
the initial-final mass relationship in the results obtained by Reid (1996)
when considering the white dwarf population of the Hyades open cluster.
Another important piece of evidence must also be taken into account.
The determination of the mass range
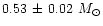 -
and the results of Alves et al. (2000), as well - is mainly based on
the maximum brightness of AGB stars and on the luminosity of post-AGB
stars, which can be directly related to the mass of the degenerate CO
core prior to the beginning of the cooling phase. However, there are
several globular clusters with an horizontal branch morphology showing
the presence of an extended blue tail, as in the case of NGC 6752.
Regardless of the physical mechanism(s) producing the stars which
populate the hot side of the HB in globular clusters, it is well known
that they are stars which have lost a large amount of their envelope
during the RGB phase. At the end of the He-burning phase these stars,
depending on the mass of their residual H-rich envelope, can behave as
post-Early AGB structures or as AGB-manqué ones - see, for
instance, Greggio & Renzini (1990) - and do not experience the
thermally pulsing phase on the AGB as most massive HB stars do. On
theoretical grounds, the minimum (initial) HB mass which does not
experience the AGB thermal pulses is a quite robust prediction (Dorman
et al. 1993; Bono et al. 1997), being equal to
-
and the results of Alves et al. (2000), as well - is mainly based on
the maximum brightness of AGB stars and on the luminosity of post-AGB
stars, which can be directly related to the mass of the degenerate CO
core prior to the beginning of the cooling phase. However, there are
several globular clusters with an horizontal branch morphology showing
the presence of an extended blue tail, as in the case of NGC 6752.
Regardless of the physical mechanism(s) producing the stars which
populate the hot side of the HB in globular clusters, it is well known
that they are stars which have lost a large amount of their envelope
during the RGB phase. At the end of the He-burning phase these stars,
depending on the mass of their residual H-rich envelope, can behave as
post-Early AGB structures or as AGB-manqué ones - see, for
instance, Greggio & Renzini (1990) - and do not experience the
thermally pulsing phase on the AGB as most massive HB stars do. On
theoretical grounds, the minimum (initial) HB mass which does not
experience the AGB thermal pulses is a quite robust prediction (Dorman
et al. 1993; Bono et al. 1997), being equal to 
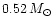 .
Since the mass of the CO core at the end of the HB phase is
of the order of
.
Since the mass of the CO core at the end of the HB phase is
of the order of
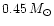 ,
globular clusters with extended blue
tails can produce also white dwarfs with masses in the range
,
globular clusters with extended blue
tails can produce also white dwarfs with masses in the range
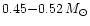 ,
on average
,
on average 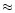
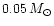 less massive
than the white dwarf progeny of stars climbing up the AGB. Thus, it is
worth considering the possibility of different masses for the globular
cluster cooling sequences.
less massive
than the white dwarf progeny of stars climbing up the AGB. Thus, it is
worth considering the possibility of different masses for the globular
cluster cooling sequences.
Turning now our attention to the CMD location of white dwarfs of
different masses, it is well known from relatively simple physical
considerations that the larger the white dwarf mass is, the smaller its
radius is. In Fig. 3 we display in the BV and VI planes, for
effective temperatures between 10000 and 20000 K, two representative
white dwarf cooling tracks with masses equal to 0.54 and
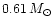 .
The higher mass is shifted to higher MV values.
The derivative
.
The higher mass is shifted to higher MV values.
The derivative
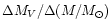 equals to 2.3 for
masses between 0.45 and 0.60
equals to 2.3 for
masses between 0.45 and 0.60 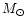 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2635f3.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg41.gif) |
Figure 3:
White dwarf cooling tracks in the BV and VI planes for
masses equal to 0.54 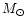 and 0.61
and 0.61 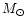 ,
and ,
and
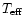 between 20000 and 10000 K between 20000 and 10000 K |
| Open with DEXTER |
As already mentioned in the introduction, field white dwarfs with
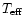 between
between 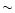 20000 and 10000 K can be present either
in the DA or non-DA types, with a number ratio of DA to non-DA
equal to 4.
Our selected standard envelope thicknesses (see next subsection) are
20000 and 10000 K can be present either
in the DA or non-DA types, with a number ratio of DA to non-DA
equal to 4.
Our selected standard envelope thicknesses (see next subsection) are
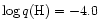 and
and
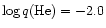 for DA white dwarfs,
and
for DA white dwarfs,
and
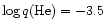 for the non-DA spectral type, where q(H)
and q(He) indicate the ratio of the mass contained in the H and He
envelope layers to the total white dwarf mass, respectively.
for the non-DA spectral type, where q(H)
and q(He) indicate the ratio of the mass contained in the H and He
envelope layers to the total white dwarf mass, respectively.
The envelope chemical composition strongly affects not only the white
dwarf cooling times, but also their location in the CMD, and the precise
shape of the cooling track, as clearly shown in Fig. 4 where we show the
cooling tracks for a
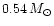 DA white dwarf (solid line) and
a non-DA white dwarf of the same mass. It is evident that in the BV
plane DA white dwarfs are brighter at a fixed colour. This is clearly
confirmed by observations of local DA white dwarfs, see e.g. panel 2 of
Fig. 1 in Renzini et al. (1996), while the reverse happens in the VIplane. Moreover, the separation between DA and non-DA white dwarfs is
larger in the BV plane, making possibly more evident their
identification in a given globular cluster. MV differences of
up to
DA white dwarf (solid line) and
a non-DA white dwarf of the same mass. It is evident that in the BV
plane DA white dwarfs are brighter at a fixed colour. This is clearly
confirmed by observations of local DA white dwarfs, see e.g. panel 2 of
Fig. 1 in Renzini et al. (1996), while the reverse happens in the VIplane. Moreover, the separation between DA and non-DA white dwarfs is
larger in the BV plane, making possibly more evident their
identification in a given globular cluster. MV differences of
up to 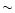 1 mag at a fixed BV value are possible in the BV plane,
while they are a factor
1 mag at a fixed BV value are possible in the BV plane,
while they are a factor 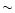 5 smaller in the VI plane. Also the
shape of the DA and non-DA cooling sequences is different, especially
in the BV plane.
5 smaller in the VI plane. Also the
shape of the DA and non-DA cooling sequences is different, especially
in the BV plane.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2635f4.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg45.gif) |
Figure 4:
Same as Fig. 3 but for a white dwarf of 0.54 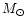 either DA or non-DA (see text for details) either DA or non-DA (see text for details) |
| Open with DEXTER |
So far, we have considered DA and non-DA white dwarfs having their very
outer layers made of either pure hydrogen or pure helium. However,
observations suggest that in this temperature range DA white dwarfs can
have a small amount of helium in their spectra, of the order of
10-5 by number, and that 20% of non-DA white dwarfs show some
hydrogen in their envelopes, with abundances of the order of 10-4by number at most. We have tested the effect of these small admixtures
of helium in the outer envelope of DA white dwarfs, and of hydrogen in
the envelope of non-DA white dwarfs, by computing appropriate models
for a
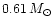 white dwarf, and using the results of
Bergeron et al. (1995) about the influence of H-He
mixtures on the derived white dwarf colours. We have found negligible
variations of the CMD location with respect to the case of our standard
He-free DA white dwarf envelopes and H-free non-DA atmospheres.
white dwarf, and using the results of
Bergeron et al. (1995) about the influence of H-He
mixtures on the derived white dwarf colours. We have found negligible
variations of the CMD location with respect to the case of our standard
He-free DA white dwarf envelopes and H-free non-DA atmospheres.
The thicknesses of the hydrogen and helium envelopes of white dwarfs has
been the subject of many investigations during the last decade. The
thickness of these layers is a key ingredient to determine the evolution
of the white dwarf since, due to their opacity, they basically regulate
the energy loss rate of the isothermal, highly conductive electron
degenerate core. Moreover, the envelope thickness also affects the
radius of the white dwarf at a given effective temperature. As
discussed by D'Antona & Mazzitelli (1990), due to the unknown details
of the mass loss process during the AGB phase and the planetary nebula
ejection, theoretical evolutionary models cannot yet provide too
stringent predictions about the thickness of the hydrogen and helium
layers surrounding the degenerate CO core.
Observational constraints based on spectroscopic (Barstow et al. 1993)
as well as on asteroseismological (Clemens 1995) analyses suggest that
local field DA white dwarfs have typically hydrogen layers of about
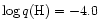 .
On the other hand, the study of the
mass-radius relationship for a sample of field white dwarfs with known
Hipparcos parallaxes provides indications that the thickness of the
hydrogen layers spans a range of values within
.
On the other hand, the study of the
mass-radius relationship for a sample of field white dwarfs with known
Hipparcos parallaxes provides indications that the thickness of the
hydrogen layers spans a range of values within
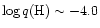 and
and
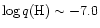 (Provencal et al. 1998). As for
the thickness of the helium layer below the hydrogen envelope the
assumed reference value comes basically from stellar evolution
constraints, and it is
(Provencal et al. 1998). As for
the thickness of the helium layer below the hydrogen envelope the
assumed reference value comes basically from stellar evolution
constraints, and it is
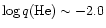 (Hansen 1999 and
references therein). We have verified, by computing white dwarf cooling
tracks with
(Hansen 1999 and
references therein). We have verified, by computing white dwarf cooling
tracks with
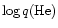 decreased by 1 dex (keeping the total
white dwarf mass constant) that the location in the CMD of DA white
dwarfs is basically unchanged. As for non-DA white dwarfs, estimates
of the envelope thickness range between
decreased by 1 dex (keeping the total
white dwarf mass constant) that the location in the CMD of DA white
dwarfs is basically unchanged. As for non-DA white dwarfs, estimates
of the envelope thickness range between 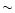
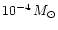 and
and
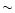
 (Pelletier et al. 1986; MacDonald et al. 1998).
(Pelletier et al. 1986; MacDonald et al. 1998).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f5.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg52.gif) |
Figure 5:
Same as Fig. 4 but for varying thicknesses of the H and He
envelopes (see text for details) |
| Open with DEXTER |
All these results are however for field white dwarfs; no indications
exist yet about
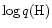 and
and
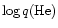 in globular
clusters, apart from the fact that theoretical evolutionary models of
white dwarfs coming from blue HB progenitors - in the hypothesis that
mass loss during the He-burning phases is negligible - predict an
upper limit to the thickness of the very outer H layers ranging from
in globular
clusters, apart from the fact that theoretical evolutionary models of
white dwarfs coming from blue HB progenitors - in the hypothesis that
mass loss during the He-burning phases is negligible - predict an
upper limit to the thickness of the very outer H layers ranging from
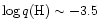 to -4.0 (Castellani et al. 1994a).
to -4.0 (Castellani et al. 1994a).
In Fig. 5 we show the effect of varying the thickness of the external H
and He layers for, respectively, a DA and and a non-DA white dwarf of
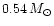 .
In the case of non-DA white dwarfs our reference
value is
.
In the case of non-DA white dwarfs our reference
value is
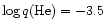 ,
which we have changed by
,
which we have changed by 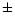 1.0 dex,
obtaining virtually no variation in the location of the cooling track
(the three tracks perfectly overlap in Fig. 5). In the case of H
envelopes the situation is different, since the thickness of the H
layers affects appreciably the location of the track. In Fig. 5
representative models with
1.0 dex,
obtaining virtually no variation in the location of the cooling track
(the three tracks perfectly overlap in Fig. 5). In the case of H
envelopes the situation is different, since the thickness of the H
layers affects appreciably the location of the track. In Fig. 5
representative models with
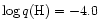 and
and
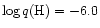 are displayed; a reduction of the thickness of the H envelope
shifts the track - at a constant value of the colour - towards
higher
are displayed; a reduction of the thickness of the H envelope
shifts the track - at a constant value of the colour - towards
higher 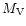 values, with a derivative
values, with a derivative
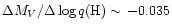 for
for
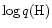 ranging between
-4.0 and -7.0.
ranging between
-4.0 and -7.0.
The chemical stratification of the CO core may potentially affect as
well the CMD location of the white dwarf track since the the mass-radius
relationship also depends on the electron mean molecular weight of the
electron-degenerate core. To this regard, it is important to realize
that the value of the CO ratio along the white dwarf core is subject to
some uncertainties due to our poor knowledge of the value of the
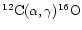 reaction rate - see the
detailed discussions in Salaris et al. (1997) or Cassisi et al. (2001),
and references therein. Moreover, for a given value of the
reaction rate - see the
detailed discussions in Salaris et al. (1997) or Cassisi et al. (2001),
and references therein. Moreover, for a given value of the
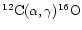 reaction rate, the CO profile is possibly
a function of the initial metallicity of the white dwarf progenitor
(Umeda et al. 1999).
reaction rate, the CO profile is possibly
a function of the initial metallicity of the white dwarf progenitor
(Umeda et al. 1999).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f6.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg59.gif) |
Figure 6:
Profile of the oxygen mass fraction (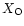 )
along the
CO core of our reference white dwarf model of )
along the
CO core of our reference white dwarf model of
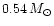 .
The
carbon abundance, .
The
carbon abundance, 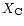 ,
is ,
is
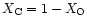 |
| Open with DEXTER |
As a numerical test, and in order to mimic these effects, we have
computed two cooling tracks for a
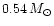 white dwarf, where,
for the first case, we have substituted our reference CO stratification
shown in Fig. 6 with a flat profile with 50% of C and 50% of O by
mass, whereas in the second case we have inverted the role of C and O,
preserving the shape of the initial chemical profile. The resulting
cooling tracks are however negligibly affected by these changes in the
effective temperature range we are dealing with. This means that,
regardless of the still large uncertainty affecting the
white dwarf, where,
for the first case, we have substituted our reference CO stratification
shown in Fig. 6 with a flat profile with 50% of C and 50% of O by
mass, whereas in the second case we have inverted the role of C and O,
preserving the shape of the initial chemical profile. The resulting
cooling tracks are however negligibly affected by these changes in the
effective temperature range we are dealing with. This means that,
regardless of the still large uncertainty affecting the
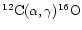 reaction rate, and regardless of the
possible effects on the CO profile of the initial progenitor
metallicity, the CMD location of the bright portion of the white dwarf
cooling sequence is not appreciably affected.
reaction rate, and regardless of the
possible effects on the CO profile of the initial progenitor
metallicity, the CMD location of the bright portion of the white dwarf
cooling sequence is not appreciably affected.
He-core white dwarfs are the byproduct of strong mass loss along the
red giant phase (due for example to the interaction with a binary
companion), which strips out the H envelope on top of the H burning
shell before the degenerate He core reaches the critical mass to
experience the He flash and the subsequent quiescent He burning phase
(Kippenhahn et al. 1967; Castellani et al.
1994b; Hansen & Phinney 1998). Their mass can range from a value close
to the degenerate He core-mass at the red giant tip (about
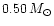 for the most metal poor globular clusters as M 92, decreasing
down to about
for the most metal poor globular clusters as M 92, decreasing
down to about
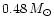 for the metal rich ones as 47 Tuc) down
to masses of the order of
for the metal rich ones as 47 Tuc) down
to masses of the order of
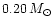 .
There is possibly at
least one direct observational indication that He-core white dwarfs
contribute to the cooling sequence of globular clusters (Moehler et al. 2000).
.
There is possibly at
least one direct observational indication that He-core white dwarfs
contribute to the cooling sequence of globular clusters (Moehler et al. 2000).
In Fig. 7 we show the CMD location of a
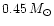 He-core
white dwarf with a H surface layer of
He-core
white dwarf with a H surface layer of
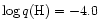 .
In the
same plot our reference DA and non-DA model sequences of
.
In the
same plot our reference DA and non-DA model sequences of
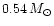 are also shown. The He-core white dwarf mass is close to
the upper possible value, lower masses being shifted to the red side of
the CMD. As expected purely on the base of the mass difference with
respect to the DA white dwarf with a CO core plotted in the figure, the
He-core white dwarf is shifted to higher brightnesses at a fixed
colour. This feature is reminiscent of the two bright white dwarfs
discarded by Renzini et al. (1996) in their fitting procedure -
compare the BV panel in Fig. 7 with Fig. 1 of Renzini et al. (1996)
- because they were clearly located to the right side of the main DA
cluster sequence. In the VI plane the He-core white dwarf sequence
overlaps with the non-DA one at the bright end of the
are also shown. The He-core white dwarf mass is close to
the upper possible value, lower masses being shifted to the red side of
the CMD. As expected purely on the base of the mass difference with
respect to the DA white dwarf with a CO core plotted in the figure, the
He-core white dwarf is shifted to higher brightnesses at a fixed
colour. This feature is reminiscent of the two bright white dwarfs
discarded by Renzini et al. (1996) in their fitting procedure -
compare the BV panel in Fig. 7 with Fig. 1 of Renzini et al. (1996)
- because they were clearly located to the right side of the main DA
cluster sequence. In the VI plane the He-core white dwarf sequence
overlaps with the non-DA one at the bright end of the
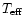 interval. In the BV plane, due to the steeper slope of the
H-envelope cooling sequences, the He-core white dwarf is on average
closer in colour to the CO one than in the VI plane.
interval. In the BV plane, due to the steeper slope of the
H-envelope cooling sequences, the He-core white dwarf is on average
closer in colour to the CO one than in the VI plane.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f7.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg63.gif) |
Figure 7:
Comparison of the CMD of a He-core white dwarf, with H
envelope and
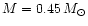 ,
with our reference DA and non-DA
sequences ,
with our reference DA and non-DA
sequences |
| Open with DEXTER |
In this section we quantify the possible systematic errors on the
distances derived from the WD-fitting technique taking into account the
results previously discussed. We study the cases in which, due to our
lack of precise empirical or theoretical determinations, the parameters
which determine the position of the white dwarf sequence on the CMD are
possibly different in the local template and in the globular cluster
sequence, but within the range allowed by independent observations.
Because the ratio between the number of DA and non-DA white dwarfs in
the field is 4:1 (and presumably this ratio is the same in globular
clusters) one is forced to use the cooling sequences of DA white dwarfs
in order to build the template sequence. This, in turn, implies that an
important role is played by the thickness of the H surface layers. To
this date, we do not have any empirical indication about the value of
q(H) for white dwarfs in globular clusters, and about its dependence
on the HB morphology. In principle, there could be sizeable systematic
differences due, for example, to the fact that in globular clusters with
blue HB (like M 92 and NGC 6752) the main component of the white dwarf
population could be produced by stars not experiencing the AGB phase, in
contrast with white dwarfs populating red HB globular clusters (like
47 Tuc). We are forced, therefore, to treat the thickness of the
envelope layers as a free parameter, in the hypothesis that the possible
range of values is within the range spanned by field white dwarfs.
Since the mass range for white dwarfs in globular clusters appears to be
mainly in the range
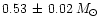 ,
it is clear that the
template white dwarf sequence should be made by stars within this mass
range. However, there are almost no field white dwarfs suitable for the
WD-fitting method, for which the value of the mass is derived
empirically (like, for instance, the case of white dwarfs in close
binary systems, as Sirius B). In order to build the template DA white
dwarf sequence, one needs therefore to employ mass determinations
obtained from semiempirical methods, as discussed in Bragaglia et al. (1995). It is possible to determine spectroscopical values for the
gravity (g) and
,
it is clear that the
template white dwarf sequence should be made by stars within this mass
range. However, there are almost no field white dwarfs suitable for the
WD-fitting method, for which the value of the mass is derived
empirically (like, for instance, the case of white dwarfs in close
binary systems, as Sirius B). In order to build the template DA white
dwarf sequence, one needs therefore to employ mass determinations
obtained from semiempirical methods, as discussed in Bragaglia et al. (1995). It is possible to determine spectroscopical values for the
gravity (g) and
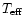 of a sample of local white dwarfs, and
then derive the masses employing theoretical
of a sample of local white dwarfs, and
then derive the masses employing theoretical
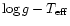 relationships. However, the assumed thicknesses of the envelope layers
of DA white dwarfs affect the
relationships. However, the assumed thicknesses of the envelope layers
of DA white dwarfs affect the
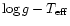 relationship. In
fact, it can be shown that a uniform distribution of
relationship. In
fact, it can be shown that a uniform distribution of
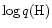 between -4.0 and -7.0 produces a mass range dispersion of about
between -4.0 and -7.0 produces a mass range dispersion of about
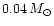 for a given couple of
for a given couple of 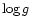 and
and
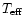 values.
values.
One could speculate if, after deriving a certain mass range for the
template white dwarfs assuming a given spread in the 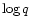 (H) values,
it is possible to judge if the results and the assumptions about the
envelope thickness are consistent with the distribution of the stars in
the CMD. As we are going to show now, this is not an easy task when
considering realistic errors on the parallax of the objects. We
determined, using our cooling tracks, three template sequences of about
100 DA white dwarfs by means of a simplified version of our Monte-Carlo
simulator (García-Berro et al. 1999), assuming a negligible error
on their colours, and allowing for an error of
(H) values,
it is possible to judge if the results and the assumptions about the
envelope thickness are consistent with the distribution of the stars in
the CMD. As we are going to show now, this is not an easy task when
considering realistic errors on the parallax of the objects. We
determined, using our cooling tracks, three template sequences of about
100 DA white dwarfs by means of a simplified version of our Monte-Carlo
simulator (García-Berro et al. 1999), assuming a negligible error
on their colours, and allowing for an error of 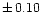 mag in
MV, which is approximately the average error of the brightness
of the template white dwarfs of Renzini et al. (1996) due to the error
on their parallaxes (which is of the order of 5%). The first sequence
(sequence A) comprises masses in the range between 0.51 and
mag in
MV, which is approximately the average error of the brightness
of the template white dwarfs of Renzini et al. (1996) due to the error
on their parallaxes (which is of the order of 5%). The first sequence
(sequence A) comprises masses in the range between 0.51 and
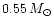 ,
and
,
and 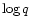 (H) uniformly distributed between -4 and -7;
sequence B has the same mass range but the value of the thickness of the
hydrogen outer layer was kept constant at
(H) uniformly distributed between -4 and -7;
sequence B has the same mass range but the value of the thickness of the
hydrogen outer layer was kept constant at
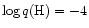 ;
finally,
sequence C is characterized by
;
finally,
sequence C is characterized by
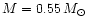 and
and
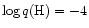 .
In Fig. 8 we show the three sequences in the BV CMD (for
.
In Fig. 8 we show the three sequences in the BV CMD (for
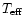 between 10000 and 20000 K), after shifting vertically
sequence B by +0.04 mag, and sequence C by +0.015 mag, in order to
reproduce the average brightness of sequence A. The average brightness
of the three sequences is different, but the dispersion around the
average looks very much the same, and dominated by the parallax error,
in spite of the fact that the mass and/or envelope thickness ranges are
different.
between 10000 and 20000 K), after shifting vertically
sequence B by +0.04 mag, and sequence C by +0.015 mag, in order to
reproduce the average brightness of sequence A. The average brightness
of the three sequences is different, but the dispersion around the
average looks very much the same, and dominated by the parallax error,
in spite of the fact that the mass and/or envelope thickness ranges are
different.
The main result of this exercise is that uncertainties in the value of
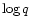 (H) produce unavoidable uncertainties on the precise value of
the masses of the template white dwarfs and, thus, on the precise
location of the template sequence, which may contribute to the error
budget of the WD-fitting technique by amounts of the order of less than
0.05 mag. For the sake of conciseness, in the following we will
consider as our reference template a sequence (determined from the
Monte-Carlo simulations) made of about 100 DA white dwarfs with masses
in the range between 0.51 and
(H) produce unavoidable uncertainties on the precise value of
the masses of the template white dwarfs and, thus, on the precise
location of the template sequence, which may contribute to the error
budget of the WD-fitting technique by amounts of the order of less than
0.05 mag. For the sake of conciseness, in the following we will
consider as our reference template a sequence (determined from the
Monte-Carlo simulations) made of about 100 DA white dwarfs with masses
in the range between 0.51 and
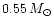 ,
,
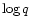 (H) uniformly
distributed between -4 and -7 and effective temperatures in the
range between 10000 and 20000 K.
(H) uniformly
distributed between -4 and -7 and effective temperatures in the
range between 10000 and 20000 K.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f8.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg70.gif) |
Figure 8:
Comparison among a white dwarf template sequence with
masses between 0.51 and
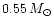 and
and 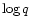 (H) between -4and -7 (sequence A, filled circles), a sequence with the same mass
range but (H) between -4and -7 (sequence A, filled circles), a sequence with the same mass
range but
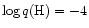 (sequence B, empty circles), and a
sequence with
(sequence B, empty circles), and a
sequence with
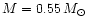 and
and
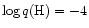 (sequence
C, starred circles). All sequences have been calculated including a
random error of 0.10 mag in their MV magnitudes. Sequences B
and C have been also shifted vertically by, respectively, 0.04 and 0.015
mag in order to overlap with sequence A
(sequence
C, starred circles). All sequences have been calculated including a
random error of 0.10 mag in their MV magnitudes. Sequences B
and C have been also shifted vertically by, respectively, 0.04 and 0.015
mag in order to overlap with sequence A |
| Open with DEXTER |
We define here as red HB globular clusters those clusters in which the
mass of the HB stars is always larger than 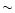
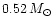 ,
corresponding to a colour of HB stars larger than
,
corresponding to a colour of HB stars larger than
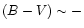 0.21.
This means that all the white dwarfs populating red HB clusters are a
product of AGB evolution (see the discussion in our previous section).
In this case, empirical estimates of the white dwarf masses show a range
between 0.51 and
0.21.
This means that all the white dwarfs populating red HB clusters are a
product of AGB evolution (see the discussion in our previous section).
In this case, empirical estimates of the white dwarf masses show a range
between 0.51 and
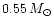 .
Thus, if the unknown thickness of
the H layers of the DA cluster white dwarfs is similar to that of the
local white dwarfs, in principle there should be no systematic
error in the distances derived using our reference template sequence.
.
Thus, if the unknown thickness of
the H layers of the DA cluster white dwarfs is similar to that of the
local white dwarfs, in principle there should be no systematic
error in the distances derived using our reference template sequence.
To obtain a reasonable estimate of the maximum possible systematic
error, our reference sequence has been fitted to a cluster DA sequence
with, respectively,
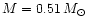 and
and
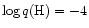 ,
and
,
and
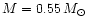 and
and
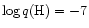 .
The systematic error in
the distance modulus is of -0.10 mag in the first case and of +0.10mag in the second case, with a
.
The systematic error in
the distance modulus is of -0.10 mag in the first case and of +0.10mag in the second case, with a 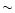 60% contribution due to the
effect of the envelope thickness. It is obvious that in the case that
the cluster white dwarfs have an intrinsic spread in mass
and/or
60% contribution due to the
effect of the envelope thickness. It is obvious that in the case that
the cluster white dwarfs have an intrinsic spread in mass
and/or
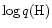 within the mentioned range, the systematic
error on their distance modulus is smaller than
within the mentioned range, the systematic
error on their distance modulus is smaller than 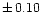 mag.
mag.
If one accepts the results of Alves et al. (2000) about M 15 as due to a
genuine spread in the initial-final mass relationship, the mass range
of globular cluster white dwarfs could possibly extend up to
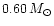 .
By repeating the previous exercise considering as an
extreme case
.
By repeating the previous exercise considering as an
extreme case
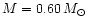 and
and
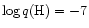 for the
cluster white dwarfs, one gets systematic errors of +0.20 mag in the
cluster distance modulus. Of course this is a very extreme case.
Probably, it is more realistic to consider a mass distribution between
0.51 and
for the
cluster white dwarfs, one gets systematic errors of +0.20 mag in the
cluster distance modulus. Of course this is a very extreme case.
Probably, it is more realistic to consider a mass distribution between
0.51 and
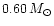 and
and
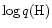 distributed between
-4 and -7. With this sample of 100 cluster white dwarfs and using
the same reference template white dwarf sequence, we determine a
systematic error on the distance modulus of +0.05 mag. Should all the
globular cluster white dwarfs have the same H layers thickness, the
systematic errors would be then +0.01 mag if
distributed between
-4 and -7. With this sample of 100 cluster white dwarfs and using
the same reference template white dwarf sequence, we determine a
systematic error on the distance modulus of +0.05 mag. Should all the
globular cluster white dwarfs have the same H layers thickness, the
systematic errors would be then +0.01 mag if
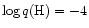 and
+0.11 mag if
and
+0.11 mag if
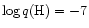 .
.
We define as blue HB globular clusters those clusters in which the mass
of the HB stars extends below 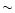
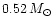 .
In general,
even globular clusters with long blue tails always have a fraction of
their HB population located at colours larger than
.
In general,
even globular clusters with long blue tails always have a fraction of
their HB population located at colours larger than
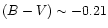 ,
and, therefore, white dwarfs populating clusters with a blue HB are the
product of both AGB evolution and AGB-manqué or post-Early AGB stars.
As discussed before, one expects that this kind of globular clusters
is populated by white dwarfs with masses down to
,
and, therefore, white dwarfs populating clusters with a blue HB are the
product of both AGB evolution and AGB-manqué or post-Early AGB stars.
As discussed before, one expects that this kind of globular clusters
is populated by white dwarfs with masses down to 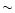
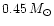 .
It appears that blue HB clusters should therefore show a
larger mass spread for the white dwarf population, with white dwarf
masses ranging between approximately 0.45 and
.
It appears that blue HB clusters should therefore show a
larger mass spread for the white dwarf population, with white dwarf
masses ranging between approximately 0.45 and
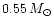 .
.
By fitting our template sequence to a cluster sequence with a mass range
between 0.45 and
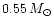 and a range of
and a range of 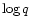 (H) as in
the template one, we obtained a systematic error on the distance modulus
of -0.06 mag. If we accept a larger mass range of up to
(H) as in
the template one, we obtained a systematic error on the distance modulus
of -0.06 mag. If we accept a larger mass range of up to
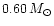 ,
the systematic error goes down to -0.04 mag, since the
higher mass objects tend to compensate for the presence of masses lower
than the template ones. This is of course just an estimate of the
average systematic error in case of globular clusters with a blue HB.
To obtain more precise evaluations one should compute synthetic CMDs for
each given cluster in order to determine, from the observed HB
morphology, the mass distribution along the HB and therefore, on the
base of the discussion in Sect. 3.1, infer the possible distribution
of white dwarf masses.
,
the systematic error goes down to -0.04 mag, since the
higher mass objects tend to compensate for the presence of masses lower
than the template ones. This is of course just an estimate of the
average systematic error in case of globular clusters with a blue HB.
To obtain more precise evaluations one should compute synthetic CMDs for
each given cluster in order to determine, from the observed HB
morphology, the mass distribution along the HB and therefore, on the
base of the discussion in Sect. 3.1, infer the possible distribution
of white dwarf masses.
Considering now the possibility of different envelope thicknesses
between template and cluster white dwarfs, if the white dwarf mass range
is between 0.45 and
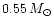 and
and
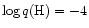 in the
cluster, the systematic error on the derived distance modulus is of
about -0.12 mag. If we adopt the same mass distribution but we change
in the
cluster, the systematic error on the derived distance modulus is of
about -0.12 mag. If we adopt the same mass distribution but we change
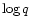 (H) to -7, the error is negligible, since the different
envelope thickness compensates for the different mass range between the
template and cluster sequence.
(H) to -7, the error is negligible, since the different
envelope thickness compensates for the different mass range between the
template and cluster sequence.
Up to know, we have made the assumption that cluster DA white dwarfs can
be distinguished from non-DA ones. In absence of spectroscopical
identification, the only way to discriminate between DA and non-DA
white dwarfs is by checking the relative CMD location of the white dwarf
sample (see Fig. 4). Here we estimate the maximum photometric error
allowing for a clear distinction between DA and non-DA objects in the
BV and VI CMDs. Moreover, we estimate the systematic errors
introduced in the globular cluster distances when using a DA template
sequence fitted to a cluster white dwarf sample made of both DA and
non-DA stars. We assume that the cluster DA/non-DA number ratio in
the
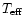 interval we are dealing with is 4:1 as in the field.
Notice, however, that below
interval we are dealing with is 4:1 as in the field.
Notice, however, that below
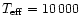 K the number of
non-DAs is similar or even larger than the number of DAs. The most
reasonable explanation for this is that the outer convective region
mixes the H layer into the He envelope (Bergeron et al. 2000).
K the number of
non-DAs is similar or even larger than the number of DAs. The most
reasonable explanation for this is that the outer convective region
mixes the H layer into the He envelope (Bergeron et al. 2000).
Figures 9 and 10 show a sequence of about 80 DA and 20 non-DA white
dwarfs (
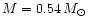 ,
,
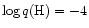 for the DAs and
for the DAs and
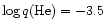 for the non-DAs) computed including 1
for the non-DAs) computed including 1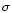 photometric errors in B, V, and I of, respectively, 0.02 and 0.05 mag. Even in the case of the smallest errors, the non-DA and DA
sequences are not well separated in the VI plane, while the DA
sequence is clearly distinguishable from the non-DA one in the BV plane.
With an error bar of the order of 0.05 mag, non-DA white dwarfs start
to be mixed up with DA ones also in the BV plane. In order to be more
precise, when fitting a template DA sequence to a cluster white dwarf
sequence including both DA and non-DA objects, one underestimates the
globular cluster distance by only 0.03 mag if the fitting is performed
in the VI plane, whereas in the case in which the fitting is performed
in the BV plane the distance is overestimated by
photometric errors in B, V, and I of, respectively, 0.02 and 0.05 mag. Even in the case of the smallest errors, the non-DA and DA
sequences are not well separated in the VI plane, while the DA
sequence is clearly distinguishable from the non-DA one in the BV plane.
With an error bar of the order of 0.05 mag, non-DA white dwarfs start
to be mixed up with DA ones also in the BV plane. In order to be more
precise, when fitting a template DA sequence to a cluster white dwarf
sequence including both DA and non-DA objects, one underestimates the
globular cluster distance by only 0.03 mag if the fitting is performed
in the VI plane, whereas in the case in which the fitting is performed
in the BV plane the distance is overestimated by 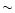 0.20 mag.
These figures are of course reduced if the ratio DA/non-DA is smaller
than the value we have adopted here.
0.20 mag.
These figures are of course reduced if the ratio DA/non-DA is smaller
than the value we have adopted here.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H2635f9.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg80.gif) |
Figure 9:
BV and VI colour-magnitude diagrams for DA (empty
circles) and non-DA (filled circles) white dwarfs (see text for
details) assuming observational errors of 0.02 mag in B, V and I |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H2635f10.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg81.gif) |
Figure 10:
Same as in Fig. 9 but for observational errors of 0.05 mag
in B, V and I |
| Open with DEXTER |
Another potential source of systematic errors in the WD-fitting
distances is the presence of He-core white dwarfs (see Fig. 7), and
although it is hard to give a precise quantitative assessment of this
error source, we can however provide an argument to give some hints
about the magnitude of this effect. We will show that the effect would
be possibly small or even negligible. White dwarfs with cores made of
He are the product of binary evolution. Actual estimates of the binary
frequency in globular clusters provide a value of the order of 10% or
less (Hut et al. 1992). If one accepts this estimate, we have verified
that, by computing a cluster cooling sequence containing about 130 CO-core white dwarfs with DA/non-DA ratio 4:1 and constant envelope
thickness (
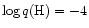 for the DAs and
for the DAs and
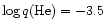 for the non-DAs), plus about 14 (about 10% of the total sample)
He-core DA objects, even if all the He-core white dwarfs have masses
of the order of
for the non-DAs), plus about 14 (about 10% of the total sample)
He-core DA objects, even if all the He-core white dwarfs have masses
of the order of
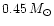 ,
their presence causes a systematic
error of the order of only -0.01 mag. In the case that there is a
spectrum of masses for He-core white dwarfs, ranging between
,
their presence causes a systematic
error of the order of only -0.01 mag. In the case that there is a
spectrum of masses for He-core white dwarfs, ranging between 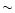 0.20 and
0.20 and
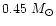 ,
then even less objects will be close
enough to the CO cooling sequences for the relevant effective
temperature range to be confused with them, while the others will lay at
larger colours, clearly separated from the more populated CO sequences
(see Fig. 11).
,
then even less objects will be close
enough to the CO cooling sequences for the relevant effective
temperature range to be confused with them, while the others will lay at
larger colours, clearly separated from the more populated CO sequences
(see Fig. 11).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H2635f11.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg83.gif) |
Figure 11:
CMD of a globular cluster cooling sequence made of CO-core
white dwarfs with masses between 0.51 and 0.55 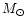 ,
DA/non-DA
ratio 4:1 (filled circles), plus a 10% fraction of He-core DA white
dwarfs with masses uniformly distributed between 0.20 and 0.45 ,
DA/non-DA
ratio 4:1 (filled circles), plus a 10% fraction of He-core DA white
dwarfs with masses uniformly distributed between 0.20 and 0.45
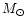 (starred circles). For all objects the envelope thickness
is constant and equal to
(starred circles). For all objects the envelope thickness
is constant and equal to
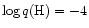 for the DAs and
for the DAs and
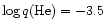 for the non-DAs
for the non-DAs |
| Open with DEXTER |
The knowledge of the reddening of the globular cluster is fundamental in
order to derive the cluster distance using the WD-fitting technique.
We tested the sensitivity of the derived distances to the uncertainty on
the cluster reddening, by considering two DA cooling tracks with
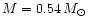 and
and
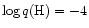 ,
shifted in colour one with
respect to the other; we then fitted the two sequences one of top of the
other for different amounts of the relative shift, obtaining in the BV
and VI planes a value for the derivative of the apparent distance
modulus with respect to the (B-V) colour excess,
,
shifted in colour one with
respect to the other; we then fitted the two sequences one of top of the
other for different amounts of the relative shift, obtaining in the BV
and VI planes a value for the derivative of the apparent distance
modulus with respect to the (B-V) colour excess,
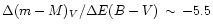 .
.
In this paper we have thoroughly discussed many possible sources of
systematic errors on the globular clusters distances obtained using the
WD-fitting technique. In order to do so we have first investigated in
detail the changes produced in the BV and VI CMDs when varying the
adopted mass of the template white dwarf cooling sequence, the influence
of the assumed thicknesses of their envelopes on the location of the
cooling tracks, as well as the consequences of changing the chemical
composition of their envelopes and of their cores. We have then applied
these results in order to derive, by means of Monte-Carlo simulations,
a realistic estimate of the systematic errors involved in the
application of this technique to galactic globular clusters. Our main
results can be summarized as follows:
- 1.
- The unknown thickness of the H layers in cluster DA white dwarfs
plays a non-negligible role, comparable to the role played by
uncertainties on the white dwarf masses. For reasonable assumptions
(derived from observations of field white dwarfs and constraints from
globular cluster CMDs) about the unknown mass and
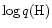 values in cluster DA white dwarfs, a realistic estimate of the maximum
systematic error on the derived distance moduli is within
values in cluster DA white dwarfs, a realistic estimate of the maximum
systematic error on the derived distance moduli is within
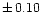 mag. However, one should be aware that particular combinations of white
dwarf masses and envelope thicknesses - still allowed by current weak
or non-existent observational constraints - could produce larger
errors.
mag. However, one should be aware that particular combinations of white
dwarf masses and envelope thicknesses - still allowed by current weak
or non-existent observational constraints - could produce larger
errors.
- 2.
- A photometric precision better than
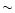 0.05 mag is needed in
order to distinguish DA from non-DA white dwarfs in the BV plane. An
even better precision is needed when using the VI plane. In the case
of larger observational errors and no clear (spectroscopical)
distinction between DA and non-DA cluster white dwarfs, fitting a
template DA sequence to a cluster sequence made of a mixture of DA and
non-DA stars introduces a very small systematic error
0.05 mag is needed in
order to distinguish DA from non-DA white dwarfs in the BV plane. An
even better precision is needed when using the VI plane. In the case
of larger observational errors and no clear (spectroscopical)
distinction between DA and non-DA cluster white dwarfs, fitting a
template DA sequence to a cluster sequence made of a mixture of DA and
non-DA stars introduces a very small systematic error 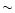 -0.03 mag
in the VI plane, but this error amounts to
-0.03 mag
in the VI plane, but this error amounts to 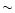 +0.20 mag, in the
BV plane. The VI plane looks therefore better suited for the
application of the WD-fitting method, since it permits to get rid of
the uncertainty due to a possible contamination of the DA sample by
non-DA white dwarfs.
+0.20 mag, in the
BV plane. The VI plane looks therefore better suited for the
application of the WD-fitting method, since it permits to get rid of
the uncertainty due to a possible contamination of the DA sample by
non-DA white dwarfs.
- 3.
- Contamination by He-core white dwarfs should not influence
appreciably the WD-fitting distances.
- 4.
- Due to the steep slopes of the white dwarf cooling curves in the
CMD, the distance derived from the WD-fitting technique has a non
negligible dependence on the adopted cluster reddening. We obtained a
derivative
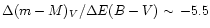 ,
a dependence
which is similar to the one of the MS-fitting technique in the BV
CMD.
,
a dependence
which is similar to the one of the MS-fitting technique in the BV
CMD.
Acknowledgements
We thank M. Zoccali for useful comments to a
preliminary version of the manuscript. Part of this work was supported
by the Spanish DGES project numbers PB98-1183-C03-02, AYA2000-1785
and ESP98-1348, by the CIRIT and by Sun MicroSystems under the Academic
Equipment Grant AEG-7824-990325-SP. One of us (S.C.) has been
supported by MURST-Cofin2000- under the scientific project
"Stellar Observables of Cosmological Relevance".
- Alves, D. R., Bond, H. E., & Livio, M. 2000, AJ, in press
In the text
- Barstow, M. A., Fleming, T. A., Diamond, C. J., et al. 1993, MNRAS, 264, 16
In the text
NASA ADS
- Bergeron, P., Saumon, D., & Wesemael, F. 1995, ApJ, 443, 764
In the text
NASA ADS
- Bergeron, P., Wesemael, F., & Beauchamp, A. 1995, PASP, 107,
1047
NASA ADS
- Bergeron, P., Leggett, S. K., & Ruiz, M. T. 2000
[astro-ph/0011286]
In the text
- Bono, G., Caputo, F., Cassisi, S., Castellani, V., & Marconi, M.
1997, ApJ, 479, 279
In the text
NASA ADS
- Bragaglia, A., Renzini, A., & Bergeron, P. 1995, ApJ, 443, 735
In the text
NASA ADS
- Cassisi, S., Castellani, V., Degl'Innocenti, S., Salaris, M.,
& Weiss, A. 1999, A&AS, 134, 103
In the text
NASA ADS
- Cassisi, S., Castellani, V., Degl'Innocenti, S., Piotto, G. P.,
& Salaris, M. 2001, A&A, 366, 578
In the text
NASA ADS
- Castellani, V., Degl'Innocenti, S., & Romaniello, M. 1994a,
ApJ, 423, 266
In the text
NASA ADS
- Castellani, V., Luridiana, V., & Romaniello, M. 1994b, ApJ,
428, 633
In the text
NASA ADS
- Clemens, J. C. 1995, in White Dwarfs, ed. D. Koester, & K.
Werner (Springer), 294
In the text
- D'Antona, F., & Mazzitelli, I. 1990, ARA&A, 28, 139
In the text
NASA ADS
- Dorman, B., Rood, R. T., & O'Connell, R. W. 1993, ApJ, 419, 596
In the text
NASA ADS
- Fernley, J., Barnes, T. G., Skillen, I., et al.
1998, A&A, 330, 515
In the text
NASA ADS
- García-Berro, E., Torres, S., Isern, J., & Burkert, A.
1999, MNRAS, 302, 173
In the text
NASA ADS
- Gratton, R. G., Fusi-Pecci, F., Carretta, E., et al.
1997, ApJ, 491, 749
In the text
NASA ADS
- Greggio, L., & Renzini, A. 1990, ApJ, 364, 527
In the text
NASA ADS
- Hansen, B. M. S. 1999, ApJ, 520, 680
In the text
NASA ADS
- Hansen, B. M. S., & Phinney, E. S. 1998, MNRAS, 294, 557
In the text
NASA ADS
- Hubbard, W. B., & Lampe M. 1969, ApJS, 18, 297
In the text
NASA ADS
- Hut, P., McMillan, S., Goodman, J., et al.
1992, PASP, 104, 981
In the text
NASA ADS
- Iglesias, C. A., & Rogers, F. J. 1993, ApJ, 412, 752
In the text
NASA ADS
- Isern, J., García-Berro, E., Hernanz, M., Mochkovitch, R.,
& Torres, S. 1998, ApJ, 486, 413
In the text
NASA ADS
- Itoh, N., Mitake, S., Iyetomi, H., & Ichimaru, S. 1983 ApJ, 273,
774
In the text
NASA ADS
- Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS,
102, 411
In the text
NASA ADS
- Kippenhahn, R., Kohl, K., & Weigert, A. 1967, Z. Ap., 66, 58
In the text
NASA ADS
- Koester, D., & Chanmugam, G. 1990, Rep. Prog. Phys., 53, 837
In the text
NASA ADS
- Luri, X., Gómez, A. E., Torra, J., Figueras, F., & Mennessier,
M. O. 1998, A&A, 335, L81
In the text
NASA ADS
- MacDonald, J., Hernanz, M., & Jose, J. 1998, MNRAS, 296, 523
In the text
NASA ADS
- Mazzitelli, I., D'Antona, F., & Caloi, V. 1995, A&A, 302, 382
In the text
NASA ADS
- Michaud, G., Bergeron, P., Wesemael, F., & Fontaine, G. 1985,
ApJ, 299, 741
NASA ADS
- Moehler, S., Heber, U., Napiwotzki, R., Koester, D., & Renzini,
A. 2000, A&A, 354, L75
In the text
NASA ADS
- Pelletier, C., Fontaine, G., Wesemael, F., Michaud, G., & Wegner,
G. 1986, ApJ, 307, 242
In the text
NASA ADS
- Provencal, J. L., Shipman, H. L., Hog, E., & Thejll, P. 1998, ApJ,
494, 759
In the text
NASA ADS
- Reid, I. N. 1996, AJ, 111, 2000
In the text
NASA ADS
- Renzini, A., Bragaglia, A. Ferraro, F. R., et al.
1996, ApJ, 465, L23
In the text
NASA ADS
- Richer, H. B., et al. 1997, ApJ, 484, 741
In the text
NASA ADS
- Salaris, M., & Weiss, A. 1997, A&A, 327, 107
In the text
NASA ADS
- Salaris, M., & Weiss, A. 1998, A&A, 335, 943
NASA ADS
- Salaris, M., Domínguez, I., García-Berro, E.,
et al. 1997, ApJ, 486, 413
In the text
NASA ADS
- Salaris, M., García-Berro, E., Hernanz, M., Isern, J.,
& Saumon, D. 2000, ApJ, 544, 1036
In the text
NASA ADS
- Saumon, D., Chabrier, G., & Van Horn, H. M. 1995, ApJS, 99, 713
In the text
NASA ADS
- Segretain, L., Chabrier, G., Hernanz, M., et al.
1994, ApJ, 434, 641
In the text
NASA ADS
- Umeda, H., Nomoto, K., Yamaoka, H., & Wanajo, S. 1999, ApJ, 513,
861
In the text
NASA ADS
- VandenBerg, D. A., Swenson, F. J., Rogers, F. J., Iglesias, C. A.,
& Alexander, D. R. 2000, ApJ, 532, 430
In the text
NASA ADS
- von Hippel, T., & Gilmore, G. 2000, AJ, 120, 1384
In the text
NASA ADS
- Wagenhuber, J. 1996, Ph.D. Thesis, Max-Planck-Institut für
Astrophysik
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{H2635f1.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f2.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2635f3.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg41.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2635f4.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg45.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f5.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg52.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f6.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f7.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H2635f8.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H2635f9.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H2635f10.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg81.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{H2635f11.ps}\end{figure}](/articles/aa/full/2001/21/aah2635/Timg83.gif)