A&A 371, 779-794 (2001)
DOI: 10.1051/0004-6361:20010427
S. Mei1,2 - P. J. Quinn2 - D. R. Silva2
1 -
Observatoire Midi-Pyrénées, 14 Av. E. Belin, 31400 Toulouse, France
2 -
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
Received 10 February 2000 / Accepted 14 March 2001
Abstract
We evaluate the method of optical and infrared Surface
Brightness Fluctuations (SBF) as a distance indicator and its
application on 8-m class telescopes,
such as the Very Large Telescope (VLT).
The novelty of our approach resides in the development of
Monte Carlo simulations
of SBF observations incorporating realistic elliptical
galaxy stellar population models, the effects induced
by globular clusters and background galaxies, instrumental
noise, sky background and PSF blurring.
We discuss, for each band and
in different observational conditions, the errors on distance
measurements arising from stellar population effects, data treatment
and observational constraints.
With 8-m class telescopes, one can extend I-band SBF
measurements out to 6000-10000 kms-1.
Integration times in the K-band are too expensive from the ground,
due to the high infrared background for large-scale distance determination projects. Nevertheless ground-based K-band measurements
are necessary to understand stellar
population effects on the SBF calibration, and to prepare
future space-based observations, where this band is
more efficient.
Key words: cosmology: observation - distance scale - large-scale structure of Universe
Distance measurements are the key to understanding many central
questions in astronomy. Correct distance measurements permit
one to map the matter distribution in the universe,
study its dynamics, and to constrain certain cosmological
parameters, such as ![]() and
and
![]() .
Beyond the limits reached by the Cepheid distance scale
(
.
Beyond the limits reached by the Cepheid distance scale
(![]() 2000 kms-1), the method of Surface Brightness Fluctuations (SBF)
is one of the most accurate currently known, with a claimed error
on single galaxy distances of 8-10%. The approach is
based on simple concepts. It can in principle be used to
calibrate other methods, such as Tully-Fisher,
2000 kms-1), the method of Surface Brightness Fluctuations (SBF)
is one of the most accurate currently known, with a claimed error
on single galaxy distances of 8-10%. The approach is
based on simple concepts. It can in principle be used to
calibrate other methods, such as Tully-Fisher,
![]() and
Supernovae I (Tonry et al. 1997), that extend beyond the limit
of SBF detection. It is therefore important to understand the method's
limitations in terms of distance and to identify the various
sources of error affecting SBF measurements.
and
Supernovae I (Tonry et al. 1997), that extend beyond the limit
of SBF detection. It is therefore important to understand the method's
limitations in terms of distance and to identify the various
sources of error affecting SBF measurements.
Recently, SBF have been successfully used to measure
distances to galaxies with radial velocities up to 4000 kms-1 with
ground-based telescopes, and up to 7000 kms-1 in optical bands using the
Hubble Space Telescope (Sodemann & Thomsen 1995; Sodemann & Thomsen 1996; Ajhar et al. 1997; Tonry et al. 1997; Thomsen et al. 1997; Lauer et al. 1998; Pahre et al. 1999; Tonry et al. 2000; Blakeslee et al. 2001; Mei et al. 2000; Tonry et al. 2001).
A recent review of the method can be found in Blakeslee et al. (1999).
The technique was introduced by Tonry & Schneider (1988) and
is based on a simple concept: the Poisson distribution of
unresolved stars in a galaxy produces fluctuations in each pixel
of the galaxy image. The variance of these fluctuations is proportional
to the square of the flux of each star (
![]() )
times the
number of stars per pixel (
)
times the
number of stars per pixel (
![]() ).
While the mean flux per pixel does not depend on distance, the variance
is inversely proportional to the square of the galaxy distance.
The SBF amplitude is defined as the variance normalized to the mean
flux of the galaxy, which then indicates the flux-weighted average stellar
flux. This implies that the brightest stars (in evolved populations,
the red giant branch) contribute most to the signal.
).
While the mean flux per pixel does not depend on distance, the variance
is inversely proportional to the square of the galaxy distance.
The SBF amplitude is defined as the variance normalized to the mean
flux of the galaxy, which then indicates the flux-weighted average stellar
flux. This implies that the brightest stars (in evolved populations,
the red giant branch) contribute most to the signal.
The SBF signal is convolved with the point spread function (PSF) created by the telescope optics and atmospheric seeing. This permits one to distinguish the galaxy fluctuations from white noise fluctuations in the image (e.g., photon shot noise, read-out noise and dark current), because in the Fourier space white noise fluctuations have a flat spectrum. At the same time, the fluctuations are contaminated by the signal from external sources, such as background galaxies, globular clusters and foreground stars, that are also convolved with the PSF. For these reasons, obtaining good SBF measurements requires good seeing and sufficiently long integration times to both extract the signal from photon shot noise, and to detect external sources and correctly estimate their luminosity function; the latter then serves to estimate and remove the contribution of faint, undetected sources from the SBF amplitude.
In addition, stellar populations vary from elliptical to elliptical, and the absolute amplitude of the fluctuations depends on these variations. This implies that the SBF amplitude is not per se a standard candle at each wavelength, but rather that it must be calibrated as a function of stellar population. Tonry and his collaborators have found an empirical calibration for the absolute magnitude of I-band SBF, via a linear relation with (V-I) color that demonstrates a universal zero point and slope (Tonry et al. 2000; Ferrarese et al. 2000). This calibration is supported by theoretical predictions from Worthey's stellar population models (Worthey 1993; Worthey 1994; Jensen et al. 1998). When making optical SBF measurements, it is thus necessary to have both V and I-band images of the observed galaxies, to obtain the precise (V-I) photometry necessary for the calibration.
In recent years the method has been extended to infrared bands for several reasons (Luppino & Tonry 1993; Pahre & Mould 1994; Jensen et al. 1996; Jensen et al. 1998; Jensen et al. 1999; Mei et al. 2001a; Mei et al. 2001b; Jensen et al. 2000). Firstly, in these bands the contrast between the brightest red giants and the underlying stellar population is more extreme than in the optical, producing larger SBF at any given distance. Secondly, the color contrast between the SBF and point sources (globular clusters and background galaxies) is larger than in the I-band. Moreover, at ground facilities, the K-band seeing is intrinsically better than I-band seeing, which further enhances the SBF contrast.
Relative to the theoretical predictions (Worthey 1993; Buzzoni 1993; Worthey 1994; Jensen et al. 1998; Mei et al. 1999; Liu et al. 1999; Liu et al. 2000; Blakeslee et al. 2001), K-band SBF absolute amplitudes are predicted to have only a weak dependence on (V-I) and a potentially larger scatter, because the effects of age and metallicity are less degenerate than in the I-band. Ellipticals measured to date (Luppino & Tonry 1993; Pahre & Mould 1994; Jensen et al. 1996; Jensen et al. 1998; Jensen et al. 1999; Jensen et al. 2000) show an almost constant K-band SBF absolute amplitude, suggesting that these fluctuations may provide a good standard candle. These arguments lead one to believe that, in the infrared, it is possible to make SBF measurements to a greater distance than in the optical, and that in the future, most SBF measurements will be taken at this wavelength. On the other hand, the ground-based background level in infrared bands is higher than in the optical, making detection of extended sources more difficult. Jensen and his collaborators have measured K-band SBF out to 7000 kms-1 from ground-based telescopes (Jensen et al. 1999; Jensen et al. 2000). Their integration times did not permit them to obtain a high signal-to-noise ratio, and they also found residual spatial variations that contaminated their SBF measurements. The low signal-to-noise ratio of most current observations, the limited size of the sample and the low (V-I) coverage of the Jensen et al. (1998) sample ( (V-I) > 1.15) prevent us from being entirely confident in the precision of K-band SBF measurements as a standard candle. Moreover, some of the ellipticals with SBF distance measurements in both I and K-bands show a discrepancy between the two (Pahre & Mould 1994; Jensen et al. 1996; Jensen et al. 1998; Mei et al. 2001a; Mei et al. 2001b), suggesting that either the measurements are affected by systematic errors (i.e., insufficient signal-to-noise), or by the presence of stellar populations that can alter the measurement and that are not taken properly into account in the present calibration. Anomalously bright cool stellar populations may already have been detected in some ellipticals (Elston & Silva 1992; Freedman 1992; Pahre & Mould 1994; Silva & Bothun 1998; Luppino & Tonry 1993; Jensen et al. 1996; Jensen et al. 1998; Mei et al. 2001a; Mei et al. 2001b).
In this paper we examine the accuracy and usefulness of the SBF method by studying the different sources of error inherent in the method. We wish to quantify the error budget for SBF measurement due to: a) stellar population effects; b) observational constraints; and c) data processing. This study permits us to better understand the potential and the limitations of the method when applied in different wave bands and at different distances. We have simulated galaxies in the I and in the K-band using theoretical models by Bruzual & Charlot (Bruzual & Charlot 1993; Charlot et al. 1996; Bruzual & Charlot 2000; Liu et al. 2000) to study the effects of population variations in the infrared. To I-band and K-band models we have added external sources and then extracted distance measurements after varying the SBF signal-to-noise ratio, the seeing, and completeness magnitude for point sources detection. In Sect. 2 we discuss the role of different stellar populations. We present our analysis of the observational constraints and data treatment in Sect. 3, and discuss the results in Sect. 4.
The attraction of a high intrinsic SBF amplitude in the infrared may be
negated by the effect of stellar population variations. By studying
stellar population effects, our aim is to understand the error on the
empirical calibration in the K-band from a theoretical point-of-view, and
the error that arises from the presence of different stellar populations.
This can be seen as a two-fold problem. On one hand, if the dispersion in
K-band absolute magnitudes, or in its dependence on galaxy colors, is small
enough, we will be able to make distance measurements with reasonable
accuracy. On the other hand, if different stellar populations have
significantly different absolute magnitudes, we might be able to distinguish
populations of different age or metallicity.
| Age | z |
|
V-I | V-K |
|
V-I | V-K |
| (SP) | (SP) | (SP) | (EMP) | (EMP) | (EMP) | ||
| (Gyr) | (mag) | (mag) | (mag) | (mag) | (mag) | (mag) | |
| 3 | 0.05 | -6.33 | 1.19 | 3.35 | - | - | - |
| 0.02 | -5.83 | 1.09 | 2.94 | -5.85 | 1.11 | 2.97 | |
| 0.008 | -5.39 | 1.03 | 2.59 | - | - | - | |
| 0.004 | -5.14 | 0.96 | 2.34 | - | - | - | |
5 |
0.05 | -6.18 | 1.27 | 3.51 | - | - | - |
| 0.02 | -5.62 | 1.14 | 3.00 | -5.63 | 1.15 | 3.04 | |
| 0.008 | -5.25 | 1.04 | 2.62 | - | - | - | |
| 0.004 | -5.07 | 1.00 | 2.41 | - | - | - | |
7 |
0.05 | -6.17 | 1.32 | 3.61 | - | - | - |
| 0.02 | -5.48 | 1.18 | 3.04 | -5.49 | 1.19 | 3.12 | |
| 0.008 | -5.50 | 1.11 | 2.78 | - | - | - | |
| 0.004 | -5.02 | 1.05 | 2.51 | - | - | - | |
12 |
0.05 | -5.90 | 1.37 | 3.67 | - | - | - |
| 0.02 | -5.50 | 1.25 | 3.25 | -5.50 | 1.27 | 3.30 | |
| 0.008 | -5.34 | 1.17 | 2.91 | - | - | - | |
| 0.004 | -4.83 | 1.10 | 2.60 | - | - | - | |
15 |
0.05 | -5.77 | 1.39 | 3.71 | - | - | - |
| 0.02 | -5.48 | 1.28 | 3.30 | -5.48 | 1.30 | 3.34 | |
| 0.008 | -5.19 | 1.20 | 2.94 | - | - | - | |
| 0.004 | -4.73 | 1.12 | 2.63 | - | - | - |
Two recent papers have explored the effects of changes in stellar populations on the SBF amplitudes, Liu et al. (2000) and Blakeslee et al. (2001). While models based on Bruzual & Charlot (2000) (Liu et al. 2000) predict a brightening of the amplitudes of K-band SBF absolute fluctuations for redder populations, independent models from Blakeslee et al. (2001) predict a dimming of the K-band absolute fluctuations for redder populations. At present, observations are not extensive enough in luminosity and color range to discriminate between the two predictions. We focus in this paper on Bruzual & Charlot (2000) models (Liu et al. 2000) that we have used in our Monte Carlo simulations.
Our simulations use single burst Bruzual and Charlot
(Bruzual & Charlot 1993; Charlot et al. 1996; Bruzual & Charlot 2000; Liu et al. 2000) stellar population models, based on Padova tracks and semi-empirical SEDs (Liu et al. 2000).
Further details on these models can be found in Liu et al.
(2000), with a wide range of predictions for SBF in different observing
bands and for different ages and metallicities.
Liu et al. (2000) also used single-burst population models. We add in this work a section on composite models.
The I and K filter used in our work correspond to the filters of the instruments FORS1 and ISAAC at the ESO 8.2 m VLT/UT1 telescope (http://www.eso.org/instruments/fors1/, http://www.eso.org/instruments/isaac/). In the I-band we used a Bessel filter.
In the K-band, we used a
![]() filter, according to the VLT ISAAC
instrument. The difference between the standard K filter and K', which
is the filter adopted by Worthey in his SBF predictions, is
filter, according to the VLT ISAAC
instrument. The difference between the standard K filter and K', which
is the filter adopted by Worthey in his SBF predictions, is ![]() mag (Jensen et al. 1998). Since the
mag (Jensen et al. 1998). Since the
![]() filter is between these two filters, our
results can be compared with Worthey's without making magnitude corrections.
Bruzual and Charlot models differ from Worthey models in their stellar
evolution prescriptions (Charlot et al. 1996). In particular, they differ in how
the stars evolve once they leave the Main Sequence and in the way
colors are assigned to stars in specific positions in the theoretical
color-magnitude diagram. Stellar population models have well-known
uncertainties, typically of
filter is between these two filters, our
results can be compared with Worthey's without making magnitude corrections.
Bruzual and Charlot models differ from Worthey models in their stellar
evolution prescriptions (Charlot et al. 1996). In particular, they differ in how
the stars evolve once they leave the Main Sequence and in the way
colors are assigned to stars in specific positions in the theoretical
color-magnitude diagram. Stellar population models have well-known
uncertainties, typically of ![]() 0.03 mag in B-V colors,
amounting to 0.1-0.14 mag in V-K colors.
0.03 mag in B-V colors,
amounting to 0.1-0.14 mag in V-K colors.
In their latest models, Bruzual and Charlot have refined the prescription for cool RGB (Red Giant Branch) and AGB (Asymptotic Giant Branch) stars in their models. In particular, they use an improved color-temperature calibration for cool stars (Feast 1996). Moreover they account for the evolution of M stars into C stars near the tip of the AGB, and its dependence on stellar mass and metallicity. The prescription is semi-empirical and based on models and observations of evolved stars in the Galaxy, the LMC and the SMC (Liu et al. 2000).
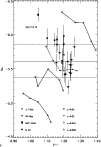 |
Figure 1: We plot K-band SBF from recent observations versus Bruzual & Charlot (2000) single burst stellar population models predictions. The filled circles are data from Jensen et al. (1998) (JLT), while the asterisks are the data from Pahre & Mould (1994) (PM). The filled square is NGC 4489 from Mei et al. (2001a) and the filled diamond is M 32 from Luppino & Tonry (1993). Ages increase from left to right, taking on values of 3, 5, 7, 12 and 15 Gyrs. Solar metallicity models are plotted as triangles, twice solar metallicity as empty circles, 40% solar metallicity as diamonds and 20% solar metallicity as squares |
| Open with DEXTER | |
We considered ages equal to 3, 5, 7, 12 and 15 Gyr,
and metallicities Z= 0.004 (20% solar), 0.008 (40% solar), 0.02
(solar) and 0.05 (twice solar).
In the case of solar metallicity, we had a choice between a
library of empirical stellar spectra (Lejeune et al. 1997) and one of
theoretical model atmospheres (Gunn & Stryker 1983; Persson et al. 1983; Fluks et al. 1994).
For the adopted initial mass function, solar metallicity and
formation redshift
![]() ,
the models provide good fits to
the spectral features and colors of nearby elliptical and S0 galaxies,
from the ultraviolet to the infrared (Kauffmann & Charlot 1998).
,
the models provide good fits to
the spectral features and colors of nearby elliptical and S0 galaxies,
from the ultraviolet to the infrared (Kauffmann & Charlot 1998).
We summarize the predictions of these models that are important in the context of our simulations in Fig. 1 and in Table 1. Additional model predictions and an interesting discussion of the models can be found in Liu et al. (2000). The comparison with Blakeslee et al. (2001) can be found in that study.
The SBF amplitude was calculated as:
In Fig. 1 we plot Bruzual and Charlot models with a Salpeter IMF in comparison to observed SBF K-band absolute magnitudes. The asterisks are the data with errors from Pahre & Mould (1994) (PM) and the filled circles are the high signal-to-noise data (as defined by Jensen et al. 1998) with errors from Jensen et al. (1998) (JLT).
We have also explored the case of composite populations by mixing two different stellar populations to study simple combinations of age and metallicity, for Bruzual & Charlot (2000) models.
In Fig. 2 we compare the
observations to Bruzual and Charlot models with
composite stellar populations, where each composite
stellar population is a mixture of two identical-age
populations of different metallicities.
To a main population of fixed age (3, 5, 7, 12, and 15 Gyrs)
and solar metallicity (Z=0.02), we have added a second
population with, respectively,
200% (open circle), 40% (open triangles) and 20%
(open squares) solar metallicity. We quantify the
presence of this second population in terms of its fractional
contribution to the total light. Thus, we see a trio
of dotted lines (one for each metallicity of the second
population) emanating from each of the five diamonds
(one for each age of the main population). The abundance
of the second population varies along each dotted line, and the
crosses indicate steps of 10% variation in the luminosity
contribution of this second population (0% at the
position of the diamond, and 100% at the position of
the symbol corresponding to the metallicity of the
second population).
The fluctuation colors of these simple
composite models are all compatible with the current observations
(
![]() and
and
![]() (Blakeslee et al. 2001)).
(Blakeslee et al. 2001)).
We conclude from these models that while young populations with high metallicities tend to increase the amplitude of the fluctuations, low metallicities lower their value. The K-band SBF amplitude becomes higher for redder populations.
At present, some galaxies with fluctuations higher than the Jensen et al. (1998) mean have been observed (Luppino & Tonry 1993; Pahre & Mould 1994; Jensen et al. 1996; Jensen et al. 1998; Mei et al. 2001a; Mei et al. 2001b), while there are no cases of galaxies observed with anomalously low fluctuations.
We have also studied the case of a composite model consisting of an old (12 and 15 Gyrs) solar metallicity population mixed with a 3 Gyr population with metallicities lower than or equal to solar (Fig. 3). The average K-band SBF amplitude for the old solar metallicity population is -5.49 mag. A one sigma detection of the 3 Gyr old population with respect to the Jensen et al. (1998) mean is a measurement of K-band SBF fluctuations brighter than -5.73; at two sigma, the K-band SBF fluctuations are brighter than -5.85. A composite 12/15 Gyr plus a 3 Gyr solar metallicity population will produce K-band SBF brighter than -5.73 when 50% of the total light is contributed by the younger population; it is never brighter than -5.85. A composite population of 12/15 Gyr solar metallicity plus a 3 Gyr at half solar metallicity population will never produce K-band SBF brighter than -5.73. Now consider a composite consisting of a 15 Gyr population at twice solar metallicity mixed with a 3 Gyr population at solar metallicity; this will produce K-band SBF between -5.77 and -5.82, i.e., between 1 and 2 sigma off the mean. Finally, single-burst populations with twice the solar metallicity all have predicted K-band SBF brighter than -5.77. These predictions differ from Blakeslee et al. (2001) stellar population model predictions, where amplitudes brighter than -5.73 are predicted for composite populations with low (V-I) colors. In conclusion, SBF amplitudes higher than the Jensen et al. (1998) mean are consistent with both a high metallicity stellar population and the presence of an intermediate age population. However, as pointed out by Liu et al. (2000), if K-band SBF are mainly sensitive to metallicity variations, they can be used in combination with age sensitive observables to break the age-metallicity degeneracy in elliptical galaxies. The predictions from Blakeslee et al. (2001) do not show this possibility. The NGC 4489 high fluctuations though are not consistent with any of these models (for discussion see Mei et al. 2000b).
To discriminate between the currently available models, the sample of ellipticals with accurate K-band SBF measurements needs to be extended to (V-I) < 1.15. In general accurate K-band SBF are only available for galaxies with (V-I) > 1.15. In that color range, our predicted SBF magnitudes and Liu et al. (2000) predicted magnitudes (both based on Bruzual & Charlot 2000 models) as well as Blakeslee et al. (2000) predicted magnitudes are consistent with each other and the available data. In our Monte Carlo simulations, we choose single-burst Bruzual & Charlot (2000) models closer to this mean and a bright magnitude. In fact, distance measurements at large distance in the K-band will be made on luminous and red galaxies.
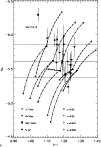 |
Figure 2:
Composite stellar population effects.
We plot K-band SBF from recent observations versus Bruzual &
Charlot (2000) single burst model predictions, shown as the open symbols. We consider
here the case of a composite population consisting of two
identical age sub-populations with different metallicities.
The filled circles are
the data from Jensen et al. (1998) (JLT), while the asterisks are the
data from Pahre & Mould (1994) (PM). The filled square is NGC 4489 from Mei et al. (2001a) and the filled diamond is M 32 from Luppino & Tonry (1993).
For the single-burst models, ages increase from left to right and take on values of 3, 5, 7, 12 and 15 Gyrs.
For the composite populations, the main sub-population is fixed at solar metallicity, and it's
position on the plot is indicated by the five diamonds (one for each
age). From each of these points emanates three dotted curves,
one for each metallicity of the second sub-population; each of
these dotted lines terminates in a symbol indicating the
metallicity of the second population. Variations along
the dotted lines show the effect of changing the abundance
of the second population. We measure this abundance
by the fractional contribution of the second population to
the total luminosity; the crosses indicate 10% steps in
luminosity contribution. The horizontal lines show the mean
(solid line) and the two standard deviation variation
(long dashed lines) of the observed
|
| Open with DEXTER | |
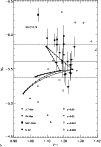 |
Figure 3:
Composite stellar population effects.
We plot K-band SBF from recent observations versus Bruzual &
Charlot (2000) single burst model predictions, shown as the open symbols. We consider
here the case of a composite population consisting of one
old age (12 Gyr and 15 Gyr) and one 3 Gyr sub-population with,
respectively, solar and solar and sub-solar metallicities.
The filled circles are
the data from Jensen et al. (1998) (JLT), while the asterisks are the
data from Pahre & Mould (1994) (PM). The filled square is NGC 4489 from Mei et al. (2001a) and the filled diamond is M 32 from Luppino & Tonry (1993).
For the single-burst models, ages increase from left to right and take on values of 3, 7, 12 and 15 Gyrs.
For the composite populations, the main sub-population is fixed at solar metallicity and age 12 Gyr and
15 Gyr. From each of these two points emanates three dotted curves,
one for each solar and subsolar metallicity of the second sub-population,
that is fixed at age 3 Gyr. Variations along
the dotted lines show the effect of changing the abundance
of the second population. We measure this abundance
by the fractional contribution of the second population to
the total luminosity; the crosses indicate 10% steps in
luminosity contribution. The horizontal lines show the mean
(solid line) and the two standard deviation variation
(long dashed lines) of the observed
|
| Open with DEXTER | |
In this section, we study errors introduced into SBF measurements by non-ideal observing conditions and data treatment. Our aim is to quantify the limits of the SBF method when measuring galaxies at large distance using large ground-based telescopes, such as the VLT, in both the I and the K-bands.
To achieve this, we have isolated the different causes of error on the measurements and have studied their contribution as a function of distance and galaxy magnitude. As observational constraints, we have considered detector efficiency, detector scale and the seeing of the observations.
Concerning data treatment, we have studied the error induced by the fitting of the galaxy power spectrum used to extract the SBF amplitude, both with and without contributions from external sources.
We then compare the results from the I and the K-bands, in order to understand the advantages and the limits of infrared and optical I-band SBF measurements.
 |
Figure 4: Simulation procedure |
| Open with DEXTER | |
We have simulated elliptical galaxies with a De Vaucouleurs
surface brightness profile.
The galaxies were constructed by randomly selecting stars from
Bruzual & Charlot (2000) theoretical luminosity functions.
Specifically, for these simulations we have chosen a model with a
Salpeter IMF, solar metallicity (Z=0.02) and an age of 12 Gyr.
This is the model that best reproduces the observed average
I and K-band SBF amplitudes.
The absolute amplitude of the K-band SBF predicted from this
model is
![]() mag, in agreement with the observed
mean of
mag, in agreement with the observed
mean of
![]() mag (Jensen et al. 1998).
In fact, K-band observations at large distance will be mainly made on
bright and red elliptical galaxies, as for the Jensen et al. (1998) sample.
The absolute amplitude of the I-band SBF predicted from this model
is
mag (Jensen et al. 1998).
In fact, K-band observations at large distance will be mainly made on
bright and red elliptical galaxies, as for the Jensen et al. (1998) sample.
The absolute amplitude of the I-band SBF predicted from this model
is
![]() mag. The (V-I) color from the model is
1.25, not too much different from the Jensen et al. (1998) sample,
but the interesting point is that our simulations predict
mag. The (V-I) color from the model is
1.25, not too much different from the Jensen et al. (1998) sample,
but the interesting point is that our simulations predict
![]() .
This value is lower than
.
This value is lower than
![]() from the Tonry
et al. (2000) calibration for the same color. All the other
parameters being fixed, brighter I-band SBF will increase
the signal-to-noise ratio (P0/P1, defined below), as well
as the ratio of SBF to external
source fluctuations. Thus, this lower value does not affect the results of this study.
from the Tonry
et al. (2000) calibration for the same color. All the other
parameters being fixed, brighter I-band SBF will increase
the signal-to-noise ratio (P0/P1, defined below), as well
as the ratio of SBF to external
source fluctuations. Thus, this lower value does not affect the results of this study.
After convolution with a Gaussian point spread
function, we added a background of white noise with contributions
from the sky, galaxy shot noise, read-out noise and dark current.
The sky magnitude was assumed to be 13 mag/arcsec2 in K-band,
and 19.2 mag/arcsec2 in I-band. These values are close to
the sky brightnesses in grey time in Paranal.
For telescope parameters, we have considered zero magnitudes,
read-out noise figures and dark currents, choosing values appropriate for
the FORS1 and ISAAC instruments at the ESO 8.2 m VLT/UT1 telescope (http://www.eso.org/instruments/fors1/, http://www.eso.org/instruments/isaac/).
The read-out noise is thus set at 10 e- and the dark current
< 0.1 e-/s for ISAAC, and respectively 6 e- and < 0.001 e-/s for FORS1. The pixel scale was assumed to be 0.15
![]() /pixel,
which is the pixel scale of ISAAC (0.147
/pixel,
which is the pixel scale of ISAAC (0.147
![]() /pixel),
and a value between the two available choices for FORS1
(0.1
/pixel),
and a value between the two available choices for FORS1
(0.1
![]() /pixel and 0.2
/pixel and 0.2
![]() /pixel). These parameters are
summarized in Table 2.
/pixel). These parameters are
summarized in Table 2.
As a first step, the error on SBF fluctuations was
calculated in the absence of external sources; this represents
an ideal lower limit on the error in estimating the fluctuation power.
The images were reduced using the standard SBF measurement procedure (see for example Tonry et al. 1997; Tonry et al. 2000; and Mei et al. 2000a for discussions).
The sky was first subtracted from the image, and then an average
galaxy brightness profile was constructed by fitting isophotes
with varying centers, ellipticity and orientation angle.
We used the IRAF![]() isophote package.
A galaxy model was thus obtained and then subtracted from the image.
Large-scale residuals were fitted and subtracted from the original image.
The final residual image was then divided by the square root of
the average galaxy profile, to normalize the fluctuations to
the average galaxy flux and to make them constant over the image.
isophote package.
A galaxy model was thus obtained and then subtracted from the image.
Large-scale residuals were fitted and subtracted from the original image.
The final residual image was then divided by the square root of
the average galaxy profile, to normalize the fluctuations to
the average galaxy flux and to make them constant over the image.
Seeing |
Scale | MV |
|
|
|
|
| (
|
(
|
(mag) | (mag) | (mag) | (mag) | (mag) |
| 0.6/1 | 0.15 | -23 | -1.03 | -5.49 | 19.2 | 13 |
The resulting image was divided into concentric
annuli, each with a radial extent of approximately 12
![]() .
Over each annulus, we calculated the power spectrum as
the square of the modulus of the spatial Fourier transform.
The PSF power spectrum was found from the Fourier
transform of the input Gaussian PSF.
This means that in our simulations we do not include errors that can come from an inaccurate estimation of the PSF Fourier transform, because of lack of good high-S/N stars in both I and K-band images.
.
Over each annulus, we calculated the power spectrum as
the square of the modulus of the spatial Fourier transform.
The PSF power spectrum was found from the Fourier
transform of the input Gaussian PSF.
This means that in our simulations we do not include errors that can come from an inaccurate estimation of the PSF Fourier transform, because of lack of good high-S/N stars in both I and K-band images.
We then fit the image power spectrum with the following
functional form: a constant P0 times the PSF power spectrum,
plus a constant term, P1, representing the
white noise power contribution:
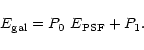 |
(2) |
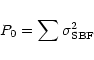 |
(3) |
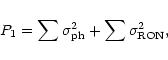 |
(4) |
where
![]() represents the surface brightness
fluctuations,
represents the surface brightness
fluctuations,
![]() the fluctuations due to photon
shot noise, and
the fluctuations due to photon
shot noise, and
![]() the contribution from read out noise.
The sum is taken over all non-zero pixels of the image.
the contribution from read out noise.
The sum is taken over all non-zero pixels of the image.
The amplitude of the fluctuations is computed as:
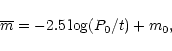 |
(5) |
The steps followed in this procedure are summarized in Fig. 4.
The error on P0 was estimated as follows: The error calculated from a linear least squares fit, for chi-squared variations, assumes that the variables to be fitted are each extracted from a Gaussian distribution. This is not directly applicable to our situation, where each power spectrum point has been calculated as the square of the FFT of Gaussian variables (the pixels in the images in which we have on average more that 10 ADU). Our power spectrum values follow instead a chi-squared distribution (Sodemann & Thomsen 1995).
In this case, the error calculated by a simple Gaussian least square fit does not represent the true fit errors. The order of magnitude of the actual error can be estimated by repeated Monte Carlo simulations. We simulate the same galaxy, with the same observational parameters, four hundred times and calculate the variance on the parameter P0 obtained from the fits.
The galaxies were simulated with an absolute magnitude of MV = -23 for distances from 10 to 130 Mpc. The percentage error on the distance measurement was calculated as a function of the distance and of the radius of the considered annulus in the galaxy.
The percentage error introduced by power spectrum
fitting was calculated as a function of the signal-to-noise ratio,
defined as:
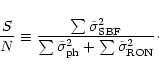 |
(6) |
Where
![]() ,
,
![]() and
and
![]() are SBF, photon shot noise and read out noise fluctuations,
normalised at the mean galaxy profile in each pixel, as defined in Tonry &
Schneider (1988).
are SBF, photon shot noise and read out noise fluctuations,
normalised at the mean galaxy profile in each pixel, as defined in Tonry &
Schneider (1988).
Our results are plotted in Figs. 5 and 6.
The total variance of the power spectrum is the sum of the variance due to
the fluctuations and due to white noise. For a S/N < 10, the white noise
dominates. At higher S/N, the fluctuations dominate and
we observe that the percentage error on the
power spectrum reaches a plateau. The plateau is
effectively reached after a signal-to-noise ratio of ![]() 10.
10.
The error due to the presence of globular clusters and background galaxies was then considered.
In this case:
When performing SBF data reduction, the contribution from external sources was evaluated and subtracted by a two step process:
First, the external sources are detected and their
magnitudes calculated. This allows us to build a luminosity
function, complete down to a cut-off magnitude
![]() .
The complete source luminosity function is then the sum of the
globular cluster luminosity function (GCLF) plus the background galaxy
luminosity function.
.
The complete source luminosity function is then the sum of the
globular cluster luminosity function (GCLF) plus the background galaxy
luminosity function.
The globular cluster Gaussian luminosity function was
assumed to be Gaussian:
![]() is defined as:
is defined as:
For the background galaxies, we assume a
power-law luminosity function (Tonry & Schneider 1988)
The detected objects are masked from the image and the measurement of the fluctuation amplitude is done as described above. The measured fluctuation amplitude will then contain the SBF amplitude plus the undetected external source fluctuations.
The second step in our SBF analysis then consists of
estimating the residual external source fluctuations,
and their subtraction from the total power spectrum amplitude.
For the globular clusters, these residuals are given by (Blakeslee & Tonry 1995):
The SBF amplitude is then estimated by:
In calculating the errors on
![]() and
and
![]() by error propagation theory, we assumed that the parameters with
errors are
by error propagation theory, we assumed that the parameters with
errors are
![]() ,
,
![]() ,
m0, and
,
m0, and
![]() all the others
being considered fixed. The errors are then given by:
all the others
being considered fixed. The errors are then given by:
![\begin{displaymath}%
\Phi= {\rm erfc}[\frac{m_{\rm cut}-m_{\rm peak}+0.8 \sigma^2 \ln(10)}{\sqrt{2}\sigma}]
\end{displaymath}](/articles/aa/full/2001/21/aa9639/img66.gif) |
(16) |
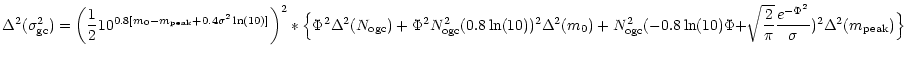 |
(17) |
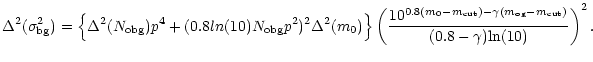 |
(18) |
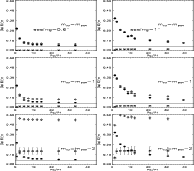 |
Figure 5:
I-band error budget found from our simulations
for seeing = 0.6
|
| Open with DEXTER | |
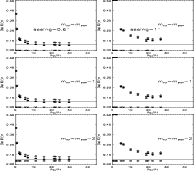 |
Figure 6:
K-band error budget found from our simulations
for seeing = 0.6
|
| Open with DEXTER | |
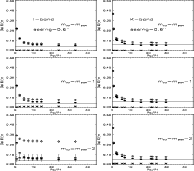 |
Figure 7: We consider here the case in which no error on the GCLF peak is included in the calculation. We plot I (on the left) and K-band (on the right) error budget found from our simulations for seeing = 0.6/arcsec. The percentage error on distance is shown as a function of the signal-to-noise ratio. Diamonds represent the total error; filled circles, the error due only to power spectrum fitting; and asterisks, the error due to external source detection and subtraction. The constant solid line is the percentage error induced by the zero point magnitude and SBF absolute magnitude |
| Open with DEXTER | |
In I and K-bands, we simulated composite
(globular cluster plus background galaxy) luminosity functions,
assuming that the error for each N as a function of magnitude
is given by a Poisson distribution. We then fit these
luminosity functions down to a completeness magnitude
![]() for four hundred independent realizations,
with the only free parameters being
for four hundred independent realizations,
with the only free parameters being
![]() and
and
![]() .
We calculated the errors on
.
We calculated the errors on
![]() and
and
![]() from the
variance of their fitted values over the simulations.
Using these latter values, we then calculated the errors
on the external source fluctuation residuals.
The error on the globular cluster peak has been taken to be
0.15 mag when
from the
variance of their fitted values over the simulations.
Using these latter values, we then calculated the errors
on the external source fluctuation residuals.
The error on the globular cluster peak has been taken to be
0.15 mag when
![]() is equal to
is equal to
![]() ,
0.20 mag when
,
0.20 mag when
![]() is equal to
is equal to
![]() ,
0.25 mag when
,
0.25 mag when
![]() is equal to
is equal to
![]() .
These values are an estimate of the error on the peak of the globular cluster luminosity function from published data (Ferrarese et al. 2000). More detailed simulations are needed to better quantify this error.
.
These values are an estimate of the error on the peak of the globular cluster luminosity function from published data (Ferrarese et al. 2000). More detailed simulations are needed to better quantify this error.
The errors due to zero-point determination and the absolute magnitude calibration of the fluctuations were added to derive a total error on distance measurements. We have taken the error in the zero-point magnitude to be 0.02 mag in the I-band, and 0.03 mag in the K-band. The error on the fluctuation absolute magnitude was set to 0.08 mag in the I-band, from the Tonry et al. (2000) calibration, and 0.12 mag from the dispersion of the K-band data available from Jensen et al. (1998). Ferrarese et al. (2000) find a similar K-band dispersion of 0.11 mag. Both these errors include the random error on Cepheid zero point, but not the systematic Cepheid zero point error of 0.16 mag (Ferrarese et al. 2000; Mould et al. 2000), that was included only in our estimation of the total percentage error in Figs. 8 and 9. If the errors on the zero-point magnitude and on the absolute magnitude calibration of the fluctuations would be the same in the K as in the I-band, the total percentage error on distance in the K-band will change by 0.01-0.03%.
Our results are presented as percentage
errors on distance versus signal-to-noise ratio in
Fig. 5 for the I-band and in Fig. 6
for the K-band; seeing equal to 0.6
![]() and 1
and 1
![]() were
considered in both cases.
The error budget shown in Figs. 5 and 6
does not include the systematic uncertainty on the Cepheid zero point. Diamonds show the total error due to power spectrum fitting,
external source detection and subtraction, plus errors
in zero-point magnitude and SBF absolute magnitude calibration.
Filled points show the relative contribution to the error budget
from power spectrum fitting; asterisks, the contribution due to
external source detection and subtraction; and the constant, solid line,
the contribution of zero-point magnitude and SBF absolute magnitude
calibration uncertainties.
From top to bottom in a column, the completeness magnitude
were
considered in both cases.
The error budget shown in Figs. 5 and 6
does not include the systematic uncertainty on the Cepheid zero point. Diamonds show the total error due to power spectrum fitting,
external source detection and subtraction, plus errors
in zero-point magnitude and SBF absolute magnitude calibration.
Filled points show the relative contribution to the error budget
from power spectrum fitting; asterisks, the contribution due to
external source detection and subtraction; and the constant, solid line,
the contribution of zero-point magnitude and SBF absolute magnitude
calibration uncertainties.
From top to bottom in a column, the completeness magnitude
![]() for external source detection decreases and is expressed relative
to the peak of the globular cluster luminosity function.
for external source detection decreases and is expressed relative
to the peak of the globular cluster luminosity function.
The percentage distance error is averaged over five
different annuli with a width of ![]() 12
12
![]() .
The error bar is given by the standard deviation over these five annuli.
The assumed SN in the plot is 6.
For lower frequencies, SN=2 and 4, the total error does
not change dramatically.
.
The error bar is given by the standard deviation over these five annuli.
The assumed SN in the plot is 6.
For lower frequencies, SN=2 and 4, the total error does
not change dramatically.
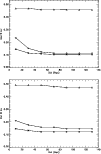 |
Figure 8:
Total I-band distance percentage error versus distance
calculated for signal-to-noise ratios corresponding to integration
times that permit a detection of external sources at 90% completeness
down to
|
| Open with DEXTER | |
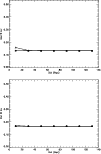 |
Figure 9:
Total K-band distance percentage error versus distance
calculated for signal-to-noise ratios corresponding to integration
times that permit a detection of external sources at 90% completeness
down to
|
| Open with DEXTER | |
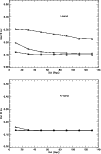 |
Figure 10:
We consider here the case in which no error on the GCLF peak is included in the calculation. From top to bottom, we plot I and K-band total distance percentage error versus distance
calculated for signal-to-noise ratios corresponding to integration
times that, in each band, permit a detection of external sources at 90% completeness
down to
|
| Open with DEXTER | |
We plot in Figs. 8 and 9
the total percentage distance error as a function of distance
calculated for signal-to-noise ratios that will permit us to obtain a completeness of 90% on
external source detection for different cut-off magnitudes
![]() .
In this percentage error the systematic error on Cepheid zero point, 0.16 mag (Ferrarese et al. 2000; Mould et al. 2000),
was included. As we can see from the figures, with a seeing equal to 0.6
.
In this percentage error the systematic error on Cepheid zero point, 0.16 mag (Ferrarese et al. 2000; Mould et al. 2000),
was included. As we can see from the figures, with a seeing equal to 0.6
![]() ,
in both I and in K-band it is possible to measure distance
with an accuracy of 10% if external sources are detected down
to one magnitude brighter than the peak magnitude of the globular
cluster luminosity function. With a seeing equal to 1
,
in both I and in K-band it is possible to measure distance
with an accuracy of 10% if external sources are detected down
to one magnitude brighter than the peak magnitude of the globular
cluster luminosity function. With a seeing equal to 1
![]() ,
for large distances, the typical errors on measurements are similar. The key quantity is therefore the integration time necessary for the detection of external sources (which depends both on distance and on seeing) and crowding
effects.
,
for large distances, the typical errors on measurements are similar. The key quantity is therefore the integration time necessary for the detection of external sources (which depends both on distance and on seeing) and crowding
effects.
Reaching the peak magnitude of the globular
cluster luminosity function is time expensive to realise in practice.
Typical observations will attain a completeness in external source detection
between one to one and half magnitude fainter than the estimated peak magnitude of the
globular cluster luminosity function. This will be the major source of error
on large distance measurements.
In our simulations, we fixed the peak and the dispersion of the globular cluster luminosity function, when fitting it. We assumed an error on the globular cluster luminosity function peak equal to 0.15 mag when
![]() is equal to
is equal to
![]() ,
0.20 mag when
,
0.20 mag when
![]() is equal to
is equal to
![]() ,
0.25 mag when
,
0.25 mag when
![]() is equal to
is equal to
![]() .
These values have been chosen from published data (Ferrarese et al. 2000) and they take into account the fact that the error will increase as
.
These values have been chosen from published data (Ferrarese et al. 2000) and they take into account the fact that the error will increase as
![]() falls below
falls below
![]() .
More detailed simulations would be needed to further quantify this point.
We show in Figs. 7 and 10 what
the calculated errors would be in both bands when not taking in account any error on
.
More detailed simulations would be needed to further quantify this point.
We show in Figs. 7 and 10 what
the calculated errors would be in both bands when not taking in account any error on
![]() ,
in the case in which the seeing is equal to 0.6
,
in the case in which the seeing is equal to 0.6
![]() .
.
We can now compare the two bands. From Figs. 8 and 9, the first difference to note between the two bands is that, while in the I-band the percentage error changes significantly as a function of the cut-off magnitude, in the K-band the error tends to degenerate to closest values. This is because of the higher color contrast of the fluctuations in K with respect to the external source color in this band. The percentage contribution of external source fluctuations to SBF fluctuations does not change as dramatically as in the I-band when the cut-off changes by one or two magnitudes. One could at this point think that this peculiar characteristic of the K-band would permit us to reach larger distances in this band than in the I-band. This is actually not true from the ground, due to the long integration time required to detect external sources down to a significant cut-off magnitude in the presence of the high background in the K-band.
In fact, given these results and knowing the
VLT I and K-band integration times required to obtain the signal-to-noise
ratios that we considered, we can put limits on the distance
attainable within a given percentage distance error.
For a galaxy of absolute V magnitude of -23,
we have predicted from simulations that it is possible in the I-band, with a total (integration time plus overheads) exposure time no larger than 12 hours, and a sky of 19.2 mag/arcsec2, to reach distances up to ![]() 90 Mpc, or, for H0=70 km/s/Mpc,
90 Mpc, or, for H0=70 km/s/Mpc, ![]() 6500 kms-1,
within an error of
6500 kms-1,
within an error of ![]() 10% for a seeing equal to 0.6
10% for a seeing equal to 0.6
![]() (assuming to detect external source up to a cutoff magnitude one magnitude below the peak of the globular cluster luminosity function). If the total exposure time can be increased to 24 hours, it will be possible, under the same conditions, to reach distances around
(assuming to detect external source up to a cutoff magnitude one magnitude below the peak of the globular cluster luminosity function). If the total exposure time can be increased to 24 hours, it will be possible, under the same conditions, to reach distances around ![]() 10000 kms-1. In the K-band, with a total exposure time no larger than 12 hours, and a sky of 13 mag/arcsec2,
it is possible to reach distances up to
10000 kms-1. In the K-band, with a total exposure time no larger than 12 hours, and a sky of 13 mag/arcsec2,
it is possible to reach distances up to ![]() 40 Mpc, or, for
H0=70 km/s/Mpc,
40 Mpc, or, for
H0=70 km/s/Mpc, ![]() 3000 km s-1, with an error of around
10% and a seeing equal to 0.6
3000 km s-1, with an error of around
10% and a seeing equal to 0.6
![]() ;
or
;
or ![]() 3500 kms-1, when a sky magnitude of 13.7 mag/arcsec2 is assumed (assuming to detect external source up to a cutoff magnitude two magnitudes below the peak of the globular cluster luminosity function). If the total exposure
time can be increased to 24 hours, it will be possible, under the
same conditions, to reach distances around
3500 kms-1, when a sky magnitude of 13.7 mag/arcsec2 is assumed (assuming to detect external source up to a cutoff magnitude two magnitudes below the peak of the globular cluster luminosity function). If the total exposure
time can be increased to 24 hours, it will be possible, under the
same conditions, to reach distances around ![]() 4000 kms-1
with an error around 15%, with a seeing equal to 1
4000 kms-1
with an error around 15%, with a seeing equal to 1
![]() .
We have assumed an overhead of approximately 50%.
.
We have assumed an overhead of approximately 50%.
We thus conclude that while I-band SBF observations at ground-based large telescopes will permit one to extend the current ground-based sample out to 6500-10000 kms-1, K-band SBF measurements from the ground alone will be limited by the high infrared background.
Hybrid approaches, as already pointed out by Jensen and
his collaborators (Jensen et al. 1996, 1998, 1999, 2000) can combine SBF observations
in the K-band with external source detection in the I-band,
reducing expensive exposure time in the K-band while maintaining a correct
estimation of the external source contribution.
On the one hand, when external sources are detected in the I-band around
one magnitude below
![]() ,
this approach has the advantage
of providing two independent (even if there will not be an independent
external source detection) SBF distance measurements, or of
providing information on the galaxy stellar population.
On the other hand, as can be seen from Fig. 9, when external sources are detected for
,
this approach has the advantage
of providing two independent (even if there will not be an independent
external source detection) SBF distance measurements, or of
providing information on the galaxy stellar population.
On the other hand, as can be seen from Fig. 9, when external sources are detected for
![]() larger than
larger than
![]() ,
I-band distance measurements present errors from 10% to 50%,
while K-band measurement errors at the same
,
I-band distance measurements present errors from 10% to 50%,
while K-band measurement errors at the same
![]() are around 10%.
A more detailed study of combining I and K-band surveys has to be explored, in order to define the optimal approach depending on distance and on observing
conditions.
are around 10%.
A more detailed study of combining I and K-band surveys has to be explored, in order to define the optimal approach depending on distance and on observing
conditions.
We must point out that the errors that we have derived
are lower limits. We are estimating errors within the available
observational constraints and standard data processing.
We have not considered other sources of error, such as anomalous
boxiness or diskiness of the galaxy, or profiles differing
from a standard de Vaucouleurs profile.
We have assumed that these effects are negligible
and corrected by the smooth fit of the residual image
after the first subtraction of the galaxy model. We did not consider crowding effects on the detection of external sources. We assumed the error on the globular cluster luminosity function peak in function of
![]() ,
but did not strengthened these values with simulations. More detailed simulations would be needed to further quantify these points.
,
but did not strengthened these values with simulations. More detailed simulations would be needed to further quantify these points.
We can compare these theoretical predictions with VLT I-band SBF
that we measured in IC 4296 (Mei et al. 2000), an elliptical galaxy in Abell 3565
(![]() 3500 kms-1). For this galaxy we have measured a distance modulus of
3500 kms-1). For this galaxy we have measured a distance modulus of
![]() mag and a galaxy
distance of
mag and a galaxy
distance of ![]() Mpc. From HST I-band SBF measurements, Lauer et al. (1998) have obtained
Mpc. From HST I-band SBF measurements, Lauer et al. (1998) have obtained
![]() mag with a derived distance of
mag with a derived distance of ![]() Mpc. The seeing of this
observation was 0.7
Mpc. The seeing of this
observation was 0.7
![]() .
We obtain a completeness magnitude at around one
magnitude brighter than the globular cluster luminosity function peak. The percentage error
on distance that we obtained on IC 4296 is
.
We obtain a completeness magnitude at around one
magnitude brighter than the globular cluster luminosity function peak. The percentage error
on distance that we obtained on IC 4296 is ![]() 8%, This error is
consistent with our Monte Carlo prediction of
8%, This error is
consistent with our Monte Carlo prediction of ![]() 10% for external
source detection up to one magnitude brighter than the globular cluster
luminosity function peak, as presented in Sect. 3.2, Fig. 6.
The error on distance that we obtain with
2.3 hours of integration time is comparable to 3.2 hours integration time from the Hubble Space Telescope (Lauer et al. 1998). This result confirms the potential of 8-m class telescope in large distance ground-based SBF observations.
Ground-based observations from large telescopes are thus competitive with space observations, but with the advantage of larger fields of view, permitting
one to measure more ellipticals in the same field. Our conclusions are also in agreement with the recent observations and conclusions from Tonry et al. (2001).
10% for external
source detection up to one magnitude brighter than the globular cluster
luminosity function peak, as presented in Sect. 3.2, Fig. 6.
The error on distance that we obtain with
2.3 hours of integration time is comparable to 3.2 hours integration time from the Hubble Space Telescope (Lauer et al. 1998). This result confirms the potential of 8-m class telescope in large distance ground-based SBF observations.
Ground-based observations from large telescopes are thus competitive with space observations, but with the advantage of larger fields of view, permitting
one to measure more ellipticals in the same field. Our conclusions are also in agreement with the recent observations and conclusions from Tonry et al. (2001).
We have evaluated in this paper the potential of SBF measurements in the I and in the K-band. The method is limited by stellar population effects and by the errors that come from observational conditions and data treatment. The I-band is currently well-calibrated by the Tonry et al. (2000) linear relation between SBF amplitudes and galaxy (V-I) color. We have studied the effect of stellar population on the K-band amplitudes with Bruzual and Charlot stellar population model predictions.
Bruzual & Charlot (2000) single
age - single metallicity models with a Salpeter IMF and solar metallicity,
predict an average
![]() mag and (V-I) colors
between 1.1 and 1.39. This value is consistent
with previous K-band observations in the Virgo and Fornax cluster by Jensen
et al. (1998). The average and standard deviation of the Jensen et al. (1998)
sample is
mag and (V-I) colors
between 1.1 and 1.39. This value is consistent
with previous K-band observations in the Virgo and Fornax cluster by Jensen
et al. (1998). The average and standard deviation of the Jensen et al. (1998)
sample is
![]() mag for (V-I) colors between 1.15
and 1.27.
mag for (V-I) colors between 1.15
and 1.27.
We have also examined the prediction of Bruzual and Charlot models with a Salpeter IMF in the case of composite populations.
These models (cf. Liu et al. 2000) predict that the presence of young populations and high metallicities will increase the amplitude of the fluctuations, while low metallicities will lower their value.
Independent models by Blakeslee et al. (2001) also predict higher amplitude fluctuations in younger populations, but a much weaker metallicity dependence.
The variation of the absolute SBF might explain the higher than average SBF, observed in some of the low signal-to-noise sample of Jensen et al. (1998) and Pahre & Mould (1994), as well as the higher than standard K-band fluctuations observed by Mei et al. (2001a) in NGC 4489. At present, galaxies with anomalous low fluctuations have not been observed. NGC 4489 has lower (V-I) than the Jensen et al. (1998) sample from which the current K-band calibration is derived. From theoretical predictions, its higher K-band SBF amplitude can be explained both by the presence of an intermediate age population (from Liu et al. 2000 predictions) or by a difference in metallicity, quantified from the difference in (V-I) (predictions from Blakeslee et al. 2001 models).
Additional K-band SBF data over a larger range of galaxy colors and luminosities are necessary to improve the precision on the empirical calibration. A better calibration at lower (V-I) would permit one to discriminate between the Liu et al. (2000) and Blakeslee et al. (2001) predictions.
We have also quantified the limit of the method in both the I and the K-band by studying the error budget that comes from observational conditions and data treatment, using Monte Carlo simulations. In our simulation K-band galaxies were considered over the range of the Jensen et al. (1998) calibration, because measurements on large distances will be based on luminous, red galaxies.
According to our results, the VLT and other very large telescopes will permit us to extend SBF distance measurements in the I-band to a distance ![]() 6500 kms-1 within a percentage error on single galaxy distance of
6500 kms-1 within a percentage error on single galaxy distance of ![]() 10%. In the K-band, distances
10%. In the K-band, distances ![]() 3000 kms-1 will be reached with a percentage error on distance of
3000 kms-1 will be reached with a percentage error on distance of ![]() 10%.
This error can be compared to the single galaxy distance percentage error
10%.
This error can be compared to the single galaxy distance percentage error ![]() 10% that can be obtained by the PNLF method and Supernovae Type Ia, and it is smaller than the 15-20% distance error that can be obtained by Tully-Fisher and
10% that can be obtained by the PNLF method and Supernovae Type Ia, and it is smaller than the 15-20% distance error that can be obtained by Tully-Fisher and
![]() .
.
This means that SBF distance measurements on large telescopes will permit us to extend the current ground-based I-band sample to twice the current distance limit, to calculate bulk flows beyond the current limit of 3000 kms-1 (Tonry et al. 2000), and to compare distances and peculiar velocities with those derived from other methods.
On the other hand, measuring in the K-band alone does not permit us to go very deep in distance from the ground, due the high background level in the infrared and the high integration times needed to detect external sources. Jensen et al. (1998) have made extensive use of optical images for external source detection. They have derived globular cluster luminosity functions from the I-band image of the galaxies that they observed in the K-band, and employed it to correct the external source contribution to the SBF fluctuations in the K-image. This method requires both I and K images of the same galaxies, and permits one to clearly identify the SBF fluctuations in the K-band with no contamination.
The optimal use of both bands for distance measurements has to be studied with more detailed simulations, but it is nevertheless useful in two other respects. Firstly, it enables us to discriminate among stellar population models. Secondly, the use of combined I and K-band SBF will help us gain knowledge on K-band SBF calibration in preparation for space-based observations, that are possible on NICMOS on the HST (Jensen et al. 2000) and will be possible with the NGST. In fact, in space the background in the K-band is significantly lower and the required source extraction will be possible in reasonable integration times.
Current K-band measurements from the ground might thus help in stellar population model discrimination and study of stellar population age and metallicity in elliptical galaxies (Liu et al. 2000; Blakeslee et al. 2001), and can lay the basis for further K-band SBF measurements from the space.
These conclusions need to be strengthened by exploring a wider range of parameters and by more extensive simulations of errors due to the corrections of the external source contribution, to the PSF template fitting, and to irregular isophotes. Our approach is novel for its application of realistic Monte Carlo simulations of SBF observations. It will be further developed in subsequent work.
Acknowledgements
We are grateful to S. Charlot for proving Bruzual & Charlot models and to our referee, John Blakeslee, for his useful comments. S. Mei thanks M. Romaniello and P. A. Duc for the interesting discussions, J. G. Bartlett for reading the manuscript, and acknowledges support from the European Southern Observatory Studentship programme and Director General's Discretionary Fund.