A stationary self-consistent outflow of a magnetised relativistic plasma from a rotating object with an initially monopole-like magnetic field is investigated in the ideal MHD approximation under the condition
A&A 371, 1155-1168 (2001)
DOI: 10.1051/0004-6361:20010201
S. V. Bogovalov
Moscow Engineering Physics Institute, Kashirskoje Shosse 31, Moscow, 115409, Russia
Received 15 December 1999 / Accepted 16 January 2001
Abstract
A stationary self-consistent outflow of a magnetised relativistic plasma
from a rotating object with an initially monopole-like magnetic field is
investigated in the ideal MHD approximation under the condition
![]() ,
where
,
where ![]() is the ratio of the Poynting flux over the mass energy
flux at the equator and the surface of the star, with
is the ratio of the Poynting flux over the mass energy
flux at the equator and the surface of the star, with
![]() and
and ![]() the initial four-velocity and
Lorentz factor of the plasma. The mechanism of the magnetocentrifugal
acceleration and self-collimation of the relativistic plasma is
investigated. A jet-like relativistic flow along the axis
of rotation is found in the steady-state solution under the condition
the initial four-velocity and
Lorentz factor of the plasma. The mechanism of the magnetocentrifugal
acceleration and self-collimation of the relativistic plasma is
investigated. A jet-like relativistic flow along the axis
of rotation is found in the steady-state solution under the condition
![]() with properties predicted analytically.
The amount of the collimated matter in the jet is rather small in
comparison to the total mass flux in the wind.
An explanation for the weak self-collimation of relativistic winds
is given.
with properties predicted analytically.
The amount of the collimated matter in the jet is rather small in
comparison to the total mass flux in the wind.
An explanation for the weak self-collimation of relativistic winds
is given.
Key words: MHD - stars: winds, outflows-plasma-relativity - galaxies: jets
Radio pulsars (Michel 1991), superluminal galactic objects (Mirabel & Rodriguez 1994, 1998) and AGNs (Begelman et al. 1984; Pelletier et al. 1996) are observed to be associated with relativistic outflows. AGNs and superluminal galactic objects produce jets, while radio pulsars demonstrate a surprisingly high efficiency of transforming the pulsar rotational energy into kinetic energy of the relativistic wind (Kennel & Coroniti 1984). Hence, the problem of acceleration and collimation of relativistic plasmas is among the most important in the physics of relativistic outflows.
Nevertheless, radio pulsars, AGNs and superluminal galactic objects are objects of rather different nature and scales. It may well be that the mechanisms of acceleration of the outflows in these sources are not the same. However, there seems to exist a mechanism which operates very well for all these objects, namely, the so-called magnetocentrifugal acceleration where the acceleration of the plasma outflow occurs in the magnetic field of the rotating object. Such conditions are realized in the magnetospheres of radio pulsars, in the winds from accretion disks (Blandford & Payne 1982) and apparently in superluminal galactic objects (Mirabel & Rodriguez 1998). However, it has not been investigated whether the magnetocentrifugal mechanism could provide the acceleration of the relativistic plasma in these objects to the observed bulk motion velocities.
The analysis of problem of the relativistic plasma acceleration and collimation in a rotating magnetosphere started with Michel (1969), where it was shown that the magnetocentrifugal acceleration of the plasma is not effective for a prescribed monopole-like magnetic field. Subsequently, the relativistic plasma outflow has been investigated in several other studies and for different astrophysical conditions (Okamoto 1978; Ardavan 1979; Beskin et al. 1983; Camenzind 1986). In particular, the ultrarelativistic plasma outflow from an accretion disk was investigated numerically in Camenzind (1987) while the structure of electromagnetically driven relativistic jets was discussed in Li (1993) under the assumption of jet confinement by an ambient medium. Collimation of stellar magnetospheres to jets in the force-free approximation was studied in Sulkanen & Lovelace (1990) and Fendt et al. (1995). Later, Fendt & Camenzind (1996) investigated the plasma dynamics in the MHD approximation in magnetic configurations obtained via the force-free approximation. A class of self-similar solutions of the relativistic plasma outflow has been obtained in Contopoulos (1994). It was found that the efficiency of the plasma acceleration can be higher than in Michel's solution due to the effect of the magnetic collimation of the wind to the axis of rotation (Begelman & Li 1994; Fendt & Camenzind 1996; Takahashi & Shibata 1998). Thus, the problem of the relativistic plasma acceleration in a rotating magnetic field appeared to be closely connected to the problem of plasma collimation.
Strong evidence has been accumulated for a correlation between collimated astrophysical outflows (jets) and accretion disks. Direct evidence for a disk-jet connection has been demonstrated by HST observations of the Herbig-Haro object HH 30 (Burrows et al. 1996), although on the theoretical front this connection was discussed earlier (Camenzind 1990; Ferreira & Pelletier 1993; Falke & Biermann 1995). A disk-jet connection is also supported by observations of the active galaxy M 87 (Ford et al. 1994) and superluminal galactic objects (Mirabel & Rodriguez 1998). These observations seem to lead to the conclusion that jets require the existence of accretion disks for their formation (e.g. Livio 1999) and therefore accretion disks should be a necessary element of the collimation mechanism. However, we have by now reliable evidence that there is at least one source producing jets without the presence of an accretion disk. Namely, recent observations of the Crab Nebula by the Chandra observatory leave no doubts that the Crab pulsar indeed produces jets (Weiskopff et al. 2000). Therefore, it would be important to understand the mechanism of plasma collimation in all known jet sources, including the Crab pulsar.
Such a mechanism is provided by magnetic collimation of outflows from
accretion disks and it was first suggested by Lovelace (1976),
Blandford (1976) and Bisnovatyi-Kogan & Ruzmaikin
(1976). Subsequently, it was shown from an analysis of the full
set of the MHD equations for
nonrelativistic (Heayvaerts & Norman 1989) and relativistic
outflows (Chiueh et al. 1991; Bogovalov 1995) that
collimation is a rather general property of magnetised winds from a
rotating object. A magnetised fast-mode supersonic
wind inevitably will be partially cylindrically collimated along the
axis of rotation at distances large compared to all
characteristic dimensions of the source, such as the size of the
accretion disk, provided that: the flow is non-dissipative,
the magnetised central object is rotating, the total magnetic flux of
one polarity reaching infinity (open field lines) is finite, the polytropic
index of the plasma exceeds unity and the pressure of ambient matter is
low enough not to be able to terminate the wind before the formation of the jet.
This result is independent of the specific properties of the
central source. Collimation occurs spontaneously due to the internal Lorentz
force arising in the magnetised plasma which is ejected from the rotating source
and therefore can be regarded as a process of self-collimation (hereafter
SC process). Note that the assumption of a polytropic gas with a constant
polytropic index ![]() does not seem really
restrictive, since several exact MHD solutions for collimated outflows have
been constructed for the case of a variable index
does not seem really
restrictive, since several exact MHD solutions for collimated outflows have
been constructed for the case of a variable index ![]() ,
Sauty & Tsinganos
(1994), Vlahakis & Tsinganos (1998).
,
Sauty & Tsinganos
(1994), Vlahakis & Tsinganos (1998).
Although the SC process has been questioned (e.g., Okamoto 1999), a numerical investigation of this process and the characteristics of jets produced via this mechanism in the cold (Bogovalov & Tsinganos 1999) or hot (Tsinganos & Bogovalov 2000; Sauty et al. 1999) nonrelativistic winds leave no doubt that this mechanism works. This mechanism provides the formation of cylindrically collimated outflows at a large distance from the central source while collimation is accompanied by essentially more efficient acceleration of the plasma at the equatorial region as compared with the original study of Michel (1969). Evidence for the focusing of MHD outflows from accretion disks to the axis of rotation at distances of the order of the dimension of accretion disks has been obtained in other studies as well, such as in Ouyed & Pudritz (1997), Ustyugova et al. (1999) and Krasnopolskii et al. (1999).
In the analysis of Bogovalov & Tsinganos (1999), the relaxation method was used to obtain the solution of the steady state outflow problem, i.e., the time-dependent problem was solved in order to get a steady-state solution. This method was first employed by Washimi & Shibata (1993) for outflows from stellar objects. Later this method was applied in Bogovalov (1996) for the investigation of the SC process in an initially monopole-like magnetic field. It seems that this numerical method allows us to solve accurately all problems connected with the critical surfaces (Bogovalov 1997b; Tsinganos et al. 1996).
In our previous study (Bogovalov 1997a), the relaxation method has been applied to the investigation of the relativistic plasma outflow and it was found that the relativistic plasma is very weakly collimated and accelerated even if the Poynting flux dominates the matter energy flux at the equator. However, an analytical study performed in this work has shown that an efficient SC of the relativistic plasma is still possible for very fast rotation of the central source. Recently it has been argued that a relativistic plasma is poorly accelerated even under this condition (Beskin et al. 1998). However, the SC process was totally neglected in this work. Therefore, the question concerning the efficiency of the acceleration and SC of the relativistic winds from fast rotators remains open.
Outflows of magnetised plasmas are described by the system of the familiar nonlinear MHD equations. It is not surprising that this system has many solutions corresponding to different physical conditions. Then, a reasonable choice of the appropriate approximation and a sound model is crucially important to arrive at some physically meaningful solution.
To formulate the basic demands of the model let us consider the general properties of winds and jets. According to observations, the length of the jets greatly exceeds all characteristic scales of the central source. Therefore, for an investigation of the SC process and the characteristics of the jets, the theory should allow us to obtain the solution on scales greatly exceeding all sizes of the central source.
Observations of winds and jets from several classes of astrophysical objects such as our Sun (Parker 1963), or, YSO's (Burrows et al. 1996), pulsars (Kennel & Coroniti 1984) and AGNs (Ferrari et al. 1996) show that they are super-magnetosonic at relatively large distances from the source. At the same time all winds must be subsonic near the central source where the basic parameters of the outflows are controlled. Therefore, the theory must describe flows of mixed type, containing the small scale regions of a subsonic flow and the large scale regions of the super magnetosonic flow. The scales of these regions may differ by several orders of magnitude. These properties of the outflows dictate the choice of the approximations and mathematical models.
The force-free approximation has been widely used for the analysis of axisymmetric relativistic outflows (Scharlemann & Wagoner 1973; Mestel & Wang 1979; Beskin et al. 1983; Lyubarskii 1990; Fendt et al. 1995). For simplification reasons, the axisymmetric stellar magnetosphere can be assumed initially to have a dipolar magnetic field (Contopoulos et al. 1999). However, this approximation is not appropriate for the investigation of the SC process for several reasons. For example, it describes only subsonic flows of plasma since the force-free transfield (Grad-Shafranov) equation is elliptic everywhere (Fendt et al. 1995). Therefore, this approximation cannot be used for the investigation of plasma outflow in the supersonic regions. Moreover, the collimating and accelerating forces are equal to zero in this approximation. For these reasons, the force-free approximation gives ambiguous results. For example, the structure of the flow of the relativistic plasma at large distances from the source obtained in Sulkanen & Lovelace (1990) and in Fendt et al. (1995) differs from the structure obtained in Contopoulos et al. (1999). Although Sulkanen & Lovelace (1990) and Contopoulos et al. (1999) used similar models, Contopoulos et al. (1999) obtained a radially outflowing plasma while Sulkanen & Lovelace (1990) obtained collimated jets. Jets were obtained as well in Fendt et al. (1995). Actually all these works are mathematically correct. The difference between them is only in the boundary conditions at infinity or at the outer boundary of the integration domain. These works clearly demonstrate that the flow of plasma at large distances from the source in the force-free approximation basically depends on the boundary conditions at infinity. But there is no such dependence in real supersonic flows. This is the most important qualitative difference between the subsonic and super fast magnetosonic flows.
In the steady state subsonic flow the MHD signals propagate down and upstream of the flow. That is why the plasma flow is defined by the forces affecting the plasma at a given point, upstream and down stream of the flow. This is not the case in the super fast magnetosonic flow. No MHD signals can propagate upstream of the supersonic flow. The supersonic flow is defined only by the forces which affect the plasma upstream and at the given point and does not depend on the forces which affect the plasma downstream of the flow. For this reason the supersonic flow does not depend on the boundary conditions located downstream of the flow (actually the situation is more complicated; the flow should cross the fast mode critical surface, Bogovalov 1997b). The simplest approximation which allows us to describe the mixed type outflows is the ideal MHD approximation. This approximation is used in this paper.
However, even the use of the MHD approximation does not always allow us to investigate the SC process in the supersonic region. There is a wide class of self-similar solutions for the nonrelativistic (e.g. Blandford & Payne 1982; Vlahakis & Tsinganos 1999) and relativistic plasma (Contopoulos 1994). All these solutions terminate not so far from the source. Independent of why this termination happens, the self-similar solutions cannot be used for the verification of the predictions of the SC theory since the central source has infinitely large size with infinite magnetic flux in the upper hemisphere. At any distance from the source, the dimension of the source exceeds the distance to the source. However, we are interested in the opposite case, when the distance is large compared with the dimension of the central source. Therefore, we demand that the appropriate model should have finite geometrical dimensions, finite magnetic flux of the open field lines of every polarity and initially uncollimated plasma outflow. The last condition is important for us since our objective is to study the process which transforms the initially uncollimated outflow into the outflow containing the jet. The word "initially'' means that if one of the conditions for the SC process is not fulfilled (for example if the central source is not rotating or the magnetic field is absent) the wind expands radially at large distances from the source. Actually, a lot of models satisfy all these conditions.
The SC is a general property of magnetised winds from rotating sources. It must take place in a wind from any source provided that the conditions specified by Heayvaerts & Norman (1989), Chiueh et al. (1991) and Bogovalov (1995) are fulfilled. Therefore "convenience'' and "simplicity'' become reasonable arguments for the choice of the model for the investigation of this process. The model of a star with a wind in an initially monopole-like (below m-l) magnetic field firstly proposed by Sakurai (1985) is the most simple and convenient. This model allows us to avoid the mathematically complicated problem connected with the coexistence of open and closed field lines near the source which actually has no direct relation to the SC process and usually is considered particular (Keppens & Goedbloed 1999).
The model with the initially monopole-like magnetic field describes a more wider class of outflows, including the time-dependent outflows from oblique rotators (Bogovalov 1999) and outflows from objects with arbitrary distribution of the polarity of the magnetic field at the base (Tsinganos & Bogovalov 2000).
In this paper we consider the outflow of an initially cold relativistic plasma and neglect only gravitation since we are interested in the effect of the electromagnetic forces only on the plasma.
The plasma outflow from astrophysical objects consists of two zones where the properties of the flow differ qualitatively. The nearest zone is located near the surface of the central source and includes all the critical surfaces of the steady state flow (Bogovalov 1997b). The outer boundary of the nearest zone can be located rather arbitrary but always downstream of the fast mode critical surface. The flow of the plasma in the nearest zone is of the mixed type. It is subsonic near the source and is super fast magnetosonic at the outer boundary. The far zone is located downstream of the nearest zone. The plasma flow in the far zone is super fast magnetosonic. Different methods should be applied for the solution of the problem in each of these zones.
The solution of the problem of the steady state plasma outflow can be divided in two steps (Bogovalov & Tsinganos 1999). In the first step, the problem is solved in the nearest zone by the relaxation method and in the second, the steady state solution in the far zone is obtained by solving directly the transfield equation as a Cauchy problem. The solution in the nearest zone is used to specify the initial values for the flow in the far zone.
The system of equations defining the dynamics of the relativistic
plasma in the ideal MHD approximation is as follows,
The problem was solved in the cylindrical system of coordinates. Some details of the solution method are given in Appendix A. The numerical simulation was performed only in the quarter of the total box of simulation due to the symmetry of the flow in relation to the equatorial plane and the axis of rotation. The boundaries of the nearest zone include the surface of the star, the axis of rotation, the equator and the outer boundaries, which are a cylinder (right hand side of the box) and a plane perpendicular the axis of rotation at some distance from the source (upper side of the box). The outer boundaries are located in the supersonic domain of the flow beyond the fast mode critical surface. This guarantees the independence of the solution in the nearest zone of the position and conditions of the outer boundaries.
The number of independent boundary conditions on the surface of the star is equal to the number of MHD waves leaving the surface to satisfy the causality in the flow (Bogovalov 1997b). They are as follows:
At the outer boundaries only one side internal derivatives were used for calculation of the derivatives in the finite differences, since the solution does not depend on the conditions down the flow from these boundaries.
The flow in the far zone is fast mode supersonic. The system of equations describing the steady state flow is hyperbolic. Therefore, a Cauchy problem can be formulated for this flow.
It is convenient to introduce the
flux function ![]() as follows
as follows
The stationary MHD equations admit well known four integrals (Tsinganos 1982). They are:
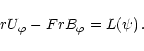 |
(8) |
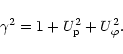 |
(11) |
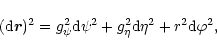 |
(12) |
According to Landau & Lifshitz (1975) the equation
![]() ,
where Tij is the energy-momentum tensor and "k'' denotes covariant
differentiation, will have the following
form in these coordinates,
,
where Tij is the energy-momentum tensor and "k'' denotes covariant
differentiation, will have the following
form in these coordinates,
The unknown variables here
are
![]() and
and
![]() .
The metric coefficient
.
The metric coefficient ![]() can be obtained from the
transfield Eq. (13),
can be obtained from the
transfield Eq. (13),
The metric coefficient ![]() can be obtained from definition (6)
in terms of the magnitude of the poloidal magnetic field as follows
can be obtained from definition (6)
in terms of the magnitude of the poloidal magnetic field as follows
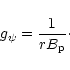 |
(16) |
with ![]() calculated by the expression (14).
Here
calculated by the expression (14).
Here
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
For the numerical solution of the system of Eq. (19)
the two step Lax-Wendroff method on the lattice with a dimension equal
to 1000 is used.
.
For the numerical solution of the system of Eq. (19)
the two step Lax-Wendroff method on the lattice with a dimension equal
to 1000 is used.
Equation (19) should be supplemented by
appropriate boundary conditions and initial values on some initial surface
of constant ![]() located in the nearest zone, but down the flow from all the critical surfaces.
The form of the initial surface of constant
located in the nearest zone, but down the flow from all the critical surfaces.
The form of the initial surface of constant ![]() was obtained
numerically through integration of the following equations,
was obtained
numerically through integration of the following equations,
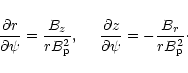 |
(20) |
Boundary conditions on the axis of rotation and the equatorial plane are the same as the conditions in the nearest zone. No conditions at infinity were specified.
A stationary solution of the relativistic plasma flow from the star with
an initially m-l magnetic field is defined by three
dimensionless parameters (Bogovalov 1999). One of them is the ratio of
the
radius of the star
![]() to the radius of the initial fast mode
magnetosonic surface
to the radius of the initial fast mode
magnetosonic surface
![]() ,
where
,
where
![]() .
The word "initial" here refers to the radius of the fast mode surface when the
star is not rotating.
But this dependence can be neglected under the condition
.
The word "initial" here refers to the radius of the fast mode surface when the
star is not rotating.
But this dependence can be neglected under the condition
![]() and
and
![]() ,
where
,
where
![]() is the radius of the light cylinder, and
is the radius of the light cylinder, and ![]() is the
angular velocity of the uniformly rotating star.
Therefore, the solution crucially
depends only on two dimensionless parameters which can be chosen rather
arbitrary. It is convenient to choose one of them as follows
is the
angular velocity of the uniformly rotating star.
Therefore, the solution crucially
depends only on two dimensionless parameters which can be chosen rather
arbitrary. It is convenient to choose one of them as follows
It is convenient to take the second parameter as follows
Representation of the solution in the parameters ![]() ,
,
![]() is
convenient since the steady state outflow in the initially m-l
magnetic field has a simple analytical solution in the limit
is
convenient since the steady state outflow in the initially m-l
magnetic field has a simple analytical solution in the limit
![]() independent of the value of
independent of the value of ![]() (Bogovalov 1997a) and the transition to the nonrelativistic
limit corresponds simply to
the limit
(Bogovalov 1997a) and the transition to the nonrelativistic
limit corresponds simply to
the limit
![]() and
and
![]() .
.
For comparison with observation, Eq. (21) should be expressed in
variables general for the m-l model and real astrophysical objects.
An astrophysical object can be considered as equivalent to the
object with the m-l magnetic field if they both produce winds with
the same magnetic flux, the same mass flux,
the same initial Lorentz factor and finally both rotate with the same
angular velocity. The magnetisation parameter in these variables
takes the form
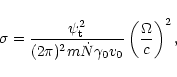 |
(25) |
The position of the radio pulsars in the parameter space ![]() ,
,
![]() was discussed in detail by Bogovalov (1999).
All radio pulsars eject Poynting-dominated winds (
was discussed in detail by Bogovalov (1999).
All radio pulsars eject Poynting-dominated winds (
![]() )
but basically
all of them are slow rotators (
)
but basically
all of them are slow rotators (
![]() ). One of the youngest and
fastest rotating pulsars with a strong magnetic field on the surface
is the pulsar in the Crab Nebula. This pulsar rotates with
). One of the youngest and
fastest rotating pulsars with a strong magnetic field on the surface
is the pulsar in the Crab Nebula. This pulsar rotates with
![]() and ejects
and ejects
![]() pairs with
the rate
pairs with
the rate
![]() per second and average
per second and average
![]() (Daugherty & Harding 1982). At
(Daugherty & Harding 1982). At
![]() G the magnetisation parameter of the wind
G the magnetisation parameter of the wind
![]() and
and
![]() The light cylinder radius of the Crab pulsar is located at the distance
The light cylinder radius of the Crab pulsar is located at the distance
![]() cm from the axis of rotation. The radius of the
fast magnetosonic surface
cm from the axis of rotation. The radius of the
fast magnetosonic surface ![]() exceeds the
light cylinder radius by a factor of 114. Marginally, the Crab pulsar
could be the fast rotator provided that
exceeds the
light cylinder radius by a factor of 114. Marginally, the Crab pulsar
could be the fast rotator provided that
![]() .
The uncertainties
in estimates of this parameter do not rule out this possibility.
But all other, more slowly rotating pulsars are certainly the slow rotators.
.
The uncertainties
in estimates of this parameter do not rule out this possibility.
But all other, more slowly rotating pulsars are certainly the slow rotators.
In AGNs and superluminal sources ![]() is defined from observations of
jets and lies in the range 1-10. If the collimation of the plasma
is really due to the SC process we should expect that
is defined from observations of
jets and lies in the range 1-10. If the collimation of the plasma
is really due to the SC process we should expect that
![]() and
and
![]() .
So, the winds from AGNs and superluminal sources
should be mainly Poynting flux dominated.
.
So, the winds from AGNs and superluminal sources
should be mainly Poynting flux dominated.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{ms9493f1r.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg115.gif) |
Figure 1:
The steady-state relativistic plasma flow in the nearest zone
of the star for the parameters |
| Open with DEXTER | |
In Fig. 1 we show the result of the numerical simulation of the
plasma outflow in the nearest zone of the star, for a time interval
![]() and for the set of the values of the two key parameters,
and for the set of the values of the two key parameters,
![]() and
and ![]() .
This time interval is larger by a factor of 2.62 compared to the typical
time the plasma and all MHD perturbations take to travel from the surface
of the star to the fast mode surface.
Note that during this time interval, a steady state solution is reached
.
This time interval is larger by a factor of 2.62 compared to the typical
time the plasma and all MHD perturbations take to travel from the surface
of the star to the fast mode surface.
Note that during this time interval, a steady state solution is reached![]() ,
since all perturbations which could be excited at the start of the simulation
have left the box of simulation. The initial fast mode surface is circular
with a radius equal to 1 in our units.
Note that the final fast mode surface shown in Fig. 1 has a small amplitude kink
structure at a polar angle around 45 degrees. Such a structure is formed
in all simulations performed with the present method and in the present geometry
(Washimi & Shibata 1993; Bogovalov & Tsinganos 1999).
Basically it is due to the shape of the surface of the star which is
actually approximated by a sequence of step functions in the cylindrical
system of coordinates.
,
since all perturbations which could be excited at the start of the simulation
have left the box of simulation. The initial fast mode surface is circular
with a radius equal to 1 in our units.
Note that the final fast mode surface shown in Fig. 1 has a small amplitude kink
structure at a polar angle around 45 degrees. Such a structure is formed
in all simulations performed with the present method and in the present geometry
(Washimi & Shibata 1993; Bogovalov & Tsinganos 1999).
Basically it is due to the shape of the surface of the star which is
actually approximated by a sequence of step functions in the cylindrical
system of coordinates.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{ms9493f2r.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg127.gif) |
Figure 2:
The relativistic plasma flow in the far zone for
|
| Open with DEXTER | |
The SC theory predicts that a wind of relativistic plasma consists of a cylindrically collimated core surrounded by a radially expanding flow (Heyvaerts & Norman 1989; Chiueh et al. 1991; Bogovalov 1995). An inspection of Fig. 1 shows that the collimation of the plasma along the axis of rotation is practically invisible in the nearest zone. The results of the same simulation in the far zone are presented in Fig. 2. At a first glance, in the far zone there is no cylindrical collimation. However, a closer examination of the results shows that a cylindrically collimated core is actually formed in the wind.
Figure 3 gives the distribution of the poloidal magnetic field
across the axis of rotation for two values of z.
This distribution differs from that expected
for a m-l wind. The m-l poloidal magnetic field is described by the
equation
![]() .
And, at a fixed z the poloidal field
normalized to its value at the axis of rotation (
.
And, at a fixed z the poloidal field
normalized to its value at the axis of rotation (
![]() )
depends on ras
)
depends on ras
![]() .
Then, at
.
Then, at
![]() the poloidal magnetic
field remains practically constant at
the poloidal magnetic
field remains practically constant at
![]() .
This dependence
is represented by the horizontal line
.
This dependence
is represented by the horizontal line
![]() in Fig. 3.
However, our numerical simulation gives a totally different picture.
Namely, the poloidal magnetic field has clearly a maximum at the rotation axis
and then drops down with the distance r from the axis, for example at
in Fig. 3.
However, our numerical simulation gives a totally different picture.
Namely, the poloidal magnetic field has clearly a maximum at the rotation axis
and then drops down with the distance r from the axis, for example at
![]() to half its value from the axis.
It is important that this distribution is practically independent of z.
This result implies that the wind near the axis of rotation has achieved
an asymptotic state and the flow is collimated exactly along the axis of
rotation here.
to half its value from the axis.
It is important that this distribution is practically independent of z.
This result implies that the wind near the axis of rotation has achieved
an asymptotic state and the flow is collimated exactly along the axis of
rotation here.
The m-l model allows us to perform a quantitative comparison of the
SC theory and our numerical experiment.
The structure of the cylindrically collimated flow at large distances
from the source is especially simple provided that the central source
rotates uniformly while the plasma velocity and the ratio of the poloidal
magnetic and mass fluxes (function cF in Eq. (7))
are constant across the jet.
In this case the dependence of ![]() on r at the fixed z for a
cold plasma is given by the simple analytical expression
(Bogovalov 1995)
on r at the fixed z for a
cold plasma is given by the simple analytical expression
(Bogovalov 1995)
All these conditions are indeed fulfilled in our case.
The outflow speed at the vicinity of the axis of rotation is close to the
speed of light (
![]() at
at
![]() and
and
![]() at
at
![]() )
and is independent of r. The function F is assumed
independent of
)
and is independent of r. The function F is assumed
independent of ![]() for all field lines and the star rotates uniformly.
A comparison of the calculated dependence of
for all field lines and the star rotates uniformly.
A comparison of the calculated dependence of ![]() on r with the
analytical prediction, Eq. (26), shows that the SC theory correctly
predicts the asymptotic properties of the wind structure.
on r with the
analytical prediction, Eq. (26), shows that the SC theory correctly
predicts the asymptotic properties of the wind structure.
The cylindrically collimated flow in Fig. 2 is not visible
since its transversal scale is extremely small. The flux of the
poloidal magnetic field contained in this flow is small as well. The
dependence of the magnetic flux on r is shown in Fig. 3 by
the dashed-dotted line.
For plotting convenience, this flux is multiplied by 100 and is also
normalised to the total magnetic flux in the upper hemisphere,
![]() ,
which coincides with the magnetic flux at the equator.
The mass flux normalised to the total mass flux
in the upper hemisphere is presented by the same curve since the
mass flux is proportional to the poloidal magnetic field in our case.
The fraction of the magnetic and mass flux in the cylindrically
collimated flow is of the order
,
which coincides with the magnetic flux at the equator.
The mass flux normalised to the total mass flux
in the upper hemisphere is presented by the same curve since the
mass flux is proportional to the poloidal magnetic field in our case.
The fraction of the magnetic and mass flux in the cylindrically
collimated flow is of the order ![]() .
The rest of the magnetic and mass flux expands radially, in accordance with
the SC theory.
.
The rest of the magnetic and mass flux expands radially, in accordance with
the SC theory.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9493f3.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg144.gif) |
Figure 3:
The distribution of the poloidal magnetic field across the jet
at
|
| Open with DEXTER | |
The same physical picture emerges for a larger value of ![]() .
In Fig. 4 we show in the nearest zone the results of
the simulation of the flow of plasma for
.
In Fig. 4 we show in the nearest zone the results of
the simulation of the flow of plasma for ![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{ms9493f4r.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg145.gif) |
Figure 4:
Steady-state relativistic plasma flow in the nearest zone
of the star and for the parameters |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{ms9493f5r.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg146.gif) |
Figure 5:
Relativistic outflow in the far zone of the star for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9493f6.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg147.gif) |
Figure 6:
The dependence of the poloidal magnetic field across the jet
at
|
| Open with DEXTER | |
The efficiency of the acceleration of the plasma by a rotating object is
important in astrophysical applications. This acceleration in the model under
consideration is expected to be most efficient near the equatorial plane since at the axis of
rotation there is no accelerating force at all.
The accelerating force in the poloidal direction
is proportional to the product
![]() ,
where
,
where ![]() is
the component of the electric current perpendicular to a field line.
The accelerating force in the azimuthal direction is proportional to
the product
is
the component of the electric current perpendicular to a field line.
The accelerating force in the azimuthal direction is proportional to
the product
![]() .
Thus, all accelerating forces are
proportional to
.
Thus, all accelerating forces are
proportional to ![]() .
This implies that the acceleration occurs
only if the electric currents cross the poloidal field lines. The
electric currents shown by the dashed line in Figs. 1 and 4
indeed cross the poloidal field lines. This is very well seen especially in Fig. 4 near the equator.
.
This implies that the acceleration occurs
only if the electric currents cross the poloidal field lines. The
electric currents shown by the dashed line in Figs. 1 and 4
indeed cross the poloidal field lines. This is very well seen especially in Fig. 4 near the equator.
The dependence of the four-velocity of the plasma on the distance from the
centre of the source is shown in Fig. 7.
The distance is given in a logarithmic scale. The
energy of the particles increases slower than logarithmically and reaches
a constant value. It follows from energy conservation (10)
that the maximum possible terminal four-velocity
![]() at the equator is
at the equator is
![]() ,
since W at the equator can be
estimated as
,
since W at the equator can be
estimated as
![]() ,
provided that
,
provided that
![]() and the toroidal
magnetic field is estimated as
and the toroidal
magnetic field is estimated as
![]() (Bogovalov 1997a). All Poynting flux
should be transformed into kinetic energy of the plasma in this case.
But this value of the velocity is never achieved.
Michel (1969) calculated for
(Bogovalov 1997a). All Poynting flux
should be transformed into kinetic energy of the plasma in this case.
But this value of the velocity is never achieved.
Michel (1969) calculated for
![]() the value
the value
![]() for the plasma flow in a prescribed and fixed
m-l poloidal magnetic field. Therefore,
for the plasma flow in a prescribed and fixed
m-l poloidal magnetic field. Therefore,
![]() (see Eq. (24)).
It is reasonable to estimate the efficiency of the plasma acceleration
as the ratio
(see Eq. (24)).
It is reasonable to estimate the efficiency of the plasma acceleration
as the ratio
![]() which is approximately
the ratio of the part of
the Poynting flux transformed into the kinetic energy of the plasma (this is
valid, provided that
which is approximately
the ratio of the part of
the Poynting flux transformed into the kinetic energy of the plasma (this is
valid, provided that
![]() )
to the
initial value of the Poynting flux at the equator in the relativistic limit.
For the Michel solution (1969)
)
to the
initial value of the Poynting flux at the equator in the relativistic limit.
For the Michel solution (1969)
![]() .
The same value is given by Beskin et al.
(1998) for the analytical solution of
the same problem under the assumption that the poloidal
magnetic field goes to a monopole-like field at
.
The same value is given by Beskin et al.
(1998) for the analytical solution of
the same problem under the assumption that the poloidal
magnetic field goes to a monopole-like field at
![]() .
It follows from Fig. 7 that
.
It follows from Fig. 7 that
![]() increases with
increases with ![]() essentially faster than
essentially faster than
![]() .
For the flow with
.
For the flow with ![]() Michel's
estimate gives
Michel's
estimate gives
![]() ,
while the numerical solution gives
more than 8. Correspondingly, the efficiency of the acceleration remarkably exceeds the
efficiency of the acceleration given by Michel and achieves
,
while the numerical solution gives
more than 8. Correspondingly, the efficiency of the acceleration remarkably exceeds the
efficiency of the acceleration given by Michel and achieves ![]() for
the flow at
for
the flow at ![]() and
and ![]() .
It follows from Fig. 7
that the remarkable part of the acceleration occurs at large distances from
the star. It happens at the collimation of the magnetic flux to the axis of rotation
due to disbalance arising between the tension and pressure gradient of the
toroidal magnetic field (Begelman & Li 1994; Fendt & Camenzind
1996). This mechanism was not taken
into account in the analysis of Michel (1969) and Beskin et al.
(1998) since
they assumed a fixed m-l magnetic field.
.
It follows from Fig. 7
that the remarkable part of the acceleration occurs at large distances from
the star. It happens at the collimation of the magnetic flux to the axis of rotation
due to disbalance arising between the tension and pressure gradient of the
toroidal magnetic field (Begelman & Li 1994; Fendt & Camenzind
1996). This mechanism was not taken
into account in the analysis of Michel (1969) and Beskin et al.
(1998) since
they assumed a fixed m-l magnetic field.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9493f7.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg166.gif) |
Figure 7:
Dependence of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms9493f8.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg170.gif) |
Figure 8:
Dependence of the four-velocity of the plasma
|
| Open with DEXTER | |
The physics of this phenomena can be understood as follows.
It can be shown from simple geometrical consideration that
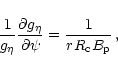 |
(27) |
where ![]() is the curvature radius of the poloidal magnetic field
lines, with
is the curvature radius of the poloidal magnetic field
lines, with ![]() positive if the centre of curvature is in the domain
between the line and the axis of rotation and negative in the opposite case.
With this expression, Eq. (13) takes the form
positive if the centre of curvature is in the domain
between the line and the axis of rotation and negative in the opposite case.
With this expression, Eq. (13) takes the form
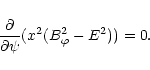 |
(31) |
The characteristic scale of collimation
![]() which defines the distance
where the flow reaches the asymptotic regime can be estimated as follows.
which defines the distance
where the flow reaches the asymptotic regime can be estimated as follows.
![]() ,
where
,
where ![]() is the
polar angle of the plasma velocity and
R is the distance to the center of the source. In the radially expanding
wind
is the
polar angle of the plasma velocity and
R is the distance to the center of the source. In the radially expanding
wind
![]() .
Taking into account also that at
large distances
.
Taking into account also that at
large distances
![]() (Bogovalov 1997a),
the rate of turning of the trajectory of the plasma follows from Eq. (29) and is defined by the equation
(Bogovalov 1997a),
the rate of turning of the trajectory of the plasma follows from Eq. (29) and is defined by the equation
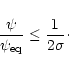 |
(35) |
For ![]() the collimation is more efficient and the effect of
collimation appears already in the nearest zone where the plasma is
not yet accelerated. At the estimation of the collimation scale
it is necessary to take into account acceleration of the plasma
to a Lorentz factor greater than 10 near the equator.
This could be done by integration of Eq. (32)
from a radius
the collimation is more efficient and the effect of
collimation appears already in the nearest zone where the plasma is
not yet accelerated. At the estimation of the collimation scale
it is necessary to take into account acceleration of the plasma
to a Lorentz factor greater than 10 near the equator.
This could be done by integration of Eq. (32)
from a radius
![]() where the energy of the plasma practically
reaches the terminal value.
If we take into account the acceleration, the asymptotic
regime (in which
where the energy of the plasma practically
reaches the terminal value.
If we take into account the acceleration, the asymptotic
regime (in which
![]() does not depend on
does not depend on ![]() in a radially expanding
wind) will be achieved at a distance
of the order
in a radially expanding
wind) will be achieved at a distance
of the order
![]() .
It follows from this expression that at
.
It follows from this expression that at ![]() the asymptotic regime
at
the asymptotic regime
at
![]() will be achieved only for
will be achieved only for
![]() .
This value agrees well with
the numerical results presented in Fig. 8 in the limits of uncertainties.
.
This value agrees well with
the numerical results presented in Fig. 8 in the limits of uncertainties.
Comparison of the present work with our previous work
(Bogovalov & Tsinganos 1999) shows that the relativistic
plasma is collimated less efficiently than the nonrelativistic one.
In particular, the fraction of the collimated mass flux in the nonrelativistic
flow was close to ![]() ,
while in the relativistic limit it is of the order
,
while in the relativistic limit it is of the order ![]() .
This difference can be understood from simple qualitative consideration.
The dynamics of the cold plasma is basically controlled by two forces.
One of them is the volumetric Lorentz force,
.
This difference can be understood from simple qualitative consideration.
The dynamics of the cold plasma is basically controlled by two forces.
One of them is the volumetric Lorentz force,
![]() and the other is the volumetric Coulomb force,
and the other is the volumetric Coulomb force,
![]() (see Eq. (1)). The collimation of the plasma to
the axis of rotation is defined by the components of these forces
perpendicular to the stream lines. The perpendicular component of the
Lorentz force is
(see Eq. (1)). The collimation of the plasma to
the axis of rotation is defined by the components of these forces
perpendicular to the stream lines. The perpendicular component of the
Lorentz force is
![]() ,
where
,
where
![]() is the
component of the poloidal electric current parallel to the
poloidal magnetic field and
is the
component of the poloidal electric current parallel to the
poloidal magnetic field and
![]() is the toroidal magnetic field.
The perpendicular component of the Coulomb force is
is the toroidal magnetic field.
The perpendicular component of the Coulomb force is
![]() .
These forces are shown schematically
in Fig. 4. It is important to note that these two forces are directed
along opposite directions. The Lorentz force collimates the plasma while the
Coulomb force decollimates it. In the nonrelativistic limit the
Coulomb force is neglected, since it is negligible in comparison to the Lorentz
force. The ratio of the Coulomb and Lorentz forces is of the
order (v/c)2 in this limit. In the relativistic limit the Coulomb force
becomes practically equal to the Lorentz force and it
strongly decreases the SC of the plasma. That is why the relativistic
generalization of the parameter
.
These forces are shown schematically
in Fig. 4. It is important to note that these two forces are directed
along opposite directions. The Lorentz force collimates the plasma while the
Coulomb force decollimates it. In the nonrelativistic limit the
Coulomb force is neglected, since it is negligible in comparison to the Lorentz
force. The ratio of the Coulomb and Lorentz forces is of the
order (v/c)2 in this limit. In the relativistic limit the Coulomb force
becomes practically equal to the Lorentz force and it
strongly decreases the SC of the plasma. That is why the relativistic
generalization of the parameter ![]() introduced earlier for the nonrelativistic winds
(Bogovalov & Tsinganos 1999) has additionally
the Lorentz factor in the denominator (see Eq. (23)).
introduced earlier for the nonrelativistic winds
(Bogovalov & Tsinganos 1999) has additionally
the Lorentz factor in the denominator (see Eq. (23)).
Although the Lorentz factor in the denominator of Eq. (23)
decreases remarkably the value of ![]() ,
it was expected that the collimation of the relativistic plasma will be
strong enough at the condition
,
it was expected that the collimation of the relativistic plasma will be
strong enough at the condition
![]() .
In the nonrelativistic case the collimation becomes
strong already in the subsonic region under this condition.
The most surprising result is that the relativistic plasma is practically
not collimated, even under this condition. The increase of the
collimating force does not provide more efficient collimation of the
relativistic plasma! This happens since another
relativistic effect comes into play.
.
In the nonrelativistic case the collimation becomes
strong already in the subsonic region under this condition.
The most surprising result is that the relativistic plasma is practically
not collimated, even under this condition. The increase of the
collimating force does not provide more efficient collimation of the
relativistic plasma! This happens since another
relativistic effect comes into play.
The curvature
![]() of the stream lines of the nonrelativistic
plasma is defined by the simple equation
of the stream lines of the nonrelativistic
plasma is defined by the simple equation
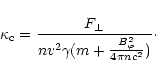 |
(38) |
This work shows that the self-collimation (SC) process
occurs in relativistic winds as
predicted by the SC theory. The wind consists
of a radially expanding part which surrounds a
cylindrically collimated flow.
The radius of the cylindrically collimated flow is
![]() ,
where
,
where ![]() is the initial radius of the fast magnetosonic surface.
The mass flux in the collimated part
is small compared with the total mass flux in the wind (
is the initial radius of the fast magnetosonic surface.
The mass flux in the collimated part
is small compared with the total mass flux in the wind (![]() 10-3),
even for relatively small Lorentz factors. SC essentially
decreases for larger Lorentz factors. Acceleration of the
plasma occurs in the radially expanding wind while
the plasma in the jet is not accelerated in this cold outflow model.
10-3),
even for relatively small Lorentz factors. SC essentially
decreases for larger Lorentz factors. Acceleration of the
plasma occurs in the radially expanding wind while
the plasma in the jet is not accelerated in this cold outflow model.
The relatively small part of the mass flux in the cylindrically collimated flow
has been also found in our simulations of nonrelativistic
outflows (Bogovalov & Tsinganos 1999), although the magnetic flux
contained in the relativistic case appears smaller by a factor of order 10.
In addition, the collimation scale at low latitudes
does not depend on the magnetic field and the angular velocity
of the central source for
![]() ,
in contrast with our results for
the nonrelativistic winds in the same model. This means
that the weak collimation of the relativistic plasma is due to the
intrinsic property of the plasma and not to a property of the model.
Collimation decreases due to the affect of the electric force which
becomes comparable with the collimating Lorentz force in the relativistic
limit and in the high
,
in contrast with our results for
the nonrelativistic winds in the same model. This means
that the weak collimation of the relativistic plasma is due to the
intrinsic property of the plasma and not to a property of the model.
Collimation decreases due to the affect of the electric force which
becomes comparable with the collimating Lorentz force in the relativistic
limit and in the high ![]() limit the collimation is saturated due to the
contribution of the electromagnetic field into the inertial mass of plasma.
limit the collimation is saturated due to the
contribution of the electromagnetic field into the inertial mass of plasma.
The most striking feature of the collimated flows obtained in the model
under consideration is that a very small fraction (![]() 10-3)
of the mass flux exists in the collimated flow in comparison to the mass flux
in the wind. This result is apparently in conflict with observations of AGN.
The source of the wind energy is the gravitational energy released by the
accreted matter. Therefore, the energy flux in the wind should be less than
the luminosity of the
accretion disk where about half of the gravitational energy is released
(Shakura & Sunyaev 1973). The total luminosity of AGN
10-3)
of the mass flux exists in the collimated flow in comparison to the mass flux
in the wind. This result is apparently in conflict with observations of AGN.
The source of the wind energy is the gravitational energy released by the
accreted matter. Therefore, the energy flux in the wind should be less than
the luminosity of the
accretion disk where about half of the gravitational energy is released
(Shakura & Sunyaev 1973). The total luminosity of AGN
![]() in
soft electromagnetic emission (below X-rays) should be
comparable with the energy released at the accretion. According to our
results the energy flux in the jet
in
soft electromagnetic emission (below X-rays) should be
comparable with the energy released at the accretion. According to our
results the energy flux in the jet
![]() should be by the factor
10-3 less than the accretion energy,
should be by the factor
10-3 less than the accretion energy,
![]() .
This disagrees with observations. X-ray and
gamma-ray emission is usually attributed to the emission from jets
(Urry & Padovani 1995). Sometimes, the luminosity of the jets is less only by a factor of 10 than the total luminosity of
AGN at other wavelengths (Elvis et al. 1994).
The energy flux in this emission can be considered as the lower limit on the
energy flux in the jet (however, we do not take into account beaming here).
If so, we have in AGN
.
This disagrees with observations. X-ray and
gamma-ray emission is usually attributed to the emission from jets
(Urry & Padovani 1995). Sometimes, the luminosity of the jets is less only by a factor of 10 than the total luminosity of
AGN at other wavelengths (Elvis et al. 1994).
The energy flux in this emission can be considered as the lower limit on the
energy flux in the jet (however, we do not take into account beaming here).
If so, we have in AGN
![]() .
.
This disagreement between theory and observations implies that either the present model has no observed counterpart or the SC mechanism is not able in principle to provide collimation of the major fraction of the outflow into the jet. It is important in this regard to understand from the theoretical point of view what modifications should be made in order to provide magnetic collimation of the major fraction of the relativistic wind. This problem has been already investigated by Bogovalov & Tsinganos (2001) in relation to nonrelativistic winds. It was shown in this study that in a model consisting of a central source ejecting a high-speed wind and an accretion disk ejecting a nonrelativistic magnetised outflow, all the mass flux from the central source can be cylindrically collimated indirectly by the surrounding disk-wind. Apparently, a collimation of the major part of a relativistic outflow from a central source can be provided by the same mechanism in the context of the present model as well.
Acknowledgements
I acknowledge support from the University Joseph Fourier and the Institut Universitaire de France as well as the warm hospitality of Prof. G. Pelletier and Dr. J. Ferreira during my stay in the Laboratoire d'Astrophysique de l'Observatoire de Grenoble, where part of this work was done. This work was partially supported by the Ministry of Education of Russia in the framework of the program "Universities of Russia - fundamental research'', project No. 990479 and by collaborative INTAS-ESA grant No. 99-120. The author is sincerely grateful to the unknown second referee and K.Tsinganos for the large amount of work they put in reading of this manuscript and their addition of useful comments. The author thanks V. B. Komberg for useful discussion of the observational properties of AGN.
This equation can be obtained as follows.
Time derivative of the frozen-in condition (2) gives that
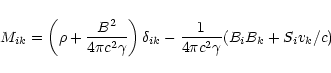
![$\displaystyle {M_{ik}^{-1}={1\over (\rho + {B^2\over 4\pi c^2 \gamma})}
\Bigg[\...
...mma +S_i v_k
/c\over (4\pi\rho c^2\gamma+B^2-({\vec{S} \cdot \vec{v}}/c)}\Bigg]$](/articles/aa/full/2001/21/aa9493/img241.gif) |
gives the equation of motion in the form (A.1) appropriate for the numerical solution.
A two-step Lax-Wendroff numerical scheme was used for the numerical solution of the problem (Press et al. 1990). The analytical solution obtained for the slow rotators (Bogovalov 1997a) was used as the initial state of the plasma.
The testing of the numerical code was performed by comparison of the
results with the results obtained with the nonrelativistic version of the
code (Bogovalov & Tsinganos 1999), by comparison with predictions
of the analytical theory (Bogovalov 1992; Bogovalov 1997a)
and by simulation of the perturbation propagation in the wind.
One of these tests is presented in Fig. A.1.
The beginning of the star rotation starts the
shock wave propagating with the Alfvenic velocity in the
isotropic wind. This velocity
is very close to 1 for the taken parameters of the wind.
The shock has an oscillating structure typical for the collisionless
shocks. The front is smoothed due to the numerical diffusion.
The first (largest) maximum can be accepted as the boundary of the shock.
It follows from the figure that the wave propagates with the velocity
very close to the light velocity which is equal
c/v0= 1.01 in the dimensionless variables normalized to v0at
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{ms9493f9.eps}\end{figure}](/articles/aa/full/2001/21/aa9493/Timg242.gif) |
Figure A.1: The simulation of propagation of the switch on shock wave in the relativistic wind. All the notations are the same as in Figs. 1 and 4. The wave is generated at the beginning of rotation of the central object |