CCD UBVRI (Cousins system) photometry for 802 stars in the region of
the open cluster HM1 was obtained in May 1993 and May 1997 using the University
of Toronto Southern Observatory (UTSO) telescope, Las Campanas (Chile). Four
zones were measured in 1993 when the telescope was equipped with a PM
![]() METACHROME UV-coated chip (4
METACHROME UV-coated chip (4
![]() on a side,
0.45
on a side,
0.45
![]() /pixel).
In 1997 we used a new Kodak CCD
/pixel).
In 1997 we used a new Kodak CCD
![]() UV-coated
(7
UV-coated
(7
![]() on a side, 0.40
on a side, 0.40
![]() /pixel) chip
/pixel) chip
![]() binned and glycol refrigerated to cover the
additional large area on the tilt depicted in the finding chart in Fig. 1. On
this occasion, a comparison field 15
binned and glycol refrigerated to cover the
additional large area on the tilt depicted in the finding chart in Fig. 1. On
this occasion, a comparison field 15
![]() north of HM1 was also exposed.
north of HM1 was also exposed.
To improve the signal-noise ratio of faint stars, we combined two long
exposure frames of 700, 450, 200, 110 and 110 s in the UBVRI
filters respectively. Moreover, to avoid saturation among bright stars, short
exposures of 40 and 50 s in the RI filters were additionally taken.
The nights were photometric with seeing values ranging from 1.2
![]() to
1.4
to
1.4
![]() .
.
We removed instrumental signatures with a combination of bias and flat field exposures. Using the point spread function, PSF method (DAOPHOT, Stetson 1987), instrumental magnitudes were obtained. They were matched with the standard system by means of calibration sequences in the open clusters NGC 5606 and Hogg 16 (Vázquez & Feinstein 1991a, 1991b; Vázquez et al. 1994) including over 20 stars spectrally well distributed. For extinction coefficients we used those of Grothues & Gocherman (1992).
We adopt as the external photometric error the typical calibration errors on the order of 0.02-0.03 mag in colour and magnitude. The internal accuracy of our photometry, 0.02 mag, was estimated from the mean differences of colours and magnitudes for stars with V < 17 that are located in the overlapping regions of the different frames.
| # | HM-TAH | X | Y | V | B-V | U-B | V-R | V-I | LSS | ST | Rem | Note |
| 1 | 1 | 854.5 | 487.0 | 11.02 | 1.48 | 0.40 | 1.18 | 2.14 | 4065 | WN7/WN8-A | 1/2 | |
| 2 | 4 | 769.3 | 237.0 | 11.30 | 0.42 | 0.46 | 0.44 | 0.53 | ||||
| 3 | 5 | 975.3 | 631.2 | 11.40 | 0.50 | 0.19 | 0.49 | 0.76 | ||||
| 4 | 2 | 722.5 | 489.2 | 11.44 | 1.49 | 0.37 | 1.28 | 2.28 | 4067 | O4If+ | 1 | * |
Figure 2 shows the magnitude and colour errors from DAOPHOT as a function of V. Up to V = 16, the U-B errors remain below 0.05 mag but quickly rise to 0.3 for V = 16-17 due to the strong absorption in this area. V = 17 is, therefore, a reliable limit for further analyses in this text. The CCD photometric catalogue containing the star identification, the x -y co-ordinates, V, U-B, B-V, V-R, V-I values, the cross correlation with other authors and the available spectral types is provided in Table 1 (available in electronic format). In the rest of this paper, the notation used by HM77 and TAH82 will be preferred; however, in those cases where ours is deemed indispensable, it will be denoted by numbers in brackets.
![\begin{figure}
\par\includegraphics[width=14.6cm,clip]{MS10428f03.eps}
\end{figure}](/articles/aa/full/2001/21/aa10428/Timg15.gif) |
Figure 3: The Serkowski's (1973) law fittings for the 21 stars in our sample. Bars indicate the polarisation errors (see Table 3) |
Eighteen out of 802 stars have UBV photoelectric photometry made
by HM77. Four of them have also VRI and near IR photometry made by TAH82.
The mean photomeric differences given by our measures minus those
of other authors, along with the standard deviations, listed in Table 2, are
quite small except for stars 2, 7, 10, 14, 15, 22 and 24. We found that three
of them, stars 2, 10 and 22, have close companions photometrically resolved.
The rest of the
stars with large differences have close neighbours (at 6
![]() ),
therefore, contamination and even variability are possible.
Surprisingly, the four TAH82 stars show VRI differences exceeding several
tenths of our measures. We were unable to account for this.
),
therefore, contamination and even variability are possible.
Surprisingly, the four TAH82 stars show VRI differences exceeding several
tenths of our measures. We were unable to account for this.
| Star |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EB-V | |
| 1 |
|
|
|
|
|
|
0.04 |
|
|
|
|
|
|
|
1.84 | |
| 2 |
|
|
|
|
|
|
0.09 |
|
|
|
|
|
|
|
1.82 | |
| 3 |
|
|
|
|
|
|
0.04 |
|
|
|
|
|
|
|
1.84 | |
| 4 |
|
|
|
|
|
|
0.02 |
|
|
|
|
|
0.38 | |||
| 5 |
|
|
|
|
|
|
0.10 |
|
|
|
|
|
|
|
0.59 | |
| 6 |
|
|
|
|
|
|
0.02 |
|
|
|
1.83 | |||||
| 7 |
|
|
|
|
|
|
0.03 |
|
|
|
|
|
|
|
0.39 | |
| 8 |
|
|
|
|
|
|
0.14 |
|
|
|
|
|
|
|
1.85 | |
| 9 |
|
|
|
|
|
|
0.08 |
|
|
|
|
|
|
|
1.86 | |
| 12 |
|
|
|
|
|
|
0.05 |
|
|
|
|
|
|
|
1.77 | |
| 13 |
|
|
|
|
|
|
0.03 |
|
|
|
|
|
|
|
1.78 | |
| 14 |
|
|
|
|
|
|
0.02 |
|
|
|
0.55 | |||||
| 15 |
|
|
|
|
|
|
1.68 |
|
|
|
|
|
|
|
||
| 16 |
|
|
|
|
|
|
0.06 |
|
|
|
|
|
|
|
2.07 | |
| 17 |
|
|
|
|
|
|
0.05 |
|
|
|
|
|
|
|
0.55 | |
| 18 |
|
|
|
|
|
|
0.06 |
|
|
|
|
|
|
|
1.76 | |
| 19 |
|
|
|
|
|
|
0.23 |
|
|
|
|
|
|
|
1.84 | |
| 20 |
|
|
|
|
|
|
0.06 |
|
|
|
|
|
|
1.57 | ||
| 21 |
|
|
|
|
|
|
0.03 |
|
|
|
|
|
|
|
0.59 | |
| (29) |
|
|
|
|
|
|
0.02 |
|
|
|
|
|
|
|
1.43 | |
| (44) |
|
|
|
|
|
|
0.12 |
|
|
|
|
|
|
|
0.84 |
On three nights of June in 1997 we carried out UBVRI polarimetric
observations of 21 stars using the Torino Observatory
Five-Channel Photopolarimeter attached to the 215-cm telescope of the
Complejo Astronómico El Leoncito (CASLEO). A set of filters with
effective wavelengths,
![]() m,
m,
![]() m,
m,
![]() m,
m,
![]() m,
m,
![]() m,
and a 15
m,
and a 15
![]() diameter diaphragm was used. The number of
observations varied from 4 to 8 for each star and each night, three stars of
null polarisation, HD 68456, 102365 and 146233, (Gliese 1969), were
observed to remove instrumental polarisation. The determination of the zero
point of the polarisation angle was carried out by observing three
stars each night, namely, HD 111613, 147084 and 187929, (Serkowski et al.
1975). The percentage of polarisation,
diameter diaphragm was used. The number of
observations varied from 4 to 8 for each star and each night, three stars of
null polarisation, HD 68456, 102365 and 146233, (Gliese 1969), were
observed to remove instrumental polarisation. The determination of the zero
point of the polarisation angle was carried out by observing three
stars each night, namely, HD 111613, 147084 and 187929, (Serkowski et al.
1975). The percentage of polarisation,
![]() ,
the
polarisation angle,
,
the
polarisation angle,
![]() ,
and their errors are included in
Table 3. The uncertainties in the polarisation angles shown in this table were
computed using (Hsu & Breger 1982):
,
and their errors are included in
Table 3. The uncertainties in the polarisation angles shown in this table were
computed using (Hsu & Breger 1982):
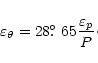
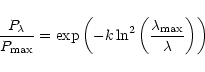
Copyright ESO 2001