A&A 371, 908-920 (2001)
DOI: 10.1051/0004-6361:20010410

The open cluster Havlen-Moffat No. 1 revisited[*],[*]

R. A. Vázquez[*] - G. Baume[*]

Observatorio Astronómico de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina

Received 2 November 2000 / Accepted 7 February 2001

Abstract
A deep CCD UBVRI photometric survey combined with UBVRI polarimetric observations of 21 bright stars was carried out in the region of the open cluster Havlen-Moffat No. 1. Our data reveal that the extinction law in this cluster is variable and that six cluster stars show very high polarisation values (>4%), probably because of the presence of a nearby small dust cloud. The cluster is at a distance of d = 3300 pc, it is 2-4 Myr old and the initial mass function of its most massive stars ( ${\cal M} > 3~{\cal M_{\hbox{$\odot$ }}}$) has a flat slope of $x\approx 0.7$. As an additional result, it was possible to reconcile the absolute magnitudes of the two WN7-type members using the R-values valid in the regions where they are located.

Key words: cluster: open - individual: Havlen-Moffat No. 1 - stars: imaging - stars: luminosity function, mass function - ISM: dust, extinction


1 Introduction

Havlen-Moffat No. 1 (hereafter HM1) = C1715-387 ( $l = 348.7^{\circ}$, $b = -0.8^{\circ}$) is a compact group of stars that is particularly interesting due to the presence of WR- and Of-type stars (Stephenson & Sanduleak 1971; Sanduleak 1974). Situated in the inner part of our Galaxy, in the spiral II-arm beyond the Sagittarius arm, this cluster is a highly reddened object projected against the HII region RCW 121 (Georgelin & Georgelin 1970; Rodgers et al. 1960). A first attempt to establish the cluster parameters comes from Havlen & Moffat (1977, hereafter HM77) who carried out UBV photometry of over 20 stars and spectroscopy for a handful of them. Lundström & Stenholm (1984) studied the two WR stars whereas Thé et al. (1982; hereafter TAH82) employing Walraven and VRI,JHKL photometry, extended the HM77 work, setting the cluster distance between 2.9 and 3.9 kpc. They suggested that four of the brightest stars have near infrared excesses and that HM1 stars are probably exciting the HII regions RCW 122 and 123. It is curious that this cluster did not receive more attention in the past, despite being a highly reddened object containing stars that are key objects to understand the stellar evolution of massive stars. More recent specific information on the WR stars appears in Crowther et al. (1995), where they were classified as WN7+(abs?), and in Walborn & Fitzpatrick (2000) who re-classified LSS 4065 as a weak line WN8-A star.

Taking into account the importance of the stellar population in HM1, we intend to improve its observational parameters using a large star sample. In the first approach of TAH82, the reddening law in this cluster was assumed as normal; however, this assertion based on VRI,JHKL photometry of only 4 of the bright stars requires further verification with more extensive UBVRI photometry. Besides, to determine a more accurate cluster age and to provide a better distance estimation, a photometric survey including faint stars is clearly needed. On the other hand, with such a survey it is possible to build the luminosity and initial mass functions of the most massive stars in the cluster. These two functions are of crucial astrophysical interest (Miller & Scalo 1978) because they provide us with information on how many of the bright stars have ended their lives as supernovae, how much mechanical energy coming from them was injected in the interstellar medium and how many unobservable faint stars (which are important in the dynamical evolution of this kind of system) are expected to be found (Will et al. 1995).

  \begin{figure} \par\includegraphics[width=12cm,clip]{MS10428f01.eps} \end{figure} Figure 1: Finding chart of HM1 showing the positioning of the five frames. The size of the symbols is approximately proportional to V. Some star numberings from HM77 (1 to 24) and TAH82 (starting at 25) are given as a guide. Those in brackets are from the present work. Cluster boundaries are indicated by a 3 ${\hbox {$^\prime $ }}$ radius circle. North and East are also indicated
Open with DEXTER

Bearing this in mind, we decided to perform extensive and deep photometry, including also polarimetric observations of several bright cluster stars. This last type of study was designed to observe the state of polarisation of the interstellar medium towards this highly reddened object. In Sect. 2 we present details of the observations and of the data reduction processes in both photometry and polarimetry; in Sect. 3 we discuss the cluster membership and the reddening law and then we derive the main cluster parameters, distance and age. In Sect. 4 we compute the luminosity and initial mass function of the cluster. Conclusions are presented in Sect. 5.

2 Observations

2.1 Photometry

CCD UBVRI (Cousins system) photometry for 802 stars in the region of the open cluster HM1 was obtained in May 1993 and May 1997 using the University of Toronto Southern Observatory (UTSO) telescope, Las Campanas (Chile). Four zones were measured in 1993 when the telescope was equipped with a PM $512\times 512$ METACHROME UV-coated chip (4 ${\hbox {$^\prime $ }}$ on a side, 0.45 ${\hbox{$^{\prime\prime}$ }}$/pixel). In 1997 we used a new Kodak CCD $2032\times 2048$ UV-coated (7 ${\hbox {$^\prime $ }}$ on a side, 0.40 ${\hbox{$^{\prime\prime}$ }}$/pixel) chip $2\times 2$ binned and glycol refrigerated to cover the additional large area on the tilt depicted in the finding chart in Fig. 1. On this occasion, a comparison field 15 ${\hbox {$^\prime $ }}$ north of HM1 was also exposed.

To improve the signal-noise ratio of faint stars, we combined two long exposure frames of 700, 450, 200, 110 and 110 s in the UBVRI filters respectively. Moreover, to avoid saturation among bright stars, short exposures of 40 and 50 s in the RI filters were additionally taken. The nights were photometric with seeing values ranging from 1.2 ${\hbox{$^{\prime\prime}$ }}$ to 1.4 ${\hbox{$^{\prime\prime}$ }}$.

We removed instrumental signatures with a combination of bias and flat field exposures. Using the point spread function, PSF method (DAOPHOT, Stetson 1987), instrumental magnitudes were obtained. They were matched with the standard system by means of calibration sequences in the open clusters NGC 5606 and Hogg 16 (Vázquez & Feinstein 1991a, 1991b; Vázquez et al. 1994) including over 20 stars spectrally well distributed. For extinction coefficients we used those of Grothues & Gocherman (1992).

We adopt as the external photometric error the typical calibration errors on the order of 0.02-0.03 mag in colour and magnitude. The internal accuracy of our photometry, 0.02 mag, was estimated from the mean differences of colours and magnitudes for stars with V < 17 that are located in the overlapping regions of the different frames.


  \begin{figure} \par\includegraphics[width=9.4cm,clip]{MS10428f02.eps} \end{figure} Figure 2: The error (as given by DAOPHOT) of our photometry against the V magnitude
Open with DEXTER


   
Table 1: Photometric catalogue of the HM1 region

#		 HM-TAH X Y V B-V U-B V-R V-I LSS ST Rem Note

1		 1 854.5 487.0 11.02 1.48 0.40 1.18 2.14 4065 WN7/WN8-A 1/2  
2 4 769.3 237.0 11.30 0.42 0.46 0.44 0.53        
3 5 975.3 631.2 11.40 0.50 0.19 0.49 0.76        
4 2 722.5 489.2 11.44 1.49 0.37 1.28 2.28 4067 O4If+ 1 *

Comment: Table 1 is available in full in an electronic version at the CDS. A portion of it is shown here.

Figure  2 shows the magnitude and colour errors from DAOPHOT as a function of V. Up to V = 16, the U-B errors remain below 0.05 mag but quickly rise to 0.3 for V = 16-17 due to the strong absorption in this area. V = 17 is, therefore, a reliable limit for further analyses in this text. The CCD photometric catalogue containing the star identification, the x -y co-ordinates, V, U-B, B-V, V-R, V-I values, the cross correlation with other authors and the available spectral types is provided in Table 1 (available in electronic format). In the rest of this paper, the notation used by HM77 and TAH82 will be preferred; however, in those cases where ours is deemed indispensable, it will be denoted by numbers in brackets.


  \begin{figure} \par\includegraphics[width=14.6cm,clip]{MS10428f03.eps} \end{figure} Figure 3: The Serkowski's (1973) law fittings for the 21 stars in our sample. Bars indicate the polarisation errors (see Table 3)
Open with DEXTER


 

 
Table 2: Mean photometric differences (our data minus other authors)
  $\Delta V$ $\Delta(B-V)$ $\Delta(U-B)$ $\Delta(V-R)$ $\Delta(V-I)$ N

HM77		 $-0.04\pm0.04$ $-0.04\pm0.02$ $0.03\pm0.09$ - - 18
TAH82 $0.05\pm0.12$ - - $0.22\pm0.08$ $0.22\pm0.12$ 4


Eighteen out of 802 stars have UBV photoelectric photometry made by HM77. Four of them have also VRI and near IR photometry made by TAH82. The mean photomeric differences given by our measures minus those of other authors, along with the standard deviations, listed in Table 2, are quite small except for stars 2, 7, 10, 14, 15, 22 and 24. We found that three of them, stars 2, 10 and 22, have close companions photometrically resolved. The rest of the stars with large differences have close neighbours (at 6 ${\hbox{$^{\prime\prime}$ }}$), therefore, contamination and even variability are possible. Surprisingly, the four TAH82 stars show VRI differences exceeding several tenths of our measures. We were unable to account for this.

 

 
Table 3: Polarimetric data and fitting results

Star		 $P_{U}(\%)~~~$ $P_{B}(\%)~~~$ $P_{V}(\%)~~~$ $P_{R}(\%)~~~$ $P_{I}(\%)~~~$ $P_{\max}(\%)~~$ $\varepsilon_{\rm P}/P_{\max}$
  $\theta_{U}(^\circ)~~~$ $\theta_{B}(^\circ)~~~$ $\theta_{V}(^\circ)~~~$ $\theta_{R}(^\circ)~~~$ $\theta_{I}(^\circ)~~~$ $\lambda_{\max}({\rm {\mu m}})~$ EB-V

1		 $1.83\pm0.20$ $2.02\pm0.25$ $1.91\pm0.06$ $2.00\pm0.03$ $1.66\pm0.04$ $2.04\pm0.07$ 0.04
  $18.4\pm3.1$ $22.0\pm3.5$ $18.3\pm0.9$ $18.2\pm0.5$ $18.2\pm0.6$ $0.56\pm0.32$ 1.84

2		 $2.81\pm0.16$ $2.91\pm0.11$ $2.11\pm0.08$ $2.21\pm0.04$ $1.75\pm0.08$ $2.64\pm0.24$ 0.09
  $44.4\pm1.6$ $41.5\pm1.1$ $35.5\pm1.1$ $40.5\pm0.5$ $39.1\pm1.3$ $0.45\pm0.48$ 1.82

3		 $4.64\pm0.84$ $5.32\pm0.48$ $5.64\pm0.09$ $6.11\pm0.05$ $4.87\pm0.08$ $6.04\pm0.26$ 0.04
  $28.4\pm5.2$ $38.8\pm2.6$ $39.0\pm0.5$ $37.8\pm0.2$ $39.1\pm0.5$ $0.59\pm0.54$ 1.84

4		 $1.26\pm0.27$ $1.66\pm0.07$ $1.71\pm0.10$ $1.81\pm0.08$ $1.72\pm0.18$ $1.84\pm0.03$ 0.02
  $156.4\pm6.2$ $8.5\pm1.3$ $12.1\pm1.7$ $9.6\pm1.3$ $16.7\pm3.0$ $0.61\pm0.20$ 0.38

5		 $1.69\pm0.39$ $1.46\pm0.19$ $0.99\pm0.35$ $1.39\pm0.22$ $0.86\pm0.34$ $1.49\pm0.15$ 0.10
  $179.2\pm6.7$ $ 12.6\pm3.7$ $171.2\pm10.0$ $173.4\pm4.5$ $0.2\pm11.4$ $0.45\pm0.72$ 0.59

6		 $4.57\pm0.44$ $4.45\pm0.10$ $4.27\pm0.14$ $4.26\pm0.11$ $3.55\pm0.17$ $4.56\pm0.10$ 0.02
  $174.3\pm2.8$ $2.9\pm0.6$ $5.4\pm0.9$ $1.7\pm0.7$ $3.9\pm1.4$ $0.52\pm0.22$ 1.83

7		 $2.31\pm0.24$ $2.94\pm0.07$ $2.92\pm0.13$ $3.17\pm0.09$ $3.23\pm0.19$ $3.26\pm0.09$ 0.03
  $10.5\pm3.0$ $21.3\pm0.7$ $27.6\pm1.3$ $21.8\pm0.8$ $24.9\pm1.7$ $0.61\pm0.30$ 0.39

8		 $3.43\pm0.25$ $4.33\pm0.15$ $2.60\pm0.06$ $2.73\pm0.06$ $2.22\pm0.08$ $3.07\pm0.42$ 0.14
  $36.1\pm2.1$ $34.9\pm1.0$ $33.5\pm0.7$ $37.5\pm0.6$ $37.3\pm1.0$ $0.47\pm0.88$ 1.85

9		 $1.84\pm0.42$ $1.47\pm0.56$ $1.68\pm0.61$ $1.63\pm0.53$ $1.64\pm0.52$ $1.87\pm0.14$ 0.08
  $42.5\pm6.5$ $37.8\pm10.9$ $37.0\pm10.4$ $37.9\pm 9.4$ $35.1\pm 9.1$ $0.51\pm0.57$ 1.86

12		 $5.88\pm0.35$ $6.34\pm0.25$ $5.37\pm0.11$ $5.62\pm0.06$ $4.76\pm0.08$ $5.86\pm0.27$ 0.05
  $13.4\pm 1.7$ $23.3\pm 1.1$ $21.8\pm 0.6$ $21.4\pm0.3$ $22.0\pm 0.5$ $0.55\pm0.41$ 1.77

13		 $5.16\pm0.27$ $5.43\pm0.29$ $4.87\pm0.05$ $5.08\pm0.04$ $4.23\pm0.06$ $5.10\pm0.15$ 0.03
  $34.2\pm1.5$ $36.7\pm1.5$ $36.3\pm0.3$ $36.8\pm0.2$ $37.8\pm0.4$ $0.58\pm0.38$ 1.78

14		 $1.56\pm0.28$ $1.56\pm0.09$ $1.94\pm0.10$ $1.99\pm0.06$ $1.92\pm0.08$ $2.01\pm0.03$ 0.02
  $178.4\pm5.2$ $5.1\pm1.6$ $0.5\pm1.4$ $3.8\pm0.9$ $2.4\pm1.1$ $0.68\pm0.22$ 0.55

15		 $3.09\pm1.53$ $1.55\pm0.15$ $0.43\pm0.55$ $0.44\pm0.38$ $0.74\pm0.52$ $10.05\pm16.85$ 1.68
  $165.9\pm14.2$ $177.3\pm 2.7$ $165.4\pm37.0$ $18.1\pm24.4$ $45.6\pm20.1$ $0.12\pm0.71$  

16		 $6.77\pm0.80$ $6.44\pm0.18$ $4.90\pm0.06$ $5.28\pm0.05$ $4.29\pm0.05$ $5.28\pm0.30$ 0.06
  $39.6\pm 3.4$ $45.3\pm 0.8$ $38.2\pm 0.3$ $41.8\pm 0.3$ $41.4\pm 0.4$ $0.56\pm0.57$ 2.07

17		 $0.64\pm0.19$ $1.45\pm0.12$ $1.28\pm0.05$ $1.35\pm0.06$ $1.07\pm0.15$ $1.34\pm0.06$ 0.05
  $16.8\pm 8.5$ $10.0\pm 2.3$ $13.2\pm 1.0$ $13.1\pm 1.2$ $17.1\pm 3.9$ $0.61\pm0.71$ 0.55

18		 $1.46\pm0.70$ $2.76\pm0.72$ $1.95\pm0.18$ $1.94\pm0.26$ $1.63\pm0.24$ $2.02\pm0.11$ 0.06
  $4.9\pm13.8$ $24.4\pm 7.4$ $29.1\pm 2.7$ $42.1\pm 3.8$ $38.5\pm 4.2$ $0.54\pm0.55$ 1.76

19		 $2.75\pm0.70$ $2.10\pm1.46$ $1.35\pm0.47$ $2.20\pm0.41$ $1.39\pm0.49$ $2.18\pm0.50$ 0.23
  $35.6\pm 7.3$ $35.5\pm20.0$ $22.3\pm10.0$ $33.9\pm 5.4$ $8.4\pm10.2$ $0.45\pm1.24$ 1.84

20		 $4.33\pm0.28$ $5.09\pm0.27$ $3.94\pm0.10$ $4.27\pm0.06$ $3.49\pm0.08$ $4.42\pm0.27$ 0.06
  $21\pm 1.8$ $31.5\pm 1.5$ $27.3\pm 0.8$ $30.3\pm 0.4$ $29.5\pm 0.7$ $0.54\pm0.51$ 1.57

21		 $2.21\pm0.12$ $2.46\pm0.11$ $2.42\pm0.05$ $2.52\pm0.05$ $2.10\pm0.08$ $2.54\pm0.07$ 0.03
  $11.2\pm 1.6$ $10.9\pm 1.3$ $11.1\pm 0.6$ $13.3\pm 0.6$ $10.2\pm 1.1$ $0.57\pm0.30$ 0.59

(29)		 $2.94\pm0.58$ $3.05\pm0.26$ $3.13\pm0.06$ $3.21\pm0.08$ $2.65\pm0.10$ $3.20\pm0.06$ 0.02
  $179.8\pm5.7$ $178.3\pm 2.5$ $177.9\pm 0.6$ $0.3\pm 0.7$ $178.5\pm1.1$ $0.58\pm0.24$ 1.43

(44)		 $3.65\pm1.04$ $2.99\pm0.43$ $2.07\pm0.17$ $2.07\pm0.15$ $2.06\pm0.35$ $2.32\pm0.27$ 0.12
  $19.2\pm 8.1$ $14.9\pm 4.1$ $17.1\pm 2.3$ $18.8\pm 2.0$ $7.5\pm 4.9$ $0.50\pm0.98$ 0.84


2.2 Polarimetry

On three nights of June in 1997 we carried out UBVRI polarimetric observations of 21 stars using the Torino Observatory Five-Channel Photopolarimeter attached to the 215-cm telescope of the Complejo Astronómico El Leoncito (CASLEO). A set of filters with effective wavelengths, $\lambda_{U} =0.360~\mu$m, $\lambda_{B} =0.440~\mu$m, $\lambda_{V} =0.530~\mu$m, $\lambda_{R} =0.690~\mu$m, $\lambda_{I} = 0.830~\mu$m, and a 15 ${\hbox{$^{\prime\prime}$ }}$ diameter diaphragm was used. The number of observations varied from 4 to 8 for each star and each night, three stars of null polarisation, HD 68456, 102365 and 146233, (Gliese 1969), were observed to remove instrumental polarisation. The determination of the zero point of the polarisation angle was carried out by observing three stars each night, namely, HD 111613, 147084 and 187929, (Serkowski et al. 1975). The percentage of polarisation, $P_{\lambda}$, the polarisation angle, $\theta_{\lambda}$, and their errors are included in Table 3. The uncertainties in the polarisation angles shown in this table were computed using (Hsu & Breger 1982):

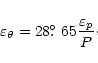
\begin{displaymath}\varepsilon_\theta = 28\hbox{$.\!\!^\circ$ }65\frac{\varepsilon_p}{P}\cdot \end{displaymath}

The cases of large uncertainties, especially in the U and B bands, require more observations in order to be reduced. However, since we are interested in the detection of large variations of polarisation across the cluster surface, the accuracy reached in this attempt is quite satisfactory. Assuming that polarisation is produced by interstellar dust and that the wavelength $\lambda_{\max}$ at which the maximum polarisation $P_{\max}$ occurs depends both on the optical properties and size distribution of dust grains (Greenberg 1968; McMillan 1978; Wilking et al. 1980), we computed $\lambda_{\max}$ and $P_{\max}$ for 21 stars from Serkowski's law (1973):

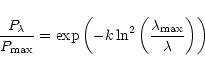
\begin{displaymath}\frac{P_\lambda}{P_{\max}} = \exp \left( -k \ln^{2} \left( \frac {\lambda_{\max}}{\lambda}\right) \right) \end{displaymath}

where k = 1.15. The $P_{\max}$ and $\lambda_{\max}$ values, the relative fitting error, $\varepsilon_{\rm P}/P_{\max}$ are included in Table 3. Figure 3 shows the Serkowski's law fittings for all the stars observed.

3 Data analysis

3.1 Cluster size

To know how much of HM1 has been covered by our photometry, we used the Digitized Sky Survey plates produced by the STScI that include the cluster and its surroundings. After taking a 15 ${\hbox {$^\prime $ }}$ radius area centred approximately on star 1, we calibrated the stellar magnitudes inside it and computed the stellar density down to $V \approx 16$ mag. We then adjusted the counts using a bidimensional Gaussian to obtain a density profile by means of which we settled the cluster angular radius at the point where the stellar density merges into the background level. In this way we found a cluster radius of 3 ${\hbox {$^\prime $ }}$, represented by the circle in Fig. 1, which is of the same order as the one found by HM77, 4 ${\hbox {$^\prime $ }}$. Thus, our photometry properly covers the cluster centre and part of its surroundings.

3.1.1 Cluster analysis

  \begin{figure} \par\includegraphics[width=12.9cm,clip]{MS10428f04.eps} \end{figure} Figure 4: The two-colour diagram. Symbols are: filled circles for likely members (the WR-stars are shown as open circles); triangles for probable members; small open squares for non-members; crosses are stars for which no membership could be estimated. The dashed line represents the Schmidt- Kaler's (1982) ZAMS, displaced by EB-V=1.75 from its normal intrinsic location (solid line). The arrows show the path of the reddening for O- and late B-type stars
Open with DEXTER

The two-colour diagram in Fig. 4 shows that the HM1 stars are affected by a combination of increasing foreground absorption followed by intense differential reddening inside the cluster. Proper motions of six of our stars (1, 2, 4, 5, 7 and 10) are reported in the Hipparcos/Tycho Catalogues. Only the WR star LSS 4065 (star 1) has a parallax measure, but its error is so huge that nothing relevant concluded.

By means of a star-by-star comparison of the star locations in all the photometric diagrams (Figs. 4 and 5) simultaneously, we confirm most of the members stated in previous works and included several new ones. There are five stars: 16, (26), (32), 39 and (52), located above the path of the reddening for an O-type star in Fig. 4 as if they had U excess. In particular, stars 16 and (26) resemble Be-type stars due to their displacement to the red side of the cluster sequence in the colour-magnitude diagrams (Fig. 5). Although stars 20 and 24 were found to be likely members by HM77 and TAH82, after our analysis, star 20 remains a probable member but star 24 becomes a definite foreground star in view of its location in Fig. 4. As was mentioned above, six stars have proper motions. Although this is clearly too small a number to derive independent membership assessment, we want to mention that the mean proper motion for the suspected members 1, 2 and 10 ( $\overline{\mu_{\alpha} \cos\delta} = -4.4 \pm 2.1({\rm s.d.})$ mas yr-1, $\overline{\mu_{\delta}} = -4.3 \pm 2.3({\rm s.d.})$ mas yr-1) do not contradict the results based on photometry, while the proper motions of suspected non-members (4, 5 and 7) differ significantly from the mean cluster motion.

We explored the possibility of having a "clean'' version of the lower main sequence of HM1 using a comparison field ( $7{\hbox{$^\prime$ }}\times 7{\hbox{$^\prime$ }}$) located 15$^\prime$ north of it (Fig. 6a) with a method already described in Vázquez et al. (1997). As it would prove useless to repeat it here, we will directly comment on the result of its application as seen in Fig. 6b, the HM1 V vs. B-V diagram after the subtraction of field stars. It is apparent from this figure that too many stars remain to the left of the main sequence while a few others are on the right side of the cluster sequence, a location usually reserved for pre-main sequence stars (compare Figs. 6b and 5a). However, these two facts are not reliable results, since our reference frame for field stars does not seem to represent the field star population against which the cluster is projected, as there are fewer field stars in the comparison frame than in the cluster itself.


  \begin{figure} \par\includegraphics[width=10cm,clip]{MS10428f05.eps} \end{figure} Figure 5: a) The V vs. B-V diagram. The Schmidt-Kaler's (1982) ZAMS, adapted to the distance modulus found in Sect. 3.4, is shown by a solid line. The two WR and the stars 16 and (26) that may be Be-type stars are indicated. Symbols as in Fig. 4; b) this is the V vs. U-Bdiagram. Symbols and lines as in Fig. 4
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS10428f06.eps} \end{figure} Figure 6: a) The V vs. B-V diagram of the comparison field stars; b) The V vs. B-V diagram of Fig. 5 a) after subtracting the field stars
Open with DEXTER


   
Table 4: Magnitudes and intrinsic colours of members and probable members in HM1

#		 VO (B-V)0 EB-V (U-B)0 EU-B (V-I)0 EV-I MV EV-I/EB-V Com.

1		 5.30 -0.20 1.68     -0.29 2.43 -7.30 1.44 lm *
4 5.44 -0.33 1.82 -1.20 1.57 -0.29 2.57 -7.16 1.41 lm
5 5.53 -0.33 1.83 -1.20 1.66 -0.29 2.61 -7.07 1.42 lm
9 5.30 -0.20 1.84     -0.29 2.93 -7.30 1.59 lm *
10 6.38 -0.32 1.85 -1.14 1.49 -0.29 2.33 -6.22 1.26 lm
11 6.68 -0.30 1.77 -1.05 1.43 -0.29 2.61 -5.92 1.47 lm
13 6.89 -0.32 1.78 -1.14 1.52 -0.29 2.59 -5.71 1.46 lm
14 6.68 -0.31 1.84 -1.15 1.50 -0.29   -5.92   lm
16 6.94 -0.31 1.86 -1.14 1.51 -0.29 2.31 -5.66 1.24 lm
20 6.32 -0.33 2.07 -1.20 1.71 -0.29 3.08 -6.28 1.48 pm
24 7.53 -0.31 1.76 -1.10 1.43 -0.29 2.18 -5.07 1.24 lm
25 8.22 -0.28 1.57 -0.99 1.25 -0.29 2.30 -4.38 1.47 pm
26 6.53 -0.33 2.09 -1.20 1.72 -0.29 2.60 -6.07 1.25 lm
32 7.53 -0.36 1.86 -1.31 1.51 -0.29 2.08 -5.07 1.12 lm
35 7.98 -0.30 1.79 -1.08 1.45 -0.29 2.23 -4.62 1.25 lm
37 8.03 -0.31 1.84 -1.11 1.50 -0.29 2.28 -4.57 1.24 lm
47 8.19 -0.29 1.88 -1.05 1.53 -0.29 2.37 -4.41 1.26 lm
52 7.86 -0.33 2.06 -1.20 1.69 -0.29   -4.74   lm
54 8.96 -0.26 1.73 -0.95 1.40 -0.29 2.56 -3.64 1.48 lm
55 8.33 -0.31 1.93 -1.14 1.58 -0.29 2.48 -4.27 1.29 lm
57 7.75 -0.34 2.12 -1.24 1.75 -0.29 3.06 -4.85 1.44 lm
65 8.09 -0.34 2.08 -1.24 1.71 -0.29 2.56 -4.51 1.23 lm
67 9.71 -0.24 1.59 -0.86 1.27 -0.25 1.90 -2.88 1.19 pm
69 9.28 -0.29 1.73 -1.05 1.40 -0.29 2.19 -3.32 1.26 lm
70 8.60 -0.31 1.94 -1.13 1.59 -0.29 2.84 -4.00 1.46 lm
76 9.11 -0.28 1.83 -1.00 1.48 -0.29 2.64 -3.49 1.44 lm
81 9.29 -0.27 1.80 -0.97 1.46 -0.29 2.66 -3.31 1.48 lm
87 9.28 -0.30 1.81 -1.05 1.47 -0.29 2.25 -3.32 1.24 lm
95 8.38 -0.33 2.11 -1.20 1.74 -0.29 2.72 -4.22 1.29 lm
96 8.39 -0.35 2.11 -1.26 1.74 -0.29 2.58 -4.21 1.23 lm
104 9.50 -0.28 1.79 -1.02 1.45 -0.29 2.27 -3.10 1.27 lm
105 9.25 -0.25 1.87 -0.91 1.52 -0.27 2.40 -3.35 1.28 lm
120 10.02 -0.26 1.72 -0.95 1.38 -0.29 2.34 -2.58 1.37 lm
123 9.71 -0.25 1.83 -0.89 1.48 -0.27 2.35 -2.89 1.29 lm
126 9.60 -0.30 1.87 -1.07 1.52 -0.29 2.52 -3.00 1.35 lm
128 9.67 -0.31 1.85 -1.13 1.50 -0.29 2.47 -2.93 1.34 lm
130 9.86 -0.23 1.80 -0.85 1.45 -0.25 2.34 -2.74 1.30 lm
132 9.55 -0.25 1.89 -0.91 1.54 -0.28 2.87 -3.05 1.51 lm
154 10.04 -0.23 1.83 -0.85 1.49 -0.24 1.82 -2.56 0.99 pm
162 11.10 -0.18 1.53 -0.62 1.22 -0.17 2.12 -1.50 1.39 pm
180 10.20 -0.28 1.84 -1.00 1.50 -0.29 2.37 -2.40 1.29 lm
186 10.79 -0.18 1.67 -0.63 1.34 -0.18 2.16 -1.81 1.29 pm
193 10.75 -0.03 1.70 -0.83 1.37 -0.02   -1.85   lm
205 9.95 -0.29 1.96 -1.03 1.60 -0.29 2.42 -2.65 1.24 lm
207 11.07 -0.17 1.63 -0.61 1.30 -0.17 3.04 -1.53 1.87 pm
213 10.40 -0.17 1.84   1.49 -0.17 2.35 -2.20 1.28 pm
216 10.42 -0.23 1.84 -0.80 1.50 -0.24 2.15 -2.18 1.17 lm
229 10.57 -0.13 1.84   1.49 -0.11 2.66 -2.03 1.45 pm
244 10.33 -0.20 1.94 -0.67 1.59 -0.19 2.94 -2.27 1.51 pm
247 11.21 -0.20 1.68 -0.69 1.35 -0.20 2.40 -1.39 1.43 pm
252 10.70 -0.21 1.84   1.49 -0.21 2.34 -1.90 1.27 pm
303 11.09 -0.16 1.84   1.49 -0.15 2.42 -1.51 1.31 pm
324 11.18 -0.08 1.84   1.49 -0.06 2.38 -1.42 1.29 pm
359 11.33 -0.04 1.84   1.49 -0.02 2.67 -1.27 1.45 pm
362 11.35 -0.18 1.84   1.49 -0.18 2.67 -1.25 1.45 pm
371 11.38 -0.11 1.84   1.49 -0.09 2.78 -1.22 1.51 pm
384 11.42 -0.03 1.84   1.49 -0.02 2.31 -1.18 1.26 pm
389 11.45 -0.09 1.84   1.49 -0.08 2.23 -1.15 1.21 pm
398 11.48 -0.18 1.84   1.49 -0.17 2.32 -1.12 1.26 pm
405 11.52 -0.08 1.84   1.49 -0.07 2.51 -1.08 1.36 pm
410 11.54 -0.12 1.84   1.49 -0.11 2.59 -1.06 1.41 pm
414 11.56 -0.13 1.84   1.49 -0.12 2.28 -1.04 1.24 pm
416 11.56 -0.19 1.84   1.49 -0.19 2.41 -1.04 1.31 pm
468 11.78 -0.18 1.84   1.49 -0.18 2.83 -0.82 1.54 pm
470 11.79 -0.10 1.84   1.49 -0.09 2.33 -0.81 1.27 pm
477 11.80 -0.11 1.84   1.49 -0.10 2.34 -0.80 1.27 pm
504 11.91 -0.15 1.84   1.49 -0.14 2.60 -0.69 1.41 pm
506 11.92 -0.18 1.84   1.49 -0.18 2.47 -0.68 1.34 pm
509 11.93 -0.01 1.84   1.49 0.00 2.51 -0.67 1.37 pm
511 11.94 -0.00 1.84   1.49 0.01 2.78 -0.66 1.51 pm
512 11.94 -0.17 1.84   1.49 -0.17 2.28 -0.66 1.24 pm
518 11.95 -0.00 1.84   1.49 0.01 2.59 -0.65 1.41 pm
519 11.95 -0.12 1.84   1.49 -0.11 2.69 -0.65 1.46 pm
520 11.96 -0.09 1.84   1.49 -0.07 2.18 -0.64 1.19 pm
537 12.01 -0.16 1.84   1.49 -0.15 2.31 -0.59 1.26 pm
Note: Star numbers in the first column are from the present work.
Open with DEXTER
Com:
lm = likely member;
lm * = likely member with intrinsic (B-V)0 colours from Lundström & Stenholm (1984);
pm = probable member.

Intrinsic colours of stars with unique reddening solution in Fig. 4 (WR stars excluded) were estimated with the colour excess relation EU-B / EB-V = 0.72 + 0.05 $\times E_{B-V}$ following the procedure explained in Vázquez & Feinstein (1991a) and assuming their luminosity is class V. Mean excesses $\overline{E_{B-V}} = 1.84\pm 0.07 ({\rm s.d.})$ and $\overline{E_{U-B}} = 1.49\pm 0.07 ({\rm s.d.})$were derived from likely members but, if we include also probable members with U-B, we obtain $\overline{E_{B-V}} = 1.83 \pm 0.2 ({\rm s.d.})$ and $\overline{E_{U-B}} = 1.49\pm 0.2 ({\rm s.d.})$; in both cases these values are close to EB-V =1.85 found by HM77. These mean values were used to correct the observed colours of probable members. For the two WR-stars we used (B-V)0= -0.22 from Lundström & Stenholm (1984) to obtain their colour excesses. Intrinsic UBV colours and colour excesses of likely and probable members are listed in Cols. 3-6 in Table 4.

3.2 The reddening law and the interstellar medium towards HM1

3.2.1 Photometry

The way absorption changes with distance in this zone is outlined in the interstellar extinction maps constructed by Neckel & Klare (1980). They suggest a rapidly increasing absorption pattern, reaching up to 2 mag in the first kiloparsec from the Sun.

Figure 7 shows the B-V vs. V-I diagram together with the intrinsic lines for stars of luminosities V and III from Cousins (1978). In terms of the reddening law (i.e., the ratio of visual to selective absorption, R = AV/EB-V), this figure shows a real star-to-star variation of R. Cluster members lie between two extreme R-values: one of them corresponds to the normal excess relation, EV-I/EB-V = 1.244, R = 3.1 (Dean et al. 1978), and the other to a higher one, EV-I /EB-V = 1.47 or $R \approx 3.7$. Judging by the increasing spread from V-I > 1.5 and B-V > 1.0 seen in Fig. 7, we do not rule out that part of the interstellar material in front of HM1 is also producing anomalous extinction.

The individual EV-I excesses can be used to compute the EV-I/EB-V ratio in order to analyse the spatial distribution of R across the cluster. Intrinsic (V-I)0 colours of normal stars were obtained with the relation of B-V and V-I from Cousins (1978). Individual EV-I and EV-I/EB-V number ratios are listed in Cols. 8 and 10 in Table 4.

The distribution of the R-values is depicted in Fig. 8. It shows that stars with high R-values tend to lie on the cluster's southwest side, while normal R-value stars are more concentrated in the cluster centre. Since the R-value varies between the two extremes mentioned above we adopted a mean value $\overline{R} = 3.3$ to obtain reddening-free V0 magnitudes for likely and probable members. The two WR stars were treated differently (see Sect. 3.4).

3.2.2 Polarimetry

The polarimetric information in Table 3 shows that stars 5, 8, 15, 19 and (29) have not only large relative fitting errors, $\varepsilon_{\rm P}/P_{\max}$, but also $\lambda_{\max}$ values smaller than the average ones for the interstellar medium, 0.545 $\mu$m (Serkowski et al. 1975). An extreme case is the foreground star 15 that seems to shows anomalous polarisation in the U and B bands. However, in this case we suspect that a companion, star (66), at 6 ${\hbox{$^{\prime\prime}$ }}$ is distorting our observations. Since we assume that polarisation is strictly due to the interstellar medium, if the relative fitting errors are larger than 0.1, as is the case for stars 8, 15, 19 and (44), intrinsic polarisation should be suspected. We are aware, however, that some peculiar stellar envelopes may sometimes reproduce a wavelength dependence similar to the interstellar medium (Orsatti et al. 1998), yielding $\varepsilon_{\rm P}/P_{\max} < 0.1$.


  \begin{figure} \par\includegraphics[width=12.5cm,clip]{MS10428f07.eps} \end{figure} Figure 7: The B-V vs. V-I diagram. Symbols as in Fig. 4. The solid lines represent the intrinsic location of stars of luminosity V and III from Cousins (1978). The path of the reddening line for R = 3.1 and R=3.7 is also shown


  \begin{figure} \par\includegraphics[width=10cm,clip]{MS10428f08.eps} \end{figure} Figure 8: The spatial distribution of polarisation vectors in the zone of HM1. The 1% polarisation is indicated. Grey filled circles denote members having anomalous EV-I/EB-V ratios. Black filled circles indicate members with normal EV-I/EB-V ratios. Open circles are foreground stars. The small $5^{\circ } \times 5^{\circ }$ box shows the distribution of polarisation vectors around HM1, taken from Klare & Neckel (1977)
Open with DEXTER

Figure 8 shows the spatial distribution of the polarisation vectors in the HM1 area. The small panel inside this figure shows the distribution of the polarisation vectors from Klare & Neckel (1977) in an area ( $5^{\circ } \times 5^{\circ }$) centred in the cluster. The polarisation patterns in both figures suggest the presence of several dust components producing different amounts of polarisation. Notice the handful of cluster members on the cluster south-west side that appear highly polarised.

Following Whittet & van Breda (1978), the mean R-value in terms of polarimetry is given by:

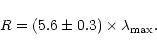
\begin{displaymath}R = \left( 5.6 \pm 0.3 \right) \times \lambda_{\max}. \end{displaymath}

If we do not take into account stars with anomalous fittings, we find a mean value $\overline{\lambda_{\max}} = 0.57\pm 0.11~\mu$m (close to Serkowski et al. 1975, value) and $\overline{R} = 3.2 \pm 0.7$(s.d.) that agrees with the R average adopted from photometry alone. On the other hand, the assessment of the polarisation efficiency of the interstellar material when it is produced by a normal size-particle distribution can be performed by inspecting the relationship between the polarisation percentage and the visual absorption, which should not surpass the upper limit given by Serkowski et al. (1975):

\begin{displaymath}P_{\max} \approx 3 \times R \times E_{B-V}, \end{displaymath}

although they found an average $P_{\max} = 5.03 \times E_{B-V}$ in the Galaxy. The $P_{\max}/ E_{B-V}$ ratio depends mainly on the alignment efficiency and the intensity of the magnetic field but it also depends on the depolarisation produced when the star-light passes through dust clouds having different magnetic field orientations.

In Fig. 9 we show the $P_{\max}$ vs. EB-V plot (star 15 excluded) along with the upper limit from Serkowski et al. (1975). The EB-V values of foreground stars were estimated assuming they are of late B- or A-types and luminosity class V. The probable colour excess of star 17, without CCD photometry, was computed from the HM77 data. We distinguish three stellar groups in this figure: one of them corresponds to members with high polarisation values, $P > 4\%$, (3, 6, 12, 13, 16 and 20), located on the south-west side of the cluster (except star 6); the other is constituted by members in the centre of the cluster having $P < 4\%$, and the third one made up of foreground stars with $P < 4\%$. The typical polarisation observed for foreground stars implies a contribution of 1.5 to 2.6% produced by nearby interstellar material (not far from this region, Feinstein et al. 2000 found a similar foreground contribution in the cluster Trumpler 27). We notice also that the members at the southwest side of the cluster, bearing the highest polarisation values, are surrounded (in projection) by foreground stars 4, 7, 17, (29) and (44). We would like to point out that finding cluster members with $P > 4\%$ that show, on the average, high EV-I/EB-V ratios ( $R \geq 3.5$) and members with $P < 4\%$ that have normal EV-I/EB-V ratios (R = 3.1) is just a matter of chance and it does not reflect any physical connection between polarisation and absorption. In fact, the high polarisation values of stars 3, 12, 13, 16 and 20 are likely to be produced by a nearby small dust cloud instead of being produced somewhere in the proximity of the cluster itself. For instance, foreground star 7, which is close to this group, has a polarisation of 3.26% (the highest among foreground stars), probably due to its location on the northern edge of this cloud where it is partially covered by the cloud. The cloud only becomes apparent through its polarimetric effects, as no hints of increasing absorption for stars 3, 12, 13, 16 and 20 relative to other members is evident in Figs. 4 and 9. Indeed, Fig. 9 confirms that whatever the polarisation state of cluster members, the reddening across HM1 remains approximately the same (from 1.6 to 2.0). Probably, another small nearby cloud is also covering star 6, north of the HM1 centre.


  \begin{figure} \par\includegraphics[width=10cm,clip]{MS10428f09.eps} \end{figure} Figure 9: The $P_{\max}$ vs. E(B-V) diagram. The solid line is the upper limit given by Serkowski et al. (1975). The two dotted lines provide the EB-V limits within which cluster stars are mainly distributed. Bars indicate polarisation errors
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{MS10428f10.eps} \end{figure} Figure 10: The absorption-free colour-magnitude diagram of HM1. The ZAMS is superposed to V0-MV= 12.6. The dashed lines are the isochrones of Schaller et al. (1992). The number shown is the $\log (age)$. The location of star 35 is indicated. Symbols as in Fig. 4
Open with DEXTER

3.3 Distance and age

Figure 10 shows the Schmidt-Kaler's (1982) ZAMS fitted to a distance modulus of $V_0-M_V = 12.6 \pm 0.2$ (error by inspection). The early ZAMS fittings (HM77 or TAH82) were performed using a few stars distributed along the vertical part of the main sequence, which makes their estimates uncertain; now, however, we have the advantage that our photometry is two magnitudes lower than in any earlier investigation. Had the distance modulus been obtained with the six stars with spectroscopy and the Schmidt-Kaler's relation of spectral types and absolute magnitudes instead, we would have found distinct values according to the luminosity class adopted ranging from $\overline{V_0-M_V} = 11.7\pm 0.4$ (LC V) to $\overline{V_0-M_V} = 12.9 \pm 0.5$ (LC I). Since the magnitude spread in this last procedure introduces severe uncertainties in the distance modulus (large deviations can be produced by binarity or stellar duplicity), we adopt V0-MV = 12.6, from the ZAMS superposition, that corresponds to a distance d = 3.3 kpc. Although our distance is larger than the one found by HM77 (2.9 kpc), it still is in the range from 2.9 to 3.9 kpc determined by TAH82, confirming that HM1 belongs to the internal spiral arm-II, beyond the Sagittarius arm.

To determine the age of HM1, we superposed the cluster sequence to the isochrones from Schaller et al. (1992) evolutionary models computed with solar metallicity, mass loss and overshooting. The best isochrone fitting that corresponds to an age of 2-4 Myr is shown in Fig. 10. With such an age, there is no chance that star 35 is a cluster member because it is 30-40 Myr old, judging from the closest isochorone. TAH82 assumed it is a red super-giant cluster, probably an early product of a non-coeval star formation process. However, this assertion is not confirmed by our photometry since neither clues of age spread among massive stars nor the presence of faint stars lying well above the cluster main sequence are observed in our diagrams (however, this last statement reveals our inability to adequately subtract field stars instead of confirming a definite lack of contraction-phase stars). Notwithstanding, star 35 shows strong colour anomalies (its U-B colour is too blue when compared to its B-V=2.59 and V-I = 3.47), a fact deserving further observations.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS10428f11.eps} \end{figure} Figure 11: The colour difference method for stars 1, 2, 3 and 6
Open with DEXTER

3.4 Some especial stars in HM1

From Lundström & Stenholm (1984) we know that the two WN7-type stars 1 (LSS 4065) and 3 (LSS 4064) are conspicuous cluster members that have different absolute magnitudes despite their similar spectral types. Later on, both stars were classified as WN7+(abs?) (see Crowther et al. 1995) and very recently LSS 4065 was re-classified WN8-A (Walborn & Fitzpatrick 2000). This star, with a polarisation value comparable to the foreground stars, is placed in the centre of HM1; LSS 4064, on the contrary, is placed in the south-west and shows the highest polarisation (6.04%) found in our survey. On the basis of a normal absorption law, TAH82 pointed out these two WR-type stars show infrared excess caused by free-free emission in their winds when compared to model fluxes. In particular, TAH82 suggest that LSS 4064 has a depression in its spectral energy distribution shortwards of $\lambda_V$ (see their Fig. 4) suggesting, in adition, that a better agreement with the 40000 K Kurucz's (1979) model would be achieved for LSS 4064 if a colour excess EB-V = 1.99 is adopted instead of 1.87. However, firstly, the colour excess adopted by TAH82 is correct (the intrinsic colour (B-V)0 for a WN7-type star is -0.22 from Lundström & Stenholm 1984) and, secondly, we have found that the reddening law is anomalous in the location of LSS 4064. So, the probable near IR excess may have another explanation: Fig. 11 shows the colour-difference method applied to the two Of and the two WR stars combining our UBVRI and JHKL data from TAH82 along with the van der Hulst curve # 15 and intrinsic colour from Johnson (1968). This figure shows that only star 3 (LSS 4064) shows clear hints of having infrared excess and that, in view of our findings of Sect. 3.3, it is very probably produced by the intracluster material and not in its own wind, as suggested by TAH82.

We computed the reddening-free magnitudes of these two WR stars using the R-values according to their locations, obtaining the same absolute magnitude MV = -7.3. Although they compare fairly well with the absolute magnitude of the WR-star WN7+abs, HD 93162 (Crowther et al. 1995), -7.2, they still are a bit far from the average given in Table 10 of Crowther et al. (1995), MV = -6.7, and of the average given by Lundström & Stenholm (1984), -6.5. However, Vacca & Torres-Dodgen (1990) found absolute magnitudes of -7.3 for stars LSS 4064 and -6.7 for LSS 4065 though assuming that HM1 is located at a distance of 2800 pc and that the R-value in the cluster remains not only invariable but also normal.

Star 2 (LSS 4067), an O4If+ (Walborn & Fitzpatrick 2000) and star 6, an O5f, show high values for their EV-I/EB-V ratios as well. Their $P_{\max}$ values are low for star 2 (it has a companion, star (14), at $1.3{\hbox{$^{\prime\prime}$ }}$ with V = 12.77) and high in the case of star 6.


 

 
Table 5: The luminosity and initial mass functions
MV $\log{\cal M}$ N $ \log N$
-8,-7 1.98, 1.80 4 0.60
-7,-6 1.80, 1.62 3 0.48
-6,-5 1.62, 1.43 6 0.78
-5,-4 1.43, 1.26 10 1.00
-4,-3 1.26, 1.08 10 1.00
-3,-2 1.08, 0.90 12 1.08
-2,-1 0.90, 0.72 18 1.26
-1,0 0.72, 0.54 12 1.08
  MV = -1 $\gamma =$ $0.12\pm0.02$
  MV = -3 $\gamma =$ $0.13\pm0.04$
  MV = -1 x= $0.67\pm0.10$
  MV = -3 x = $ 0.73\pm0.21$



  \begin{figure} \par\includegraphics[width=9cm]{MS10428f12.eps} \end{figure} Figure 12: The initial mass function. The solid and dotted lines are the least squares fitting to MV = -3 and -1 respectively
Open with DEXTER

4 The cluster luminosity function and the initial mass function

The luminosity function, LF, is a powerful tool to compare the distribution of massive stars in relation to less massive ones. Special care must be taken as the different evolutionary status of the stars present in a given sample can lead to wrong results. This is not the case in an open cluster. The LF shows the additional advantage that it is independent of the evolutionary model or theory used (Burki 1977). In order to build this function, it is assumed that such function may be considered a power law expressed as follows:

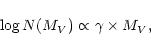
\begin{displaymath}\log N(M_V)\propto \gamma \times M_V, \end{displaymath}

where $\gamma$, the slope of the fitting, is a quantity to be determined from our data. We list in Table 5 the star counts by MV magnitude bins of size $\Delta M_V= 1$ mag. The most evolved members, the two WR stars, were included in the brightest bin while the faintest one was ignored because of its obvious incompleteness. The counts were fitted by means of an unweighted least squares method throughout two luminosity ranges, -8 < MV < -1 or -8 < MV < -3 to estimate the influence of incompleteness among faint stars. The $\gamma$ values obtained from the respective fittings are quite flat, $\approx$0.12, in relation to other regions in our galaxy and the Magellanic Clouds: Vallenari et al. (1993) found $\gamma =0.3$ in the range -2.5 < MV < + 1 in the young association NGC 1948 in the LMC; Perry & Hill (1992) found $\gamma =0.3$ in the range -7 < MV < - 4 in the association Scorpius OB1 and NGC 6231; Baume et al. (1999) found $\gamma \approx 0.2$ in NGC 6231 in the range -7.5 < MV < 1.5. The slope of the luminosity function in HM1 is, indeed, flat because, apart from multiplicity and binarity effects or incompleteness due to the strong absorption, even if we raise the lower limit up to -4, the slope $\gamma$ remains unchangeable. The initial mass function, IMF, on the other hand, gives the number dN of stars of mass ${\cal M}$ in the mass bin ${\cal M}\pm {\rm d} {\cal M }/2$, found in an open cluster at the moment of its formation. This function can be well represented by a power law (see, e.g., Scalo 1986):

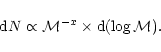
\begin{displaymath}{\rm d}N \propto {\cal M}^{-x} \times {\rm d}(\log {\cal M}). \end{displaymath}

When dealing with galactic field stars, the slope of the IMF, x, has a typical value of 1.35 as found by Salpeter (1955). However, when dealing with open clusters, strong variations of x have been reported by Conti (1992) and Massey et al. (1995). In our case, to compute the x value in HM1 we used the mass-luminosity relation given by Scalo (1986) to transform the LF into the IMF. It assigns a mean mass to each luminosity bin. The stellar mass values and the corresponding counts, dN, listed in Table 5, were fitted with a least squares method. The result of the fittings yields extremely flat IMF slopes of x = 0.6-0.7. Anyway, if fitting errors are allowed, the slope value can still fit into the range 1.0 < x < 1.3 of typical slopes found in our galaxy according to Conti (1992). In terms of similarity with other objects of this type, the IMF of HM1 massive stars is indeed steep but not unusual: Massey et al. (1995) found IMF slopes ranging from 0.7 to 2 for 11 open clusters of our galaxy in the dominion of massive stars. Other flat slopes in open clusters are also reported in, for example, the works of Sagar et al. (1986) or Will et al. (1995).

5 Conclusions

Our observations indicate that the extinction law in the HM1 region is anomalous and takes place in the intracluster material. It is also possible that part of the interstellar material just in front of HM1 contributes to this fact. We also noticed that the properties of the interstellar material in this zone strongly change in a very reduced portion of the sky. At only $2{\hbox{$^\prime$ }}$ southwest of the cluster centre where the polarisation of the stars is similar to the foreground polarisation, we found stars with the highest polarisation values that, in turn, show high R-values. However, at the same time, no extra absorption across the cluster surface is evident from our diagrams. So, to find stars with high polarisation and anomalous extinction law sharing a same location does not imply a physical relationship at all. This assumption is favoured by the polarisation maps of Klare & Neckel (1977) that reveal that nearby small dust clouds produce high polarisation values across the area that surrounds HM1.

It still has to be explained why highly reddened stars ( $A_V \geq 6$), as seen in the cluster centre, have, however, a polarisation comparable to foreground stars. It is probable that, when looking at the cluster centre, the star light passes through clouds with different orientations of their magnetic fields undergoing a depolarisation process. We have already found a situation of this type in other young cluster in this zone, Trumpler 27 (Feinstein et al. 2000) as well. There are examples of this: the average $P_{\max}/ E_{B-V}$ ratio is in the order of 5 (Serkowski et al. 1975) but there are zones in our galaxy with smaller values e.g. Cygnus OB2 ( $P_{\max} = 1.7 \times E_{B-V}$, McMillan & Tapia 1977) or R Coronae Australis ( $P_{\max} = 2 \times E_{B-V}$, Vrba et al. 1981), where the polarisation and reddening can be produced by more than one source. Unfortunately, there is no available spectroscopy of foreground stars close to the cluster front to study the material between the sun and the cluster and subtract its contribution to the total polarisation shown by cluster stars.

We obtained a better distance estimation as we were able to reach stars 2 mag fainter than in any previous work: the cluster is at a distance d=3.3kpc, beyond the Sagittarius spiral arm. HM1 is 2-4 Myr old, an age that agrees with the presence of two WN7-8 stars and several O and Of stars, but excludes the possibility that star 35 is a red super-giant member. Our data show that it is a foreground star. Further, both WR stars have the same absolute magnitude, -7.3, and only LSS 4064 shows hints of infrared excess that can be attributed to the intracluster material.

Acknowledgements
The authors acknowledge the financial suport from La Plata Observatory and the CONICET. Special thanks are given to Bob Garrison for the kind allocation of telescope time at UTSO and to the CASLEO staff for the technical support. We also acknowledge useful comments from Dr. H. G. Marraco. We are grateful to our referee, Dr. M. Geffert, for his valuable suggestions which improved the final version of this article

References

 

Copyright ESO 2001