A&A 371, 476-486 (2001)
DOI: 10.1051/0004-6361:20010391
Theoretical Physics, University of Oxford, 1 Keble Road, Oxford, UK
Received 22 January 2001 / Accepted 9 March 2001
Abstract
The interstellar gas flow in the inner disk of M 31 is
modelled using a new, two dimensional, grid based, hydrodynamics
code. The potential of the stellar bulge is derived from its surface
brightness profile. The bulge is assumed to be triaxial and rotating
in the same plane as the disk in order to explain the twisted nature
of M 31's central isophotes and the non circular gas
velocities in the inner disk. Results are compared with CO
observations and the bulge is found to be a fast rotator with a
B-band mass-to-light ratio,
![]() = 6.5
= 6.5 ![]() 0.8, and a
ratio of co-rotation radius to bulge semi-major axis,
0.8, and a
ratio of co-rotation radius to bulge semi-major axis,
![]() = 1.2
= 1.2 ![]() 0.1, implying that any dark halo must have a
low density core in contradiction to the predictions of CDM. These
conclusions would be strengthened by further observations confirming
the model's off axis CO velocity predictions.
0.1, implying that any dark halo must have a
low density core in contradiction to the predictions of CDM. These
conclusions would be strengthened by further observations confirming
the model's off axis CO velocity predictions.
Key words: hydrodynamics - galaxies: M 31 - galaxies: ISM - galaxies: structure
For many years, there has been ample evidence that bulges of barred spiral galaxies (SB bulges) are triaxial (Kormendy 1982). A spiral galaxy cannot have an oblate spheroidal bulge if the position angles of the major axes of the bulge, bar and disk are all different unless the bulge is tipped with respect to the plane of the disk. Given that observations of edge on galaxies show that bulges are rather flat (Kormendy 1981), it is most likely that the shortest axis is perpendicular to the plane of the disk.
Using stellar kinematic data, Kormendy & Illingworth (1982) provide evidence that many SA bulges (in unbarred galaxies) are rotationally flattened, and consistent with being oblate spheroids. However, there is also photometric and kinematic evidence to show that triaxial bulges may be common in unbarred galaxies. In a similar way to barred galaxies, a misalignment between the apparent major axes of the bulge and the disk is an indicator of triaxiality, as is a twisting of the inner bulge isophotes with respect to those of the disk. These effects have been seen in NGC 2784 (Bertola et al. 1988) and in a sample of 10 unbarred galaxies (Zaritsky & Lo 1986).
Stronger evidence for triaxiality comes from combining photometry with kinematic data. In an non-axisymmetric potential, the shape of the rotation curve will depend on the position of the line of sight and the major axis of the non-axisymmetric component. A slowly rising rotation curve or one in which a bump of extreme velocities is seen near the centre are indications of triaxiality (Gerhard et al. 1989). By comparing the theoretical gas velocity field derived from a triaxial potential with the observed kinematic data, one can determine whether or not the assumption of triaxiality is justified. Triaxiality has been demonstrated for both NGC 4845 (Gerhard et al. 1989) and for our Galaxy (Gerhard & Vietri 1986).
It is important to know whether triaxiality is common in SA bulges, since any asymmetries in the underlying potential of the inner galaxy have a large effect on the motions of interstellar gas and could provide a method of transporting gas into galaxy cores. Hence, triaxial bulges could provide clues to the fueling of central starbursts and active galactic nuclei. Furthermore, large scale movement of gas within a spiral galaxy could lead to changes in the overall morphology. In particular, a build up of gas in the galactic centre can result in the creation of a bar or its destruction.
Triaxial bulges can also help to constrain the masses of dark halos in galaxies. Kinematic observations contain the best evidence for the existence of dark halos. Flat rotation curves imply that the mass distribution in a galaxy must extend well beyond the observed stellar or gaseous distributions. However, in an axisymmetric galaxy it is not possible to determine how much of the mass of the galaxy resides in the disk and how much in the halo. Many rotation curves can be fitted by models ranging from zero-mass disks to "maximum disks'' (van Albada & Sancisi 1986), that is disks that are as massive as possible whilst ensuring that the halo is not hollow.
The velocity fields of barred galaxies provide extra information that can be used to break this disk-halo degeneracy (Weiner et al. 2001). Large jumps in velocity are an indication of triaxiality (either bar or bulge). These velocity jumps can help to determine a mass model for the non-axisymmetric component. Assuming a spherical halo, this can then be used to constrain the mass-to-light ratio of the disk and the mass fraction of the halo.
There is both photometric and kinematic evidence for triaxiality in
M 31, the Andromeda galaxy. Lindblad (1956) noted
that the apparent major axes of bulge and disk are misaligned and that
the central isophotes are twisted with respect to the isophotes of the
outer disk. He attributed this to the presence of a triaxial bulge
rotating in the plane of the disk. Stark (1977) showed that the
"Lindblad twist'' is generated by a one parameter family of triaxial
models of the bulge of M 31, where the parameter, ![]() ,
is
the angle between the major axis of the bulge and the line of nodes of
the disk.
,
is
the angle between the major axis of the bulge and the line of nodes of
the disk.
In addition, many observations of interstellar gas have detected
anomalously high velocities in both ![]() atomic gas
(Brinks & Burton 1984) and CO molecular gas (Loinard et al. 1995) in
the central 10' of M 31. Stark & Binney (1994) showed that these
velocities would occur in a simple, analytic, rotating barred
potential by calculating closed, non-intersecting, periodic orbits in
the plane of the disk and arguing that interstellar gas would largely
follow these orbits.
atomic gas
(Brinks & Burton 1984) and CO molecular gas (Loinard et al. 1995) in
the central 10' of M 31. Stark & Binney (1994) showed that these
velocities would occur in a simple, analytic, rotating barred
potential by calculating closed, non-intersecting, periodic orbits in
the plane of the disk and arguing that interstellar gas would largely
follow these orbits.
This paper aims to build on the work of Stark (1977) and Stark & Binney (1994) in two ways. The potential of the bulge is derived from observations, using the method of Stark (1977) and the surface brightness profile of Walterbos & Kennicutt (1988) whilst the gas flows are modelled using a 2D, isothermal, hydrodynamics code.
Section 2 provides details of the construction of the mass distribution of the bulge from the observed surface brightness profile. Section 3 describes the hydrodynamics code that was used to determine the response of the gas in the ISM to the background potential. Section 4 discusses the results and their comparison with observations. Section 5 comments on the constraints on the dark halo implied by these results. Section 6 concludes.
The Andromeda galaxy has been studied for over a thousand
years. It is one of the few galaxies which can be seen with the naked
eye and was mentioned by Abu I-Husain al-Sufi in his Book on the
Constellations of the Fixed Stars in 964 AD. As the closest large
spiral to our own Galaxy, Andromeda provides us with an ideal
laboratory for probing the structure and dynamics of spiral
galaxies. Due to its close proximity, high resolution photometric
observations are available of both the stellar and gaseous
components. These include maps in U, V, B and R bands (Walterbos & Kennicutt 1988), ![]() (Brinks & Burton 1984)
and CO (Loinard et al. 1995). Its large inclination angle
(
(Brinks & Burton 1984)
and CO (Loinard et al. 1995). Its large inclination angle
(
![]() )
means that although it is difficult to determine
accurate positional data on its apparent minor axis, more information
is available on the kinematics of the galaxy. This and other
observational data is summarized in Table 1.
)
means that although it is difficult to determine
accurate positional data on its apparent minor axis, more information
is available on the kinematics of the galaxy. This and other
observational data is summarized in Table 1.
| Distance of M 31 |
D | 690 kpc |
| Total B-band absorption |
AB | 1.3 mag |
| Inclination angle |
|
|
| Systemic velocity |
|
-315 km s-1 |
| Bulge effective radius* | 10' | |
| Bulge surface brightness* | 22.2 mag arcsec-2 | |
| Axis ratio of inner isophotes* | 1.54 | |
| Bulge to disk isophote angle** |
|
|
| Max. bulge isophote semi-major axis |
|
|
|
At the distance of M 31, 1' = 200 pc on the major axis.
** Lindblad (1956), |
The model of M 31 consists of two components: a rotating bulge and an axisymmetric component combining the effects of both disk and halo.
As shown in Stark (1977), a surface brightness profile in which the
isophotes are elliptical can be transformed into a one parameter
family of volume density profiles in which the density is constant on
similar, ellipsoidal shells. Stark's procedure relies on the use of a
number of observationally determined variables and the input of two
other parameters: the appropriate mass-to-light ratio, ![]() ,
and
the angle,
,
and
the angle, ![]() ,
between the major axis of the bulge and the disk's
line of nodes, both of which are determined by comparison with gas
kinematics.
,
between the major axis of the bulge and the disk's
line of nodes, both of which are determined by comparison with gas
kinematics.
The B-band surface brightness profile of the bulge of M 31
follows the
![]() law of de Vaucouleurs (1958):
law of de Vaucouleurs (1958):
![\begin{displaymath}I(s) = I_{\rm e} \, \exp(-7.67 [ (s/r_{\rm e})^{\frac{1}{4}} - 1] ) \, , \end{displaymath}](/articles/aa/full/2001/20/aah2653/img28.gif)
where ![]() is the effective radius,
is the effective radius, ![]() is the surface brightness
at
is the surface brightness
at ![]() and s is the semi-major axis length of the isophote. Table
1 gives the observationally determined values for
M 31. However, to recover the true bulge surface brightness
profile, this must be corrected for absorption both in M 31
and in our own Galaxy. Using the values of
AB = 0.32 mag for our
Galaxy in the direction of M 31 (Burstein & Heiles 1982),
AB = 0.98 mag for the bulge region of M 31
(van Genderen 1973) and
and s is the semi-major axis length of the isophote. Table
1 gives the observationally determined values for
M 31. However, to recover the true bulge surface brightness
profile, this must be corrected for absorption both in M 31
and in our own Galaxy. Using the values of
AB = 0.32 mag for our
Galaxy in the direction of M 31 (Burstein & Heiles 1982),
AB = 0.98 mag for the bulge region of M 31
(van Genderen 1973) and
![]() for the absolute
B-band solar magnitude (Allen 1973), the value of
for the absolute
B-band solar magnitude (Allen 1973), the value of
![]() mag arcsec-2 in Walterbos & Kennicutt (1988) is transformed
into
mag arcsec-2 in Walterbos & Kennicutt (1988) is transformed
into
![]()
![]() pc-2.
pc-2.
To recover an ellipsoidal luminosity distribution from this brightness
profile, an Abel-type integral equation has to be solved. The solution
is itself an integral, which is numerically integrated using Romberg's
method and multiplied by a constant B-band mass-to-light ratio,
![]() ,
to generate a 3D mass density profile.
,
to generate a 3D mass density profile.
The inner isophotes, which are twisted with the respect to those of
the outer disk, are used to define the spatial extent of the
bulge. Hence, the bulge model is truncated at an elliptical radius
![]() ,
the length of the semi-major axis of the
largest twisted isophote. For the model of minimum
,
the length of the semi-major axis of the
largest twisted isophote. For the model of minimum ![]() ,
this
corresponds to a bulge semi-major axis of 3.5 kpc.
,
this
corresponds to a bulge semi-major axis of 3.5 kpc.
Since the hydrodynamic calculations are carried out in 2D, only the
forces in the plane of the disk are relevant. Therefore the force due
to the bulge is calculated in the plane z=0. The force at a point
(x,y) is found by splitting the bulge into 300 concentric, triaxial
shells and summing the contributions of all shells interior to that
point. From Hunter et al. (1988), the component of the force acting at
(x,y) in the x direction due to an ellipsoidal shell of semi-axes
ai,bi,ci, where
ai > bi > ci and ci lies perpendicular to
the plane of the disk, is
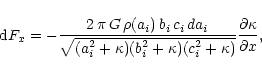
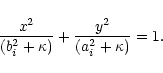
The region inside the central shell is modelled as a homogeneous
ellipsoid of density,
![]() .
This central region is split into
three smaller shells and the volume weighted densities of these
smaller shells are summed to give
.
This central region is split into
three smaller shells and the volume weighted densities of these
smaller shells are summed to give
![]() .
.
Table 2 details the effect that changes in ![]() have on the
other physical variables in the model. Larger values of
have on the
other physical variables in the model. Larger values of ![]() are
associated with fatter, shorter and more rapidly tumbling bulges.
are
associated with fatter, shorter and more rapidly tumbling bulges.
| a* | b* | c* | a/b |
|
|
|
||
| 25.0 | 12.7 | 4.80 | 2.35 | 51.2 | 44.3 | 37.4 | 0.67 | |
|
|
19.2 | 10.4 | 6.05 | 1.86 | 62.4 | 51.0 | 45.8 | 1.11 |
|
|
16.8 | 10.1 | 6.45 | 1.66 | 70.2 | 56.2 | 49.3 | 1.35 |
|
|
15.5 | 9.75 | 6.65 | 1.58 | 76.3 | 60.4 | 52.2 | 1.52 |
|
|
14.6 | 9.40 | 6.80 | 1.55 | 81.3 | 63.8 | 54.7 | 1.65 |
|
|
13.9 | 8.95 | 6.90 | 1.55 | 85.6 | 66.8 | 56.8 | 1.76 |
|
|
13.4 | 8.45 | 7.00 | 1.58 | 89.6 | 69.5 | 58.7 | 1.85 |
|
|
12.9 | 7.75 | 7.10 | 1.66 | 93.4 | 72.1 | 60.5 | 1.94 |
|
* Semi axis lengths (arcmin).
|
A simple interpretation of observations of gas velocities in
M 31 (Brinks & Burton 1984) suggests that the circular speed,
![]() ,
along the line of nodes of the disk is equal to a constant
velocity, v0, at radii greater than r0. At radii less than
r0, the circular speed falls linearly to zero. The axisymmetric
component has a mass distribution contrived to ensure that the model's
circular speed behaves thus. To determine v0 and r0, a two
component straight line is fitted to the CO observations of
Loinard et al. (1995). The data are folded about X = 0 and the four most
central points are excluded from the fit as they fall inside the
bulge and will therefore be experiencing severe non-axisymmetric
motion. The best fit occurs for v0=248 km s-1 and
r0=30.0'. This value of v0 is deprojected by a factor
,
along the line of nodes of the disk is equal to a constant
velocity, v0, at radii greater than r0. At radii less than
r0, the circular speed falls linearly to zero. The axisymmetric
component has a mass distribution contrived to ensure that the model's
circular speed behaves thus. To determine v0 and r0, a two
component straight line is fitted to the CO observations of
Loinard et al. (1995). The data are folded about X = 0 and the four most
central points are excluded from the fit as they fall inside the
bulge and will therefore be experiencing severe non-axisymmetric
motion. The best fit occurs for v0=248 km s-1 and
r0=30.0'. This value of v0 is deprojected by a factor
![]() for use in the calculation of the forces due to the
axisymmetric component.
for use in the calculation of the forces due to the
axisymmetric component.
Since the bulge forces have already been calculated, the forces due to
the axisymmetric component can be found by considering that at radii
greater than r0,
![]() ,
where
vA and vB are the contributions to the circular speed along the
line of nodes from the axisymmetric component and the bulge,
respectively. At radii less than r0, the forces due to the
axisymmetric component are assumed to fall linearly to zero.
,
where
vA and vB are the contributions to the circular speed along the
line of nodes from the axisymmetric component and the bulge,
respectively. At radii less than r0, the forces due to the
axisymmetric component are assumed to fall linearly to zero.
 |
Figure 1: Circular speed for best fit model. The solid and dot-dashed lines are along the bulge major axis whilst the dotted lines are along the bulge minor axis |
| Open with DEXTER | |
Figure 1 shows the circular speed curve for the model and the contributions of both the bulge and the axisymmetric components.
Section 5 considers whether and how the axisymmetric component can be broken up into seperate contributions from the disk and dark halo.
The ISM of M 31 is assumed to be an isothermal gas responding
to the fixed stellar potential described above. Cowie (1980) argued
that an isothermal fluid is a reasonable assumption for a cold, dense
ensemble of clouds. The sound speed, ![]() ,
is taken to be the cloud
dispersion velocity,
,
is taken to be the cloud
dispersion velocity, ![]() 10 km s-1, and the surface density,
10 km s-1, and the surface density,
![]() ,
is the average density of the surrounding clouds.
,
is the average density of the surrounding clouds.
The response of the gas is determined using a parallel, hydrodynamics
code, GALAHAD, based on the shock capturing FS2 algorithm
(van Albada & Roberts 1981; van Albada et al. 1982). The code solves the discrete,
isothermal Euler equations with gravitational source terms on a 2D
Cartesian grid, which represents half of a rotationally symmetric
galaxy. The
![]() grid cells cover
grid cells cover
![]() kpc so
that each grid cell is a square, 125 pc on a side. This is
approximately the same resolution as that of the CO observations
described later. The bulge is positioned so that the major axis is
aligned with the symmetry axis of the grid.
kpc so
that each grid cell is a square, 125 pc on a side. This is
approximately the same resolution as that of the CO observations
described later. The bulge is positioned so that the major axis is
aligned with the symmetry axis of the grid.
The FS2 algorithm is well suited to problems in galactic hydrodynamics. It is a second-order, flux-splitting scheme with no added numerical viscosity, which utilises operator splitting to include source terms and dimensional splitting to perform calculations in 2D. Discontinuities in the flow are handled by a limiter in the FS2 algorithm rather than by jump conditions. The self gravity of the gas is neglected in all simulations.
The isothermal Euler equations are essentially the conservation laws
of mass and momentum in the x and y directions for compressible,
frictionless fluids plus an equation of state defining the pressure as
p =
![]() .
In a frame rotating with the bulge at a pattern
speed
.
In a frame rotating with the bulge at a pattern
speed
![]() ,
and with gravitational source terms, the equations
are
,
and with gravitational source terms, the equations
are
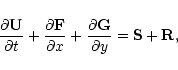
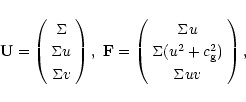
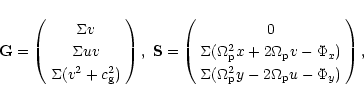
The pattern speed,
![]() ,
fixes a co-rotation radius,
,
fixes a co-rotation radius,
![]() ,
at which, on the major axis, the gravitational and centrifugal
forces are equal and, in the rotating frame, gas there can stand
still. The co-rotation radius occurs at the distance along the major
axis at which
,
at which, on the major axis, the gravitational and centrifugal
forces are equal and, in the rotating frame, gas there can stand
still. The co-rotation radius occurs at the distance along the major
axis at which
![]() 0, where
the effective potential
0, where
the effective potential
![]() .
Following Athanassoula (1992), we set
.
Following Athanassoula (1992), we set
![]() ,
where a is the length of the bulge
semi-major axis. However, unlike the galaxy models of
Athanassoula (1992), M 31 is a real galaxy, modelled with a
somewhat arbitrary bulge edge. Hence, it cannot be assumed that the
value of
,
where a is the length of the bulge
semi-major axis. However, unlike the galaxy models of
Athanassoula (1992), M 31 is a real galaxy, modelled with a
somewhat arbitrary bulge edge. Hence, it cannot be assumed that the
value of
![]() will be
will be
![]() as quoted in
Athanassoula (1992).
as quoted in
Athanassoula (1992).
During every simulation, the gas gradually loses angular momentum and
falls inwards to the galactic centre. As in Athanassoula (1992),
GALAHAD includes a routine to compensate for this by crudely
simulating the interaction of stars with the ISM: star formation
occurs and gas is removed in areas of high density, whereas stellar
mass loss is assumed to take place at a steady rate across the
galaxy. These phenomena are modelled by setting
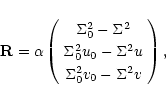
| Number of grid cells |
|
|
| Gas recycling parameter |
0.3 pc
|
|
| Initial gas density |
|
|
| Constant mass radius | 10 kpc | |
| Sound speed |
10 km s-1 | |
| Galaxy radius | 10 kpc | |
| Courant number | C | 0.5 |
Simulations start with the gas at a uniform surface density
![]() pc-2 and on circular orbits at a speed
given by
pc-2 and on circular orbits at a speed
given by
![]() with
with ![]() chosen such that
chosen such that
![]() =
=
![]() ,
where
,
where
![]() kpc and
kpc and
![]() is the
mass of the model at
is the
mass of the model at ![]() .
.
The boundary conditions are set using two rows of ghost cells, outside the boundary of the grid, on which the dynamical variables are held constant at their initial values.
The bulge is linearly introduced over half a rotation period and the
model is evolved to a quasi steady state over three rotation periods,
corresponding to about 0.3 Gyr. A comparison of a run at three and
four rotation periods shows very little change in the velocity fields
over much of the galaxy. However, in the region in which gas orbits
around the Lagrangian points, significant discrepancies are
found. Oscillations with amplitude ![]() 10 km s-1 occur in the
total gas velocity with a period of 70 Myr. These oscillations persist
until at least ten rotation periods.
10 km s-1 occur in the
total gas velocity with a period of 70 Myr. These oscillations persist
until at least ten rotation periods.
A number of tests were performed to ensure that GALAHAD performs as it
should. One simple and effective test for codes used in spiral galaxy
simulations is to model an axisymmetric galaxy to determine how much
gas infall there is due to numerical viscosity. After 2 Gyr, 98% of
the grid still had the same gas density as at the start and only 8%
of the initial gas mass had fallen into the central 2% of the
grid. The density in the central cells rose from
1 ![]() pc-2 to 40
pc-2 to 40 ![]() pc-2.
pc-2.
| |
Figure 2: 1D Shock-tube test with sound speed, c = 350 m s-1. The left hand panel shows the initial density conditions, the central panel shows the gas density after 0.01s and the right hand panel shows the gas velocity after 0.01s. In all panels, the solid line is the analytic solution and each diamond represents a cell in the simulated results |
| Open with DEXTER | |
Shock-tube tests were performed on GALAHAD to test the coding of the FS2 algorithm in the absence of source terms. A shock-tube test involves setting up gas on either side of a thin membrane at a constant density and at zero velocity. Model results were compared to the analytical solution for isothermal gas in two separate scenarios: the 1D shock-tube and the 2D oblique shock-tube. The results are presented for the 1D test in Fig. 2 and show that GALAHAD adequately replicates the analytical solutions.
Overall, 87 simulation runs were performed within the three
dimensional parameter space, (![]() ,
,
![]() ,
,
![]() ). The
ranges of the parameters are
). The
ranges of the parameters are
![]() ,
,
![]() and
and
![]() .
.
The model which most closely fits the observations is detailed in
Table 4. The method which was used to determine this model
of minimum ![]() is described in Sect. 4.3.
is described in Sect. 4.3.
| Semi-major axis | a | 3.5 kpc |
| Bulge mass |
|
|
| Bulge mass-to-light ratio |
|
6.5 |
| Pattern speed |
|
53.7 km s-1 kpc-1 |
| Rotation ratio |
|
1.2 |
| Phi angle |
|
 |
Figure 3:
The
model of minimum |
| Open with DEXTER | |
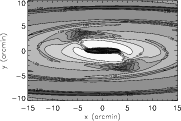 |
Figure 4:
Absorption map for the bulge of M 31. Derived from the
gas density field of the model of minimum |
| Open with DEXTER | |
In the plane z = 0 of triaxial or barred potentials, periodic orbits
exist in two main families, x1 and x2. x1 orbits exist at all
radii and are elongated along the bulge major axis. x2 orbits exist
inside the Inner Lindblad Resonance (ILR) and are oriented
perpendicular to the major axis. In the model of minimum ![]() ,
these effects can be seen in panel (b) of Fig. 3, where
gas near the outline of the bulge is moving in orbits elongated along
the major axis. Near the centre of the bulge, the gas flows along
orbits elongated along the minor axis.
,
these effects can be seen in panel (b) of Fig. 3, where
gas near the outline of the bulge is moving in orbits elongated along
the major axis. Near the centre of the bulge, the gas flows along
orbits elongated along the minor axis.
When gas falls inwards and passes the ILR, it shifts from x1 to lower energy x2 orbits. In doing so, it creates the "spray'' region seen as the diagonal gas flows just above and to the right and below and to the left of the centre in panel (b) of Fig. 3. Since this area contains transient gas which is not on any periodic orbits, it is an area of very low density and corresponds to the low density regions in panel (a) of Fig. 3.
As the gas travels through the "spray'' region, it slows down and climbs out of the bulge's potential well. At the end of the "spray'' region, the gas reaches its minimum kinetic energy, abruptly changes direction and follows the gas it has encountered back down into the potential well. This abrupt change in velocity is seen in panel (b) of Fig. 3 as the peak in the negative of the divergence of the velocity, a signature of shocked gas. This corresponds to the high density lanes of gas in panel (a) of Fig. 3, which forms where the shock causes gas to pile up. Athanassoula (1992) shows that these shocks are intimately linked to the dust lanes which appear in many barred galaxies.
The high density gas appearing in Fig. 3 panel (a) suggests the existence of dust lanes in M 31. Using the value for the mean B-band absorption in the bulge region of AB = 0.98 mag, (van Genderen 1973), the gas density can be calibrated and an absorption map for the bulge can be determined.
Taking the column density of interstellar hydrogen to be
![]() =
=
![]() +
+
![]() m-2 mag-1 and
m-2 mag-1 and
![]() (Binney & Merrifield 1998), it
follows that the mean gas density in the bulge region should be
(Binney & Merrifield 1998), it
follows that the mean gas density in the bulge region should be
![]() pc-2.
pc-2.
Assuming that CO is a reasonable tracer of both interstellar hydrogen
and dust in M 31 (Neininger et al. 1998),
![]() can be used to calibrate the gas densities in the bulge
region and determine the corresponding B-band absorption map,
which is shown in Fig. 4.
can be used to calibrate the gas densities in the bulge
region and determine the corresponding B-band absorption map,
which is shown in Fig. 4.
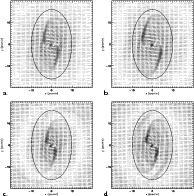 |
Figure 5:
Velocity fields for four different runs in the frame
rotating with the bulge. The models in panels a) and b) are slower
bulges with
|
| Open with DEXTER | |
Figure 5 shows the velocity field for a selection of four
different models in the frame rotating with the bulge. Each model has
![]() implying that the semi-major axis of the bulge
a =16' for every model. The solid ellipse in each panel marks the
extent of the bulge and the greyscale is minus the divergence of the
velocity, highlighting the shocks.
implying that the semi-major axis of the bulge
a =16' for every model. The solid ellipse in each panel marks the
extent of the bulge and the greyscale is minus the divergence of the
velocity, highlighting the shocks.
The top two panels panels (a) and (b) are the slower bulges
(
![]() = 1.4 and
= 1.4 and
![]() and 52 km s-1 kpc-1) whereas (c) and (d) are faster (
and 52 km s-1 kpc-1) whereas (c) and (d) are faster (
![]() = 1.0 and
= 1.0 and
![]() and 77 km s-1 kpc-1). The left hand
panels, (a) and (c), describe lighter bulges (
and 77 km s-1 kpc-1). The left hand
panels, (a) and (c), describe lighter bulges (
![]() )
and
the two on the right, panels (b) and (d) describe heavier bulges
(
)
and
the two on the right, panels (b) and (d) describe heavier bulges
(
![]() ).
).
A comparison of the top two panels with the bottom two shows the effect of a faster bulge on the shock morphology. A faster bulge has a smaller co-rotation radius and radius of the ILR at which gas transfers between x1 and x2 orbits. Since this transfer of gas between families of periodic orbits is the primary cause of the shocks seen in Fig. 5, we see that fast bulges have shocks which occur closer to their centres. This is the case irrespective of whether the bulge is heavy or light. The faster bulges also have pronounced secondary shocks, which emerge near the end of the major axis of the bulge.
The left hand panels (a) and (c) show the lighter bulges. In comparison with the heavier bulges of panels (b) and (d), they have weaker shocks. The shocks for the lighter bulges are also slightly closer to the centre and slightly straighter than for the heavier ones.
 |
Figure 6:
Gas velocity from the model of minimum |
| Open with DEXTER | |
The observational data used to judge the success of the simulations is CO data from Loinard et al. (1995). The molecular gas is likely to be confined to the plane of the disk and follow the periodic orbits described above. CO is a good tracer of the majority of molecular gas in a galaxy, particularly in the case of Andromeda (Neininger et al. 1998). Hence, it is amenable to modelling using isothermal hydrodynamics.
However, although there have been recent CO maps made of most of the Andromeda galaxy (Loinard et al. 1999; Dame et al. 1993), there is very little CO data available in the central bulge region. The reason for this deficiency in data could be that the CO is very cold and difficult to detect in the inner disk (Loinard & Allen 1998) or simply not there (Melchior et al. 2000).
The data from Loinard et al. (1995) were taken using the 30-m IRAM
millimeter radio telescope in 1993. 26 positions along the apparent
major axis of M 31 were surveyed and CO was detected in 16 of
them with a resolution of 35'' ![]() 2.6 km s-1. All 16 data
points are used in the comparison with the models.
2.6 km s-1. All 16 data
points are used in the comparison with the models.
Each model was rotated by ![]() and inclined by
and inclined by ![]() to match the
viewing position on the sky. A cut was then taken along the line
of nodes of the disk, involving an interpolation from off-axis positions,
and a comparison made with the CO data. Figure 6 shows a
comparison between the output of the best fit model and the CO data.
to match the
viewing position on the sky. A cut was then taken along the line
of nodes of the disk, involving an interpolation from off-axis positions,
and a comparison made with the CO data. Figure 6 shows a
comparison between the output of the best fit model and the CO data.
The model fits the data quite well except for one point at
X=-21.6'',
![]() km s-1 which cannot be
fit using the model described above. This anomalous point may be due
to a molecular cloud orbiting above the plane of the disk. In this
case, its line of sight velocity would be smaller than if it moved in
the plane, since it would be partly moving in the z direction.
km s-1 which cannot be
fit using the model described above. This anomalous point may be due
to a molecular cloud orbiting above the plane of the disk. In this
case, its line of sight velocity would be smaller than if it moved in
the plane, since it would be partly moving in the z direction.
To make a quantitative statement about how good a fit a particular
model is and which model gives the best fit to the data, a likelihood
function is derived, where the errors in the position and velocity of
the CO data are assumed to be Gaussian. Given that there are errors in
both X and
![]() ,
the difference between the data and the
model is found by comparing each datum with the point in the model
which is closest to it. This takes place within error space, where all
distances are divided by the error on X (35'') and all velocities by
the error on
,
the difference between the data and the
model is found by comparing each datum with the point in the model
which is closest to it. This takes place within error space, where all
distances are divided by the error on X (35'') and all velocities by
the error on
![]() (2.6 km s-1).
(2.6 km s-1).
This procedure gives a value of ![]() for each model and a simple
method of ascertaining the model of minimum
for each model and a simple
method of ascertaining the model of minimum ![]() .
For this
model,
.
For this
model, ![]() = 15
= 15![]() ,
,
![]() = 6.5,
= 6.5,
![]() = 1.2
and
= 1.2
and ![]() = 4.7 or 2.7 with or without the far flung data point
respectively. Given the various assumptions that have gone into this
model, it is unlikely that values much closer to
= 4.7 or 2.7 with or without the far flung data point
respectively. Given the various assumptions that have gone into this
model, it is unlikely that values much closer to ![]() = 1 could
be attained. Table 4 provides details of the parameters of
this model.
= 1 could
be attained. Table 4 provides details of the parameters of
this model.
Contour plots of ![]() are shown in Fig. 7 for
are shown in Fig. 7 for
![]() = 1.0, 1.2 and 1.4. In each plot, the value for the
bulge mass-to-light ratio is constrained to 0.5 either side of the
best fit model value at the 90% confidence level. However, as the
value of
= 1.0, 1.2 and 1.4. In each plot, the value for the
bulge mass-to-light ratio is constrained to 0.5 either side of the
best fit model value at the 90% confidence level. However, as the
value of
![]() rises from 1.0 to 1.4,
rises from 1.0 to 1.4, ![]() becomes less well
constrained. This effect happens concurrently with a narrower spread
of pattern speeds. The result is that the pattern speed varies by 3 or
4 km s-1 kpc-1 in each of the panels in Fig. 7
in the 90% confidence regions.
becomes less well
constrained. This effect happens concurrently with a narrower spread
of pattern speeds. The result is that the pattern speed varies by 3 or
4 km s-1 kpc-1 in each of the panels in Fig. 7
in the 90% confidence regions.
Figure 8 shows the value of ![]() as a function of
as a function of
![]() and
and
![]() at a constant value of
at a constant value of
![]() = 18
= 18![]() .
Although the plot was only constructed at a
single value of
.
Although the plot was only constructed at a
single value of ![]() ,
it does indicate that the favoured value of
,
it does indicate that the favoured value of
![]() lies between 1.1 and 1.3. This shows that the bulge of
Andromeda is a fast rotator.
lies between 1.1 and 1.3. This shows that the bulge of
Andromeda is a fast rotator.
Combining all of the above results implies that, at the 90%
confidence level,
![]() ,
,
![]() and
and
![]() .
.
Unfortunately, the derived values of
![]() are not very
robust. Using the above method, it is possible to vary the value of
are not very
robust. Using the above method, it is possible to vary the value of
![]() by two simply by taking the result of a particular model
at four rather than at three bar rotations. This is enough to turn a
model which fits the data very well into one which is a much worse
fit. Therefore it becomes much more difficult to determine whether a
particular model is a good representation of M 31 or not and
how well the above results can be trusted.
by two simply by taking the result of a particular model
at four rather than at three bar rotations. This is enough to turn a
model which fits the data very well into one which is a much worse
fit. Therefore it becomes much more difficult to determine whether a
particular model is a good representation of M 31 or not and
how well the above results can be trusted.
A much stronger case could be made if more off axis CO data was
available in the inner regions of M 31. In order to anticipate
such observations, I have provided in Fig. 9 a set of
predictions from the model of minimum ![]() for off axis gas
velocities, for comparison with observations. All predictions are for
cuts parallel to the major axis, taken at 1' intervals from 0' to
4' inclusive.
for off axis gas
velocities, for comparison with observations. All predictions are for
cuts parallel to the major axis, taken at 1' intervals from 0' to
4' inclusive.
These results were all calculated using a distance to M 31 of 690 kpc for ease of comparison with previous work. However, using recent results from Hipparcos, Stanek & Garnavich (1998) deduce that the distance is 784 kpc. Adopting this value means that 1' = 230 pc. Lengths, whether observed or deprojected and the mass of the bulge, all scale in proportion to the distance whereas the central density scales as the inverse square of the distance to M 31.
 |
Figure 7:
|
| Open with DEXTER | |
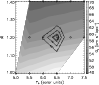 |
Figure 8:
|
| Open with DEXTER | |
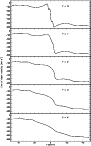 |
Figure 9:
Gas velocities from the model of minimum |
| Open with DEXTER | |
In order to do this, the total circular speed curve of the model of
minimum ![]() ,
shown in Fig. 1, is taken to
represent the combined mass distribution of the bulge, disk and
halo. Hence, the total mass at 3.5 kpc,
,
shown in Fig. 1, is taken to
represent the combined mass distribution of the bulge, disk and
halo. Hence, the total mass at 3.5 kpc,
![]() .
The contribution of the bulge to this has already been
deduced to be
.
The contribution of the bulge to this has already been
deduced to be
![]() ,
however there remains a
degeneracy between the contributions of the disk and the halo.
,
however there remains a
degeneracy between the contributions of the disk and the halo.
One method of breaking this degeneracy is to represent the halo by an
NFW profile (Navarro et al. 1996) derived from cosmological N-body
simulations,
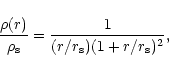
The circular velocity curve for an NFW profile is given by
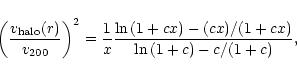
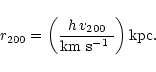
If
![]() km s-1, then the method of
Navarro et al. (1997) gives a halo mass fraction at 3.5 kpc of 58% and a
disk mass of only
km s-1, then the method of
Navarro et al. (1997) gives a halo mass fraction at 3.5 kpc of 58% and a
disk mass of only
![]() .
However,
Navarro et al. (1996) state that the maximum rotation velocity can be as
high as
.
However,
Navarro et al. (1996) state that the maximum rotation velocity can be as
high as
![]() .
If
.
If
![]() km s-1, the halo mass fraction at 3.5 kpc falls
to 44% and the disk mass rises to
km s-1, the halo mass fraction at 3.5 kpc falls
to 44% and the disk mass rises to
![]() .
But
in either case, the inner region of M 31 would be heavily dark
matter dominated if NFW halo profiles are to be believed.
.
But
in either case, the inner region of M 31 would be heavily dark
matter dominated if NFW halo profiles are to be believed.
Debattista & Sellwood (2000) convincingly demonstrate that fast, long lived bars cannot co-exist with massive dark halos. Their argument is based on the idea that dynamical friction from a dense, dark matter halo slows down any rapidly rotating bar. Hence, any old bar which is found to be a fast rotator precludes the existence of a dark halo, other than one with the lowest possible central density consistent with not being hollow.
"Fast'' bars have
![]() and, of the few galaxies
where
and, of the few galaxies
where
![]() has been measured, all have fallen within this
range implying that all barred galaxies have minimal halos and, hence,
maximum disks. Further, unless the distribution of halo densities is
bimodal, this conclusion of minimum halos should be extended to all
spiral galaxies.
has been measured, all have fallen within this
range implying that all barred galaxies have minimal halos and, hence,
maximum disks. Further, unless the distribution of halo densities is
bimodal, this conclusion of minimum halos should be extended to all
spiral galaxies.
Since the model of minimum ![]() for M 31 has
for M 31 has
![]() and the bulge of M 31 is older than 6 Gyr
(Trager et al. 2000), M 31 must have a low density dark matter
halo and a maximum disk. The exact value of the halo mass fraction
inside 3.5 kpc is dependent on the profile adopted for disk and halo,
even for a maximum disk. The maximum disk model of Kent (1989)
implies a halo mass fraction of just 0.5% at 3.5 kpc and, although
the model of minimum
and the bulge of M 31 is older than 6 Gyr
(Trager et al. 2000), M 31 must have a low density dark matter
halo and a maximum disk. The exact value of the halo mass fraction
inside 3.5 kpc is dependent on the profile adopted for disk and halo,
even for a maximum disk. The maximum disk model of Kent (1989)
implies a halo mass fraction of just 0.5% at 3.5 kpc and, although
the model of minimum ![]() is unable to make such a quantitative
prediction, it is clearly at odds with the NFW halo predicted by CDM.
is unable to make such a quantitative
prediction, it is clearly at odds with the NFW halo predicted by CDM.
The mass distribution for the bulge of M 31 has been determined from observations of the bulge surface brightness profile. The bulge is triaxial and rotates about the same axis as the disk. The GALAHAD code, based on the FS2 algorithm, has been used to reproduce observations of CO position and velocity in the bulge of the unbarred Andromeda galaxy, particularly the extreme velocities which appear in the central 10'.
By matching the model gas velocity field to the observations, it has
been possible to constrain the B-band bulge mass-to-light ratio,
![]() ,
and the bulge pattern speed,
,
and the bulge pattern speed,
![]() ,
at the 90%
confidence level, to
,
at the 90%
confidence level, to
![]() and 51
and 51
![]() km s-1 kpc-1. The angle between the major axis of the
bulge and the line of nodes of the disk has been constrained to
km s-1 kpc-1. The angle between the major axis of the
bulge and the line of nodes of the disk has been constrained to
![]() .
For the model of minimum
.
For the model of minimum ![]() ,
,
![]() = 6.5,
= 6.5,
![]() = 1.2, the semi-major axis
a=3.5 kpc and
= 1.2, the semi-major axis
a=3.5 kpc and
![]() .
.
The procedure described above improves on previous bulge models by constructing the mass distribution from observations. Further, the use of a hydrodynamics code to determine the response of the gas to the underlying potential provides a more accurate representation of the gas velocity field than calculations of periodic orbits. However, the oscillations inherent in a hydrodynamic model of a galaxy limit the accuracy of any simulation and may lead to more slack in the predictions than the formal errors imply.
If the bulge really is triaxial, it should be possible to constrain its parameters further by attempting to observe the offset dust lanes that should accompany the gas shocks described above. An absorption map has been provided to assist dust lane observations.
Since the bulge of M 31 has been shown to be a fast rotator, it follows from Debattista & Sellwood (2000) that M 31 has a maximum disk and a halo mass fraction within 3.5 kpc of just a few percent. This is in stark contrast to the predictions of Navarro et al. (1996), which imply that the halo mass fraction within 3.5 kpc is between 44% and 58%.
These conclusions would be strengthened by the confirmation of the off axis gas velocity predictions which have been made above. This could be done by confronting the model with further CO observations of the central 15' of M 31.
Given that triaxiality has now been demonstrated in both our Galaxy and our nearest large neighbour, M 31, it seems likely that triaxial bulges are a common feature of both SA and SB spiral galaxies.
Acknowledgements
I thank James Binney for many useful discussions and helpful advice, Julio Navarro for the NFW subroutine and the Oxford Supercomputing Centre for the use of OSCAR, an SGI Origin 2000 parallel computer, to carry out the hydrodynamic calculations.