A&A 371, 753-759 (2001)
DOI: 10.1051/0004-6361:20010382

Photometric study of Centaurs 10199 Chariklo (1997CU $_\mathsf{26}$) and 1999UG $_\mathsf{5}$

N. Peixinho1 - P. Lacerda2 - J. L. Ortiz3 - A. Doressoundiram4 - M. Roos-Serote1 - P. J. Gutiérrez3


1 - Centre for Astronomy and Astrophysics of the University of Lisbon/Lisbon Astronomical Observatory, Tapada da Ajuda, 1349-018 Lisbon, Portugal
2 - Leiden Observatory, The Netherlands
3 - Instituto de Astrofísica de Andalucía, CSIC, Granada, Spain
4 - Paris-Meudon Observatory, France

Received 9 November 2000 / Accepted 6 March 2001

Abstract
We present the results of visible broad band photometry of two Centaurs, 10199 Chariklo (1997CU$_{\rm 26}$) and 1999UG$_{\rm 5}$from data obtained at the 1.52 meter telescope of the National Astronomical Observatory at Calar Alto, Spain, during 2 separate runs in April 1999 and February 2000 and at the 1.5 meter telescope of the Sierra Nevada Observatory, Spain, in March of 1999. For Chariklo, the absolute magnitudes determined from the February 2000 data are found to be higher by about 0.27 mag than the average in the 1999 run. This may indicate long period rotational variability and possibly a G parameter higher than the assumed value of 0.15. From the best sampled R-lightcurve obtained in the February 2000 run, no short term rotational variability was found. The V-R colours for this object in all runs are similar to previously published values. For 1999UG$_{\rm 5}$, colours were found to be very red: $B-V = 0.88 \pm 0.18$, $V-R = 0.60 \pm 0.08$ and $R-I = 0.72 \pm 0.13$. These results place this object in the group of the reddest known bodies in the Solar System. HR and HV are found to be $10.06 \pm 0.09$ and $10.61 \pm 0.07$respectively, and its diameter is estimated to be on the order of $47 \pm 2$ km.

Key words: Minor bodies - Centaurs - photometry - rotation - colours


1 Introduction

The Centaurs are a family of minor bodies, usually defined as those objects having orbits between Jupiter and Neptune, even though a strict dynamical definition does not exist. They are thought to be in transition from Kuiper Belt Objects into short period comets, and their orbits are dynamically unstable on a 106-107 year time scale (Asher & Steel 1993; Levison & Duncan 1997; Morbidelli 1997). Therefore, the study of the chemical and physical properties of these objects together with those of the Kuiper Belt, which probably contain some of the most pristine material in the Solar System, is of great importance for the study of the earlier stages of the formation of the Solar System. At the time of writing about 20 Centaur objects have been identified.

Centaur 10199 Chariklo (1997CU$_{\rm 26}$) was discovered on February 15, 1997 (Scotti et al. 1997) and has been observed on several occasions since then (Brown 2000; Brown et al. 1998; Davies et al. 1998; McBride et al. 1999; Tegler & Romanishin 1998). It is one of the few distant minor bodies for which a spectrum has been obtained, and it shows signatures of water ice (Brown 2000; Brown et al. 1998). Also, infrared and visible measurements indicate an albedo of about 0.045 and a corresponding size of $302 \pm 30$ km diameter (Jewitt & Kalas 1998). No cometary activity has been detected (McBride et al. 1999). The rotation period has been difficult to determine, due to the apparently very weak variations in the lightcurve, which suggest either a very long period or one close to 24 hours (Davies et al. 1998; McBride et al. 1999, from observations taken in 1997). Another possibility is that the object is (nearly) spherical without significant albedo variations on the surface, or that one of its poles was facing the Sun in 1997. In this paper we discuss these possibilities.

Centaur 1999UG$_{\rm 5}$ was discovered on October 29, 1999. This is the first report on photometry of this object.

2 Observations and data reduction

The observations were obtained during three separate runs:

1.
March 15 through 21, 1999 (with 3 photometric nights) at the 1.5 meter telescope of the Sierra Nevada Observatory (SNO), Spain;

2.
April 14 through 17, 1999 (with 2 photometric nights) at the National Astronomical Observatory 1.52 meter telescope (NAO) at Calar Alto, Spain;

3.
February 2 through 7, 2000 (4 photometric nights), NAO, Spain.

At SNO we used the Albireo spectrograph, used in its imaging mode, with Johnson V and R filters. The detector was a $1152 \times 820$ Thomson THX31133 CCD, with pixel scale of $\sim$1.5 arcsec. Typical integration times ranged from 500 s to 1500 s. Object tracking was not possible. However the exposure times, combined with the apparent rate of motion of the Centaur, as well as the seeing conditions allowed us to avoid trailing of the object in the images. Typical seeing conditions were around 2 to 3 arcsec.

The detector at NAO was a Tektronix $1024 \times 1024$ CCD with square $\sim$0.4$\,$arcsec pixels and a $6.9 \times 6.9$ arcmin field of view. We used standard Johnson BVRI filters. The typical seeing conditions during the photometric nights were about 2-3 arcsec in 1999 and 2 arcsec in 2000.


 

 
Table 1: Calibration parameters
Night Telescope Landolt Fields Extinction Coeficients Colour Terms Filter
1999 Mar. 19-20 SNO       V
1999 Mar. 20-21 SNO pg1657+078, 104325 $k_{V} = 0.206 \pm 0.006$   V
  SNO pg1657+078, 104325 assumed kR = 0.15   R
1999 Mar. 21-22 SNO       V
           
1999 Apr. 14-15 NAO       V
  NAO       R
1999 Apr. 17-18 NAO pg1657+078, pg0918+029 $k_{V} = 0.165 \pm 0.033$   V
  NAO pg1657+078, pg0918+029 $k_{R} = 0.125 \pm 0.038$   R
           
2000 Feb. 02-03 NAO pg0231+051, pg0918+029 $k_{V} = 0.127 \pm 0.004$ $k_{\it VR} = 0.054 \pm 0.003$ V
  NAO pg0231+051, pg0918+029 $k_{R} = 0.097 \pm 0.005$ $k_{\it VR} = 0.054 \pm 0.004$ R
2000 Feb. 03-04 NAO pg0231+051, pg0918+029 $k_{V} = 0.133 \pm 0.004$ $k_{\it VR} = 0.066 \pm 0.004$ R
  NAO pg0231+051, pg0918+029 $k_{R} = 0.099 \pm 0.004$ $k_{\it VR} = 0.075 \pm 0.005$ R
2000 Feb. 04-05 NAO pg0231+051, pg0918+029 $k_{B} = 0.322 \pm 0.007$ $k_{\it BV} = -0.097 \pm 0.004$ B
    pg1657+078, ru149      
  NAO pg0231+051, pg0918+029 $k_{V} = 0.255 \pm 0.005$ $k_{\it VR} = 0.054 \pm 0.007$ V
    pg1657+078, ru149      
  NAO pg0231+051, pg0918+029 $k_{R} = 0.225 \pm 0.006$ $k_{\it VR} = 0.080 \pm 0.008$ R
    pg1657+078, ru149      
  NAO pg0231+051, pg0918+029 $k_{I} = 0.155 \pm 0.007$ $k_{\it VI} = -0.036 \pm 0.004$ I
    pg1657+078, ru149      
2000 Feb. 06 - 07 NAO pg0918+029 $k_{R} = 0.093 \pm 0.009$ $k_{\it VR} = 0.058 \pm 0.006$ R


The reduction of the 1999 data was carried out following standard processing of average bias subtraction and flatfield correction using high signal-to-noise flatfields for each filter (Johnson R and V). The DAOPHOT package was used for the synthetic aperture calculations. The synthetic aperture used for the Centaur and field stars had a diameter of six pixels for the SNO run and 2 times the Full Width at Half Maximum (FWHM) of the stellar profiles for the NAO run. These small apertures allow us to maximize the signal to noise on faint objects. The photometry was computed relatively to two field stars (observed on all nights) and was placed in an absolute scale by means of observations of the Landolt standard pg1657+078 and 104325 (Landolt 1992) for which we used a large enough aperture to get all the flux. The fraction of flux loss in the relatively small apertures used for the Centaur and field stars was estimated by measuring the percentage of flux loss in the brightest stars. The final results are therefore corrected for this effect. Extinction coefficients were derived for the V band from strömgren photometry which was being carried out at the 0.9 meter telescope in the SNO on the same nights, whereas for R, it was assumed to have a slightly smaller value (the resulting uncertainty is very small because the difference in airmasses between the calibration star and the centaur was lower than 0.2). The uncertainty in the absolute calibration is estimated to be 0.03 mag. For the NAO 1999 run, the extinction coefficients were derived from our own data in R and V, as we had adequate sky coverage. The uncertainty in the absolute calibration is estimated as 0.04.

For the February 2000 run, we used IRAF's CCDRED package and averaged biases and high signal-to-noise flat fields taken frequently during the run. We observed Landolt fields (Landolt 1992) close to our objects, and tracked them during the night for absolute calibration. Synthetic aperture photometry was performed using IRAF's PHOT routine. We used an aperture of 2 times the FWHM of the field stars' profiles for 10199 Chariklo (1997CU$_{\rm 26}$) and the standard stars, and 1.5 times the FWHM for the fainter 1999UG$_{\rm 5}$. Growth curves were derived using the brightest stars in each frame, and the correction for the flux loss was determined with IRAF's MKAPFILE routine, considering the profile out to 4 times the FWHM, where the profile reached its plateau. The colour terms on this run turned out to be considerably high and we took them into account.

Table 1 lists all the details of the calibration parameters.

3 Results and discussion for 10199 Chariklo (1997CU $_\mathsf{26}$)

Table 2 lists the observations for 1997CU$_{\rm 26}$, together with the values for the calibrated magnitudes. Since our observations were focused on the determination of a possible rotation period, we mainly observed through the R filter. In order to monitor the correctness of our data, we did some observations in the V filter to check the V-R colour.

From the March 1999 run (SNO), we obtain an average V value of $18.02 \pm 0.07$ and an average R value of $17.52 \pm 0.05$. The above values translate into absolute magnitudes $H_{V} = 6.57 \pm 0.07$ and $H_{R} = 6.07 \pm 0.05$, assuming a phase correction parameter G = 0.15. The V-R colour as calculated from these values is $0.50 \pm 0.09$.

From the April 1999 run (NAO), the average V value is $18.02 \pm 0.07$, and the average R value is $17.55 \pm 0.06$, so that the absolute magnitudes are $H_{V} = 6.42 \pm 0.07$ and $H_{R} = 5.95 \pm 0.06$, assuming the same phase correction parameter. The V-R colour is $0.47 \pm 0.09$.

For the February 2000 run (NAO), we find an average value for V of $18.04 \pm 0.03$ and for R of $17.55 \pm 0.05$. Considering only consecutive V and R measurements from the first night, we obtain $V-R = 0.49 \pm 0.04$. The values for HV and HR are $6.76 \pm 0.03$ and $6.29 \pm 0.05$ respectively, again assuming G = 0.15.

In all runs, the V-R colour indices are consistent and similar to previously published values (Table 7; Davies et al. 1998; McBride et al. 1999; Tegler & Romanishin 1998).


 

 
Table 2: Photometry of 10199 Chariklo (1997CU$_{\rm 26}$); SNO, March 1999
UT date Julian date R (AU) $\Delta$ (AU) $\alpha$ $\hbox{$^\circ$ }$ Exp.(s) Filter Mag$^{\star}$
1999 Mar. 19-20 2451257.49236 13.49 12.72 2.74 600 V 18.014
1999 Mar. 19-20 2451257.50208       1000 V 18.070
1999 Mar. 19-20 2451257.51458       1500 V 18.025
1999 Mar. 19-20 2451257.53472       1500 V 17.968
1999 Mar. 19-20 2451257.55417       1000 R 17.515
               
1999 Mar. 20-21 2451258.46806 13.49 12.73 2.80 1000 V 18.007
1999 Mar. 20-21 2451258.48750       1000 V 17.947
1999 Mar. 20-21 2451258.50764       1000 R 17.499
1999 Mar. 20-21 2451258.52361       1000 R 17.465
1999 Mar. 20-21 2451258.53681       1000 V 17.940
1999 Mar. 20-21 2451258.55000       1000 R 17.475
1999 Mar. 20-21 2451258.56389       1500 V 18.140
1999 Mar. 20-21 2451258.57778       1500 V 18.010
1999 Mar. 20-21 2451258.58700       1000 V 18.074
               
1999 Mar. 21-22 2451259.39236 13.49 12.74 2.86 1000 V 18.197
1999 Mar. 21-22 2451259.40764       1000 R 17.519
1999 Mar. 21-22 2451259.42361       1000 V 17.944
1999 Mar. 21-22 2451259.43611       1000 R 17.521
1999 Mar. 21-22 2451259.44931       500 R 17.641
1999 Mar. 21-22 2451259.45625       500 V 17.995

$^{\star}$ The errors on these values are typically 0.06.


 
Table 2: Photometry of 10199 Chariklo (cont.); NAO, April 1999
UT date Julian Date R (AU) $\Delta$ (AU) $\alpha$ $\hbox{$^\circ$ }$ Exp. (s) Filter Mag$^{\star}$
1999 Apr. 14-15 2451283.457 13.48 13.05 3.90 500 R 17.625
1999 Apr. 14-15 2451283.470       1000 R 17.621
1999 Apr. 14-15 2451283.481       1000 V 18.107
1999 Apr. 14-15 2451283.490       1000 V 18.137
               
1999 Apr. 17-18 2451286.336 13.48 13.08 3.99 500 R 17.466
1999 Apr. 17-18 2451286.352       500 R 17.476
1999 Apr. 17-18 2451286.358       1000 V 17.976
1999 Apr. 17-18 2451286.366       1000 V 17.963
1999 Apr. 17-18 2451286.373       500 R 17.496
1999 Apr. 17-18 2451286.414       500 R 17.561
1999 Apr. 17-18 2451286.421       500 R 17.525
1999 Apr. 17-18 2451286.428       1000 V 17.938
1999 Apr. 17-18 2451286.435       1000 V 18.009
1999 Apr. 17-18 2451286.457       500 R 17.618

$^{\star}$ The errors on these values are typically 0.05.


 
Table 2: Photometry of 10199 Chariklo (cont.); NAO, February 2000
UT date Julian date R (AU) $\Delta$ (AU) $\alpha$ $\hbox{$^\circ$ }$ Exp. (s) Filter Mag Error$^{\star}$
2000 Feb. 02.94132 2451577.44132 13.36 12.43 1.48 300 R 17.524 0.023
2000 Feb. 02.94571 2451577.44571       300 V 18.057 0.023
2000 Feb. 03.02298 2451577.52298       500 R 17.551 0.021
2000 Feb. 03.02965 2451577.52965       500 V 18.002 0.019
2000 Feb. 03.08629 2451577.58629       500 R 17.526 0.021
2000 Feb. 03.09727 2451577.59727       500 R 17.560 0.014
2000 Feb. 03.10402 2451577.60402       500 V 18.065 0.019
2000 Feb. 03.13865 2451577.63865       500 V 18.010 0.018
2000 Feb. 03.14532 2451577.64532 13.36 12.43 1.47 500 R 17.547 0.021
2000 Feb. 03.17434 2451577.67434       500 R 17.553 0.021
2000 Feb. 03.18398 2451577.68398       500 V 18.051 0.020
                 
2000 Feb. 03.96915 2451578.46915 13.36 12.42 1.42 500 R 17.519 0.016
2000 Feb. 04.00981 2451578.50981       500 R 17.515 0.015
2000 Feb. 04.05909 2451578.55909       500 R 17.531 0.016
2000 Feb. 04.10560 2451578.60560       500 R 17.509 0.016
2000 Feb. 04.15458 2451578.65458       500 R 17.545 0.016
                 
2000 Feb. 04.94554 2451579.44554 13.36 12.42 1.37 500 R 17.521 0.043
2000 Feb. 04.96629 2451579.46629       500 R 17.574 0.043
2000 Feb. 05.01117 2451579.51117       500 R 17.565 0.043
2000 Feb. 05.03236 2451579.53236       500 R 17.579 0.043
2000 Feb. 05.06306 2451579.56306 13.36 12.42 1.36 500 R 17.520 0.043
2000 Feb. 05.08058 2451579.58058       500 R 17.578 0.043
2000 Feb. 05.10391 2451579.60391       500 R 17.565 0.043
2000 Feb. 05.12286 2451579.62286       500 R 17.544 0.044
                 
2000 Feb. 06.97955 2451581.47955 13.36 12.41 1.26 500 R 17.574 0.016
2000 Feb. 07.02205 2451581.52205       500 R 17.556 0.016
2000 Feb. 07.04083 2451581.54083       500 R 17.597 0.016
2000 Feb. 07.06536 2451581.56536       500 R 17.569 0.014
2000 Feb. 07.08455 2451581.58455       500 R 17.548 0.016
2000 Feb. 07.14320 2451581.64320 13.36 12.41 1.25 500 R 17.563 0.017
2000 Feb. 07.16938 2451581.66938       500 R 17.560 0.017

$^{\star}$ Iraf formal error.


As shown in Table 5, McBride et al. (1999) report a value for HV of $6.64 \pm 0.04$ from data taken in May 1997 (6 observations during 3 nights). Our observations from 1999 give smaller values and the 2000 run gives a significantly higher value, the maximum difference being 0.34 mag, between the April 1999 and February 2000 data.


  \begin{figure} \includegraphics[width=8.8cm,clip]{H2535.eps}\end{figure} Figure 1: The Lomb-Normalized Power Spectrum as determined from the February 2000 data set in the R-filter using Lomb's (1976) method (Press et al. 1992) for unevenly spaced data. The maximum power at 0.769 cycles/day, corresponding to a 31.2 hours period, has no significance
Open with DEXTER

Also presented in Table 5 are the ecliptic latitude and longitude of the object as seen from Earth at the dates of the observations, as well as the $V(1,\alpha$) mag. The maximum difference in $V(1,\alpha$) mag is 0.23, between the May 1997 (McBride et al. 1999) and the April 1999 data. From this table, no obvious relation is seen between the different magnitudes and the geometry of the observations.

Taking G values of 0.15 and 0.30 results in maximum differences between HV's (April 1999 and February 2000 data) of 0.34 and 0.31 respectively.

In the case of G = 0.30 McBride et al.'s (1999) value comes much closer to our February 2000 value, although the difference is still slightly larger than the error bars. They find G = 0.36 for J band, so it appears that G = 0.30 for the V band would be better than 0.15 and would not require the large phase redding they introduce.


 

 
Table 3: Comparing the V magnitudes of 10199 Chariklo
Period $\alpha$ $\hbox{$^\circ$ }$ lat.$^{\star}$ $\hbox{$^\circ$ }$ lon.$^{\star}$ $\hbox{$^\circ$ }$ $V(1,\alpha$) HV (G = 0.15) HV (G = 0.30)
May 1997 4.1 125 -3.6 7.02 $\pm$ 0.04 6.64 $\pm$ 0.04 6.70 $\pm$ 0.04
(McBride et al. 1999)            
Mar. 1999 2.8 139 -9.6 6.85 $\pm$ 0.07 6.56 $\pm$ 0.07 6.60 $\pm$ 0.07
Apr. 1999 3.94 139 -9.6 6.79 $\pm$ 0.07 6.42 $\pm$ 0.07 6.48 $\pm$ 0.07
Feb. 2000 1.4 150 -12.4 6.94 $\pm$ 0.03 6.76 $\pm$ 0.03 6.79 $\pm$ 0.03

$^{\star}$ Ecliptic latitude and longitude as seen from Earth.

We judge it unlikely that large calibration errors are present, and so the observed differences can argue for rotational variability, although other possibilities exist, such as an outburst of activity in 1999.

Applying the formula used by Jewitt & Kalas (1998):

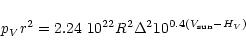\begin{displaymath}p_{V} r^2 = 2.24 ~ 10^{22} R^2 \Delta^2 10^{0.4(V_{\rm sun} - H_{V})} \end{displaymath} (1)

where pV is the V-band geometric albedo (0.045, Jewitt & Kalas 1998), HV the absolute magnitude of the object (R and $\Delta$ the heliocentric and geocentric distances in Astronomical Units, both unity when applying HV), and $V_{\rm sun}$ the apparent V-magnitude of the Sun (-26.76), radii between approximately $139 \pm 2$ km and $163 \pm 5$ km (diameter between $278 \pm 4$ km and $326 \pm 10$ km) are found. This is in close agreement with Jewitt & Kalas (1998) who report a diameter of $302 \pm 30$ km.

Concerning the rotation rate of 10199 Chariklo (1997CU$_{\rm 26}$), Davies et al. (1999) have reported no clear variable periodic signal. Since they observed the object only a few times in three days, they argued that a rotation period might exist but would be very long or close to 24 hours. The lack of variability in their data set would also be consistent with a nearly spherical body or with the possibility that one of its poles was facing the Sun in 1997.

We tried to explore our data to find if any periodicity could be detected. We applied the Lomb method (Lomb 1976) as described in Press et al. (1992), for the 1999 runs and the February 2000 runs separately.

The Lomb periodogram of the 1999 R-band data shows a weak signal at 18.5 hours which is below the 50% confidence level. Its confidence level was overestimated in Peixinho et al. (1999), rating it as 70%. Besides, the 18.5 periodic signal is absent in the V lightcurve. We therefore conclude that the 18.5 hour period is very likely spurious.

The 2000 Calar Alto data set is better suited for period analysis because of the larger amount of data in R band. The highest peak at a frequency of 0.769 cycles/day, corresponding to a period of 31.2 hours, has a false period probability of 67.6%, hence it is not significant (Fig. 1).

Assuming the results for the variation in the absolute magnitude from 1999 to 2000 are real and due to a change in cross section, the minimum value of the ratio of the major to minor axis can be calculated from the amplitude of the variation. This is in the order of 1.33 (peak to peak amplitude of $\sim$0.31 mag). This probably indicates that the object has a slow rotation rate rather than being pole on.

4 Results and discussion for 1999UG $_\mathsf{5}$

At the time of our February 2000 observing run 1999UG$_{\rm 5}$ was visible only in the first few hours of the astronomical night. Therefore, not enough observations could be obtained through the same filter for the determination of a possible rotation period. We focused on the determination of the colours for this object.

In order to avoid errors induced by possible rotational variability, the colours were determined using only consecutive images, or almost consecutive, on the corresponding filters, with the exception of B-V.

Table 6 lists the observations for 1999UG$_{\rm 5}$, and the values for the absolute magnitudes.

 

 
Table 4: Photometry of 1999UG$_{\rm 5}$; NAO, February 2000
UT date Julian date R (AU) $\Delta$ (AU) $\alpha$ $\hbox{$^\circ$ }$ Exp. (s) Filter Mag Error$^{\star}$
2000 Feb. 02.81945 2451577.31945 7.66 7.78 7.28 300 R 19.370 0.053
2000 Feb. 02.82188 2451577.32188       500 V 19.967 0.060
                 
2000 Feb. 03.81248 2451578.31248 7.66 7.79 7.25 500 V 20.062 0.048
2000 Feb. 03.81898 2451578.31898       500 R 19.476 0.044
2000 Feb. 03.85439 2451578.35439       900 V 20.082 0.041
2000 Feb. 03.86737 2451578.36737       900 R 19.570 0.038
                 
2000 Feb. 04.81285 2451579.31285 7.66 7.80 7.23 500 I 18.582 0.055
2000 Feb. 04.83004 2451579.33004       500 R 19.428 0.059
2000 Feb. 04.84458 2451579.34458       500 I 18.943 0.068
2000 Feb. 04.85185 2451579.35185       500 R 19.538 0.063
2000 Feb. 04.87417 2451579.37417       500 B 21.085 0.14
2000 Feb. 04.88096 2451579.38096       500 R 19.396 0.066
2000 Feb. 04.89412 2451579.39412       500 B 20.750 0.13
2000 Feb. 04.90148 2451579.40148       500 R 19.591 0.078

$^{\star}$ Iraf formal error.


 

 
Table 5: Comparison of colours of 1999UG$_{\rm 5}$
Object B-V V-R R-I reference
1999UG5 0.88 $\pm$ 0.18 0.60 $\pm$ 0.08 0.72 $\pm$ 0.13 this paper
5415 Pholus - 0.75 $\pm$ 0.04 0.76 $\pm$ 0.06 Luu & Jewitt (1996)
  1.19 $\pm$ 0.1 0.78 $\pm$ 0.04 - Romanishin et al. (1997)
    0.75 $\pm$ 0.02 0.84 $\pm$ 0.03 Davies et al. (1998)
         
7066 Nessus 0.88 $\pm$ 0.07 0.72 $\pm$ 0.05 - Luu & Jewitt (1996)
  - 0.80 $\pm$ 0.07 0.69 $\pm$ 0.12 Davies et al. (1998)
         
1995 GO 0.75 $\pm$ 0.04 0.47 $\pm$ 0.04 - Romanishin et al. (1997)
  0.78 $\pm$ 0.05 0.73 $\pm$ 0.04 - Brown & Luu (1997)
  - 0.41 $\pm$ 0.02 0.55 $\pm$ 0.04 Davies et al. (1998)
         
1997 CU26 - 0.46 $\pm$ 0.02 0.55 $\pm$ 0.03 Davies et al. (1998)
  - 0.48 $\pm$ 0.02 0.56 $\pm$ 0.03 Tegler & Romanishin (1998)
  - 0.46 $\pm$ 0.02 - McBride et al. (1999)
    0.50 $\pm$ 0.09 - March 1999, this paper
    0.47 $\pm$ 0.09 - April 1999, this paper
    0.49 $\pm$ 0.04 - February 2000, this paper
         
1995 DW2 - 0.41 $\pm$ 0.10 0.46 $\pm$ 0.18 Davies et al. (1998)
         
2060 Chiron 0.67 $\pm$ 0.06 0.34 $\pm$ 0.03 - Luu & Jewitt (1996)
         
Sun 0.67 0.36 0.53 Hartmann et al. (1990)


Table 7 summarizes the results and compares them to other objects in the solar system. The red colours for 1999UG$_{\rm 5}$ place this object among the reddest known in the solar system, indicating that its surface may be covered by some organic material (Cruikshank 1989; Thompson et al. 1987).

From V and R filters, disregarding any rotational variations, average values for $R = 19.48 \pm 0.09$ and $V = 20.04 \pm 0.07$ are obtained, and assuming a phase parameter value G = 0.15, this implies $H_{R} = 10.06 \pm 0.09$ and $H_{V} = 10.61 \pm 0.07$.

The diameter of 1999UG$_{\rm 5}$ as estimated from Eq. (1), assuming the same value for pV as for Chariklo, is $47 \pm 2$ km.

Acknowledgements

The authors acknowledge the use of the National Astronomical Observatory 1.52 meter telescope at the Calar Alto Observatory, Spain. This work is partially based on observations made with the 1.5 meter telescope of the Observatorio de Sierra Nevada Observatory, Granada, Spain, which is operated by the Instituto de Astrofísica de Andalucía (CSIC).

We also would like to thank Dr. Luisa Almeida, from CAAUL, for her valued help with the subtleties of IRAF's PHOTCAL routines and her very careful method for standard calibration.

References

 
Copyright ESO 2001