

Up: CI and CO in
Subsections
Notes
a Ratio denotes the relative contributions of the two
components to the observed emission in the
J=2-1
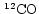
line.
b Model-calculated intensities of the
J=1-0,
J=3-2 and
J=4-3
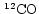
transitions normalized to
the
J=2-1
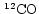
intensity.
c
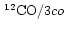
intensity ratios in the
J=1-0,
J=2-1 and
J=3-2 transitions.
Notes:
a Boulanger
Viallefond (
1992);
b Rogstad et al. (
1974);
Tilanus
Allen (
1993).
The observed
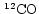 and
and 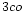 line intensities and ratios can be modelled
by radiative transfer models such as described by Jansen (1995) and
Jansen et al. (1994). The models provide line intensities as a function
of three input parameters: gas kinetic temperature
line intensities and ratios can be modelled
by radiative transfer models such as described by Jansen (1995) and
Jansen et al. (1994). The models provide line intensities as a function
of three input parameters: gas kinetic temperature 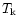 ,
molecular
hydrogen density n(H2) and CO column density per unit velocity
(N(CO)/dV). By comparing model line ratios to the observed ratios we
may identify the physical parameters best describing the actual conditions in
the observed source. The additional filling factor is found by comparing model
intensities to those observed. If
,
molecular
hydrogen density n(H2) and CO column density per unit velocity
(N(CO)/dV). By comparing model line ratios to the observed ratios we
may identify the physical parameters best describing the actual conditions in
the observed source. The additional filling factor is found by comparing model
intensities to those observed. If
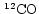 and
and 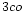 have the same beam
filling factor, a single component fit requires determination of five
independent observables. As we have measured seven line intensities, such
a fit is, in principle, overdetermined. In practice, this is not quite the
case because of significant finite errors in observed intensities, and
because of various degrees of degeneracy in the model line ratios. We found
that a single-component fit could be made to the data of the two galaxies
only if we allow CO J=1-0 intensities to be rather higher than observed.
As we also consider a single temperature, single density gas to be
physically implausible for the large volumes sampled, we reject such a fit.
have the same beam
filling factor, a single component fit requires determination of five
independent observables. As we have measured seven line intensities, such
a fit is, in principle, overdetermined. In practice, this is not quite the
case because of significant finite errors in observed intensities, and
because of various degrees of degeneracy in the model line ratios. We found
that a single-component fit could be made to the data of the two galaxies
only if we allow CO J=1-0 intensities to be rather higher than observed.
As we also consider a single temperature, single density gas to be
physically implausible for the large volumes sampled, we reject such a fit.
It is much more probable that the large linear beams used sample molecular
gas with a range of temperatures and densities. We approximate such
a situation by assuming the presence of two independent components.
As this already doubles the number of parameters to be determined to ten,
a physically realistic more complex analysis is not possible. In our
analysis, we assume identical
CO isotopical abundances for both components, and by assuming a specific
value (i.e. [12CO]/[13CO] = 40, cf. Mauersberger 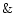 Henkel
1993) reduce the number of parameters to eight. This leaves a single free
parameter, for which we take the relative contribution (filling factor) of
the two components in the emission from the J=2-1
Henkel
1993) reduce the number of parameters to eight. This leaves a single free
parameter, for which we take the relative contribution (filling factor) of
the two components in the emission from the J=2-1
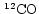 line.
Acceptable fits are then identified by searching a grid of model
parameter combinations (10 K
line.
Acceptable fits are then identified by searching a grid of model
parameter combinations (10 K
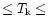 250 K,
250 K,
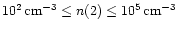 ,
,
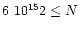 (CO)/d
(CO)/d
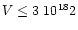 ;
relative emission contributions 0.1 to 0.9) for sets
of line ratios matching the observed set.
;
relative emission contributions 0.1 to 0.9) for sets
of line ratios matching the observed set.
The CO line ratios observed for NGC 6946 and M 83 can be fit by various
combinations of gas parameters or rather various regions in gas parameter
space. We have rejected from further consideration all solutions where the
denser component is also required to be the hotter, as we consider this to
be physically unlikely on the scales observed. Although the various line
ratios are very similar, in particular the isotope ratios for M 83
appear to be systematically somewhat lower than for NGC 6946. For this
reason, and also in order to demonstrate the possible variation in model
parameters, we have listed characteristic solutions for both galaxies
separately. The quality of each solution can be judged by comparing the
calculated model line ratios in Table 5 with those observed in Table 4.
The single-component fit is included for comparison.
The densest and coolest component has a fairly well-determined density of
3000
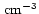 and an even better determined column density N(CO)/dV =
6-1
and an even better determined column density N(CO)/dV =
6-1
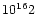 irrespective of density. The low-density
component (
irrespective of density. The low-density
component (
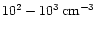 )
must have higher column
densities N(CO)/dV = 1-10
)
must have higher column
densities N(CO)/dV = 1-10
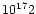 but its precise
temperature is difficult to determine as long as the relative emission
ratios of the components are a free parameter.
but its precise
temperature is difficult to determine as long as the relative emission
ratios of the components are a free parameter.
The observed C and C+ intensities are modelled with the same
radiative transfer model. For both we assume the CO-derived,
two-component solutions to be valid as far as kinetic temperatures,
and C+ intensities are modelled with the same
radiative transfer model. For both we assume the CO-derived,
two-component solutions to be valid as far as kinetic temperatures,  densities and filling factors are concerned. We may then solve for
C
densities and filling factors are concerned. We may then solve for
C and C+ column densities. The column density of the hotter
component is usually well-determined, but that of the cooler component is
more or less degenerate. Rather than a single solution, a range of possible
column density solutions is found. These are constrained by requiring similar
velocity dispersions (of about 3-5 km s-1) for both hot and cold
components and by requiring the resulting total carbon column densities to
be consistent with the chemical model solutions presented by Van
Dishoeck
and C+ column densities. The column density of the hotter
component is usually well-determined, but that of the cooler component is
more or less degenerate. Rather than a single solution, a range of possible
column density solutions is found. These are constrained by requiring similar
velocity dispersions (of about 3-5 km s-1) for both hot and cold
components and by requiring the resulting total carbon column densities to
be consistent with the chemical model solutions presented by Van
Dishoeck  Black (1988). These models show a strong dependence of the
N(C)/N(CO) column density ratio on total carbon and molecular hydrogen
column densities.
Black (1988). These models show a strong dependence of the
N(C)/N(CO) column density ratio on total carbon and molecular hydrogen
column densities.
The very strong [CII] intensity observed in M 83 exceeds that expected
from the CO-derived solutions. It thus implies the presence of ionized
carbon in high-density molecular volumes poorly represented by CO emission.
Consequently, in Model 6 (Table 5) we ascribed essentially all [CII]
emission to a gas with density
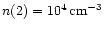 at temperature
at temperature
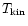 = 60 K whereas in Model 7 we assumed
= 60 K whereas in Model 7 we assumed
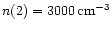 at
at
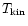 = 150 K.
= 150 K.
In order to relate total carbon (i.e. C + CO) column densities to those of
molecular hydrogen, we have estimated [C]/[H] gas-phase abundance ratios
from [O]/[H] abundances. Both galaxies have virtually identical
central abundances [O]/[H] = 1.75 10-3 Zaritsky et al. 1994;
Garnett et al. 1997). Using results given by Garnett et al. (1999), notably
their Figs. 4 and 6, we then estimate carbon abundances [C]/[H] =
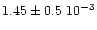 .
As a significant fraction of all carbon
will be tied up in dust particles, and not be available in the gas-phase,
we adopt a fractional correction factor
.
As a significant fraction of all carbon
will be tied up in dust particles, and not be available in the gas-phase,
we adopt a fractional correction factor
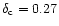 (see for
instance van Dishoeck
(see for
instance van Dishoeck 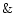 Black 1988), so
that
Black 1988), so
that
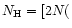 H2) + N(HI)]
H2) + N(HI)] 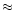 2500 [N(CO) + N(C)]
with a factor of two uncertainty in the numerical factor.
2500 [N(CO) + N(C)]
with a factor of two uncertainty in the numerical factor.
The results of our model calculations are given in Table 6, which presents
beam-averaged column densities for both CO and C (C and C+)
and the
and C+)
and the  column densities derived from these.
Table 6 also lists the total mass estimated to be present in the central
molecular concentration (R < 300 pc) obtained by scaling the
column densities derived from these.
Table 6 also lists the total mass estimated to be present in the central
molecular concentration (R < 300 pc) obtained by scaling the 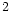 column densities with the J=2-1
column densities with the J=2-1
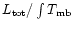 dV ratio
from Table 3, and the face-on mass densities implied by
hydrogen column density and the galaxy inclination. Beam-averaged
neutral carbon to carbon monoxide column density ratios are
N(C
dV ratio
from Table 3, and the face-on mass densities implied by
hydrogen column density and the galaxy inclination. Beam-averaged
neutral carbon to carbon monoxide column density ratios are
N(C
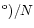 (CO)
(CO)
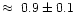 for both NGC 6946 and M 83,
somewhat higher than the values 0.2-0.5 found for M 82, NGC 253 and M 83
(White et al. 1994; Israel et al. 1995; Stutzki et al. 1997; Petitpas
for both NGC 6946 and M 83,
somewhat higher than the values 0.2-0.5 found for M 82, NGC 253 and M 83
(White et al. 1994; Israel et al. 1995; Stutzki et al. 1997; Petitpas  Wilson 1998).
Wilson 1998).
Notwithstanding the significant differences between the model
parameters, the hydrogen column densities, masses and mass-densities
derived in Table 6 are very similar. The [CI] and [CII] line and
the far-infrared continuum (Smith  Harvey 1996) intensities
suggest that they predominantly arise in a medium of density close to
Harvey 1996) intensities
suggest that they predominantly arise in a medium of density close to
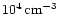 subject to a radiation field log
subject to a radiation field log 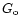 = 1-1.5
(cf. Kaufman et al. 1999). Emission from the molecules CS, H2CO
and HCN has been detected from the CO peaks in Fig. 2 (Mauersberger
et al. 1989; Hüttemeister et al. 1997; Paglione et al. 1995, 1997);
their intensities likewise indicate a density
= 1-1.5
(cf. Kaufman et al. 1999). Emission from the molecules CS, H2CO
and HCN has been detected from the CO peaks in Fig. 2 (Mauersberger
et al. 1989; Hüttemeister et al. 1997; Paglione et al. 1995, 1997);
their intensities likewise indicate a density
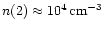 which is only provided by models 2 and 3 which we consider to be
preferable. Note that the single-component CO fit (model 4), which we
have already rejected, also does not fit the C
which is only provided by models 2 and 3 which we consider to be
preferable. Note that the single-component CO fit (model 4), which we
have already rejected, also does not fit the C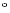 and C+
intensities predicted by the PDR models (Kaufman et al. 1999). The
high-density component probably corresponds to the molecular cloud
complexes that are the location of the present, mild starburst in the
center of NGC 6946 (Telesco et al. 1993; Engelbracht et al. 1996). It
represents about a third of the total molecular mass, and contributes
a similar fraction to the observed J=2-1 CO emission. The low-density
component has a temperature in the range
and C+
intensities predicted by the PDR models (Kaufman et al. 1999). The
high-density component probably corresponds to the molecular cloud
complexes that are the location of the present, mild starburst in the
center of NGC 6946 (Telesco et al. 1993; Engelbracht et al. 1996). It
represents about a third of the total molecular mass, and contributes
a similar fraction to the observed J=2-1 CO emission. The low-density
component has a temperature in the range
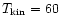 -150 K,
and a density of order
-150 K,
and a density of order
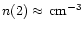 .
This is conformed by a
reanalysis of the midinfrared
.
This is conformed by a
reanalysis of the midinfrared 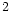 measurements by Valentijn et al.
(1996). The J=2-0 S(0)
measurements by Valentijn et al.
(1996). The J=2-0 S(0) 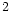 line intensity at 28
line intensity at 28 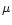 m is entirely
consistent with these values for an ortho/para ratio of two (P.P. van der
Werf, private communication). However, in order to also match the observed
J=3-1 S(1) line strength at 17
m is entirely
consistent with these values for an ortho/para ratio of two (P.P. van der
Werf, private communication). However, in order to also match the observed
J=3-1 S(1) line strength at 17 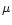 m, a small amount of high-temperature
molecular gas with
m, a small amount of high-temperature
molecular gas with
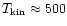 K,
K,
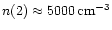 need
be present as well, but with a mass no more than a few per cent of
the mass given in Table 6. Our measurements are insensitive to such a
component.
need
be present as well, but with a mass no more than a few per cent of
the mass given in Table 6. Our measurements are insensitive to such a
component.
We thus conclude that the total mass of molecular gas within R = 0.5 kpc from the nucleus of NGC 6946 is 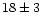 million solar masses; this
is about 1.5 per cent of the dynamical mass, so that the total mass of
the inner part of the galaxy must be completely dominated by stars.
No more than a quarter of all hydrogen is HI; most is in the form of
million solar masses; this
is about 1.5 per cent of the dynamical mass, so that the total mass of
the inner part of the galaxy must be completely dominated by stars.
No more than a quarter of all hydrogen is HI; most is in the form of 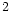 .
Between 15 and 25
.
Between 15 and 25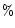 of all hydrogen is associated with ionized carbon
and almost equal amounts with neutral carbon and CO. Madden et al. (1993)
reach very similar conclusions from C+ mapping of NGC 6946, but find
different masses. Part of this difference arises in our use of two
components rather than a single component. Another important difference
between this and other studies is our use of the gas-phase carbon abundance
rather than an assumed conversion factor to obtain hydrogen column densities
and masses. For NGC 6946, this results in effective conversion factors of
the order of
X = 1 1019
of all hydrogen is associated with ionized carbon
and almost equal amounts with neutral carbon and CO. Madden et al. (1993)
reach very similar conclusions from C+ mapping of NGC 6946, but find
different masses. Part of this difference arises in our use of two
components rather than a single component. Another important difference
between this and other studies is our use of the gas-phase carbon abundance
rather than an assumed conversion factor to obtain hydrogen column densities
and masses. For NGC 6946, this results in effective conversion factors of
the order of
X = 1 1019 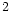 mol
mol 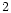 /
/
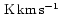 ,
which is more than an order of magnitude lower than traditionally assumed
values. The difference greatly exceeds the uncertainty of a factor of two
or three associated with the carbon abundance, illustrating the danger of
using "standard'' conversion factors in centers of galaxies where conditions
may be very different (higher metallicities, higher temperatures) from those
in galaxy disks.
,
which is more than an order of magnitude lower than traditionally assumed
values. The difference greatly exceeds the uncertainty of a factor of two
or three associated with the carbon abundance, illustrating the danger of
using "standard'' conversion factors in centers of galaxies where conditions
may be very different (higher metallicities, higher temperatures) from those
in galaxy disks.
The observed CO temperatures are typically a factor of 15 lower than
the model brightness temperatures, implying that only a small fraction of
the observing beam is filled by emitting material. We find small beam-filling
factors for the molecular material of order 0.06 - not very dependent on
choice of model. However, velocity-integrated intensities are a factor
of two or three higher than that of a model cloud, implying that the
average line of sight through NGC 6946 contains two or three clouds at
various velocities.
 |
Figure 6:
J=2-1 emission profiles at offset positions; vertical scale is in
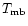 .
Left: NGC 6946 at .
Left: NGC 6946 at
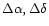 = +10'',
+10''. Right: M 83 at
= +10'',
+10''. Right: M 83 at
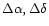 = +7'', -7''.
In both cases, the
= +7'', -7''.
In both cases, the 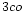 profile, multiplied by a factor of seven, is
included as the lower of the two curves
profile, multiplied by a factor of seven, is
included as the lower of the two curves |
The eastern extension seen in our J=3-2 and J = 2-1 maps is caused
by a discrete cloud at
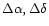 = +12'', +6''.
At this position, CO profiles show a strong, relatively narrow spike
asymmetrically superposed on the weaker broad profile from the
more extended emission (Fig. 6). This spike can also be discerned in
J=1-0 CO profiles published by Sofue et al. (1988) and in the J=3-2
and J=4-3 CO profiles by Nieten et al. (1999). By subtracting the
broad emission, we have attempted to determine the parameters of this
cloud. We find a deconvolved size of about 400 pc along the major axis
and
= +12'', +6''.
At this position, CO profiles show a strong, relatively narrow spike
asymmetrically superposed on the weaker broad profile from the
more extended emission (Fig. 6). This spike can also be discerned in
J=1-0 CO profiles published by Sofue et al. (1988) and in the J=3-2
and J=4-3 CO profiles by Nieten et al. (1999). By subtracting the
broad emission, we have attempted to determine the parameters of this
cloud. We find a deconvolved size of about 400 pc along the major axis
and 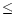 160 pc (i.e.
160 pc (i.e. 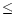 260 pc deprojected) along the minor axis.
Its deprojected distance to the nucleus is about 350 pc. Peak emission
occurs at
260 pc deprojected) along the minor axis.
Its deprojected distance to the nucleus is about 350 pc. Peak emission
occurs at
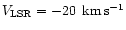 ,
and the linewidth is
,
and the linewidth is
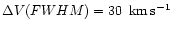 .
These results suggest that the object is a molecular cloud complex
in the bulge of NGC 6946, comparable to the Sgr B2 complex in the Milky Way.
Although the subtraction procedure is not accurate enough to obtain
good line ratios, these do not appear to be very different from those
of the major central concentration. They indicate a total mass
.
These results suggest that the object is a molecular cloud complex
in the bulge of NGC 6946, comparable to the Sgr B2 complex in the Milky Way.
Although the subtraction procedure is not accurate enough to obtain
good line ratios, these do not appear to be very different from those
of the major central concentration. They indicate a total mass
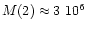
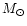 for the complex. Most of this mass
should be at a kinetic temperature of about 10 K, but about 15
for the complex. Most of this mass
should be at a kinetic temperature of about 10 K, but about 15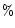 of
the total mass should experience a temperature of order 100 K.
of
the total mass should experience a temperature of order 100 K.
Not surprisingly in view of the very similar CO line ratios, the
radiative transfer solutions for M 83 do not differ much from those
for NGC 6946 (Table 5). The major difference is found in Table 6,
and is caused by the much stronger [CII] emission. With model 5,
the [CII] intensity can be reproduced using the CO derived gas
parameters, but only if in the hot 100 K component essentially
all (94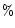 )
carbon is in the ionized atomic form C+; very
little CO can be left. Use of the CO two-component parameters requires
solutions with implausibly high C+ column densities for models 6
and 7. As already mentioned in the previous section, we have instead
assumed that the [CII] emission from M 83 mostly samples conditions
inbetween those of the two components, i.e. those at the interface of
hot, tenuous and colder, denser gas.
)
carbon is in the ionized atomic form C+; very
little CO can be left. Use of the CO two-component parameters requires
solutions with implausibly high C+ column densities for models 6
and 7. As already mentioned in the previous section, we have instead
assumed that the [CII] emission from M 83 mostly samples conditions
inbetween those of the two components, i.e. those at the interface of
hot, tenuous and colder, denser gas.
Whichever model is preferred, typically 50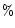 -65
-65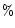 of all carbon in
the center of M 83 must be in ionized form. Because of this,
and the rather low HI column density observed towards the center of
M 83, molecular hydrogen column densities must be quite high, of
order 5-7
of all carbon in
the center of M 83 must be in ionized form. Because of this,
and the rather low HI column density observed towards the center of
M 83, molecular hydrogen column densities must be quite high, of
order 5-7
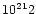 .
Although only a relatively small
fraction of all
.
Although only a relatively small
fraction of all 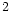 is related to CO emission, the conversion factor
is nevertheless higher for M 83 than for NGC 6946:
is related to CO emission, the conversion factor
is nevertheless higher for M 83 than for NGC 6946:
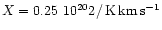 ,
but still well below the Galactic standard
value.
,
but still well below the Galactic standard
value.
The models are consistent with densities
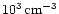 subject to
radiation fields log
subject to
radiation fields log
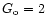 implied by comparing the CO,
[CI] and [CII] line and far-infrared continuum (Smith
implied by comparing the CO,
[CI] and [CII] line and far-infrared continuum (Smith  Harvey 1996)
intensities with the PDR models given by Kaufman et al. (1999). Few
density estimates from other molecules exist. Paglione et al. (1997)
estimate
Harvey 1996)
intensities with the PDR models given by Kaufman et al. (1999). Few
density estimates from other molecules exist. Paglione et al. (1997)
estimate
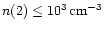 from HCN J=3-2 and J=1-0
measurements, whereas the beam-corrected ratio I(CO)/I(HCN) = 9
(J=1-0) from Israel (1982) suggests
from HCN J=3-2 and J=1-0
measurements, whereas the beam-corrected ratio I(CO)/I(HCN) = 9
(J=1-0) from Israel (1982) suggests
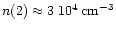 (see Mauersberger & Henkel 1993, their Fig. 4).
(see Mauersberger & Henkel 1993, their Fig. 4).
An important difference between NGC 6946 and M 83 is that the strong [CII]
emission characterizing the latter cannot be explained by assuming
that only relatively modest amounts of carbon monoxide have been
photodissociated into atomic carbon. The considerably stronger starburst
in M 83 (Gallais et al. 1991; Telesco et al. 1993; Turner  Ho 1994)
has apparently created a PDR-zone in which large amounts of high-temperature,
high-density ionized carbon gas have largely replaced efficiently eroded
CO clouds, so that a significant fraction, of order 80%, of the
molecular hydrogen in this PDR-zone is effectively not sampled by CO
emission. Dense, [CII] emitting gas is thereby a major contributor to
the total gas content of the center of M 83. The actual contribution
is somewhat uncertain because of the uncertainty in [CII] gas temperature.
If we take
Ho 1994)
has apparently created a PDR-zone in which large amounts of high-temperature,
high-density ionized carbon gas have largely replaced efficiently eroded
CO clouds, so that a significant fraction, of order 80%, of the
molecular hydrogen in this PDR-zone is effectively not sampled by CO
emission. Dense, [CII] emitting gas is thereby a major contributor to
the total gas content of the center of M 83. The actual contribution
is somewhat uncertain because of the uncertainty in [CII] gas temperature.
If we take
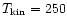 K and
K and
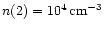 instead of the
actual values adopted, the resulting masses for models 6 and 7 in Table 6 would be about 60
instead of the
actual values adopted, the resulting masses for models 6 and 7 in Table 6 would be about 60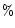 of the listed values.
of the listed values.
We conclude that the total amount of molecular gas in the center of M 83
(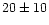 million solar masses) is very similar to that in NGC 6946
(
million solar masses) is very similar to that in NGC 6946
(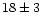 million solar masses). As in the case of NGC 6946, this is of
order 1-2 per cent of the dynamical mass, so that the mass of gas is
negligible with respect to the stellar mass. About 6
million solar masses). As in the case of NGC 6946, this is of
order 1-2 per cent of the dynamical mass, so that the mass of gas is
negligible with respect to the stellar mass. About 6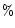 all hydrogen
is HI; the remainder must be in the form of
all hydrogen
is HI; the remainder must be in the form of 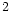 .
About half of
all hydrogen is associated with ionized carbon; the other half is mostly
associated with CO. We thus confirm the predominant role for C
.
About half of
all hydrogen is associated with ionized carbon; the other half is mostly
associated with CO. We thus confirm the predominant role for C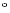 that was already found by Crawford et al. (1985) and Stacey et al. (1991).
As for NGC 6946, we note that the total molecular mass found in the central
region (R < 0.5 kpc) is much less than suggested by others on the
basis of assumed conversion factors.
that was already found by Crawford et al. (1985) and Stacey et al. (1991).
As for NGC 6946, we note that the total molecular mass found in the central
region (R < 0.5 kpc) is much less than suggested by others on the
basis of assumed conversion factors.
In M 83, observed CO temperatures are typically a factor of 7.5 (Model 5)
to 15 (Model 7) lower than the model brightness temperatures, indicating
beam-filling factors for the molecular material of order 0.12-0.06,
i.e. larger than for NGC 6946. At the same time, the velocity-integrated
intensity is a factor of two to five larger than that of a model cloud,
implying the presence of that number of clouds in an average line of sight
through M 83. Although the central gas masses in NGC 6946 and M 83 are
very similar, the face-on mass density in the center of M 83 is more than
double that of NGC 6946.


Up: CI and CO in
Copyright ESO 2001