A&A 371, 652-666 (2001)
DOI: 10.1051/0004-6361:20010409
D. Barrado y Navascués 1 - R. J. García López 2,3 - G. Severino 4 - M. T. Gomez 4
1 - Departamento de Física Teórica, C-XI-506,
Universidad Autónoma de Madrid, Cantoblanco, 28049 Madrid,
Spain
2 -
Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife,
Spain
3 -
Departamento de Astrofísica, Universidad de La Laguna, Av.
Astrofísico Francisco Sánchez s/n, 38071
La Laguna, Tenerife, Spain
4 -
Osservatorio Astronomico di Capodimonte, Via Moiariello, 16, 80131 Napoli,
Italy
Received 9 June 2000 / Accepted 12 March 2001
Abstract
An analytical model has been developed to empirically study the effects of
stellar spots and faculae on the observed equivalent
widths of
Li I 6708, Na I 5896 and K I 7699 Å lines
(and abundances in the case of lithium)
in late-type stars, taking into account
the changes in the observed magnitudes and colors.
Solar spectra corresponding to
different active regions are used as input data and a range of filling factors
are applied to simulate the surfaces of stars with different levels of
activity. Detailed comparisons between predicted and observed photometric
colors and equivalent widths are made for late-type stars of the Pleiades and the field. The
observed dispersions in K I and Li I equivalent widths for Pleiades stars can be
partially accounted by the simultaneous effects of activity on colors and the
line formation, indicating that the lithium-rotation connection suggested for
![]()
![]() Pleiades stars could be due in part to the stellar
activity. However, under realistic values for the filling factors, only a
small portion of the observed spread could be explained by these effects.
Pleiades stars could be due in part to the stellar
activity. However, under realistic values for the filling factors, only a
small portion of the observed spread could be explained by these effects.
Key words: Sun: activity - Sun: faculae, plages - sunspots - stars: abundances - stars: activity - stars: late type
The formation of neutral alkali resonance lines in the solar photosphere is known to be affected by the presence of active regions and spots on the solar surface, because the fractions of neutral alkali atoms in their ground states are very sensitive to the photospheric temperature structure (see e.g. Giampapa 1984; Caccin et al. 1993; Severino et al. 1994, and references therein). This is expected also to be the case for the photospheres of other late-type (F- to early M-type) stars with similar atmospheric characteristics. Different authors have dealt with the comparison of observed and synthetic spectra of Na I D ( 5890-5896 Å) and K I 7699 Å lines in stars of different spectral types (Covino et al. 1993; Andretta et al. 1997; Tripicchio et al. 1997, 1999; Short & Doyle 1998), showing the benefits and difficulties in using the lines of neutral alkali to probe the effect of activity on the photospheres of these stars.
Both the Li I 6708 and K I 7699 Å features are resonance lines
with similar excitation potentials and similar formation conditions: any line
formation effect which affects the K I line should also affect the
Li I line. In contrast with potassium, lithium is destroyed inside the
stellar interior by
![]() nuclear reactions in those layers where the
temperature reaches
nuclear reactions in those layers where the
temperature reaches ![]() 2.5 106 K. The K I line appears then
as a key tool for identifying and isolating the possible effects of activity
on the observed Li abundances in late-type stars, since its surface abundance
does not depend on stellar age, rotational velocity, etc.
Open clusters, due to the common properties shared by the stars belonging to
them (same age and metallicity), provide excellent opportunities to study the
details of stellar structure and evolution. Lithium abundances have been
derived for a significant number of clusters and different mixing mechanisms
have been invoked to explain the observed patterns (see recent reviews by
Balachandran 1995; Pinsonneault 1997; Martín 2001; Vauclair 2001).
These observations indicate that the abundance decreases with
temperature and stellar age, and that there is a
star-to-star scatter of the Li abundance
for the same temperature.
In particular, the existence of a lithium-rotation
connection has been suggested
for
2.5 106 K. The K I line appears then
as a key tool for identifying and isolating the possible effects of activity
on the observed Li abundances in late-type stars, since its surface abundance
does not depend on stellar age, rotational velocity, etc.
Open clusters, due to the common properties shared by the stars belonging to
them (same age and metallicity), provide excellent opportunities to study the
details of stellar structure and evolution. Lithium abundances have been
derived for a significant number of clusters and different mixing mechanisms
have been invoked to explain the observed patterns (see recent reviews by
Balachandran 1995; Pinsonneault 1997; Martín 2001; Vauclair 2001).
These observations indicate that the abundance decreases with
temperature and stellar age, and that there is a
star-to-star scatter of the Li abundance
for the same temperature.
In particular, the existence of a lithium-rotation
connection has been suggested
for ![]()
![]() stars in young clusters such as the Pleiades
(Butler et al. 1987; García López et al. 1991a,b; Soderblom et al. 1993;
García López et al. 1994; Jones et al. 1996) and Alpha Persei cluster
(Balachandran et al. 1988; Randich et al. 1998), indicating that fast rotators,
as a group, show higher lithium abundances
than slow rotators. Balachandran et al. (1998)
discuss different aspects of the lithium-rotation connection and mixing in
late-type stars. Note, however, that slightly older clusters do not
clearly show this connection, as in the case of M 35 (Barrado y
Navascués et al. 2001b). Alternatively, it has also been suggested that
chromospheric activity could affect the formation of the Li line, partially
accounting for the observed dispersion (Houdebine & Doyle 1995; Barrado y
Navascués 1996; Russel 1996; Jeffries 1999; King et al. 2000). In this case
the Li-rotation connection would be a Li-activity-rotation relation (higher
rotation means higher activity) and the observed dispersion in Li equivalent
widths (Ws) would not (or only in part) correspond to a real dispersion in Li
abundances.
stars in young clusters such as the Pleiades
(Butler et al. 1987; García López et al. 1991a,b; Soderblom et al. 1993;
García López et al. 1994; Jones et al. 1996) and Alpha Persei cluster
(Balachandran et al. 1988; Randich et al. 1998), indicating that fast rotators,
as a group, show higher lithium abundances
than slow rotators. Balachandran et al. (1998)
discuss different aspects of the lithium-rotation connection and mixing in
late-type stars. Note, however, that slightly older clusters do not
clearly show this connection, as in the case of M 35 (Barrado y
Navascués et al. 2001b). Alternatively, it has also been suggested that
chromospheric activity could affect the formation of the Li line, partially
accounting for the observed dispersion (Houdebine & Doyle 1995; Barrado y
Navascués 1996; Russel 1996; Jeffries 1999; King et al. 2000). In this case
the Li-rotation connection would be a Li-activity-rotation relation (higher
rotation means higher activity) and the observed dispersion in Li equivalent
widths (Ws) would not (or only in part) correspond to a real dispersion in Li
abundances.
Soderblom et al. (1993) found that the K I 7699 Å equivalent widths of K-type stars in the Pleiades exhibited a similar trend to that of Li I 6708 Å but with a lower spread. They concluded in their study that activity could only partially influence the observed Li spread. Stuik et al. (1997) compared observed and synthetic Li I and K I spectra (affected by the presence of spot and plages) for late-type Pleiades stars. They found that these lines are not sensitive to the presence of a chromosphere, and that they respond to the effects of activity on the stratification in the deep photosphere. However, they could not establish whether or not magnetic activity is the major contributor to the observed K I (and Li I) scatter. More recently, King et al. (2000) addressed this problem by using differential Li abundances (with respect to fitted values vs. effective temperature) and differential K I equivalent widths. They invoked an incomplete treatment of line formation (in particular, the role of ionization in reducing the the Li I line optical depth; Houdebine & Doyle 1995) to explain the correlations found between differential Li and K values and differences in stellar activity (measured using the Ca II IR triplet).
None of these previous works has clearly established the quantitative effects
of stellar activity on the K I and Li I lines. In this paper, we
have adopted an empirical approach to this study and included the Na I
5896 Å line as a complementary indicator. An analytical model has been
developed to evaluate the simultaneous effect of surface inhomogeneities on the
observed line equivalent widths and stellar photometric colors. The inputs to
this model come from high-quality, high-resolution observations carried out on
different regions of the solar disk. Section 2 briefly describes the
observational material, while Sect. 3 provides the details of the model. A
comparison between model predictions and photometric data for the Pleiades is
shown in Sect. 4. Section 5 discusses the effect of stellar spots and
faculae on the alkali and compares these results with K I and Li
I measurements in late-type Pleiades stars. Finally, Sect. 6 summarizes our
main conclusions.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS09992f1a.eps}\par\includegraphics[width=7cm,clip]{MS09992f1b.eps}
\end{figure}](/articles/aa/full/2001/20/aa9992/Timg18.gif) |
Figure 1:
Results of our model for a star with
|
| Open with DEXTER | |
| Line | Equivalent width (mÅ) | ||||
| Quiet | Faculae | Average Umbra | Central Umbra | Spot 2 | |
| (Å) | |||||
| Li I 6708 | 3.977 | 3.569 | 20.247 | 49.080 | - |
| K I 7699 | 179.5 | 177.3 | 294.5 | 373.4 | 1139.0(1) |
| Na I 5896 | 599.0 | 531.4 | 1118.4 | 1786.6 | 5180.9(1) |
| Temperature (K) | 5655 | - | 4870 | 4575 | 3700(1) |
The observations used in this work were carried out in September 1994, using
the echelle spectrograph of the Gregory-Coudé telescope located at the Teide
Observatory, Tenerife (Spain). This instrument provides a great stability
together with very high spectral resolution. Spectra with a resolving power of
![]() were recorded in each spectral range
using a 1024
were recorded in each spectral range
using a 1024![]() 1024 pixel Thomson CCD (19
1024 pixel Thomson CCD (19 ![]() m pixel-1). Long slit
observations were performed in order to obtain a spatial coverage of
160
m pixel-1). Long slit
observations were performed in order to obtain a spatial coverage of
160
![]() in a given measurement. Each final spectrum is typically the
average of 20 independent images (50 in the case of Li), which were reduced
using MIDAS following the usual procedure for solar observations carried out
with this instrumentation. Final signal-to-noise ratios are in the range
1000-4000. Additional details on the observations and data reduction can be
found in Barrado y Navascués et al. (1995) and Barrado y Navascués (1996).
Table 1 shows the equivalent widths measured for different locations of the
observed active region and its surroundings. Since our original spectra have
very high resolution, we were able to remove either
the nearby TiO and CN bands-which appear at low temperatures- in the case of
Li I, or the weak lines in the case of K I and Na I.
These equivalent widths will be used as the input data for the model proposed in the next
section.
Additional measurements (for Na and K) were selected from Tripicchio
et al. (1997, 1999) for a sunspot at 3700 K.
in a given measurement. Each final spectrum is typically the
average of 20 independent images (50 in the case of Li), which were reduced
using MIDAS following the usual procedure for solar observations carried out
with this instrumentation. Final signal-to-noise ratios are in the range
1000-4000. Additional details on the observations and data reduction can be
found in Barrado y Navascués et al. (1995) and Barrado y Navascués (1996).
Table 1 shows the equivalent widths measured for different locations of the
observed active region and its surroundings. Since our original spectra have
very high resolution, we were able to remove either
the nearby TiO and CN bands-which appear at low temperatures- in the case of
Li I, or the weak lines in the case of K I and Na I.
These equivalent widths will be used as the input data for the model proposed in the next
section.
Additional measurements (for Na and K) were selected from Tripicchio
et al. (1997, 1999) for a sunspot at 3700 K.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{MS09992f2.eps}
\end{figure}](/articles/aa/full/2001/20/aa9992/Timg23.gif) |
Figure 2:
Visual absolute magnitude against the color index
(B-V) for four cases presented in this study (thin-solid, dotted, short dashed
and long dashed lines for spots with 4870, 4575, 4000 and 3700 K, respectively).
We have computed the observed
photometry for stars with
|
| Open with DEXTER | |
We estimate in this section the behavior of the equivalent widths of Na I 5896, Li I 6708 and K I 7699 Å lines associated with the presence of active regions in late-type stars. Stellar spots (and other surface inhomogeneities) affect the observed photometry due to the lower luminosity of the spot in comparison with that of a quiet region of equivalent size. On the other hand, it is known that the equivalent widths (Ws) of the alkali show different values in different solar regions (as can be seen in Table 1) associated with the different temperatures of the line forming regions. A simple mathematical model is used here to compute an "observed'' (predicted) color index - in our case, (B-V) - and the corresponding effective temperature, as well as the "observed'' (predicted) equivalent widths of the alkali lines for a given set of parameters. This model is intended to reproduce what happens in late-type stars from our knowledge of the solar surface.
The computation starts from a fictitious star free of active regions and having a given effective temperature. Then, different active regions (spots and faculae) are added to its photosphere in a similar fashion to that followed by Pallavicini et al. (1993).
Estimating the observed photometry for a stellar disk which contains spots
requires the previous computation of the contribution of the region covered by
them, i.e. its filling factor,
![]() .
In a similar way, we should
consider the fraction covered by faculae,
.
In a similar way, we should
consider the fraction covered by faculae,
![]() ,
and the fraction
filled with quiet regions. For simplicity, we have supposed that the
photometric properties of these two last regions are identical. Therefore, it
is only necessary to take into account
,
and the fraction
filled with quiet regions. For simplicity, we have supposed that the
photometric properties of these two last regions are identical. Therefore, it
is only necessary to take into account
![]() and {1-
and {1-
![]() }. We have not considered the effect of limb darkening either.
}. We have not considered the effect of limb darkening either.
The absolute magnitude of the region covered by spots can be expressed by:
| (1) |
In the case of the region covered by faculae and the quiet photosphere:
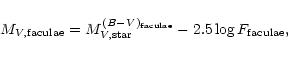 |
(2) |
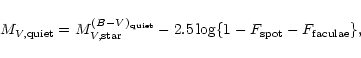 |
(3) |
Finally, the observed magnitudes can be predicted using the expression:
| (4) |
There are several factors which affect the observed equivalent widths. They
depend, among other parameters, on the filling factors of spots and faculae.
Moreover, the Ws depend on the local continuum level. Therefore, it is
necessary to compute the ratios ![]()
![]() ,
between the fluxes from
the region covered by spots and the quiet region (and faculae) at the studied
wavelengths -
,
between the fluxes from
the region covered by spots and the quiet region (and faculae) at the studied
wavelengths -
![]() (spot)/Flux(quiet):
(spot)/Flux(quiet):
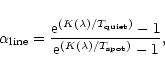 |
(5) |
![$\displaystyle %
W_{\rm obs}^{\rm line} = \frac{\alpha_{\rm line}F_{\rm spot}W^{...
... F_{\rm spot}
{+} F_{\rm faculae} {+} [1 - F_{\rm spot} {-} F_{\rm faculae}]} ,$](/articles/aa/full/2001/20/aa9992/img41.gif) |
(6) |
Tripicchio et al. (1999) have shown that the potassium equivalent
width at 7699 Å is an excellent temperature indicator
(in a very well defined spectral range).
Therefore, we have computed
the effective temperatures from their expression:
| (7) |
Color indices (B-V) were derived from the Thorburn et al. (1993)
scale temperature, namely:
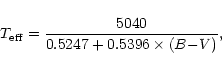 |
(8) |
Absolutes magnitudes were derived using a Pleiades empirical
main sequence (MS, see Fig. 2), with a color excess of
E(B-V)=0.04and a distance modulus of
(m-M)=5.728. Other examples of empirical
main sequences for the Pleiades, Alpha Persei cluster, M 35 and field
stars can be found in Bouvier et al. (1998); Stauffer et al. (1999);
Barrado y Navascués et al. (2001b) and
Barrado y Navascués et al. (1999), respectively.
| Model | MV | (B-V)0 | Radii ( |
Temperature (K) | |||||
| Quiet | Quiet | Spot | Quiet | Spot | Quiet | Spot | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | ||
| 1a | 4.192 | 0.500 | 0.946 | 1.218 | 0.794 | 6344 | 4870 | ||
| 1b | 4.192 | 0.500 | 1.069 | 1.218 | 0.750 | 6344 | 4575 | ||
| 1c | 4.192 | 0.500 | 1.363 | 1.218 | 0.630 | 6344 | 4000 | ||
| 1d | 4.192 | 0.500 | 1.552 | 1.218 | 0.408 | 6344 | 3700 | ||
| 2a | 5.253 | 0.679 | 0.946 | 0.921 | 0.794 | 5655 | 4870 | ||
| 2b | 5.253 | 0.679 | 1.069 | 0.921 | 0.750 | 5655 | 4575 | ||
| 2c | 5.253 | 0.679 | 1.363 | 0.921 | 0.630 | 5655 | 4000 | ||
| 2d | 5.253 | 0.679 | 1.552 | 0.921 | 0.408 | 5655 | 3700 | ||
| 3a | 6.411 | 0.900 | 0.946 | 0.811 | 0.794 | 4988 | 4870 | ||
| 3b | 6.411 | 0.900 | 1.069 | 0.811 | 0.750 | 4988 | 4575 | ||
| 3c | 6.411 | 0.900 | 1.363 | 0.811 | 0.630 | 4988 | 4000 | ||
| 3d | 6.411 | 0.900 | 1.552 | 0.811 | 0.408 | 4988 | 3700 | ||
| 4c | 7.612 | 1.103 | 1.363 | 0.737 | 0.630 | 4500 | 4000 | ||
| 4d | 7.612 | 1.103 | 1.552 | 0.737 | 0.408 | 4500 | 3700 | ||
| Model | Temperature (K) | W(Na I5896) (mÅ) | W(K I7699) (mÅ) | |||||
| Quiet | Spot | Quiet | Spot | Quiet | Spot | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | ||
| 1a | 6344 | 4870 | 348.9(1) | 1118.4(2) | 131.1(5) | 294.5(2) | ||
| 1b | 6344 | 4575 | 348.9(1) | 1786.6(2) | 131.1(5) | 373.4(2) | ||
| 1c | 6344 | 4000 | 348.9(1) | 3522.9(3) | 131.1(5) | 595.9(5) | ||
| 1d | 6344 | 3700 | 348.9(1) | 5198.9(4) | 131.1(5) | 1139.0(4) | ||
| 2a | 5655 | 4870 | 599.0(1,2) | 1118.4(2) | 179.5(2,5) | 294.5(2) | ||
| 2b | 5655 | 4575 | 599.0(1,2) | 1786.6(2) | 179.5(2,5) | 373.4(2) | ||
| 2c | 5655 | 4000 | 599.0(1,2) | 3522.9(3) | 179.5(2,5) | 595.9(5) | ||
| 2d | 5655 | 3700 | 599.0(1,2) | 5198.9(4) | 179.5(2,5) | 1139.0(4) | ||
| 3a | 4988 | 4870 | 1167.4(1) | 1118.4(2) | 264.5(5) | 294.5(2) | ||
| 3b | 4988 | 4575 | 1167.4(1) | 1786.6(2) | 264.5(5) | 373.4(2) | ||
| 3c | 4988 | 4000 | 1167.4(1) | 3522.9(3) | 264.5(5) | 595.9(5) | ||
| 3d | 4988 | 3700 | 1167.4(1) | 5198.9(4) | 264.5(5) | 1139.0(4) | ||
| 4c | 4500 | 4000 | 2154.7(1) | 3522.9(3) | 377.7(5) | 595.9(5) | ||
| 3d | 4500 | 3700 | 2154.7(1) | 5198.9(4) | 377.7(5) | 1139.0(4) | ||
| (1) From W(Na I5896) = 0.473 10 (-0.788+1.311(B-V)), adapted from Tripicchio et al. (1997). |
| (2) Measured. See Table 1. |
| (3) From field stars. See Fig. 3c. |
| (4) From direct measurement. See Tripicchio et al. (1999). |
| (5) From W(K I7699) = 1.042 10 (1.719+0.762(B-V)), adapted from Tripicchio et al. (1999). |
We have performed a series of simulations under different conditions and
obtained final values of "observed'' (predicted) photometry for a main
sequence star. This star has an effective temperature corresponding to that of
the quiet region, and we have assumed different filling factors for the spots
(in principle, the photometry is not affected by the presence of faculae). We
have used different spots: one of them corresponds to the average of the actual
sunspot. The other one is the central part of it - the nucleus of the umbra -,
with lower temperature (4870 and 4575 K, respectively).
We have also carried out the computations for spots at 4000 and 3700 K.
The model was applied
to stars with the following initial temperatures: 6344, 5655, 4988 and 4500 K,
corresponding to (
B-V)=0.500, 0.679, 0.900 and 1.100, respectively.
Table 2 lists the initial model parameters (magnitudes, colors, radii, effective temperatures).
The initial values of potassium and sodium equivalent widths
adopted for them are shown in Table 3.
Lithium equivalent widths and abundances are listed in Tables 4a and 4b, in the case of the solar-like case and the Pleiades, respectively.
| Model | Temperature (K) | A(Li) | W(Li) | A(Li) | W(Li) | |||
| Quiet | Spot | Quiet | Quiet | Spot | Spot | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | ||
| 1a | 6344 | 4870 | 1.0 | 1.010(1) | 0.85 | 20.5(2) | ||
| 1b | 6344 | 4575 | 1.0 | 1.010(1) | 0.87 | 49.1(2) | ||
| 1c | 6344 | 4000 | 1.0 | 1.010(1) | 1.00 | 173.0(1) | ||
| 1d | 6344 | 3700 | 1.0 | 1.010(1) | 1.00 | 249.8(3) | ||
| 2a | 5655 | 4870 | 1.0 | 3.977(2) | 0.85 | 20.5(2) | ||
| 2b | 5655 | 4575 | 1.0 | 3.977(2) | 0.87 | 49.1(2) | ||
| 2c | 5655 | 4000 | 1.0 | 3.977(2) | 1.00 | 173.0(1) | ||
| 2d | 5655 | 3700 | 1.0 | 3.977(2) | 1.00 | 249.8(3) | ||
| 3a | 4988 | 4870 | 1.0 | 20.4(1) | 0.85 | 20.5(2) | ||
| 3b | 4988 | 4575 | 1.0 | 20.4(1) | 0.87 | 49.1(2) | ||
| 3c | 4988 | 4000 | 1.0 | 20.4(1) | 1.00 | 173.0(1) | ||
| 3d | 4988 | 3700 | 1.0 | 20.4(1) | 1.00 | 249.8(3) | ||
| 4c | 4500 | 4000 | 1.0 | 77.0(1) | 1.00 | 173.0(1) | ||
| 3d | 4500 | 3700 | 1.0 | 77.0(1) | 1.00 | 249.8(3) | ||
|
|
|
(1) From Soderblom et al. (1993) curves of growth, using
|
| (2) Measured. See Table 1. |
|
(3) From Pavlenko et al. (1996) curves of growth, using
|
Figure 1a shows the variation of the visual magnitude (
![]() ,
defined as
the difference between the magnitude of a star only covered by quiet regions
and the observed magnitude; always positive) against the filling factor of the
spots,
,
defined as
the difference between the magnitude of a star only covered by quiet regions
and the observed magnitude; always positive) against the filling factor of the
spots,
![]() .
The solid line shows the results for a spot at 4870 K,
the dotted line represents the calculation for a spot at 4575 K,
whereas the short and long dashed lines represent the values for spots with
4000 and 3700 K, respectively. Although
the luminosity can decrease by a factor 10 in the most extreme case, a more
realistic situation can be considered in the range
.
The solid line shows the results for a spot at 4870 K,
the dotted line represents the calculation for a spot at 4575 K,
whereas the short and long dashed lines represent the values for spots with
4000 and 3700 K, respectively. Although
the luminosity can decrease by a factor 10 in the most extreme case, a more
realistic situation can be considered in the range
![]() ,
which, depending on these particular four spots, corresponds to
maximum variations of
,
which, depending on these particular four spots, corresponds to
maximum variations of
![]() mag. These values have been
observed in several active binary systems such as CF Tuc, BD+25
mag. These values have been
observed in several active binary systems such as CF Tuc, BD+25![]() 161,
AY Cet, CC Eri, UX Ari, etc. (e.g., Strassmeier et al. 1993; Strassmeier 1995,
and references therein).
161,
AY Cet, CC Eri, UX Ari, etc. (e.g., Strassmeier et al. 1993; Strassmeier 1995,
and references therein).
Figure 1b displays the dependence of the observed color index (B-V) on the
spot filling factor. It is seen that the color can change considerably, a
phenomenon which could have important consequences when comparing stars having
a high level of activity with inactive stars (i.e., rapid versus slow rotators)
at the same observed color, because the color of the quiet photosphere is
bluer than the observed color.
Note the different behavior for different
![]() ,
due to the fact that the V filter is centered around
,
due to the fact that the V filter is centered around ![]() 5500 Å,
which corresponds to a black-body temperature between the spots
at 4870 and 4575 K, whereas the B filter is centered at
5500 Å,
which corresponds to a black-body temperature between the spots
at 4870 and 4575 K, whereas the B filter is centered at ![]() 4300 Å.
Therefore, the relative contributions at the filters B and V are very different
depending on the spot and quiet photosphere temperatures.
Under realistic conditions, this change can be
up to
4300 Å.
Therefore, the relative contributions at the filters B and V are very different
depending on the spot and quiet photosphere temperatures.
Under realistic conditions, this change can be
up to
![]() .
Since there is a relationship between the color
indices and the stellar mass, the mass estimated for the more active star
would be lower than its actual value in the case of MS stars. Using the
presence of photometric variations due to the modulation with phase, as the
star rotates, can help to avoid this bias, although the lack of modulation does
not guarantee the absence of this bias, since the spots can be distributed in a
homogeneus way on the stellar disk, producing null or very small photometric
variations. In fact, studies made with tomographic spectroscopy or Doppler
imaging (Strassmeier 1995; Vogt & Hatzes 1995) and theoretical works
(Schüssler 1995), show that the spots in very active systems tend to be
concentrated in the poles, staying there for a long period of time (time scale of
years), and producing minimum photometric variations.
.
Since there is a relationship between the color
indices and the stellar mass, the mass estimated for the more active star
would be lower than its actual value in the case of MS stars. Using the
presence of photometric variations due to the modulation with phase, as the
star rotates, can help to avoid this bias, although the lack of modulation does
not guarantee the absence of this bias, since the spots can be distributed in a
homogeneus way on the stellar disk, producing null or very small photometric
variations. In fact, studies made with tomographic spectroscopy or Doppler
imaging (Strassmeier 1995; Vogt & Hatzes 1995) and theoretical works
(Schüssler 1995), show that the spots in very active systems tend to be
concentrated in the poles, staying there for a long period of time (time scale of
years), and producing minimum photometric variations.
| Model | Temperature (K) | A(Li) | W(Li) | ||||
| Quiet | Spot | Quiet | Quiet | Spot | |||
| (1) | (2) | (3) | (4) | (5) | (6) | ||
| 1a | 6344 | 4870 | 3.02(1) | 80.0 | 313(1) | ||
| 1b | 6344 | 4575 | 3.02(1) | 80.0 | 383(1) | ||
| 1c | 6344 | 4000 | 3.02(1) | 80.0 | 605(1) | ||
| 1d | 6344 | 3700 | 3.02(1) | 80.0 | 993(2) | ||
| 2a | 5655 | 4870 | 2.80(1) | 140.0 | 284(1) | ||
| 2b | 5655 | 4575 | 2.80(1) | 140.0 | 345(1) | ||
| 2c | 5655 | 4000 | 2.80(1) | 140.0 | 510(1) | ||
| 2d | 5655 | 3700 | 2.80(1) | 140.0 | 632(2) | ||
| 3a | 4988 | 4870 | 1.70(1) | 84.0 | 107(1) | ||
| 3b | 4988 | 4575 | 1.70(1) | 84.0 | 177(1) | ||
| 3c | 4988 | 4000 | 1.70(1) | 84.0 | 276(1) | ||
| 3d | 4988 | 3700 | 1.70(1) | 84.0 | 382(2) | ||
| 4c | 4500 | 4000 | 0.64(1) | 37.0 | 112(1) | ||
| 3d | 4500 | 3700 | 0.64(1) | 37.0 | 157(2) | ||
We have performed several comparisons between the observed data and the
predictions of this model on the effect of the presence of surface
inhomogeneities on the photometry and the equivalent widths. A first check is
provided by the Pleiades open cluster by looking at the location of the active
stars in the Color-Magnitude diagram (CMD), where the photometric properties of
the late-type stars change due to the presence of surface features with
different temperatures. Figure 2 shows the visual absolute magnitude against
the dereddened color index (B-V) for the four cases presented in this study. The
behavior of the observed photometry was computed using a quiet photosphere
with four different color indices (0.500, 0.679, 0.900 and 1.100) corresponding to the
effective temperatures listed in Table 2. The main sequence appears as a thin solid
line, whereas the locus for twin stars (MS-0.75
![]() )
is represented as a dotted line
parallel to it. Real data for stars belonging to the Pleiades
(Soderblom et al. 1993) are included as open circles and the size increases
with increasing stellar activity, measured using the Ca II IR triplet at
8542 Å (
)
is represented as a dotted line
parallel to it. Real data for stars belonging to the Pleiades
(Soderblom et al. 1993) are included as open circles and the size increases
with increasing stellar activity, measured using the Ca II IR triplet at
8542 Å (
![]() ). Those Pleiades stars without measured
calcium appear as plus symbols.
Solid diamonds in the figure represent model predictions for
). Those Pleiades stars without measured
calcium appear as plus symbols.
Solid diamonds in the figure represent model predictions for
![]() .
Our model shows that the presence of spots
shifts the location of these stars almost in parallel with the MS, except when the
difference between the quiet atmosphere and the stellar spot becomes very large. In this last
case, when the spots are at
temperatures much lower than the photospheric value, large
increments of the observed magnitude with respect to the MS at the same observed color
could appear, with almost no change in the color.
However, the lack of stars in this region suggests that either
such differences are not possible (i.e.,
.
Our model shows that the presence of spots
shifts the location of these stars almost in parallel with the MS, except when the
difference between the quiet atmosphere and the stellar spot becomes very large. In this last
case, when the spots are at
temperatures much lower than the photospheric value, large
increments of the observed magnitude with respect to the MS at the same observed color
could appear, with almost no change in the color.
However, the lack of stars in this region suggests that either
such differences are not possible (i.e.,
![]() K
and
K
and
![]() K) or the filling factor must be very small in this case.
Therefore, for a given observed color index, the active stars
would tend to be located in the lower part of the MS (the less luminous
region), even below the MS of single and inactive stars. In the most extreme
case, they could be found below the Zero Age Main Sequence (ZAMS). However, the
comparison with the Pleiades shows that this phenomenon is not observed.
Several factors can explain this situation: first, the physical size of the
cluster can introduce a scatter in the CMD equivalent to several tenths of
magnitude, which can hide the effect of the activity on the photometry (i.e.
Barrado y Navascués & Stauffer 1996). On the other hand, an important
fraction of the stars are in fact binaries and each component can have a
different degree of activity, a case not included in the assumptions made in
our simple model.
However, the effect of stellar spot on the observed photometry of star
suggests that it might be influencing on the Hipparcos problem
(i.e., the fact that the locus of very well known,
nearby open clusters whose distance have been measured by the Hipparcos satellite.
See Pinsonneault et al. 2000; Robichon et al. 2000, and references therein),
in the sense that two open clusters of similar ages but very different
rotational velocity distributions might have a shift in the locus of their
main sequence when compared with each other.
In summary, Fig. 2 shows that the photometry obtained
using our model is compatible with the observational data and their
uncertainties for situations showing not large differences between
K) or the filling factor must be very small in this case.
Therefore, for a given observed color index, the active stars
would tend to be located in the lower part of the MS (the less luminous
region), even below the MS of single and inactive stars. In the most extreme
case, they could be found below the Zero Age Main Sequence (ZAMS). However, the
comparison with the Pleiades shows that this phenomenon is not observed.
Several factors can explain this situation: first, the physical size of the
cluster can introduce a scatter in the CMD equivalent to several tenths of
magnitude, which can hide the effect of the activity on the photometry (i.e.
Barrado y Navascués & Stauffer 1996). On the other hand, an important
fraction of the stars are in fact binaries and each component can have a
different degree of activity, a case not included in the assumptions made in
our simple model.
However, the effect of stellar spot on the observed photometry of star
suggests that it might be influencing on the Hipparcos problem
(i.e., the fact that the locus of very well known,
nearby open clusters whose distance have been measured by the Hipparcos satellite.
See Pinsonneault et al. 2000; Robichon et al. 2000, and references therein),
in the sense that two open clusters of similar ages but very different
rotational velocity distributions might have a shift in the locus of their
main sequence when compared with each other.
In summary, Fig. 2 shows that the photometry obtained
using our model is compatible with the observational data and their
uncertainties for situations showing not large differences between
![]() and
and
![]() and realistic values of
and realistic values of
![]() .
.
The direct comparison between the W(K I 7699 Å) corresponding to
different regions of the solar photosphere indicates that the variations due to
the presence of spots have to be small, except for large values of the spot
filling factor. Figure 3a shows the relative variation of the observed W(K)
against
![]() for the solar-like case.
In the most extreme cases, when
for the solar-like case.
In the most extreme cases, when
![]() ,
changes close to a 300% can be reached. However, the more realistic values
shown in the figure indicate changes between 0% and 50%. In any case, this
kind of variation due to spots should be easily observed, as we show below.
,
changes close to a 300% can be reached. However, the more realistic values
shown in the figure indicate changes between 0% and 50%. In any case, this
kind of variation due to spots should be easily observed, as we show below.
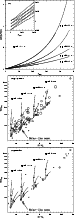 |
Figure 3:
The effect on potassium.
a)
Relative variation of the observed potassium
equivalent width against the filling factor of the spot. The set displayed
with solid lines were computed with
|
| Open with DEXTER | |
Figure 3a includes several sets of curves: the dotted lines represent the
results obtained using a spot at 4575 K and different values of the faculae
filling factor. From top to bottom,
![]() ,
0.25, 0.50 and 0.75.
The solid lines correspond to the computations for
,
0.25, 0.50 and 0.75.
The solid lines correspond to the computations for
![]() K.
Other sets, computed with
K.
Other sets, computed with
![]() K and
K and
![]() K
are shown as short and long dashed lines, respectively.
A detail of the graph appears in the box (we only display the first two cases).
Essentially, the values of
K
are shown as short and long dashed lines, respectively.
A detail of the graph appears in the box (we only display the first two cases).
Essentially, the values of
![]() do not affect the observed value
of W(K), as a consequence of the small difference between the measured
equivalent widths in the quiet region and the faculae.
do not affect the observed value
of W(K), as a consequence of the small difference between the measured
equivalent widths in the quiet region and the faculae.
In an analogous way to the previous figure, it is possible to compare the
variations of the W(K) with (B-V) - the values that would be observed, in
both cases. There is a quasi-linear relation between both quantities.
However, a more interesting comparison is made in Fig. 3b, where we have
included real data corresponding to the Pleiades cluster (Soderblom et al.
1993). The size of the symbols, as in Fig. 2, increases with increasing
stellar activity (measured using
![]() ). As noted by Soderblom et al. (1993), in the range
). As noted by Soderblom et al. (1993), in the range
![]() there is a clear trend
between activity and the potassium equivalent width for a given value of
(B-V): the larger the activity, the larger W(K). The reproduction of this
behavior has been attempted previously by Stuik et al. (1997), using a purely
theoretical model under NLTE conditions. However, their models were not able
to match the Pleiades observations (see their Fig. 8).
there is a clear trend
between activity and the potassium equivalent width for a given value of
(B-V): the larger the activity, the larger W(K). The reproduction of this
behavior has been attempted previously by Stuik et al. (1997), using a purely
theoretical model under NLTE conditions. However, their models were not able
to match the Pleiades observations (see their Fig. 8).
In order to verify if our empirical approximation would be able to match the behavior observed in the Pleiades, we proceeded as described in Sect. 3. We computed the results using four different situations: a star having a color ( B-V)=0.500, another star having a color corresponding to that one of the quiet region surrounding the sunspot - ( B-V)=0.679 -, a third star with (B-V)=0.900, and another with ( B-V)=1.100, the same values used for the simulations shown in Fig. 2. We used spots at four different temperatures (4870, 4575, 4000 and 3700 K), indicated with solid, dotted, short dashed and long dashed lines. The solar symbols (dots plus circles) indicate the location of the quiet sun and the data for the solar spots. A comparison with field dwarfs, from Tripicchio et al. (1999) are displayed in Fig. 3c. In this case, field stars are shown as crosses. Unfortunately, information regarding the activity of these stars is available for only a handful of them.
As can be concluded from Figs. 3b and 3c, the behavior of W(K) is well
reproduced despite the simplicity of the procedure. It explains why active
stars tend to have larger equivalent widths.
The model also explains why there is not a sharp
distinction between the location of inactive and active stars: it is predicted
that there are locations where it is possible to find stars having high and
intermediate activity, or intermediate and low activity. This is because stars
having different masses are compared: since the activity of the more massive
stars modifies the observed photometry to a greater extent, both stars (the
very active and the less active) have similar apparent colors. Note, however,
that realistic values of the spot filling factor (
![]() ;
indicated by solid diamonds in Fig. 3b) cannot reproduce those stars having the
largest values of the W(K I 7699) for a given color.
On the other hand, the figures should be interpreted with some caution, since
the model is rather sensitive to the initial conditions (i.e., the initial
effective temperature of the spot and the quiet photosphere and the
potassium equivalent width of the spot).
;
indicated by solid diamonds in Fig. 3b) cannot reproduce those stars having the
largest values of the W(K I 7699) for a given color.
On the other hand, the figures should be interpreted with some caution, since
the model is rather sensitive to the initial conditions (i.e., the initial
effective temperature of the spot and the quiet photosphere and the
potassium equivalent width of the spot).
As it is shown in Table 1, the W(Na) is much larger in a sunspot
than in the quiet region. Therefore, the observed value of the equivalent width
changes in a
much larger amount than in the case of potassium for the same filling factor
of the spot, although the relative variation is similar for both K I and
Na I (with respect to their respective equivalent widths). Figures 3a
and 4a illustrate this fact. In addition, the model predicts that the observed
value for Na I could be smaller than the equivalent width corresponding
to the star when it is inactive. This unlikely situation would appear if an
important fraction of the surface were covered by active regions (faculae) but
having very small spot coverage. In any case, the important result coming from
this figure is that it is possible to have a situation in which a high degree
of activity corresponds with no variations of the W(Na). This would happen if
the active regions were distributed homogeneously, or for certain combinations
of the values of
![]() and
and
![]() .
.
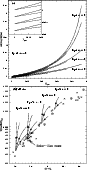 |
Figure 4: a) Variations of the sodium equivalent width against the spot filling factor. Symbols as in Fig. 3a. b) Variations of the sodium equivalent width against (B-V) color index. Field dwarfs from Tripicchio et al. (1997) are displayed as crosses |
| Open with DEXTER | |
Figure 4b plots predicted W(Na) against (B-V). We have included in the figure, as crosses, data corresponding to field dwarfs (Tripicchio et al. 1997). Note that the field stars could have different abundances of sodium. However, assuming a similar abundance, our model is able, in principle, to explain the scatter of the observed W(Na). Although, to our knowledge, there are no studies about the behavior of this doublet in late-type stars for young clusters, we would expect in principle a similar behavior to the case of K I 7699 Å (i.e., for a given color, the larger the activity, the larger the equivalent width). However, there is a significant difference between Na I 5896 and K I 7699 Å lines: the significant difference of equivalent widths between faculae and quiet regions for Na I, which is not observed for K I. So, the scatter displayed in Fig. 3b (potassium equivalent width against color index) might be different in a similar plot for sodium. Therefore, a sample of coeval stars of different colors might not show a clear relationship between activity and W(Na), since a star can have a large activity and, simultaneously, change minimally the equivalent width of Na I 5896 Å (if a large fraction of the stellar surface is covered with active regions). This is a very interesting tool to verify the effect of spots and faculae on the equivalent widths of alkali.
The study of the variation of the lithium equivalent width due to the presence of surface inhomogeneities (spots and faculae) can provide essential hints to understand the abundances derived for stars with a high level of activity, such as chromospherically active binary systems and rapid rotators belonging to young clusters.
Our model predicts a large variation in W(Li), even close to 3500%, due to the
presence of spots. This can be clearly seen in Fig. 5a. This kind of
variation has already been predicted by Giampapa (1984). The behavior of the
lithium line is very sensitive to the temperature of the spot.
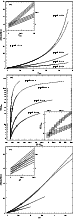 |
Figure 5: a) Variations of the lithium doublet equivalent width against the spot filling factor. b) Lithium equivalent width versus (B-V) color index. c) Variations of the lithium doublet equivalent width against photometric variations. A detail of these graphs are displayed in the small boxes. Symbols as in Fig. 3a |
| Open with DEXTER | |
Figure 5b shows the extraordinary change of the W(Li) as the observed (B-V)
color increases in the solar-like case,
as a consequence of the presence of active regions. The
dependence on the spot temperature is evident: the smaller the
temperature, the larger the observed W(Li) and color.
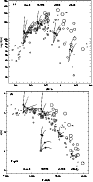 |
Figure 6: Comparison with Pleiades data: a) Lithium equivalent width against color. b) Lithium abundance against effective temperature. Symbols as in Fig. 2. We have also included the case for the Sun |
| Open with DEXTER | |
Pallavicini et al. (1993), in a quasi-simultaneous study involving photometry
and spectroscopy (measuring Li I 6708 and Ca I 6718 Å) of 4
active stars, did not observe any change in the equivalent width of the Li
line, even when these objects presented important photometric variations (up to
0.10 mag). Our model provides an explanation for this apparent puzzle. Although
the values of
![]() which correspond to
which correspond to
![]() mag could
produce important increments in W(Li), taking into account the
faculae in the simulation changes the scenario completely. The region covered
by faculae has a very reduced value of the W(Li) and tends to dilute the line
produced by the quiet region and by the spot.
Moreover, the presence of faculae is not detected in the photometric
modulation. It is reasonable to assume that the fraction of the stellar disk
covered by faculae has to be at least as large as the fraction covered by
spots. The final consequence is that a star having high or moderate activity
can experience important photometric variations together with reduced
variations in the Li equivalent width (either positive or negative), as Fig. 5c demonstrates, where we represent the relative
variation of the equivalent width of lithium against the photometric variation.
mag could
produce important increments in W(Li), taking into account the
faculae in the simulation changes the scenario completely. The region covered
by faculae has a very reduced value of the W(Li) and tends to dilute the line
produced by the quiet region and by the spot.
Moreover, the presence of faculae is not detected in the photometric
modulation. It is reasonable to assume that the fraction of the stellar disk
covered by faculae has to be at least as large as the fraction covered by
spots. The final consequence is that a star having high or moderate activity
can experience important photometric variations together with reduced
variations in the Li equivalent width (either positive or negative), as Fig. 5c demonstrates, where we represent the relative
variation of the equivalent width of lithium against the photometric variation.
An additional check to our model can be performed by comparing it, again, with Pleiades data. Figure 6 shows actual Li data (Soderblom et al. 1993), where the size of the symbols increases with increasing activity. Simulations with different photospheric temperatures are displayed, computed with spots with four temperatures (4870, 4575, 4000 and 3700 K; solid, and dotted, short and long dashed lines, respectively). As with potassium, the spread on the observed lithium equivalent widths in the Pleiades can be reproduced (Fig. 6a). However, in the lithium case, only part of the spread could be due to the effect of the stellar inhomogeneities, since our curves, even for very large filling factors, do not cover the whole area where the Pleiades stars are located. However, the simulations can explain the trend with stellar activity (for a given color): active stars have a larger value of W(Li). Therefore, part of the spread in the equivalent widths could be due to the simultaneous effect of the surface inhomogeneities on the observed equivalent width and color. Some of the cases would require, however, a (non-realistic) very large filling factor or a large difference between the temperature of the quiet photosphere and the spot.
The A(Li)-
![]() plane (Fig. 6b, where A(Li)
plane (Fig. 6b, where A(Li)
![]() )
provides complementary information. Predicted equivalent widths were translated into Li
abundances using the curves of growth by Soderblom et al. (1993).
In the case of temperatures below 4000 K (the lowest temperature of these
curves of growth), we used those published by Pavlenko et al. (1996).
Predicted
abundances tend to move the observed values to lower effective temperatures for
the most active stars, therefore reducing the spread in the abundance and the
rotation-activity relation.
The lithium abundances for active stars appear then to be correct but
their location should be shifted toward higher temperatures in the
A(Li)-
)
provides complementary information. Predicted equivalent widths were translated into Li
abundances using the curves of growth by Soderblom et al. (1993).
In the case of temperatures below 4000 K (the lowest temperature of these
curves of growth), we used those published by Pavlenko et al. (1996).
Predicted
abundances tend to move the observed values to lower effective temperatures for
the most active stars, therefore reducing the spread in the abundance and the
rotation-activity relation.
The lithium abundances for active stars appear then to be correct but
their location should be shifted toward higher temperatures in the
A(Li)-
![]() plane due to the effect of the spots on the colors. We must note,
however, that only very large activity levels would change the morphology of
the
plane due to the effect of the spots on the colors. We must note,
however, that only very large activity levels would change the morphology of
the
![]() -A(Li) plane. Even spot filling factors close to
-A(Li) plane. Even spot filling factors close to
![]() move the location of a star in this diagram by
move the location of a star in this diagram by ![]() 180 K only
towards cooler temperatures.
On the other hand, as discussed before, our simulations do not explain the high
lithium abundances in the range 5200-4600 K. Therefore, it seems that
these abundances are real and that an important fraction the lithium spread
which is present in the figure is real, and that the rotation is a key
factor in the evolution of the lithium abundance in the late spectral type stars.
180 K only
towards cooler temperatures.
On the other hand, as discussed before, our simulations do not explain the high
lithium abundances in the range 5200-4600 K. Therefore, it seems that
these abundances are real and that an important fraction the lithium spread
which is present in the figure is real, and that the rotation is a key
factor in the evolution of the lithium abundance in the late spectral type stars.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS09992f7.eps}
\end{figure}](/articles/aa/full/2001/20/aa9992/Timg69.gif) |
Figure 7:
Behavior of the differences of lithium abundances
(A(Li)
|
| Open with DEXTER | |
We have shown above (see Figs. 5 and 6) that the presence of inhomogeneities on the stellar surface could induce important variations in the measured Li equivalent widths. It is extremely important to establish how these features affect the accuracy of the derived lithium abundances. The presence of spots affects the equivalent width in two different ways: the lithium equivalent width increases, producing a pseudo-abundance larger than the real value. Simultaneously, the color indices are reddened and the lower temperature favors values lower than those corresponding to the quiet photosphere, inducing a reduction in the estimated abundance.
Figure 7a shows the behavior of the abundance provided by the solar model against
the spot filling factor for a given initial abundance (
![]() in this
case). A temperature of 5655 K for the quiet photosphere, and temperatures of
4870 K (solid lines), 4575 K (dotted lines), 4000 K (short dashed lines),
and 3700 K (long dashed lines) for the spots were used.
Different filling factors for the faculae (from top to bottom, 0.00, 0.25, 0.50
and 0.75) were considered. It is clearly seen that the presence of
inhomogeneities could introduce important errors in the derived lithium
abundance. In this case, they span from -0.05 to +1.2 dex in the worst
cases. The decrease in the observed abundance appears when a large fraction of
the photosphere is covered by faculae and the filling factor of the spots is
small. It is more important when there is a large difference between the
spot and quiet photosphere temperatures.
These uncertainties are restricted, however, by realistic estimates of
the spot filling factor which would yield
in this
case). A temperature of 5655 K for the quiet photosphere, and temperatures of
4870 K (solid lines), 4575 K (dotted lines), 4000 K (short dashed lines),
and 3700 K (long dashed lines) for the spots were used.
Different filling factors for the faculae (from top to bottom, 0.00, 0.25, 0.50
and 0.75) were considered. It is clearly seen that the presence of
inhomogeneities could introduce important errors in the derived lithium
abundance. In this case, they span from -0.05 to +1.2 dex in the worst
cases. The decrease in the observed abundance appears when a large fraction of
the photosphere is covered by faculae and the filling factor of the spots is
small. It is more important when there is a large difference between the
spot and quiet photosphere temperatures.
These uncertainties are restricted, however, by realistic estimates of
the spot filling factor which would yield
![]() dex.
dex.
Figures 7b-d show the behavior of the lithium abundance against the observed color (B-V), the increment in the visual magnitude, and the effective temperature, respectively. These values were determined from (B-V) and the Thorburn et al. (1993) temperature scale. The different observed parameters can change by a considerable amount due to the presence of inhomogeneities. However, the final uncertainties in the derived lithium abundances are limited by the expected values of the filling factors.
Doppler imaging techniques show that active stars have a tendency to
concentrate their spots in the poles (Vogt & Hatzes 1995). Doppler imaging of
active Pleiades stars shows that they are, indeed, covered with huge polar
spots of presumably long life span (Stout-Batalha & Vogt 1999). If this
controversial fact is true (see Byrne 1995 for a comprehensive discussion about
this subject), active stars would show little photometric variations due to
inhomogeneities and, simultaneously, the measured equivalent widths would be
affected. Therefore, these stars would be several tenths of magnitude fainter
than analogous inactive stars (same mass, chemical composition and age), and
could show different equivalent widths of the alkali for the same abundances
- in the case of lithium, W(Li)
![]() could be larger -. However,
this situation is not observed when a comparison of the locations of active
and inactive stars in Color-Magnitude diagrams or W(Li)-(B-V) plane is
performed.
could be larger -. However,
this situation is not observed when a comparison of the locations of active
and inactive stars in Color-Magnitude diagrams or W(Li)-(B-V) plane is
performed.
One of the aims of this work was to compare the behavior of the three alkali
elements under several circumstances, establishing the relative variations of
the observed equivalent widths in stars with different filling factors of spots
and faculae. Figure 8a shows the comparison between
potassium and lithium equivalent widths. Pleiades data are included.
Symbols are
as in Fig. 3b. Active stars tend to be in the top, right-hand side
of the diagram. This behavior is qualitatively reproduced with our model.
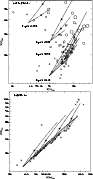 |
Figure 8:
a)
Comparison between the relative variations of
potassium and lithium for the Pleiades.
Symbols as in Fig. 3b.
b)
Comparison between the relative variations of
potassium and sodium for field stars.
Symbols as in Fig. 3c.
The last point in our calculations
corresponds to
|
| Open with DEXTER | |
Figure 8b displays the equivalent widths of sodium and potassium. Data corresponding to field stars are shown as crosses. The dependence of the trend with the spot temperature seems to be very small. It would be very interesting to have similar data for members of a cluster, to determine the effect of the activity on a sample of stars with the same age.
A simple model has been constructed to study the effects of surface active regions on the behavior of the Li I 6708, Na I 5896, and K I 7699 Å lines in the atmospheres of late-type stars. These effects strongly depend on the actual distributions of surface inhomogeneities (spots and faculae in particular) which, unfortunately, are not well known for those objects. They could be distributed in irregular or homogeneous ways and the changes in the alkali line equivalent widths will be affected by the filling factors of the spots and faculae, temperatures of the different regions and the element abundances. Additional observations providing independent estimates of the filling factors, such as direct measurements of the magnetic field via Zeeman splitting (Saar 1995) or empirical relations between the Rossby number and the filling factors (Montesinos & Jordan 1993), would help to determine the actual values of the colors and equivalent widths and to constrain the input model parameters.
Our simulations predict that active stars can suffer changes in their lithium equivalent widths compared with quiescent objects. However, under normal circumstances (spot filling factors less than 0.5), these variations would not induce significant changes in the derived abundances. A similar conclusion was reached by Pallavicini et al. (1993) by studying the photometry and the Li I 6708 Å line in several stars. Moreover, Pallavicini et al. (1987, 1992), Randich et al. (1993, 1994), Fernández-Figueroa et al. (1993), and Barrado y Navascués et al. (1997, 1998) have studied a large sample of chromospherically active binaries in a time span of several years, and have found no evidences of changes in the lithium equivalent widths that could be related to the phase or to secular changes in the activity.
The comparison between the model predictions and the observations suggests that part of the spread observed in the equivalent widths of K and Li lines, as well as in the Li abundances, for the Pleiades could be due to the simultaneous effect of surface inhomogeneities on the observed equivalent widths and photometric colors. At this point it is important to obtain additional information on these lines for other young open clusters where a similar dispersion in Li abundances has been found (eg. Alpha Persei cluster; Randich et al. 1998) to check the model predictions in those cases. Na I D measurements in the Pleiades and other clusters will provide complementary data to witness the behavior of the other two alkali elements.
Acknowledgements
DBN acknowledges the support by the the "Real Colegio Complutense'' at Harvard University, the MEC/Fulbright Commission, and "Instituto de Astrofísica de Canarias'' and the "Deutsche Forschungsgemeinschaft''. This work has been partially supported by the Spanish DGES under projects PB95-1132-C02-01, PB98-0531-C02-02, and "Plan Nacional del Espacio'', under grant ESP98-1339-CO2. DBN and RGL appreciate the hospitality of the "Osservatorio Astronomico di Capodimonte''. We thank Alfredo Tripicchio for making available his data. We do appreciate the very useful suggestions by the referee, Dr. Sofia Randich.
In order to compute the observed photometry for a star covered with spots and
faculae, we have to estimate the individual contribution of each region. The
total luminosity can be expressed as:
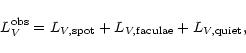 |
(9) |
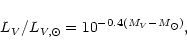 |
(10) |
| (11) |
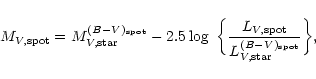 |
(12) |
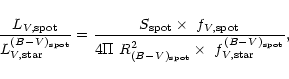 |
(13) |
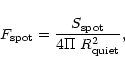 |
(14) |
![\begin{displaymath}%
\frac{L_{V,{\rm spot}}}{L_{V,{\rm star}}^{(B{-}V)_{\rm spot...
... quiet}}{R_{(B{-}V)_{\rm spot}}}\right]^2\times~F_{\rm spot} .
\end{displaymath}](/articles/aa/full/2001/20/aa9992/img91.gif) |
(15) |
| (16) |
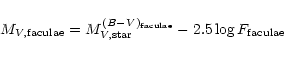 |
(17) |
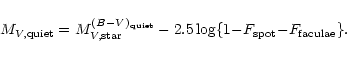 |
(18) |
Given a star with a quiet region and faculae and spots on its surface,
the observed equivalent width contains contributions from each region.
The equivalent width is defined as:
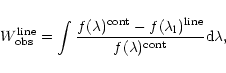 |
(19) |
| = | (20) | ||
| = | (21) |
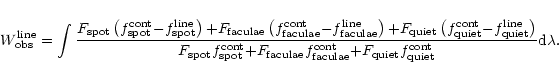
| (22) |
![$\displaystyle %
[1] =
\int {F_{\rm spot} (f_{\rm spot}^{\rm cont}{-}F_{\rm spot...
...F_{\rm quiet} f_{\rm quiet}^{\rm cont}/f_{\rm spot}^{\rm cont}} {\rm d}\lambda.$](/articles/aa/full/2001/20/aa9992/img104.gif) |
(23) |
![\begin{displaymath}%
[1] =
{\alpha_{\rm line}~F_{\rm spot} \over
\alpha_{\rm li...
...faculae} +
F_{\rm quiet} }\times~W_{\rm spot}^{\rm line}\cdot
\end{displaymath}](/articles/aa/full/2001/20/aa9992/img107.gif) |
(24) |
![\begin{eqnarray*}%
[2] =
\int {F_{\rm faculae}(f_{\rm faculae}^{\rm cont}{-}f_{...
... cont})/f_{\rm faculae}^{\rm cont}} {\rm d}\lambda .\nonumber\\
\end{eqnarray*}](/articles/aa/full/2001/20/aa9992/img108.gif)
| (25) |
![\begin{displaymath}%
[2] = {F_{\rm faculae} \over
\alpha_{\rm line}~F_{\rm spo...
...lae} +
F_{\rm quiet} }\times~W_{\rm faculae}^{\rm line} \cdot
\end{displaymath}](/articles/aa/full/2001/20/aa9992/img109.gif) |
(26) |
![$\displaystyle %
[3] =
\int {F_{\rm quiet}(f_{\rm quiet}^{\rm cont}{-}f_{\rm qui...
...rm quiet}f_{\rm quiet}^{\rm cont})/f_{\rm faculae}^{\rm cont}} {\rm d}\lambda .$](/articles/aa/full/2001/20/aa9992/img110.gif) |
(27) |
![\begin{displaymath}%
[3] =
{F_{\rm quiet} \over
\alpha_{\rm line}~F_{\rm spot} ...
...m faculae} +
F_{\rm quiet} }\times~W_{\rm quiet}^{\rm line} .
\end{displaymath}](/articles/aa/full/2001/20/aa9992/img111.gif) |
(28) |
![\begin{displaymath}%
W_{\rm line}^{\rm obs} = {\alpha_{\rm line}~F_{\rm spot}~W^...
...rm faculae} {+} [1 - F_{\rm spot} {-} F_{\rm faculae}] } \cdot
\end{displaymath}](/articles/aa/full/2001/20/aa9992/img112.gif) |
(29) |