A&A 371, 152-173 (2001)
DOI: 10.1051/0004-6361:20010309

Zero-metallicity stars

I. Evolution at constant mass

P. Marigo¹ - L. Girardi¹ - C. Chiosi¹ - P. R. Wood²

1 - Dipartimento di Astronomia, Università di Padova, Vicolo dell'Osservatorio 2, 35122 Padova, Italia
2 - Mount Stromlo and Siding Spring Observatories, Australian National University, Private Bag, Weston Creek PO, ACT 2611, Australia

Received 12 December 2000 / Accepted 28 February 2001

Abstract
We present extensive evolutionary models of stars with initial zero-metallicity, covering a large range of initial masses (i.e. $0.7~M_{\odot} \le M \le 100~M_{\odot}$). Calculations are carried out at constant mass, with updated input physics, and applying an overshooting scheme to convective boundaries. The nuclear network includes all the important reactions of the p-p chain, CNO-cycle and $\alpha$-captures, and is solved by means of a suitable semi-implicit method. The evolution is followed up to the thermally pulsing AGB in the case of low- and intermediate-mass stars, or to the onset of carbon burning in massive stars. The main evolutionary features of these models are discussed, also in comparison with models of non-zero metallicity. Among several interesting aspects, particular attention has been paid to describe: i) the first synthesis of ¹²C inside the stars, that may suddenly trigger the CNO-cycle causing particular evolutionary features; ii) the pollution of the stellar surface by the dredge-up events, that are effective only within particular mass ranges; iii) the mass limits which conventionally define the classes of low-, intermediate-, and high-mass stars on the basis of common evolutionary properties, including the upper mass limit for the achievement of super-Eddington luminosities before C-ignition in the high-mass regime; and iv) the expected pulsational properties of zero-metallicity stars. All relevant information referring to the evolutionary tracks and isochrones is made available in computer-readable format.

Key words: stars: evolution - stars: interiors - stars: Hertzsprung-Russell (HR) diagram - stars: low-mass

   
1 Introduction

The standard Big Bang Nucleosynthesis (e.g. Olive 1999) predicts that essentially no elements heavier than $\rm ^{7}Li$ should exist in the gas mixture in which the first stars are generated. Only in the framework of inhomogeneous Big Bang nucleosynthesis (see Jedamzik 2000 and references therein) we can expect some non-negligible primordial metal production.

The stars with negligible, if not zero, initial metal abundance - named population III objects (Pop-III for short) - are expected to have structure and evolution distinct from those in which traces of heavier elements, like those of the CNO group, are present.

The major difference between zero-metal stars and those of normal metal content (even down to very low values of Z) lies in the mechanism of nuclear energy generation. In fact, owing to the lack of CNO nuclei, the pre-main sequence gravitational contraction cannot stop until the central temperature and density are high enough to allow the p-p chain to provide the energy budget. Since the p-p chain is a poor thermostat as compared to the CNO-cycle, very high temperatures can be reached in the central regions. This may eventually lead (depending on the mass of the star) to the first synthesis of primary carbon through the 3-$\alpha$ reaction, while the star is still on the main sequence. As a consequence, the CNO-cycle is activated at the very high temperatures characterising the 3-$\alpha$ process, possibly causing a dramatic change in the dominant energy source (from p-p chain to CNO-cycle), hence affecting the stellar structure amid the main sequence evolution. As demonstrated below, similar changes in the evolutionary behaviour may also occur at later stages, whenever carbon is first produced (or transported) into different regions of the star.

The threshold abundance of $\rm ^{12}C$ at which the distinct behaviour of zero metal stars appears is as low as $Z \approx X_{\rm C} \sim 10^{-10}{-}10^{-9}$ (see Cassisi & Castellani 1993). Starting from these values and higher, the efficiency of CNO-cycle is sufficient to recover the standard behaviour.

Needless to say, the distinct evolutionary behaviour of these stars may also imply a very distinct nucleosynthesis and chemical pollution of the interstellar medium, if compared to stars with initial Z>10^-10. Also their properties in the HR-diagram should be quite peculiar. Both aspects are particularly important in the modelling of

1.

the initial chemical enrichment of galaxies, when the first metals and additional light elements have been made available to the second generation of stars, and probably also to the intergalactic medium;

2.

the initial spectrophotometric evolution of galaxies, when the first ionizing photons of stellar origin probably contributed to the reionization of the Universe;

3.

the observational characteristics that the remaining low-mass Pop-III stars (if any were formed) would present today, in order to guide observational searches for these objects.

In this context, the present paper is aimed to provide the necessary tools for the investigation of the above-mentioned questions. We start by presenting an extensive and homogeneous set of evolutionary tracks for Pop-III stars, covering the complete mass range from 0.7 to 100 $M_{\odot }$. All of the models are computed with convective overshooting and under the assumption of constant-mass evolution. A subsequent paper will deal with the case of more massive stars ( $M > 100\,M_{\odot}$), in which stellar winds had likely been driven by a state of pulsation instability.

The plan of the paper is as follows. After briefly reviewing the available literature on evolutionary models of primordial stars (Sect. 2), the main assumptions of present calculations are described in Sect. 3 concerning the nucleosynthesis, and Sect. 4 for the other physics prescriptions. Then, the presentation and discussion of the results start with Sect. 5 - dealing with general evolutionary aspects (e.g. the onset of the 3-$\alpha$ reaction and the activation of the CNO cycle, lifetimes, etc.) - and proceed through Sects.  6 and 7, which focus on particular issues of low- and intermediate-/high-mass models, respectively (e.g. the AGB phase, the Eddington critical luminosity). Our predictions for possible changes in the surface chemical composition are given in Sect. 8. Finally, Sect. 9 is dedicated to an analysis of the expected pulsational properties of Z=0 stars with different masses and evolutionary stages, to investigate whether pulsation might be a discriminating feature in observational searches of Pop-III objects. Appendices describe the tables of the Z=0 evolutionary tracks and related isochrones available in electronic format.

   
2 A quick review of past work on Pop-III stars

The mass-scale of Pop-III stars is still a matter of debate. The once widely accepted idea that only massive, very massive or even super-massive stars could form in the primordial medium has long limited the study of Pop-III stars to objects more massive than say $10\,M_{\odot}$, possibly in the range 10² to $10^5\, M_{\odot}$ (Carr et al. 1982). Similar suggestions were made by Hutchins (1976); Silk (1977) and Tohline (1980) whose work indicated a minimum mass of 150-200 $M_{\odot }$.

However, over the years, interest has turned towards more "normal'' stars. In fact, various fragmentation models of primordial gas have suggested that the first stars might have formed with low/intermediate masses, e.g. Yoshi & Saio (1986) find the peak of the mass function at roughly $4{-}10 \, M_{\odot}$; Nakamura & Umemura (1999) find a the typical mass of $3 \, M_{\odot}$, which may grow to $16 \, M_{\odot}$ by accretion; and Nakamura & Umemura (2000) find a lower mass-limit extending down to $1\, M_{\odot }$. With more detailed and extended calculations for the collapse and fragmentation of primordial gas clouds, Nakamura & Umemura (2001) suggest that the initial mass function of Pop-III stars may be bimodal with peaks at about $1\, M_{\odot }$ and $100 \, M_\odot$, the relative heights of these peaks being a function of the collapse epoch.

The provisional conclusion we may get from all this is that the mass peak of Pop-III stars is likely greater than say $1\, M_{\odot }$ and possibly in the range 1 to $10\,M_{\odot}$. However, both lower and much higher values cannot be firmly excluded.

Ezer & Cameron (1971) first studied models of Pop-III stars in the mass range 5 to $200 \, M_{\odot}$ from the pre-main sequence until core H-exhaustion. In a subsequent paper Ezer (1972) investigated the evolution of a $3 \, M_{\odot}$ star up to the stage of core He-exhaustion. Cary (1974) and Castellani & Paolicchi (1975) computed zero-age-main-sequence (ZAMS) models in the mass range 2 to $20 \, M_{\odot}$ and 1 to $8 \, M_{\odot}$, respectively.

Woosley & Weaver (1981) followed the evolution at constant mass of a $200 \, M_{\odot}$ star until the supernova explosion stage, thus allowing the first estimate of the contamination power of this type of star. Very massive Pop-III stars were first investigated by Bond et al. (1982, 1983). El Eid et al. (1983) and Ober et al. (1983) explored the mass range from 80 to $500 \, M_{\odot}$, including mass loss by stellar winds up to the stage of supernova explosion or collapse to a black hole. Similar studies were undertaken by Klapp (1983, 1984) for very massive stars in the range 500 to $10^4\, M_{\odot}$. These papers made it possible to get an estimate of the chemical yields both in the wind and explosive stages. Forieri (1982) studied the evolution of massive Pop-III stars in mass range 10 to $100 \, M_\odot$ up to the central He-exhaustion stage. These models were evolved at constant mass but included convective overshoot. Castellani et al. (1983) presented models for 10, 15 and $25 \, M_{\odot}$ stars from ZAMS to C-ignition.

The advanced phases of low-mass stars remained almost unexplored till the early study by D'Antona (1982) of a $1~ M_{\odot}$ star up to the stage of core He-flash, where for the first time the much less extended RGB was noticed (see also Castellani & Paolicchi 1975 for an earlier suggestion). Chieffi & Tornambé (1984) investigated the evolution of a $5~M_{\odot}$ object, noticing the absence of thermal instabilities during the double-shell (AGB) phase. Fujimoto et al. (1984) pointed out that threshold values for the core mass and CNO abundances exist for the occurrence of He-shell flashes during the AGB phase. Cassisi & Castellani (1993) presented grids of models with masses in the range $0.7 \leq M \leq 15~M_{\odot}$ and metallicity from Z=10^-4 down to Z=10^-10. The models were followed from ZAMS till He-flash, final cooling of the CO core or C-ignition as appropriate. Cassisi et al. (1996) analysed the RR Lyrae properties and the unusually strong He-shell flashes of low-mass stars with very low initial metal content ( $-10 \le \log Z \le -5$).

Many recent/ongoing work on zero-metallicity stars have been recently presented in the symposium proceedings edited by Weiss et al. (2000a), to which the reader should refer for a comprehensive picture of the present state of understanding of these objects. Particularly impressive are the studies being carried out by Heger et al. (2000) and Umeda et al. (2000), where massive zero-metallicity stars are made to evolve up to the pre-supernova stage and supernova explosion, respectively. These studies describe in detail the nucleosynthesis of heavy elements occurring in these stars.

In the work by Weiss et al. (2000b) the authors investigate the role of diffusion and external pollution in the evolution of metal-free low-mass stars, finding that no sizable effects occur (the accreted metals cannot reach the central H-burning regions, which would have otherwise affected the structure of zero-metallicity stars). Using an extended nuclear network, they also demonstrate that hot p-p chains are less effective than the 3-$\alpha$ process in producing carbon inside a zero-metallicity star.

Finally, we should mention the work by Schlattl et al. (2001), who investigate the possible changes in the envelope chemical composition as the result of convective dredge-up during the He-flash of Pop-III RGB stars (see also Fujimoto et al. 2000).

   
3 Nuclear network and nucleosynthesis

In general, the evaluation of temporal changes in the chemical abundances due to nuclear reactions requires the integration of the system of equations below:

$$% \frac {\rm d}{\rm dt} Y_i = -[ij]~ Y_i Y_j + [rs]~ Y_r Y_s, \quad i = 1,...N_{\rm el}$$ (1)

where $N_{\rm el}$ is the number of elemental species involved; Y_i = X_i/A_i, X_i, and A_i denote the abundance by number (mole g^-1), the abundance by mass, and the atomic mass of the elemental species i, respectively. In the right-hand side of the equation (1), [ij]stands for the rate of the generic reaction which converts the element i into another nucleus because of the interaction with the element j, whereas [rs]is the rate of the generic reaction transforming nuclei s and r into the element i.

In this work the adopted nuclear network consists of the sets of reactions for the pp1-chain

$$% \begin{array}{llll} {\rm\, ^1H\, +\, ^1H\, \longrightarrow\... ...e\, +\, ^4He\, \longrightarrow\, ^{7}Be + \gamma}, \end{array}$$ (2)

for the CNO tri-cycle

$$% \begin{array}{lllllllllll} {\rm\, ^{12}C\, +\, ^1H\, \longr... ... +\, ^1H\, \longrightarrow\, ^{4}He\, +\, ^{16}O}, \end{array}$$ (3)

and the most important $\alpha$-capture reactions

$$% \begin{array}{llllllllll} {\rm\, ^{4}He\, +\, 2 ^4He\, \lon... ...+\, ^4He\, \longrightarrow\, ^{26}Mg + \gamma}. \\ \end{array}$$ (4)

The abundance Eq. (1) are solved with the aid of a semi-implicit extrapolation scheme (Bader & Deuflhard 1983), which combines all the considered H- and He-burning reactions (Eqs. (2), (3), and (4)) without any assumption for nuclear equilibria. Such procedure is necessary to follow the nucleosynthesis occurring in stars with original zero (or extremely low) metal content, for various reasons.

The simultaneous consideration of H- and He-burning reactions is required by the fact that in these stars H-burning may occur at temperatures and densities high enough to allow the synthesis, via $\alpha$-captures, of the missing catalysts (i.e. ¹²C and ¹⁶O) for the activation of the CNO cycle.

The choice of a semi-implicit method is motivated by the search for a convenient compromise between the higher accuracy typical of the explicit scheme, and the better stability of the solution guaranteed by the implicit scheme. We recall that, from a technical point of view, in implicit/explicit methods the increments of the dependent variables over a given integration step are calculated from the derivatives evaluated at the new/old location of the independent variable. The net effect is that implicit methods are stable for large integration steps, but with a certain loss of accuracy in following the solution towards the equilibrium. The reverse situation occurs for explicit methods.

Actually, implicit methods are required when dealing with stiff differential equations, in which the changes of the dependent variables involve quite different scales of the independent variable. This feature matches the case of the abundance equations, as different elemental species are characterised by very different nuclear lifetimes. For instance, at temperatures near 25 10⁶ K, the e-folding time for ¹⁵N is on the order of years, whereas for ¹⁴N it is on the order of 10⁵ years. In general, implicit methods converge to the true equilibrium solutions of the nuclear network for relatively large time steps, whereas purely explicit methods would require extremely short time steps to both find the solution and maintain stability. Alternatively, in order to make the explicit scheme less time consuming this may be coupled with external assumptions on nuclear equilibria (usually made for the CNO nuclei). This possible choice is however quite risky, specially in the case of zero-metallicity stars in which the total abundance by number of the CNO elements during H-burning is not constant, but rather increasing thanks to the contribution from He-burning.

   
4 General physical input of the stellar models

Chemical composition.

The adopted initial composition consists of a mixture of just hydrogen and helium, with mass fractions of X=0.77 and Y=0.23, respectively. The adopted Y value is consistent with most recent determinations of the primordial helium content, that typically range from 0.230 to 0.234 (see e.g. Peimbert 1996 for a review; or Olive et al. 1997 and Viegas et al. 2000 for recent determinations).

Opacity.

The radiative opacities are from the OPAL group (Rogers & Iglesias 1992; Iglesias & Rogers 1993) for temperatures higher than $\log T = 4.1$, and from Alexander & Ferguson (1994) for $\log T \le 4.0$. In the temperature interval $4.0 < \log T < 4.1$, a linear interpolation between the opacities derived from both sources is adopted. The conductive opacities of electron-degenerate matter are from Hubbard & Lampe (1969).

Equation of state.

The equation of state (EOS) for temperatures higher than 10⁷ K is that of a fully-ionized gas, including electron degeneracy in the way described by Kippenhahn et al. (1965). The effect of Coulomb interactions between the gas particles at high densities is introduced following the prescription by Straniero (1988; cf. also Girardi et al. 1996).

Nuclear reaction rates and neutrino losses.

The reaction rates are from the compilation of Caughlan & Fowler (1988), except for $^{17}{\rm O}({\rm p},\alpha)^{14}{\rm N}$ and $^{17}{\rm O}({\rm p},\gamma)^{18}{\rm F}$, for which we use the more recent determinations by Landré et al. (1990). The uncertain ¹²C( $\alpha,\gamma$)¹⁶O rate was set to 1.7 times the values given by Caughlan & Fowler (1988), as indicated by the study of Weaver & Woosley (1993) on the nucleosynthesis by massive stars. The electron screening factors for all reactions are those from Graboske et al. (1973).

The energy losses by pair, plasma, and bremsstrahlung neutrinos, are from Haft et al. (1994).

External convection and overshooting.

The energy transport in the outer convection zone is described according to the mixing-length theory of Böhm-Vitense (1958). The mixing length parameter $\alpha=1.68$ comes from the calibration of a solar model (Girardi et al. 2000).

The extension of convective boundaries is estimated by means of an algorithm which takes into account overshooting from both core and envelope convective zones. The formalism is fully described in Bressan et al. (1981) and Alongi et al. (1991). The main parameter describing overshooting is its extent $\Lambda_{\rm c}$ across the border of the convective zone, expressed in units of pressure scale height.

We adopt the following prescription for the parameter $\Lambda_{\rm c}$ as a function of stellar mass:

• $\Lambda_{\rm c}=0 \,\,\,\,\,\,$ for M< 1.1 $M_{\odot }$,
• $\Lambda_{\rm c}=0.5 \,\,\,$ for $M\ge~1.1$ $M_{\odot }$.

This is for the stages of core hydrogen burning. During core helium burning (CHeB), the value $\Lambda_{\rm c}=0.5$ is used for all stellar masses.

Overshooting at the lower boundary of convective envelopes is also considered. The value of $\Lambda_{\rm e}=0.25$ (see Alongi et al. 1991, for a description of the formalism) is adopted for stars with $0.7\le(M/M_{\odot})<2.0$. For M>2.0 $M_{\odot }$ a value of $\Lambda_{\rm e}=0.7$ is assumed.

Mass loss by stellar winds.

Perhaps the most uncertain aspect of the evolution of Pop-III stars is mass loss by stellar winds. Two typical situations can be envisaged: (i) Mass loss from massive stars during their whole evolutionary history, and (ii) mass loss during the RGB and AGB phases of low and intermediate-mass stars.

Of course, the first question is whether our knowledge for normal-metallicity stars can be extrapolated and safely used for Pop-III stars. This depends on the physical nature of the mechanism driving mass-loss. In massive stars of normal metallicity (no matter whether low or high) mass loss at high effective temperature is due to radiation pressure on resonance lines of ions like CIV, NV, SiIV, etc., whereas that at low temperatures is likely caused by radiation pressure on dust grains and/or due to pulsational properties (see Chiosi & Maeder 1986; Chiosi et al. 1992; Maeder & Conti 1994; Feast 1991; Kudritzki 1998; for recent reviews). Furthermore, the body of observational and theoretical information allows us to establish empirical relations according to which the mass loss rates are seen to decrease with the metallicity. On this basis one could perhaps argue that as long as the surface layers keep the original composition mass loss cannot occur. If and when the surface abundances are contaminated by mixing of heavy elements, mass loss by the above mechanisms could be activated. However, the above reasoning would immediately fail if other mechanisms (metallicity independent) concur to drive mass loss.

Even for non-zero metallicities, modelling the RGB and AGB phases of low- and intermediate-mass stars is usually problematic, as we do not have a definitive theoretical scenario to account for mass loss during these stages. Moreover, the question arises as to whether the mass-loss prescriptions normally used for metal-poor globular cluster giants (e.g. Reimers 1975), or for pulsating AGB stars (e.g. Vassiliadis & Wood 1993) can be applied to Pop-III stars. Anyway, if any of these empirical relations is actually used in zero-metallicity models, very little mass is found to be lost during the RGB and AGB phases. This justifies to some extent the assumption of evolution at constant mass, that we adopt in the present paper.

However, in Sect. 7 we explore the possibility that the more massive and evolved Pop-III stars may become gravitationally unbound and hence lose mass. These stars will be the subject of a forthcoming paper (Marigo et al. 2001, in preparation).

	Figure 1: Zero-metallicity stellar tracks in the HR diagram, for initial masses in the range 0.7 $M_{\odot }$-100 $M_{\odot }$. Evolutionary calculations are carried out at constant mass. For the sake of simplicity, the He-burning tracks of low-mass ( $M<1.1\, M_\odot$) are not plotted. See also Fig. 2
Open with DEXTER

   
5 General properties of the stellar tracks

   
5.1 Mass ranges, evolutionary stages, and lifetimes

Figure 1 shows the whole set of zero-metallicity tracks at constant mass in the $L-T_{\rm eff}$diagram. The initial masses range from 0.7 $M_{\odot }$ to 100 $M_{\odot }$.

For the sake of clarity in the presentation of the results, we adopt the standard convention of sub-grouping the models as a function of the initial mass, by defining two mass limits, namely $M_{\rm HeF}$ and $M_{\rm up}$.

• Low-mass stars, with $M \le M_{\rm HeF}$, suffer He-ignition in an electron-degenerate core at the tip of the Red Giant Branch (RGB);
• Intermediate-mass stars, with $M_{\rm HeF} < M \le M_{\rm up}$, ignite He in a non-degenerate core, but later develop an electron-degenerate C-O core and experience the Asymptotic Giant Branch (AGB) phase;
• Massive stars, with $M > M_{\rm up}$, are able to ignite central carbon in non-degenerate conditions and proceed through the sequence of advanced nuclear burnings.

Our models are evolved from the ZAMS, at constant mass. The evolution through the whole H- and He-burning phases is followed in detail. The calculations are carried out up to the initial stages of the TP-AGB phase in intermediate- and low-mass models (a small number of thermal pulses have been followed), or the onset of carbon ignition in the helium-exhausted core for the most massive models.

For low-mass stars, the evolution is interrupted at the stage of He-flash in the electron-degenerate hydrogen-exhausted core. The evolution is then re-started from a Zero Age Horizontal Branch (ZAHB) model having the same core mass $M_{\rm c}^{\rm HeF}$ and envelope chemical composition as the last RGB model (see also Sect. 6.3).

Nuclear lifetimes of the H- and He-burning phases as a function of the stellar mass are reported in Table 1.

 

 

Table 1: Nuclear lifetimes as a function of the initial stellar mass

$M/M_{\odot}$	$\tau_{\rm H}/{\rm yr}$	$\tau_{\rm He}/{\rm yr}$
0.7	2.2751 1010	1.1598 108
0.8	1.3749 1010	1.1536 108
0.9	8.9023 109	1.0576 108
1.0	6.1077 109	1.1029 108
1.1	4.3791 109	2.0626 108
1.2	3.3170 109	1.5657 108
1.3	2.5358 109	1.2843 108
1.4	1.9741 109	1.0660 108
1.5	1.5810 109	9.4372 107
1.6	1.2830 109	7.5237 107
1.7	1.0510 109	6.3585 107
1.8	8.8129 108	6.2271 107
1.9	7.4387 108	4.8001 107
2.0	6.3454 108	4.2688 107
2.1	5.4827 108	3.7334 107
2.2	4.7794 108	3.5347 107
2.3	4.2032 108	3.0438 107
2.4	3.7470 108	2.6636 107
2.5	3.3439 108	2.4283 107
2.7	2.7806 108	2.0256 107
3.0	2.0931 108	1.6214 107
3.5	1.4855 108	1.2113 107
4.0	1.0755 108	1.1333 107
5.0	6.7291 107	6.9363 106
6.0	4.7335 107	4.4815 106
6.5	4.1719 107	3.5485 106
7.0	3.5567 107	2.9240 106
8.0	2.6947 107	2.0781 106
8.3	2.5305 107	1.9528 106
9.0	2.2221 107	1.6740 106
9.5	2.0475 107	1.5268 106
10.0	1.8923 107	1.4089 106
12.0	1.4710 107	1.0536 106
15.0	1.1307 107	7.7869 105
20.0	8.4720 106	5.7555 105
30.0	5.9030 106	4.2264 105
50.0	4.1315 106	3.3023 105
70.0	3.4538 106	2.9938 105
100.0	2.9509 106	2.6841 105

Let us now discuss the main features of the models here presented. It should be recalled that many aspects of the evolution of zero-metallicity stars are already described by Cassisi & Castellani (1993; hereinafter also CC93). In order to avoid redundant discussion, the present analysis is more focused on particular issues and/or open questions which, to our opinion, still deserve further investigation.

5.2 The evolution on the H-R diagram

Let us now discuss the main evolutionary features of zero-metallicity stars also in comparison to those of models with $Z \neq 0$. The Z=0 stellar tracks in the H-R diagram are displayed in Fig. 2, where we mark the onset/end of major core burning phases.

First, we can see that, as expected, the Z=0 tracks in the $\log L - \log T_{\rm eff}$ diagram are systematically hotter and more luminous. The latter feature results in shorter nuclear lifetimes (given in Table 1) with respect to those of solar-composition models.

Other obvious differences refer to (i) some morphological features of the tracks, and (ii) the relative excursion in in effective temperature characterising the nuclear H- and He-burning phases.

Concerning point (i), we notice that well-defined loops may show up on the Z=0 tracks (e.g. 1 $M_{\odot }$ and 3 $M_{\odot }$ models in Fig. 2). The physical interpretation of these unusual features will be discussed in Sect. 6.

Concerning point (ii), it is worth making the following remarks. As we can see, the locus of points corresponding to the termination of the main sequence (squares) describes a path in the $\log T_{\rm eff}-\log L$ plane, which significantly bends towards lower effective temperatures at increasing stellar mass (i.e. ). This can be explained as due to the gradual decrease of the mass exponent a in the mass-luminosity relation (i.e. $L \propto M^a$), as pointed out long ago by Stothers (1966).

Comparing the evolution of $1~ M_{\odot}$ models with Z=0 and Z=0.0004, we see that once they experience powerful He-ignition at the tip of the RGB, the subsequent quiescent core He-burning occurs either close to the Hayashi line (Z=0.0004), or to an HB structure blueward of the RR Lyrae instability strip (extending from $\log T_{\rm eff} \sim 3.75$ to $\log T_{\rm eff} \sim 3.85$; see Bono et al. 1995) when Z=0.

Moreover, in stars with , the onset of central He-burning (circles) occurs soon after hydrogen exhaustion in the core, and proceeds as these stars are evolving towards lower effective temperatures at nearly constant luminosities. Into this regard, a feature of particular interest is that the Z=0 models of intermediate mass ( ) start and complete their core He-burning phase always in the bluest parts of the tracks, i.e. quite far from their Hayashi lines. This implies, for instance, that Z=0 intermediate-mass stars would never appear as either red-clump stars or blue-loop stars.

For even more massive models, the locus of points marking the end of the He-burning phase (starred symbols in Fig. 2) also presents a systematic bending towards cooler regions at increasing stellar masses. In particular, we find that massive models with may reach their Hayashi lines already during the helium-burning phase, remaining there until central carbon ignition.

In general, it should be remarked that whether or not a star spends some part of its evolution on (or in proximity to) the Hayashi line may have important implications. In fact, the corresponding development of a deeply extended convective envelope may cause dredge-up events, with consequent changes in the surface chemical composition. This point will be discussed in Sect. 8.

5.3 The evolution on the $\mathsfsl{T_{c}-\rho_{c}}$ diagram

In addition to the $\log L - \log T_{\rm eff}$ plane, another powerful diagnostic of the stellar structure is the central temperature - central density diagram, as it illustrates the state of the gas in the innermost regions. Figure 3 displays the evolutionary behaviour in this plane by the models here considered. Lines are drawn to mark the approximate boundaries of the regions in which the equation of state is dominated by perfect gas, degenerate electron gas, and radiation pressure. Point loci as a function of the stellar mass are shown for relevant evolutionary stages.

One can notice, in this figure, some typical behaviours that depend mainly on the equation of state, and that are found in stellar models of any metallicity. For instance, in correspondence to the stages of gravitational contraction of stellar cores between nuclear burnings, the evolution of the central conditions in the domain of ideal gas can be described by $T_{\rm c} \propto \rho_{\rm c}^{1/3}$, as expected from homology considerations (e.g. Kippenhahn & Weigert 1990).

However, the $T_{\rm c}-\rho_{\rm c}$ diagram of zero-metallicity stars contain several unusual features worthy of note, such as: the peculiar loci marking the onset of central H-burning (line a) and the onset of the 3-$\alpha$ reaction and the CNO-cycle (line b), as well as some short-lived periods of core expansion and/or heating (that are evident, for instance, soon above line b), and the unusually low mass limit ( $1.1~M_\odot$) for stars to become degenerate before He-ignition. Each one of these features will be discussed below.

	Figure 2:  Zero-metal evolutionary tracks (solid lines) for selected initial masses (in $M_{\odot }$) as indicated. The evolutionary track of the ( $1\, M_{\odot }$, Z=0.004) model, calculated by Girardi et al. (2000), is also shown for comparison (dotted line)
Open with DEXTER

Figure 3:  Evolution of central conditions (i.e. density and temperature) for the whole set of Z=0 models. Approximate relations are used to determine the boundaries (thick straight lines) of the regions in which the equation of state is expected to be dominated by different pressure components, i.e. degenerate gas, perfect gas, and radiation pressure. Labelled lines indicate point loci as a function of the stellar mass corresponding to the onset of central H-burning (a); onset of the 3-$\alpha$ reaction and hence the CNO-cycle (b); end of core H-burning (c); onset of central He-burning (d); end of core He-burning (e); energy balance (f) between carbon burning and neutrino losses ( $\epsilon _{\rm c}=\epsilon _{\nu }$). A few values of the initial stellar masses are indicated (in $M_{\odot }$)

Open with DEXTER

   
5.4 Up to the onset of the 3-$\alpha$ reaction

Owing to the complete lack of metals (and hence CNO elements) during the "initial'' stages of central H-burning, the only energy sources able to satisfy the condition of thermal equilibrium are (i) gravitational contraction, and (ii) nuclear burning via the p-p chains. In low-mass stars, the p-p chain soon provides the nuclear energy necessary to slow down gravitational contraction, whereas at increasing mass this energy is reached only at higher and higher temperatures.

The onset of the p-p reactions as a function of mass is very inclined in the $T_{\rm c}-\rho_{\rm c}$ diagram (line a in Fig. 3). Due to the well known rather weak dependence of the p-p reaction rates on temperature (i.e. $\epsilon_{\rm pp} \propto T^{4-6}$), the contraction of the central regions can easily proceed, so that high temperatures may be then attained during the H-burning phase.

Once the central temperatures have increased up to typical values of $\log T \sim 8$, the ignition of the 3-$\alpha$ reaction takes place. This occurrence marks a fundamental event, as it is represents the first significant production of metals in these stars. As a consequence, the synthesis of primary ¹²C leads to the activation of the CNO-cycle, which then starts providing nuclear energy in competition with the p-p reactions (line b in Fig. 3).

The onset of the 3-$\alpha$ reaction occurs at earlier and earlier stages at increasing stellar mass (see Fig. 4). This occurs essentially because the 3-$\alpha$ reaction requires much higher temperatures than the p-p chain. In the lowest mass models, the first production of ¹²C takes place towards the very end of the H-burning phase, and may not even occur for . In this latter case, all central hydrogen is entirely burnt via the p-p chain. At a sufficiently high mass ( $M \ge 20~M_\odot$ in our models), the 3-$\alpha$ reaction ignites even before the p-p reactions have slowed down the initial stellar contraction. In these models then, H-burning simply proceeds via the CNO-cycle, without any significant phase of central burning via the p-p chain.

The above features explain the striking change in the slope of the curve corresponding to the onset of the H-burning phase as a function of the stellar mass (line a in Fig. 3). For models with , H-burning starts above a nearly vertical line in the $T_{\rm c}-\rho_{\rm c}$ diagram (i.e. at varying $T_{\rm c}$ and for an almost constant $\rho_{\rm c}$), that is characteristic of ZAMS stars that burn hydrogen predominantly through the p-p chain. For models with , H-burning starts above a line of modest slope (i.e. a modest increase of $T_{\rm c}$ corresponds to a substantial decrease of $\rho_{\rm c}$), that simply traces the minimum $T_{\rm c}$ and $\rho_{\rm c}$ necessary to ignite the 3-$\alpha$ reaction (and hence the CNO-cycle) in a core with $Y\sim0.23$. This also explains why line (a) simply merges with line (b) at .

	Figure 4: The central abundance of hydrogen when the fractional abundance of newly synthesised CNO elements grows up to 10-14
Open with DEXTER

5.5 Soon after the onset of the 3-$\alpha$ reaction

Subsequent to the first carbon production, as the energy contribution of the CNO reactions increases (at the expense of the p-p reactions) the central regions are forced to expand, with a consequent decrease of the central density (and central temperature in the most massive models). This leads to the behaviour of the tracks in Fig. 3, around the line (b). The activation of the CNO-cycle may result in the appearance of some peculiar features in the H-R diagram of low-mass models (i.e. loops; see Sect. 6) and, given its quite large temperature dependence (i.e. $\epsilon_{\rm CNO} \propto T^{14-22}$), it also favours the development or a larger extension of core convection. For instance, in the case of the models with $M \sim 2{-}5~M_{\odot}$ displayed in Fig. 5, after the initial recession of the convective core, central H-burning via the p-p reactions occurs in radiative conditions. Then, as the CNO cycle turns on, central regions become convectively unstable again. This effect is anticipated at increasing stellar mass, and eventually in more massive models ( $M > 5~M_{\odot}$) the transition of the core from convective to radiative and back to convective does not occur at all.

	Figure 5: Evolution of core convection during central H-burning for a few selected models with masses (in $M_{\odot }$) as indicated
Open with DEXTER

5.6 The critical masses: $\mathsfsl{M_{HeF}}$ and $\mathsfsl{M_{up}}$

From the location of the non-degenerate/degenerate boundary and of the curves for He- and C-ignition shown in Fig. 3, it is possible to estimate the critical masses $M_{\rm HeF}$ and $M_{\rm up}$. Figure 6 illustrates the predicted trend of the mass limits $M_{\rm HeF}$ and $M_{\rm up}$ as a function of the metallicity, combining the results by Girardi et al. (2000) with those of the present work for Z=0.

Concerning $M_{\rm HeF}$, this is found to decrease with the metallicity, dropping down to $\sim$ $1.1~M_\odot$ for Z=0. This is the combined result of the larger convective cores during the MS phase at decreasing metallicities when the CNO cycle is the dominant energy source (up to $Z \sim 10^{-4}$, see CC93) and, at even lower Z, of the higher temperatures reached in the centre when H-shell burning mainly occurs via the p-p reactions (as is the case for the Z=0 models).

Concerning $M_{\rm up}$, its trend is not monotonic as it first decreases with metallicity, reaches a minimum, and finally increases again up to $7~M_{\odot} - 8~M_{\odot}$ when Z=0. This behaviour is essentially controlled by the mass of the He-core left at the end of the MS. For CNO-dominated H-burning, lower metallicities correspond to more concentrated energy sources and larger convective cores, which explains the initial decrease of $M_{\rm up}$. As soon as the energy contribution from the p-p reactions becomes competitive with the CNO cycle, the central burning regions on the MS are more extended, while the sizes of the convective cores tend to be smaller. This explains the presence of the minimum and the subsequent increase of $M_{\rm up}$ at decreasing Z.

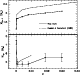	Figure 6: Critical masses $M_{\rm HeF}$ and $M_{\rm up}$ as a function of the metallicity according to the predictions of Girardi et al. (2000) for values of $Z \neq 0$, and those presently derived for Z=0. The results of Cassisi & Castellani (1993; and references therein) are shown for comparison
Open with DEXTER

Both behaviours of $M_{\rm HeF}$ and $M_{\rm up}$ are in agreement with the results of CC93. Their larger values of $M_{\rm HeF}$ and $M_{\rm up}$ at given metallicity essentially reflect the different treatment of convective boundaries (i.e. Schwarzschild criterion) with respect to ours (i.e. overshoot scheme; see Sect. 4).

	Figure 7: Kippenhahn diagrams showing the location (in fractional mass) of the burning and convective zones during the evolution of the $2.2 \, M_{\odot }$, Z=0 model
Open with DEXTER

5.7 Growth of core convection during the He-burning phase

Another remarkable evolutionary feature is found in stars with masses $M \sim 1.2$-2.5 $M_{\odot }$, and . During the central He-burning phase, the outer boundary of the core overshooting zone is located very close to the bottom of the H-burning shell.

Initially, we found that, if the convective core was left to grow, it eventually reaches the H-shell and engulfs some H-rich material, which is rapidly burnt in the core via the CNO cycle. This causes a flash that expands the core, so that central He-burning weakens and the convective core recedes temporarily (in mass). After the flash has occurred, the convective core starts growing again, possibly approaching the bottom of the H-shell. This leads to quasi-periodic H-flashes, the related growth/recession of the core resembling some sort of breathing convection.

However, this picture is likely to be physically unsound because of the treatment adopted in the evolution code. In fact, the H-flash is caused by the fact that the engulfed hydrogen is first mixed throughout the convective core, and then burnt according to nuclear reaction rates which are mass-averaged all over the convective layers. This procedure is a good approximation as long as the convective lifetimes are shorter than the nuclear lifetimes, which is usually the case for CNO-burning occurring in "ordinary'' conditions.

But at the very high temperatures ($\sim$10⁸ K) reached at the bottom the H-burning shell, the nuclear lifetimes involved in the CNO cycle (on the order of hours, days) can be comparable or even shorter than the typical convective timescales (on the order of months). Under these conditions, a correct approach would require a time-dependent solution scheme which couples simultaneously nucleosynthesis and mixing (see e.g. Schlattl et al. 2001).

Leaving the full analysis of this point to a future investigation, we make the reasonable assumption in the present study that hydrogen burns locally at the bottom of the H-shell, before a complete mixing by core convection can occur. Technically, this translates into the condition that the maximum allowed extension of core convection is set by the bottom of the H-burning shell. Figure 7 illustrates the evolution of the convective and burning regions of the 2.2 $M_{\odot }$ model. We can notice the approach of core convection towards the inner location of the H-burning shell, during the He-burning phase (third panel from left). We can also notice the remarkable thickness (in mass) of the H-burning shell, which extends deeply inward during both shell H-burning and core He-burning phases. This is due to the fact that hydrogen in the shell is mainly burnt via the p-p chain, which due to its low temperature sensitivity, allows quite high temperatures to be attained at the bottom of the shell. At an age of 5.1 10⁸ yr, our numerical treatment starts to limit the extension of the core convection. In this way, the evolution can be quietly followed up to the end of He-burning.

    
6 Low- and intermediate-mass models

6.1 The first activation of the CNO cycle

We have shown in Sect. 5.4 that the onset of the 3-$\alpha$ reaction in low-mass models possibly occurs near the end of the central H-burning phase. This circumstance is marked by short-lived loops in the H-R diagram (see Figs. 1 and 2). We can better analyse this feature looking at Fig. 8, which displays how relevant properties of the 1 $M_{\odot }$ model vary during the brief time interval in which the loop shows up.

Figure 8:  Physical properties of the 1 $M_{\odot }$ model with Z=0 at the first onset of the 3-$\alpha$ reaction. Top-left panel: central abundance of CNO elements. Bottom-left panel: fractional energy contributions from nuclear burnings, where L, $L_{\rm H}$, $L_{\rm CNO}$, and $L_{\rm pp}$ refer, respectively, to the surface stellar luminosity, the rate of energy production via H-burning, CNO cycle, and p-p chain. Top-right panel: evolution of surface quantities as indicated. Bottom-right panel: evolution of central density andtemperature

Open with DEXTER

As soon as a CNO abundance of about 10^-10,-9 is built at the centre of the star, a sudden spike arises in the rate of energy generation by nuclear H-burning. This occurs when the growing efficiency of the CNO cycle exceeds that of the p-p reactions ( $L_{\rm CNO}/L > L_{\rm pp}/L$), which have dominated the energetics of the star up to then. The central conditions react to this sudden increase of energy production: the innermost regions expand so that both $T_{\rm c}$ and $\rho_{\rm c}$ decrease.

   
6.2 The evolution on the RGB

As already pointed out by D'Antona (1982) and CC93, a prominent feature of zero-metallicity low-mass models is that, for given stellar mass, the tip of the RGB is reached with a larger core mass and much fainter luminosity with respect to models with non-zero metallicity (see, for instance, the $1~ M_{\odot}$ tracks for Z=0 and Z=0.0004 in Fig. 2). The peculiar behaviour of the luminosity as a function of the core mass ( $M_{\rm c} - L$ relation) displayed by RGB models with Z=0 can be explained as the combined effect of the lower mean molecular weight ($\mu$), and the dominant nuclear energy source (i.e. p-p chain). As is shown by Marigo (2000), the $M_{\rm c} - L$ relation at Z=0 can be remarkably well reproduced by the homology prediction $L \propto (\mu M_{\rm c})^{\delta}$ with $\delta \sim 4.5$, the value of the exponent being essentially determined by the typical temperature dependence of the p-p reactions. For dominating CNO cycle, we would get $\delta \sim 7-8$, which well accounts for the luminosity evolution of RGB models with Z > 0.

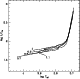	Figure 9: H-R tracks of Z=0 low-mass models extending from the ZAHB up to the beginning of the TP-AGB phase
Open with DEXTER

   
6.3 The evolution on the HB

In principle, as a low-mass star settles on the ZAHB, it starts to quiescently burn helium in the core with an abundance somewhat lower than the original one, since a small amount of helium, $\Delta Y_{\rm c}^{\rm HeF}$, has been already converted into carbon during the flash at the tip of the RGB.

 

 

Table 2: Characteristics of low-mass stars at the He-flash

M	$M_{\rm c}^{\rm HeF}$	$\Delta E_{\rm RGBt}^{\rm ZAHB}$	$\Delta Y_{\rm c}^{\rm HeF}$
$(M_{\odot})$	$(M_{\odot})$	$(10^{49}\,{\rm erg})$
0.7	0.5015	2.573	-0.0325
0.8	0.4991	2.549	-0.0322
0.9	0.4951	2.497	-0.0315
1.0	0.4882	2.400	-0.0303
1.1	0.3683	0.989	-0.0100

We have computed this quantity for each evolutionary track, by simply assuming that the flash provides just the energy necessary to lift the electron degeneracy from the core. In practice, this energy can be evaluated as the difference in total energy between the last RGB-tip configuration and the initial ZAHB one, $\Delta E_{\rm RGBt}^{\rm ZAHB}$. Then, the mass of burnt helium, and hence $\Delta Y_{\rm c}^{\rm HeF}$, follows straightforwardly from the Q-value of 3-$\alpha$ reactions. Table 2 presents some relevant characteristics of the models at the stages of He-flash and ZAHB. We can notice that the predicted fractional abundance of helium is burnt in the flash amounts to few percent (typically 3%).

The subsequent evolution on the HB (see Fig. 9) is quite similar to that of Pop-II models. However, as already pointed out by Cassisi et al. (1996), all low-mass Z=0 stars burn their central He at quite high effective temperatures (with ), so that a negligible fraction of RR Lyrae pulsators on the ZAHB is expected. This aspect is further commented on Sect. 9.

   
6.4 The AGB phase and the occurrence of thermal pulses

The evolutionary properties of metal deficient AGB stars have been analysed in the past by Fujimoto et al. (1984); Chieffi & Tornambé (1984); Cassisi et al. (1996), and more recently by Domínguez et al. (1999). A crucial question addressed in these works is about the possible occurrence of the He-shell flashes (thermal pulses), which are usually found in AGB models of various (but not zero) metallicities.

According to the semi-analytical investigation of Fujimoto et al. (1984) on the stability of nuclear burning shells, thermal pulses are conditional on the existence of thresholds in core mass $M_{\rm c}$, and CNO abundance $Z_{\rm CNO}$ in the envelope. To summarise, He-shell flashes are expected to occur when i) $M_{\rm c} < 0.73~M_{\odot}$ for any value of $Z_{\rm CNO}$, and ii) $M_{\rm c} > 0.73~M_{\odot}$ if $Z_{\rm CNO} > Z_{\rm CNO}^{\rm crit}$, the critical lower limit depending on $M_{\rm c}$. The dependence on $Z_{\rm CNO}$ can be qualitatively understood considering that in the absence (or strong deficit) of CNO elements in the envelope, the H-burning shell itself produces new carbon via the 3-$\alpha$ reaction, so that the CNO cycle can operate. It follows that the H- and He-burning shells are not energetically decoupled, and proceed outward in mass at the same rate (see also Chieffi & Tornambé 1984). Since He-rich material is not accumulated in the inert intershell buffer, but rather steadily burnt by the underlying He-shell, the occurrence of thermal pulses is thus prevented.

In this study we present the results for two intermediate-mass models, with initial zero metallicity and masses of $2.5~M_{\odot}$ and $5~M_{\odot}$, which are made evolve through the initial stages of the AGB phase, including a few episodes of thermal instabilities of the He-burning shell. Whether such events may be ascribed to true He-shell flashes is discussed below.

As the $2.5~M_{\odot}$ and $5~M_{\odot}$ models reach their Hayashi tracks (E-AGB phase) after central helium exhaustion, envelope convection progressively moves inward in both cases, and extends into regions which have experienced earlier nucleosynthesis. The so-called "second dredge-up'' takes place, but with a substantial difference between the two models. This can be appreciated by looking at Table 3, which presents the predicted surface chemical compositions after the second dredge-up event for all our models.

In the $2.5~M_{\odot}$ model the envelope penetrates into the chemical profile left by the recession of the convective core during the MS, and into regions previously affected by the p-p chain, so that the surface enrichment is essentially in helium with no trace of heavier metals (see also Fig. 7 for a similar case). In the $5~M_{\odot}$ model the envelope penetration proceeds further, reaching down to the former location of the H-burning shell (which temporarily extinguishes), so that newly synthesized CNO elements are also dredged-up to the surface. After the occurrence of the second dredge-up, the evolution of these AGB models proceeds quite differently.

 

 

Table 3: Surface chemical compositions (in mass fraction) after the 1st and 2nd dredge-up events

$M/M_{\odot}$	H	3He	4He	12C	13C	14N	15N	16O	17O	18O	22Ne	24+25Mg	20Ne
Initial:
all	0.770	2.46 10-5	0.230	0	0	0	0	0	0	0	0	0	0
After the first dredge-up:
0.7	0.769	8.63 10-5	0.231	0	0	0	0	0	0	0	0	0	0
0.8	0.768	1.40 10-4	0.232	0	0	0	0	0	0	0	0	0	0
0.9	0.768	1.54 10-4	0.232	0	0	0	0	0	0	0	0	0	0
1.0	0.768	1.17 10-4	0.232	0	0	0	0	0	0	0	0	0	0
1.1	0.769	8.29 10-5	0.231	0	0	0	0	0	0	0	0	0	0
After the second dredge-up:
1.2	0.769	6.49 10-4	0.231	0	0	0	0	0	0	0	0	0	0
1.3	0.767	4.89 10-4	0.233	0	0	0	0	0	0	0	0	0	0
1.4	0.769	4.72 10-4	0.231	0	0	0	0	0	0	0	0	0	0
1.5	0.767	3.45 10-4	0.233	0	0	0	0	0	0	0	0	0	0
1.6	0.767	3.16 10-4	0.232	0	0	0	0	0	0	0	0	0	0
1.7	0.767	2.75 10-4	0.233	0	0	0	0	0	0	0	0	0	0
1.8	0.769	2.64 10-4	0.231	0	0	0	0	0	0	0	0	0	0
1.9	0.768	2.19 10-4	0.232	0	0	0	0	0	0	0	0	0	0
2.0	0.768	2.02 10-4	0.232	0	0	0	0	0	0	0	0	0	0
2.1	0.704	1.07 10-4	0.296	0	0	0	0	0	0	0	0	0	0
2.2	0.697	9.59 10-5	0.303	0	0	0	0	0	0	0	0	0	0
2.3	0.691	8.13 10-5	0.309	0	0	0	0	0	0	0	0	0	0
2.4	0.690	6.82 10-5	0.310	0	0	0	0	0	0	0	0	0	0
2.5	0.681	5.97 10-5	0.319	0	0	0	0	0	0	0	0	0	0
2.7	0.669	5.04 10-5	0.331	4.17 10-21	1.34 10-21	4.95 10-19	2.02 10-23	1.28 10-20	1.33 10-22	7.16 10-26	2.43 10-35	1.62 10-50	7.70 10-38
3.0	0.660	4.10 10-5	0.340	1.13 10-18	3.62 10-19	1.28 10-16	5.19 10-21	3.15 10-18	2.82 10-20	1.60 10-23	4.25 10-32	6.91 10-46	3.19 10-34
3.5	0.649	2.99 10-5	0.351	8.06 10-16	2.59 10-16	8.58 10-14	3.46 10-18	1.97 10-15	1.41 10-17	8.69 10-21	2.06 10-28	1.86 10-40	6.19 10-30
4.0	0.644	2.29 10-5	0.356	6.33 10-14	2.03 10-14	6.17 10-12	2.46 10-16	1.31 10-13	7.41 10-16	5.23 10-19	5.33 10-26	7.42 10-37	4.13 10-27
5.0	0.637	1.56 10-5	0.363	3.58 10-9	7.81 10-12	6.06 10-10	1.57 10-14	4.54 10-12	3.90 10-14	5.11 10-15	5.22 10-19	6.68 10-28	1.14 10-23
6.0	0.632	1.11 10-5	0.368	2.63 10-7	1.19 10-11	9.35 10-10	2.41 10-14	7.36 10-11	5.91 10-14	4.67 10-13	2.96 10-16	1.66 10-23	4.73 10-21
6.5	0.626	9.25 10-6	0.374	7.07 10-7	1.46 10-11	1.13 10-9	2.90 10-14	2.99 10-10	7.37 10-14	2.21 10-12	1.95 10-15	2.63 10-22	4.09 10-20
7.0	0.668	8.74 10-6	0.332	1.26 10-13	4.04 10-14	1.09 10-11	4.30 10-16	2.08 10-13	8.57 10-16	7.51 10-19	6.02 10-26	2.75 10-36	9.03 10-27
8.0	0.681	7.49 10-6	0.319	9.66 10-14	5.68 10-17	8.08 10-12	6.32 10-19	1.47 10-13	1.41 10-18	1.15 10-21	9.09 10-30	6.05 10-42	4.43 10-31
8.3	0.687	7.00 10-6	0.313	1.19 10-14	3.81 10-15	1.01 10-12	3.98 10-17	1.88 10-14	7.39 10-17	6.71 10-20	1.95 10-27	2.12 10-38	2.36 10-28
9.0	0.770	4.30 10-5	0.230	0	0	0	0	0	0	0	0	0	0
9.5	0.770	4.30 10-5	0.230	0	0	0	0	0	0	0	0	0	0
10.0	0.770	4.25 10-5	0.230	0	0	0	0	0	0	0	0	0	0
12.0	0.770	3.63 10-5	0.230	0	0	0	0	0	0	0	0	0	0
15.0	0.770	2.47 10-5	0.230	0	0	0	0	0	0	0	0	0	0
20.0	0.770	1.66 10-5	0.230	0	0	0	0	0	0	0	0	0	0
30.0	0.770	1.02 10-5	0.230	0	0	0	0	0	0	0	0	0	0
50.0	0.770	5.95 10-6	0.230	0	0	0	0	0	0	0	0	0	0
70.0	0.713	1.06 10-6	0.287	7.65 10-12	2.45 10-12	6.39 10-10	2.53 10-14	1.30 10-11	5.29 10-14	5.34 10-17	5.11 10-24	2.08 10-14	2.58 10-14
100.0	0.640	6.39 10-7	0.360	2.27  10-11	7.25 10-12	1.87 10-9	7.21 10-14	3.53  10-11	1.33 10-13	1.33 10-16	2.03 10-23	1.42 10-32	1.13 10-23

As we can see from Fig. 10, the $2.5~M_{\odot}$ model experiences rather weak fluctuations in the surface luminosity, reflecting the alternation between the H- and He-burning shells in providing nuclear energy to the star. The long-term behaviour of the surface properties indicates the model is evolving down on its Hayashi track, i.e. to decreasing luminosity and increasing effective temperature. As already mentioned, the CNO surface abundance is zero, so that the H-burning shell must itself produce the necessary ¹²C to sustain the CNO-cycle. The latter is actually the dominant energy source during most part of the AGB evolution followed by our calculations (bottom-left panel of Fig. 10).

	Figure 10:  Evolutionary properties during the first thermal instabilities of the He-burning shell, for two Z=0 AGB models with initial masses of $2.5~M_{\odot}$, and $5.0~M_{\odot}$. See text for further explanation
Open with DEXTER

The $5~M_{\odot}$ model suffers well-defined He-shell flashes, which drive the features usually found in the light curves of AGB stars. Namely, over a pulse cycle, the luminosity undergoes the initial post-flash rapid dip and peak, which is followed by the low-luminosity dip, and the final recovering of the luminosity level that characterizes the quiescent shell H-burning (see, for instance, Boothroyd & Sackmann 1988). In this case, the long-term evolution is characterised by the increase of the surface luminosity and slight decrease of the effective temperature, i.e. the model is climbing on the AGB. The envelope CNO abundance (by mass) left after the completion of the second dredge-up is $Z_{\rm CNO} = 4.198~10^{-9}$.

As for the 2.5 $M_{\odot }$ model, the CNO cycle provides most of the stellar energy during the stages of quiescent H-burning (bottom-right panel of Fig. 10). However, it should be noticed that a fraction of the CNO nuclei involved as catalysts in the CNO cycle are not brought up to the surface by the second dredge-up, but are synthesized in situ by the H-burning shell via the $3-\alpha$ process. This can be seen by comparing the total CNO abundance (by number) in the envelope, $Z_{\rm CNO}$, and that, for instance, at the point of maximum nuclear efficiency within the H-burning shell, $Z_{\rm CNO}^{\rm shell}$. If there were not production of ¹²C inside the shell, we should have $Z_{\rm CNO} = Z_{\rm CNO}^{\rm shell}$, whereas we find $Z_{\rm CNO} < Z_{\rm CNO}^{\rm shell}$, with $Z_{\rm CNO}^{\rm shell}$ ranging from $\sim$2 10^-8 to $\sim$ 6.5 10^-8 at subsequent stages immediately preceding a thermal pulse.

Let us now check whether our results can be recovered within the Fujimoto scheme. The $2.5~M_{\odot}$ and $5~M_{\odot}$ models have core masses of about $0.69~M_{\odot}$ and $0.87~M_{\odot}$, and $Z_{\rm CNO}$in the envelope equal to 0 and $\sim$ 4.198 10^-9, respectively. According to Fujimoto et al. (1984) the lowest mass model is expected to suffer thermal pulses, since $M_{\rm c} < M_{\rm c}^{\rm crit}$ (regardless of $Z_{\rm CNO}$), whereas the most massive one should not, since it is located inside the region of the plane $M_{\rm c}-Z_{\rm CNO}$ where thermal pulses are prohibited (see their Fig. 5). Thus, our results would seem to disagree with the Fujimoto scheme. This is perhaps not surprising as the predictions by Fujimoto et al. (1984) are derived from a semi-analytical method, in which the input physics - adopted for the integrations of deep envelope structures - may differ from those presently used in our stellar code, as well as for other model prescriptions, such as the initial helium abundance (Y=0.25 in Fujimoto et al., Y=0.23 in our models). Other differences may also arise from the use of analytical approximations in the Fujimoto procedure.

However, even if our results do not strictly obey the quantitative thresholds in $M_{\rm c}$ and $Z_{\rm CNO}$ as pointed out by Fujimoto et al. (1984), a qualitative agreement in the behaviour of AGB models with initial zero metallicity can be found. In particular, we confirm the prediction that the occurrence of thermal pulses in massive AGB models is conditional on the pre-existence of some CNO abundance in the envelope, that in the case of our $5~M_{\odot}$ model is supplied by the second dredge-up during the E-AGB. This finding is also supported by the evolutionary calculations of zero-metallicity intermediate-mass stars by Chieffi & Tornambé (1984) and Domínguez et al. (1999). The strength of thermal instabilities should also depend on the $Z_{\rm CNO}$ value in the envelope, as this quantity controls the degree of thermal coupling between the H- and He-burning shell. In models with initial zero metallicity, we expect that the more $Z_{\rm CNO}$ is dredged-up, the less ¹²C is synthesised by the 3-$\alpha$ reaction in H-shell during a interpulse period, hence the stronger the He-shell flash should be.

   
7 Massive models

7.1 Core masses

In Fig. 11 and Table 4 we report the masses of the He and C-O cores of the zero-metallicity models with $M > M_{\rm up} \sim 7 \, M_{\odot}$, which are expected to end their evolution as supernovae.

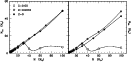	Figure 11: Masses of the He core ( $M_{\rm He}$) and C-O core ( $M_{\rm CO}$) at the central carbon ignition in zero-metallicity massive models, compared with predictions for Z=0.02, and Z=10-4
Open with DEXTER

These quantities represent fundamental information for both hydrodynamic calculations of the explosion event (see, for instance, Umeda et al. 2000), and synthetic derivation of the supernova yields (see the procedure described by Portinari et al. 1998).

 

 

Table 4: Core masses and central C/O ratio at the stage of C-ignition

$M/M_{\odot}$	$M_{\rm He}/M_{\odot}$	$M_{\rm CO}/M_{\odot}$	$(X_{\rm C}/X_{\rm O})_{\rm c}$
7.0	1.09	0.98	0.715
8.0	1.66	1.13	0.688
8.3	1.75	1.18	0.677
9.0	1.96	1.29	0.658
9.50	2.11	1.38	0.643
10.0	2.25	1.47	0.630
12.0	2.90	1.92	0.574
15.0	4.01	2.73	0.506
20.0	6.13	4.40	0.422
30.0	10.79	8.17	0.330
50.0	21.25	17.23	0.234
70.0	32.10	27.39	0.187
100.0	48.73	42.84	0.149

Comparing the results for Z=0 with those for other metallicities, we can notice that: i) for initial masses 25-30 $M_{\odot }$ the core masses are almost independent of metallicity; ii) the major differences show up at higher masses, being largely determined by the effect of mass loss that is expected to be less efficient at lower Z (and not applied to the Z=0 models); iii) in the case of the Z=0 models evolved at constant mass, both $M_{\rm He}$ and $M_{\rm CO}$follow a nearly linear relation with the stellar mass.

   
7.2 The Eddington critical luminosity

We also check whether the most massive models may become gravitationally unbound, i.e. the rate of energy outflow at the surface exceeds the corresponding Eddington luminosity

$$% L_{\rm E} = \frac{4 \pi G c M}{\kappa}$$ (5)

where M is the stellar mass, and $\kappa$ the opacity of the surface layer.

In Fig. 12 we compare the evolutionary paths in the H-R diagram for selected models of different initial masses with the loci obtained from Eq. (5), i.e. calculating the Eddington luminosity of the photosphere for each value of the effective temperature along the evolutionary sequence.

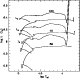	Figure 12: Evolutionary tracks in the H-R diagram (thick lines) for selected massive models with initial masses (in $M_{\odot }$) as indicated. Thin-line curves labelled with $L_{\rm E}$ show the behaviour of the Eddington luminosity calculated at the photospheric layer with Eq. (5)
Open with DEXTER

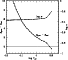Figure 13: Effective acceleration at the photosphere, defined as the difference between the inward gravitational acceleration, $g_{\rm grav}$, and the outward radiative acceleration, $g_{\rm rad}$. A sequence of models are shown up to the point in which the net acceleration becomes negative, as the surface luminosity exceeds the Eddington limit. Correspondingly, the evolution of the photospheric opacity, $\kappa$, is shown

Open with DEXTER

From this simple test, it turns out that, in contrast with the $50~M_{\odot}$ model, the $70~M_{\odot}$ and $100~M_{\odot}$ models may achieve super-Eddington luminosities (typically at $\log T_{\rm eff} \sim 3.9$) on their way to the Hayashi line, towards the end of the He-burning phase. Correspondingly, the effective acceleration at the surface becomes negative, due to the increase of the surface radiative opacity (see Fig. 13).

From this point onward the predicted evolution should not be considered reliable, as the adopted assumption of hydrostatic equilibrium does not hold any longer for the outermost layers. Likely, these stars would start losing mass from their surface.

For the sake of simplicity, we do not attempt to include any prescription for mass-loss driven by super-Eddington luminosities in the most massive stars in this work. This, and other stellar wind driving mechanisms, will be analysed in more detail in a future paper dedicated to the evolution of zero-metallicity stars with mass loss (Marigo et al. 2001, in preparation).

   
8 Surface chemical changes

We will now discuss the changes in the surface chemical composition due to convective dredge-up episodes. Usually these result from the penetration of the convective envelope into stellar layers which have previously been modified by nucleosynthetic processes. In this respect it is relevant to recall that the deepest inward extension of envelope convection occurs as a star reaches close to its Hayashi line. Keeping this in mind and looking Table 3 we can make the following considerations.

Between the end of the H-burning phase and the central He-ignition, the only models that evolve to the red part of the H-R diagram and settle onto the giant branches (closely approximating the location of the Hayashi tracks) are those of low-mass ( ). At this stage envelope convection starts to proceed inward, but it does not extend significantly into the chemical profile left by the radiative burning core. As can be noticed in Table 3, this first dredge-up episode in low-mass stars changes the surface chemical abundance of helium by negligible amounts. For more massive models ( $M > 1.2~M_{\odot}$) the onset of the He-burning phase takes place far away from the Hayashi tracks. As a consequence, the first notable feature of zero-metallicity models is that the first dredge-up essentially does not take place.

As far as the second dredge-up is concerned, we can notice from Fig. 2 that after central helium exhaustion the evolution for all models with $M < 70~M_{\odot}$is characterised by a redward excursion in the H-R diagram. However, the minimum value of the effective temperature attained - either at the start of the AGB phase or at central carbon ignition - has a non-monotonic dependence on the stellar mass. Specifically, stars with initial masses are able to approach their Hayashi tracks, then becoming red giants. In this mass range the second dredge-up is found to actually occur in models with , the envelope penetration being insufficient at lower masses. Moreover, we can notice from Table 3 that for only helium increases its abundance in the envelope, whereas for some primary CNO is also dredged-up to the surface.

It is worth remarking that further changes in the surface chemical abundances may be caused by the occurrence of the third dredge-up at thermal pulses (if they take place, see Sect. 6.4) during the TP-AGB phase (see, for instance, Domínguez et al. 1999). Actually, in our calculations we do not find any evidence of this process, but this is more likely due to the small number of He-shell flashes that have been followed for each evolutionary sequence.

More massive stars ( ) met the necessary conditions for carbon ignition in the core at higher effective temperatures, i.e. before entering the giant branch phase. As expected, these models do not suffer any dredge-up episode, i.e. their surface layers preserve the original composition.

Finally, stars with settle on their Hayashi tracks already during the core He-burning phase, and there they remain until the onset of carbon burning. The second dredge-up takes place enriching the surface composition both in helium and CNO elements (see Table 3). As already discussed in Sect. 7.2, the results for these massive and luminous models - made to evolve at constant mass - should be taken with some caution. Our analysis has in fact revealed that these models may become dynamically unstable against radiation pressure towards the end of core helium burning. From that point, stellar winds driven by super-Eddington luminosities will indirectly affect the surface chemical composition by i) reducing the stellar mass, and ii) influencing the efficiency of the second dredge-up. To this regard, a more careful study is going to be carried out in a forthcoming work (Marigo et al. 2001, in preparation).

In conclusion, owing to the particular evolutionary features of the zero-metallicity stars, we find that significant changes in the chemical composition of the envelope - during the evolutionary phases here considered - may occur within two well defined mass ranges, i.e. , and . Our results are fully illustrated in Fig. 14.

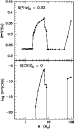	Figure 14: Surface abundances of 4He and CNO elements as a function of the stellar mass, for the last computed model
Open with DEXTER

   
9 Might we ever detect primordial stars?

Zero-metallicity stars with initial masses $M < 0.8~M_{\odot}$, if ever born, should be still alive, as their nuclear lifetimes are longer than the age of the universe (see Table 1). However, to date the hypothesis of the possible formation of primordial low-mass stars has not been proven observationally. In order to devise a test for the existence of such stars, one should single out observable distinctive features which can point unambiguously to their existence. For instance, the absence of metal lines in the stellar spectra would immediately give us the confirmation, but this circumstance is hard to meet. In fact, the interaction of long-lived first stars with a chemically enriched interstellar medium would have probably polluted their primordial surface compositions with newly synthesized metals.

Another peculiar feature of low-mass zero-metallicity stars (with $M \sim 1~M_{\odot}$) is the development of loops in the H-R diagram, corresponding to the first activation of the CNO cycle as soon as some primary ¹²C is produced by the 3-$\alpha$ reaction (see Sect. 5.4). Unfortunately, the probability of detecting such loops in a primordial simple stellar population is negligible, as this feature is quite short-lived (a few 10⁶ yr), hence scarcely populated.

Finally, distinctive observational properties of low-mass zero-metallicity stars may be derived from their loci in the HR-diagram: they are slightly hotter than the Pop-II stars of even the lowest metallicity. For instance, Cassisi et al. (1996) find that most of the evolution of Z=10^-10 HB stars occurs to the left (higher $T_{\rm eff}$) of the RR Lyrae instability strip, thus implying a very low probability of finding RR Lyrae pulsators among an hypothetical population of these stars.

However, we notice that high effective temperatures are also met at the turn-offs of low-mass stars. This might open the possibility that, at ages >10 Gyr, the main-sequence of Z=0 populations falls inside the faintest part of the instability strip which contains (in order of decreasing luminosity) three classes of variables, namely: Cepheids, RR Lyrae and $\delta$ Scuti stars. In such a case, the possibility arises that a large number of short-period, low-amplitude pulsators might be present among Pop-III stars.

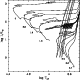	Figure 15: Instability strips in the $\log L - \log T_{\rm eff}$ diagram. Theoretical edges for (Z=0, Y=0.23) are drawn assuming pulsation occurs in the fundamental mode (solid line), first overtone (dashed line), and second overtone (dotted line). The shaded area shows the expected location of RR Lyrae according to Bono et al. (1995). See text for more details
Open with DEXTER

To investigate this possibility, the results of a preliminary analysis of pulsation and evolution of Z = 0 stars are shown in Figs. 15 and 16. We have made use of the large data set of theoretical models of Cepheid variables calculated by Chiosi et al. (1993), corresponding to luminosities $\log L/L_{\odot} > 2$, various values of the stellar mass ( ), and different metal and helium abundances (Z= 0.02, 0.008, 0.004; Y=0.23, 0.24). This data set has been extended towards lower luminosities by means of a preliminary stability analysis, specifically performed for zero-metallicity models with $M = 1~M_{\odot}$. The linear nonadiabatic pulsation calculations have been carried out with the aid of the same code as in Chiosi et al. (1993; and references therein), but incorporating the low temperature opacities of Alexander & Ferguson (1994). The new calculations cover the region of the HR diagram delimited by $0.3 \le \log(L/L_\odot) \le 1.3$ and .

Combining the earlier pulsation models with the new ones, we are now able to determine the edges of the instability strip from $\log L/L_{\odot} \sim 4.5$ down to $\log L/L_{\odot} \sim 0$, as illustrated in Fig. 15. Analogously to Chiosi et al. (1993), we have also derived several parameterised fitting formulas (given in Table 5) as a function of helium Y and metal content Z. They describe, for different pulsation modes, the location of the instability strips and other relevant relations between period, luminosity, colour, and mass. The instability strips displayed in Fig. 15 are obtained from the aforementioned analytical relations for the red and blue edge setting Z=0 and Y=0.23.

The main interesting points are the following. At luminosities $\log L/L_{\odot} > 2$ the instability strip crosses the evolutionary tracks of primordial stars which should already be dead and hence undetectable. Towards lower luminosities the theoretical location of the instability strip is consistent with the predictions for RR Lyrae variables according to Bono et al. (1995) for fixed helium and metal content (Y=0.24, Z=0.001). The shaded region corresponds to the maximum extension of the strip (to the red and to the blue), combining the results of Bono et al. (1995) for both fundamental and first overtone pulsators. We can notice that the RR Lyrae instability strip is almost twice as extended to the red as our instability strip at the same luminosities. It is worth remarking here that, whereas the blue edge is well determined by our stability analysis, the red edge is not (for more details see Chiosi et al. 1993). As a conservative approach, we define the red edge to coincide with the maximum of the growth rate. In this way, we are certainly underestimating the width of the instability strip.

Anyhow, at the typical luminosities of RR Lyrae, the instability strip for the Z=0 models would cover the red portions of the HBs described by the zero-metallicity low-mass tracks plotted in Fig. 15 (see Cassisi et al. 1996, for a similar result). In other words, pulsation should set in during a period of very rapid evolution, i.e. only after these stars have burnt most of their central helium in the bluer regions close to the ZAHB. This again would make the observability almost out of reach.

Finally, going to even fainter luminosities ( ) it turns out that zero-metallicity models with mass as low as $0.9~M_\odot$ are expected to exhibit pulsational properties during the main-sequence phase. At the luminosities and effective temperatures under consideration (see Fig. 15), the pulsation periods can range from about 0.6 to 0.03 days. The reliability of these provisional results is supported to some extent by the fact that the location on the H-R diagram and the period determinations are consistent with the observational data of $\delta$ Scuti stars - a rich class of faint variables with amplitudes ranging from hardly detectable to several tenths of a magnitude - which are usually present among the Blue Stragglers of many Galactic globular clusters. A sample of observed $\delta$ Scuti stars (Nemec & Mateo 1990; McNamara 2000) is shown in the M_V versus B-V diagram of Fig. 16, and compared to the theoretical instability strip. It is interesting to notice that, applying the fundamental-mode period-mass-luminosity-colour relation presented in Table 5, to the $\delta$ Scuti data (Nemec & Mateo 1990; McNamara 2000) and assuming Z=0.001, we can immediately estimate the pulsational masses for these variables, with a typical range between 1.2 and $1.8~M_\odot$.

Figure 16: Instability strips in the MV - (B-V) diagram, with the same notation as in Fig. 15. Isochrones of ages 15.8 Gyr and 10.0 Gyr are shown for Z=0 (continuous line) and Z=10-4 (from Girardi et al. 1996; dot-dashed line). Points correspond to observed $\delta$ Scuti stars in various galactic globular clusters and in the Carina DSph galaxy (Nemec & Mateo 1990, filled circles; McNamara 2000, starred symbols)

Open with DEXTER

A direct comparison with observations is presented in Fig. 16, showing isochrones representative of Pop-II (Z=10^-4) and Pop-III (Z=0; see the Appendix) stellar populations, for two values of the age, i.e. 10.0 Gry and 15.8 Gyr. These latter define the best range for the age of Galactic globular clusters, as recently reviewed by Carretta et al. (2000). We can see that in none of the four cases displayed, the turn-off region is located inside the instability strip, except for the Z=0, 10.0 Gyr old isochrone, which marginally intersects the red edge of the strip. However, we note that, since our calculations probably underestimate the red extension of the instability strip (see earlier in this section), there is still some possibility that the Z=0 isochrones for ages within the range under consideration will enter significantly into the red part of the instability strip. If this is indeed the case, then it implies that a large number of primordial pulsators could be present in the present era. Such stars would presumably be similar to $\delta$ Scuti variables but with lower masses at a given colour (since Z = 0 stars near the main-sequence are bluer and more luminous than solar metallicity stars of the same mass). They would also have longer periods at a given luminosity and colour (since pulsation period varies approximately as M^-0.5).

Will we ever detect them?

 

 

Table 5: Fitting relations for pulsational models. Coefficients are given for the fundamental mode, first and second overtone. Respective periods (P₀, P₁, and P₂) are expressed in days, masses and luminosities are in solar units, helium (Y) and metal (Z) abundances are by mass. Standard notation of the quantities is used

Mode	A	B	C	D	E	F	G	H	I
Blue Edge: $\log T_{\rm BE} {=} A {+} B{\times} Y {+} C{\times} Z {+} D{\times}(\log M) {+... ... L) {+} F{\times}(\log L)^2 {+} G{\times} Y(\log L)^2 {+} H{\times} Z(\log L)^2$
P0	3.928	2.985E-2	-5.021E-1	2.986E-2	-5.130E-2	-1.311E-3	5.915E-3	-2.319E-2
P1	3.962	-2.0117E-1	-6.903E-1	8.774E-2	-1.298E-2	-1.945E-2	3.073E-2	-2.658E-2
P2	3.936	4.816E-2	-8.542E-1	8.414E-2	-3.018E-2	-1.515E-2	1.758E-2	6.488E-2
Red Edge: log $T_{\rm BE} {=} A {+} B{\times} Y {+} C{\times} Z {+} D{\times}(\log M) {+} E{\... ... L) {+} F{\times}(\log L)^2 {+} G{\times} Y(\log L)^2 {+} H{\times} Z(\log L)^2$
P0	3.879	5.948E-2	2.274E-1	6.708E-2	-4.646E-2	-3.762E-3	-4.628E-4	-1.511E-1
P1	3.901	-7.233E-3	5.884E-2	6.731E-2	-4.071E-2	-6.632E-3	6.754E-3	-1.177E-1
P2	3.876	1.134E-1	-5.327E-1	2.224E-2	-3.824E-2	-3.246E-3	2.557E-3	3.747E-2
Blue Edge: $(B{-}V)_{\rm BE} {=} A {+} B{\times} Y {+} C{\times} Z {+} D{\times} (M_V) {+} ... ... G{\times}(M_V^2) {+} H{\times}(Y{\times} M_V^2) {+} I{\times}(Z{\times} M_V^2)$
P0	3.102E-1	-1.925E-1	5.349	-5.217E-2	4.720E-2	-2.590E-1	6.541E-3	-1.019E-2	1.516E-1
P1	-2.215E-1	1.653E	8.027	-3.594E-1	1.406	2.767	-2.355E-2	1.524E-1	7.409E-1
P2	1.062E-1	3.175E-1	4.482	-2.750E-1	1.004	2.314	-2.932E-2	1.664E-1	7.820E-1
Blue edge: $(V{-}I)_{\rm BE} {=} A {+} B{\times} Y {+} C{\times} Z {+} D{\times}(M_V) {+} E... ...imes}(M_V^{2}) {+} H{\times}(Y{\times} M_V^{2}) {+} I{\times}(Z{\times} M_V^{2}$)
P0	5.029E-1	-4.736E-1	2.331	-3.438E-2	-9.280E-2	-1.857E-1	6.263E-3	-2.051E-2	3.047E-2
P1	8.104E-2	8.586E-1	3.731	-2.736E-1	9.622E-1	1.408	-1.644E-2	1.071E-1	3.687E-1
P2	3.184E-1	-1.931E-1	1.809	-2.387E-1	7.655E-1	2.243	-2.424E-2	1.377E-1	6.635E-1
Red edge: $(B{-}V)_{\rm RE} {=} A {+} B{\times} Y {+} C{\times} Z {+} D{\times} (M_V) {+} ... ...} G{\times}(M_V^2) {+} H{\times}(Y{\times} M_V^2) {+} I{\times}(Z{\times} M_V^2$)
P0	3.349E-1	1.407E-1	4.187	-1.405E-1	3.711E-1	-1.638	-5.235E-3	5.933E-2	3.714E-1
P1	1.341E-1	8.584E-1	6.649	-2.564E-1	8.899E-1	1.708	-2.054E-2	1.237E-1	9.079E-1
P2	3.258E-1	7.263E-2	4.307	-1.777E-1	5.641E-1	2.764E-1	-1.799E-2	9.780E-2	2.353E-1
Red edge: $(V{-}I)_{\rm RE} {=} A {+} B{\times} Y {+} C{\times} Z {+} D{\times}(M_V) {+} E... ...} G{\times}(M_V^2) {+} H{\times}(Y{\times} M_V^2) {+} I{\times}(Z{\times} M_V^2$)
P0	5.525E-1	-1.107E-1	3.013E-1	-9.441E-2	1.655E-1	-1.415	-1.833E-3	3.032E-2	1.165E-1
P1	3.827E-1	4.601E-1	2.334	-1.970E-1	6.056E-1	1.088	-1.605E-2	8.835E-2	5.258E-1
P2	5.315E-1	-1.852E-1	6.837E-1	-1.495E-1	4.114E-1	1.909E-2	-1.790E-2	8.645E-2	2.669E-2
$\log P {=} A {+} B{\times}(\log L) {+} C{\times}(\log L)^2 {+} D{\times}\log M {+} E{\times}\log T_{\rm eff}$
P0	12.150	0.659	3.000E-2	-0.723	-3.567
P1	10.256	0.683	2.269E-2	-0.671	-3.112
P2	10.002	0.692	1.978E-2	-0.685	-3.070
$\log P {=} A{\times}\log M {+} B {+} C{\times} Z {+} D{\times} M_V {+} E{\times... ...\times}(Z^2{\times}(B-V)) {+} H{\times}(B-V)^2 {+} I{\times}(Z^2{\times}(B-V)^2$)
P0	-6.656E-1	-3.771E-1	-7.788	-3.411E-1	4.206E-1	6.834E-1	5.034E+2	1.095E-1	-2.927E+2
P1	-6.072E-1	-5.719E-1	-8.367	-3.254E-1	2.656E-1	8.998E-1	4.089E+2	-7.956E-2	-1.571E+2
P2	-5.760E-1	-7.067E-1	-1.016E+1	-3.099E-1	-4.138E-1	1.035	1.092E+3	-1.451E-1	-1.345E+3
$\log P {=} A{\times}\log M {+} B {+} C{\times} Z {+} D{\times} M_V{+} E{\times}... ...times}(Z^2{\times}(V-I)) {+} H{\times}(V-I)^2 {+} I{\times}(Z^2{\times}(V-I)^2$)
P0	-6.864E-1	-3.636E-1	-2.742	-3.347E-1	-8.353E-1	2.243E-1	1.317E+2	5.397E-1	-1.859E+2
P1	-6.103E-1	-5.764E-1	-5.814	-3.159E-1	-1.017	4.879E-1	2.659E+2	3.382E-1	-2.217E+2
P2	-5.661E-1	-7.197E-1	-6.262	-3.007E-1	-1.382	6.468E-1	6.420E+2	1.995E-1	-8.657E+2

Acknowledgements

It is a pleasure to thank B. Salasnich for his help with the evolutionary code, and A. Weiss for useful conversations on Pop-III stars. A sincere thank goes to the referee whose comments contributed to improving the presentation of the work. This study is funded by the Italian Ministry of University, Scientific Research and Technology (MURST) under contract "Formation and evolution of Galaxies'', No. 9802192401.

   
Appendix A: Tables of evolutionary tracks

The data tables for the present evolutionary tracks are available only in electronic format, either upon request to the authors, or by accessing a WWW site containing a complete data-base (including additional data and the future extensions) at http://pleiadi.pd.astro.it.

For each evolutionary track, the corresponding data file is organised into 21 columns with the following information:

1.

age/yr: stellar age in yr;

2.

logL: logarithm of surface luminosity (in solar units), $\log(L/L_{\odot})$;

3.

logTef: logarithm of effective temperature (in K), $\log~T_{\rm eff}$;

4.

grav: logarithm of surface gravity (in cgs units);

5.

logTc: logarithm of central temperature (in K);

6.

logrho: logarithm of central density (in cgs units);

7.

Xc,Yc: mass fraction of either hydrogen (up to the central H-exhaustion) or helium (later stages) in the stellar centre;

8.

Xc_C: mass fraction of carbon in the stellar centre;

9.

Xc_O: mass fraction of oxygen in the stellar centre;

10.

Q_conv: fractional mass of the convective core;

11.

Q_disc: fractional mass of the first mesh point where the chemical composition differs from the surface value;

12.

L_H/L: the luminosity provided by H-burning reactions as a fraction of the surface luminosity;

13.

Q1_H: fractional mass of the inner border of the H-rich region;

14.

Q2_H: fractional mass of the outer border of the H-burning region;

15.

L_He/L: the luminosity provided by He-burning reactions as a fraction of the surface luminosity;

16.

Q1_He: fractional mass of the inner border of the He-burning region;

17.

Q2_He: fractional mass of the outer border of the He-burning region;

18.

L_C/L: the luminosity provided by C-burning reactions as a fraction of the surface luminosity;

19.

L_nu/L: the luminosity lost by neutrinos (hence negative) as a fraction of the surface luminosity;

20.

Q_Tmax: fractional mass of the point with the highest temperature inside the star;

21.

stage: label indicating particular evolutionary stages.  

A number of evolutionary stages are indicated along the tracks (Col. 21), namely: the initial evolutionary stages (ZAMS or ZAHB), local maxima and minima of L and $T_{\rm eff}$ (Te-M, Te-m, L-M, and L-m), the exhaustion of central hydrogen (Xc=0) and helium (Yc=0), the lowest L and highest $T_{\rm eff}$ during the He-burning of intermediate-mass stars (Bhe and LpT, respectively), the base and tip of the first ascent of the red giant branch (Brg and Tip, respectively), the maximum L immediately preceding a thermal pulse (1tp), and the onset of C-burning (Cb). These stages delimit characteristic evolutionary phases, and can be useful for the derivation of physical quantities (as e.g. typical lifetimes) as a function of either mass or metallicity. Notice that some of these evolutionary stages may be absent from particular tracks, depending on the precise value of stellar mass and metallicity.

   
Appendix B: Tables of isochrones

Figure B.1: Theoretical isochrones in the HR diagram for the initial composition [Z=0, Y=0.23]. The age range goes from $\log(t/{\rm yr})=6.3$ to 10.2, at equally spaced intervals of $\Delta\log t=0.3$. In all isochrones, the main sequence is complete down to 0.7 $M_{\odot }$

From the tracks presented in this paper, we have constructed isochrones adopting the same algorithm of "equivalent evolutionary points'' as used in Bertelli et al. (1994) and Girardi et al. (2000). The initial point of each isochrone is a 0.7 $M_{\odot }$ model in the main sequence. The terminal stage of the isochrones corresponds either to stars at the beginning of the TP-AGB for ages 10⁸ yr, or to stars at C-ignition for 10⁸ yr. The youngest isochrones (up to 6 Myr) are basically limited to the main sequence stages, since at these ages the inclusion of more evolved stars would require tracks for  $M_{\odot }$, that will be presented in a forthcoming paper. Complete tables with the isochrones can be obtained upon request to the authors, or through the WWW site http://pleiadi.pd.astro.it. They cover the complete age range from about 2 Myr to 16 Gyr ( $6.3<\log(t/{\rm yr})<10.25$). Isochrones are provided at $\Delta\log t=0.05$ intervals; this means that any two consecutive isochrones differ by only 12 percent in their ages.

Figure B.1 shows some of these isochrones on the HRD, sampled at age intervals of $\Delta\log t=0.3$.

Theoretical luminosities and effective temperatures along the isochrones are translated to magnitudes and colors by using extensive tabulations of bolometric corrections and colors, as in Bertelli et al. (1994). The tabulations were obtained from convolving the spectral energy distributions contained in the $\rm [M/H]=-2.0$ library of stellar spectra of Kurucz (1992) with the response function of several broad-band filters. The response functions are from Buser & Kurucz (1978) for the UBV pass-bands, from Bessell (1990) for the R and I Cousins, and finally from Bessell & Brett (1988) for the JHK ones.

For each isochrone table, the layout is as follows: A header presents the basic information about the age and metallicity of each isochrone. Column 1 presents the logarithm of the age in yr; Cols. 2 and 3 the initial and actual stellar masses, respectively. We recall that the initial mass is the useful quantity for population synthesis calculations, since together with the initial mass function it determines the relative number of stars in different sections of the isochrones. Then follow the logarithms of surface luminosity (Col. 4), effective temperature (Col. 5), and surface gravity (Col. 6). From Cols. 7 to 15, we have the sequence of absolute magnitudes, starting with the bolometric one and following those in the UBVRIJHK pass-bands. In the last Col. (16), the indefinite integral over the initial mass M of the initial mass function (IMF) by number, i.e.

$$% \mbox{\sc flum} = \int\phi(M) \mbox{d} M$$ (B.1)

is presented, for the case of the Salpeter IMF, $\phi(M)=AM^{-\alpha}$, with $\alpha=2.35$. When we assume a normalization constant of A=1, FLUM is simply given by $\mbox{\sc flum} = M^{1-\alpha}/(1-\alpha)$. This is a useful quantity since the difference between any two values of FLUM is proportional to the number of stars located in the corresponding mass interval. It is worth remarking that FLUM relations can be derived for alternative choices of the IMF, by using the values of the initial mass we present in the Col. 2 of the isochrone tables.

We also provide summary tables containing basic information for the most significant stages along the isochrones. The evolutionary stages listed are, in sequence:

• TO: the turn-off point, i.e. the point of highest $T_{\rm eff}$ during the core-H burning phase;
• If present, Te-m and Te-M signal the coldest and hottest points, respectively, of stars in the overall contraction phase at the end of core-H burning;
• RGBb and RGBt: the base and tip of the RGB, respectively;
• BHeb: the beginning of the CHeB phase;
• If present, Te-m and Te-M signal the coldest and hottest points, respectively, for CHeB stars; For the youngest isochrones, Te-M represents the maximum extension of the Cepheid loop;
• EHeb: the end of the CHeB phase;
• In the oldest isochrones, L-M and L-m limit the luminosity range of early-AGB stars; this interval corresponds to the clump of early-AGB stars in colour-magnitude diagrams;
• 1TP: the beginning of the thermally pulsing AGB phase;
• Cb: the stage of C-ignition in the cases the AGB phase do not occur.

In addition, we provide tables with the integrated broad-band colours of single-burst stellar populations. Such tables are derived by integrating the stellar luminosities, weighted by the predicted number of stars in each bin, along the isochrones.

References

 
• Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 In the text NASA ADS  
• Alongi, M., Bertelli, G., Bressan, A., & Chiosi, C. 1991, A&A, 244, 95 In the text NASA ADS  
• Bader, G., & Deuflhard, P. 1983, Numerische Matematik, 33, 55  
• Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F, & Nasi, E. 1994, A&AS, 106, 275 In the text NASA ADS  
• Böhm-Vitense, E. 1958, Z. Astroph., 46, 108 In the text NASA ADS  
• Bond, J. R., Carr, B. J., & Arnett, W. D. 1982, Nature, 301, 584 In the text  
• Bond, J. R., Carr, B. J., & Arnett, W. D. 1983, Nature, 304, 514 In the text NASA ADS  
• Bono, G., Caputo, F., & Marconi, M. 1995, AJ, 110, 2365 In the text NASA ADS  
• Boothroyd, A. I., & Sackmann, I.-J. 1988, ApJ, 328, 632 In the text NASA ADS  
• Bressan, A., Bertelli, G., & Chiosi, C. 1981, A&A, 102, 25 In the text NASA ADS  
• Carr, B. J., Arnett, W. D., & Bond, J. R. 1982, in Supernovae: A survey of current research, Proc. of the Advanced Study Institute (Dordrecht: Reidel), 313 In the text  
• Carretta, E., Gratton, R., Clementini, G., & Fusi Pecci, F. 2000, ApJ, 533, 215 In the text NASA ADS  
• Cary, N. 1974, Astrophys. Space Sci., 31, 3 In the text  
• Castellani, V., Chieffi, A., & Tornambé, A. 1983, ApJ, 272, 249 In the text NASA ADS  
• Castellani, V., & Paolicchi, P. 1975, Astrophys. Space Sci., 185, 196 In the text  
• Cassisi, S., & Castellani, V. 1993, ApJS, 88, 509 (CC93) In the text NASA ADS  
• Cassisi, S., Castellani, V., & Tornambé, A. 1996, APJ, 459, 298 In the text NASA ADS  
• Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 In the text NASA ADS  
• Chieffi, A., & Tornambé, A. 1984, ApJ, 287, 745 In the text  
• Chiosi, C., Bertelli, G., & Bressan, A. 1992, ARA&A, 30, 305 In the text  
• Chiosi, C., & Maeder, A. 1986, ARA&A, 26, 329 In the text  
• Chiosi, C., Wood, P. R., & Capitanio, N. 1993, ApJS, 86, 541 In the text NASA ADS  
• D'Antona, F. 1982, A&A, 115, L1 In the text NASA ADS  
• Dominguez, I., Straniero, O., Limongi, M., & Chieffi, A. 1999, in The Changes in Abundances in Asymptotic Giant Branch Stars, to be published by MemSAIt, ed. F. D'Antona, & R. Gallino [astro-ph/9912425] In the text  
• El Eid, M. F., Fricke, K. J., & Ober, W. 1983, A&A, 119, 54 In the text NASA ADS  
• Ezer, D. 1972, Astrophys. Space Sci., 18, 226 In the text  
• Ezer, D., & Cameron, A. G. W. 1971, Astrophys. Space Sci., 14, 399 In the text  
• Feast, M. W. 1991, in Instabilities in Evolved Super and Hyper-Giants, ed. C. de Jager, & H. Nieuwenhuijzen, Amsterdam In the text  
• Forieri, C. 1982, Master Thesis, University of Padova, Italy In the text  
• Fujimoto, M. Y., Iben, I. Jr., Chieffi, A., & Tornambé, A. 1984, ApJ, 287, 749 In the text NASA ADS  
• Fujimoto, M. Y., Ikeda, Y., & Iben, I. Jr. 2000, ApJ, 529, L25 In the text NASA ADS  
• Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 In the text NASA ADS  
• Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 In the text NASA ADS  
• Graboske, H. C., de Witt, H. E., Grossman, A. S., & Cooper, M. S. 1973, ApJ, 181, 457 In the text NASA ADS  
• Haft, M., Raffelt, G., & Weiss, A. 1995, ApJ, 438, 1017 NASA ADS  
• Heger, A., Woosley, S. E., & Waters, R. 2000, in The First Stars, proc. of the MPA/ESO Workshop held at Garching, 4-6 august 1999, ESO Astrophysics Symposia (Springer), 121 In the text  
• Hubbard, W. B., & Lampe, M. 1969, ApJS, 18, 297 In the text NASA ADS  
• Hutchins, J. B. 1976, ApJ, 205, 103 In the text NASA ADS  
• Iglesias, C. A., & Rogers, F. J. 1993, ApJ, 412, 752 In the text NASA ADS  
• Jedamzik, K. 2000, in The First Stars, proc. of the MPA/ESO Workshop held at Garching, 4-6 august 1999, ESO Astrophysics Symposia (Springer), 15  
• Kippenhahn, R., Thomas, H.-C., & Weigert, A. 1965, Z. Astrophys., 61, 241 In the text NASA ADS  
• Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Springer-Verlag) In the text  
• Klapp, J. 1983, Astrophys. Space Sci., 93, 313 In the text  
• Klapp, J. 1984, Astrophys. Space Sci., 106, 215 In the text  
• Kudritzki, R. P. 1998, in Stellar Physics for the Local Group, proc. of the VIII Canary Islands Winter School of Astrophysics ed. A. Aparicio, A. Herrero, & F. Sanchez (Cambridge University Press), 149 In the text  
• Landré, V., Prantzos, N., Aguer, P., et al. 1990, A&A, 240, 85 In the text NASA ADS  
• McNamara, D. H. 2000, PASP, 112, 1096 In the text NASA ADS  
• Maeder, A., & Conti, P. S. 1994, ARA&A, 32, 227 In the text NASA ADS  
• Marigo, P. 2000, A&A, 360, 617 In the text NASA ADS  
• Nakamura, F., & Umemura, M. 1999, ApJ, 515, 239 In the text NASA ADS  
• Nakamura, F., & Umemura, M. 2000, in The First Stars, proc. of the MPA/ESO Workshop held in Garching, 4-6 August 1999, ESO Astrophysics Symposia (Springer), 263 In the text  
• Nakamura, F., & Umemura, M. 2001, ApJ, 548, 19 In the text NASA ADS  
• Nemec, J., & Mateo, M. 1990, in Confrontation between stellar pulsation and evolution, proc. of the Conference, held in Bologna, (May 1990), Astronomical Society of the Pacific, 64 In the text  
• Peimbert, M. 1996, Rev. Mex. A&A, 4, 55 In the text  
• Portinari, L., Chiosi, C., & Bressan, A. 1998, A&A, 334, 505 In the text NASA ADS  
• Reimers, D. 1975, Mem. Soc. R. Sci. Liège, Ser., 6, 8, 369 In the text NASA ADS  
• Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 In the text NASA ADS  
• Schlattl, H., Cassisi, S., Salaris, M., & Weiss, A. 2001, ApJ, submitted (MPA preprint No. 1345e) In the text  
• Silk, J. 1977, ApJ, 211, 638 In the text NASA ADS  
• Straniero, O. 1988, A&AS, 76, 157 In the text NASA ADS  
• Stothers, R. 1966, ApJ, 144, 959 In the text NASA ADS  
• Tohline, J. E. 1980, ApJ, 239, 417 In the text NASA ADS  
• Ober, W. W., El Eid, M. F., & Fricke, K. J. 1983, A&A, 119, 61 In the text NASA ADS  
• Olive, K. A. 1999 [astro-ph/9901231] In the text  
• Olive, K. A., Steigman, G., & Skillman, E. D. 1997, ApJ, 483, 788 In the text NASA ADS  
• Umeda, H., Nomoto, K., & Nakamura, T. 2000, in The First Stars, proc. of the MPA/ESO Workshop held at Garching, 4-6 august 1999, ESO Astrophysics Symposia (Springer), 150 In the text  
• Viegas, S. M., Gruenwald, R., & Steigman, G. 2000, ApJ, 531, 813 In the text NASA ADS  
• Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 In the text NASA ADS  
• Weaver, T. A., & Woosley, S. E. 1993, Phys. Rep., 227, 65 In the text NASA ADS  
• Weiss, A., Abel, T., & Hill, V. (eds.) 2000a, The First Stars, proc. of the MPA/ESO Workshop held at Garching, 4-6 august 1999, ESO Astrophysics Symposia (Springer) In the text  
• Weiss, A., Cassisi, S., Schlattl, H., & Salaris, M. 2000b, ApJ, 533, 413 In the text NASA ADS  
• Woosley, S. E., & Weaver, T. A. 1981, Ann. N.Y. Acad. Sci., 375, 357 In the text NASA ADS