A&A 371, 133-151 (2001)
DOI: 10.1051/0004-6361:20010316
Mineral formation in stellar winds
II. Effects of Mg/Si abundance variations on dust composition in AGB stars
A. S. Ferrarotti - H.-P. Gail
Institut für Theoretische Astrophysik,
Universität Heidelberg, Tiergartenstraße 15, 69121 Heidelberg,
Germany
Received 1 December 2000 / Accepted 27 February 2001
Abstract
Galactic F and G dwarf stars show a considerable
star-to-star scatter of their individual abundance ratios of Mg to Si. We study
the consequences of such abundance variations on the composition of the dust
mixture formed in the circumstellar dust shells if the stars enter the AGB stage
of stellar evolution.
From thermodynamic equilibrium condensation calculations for the abundant dust
components we find: (i) For
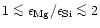 a mixture of forsterite (Mg2SiO4) and enstatite (MgSiO3) is
formed which consumes all of the available Mg and Si, (ii) for
a mixture of forsterite (Mg2SiO4) and enstatite (MgSiO3) is
formed which consumes all of the available Mg and Si, (ii) for
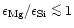 enstatite and quartz (SiO2) are formed,
while (iii) for
enstatite and quartz (SiO2) are formed,
while (iii) for
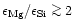 forsterite and
solid MgO are formed. According to observed Mg/Si abundance ratios, about 90%
of all stars fall into the first category, about 10% of all stars seem to fall
into the second category, and virtually no stars fall into the third category.
For the range of observed Mg/Si abundance ratios
forsterite and
solid MgO are formed. According to observed Mg/Si abundance ratios, about 90%
of all stars fall into the first category, about 10% of all stars seem to fall
into the second category, and virtually no stars fall into the third category.
For the range of observed Mg/Si abundance ratios
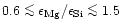 we have studied the formation of a multicomponent
mixture of dust in circumstellar dust shells by calculating simple stationary
wind models including the non-equilibrium condensation of enstatite, forsterite,
quartz, solid iron, and solid MgO. The variation of the composition of the
non-equilibrium mineral mixture with varying Mg/Si abundance ratio is studied.
The mineral mixture found to be formed under non-equilibrium conditions
is somewhat different from the chemical equilibrium composition, but follows
the general trends found in equilibrium calculations.
Particular emphasis is laid on stars with a low Mg/Si abundance ratio
(
we have studied the formation of a multicomponent
mixture of dust in circumstellar dust shells by calculating simple stationary
wind models including the non-equilibrium condensation of enstatite, forsterite,
quartz, solid iron, and solid MgO. The variation of the composition of the
non-equilibrium mineral mixture with varying Mg/Si abundance ratio is studied.
The mineral mixture found to be formed under non-equilibrium conditions
is somewhat different from the chemical equilibrium composition, but follows
the general trends found in equilibrium calculations.
Particular emphasis is laid on stars with a low Mg/Si abundance ratio
(
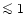 )
where quartz grains are shown to form a significant dust component
which should also be detectable by the absorption bands of quartz in the IR.
)
where quartz grains are shown to form a significant dust component
which should also be detectable by the absorption bands of quartz in the IR.
Key words: circumstellar matter - dust - stars: mass-loss - stars: winds
- stars: AGB and post-AGB
All stars with initial masses
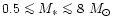 on the
main sequence finally evolve through the AGB stage of stellar evolution, shortly
before they become white dwarfs. During this stage of their evolution they
loose mass at an extremely high rate by a stellar wind and they develop
optically thick circumstellar dust shells by condensation of solid particulates
in the outflowing gas. The element mixture in the photospheric layers of the
star initially is oxygen rich with
on the
main sequence finally evolve through the AGB stage of stellar evolution, shortly
before they become white dwarfs. During this stage of their evolution they
loose mass at an extremely high rate by a stellar wind and they develop
optically thick circumstellar dust shells by condensation of solid particulates
in the outflowing gas. The element mixture in the photospheric layers of the
star initially is oxygen rich with
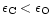 ,
as on
the main sequence. In this case the stars appear as Giants of spectral type M.
According to observation, such stars form silicate dust grains in the outflow,
and probably they also form some additional minerals. Stars with initial masses
in the range
,
as on
the main sequence. In this case the stars appear as Giants of spectral type M.
According to observation, such stars form silicate dust grains in the outflow,
and probably they also form some additional minerals. Stars with initial masses
in the range
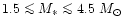 (e.g. Groenewegen et al. 1995) after a few thermal pulses on the AGB mix products of the
nuclear burning processes in their centre to the surface during the "third
dredge-up'' process. They develop through spectral type S, where
(e.g. Groenewegen et al. 1995) after a few thermal pulses on the AGB mix products of the
nuclear burning processes in their centre to the surface during the "third
dredge-up'' process. They develop through spectral type S, where
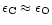 ,
to spectral type C (sometimes also denoted as spectral
type N) where
,
to spectral type C (sometimes also denoted as spectral
type N) where
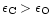 .
According to observations,
the carbon stars form soot and silicon carbide particles in their outflow, and
probably some other solid compounds.
.
According to observations,
the carbon stars form soot and silicon carbide particles in their outflow, and
probably some other solid compounds.
The chemical composition of the mineral mixture condensing in the cooling
outflow is determined by the abundance of such elements, which (i) form very
stable solid compounds which exist at temperatures of the order of 1000K
even at the low pressure conditions of circumstellar dust shells, and which (ii)
are sufficiently abundant to form dust in such quantities that emission from
this dust contributes in detectable amounts to the infrared emission from the
dust shell. Besides the obvious compositional differences between the
dominating dust components formed around Giants of spectral type M or C
(silicates for M stars, solid carbon and SiC for C stars) which are governed by
the considerable variation of the carbon to oxygen element abundance ratio
during evolution along the AGB, there may be further variations in the chemical
composition of the circumstellar dust due to abundance variations of the other
dust forming elements. In this paper we consider the composition of
circumstellar dust formed in the shells around giant stars of spectral type M,
where the abundances of C and O are not yet significantly changed by the "third
dredge-up'' episodes.
Detailed abundance determinations for AGB stars with respect to those elements
which form the main dust components in AGB stars of spectral type M seem not to
be available. Of particular interest for the formation of dust around M-type
stars are the abundances of the elements Si, Mg, and Fe and to some extent also
of Al, Ca, and Ni. Fortunately the nuclear electric charges of these elements
are big enough in order that the nuclei are not affected by nuclear processes in
the stellar burning zones during stellar evolution up to and on the AGB, which
involve charged particles. Temperatures in the burning zone are much too low
for an efficient processing of Mg, Si, and Fe. Additionally, the lighter nuclei
have low neutron capture cross sections such that the overall abundances of the light
elements also are not significantly modified by the s-process operating on the
thermally pulsing AGB. Further, the s-process consumes only a small fraction
of the Fe to form the heavy s-process nuclei. This allows us to use abundance
determinations for main sequence stars if we look for abundances of the dust forming elements on the AGB.
Systematic studies for element abundances of main sequence stars and their
dependence on metallicity, involving large samples of stars, are available for
galactical F and G stars. This range of spectral classes and associated main
sequence stellar masses is narrower than the range of initial masses of the
progenitors of AGB stars, which corresponds to main sequence stars of a spectral
type ranging roughly from late K to B3 (Lang 1992). However, stars of
the same metallicity, i.e. formed at roughly the same period of the
chemical evolution of the galaxy, should have all been formed with the same
initial chemical composition (and the same abundance variations, if such exist)
irrespective of their initial mass. Thus we can consider the abundances of the
dust forming elements in F and G type main sequence stars as representative (at
the same metallicity) for the abundances of these elements in AGB stars.
We refrain from the small metallicity gradients in the galaxy, which
makes a simple age-metallicity assignment somewhat difficult.
Two particular useful studies for our purpose are the abundance determinations
by Edvardson et al. (1993) and Chen et al. (2000) which give
abundances for the elements in which we are mainly interested in for a rather
big sample of stars. Their results show that the abundances of the dust forming
elements show a rather systematic variation of the abundances of Si, Fe, Al, and
Ca with metallicity and a scattering of the abundances of individual stars
around the mean which, however, is small. One cannot expect drastic variations
of the chemical composition of the dust mixture resulting from such limited
abundance variations. An important exception is magnesium which seems to show a
very large scattering of the Mg abundance for individual stars. This strong
scattering of individual Mg abundances is in sharp contrast to a rather uniform
Si abundance of all stars of the same metallicity. Since Mg and Si are the two
most important components for the formation of silicate dust in M-type AGB
stars, this may have severe consequences for the chemical composition of the
dust formed by such stars.
The studies of Edvardson et al. (1993) and Chen et al. (2000)
indicate, that Mg/Si abundance ratios for most of the stars with population I and
population II metallicities are evenly distributed in the interval
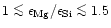 .
In this case sufficient
magnesium is available to condense the silicon completely in some type of
magnesium-silicate dust. A fraction of
.
In this case sufficient
magnesium is available to condense the silicon completely in some type of
magnesium-silicate dust. A fraction of
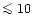 % of all stars with population
I and population II metallicity, however, seems to show magnesium abundances less
than their silicon abundances, in some extreme cases the Mg/Si abundance ratio
seems to be as low as 0.6, while e.g. the Solar System Mg/Si abundance ratio as
given by Anders & Grevesse (1989) is 1.08 and for the present
interstellar medium the data of Snow & Witt (1996) show
% of all stars with population
I and population II metallicity, however, seems to show magnesium abundances less
than their silicon abundances, in some extreme cases the Mg/Si abundance ratio
seems to be as low as 0.6, while e.g. the Solar System Mg/Si abundance ratio as
given by Anders & Grevesse (1989) is 1.08 and for the present
interstellar medium the data of Snow & Witt (1996) show
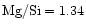 .
For
Mg/Si abundance ratios less than unity, the Si cannot completely be bound in
magnesium-silicates and some other dust species have to be formed. We shall show
that in this case quartz is formed as an additional dust component.
.
For
Mg/Si abundance ratios less than unity, the Si cannot completely be bound in
magnesium-silicates and some other dust species have to be formed. We shall show
that in this case quartz is formed as an additional dust component.
In the present paper we consider the consequences that follow from large variations
of the Mg/Si abundance ratio for the chemical composition of the dust in
circumstellar shells of objects with an oxygen rich chemistry. S and C stars are
not considered in this paper. The general principles of calculating
non-equilibrium dust formation are discusses in the first paper of this series
(Gail & Sedlmayr 1999, henceforth called Paper I).
The plan of this paper is as follows: in Sect. 2 we briefly discuss the
element abundances in AGB stars, in Sect. 3. we consider the chemical
equilibrium condensation in element mixtures with varying Mg/Si abundance ratios,
in Sect. 4 we discuss our model for calculating non-equilibrium dust
condensation, Sect. 5 presents results for the non-equilibrium dust mixture
formed in stationary stellar winds, Sect. 6 briefly discusses some consequences
for the IR spectra, and Sect. 7 contains some concluding remarks.
Table 1:
Abundances of some elements (by number relative to H) used in the
condensation calculations. Last column shows solar system abundances for
comparison
|
|
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2570f2.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg28.gif) |
Figure 1:
Magnesium and silicon abundances in galactic F and G dwarf stars. The two lines
correspond to
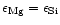 and
and
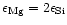 which bracket the Mg/Si abundance ratios for the
coexistence of olivine and pyroxene dust. Stars with abundances above the upper
limit line form no olivine dust but quartz and pyroxene dust. Stars with
abundances below the lower limit line cannot form pyroxene but would form
olivine and MgO dust. The cross in the lower right corner shows the estimated
order of magnitude of the error of the abundance determinations by Edvardsson et al. (1993) and Chen et al. (2000)
which bracket the Mg/Si abundance ratios for the
coexistence of olivine and pyroxene dust. Stars with abundances above the upper
limit line form no olivine dust but quartz and pyroxene dust. Stars with
abundances below the lower limit line cannot form pyroxene but would form
olivine and MgO dust. The cross in the lower right corner shows the estimated
order of magnitude of the error of the abundance determinations by Edvardsson et al. (1993) and Chen et al. (2000) |
| Open with DEXTER |
2 Element abundances on the AGB
On the AGB the element abundances of the lightest and the heaviest elements
significantly deviate from the abundances of these elements in the progenitor
stars on the main sequence due to mixing of nuclear processed material from the
burning zone to the stellar surface. The first and second dredge up processes
at the bottom of the Red Giant Branch (first dredge up) and at the bottom of the
Asymptotic Giant Branch (second dredge up) modify the abundances of He and of
CNO by mixing material having burnt H to He by the CNO cycle into the stellar
envelope. This slightly increases the He abundance. Since during H burning by
the CNO cycle the inventory of C, N, and O nuclei is converted into the
equilibrium isotopic mixture resulting from the CNO cycle, i.e. mainly into
14N, mixing of such material to the envelope increases the N abundance and
decreases the C and O abundances. After the second dredge up episode one
expects a composition like that shown in Table 1. The "solar''
values in the table correspond to the abundances given by Anders & Grevesse
(1989) and Grevesse & Noels (1993). The "AGB'' values are
determined as follows: for He, C, N, and O we scaled the standard abundances
according to the change in stellar surface abundances found in the evolutionary
calculations of Schaller et al. (1992) for stars of small and
intermediate masses. The CNO abundances determined in this way agree well with
the observationally determined mean abundances of these elements in AGB stars as
given by Smith & Lambert (1990, their Table 14).
As the star climbs up the AGB, at some instant the first thermal pulse occurs.
At the same time third dredge up starts which mixes (i) freshly produced carbon
from He burning and (ii) freshly produced s-process elements into the
envelope. This converts after a few pulse cycles the chemistry of the stellar
surface from an oxygen rich one into a carbon rich one for all stars whose
initial masses are between
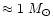 and
and
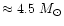 .
Stars with lower initial mass probably never become C-stars. More massive stars
convert the carbon, which is mixed from the He burning zone into the bottom
region of the outer envelope, via H burning by the CNO cycle into N (the "hot
bottom burning'' process) and retain their oxygen rich surface chemistry (cf.
Lattanzio & Forestini 1999).
.
Stars with lower initial mass probably never become C-stars. More massive stars
convert the carbon, which is mixed from the He burning zone into the bottom
region of the outer envelope, via H burning by the CNO cycle into N (the "hot
bottom burning'' process) and retain their oxygen rich surface chemistry (cf.
Lattanzio & Forestini 1999).
The abundances of nuclei with intermediate masses between the light nuclei
participating in the CNO cycle and its side paths at one hand and the heavy
nuclei beyond the iron peak on the other hand, are not affected by nuclear
burning processes in AGB stars. Central temperatures in AGB stars are too low
for proton capture to occur except for the lightest nuclei, and the medium mass
nuclei up to about the iron peak have low neutron capture cross sections and do
not participate in the s-process. This means that for the elements from Mg to
Ni the abundances of the abundant isotopes are not significantly affected by
nuclear processing on the AGB; these nuclei are mainly synthesised in
supernovae. Only some rare isotopes undergo significant abundance changes, for
instance the long lived unstable 26Al isotope is formed (e.g. Forestini
& Charbonnel 1997). The total abundances of the elements from Mg to Ni
in AGB stars, thus, are nearly identical to their initial abundances at the time
of formation of the progenitor star.
With respect to the formation of dust in the circumstellar shells of AGB stars
only the following elements are of interest: C, N, O, Mg, Al, Si, S, Ca, Fe,
and Ni, because only these are sufficiently abundant to participate in the
formation of observable quantities of dust. Less abundant elements like Ti, V,
Zr may be important for the formation of seed nuclei, however.
Abundance determinations of the elements Mg, Al, Si, S, Ca, Fe, and Ni for AGB
stars are scarce. The recent study of Edvardsson et al. (1993) with the
improvements by Tomkin et al. (1997) give abundances for the elements
of interest for a large sample of galactic F and G dwarf stars. The study of
Chen et al. (2000) give abundances of the relevant elements for a
considerable number of additional F and G dwarfs. The only exception is the
element S for which no abundance determinations are given, but sulphur probably
plays no role for dust formation in M-stars (but may be important for C-stars).
For the stars in common between the two studies we have used the data of
Edvardsson et al. (1993) and Tomkin et al. (1997) since
abundance differences for individual stars between the two sets of abundance
determinations are quite small. The error in the abundance determination for
individual stars in Edvardsson et al. (1993) has been estimated to be
at most of the order of
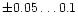 dex and the errors in Chen et al.
(2000) are of the same order of magnitude. The correlation between the
abundance ratios [Si/H] and [Mg/H], which are of particular interest for the
silicate dust formation, for the 235 stars from the studies of Edvardsson et al.
or Chen et al. where Mg and Si abundances both are determined, is shown in Fig. 1.
dex and the errors in Chen et al.
(2000) are of the same order of magnitude. The correlation between the
abundance ratios [Si/H] and [Mg/H], which are of particular interest for the
silicate dust formation, for the 235 stars from the studies of Edvardsson et al.
or Chen et al. where Mg and Si abundances both are determined, is shown in Fig. 1.
Abundances for some very metal poor stars have been given by Gratton & Sneden
(1988) and Magain (1987). The errors of the abundance
determinations are, however, much bigger then in the above mentioned studies (up to
0.15 for Gratton & Sneden and up to 0.26 for Magain). Figure 1
shows the ratios [Si/H] and [Mg/H] for 18 very metal poor stars for comparison.
The composition of the main dust components in M-stars is determined by the
abundances of the three elements Si, Mg, and Fe. The oxygen abundance in these
stars is so much higher than that of Si, Mg, and Fe that the formation of oxide
compounds is not limited by the amount of available O. Figure 1 shows the correlation between the abundances [Si/H] and
[Mg/H] for 177 stars from Edvardsson et al. (1993) and Tomkin et al.
(1997), 58 stars from Chen et al. (2000), 13 stars from Gratton
& Sneden (1988), and 5 stars from Magain (1987). Additionally
the figure shows the two lines where
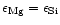 and
and
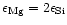 .
As is clearly seen, for stars with
population I and population II metallicities (the studies of Edvardsson et al.
and Chen et al.) the abundance ratio
.
As is clearly seen, for stars with
population I and population II metallicities (the studies of Edvardsson et al.
and Chen et al.) the abundance ratio
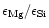 for
most stars is strongly concentrated in the region
for
most stars is strongly concentrated in the region
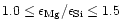 .
A small fraction of stars (
.
A small fraction of stars (
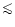 10%) have
Mg abundances less than the Si abundance down to
10%) have
Mg abundances less than the Si abundance down to
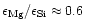 .
Only one star seems to show a Mg abundance
slightly in excess of twice the Si abundance. As we shall see below, the two
limits
.
Only one star seems to show a Mg abundance
slightly in excess of twice the Si abundance. As we shall see below, the two
limits
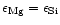 and
and
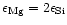 correspond to limits where a change of the mineral
composition of the circumstellar dust is to be expected.
correspond to limits where a change of the mineral
composition of the circumstellar dust is to be expected.
For the very metal poor stars (the studies of Gratton & Sneden, Magain) the Mg
abundance generally seems to be less than the Si abundance, in many cases even
much lower. In the following these stars are not considered, since it is not
clear whether they will form dust in their stellar wind if stars of such a low
metallicity enter the AGB stage of stellar evolution.
The cross in the lower right corner of Fig. 1 shows the
estimated maximum error of the abundance determinations according to Edvardsson
et al. (1993) and Chen et al. (2000). The scatter in the
Mg/Si abundance ratios considerably exceeds the errors in the abundance
determinations. This indicates large individual star-to-star variations of the
Mg/Si abundance ratio. Such variations might result, for instance, from strong
variations with initial mass of the progenitor star of the Mg/Si abundance
ratios in the ejecta of supernovae of type II (e.g. Thielemann et al.
1993) and incomplete mixing of interstellar material, or from varying
contributions of material from supernovae of type Ia which is very Mg poor (e.g.
Thielemann et al. 1993). The AGB giant stars which are descendants of
such dwarf stars can be expected to show the same range of Mg/Si abundance ratio
variations. Since this ratio determines the composition of the dust mixture in
an AGB star dust shell, considerable compositional variations of the mineral
mixture can be expected to occur.
Dust condensation in circumstellar dust shells occurs under conditions far
from a chemical equilibrium state. Nontheless, consideration of the equilibrium
condensation process is useful to determine the most stable condensates, since
these can be expected also to be the likely candidates for condensation in a
non-equilibrium state. Thus, we start with a determination of the composition
of the equilibrium mineral mixture if considerable deviations of the Mg/Si
abundance ratio from its value of 1.075 for the standard cosmic element
abundance occur.
The main dust components in AGB stars of spectral type M are those formed from
the most abundant of the refractory elements, i.e. Si, Mg, Fe. They form
together with oxygen some very stable compounds with high melting and boiling
temperatures. The less abundant elements Al, Ca, Na, Ti, Zr form some
condensates which are even more stable than the magnesium-iron-silicon
compounds, but their abundances are much too low to form dust in quantities
which can easely be detected by a contribution of such dust components to the
infrared emission from the circumstellar dust shell. Some of them may, however,
be important for the formation of seed nuclei.
For the standard cosmic element mixture numerous calculations of condensation
sequences (e.g. Grossman 1972;
Lattimer et al.
1978; Saxena & Ericksson 1986; Sharp & Huebner 1990;
Lodders & Fegley 1995; Lodders & Fegley 1999; Ebel & Grossman
2000) have shown that in chemical equilibrium forsterite with
composition Mg2SiO4, enstatite with composition MgSiO3, and free
metallic iron are the most stable condensates from the abundant elements. The
element mixture used in such calculations corresponds to a magnesium to silicon
abundance ratio for the standard cosmic element mixture of
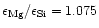 ,
if the latest abundance tabulation of Anders &
Grevesse (1989) and Grevesse & Noels (1993) is used, or to some
value close to this for other tabular values.
,
if the latest abundance tabulation of Anders &
Grevesse (1989) and Grevesse & Noels (1993) is used, or to some
value close to this for other tabular values.
If one considers in a thermodynamic equilibrium calculation that forsterite and
enstatite form solid solutions with their iron bearing counterparts, fayalite
with composition Fe2SiO4 and ferrosilite with composition FeSiO3,
respectively, it turns out that in equilibrium not the pure end-members of the
two solution series are the stable compounds but that olivine with composition
Mg2xFe2(1-x)SiO4 and pyroxene with composition
MgxFe1-xSiO3 are formed. However, in chemical equilibrium the iron
content is small, i.e. 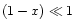 (e.g. Saxena & Ericksson 1986).
We neglect in our following considerations the small quantities of Fe bound in
olivine and pyroxene and consider only the pure compounds forsterite and
enstatite.
(e.g. Saxena & Ericksson 1986).
We neglect in our following considerations the small quantities of Fe bound in
olivine and pyroxene and consider only the pure compounds forsterite and
enstatite.
A mixture of forsterite and enstatite is obtained in chemical equilibrium only
if the magnesium to silicon abundance ratio satisfies the inequality
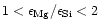 .
In principle forsterite is more
stable than enstatite, but forsterite requires two Mg atoms per Si atom for
its formation in contrast to enstatite, which requires only one. If
.
In principle forsterite is more
stable than enstatite, but forsterite requires two Mg atoms per Si atom for
its formation in contrast to enstatite, which requires only one. If
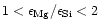 there is insufficient Mg available
in the element mixture to condense all Si atoms into the more stable
forsterite. In this case some enstatite is formed besides forsterite in such
quantities that at low temperatures forsterite and enstatite consume
all the available silicon and magnesium.
there is insufficient Mg available
in the element mixture to condense all Si atoms into the more stable
forsterite. In this case some enstatite is formed besides forsterite in such
quantities that at low temperatures forsterite and enstatite consume
all the available silicon and magnesium.
If
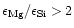 ,
more magnesium is present in the
mixture than can be bound in forsterite. No enstatite is formed in this case
and the excess magnesium forms some other stable compound, which turns out
to be solid MgO, which is well known to be very stable up to high temperatures.
,
more magnesium is present in the
mixture than can be bound in forsterite. No enstatite is formed in this case
and the excess magnesium forms some other stable compound, which turns out
to be solid MgO, which is well known to be very stable up to high temperatures.
If
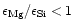 ,
insufficient quantities of magnesium
are available to condense all the silicon into enstatite. In this case at low
temperatures the formation of enstatite consumes all the available magnesium and
no forsterite is formed. The left over silicon forms some other stable silicon
compound. It turns out that this is quartz in this case, which also is a rather
stable compound.
,
insufficient quantities of magnesium
are available to condense all the silicon into enstatite. In this case at low
temperatures the formation of enstatite consumes all the available magnesium and
no forsterite is formed. The left over silicon forms some other stable silicon
compound. It turns out that this is quartz in this case, which also is a rather
stable compound.
The main features of the mineral mixture formed at different magnesium to
silicon abundance ratios are determined by stoichiometric requirements in
order to distribute Mg and Si between the most stable (forsterite) and second
most stable (enstatite) magnesium-silicon compounds, which consume Mg and Si
completely in the abundance ratio interval
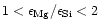 of their coexistence. Only outside this region some different Si or Mg
bearing compounds may be formed. The further details of the equilibrium
condensation have to be determined from a calculation of the equilibrium
mineral mixture by the methods of chemical thermodynamics.
of their coexistence. Only outside this region some different Si or Mg
bearing compounds may be formed. The further details of the equilibrium
condensation have to be determined from a calculation of the equilibrium
mineral mixture by the methods of chemical thermodynamics.
The less abundant elements Al and Ca form some very stable solid compounds
together with Si, Mg, and O. In the temperature region where forsterite is
stable these are mainly spinel (MgAl2O4) and diopside (CaMgSi2O6) or
anorthite (CaAl2Si2O8). Their formation consumes some fraction of the
elements Mg and Si which then are not available for the formation of other
magnesium and silicon compounds, since these Al and Ca compounds are more
stable. This shifts the above mentioned limits for the magnesium to silicon
abundance ratio to somewhat lower values, without changing the general picture.
We therefore arbitrarily assume for simplicity the Al and Ca to be completely
condensed into spinel and diopside and do not consider the details of the Al-Ca
chemistry (and of the less abundant elements), since these are unimportant for
our purposes.
We calculate the chemical composition of a mixture of solids and gas phase
species from two sets of equations: (i) the set of laws of mass action for
each of the individual species, and (ii) the constraints set by the abundances
of the elements.
For any gaseous or solid chemical compound with composition
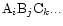 the chemical reaction of formation of this particular
compound from free atoms of the elements denoted by A, B, C, ... may be written as:
the chemical reaction of formation of this particular
compound from free atoms of the elements denoted by A, B, C, ... may be written as:
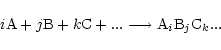 |
(1) |
In a state of chemical equilibrium the law of mass action for each of the
species reads as follows (Atkins
1994)
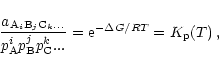 |
(2) |
where
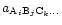 is the activity of the compound
is the activity of the compound
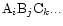 and
and 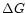 is the change of free enthalpy
in the formation of the compound from free gaseous atoms.
is the change of free enthalpy
in the formation of the compound from free gaseous atoms.
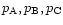 ,
... are the gas phase partial pressures of the free
atoms of the elements A, B, C, ...
,
... are the gas phase partial pressures of the free
atoms of the elements A, B, C, ...
If
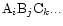 is a molecule from the gas phase, the
activity
is a molecule from the gas phase, the
activity
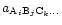 equals its partial pressure
equals its partial pressure
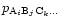 in the chemical equilibrium mixture
(Atkins 1994) and we have
in the chemical equilibrium mixture
(Atkins 1994) and we have
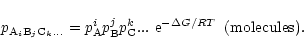 |
(3) |
If we have determined the partial pressures
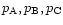 ,
... of the free atoms, the partial pressures of all molecules in the mixture are
uniquely determined by Eqs. (3).
,
... of the free atoms, the partial pressures of all molecules in the mixture are
uniquely determined by Eqs. (3).
If AiBjCk... is a solid, its activity in chemical equilibrium equals
unity (Atkins 1994) and we have
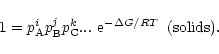 |
(4) |
This defines a relation between the partial pressures of the free atoms involved
in the formation for each of the solids existing in a state of chemical
equilibrium. For the solid compounds which are not stable for the given element
mixture and for given pressure P and temperature T, their activity calculated
from (2) satisfies
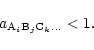 |
(5) |
Thus, in an equilibrium state the possible solid compounds which may be formed
from the given elements at pressure P and temperature T either satisfy
a=1, in which case they are present in the mixture, or they satisfy a<1, in
which case they are absent from the mixture.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{H2570f1.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg51.gif) |
Figure 2:
Lines of constant degree of condensation f of the abundant magnesium
and silicate compounds at
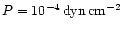 and varying abundance
ratio of magnesium to silicon. Full lines: forsterite. Dashed lines:
enstatite. Dotted lines: quartz. Dashed dotted lines: MgO. The
numbers at the lines denote the degree of condensation of the key element (Si
for forsterite, enstatite, and quartz; Mg for MgO) in the solid. The inset
shows the stability limits of the different condensates and the regions of
coexistence of different mineral mixtures. It is assumed that part of the Si
and Mg is bound in spinel and diopside
and varying abundance
ratio of magnesium to silicon. Full lines: forsterite. Dashed lines:
enstatite. Dotted lines: quartz. Dashed dotted lines: MgO. The
numbers at the lines denote the degree of condensation of the key element (Si
for forsterite, enstatite, and quartz; Mg for MgO) in the solid. The inset
shows the stability limits of the different condensates and the regions of
coexistence of different mineral mixtures. It is assumed that part of the Si
and Mg is bound in spinel and diopside |
| Open with DEXTER |
For each of the solids which may condense for a given element mixture we define
a degree of condensation f of that compound as the fraction of the nuclei of
some key element required for its formation that is bound in this solid. Usually
the least abundant of the elements required for the formation of the solid is
chosen as the key element. We denote the different elements by an index k.
Then we have an equation for the total number of nuclei for each element
which is of the form
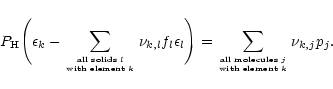 |
(6) |
Here 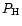 is the fictitious partial pressure of H nuclei.
is the fictitious partial pressure of H nuclei. 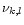 is
the number of atoms of element k in solid l per atom of the least abundant
of its constituents, and
is
the number of atoms of element k in solid l per atom of the least abundant
of its constituents, and
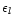 the element abundance of this element.
the element abundance of this element.
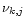 is the number of atoms of element k contained in molecule j.
The partial pressures pj of the molecules are expressed by means of the
law of mass action (3) by the partial pressures of the free
atoms. This set is completed by the equation
is the number of atoms of element k contained in molecule j.
The partial pressures pj of the molecules are expressed by means of the
law of mass action (3) by the partial pressures of the free
atoms. This set is completed by the equation
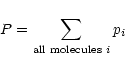 |
(7) |
for the total pressure P.
The set of Eqs. (6) and (7) together with an
equation of the form (2) for each of the solids is subject to the
condition that for each of the solids the solution of the equations satisfies:
- either a=1 and
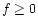 ,
,
- or f=0 and a<1.
The set of equations is solved for a state with given temperature T and
pressure P as follows: first we take advantage from the fact that hydrogen
and He are much more abundant than any other of the elements, that these two
elements do not condense under the conditions encountered in circumstellar
shells, and that at the rather low pressures and temperatures of interest only
H, H2, and He are present. Any compound of hydrogen with less abundant
elements can be neglected in calculating 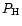 and P. Then we calculate
from the subset of equations
and P. Then we calculate
from the subset of equations
the partial pressure 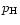 and the auxiliary quantity
and the auxiliary quantity 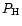 .
This
solution then is used in Eqs. (6) for all other elements.
.
This
solution then is used in Eqs. (6) for all other elements.
The remaining set of Eqs. (6) and (2) is solved
for the partial pressures of the free atoms of elements C, O, Mg, Si, S, and Fe
and for the degree of condensation f of the different possible condensates
formed from these elements. All other elements are not important for the
problem of determining the mixture of abundant minerals in chemical equilibrium
for M-star abundances, except that we have assumed that some fraction of Si and
Mg is consumed by complete condensation of Al and Ca into spinel and diopside.
The equations are solved numerically by Newton-Raphson iteration.
Polynomial approximations for calculating 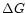 for the formation of
molecules and solids from free atoms are taken from Sharp & Huebner
(1990). For a number of molecules and solids not contained in that list
polynomial approximations for
for the formation of
molecules and solids from free atoms are taken from Sharp & Huebner
(1990). For a number of molecules and solids not contained in that list
polynomial approximations for 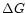 are taken from Tsuji (1973) or
polynomial approximations of the type used by Sharp & Huebner have been
calculated from data taken from the JANAF tables (Chase 1985). The error
in the JANAF data for HS detected by Ebel & Grossman (2000) has been
corrected.
are taken from Tsuji (1973) or
polynomial approximations of the type used by Sharp & Huebner have been
calculated from data taken from the JANAF tables (Chase 1985). The error
in the JANAF data for HS detected by Ebel & Grossman (2000) has been
corrected.
3.3 Results for the mineral mixture
The results for the mineral composition formed in chemical equilibrium for
different magnesium to silicon abundance ratios are shown in Fig. 2. The total gas pressure is assumed to equal
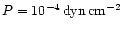 which is representative for the gas pressure in the
condensation zone of circumstellar dust shells (cf. Fig. 7 of Paper I, for
instance). Element abundances are those given by Anders & Grevesse
(1989) and Grevesse & Noels (1993) except that we have varied
the Mg/Si ratio between the limits
which is representative for the gas pressure in the
condensation zone of circumstellar dust shells (cf. Fig. 7 of Paper I, for
instance). Element abundances are those given by Anders & Grevesse
(1989) and Grevesse & Noels (1993) except that we have varied
the Mg/Si ratio between the limits
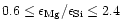 ,
which encompasses the region of Mg/Si ratios which may occur in AGB
stars.
,
which encompasses the region of Mg/Si ratios which may occur in AGB
stars.
The inset in Fig. 2 shows the stability limits and the
regions of existence for the different Mg-Si-condensates. Forsterite is the
most stable compound at any Mg/Si abundance ratio and the uppermost line
corresponds to its stability limit. Above this limit, none of the abundant
Mg-Si condensates exists, but only the much less abundant Al-Ca-condensates.
The upper stability limit of enstatite occurs at a slightly lower temperature.
Enstatite and forsterite coexist in the abundance ratio interval
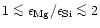 at all temperatures
below the stability limit of enstatite, and they coexist in the abundance ratio
region
at all temperatures
below the stability limit of enstatite, and they coexist in the abundance ratio
region
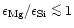 only in a small
temperature strip just below the stability limit of enstatite. The forsterite
disappears in the region
only in a small
temperature strip just below the stability limit of enstatite. The forsterite
disappears in the region
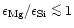 at a
certain limit temperature because enstatite takes up all the available Mg below
that limit.
at a
certain limit temperature because enstatite takes up all the available Mg below
that limit.
In the abundance ratio region
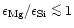 quartz is formed since only part of the Si can be bound in enstatite. Because
of the significantly less stability of quartz as compared to the magnesium
silicates, the upper stability limit of quartz appears approx. 30K below the
limit where forsterite disappears, such that there is a small intermediate
region where only enstatite exists. In the abundance ratio region
quartz is formed since only part of the Si can be bound in enstatite. Because
of the significantly less stability of quartz as compared to the magnesium
silicates, the upper stability limit of quartz appears approx. 30K below the
limit where forsterite disappears, such that there is a small intermediate
region where only enstatite exists. In the abundance ratio region
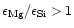 no quartz is present in the equilibrium
mineral mixture since Si forms the more stable forsterite and enstatite.
no quartz is present in the equilibrium
mineral mixture since Si forms the more stable forsterite and enstatite.
In the abundance ratio region
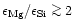 solid MgO is formed since only part of the Mg can be bound in
forsterite. MgO then takes up the excess Mg not bound in forsterite.
solid MgO is formed since only part of the Mg can be bound in
forsterite. MgO then takes up the excess Mg not bound in forsterite.
Figure 2 shows lines of constant degree of condensation fof the abundant dust species between the stability limit f=0 and the limit of
nearly complete condensation f=0.99, from which the details of the
equilibrium condensation process can be seen. Note that f is defined for a
particular condensate such that it describes the fraction of the key element
required for its formation which is bound in that condensate. For quartz,
forsterite and enstatite the key element is chosen to be Si, for solid MgO this
is Mg. Especially it can be seen from Fig. 2 how the
silicon and magnesium are distributed between forsterite and enstatite in
chemical equilibrium in the region of Mg/Si abundance ratios
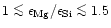 encountered in the
majority of stars.
encountered in the
majority of stars.
We have not shown the stability limit and degree of condensation of solid iron,
since iron condenses independently from the other minerals at a temperature
somewhat below that of olivine (see Fig. 2 of Paper I).
In circumstellar grains the iron content usually is different from zero,
though its precise value is not well known. Therefore, in the following, we
have not to deal with the pure end-members forsterite or enstatite of their
respective solution series, but with the iron bearing compounds olivine and
pyroxene, respectively.
We calculate models for the formation of dust in a spherically symmetric
stationary outflow from a nonvariable star. In view of the fact that most cool
giants on the AGB are large amplitude regular or semiregular variables where
shock waves regularly traverse the outer layers of the star, this assumption is
highly idealistic. A realistic treatment of multicomponent dust formation
problems including stellar pulsation, however, is presently not possible, and
stationary models such as that which are considered in the following are well
suited to study the basic principles of dust formation in circumstellar shells.
A comparison of some results of a model calculation (Winters et al.
1997) for a time-dependent model of dust condensation in a carbon star
(one dust component) with results for a model based on a stationary outflow
shows that the global characteristics of stationary models are not too different
from that of models including pulsation, though the details are quite
different. Stationary wind models are adequate, however, for the more luminous
supergiants where variability is not as important as on the AGB (Le Bertre &
Winters 1998).
The model for the stellar wind is the simplified model described in Paper I: we
assume the gas to flow with a constant velocity v0 of the order of the sonic
velocity into the dust forming layer of the circumstellar shell as long as the
gravitational pull of the star exceeds the radiation pressure on the gas-dust
mixture. Once the ratio
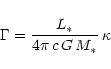 |
(11) |
of radiative to gravitational acceleration exceeds unity we solve the equation
of motion
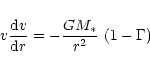 |
(12) |
for the outflow velocity v subject to the initial condition
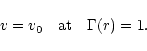 |
(13) |
M* is the stellar mass and L* the stellar luminosity. Note that 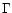 varies with distance from the star. In the dust free region one has
varies with distance from the star. In the dust free region one has
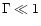 ,
after the onset of dust formation
,
after the onset of dust formation 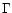 rapidly increases to
values
rapidly increases to
values 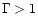 .
.
In the momentum Eq. (12) the pressure gradient is neglected in
order to avoid the necessity to integrate through the singular point of the
velocity equation, as it is explicitly done for instance in Gail & Sedlmayr
(1987). The explicit consideration of the singular point is an
unnecessary complication if the details of the dust nucleation process are
neglected, as it is done in the present paper.
The mass density in the outflow is calculated from the equation of mass
conservation
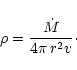 |
(14) |
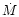 is the rate of mass-loss by the stationary outflow.
is the rate of mass-loss by the stationary outflow.
The parameters of the wind model are M*, L*, 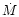 ,
and v0. The
choice of parameters is dictated by the circumstance, that we consider mass-loss
and dust formation on the AGB. In particular we wish to study the consequences of variations
of the abundance ratio of Mg to Si on dust formation in circumstellar shells of
AGB stars. We assume in our model calculation a stellar mass of
,
and v0. The
choice of parameters is dictated by the circumstance, that we consider mass-loss
and dust formation on the AGB. In particular we wish to study the consequences of variations
of the abundance ratio of Mg to Si on dust formation in circumstellar shells of
AGB stars. We assume in our model calculation a stellar mass of
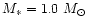 which is at the lower end of initial masses of AGB stars but considers
that the stars of interest already have lost part of their mass by a massive
stellar wind. Severe mass-loss and circumstellar dust shells are observed for
AGB stars if their luminosity has increased up to
which is at the lower end of initial masses of AGB stars but considers
that the stars of interest already have lost part of their mass by a massive
stellar wind. Severe mass-loss and circumstellar dust shells are observed for
AGB stars if their luminosity has increased up to
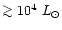 .
In our model calculation we assume
.
In our model calculation we assume
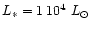 .
The effective
temperature of the star is assumed to be
.
The effective
temperature of the star is assumed to be
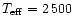 K. Typical
mass-loss rates observed for stars with dust shells cover a wide range. This
parameter is varied in the model calculations (see later). The initial velocity
v0 for integrating (12) is set to
K. Typical
mass-loss rates observed for stars with dust shells cover a wide range. This
parameter is varied in the model calculations (see later). The initial velocity
v0 for integrating (12) is set to
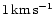 ,
which is of
the order of the sound velocity in the dust forming layer.
,
which is of
the order of the sound velocity in the dust forming layer.
4.2 Extinction by dust
The flux averaged mass extinction coefficient 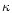 in
(11) is assumed to be given by
in
(11) is assumed to be given by
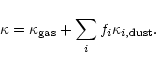 |
(15) |
The contributions
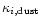 of all dust species i are approximated
by their Rosseland mean opacities. Additionally we have assumed that the
contributions of all the species simply add up, which generally is not valid for
the Rosseland mean, except in the case of grey extinction. Since the dust
extinction in the wavelength region where most of the stellar energy is emitted
(around
of all dust species i are approximated
by their Rosseland mean opacities. Additionally we have assumed that the
contributions of all the species simply add up, which generally is not valid for
the Rosseland mean, except in the case of grey extinction. Since the dust
extinction in the wavelength region where most of the stellar energy is emitted
(around
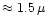 m) varies only slowly with wavelength, the dust
absorbs nearly grey and the calculation of
m) varies only slowly with wavelength, the dust
absorbs nearly grey and the calculation of 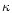 by simply adding up the
separate contributions of the different dust species is sufficiently accurate.
by simply adding up the
separate contributions of the different dust species is sufficiently accurate.
The mass extinction coefficient
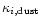 for the different dust
components is calculated by assuming that the least abundant of the elements
required for its formation is completely condensed into this dust species (for
silicate dust, for instance, this usually is the element Si). Since generally
condensation of the key element into dust is not complete, the extinction
coefficient
for the different dust
components is calculated by assuming that the least abundant of the elements
required for its formation is completely condensed into this dust species (for
silicate dust, for instance, this usually is the element Si). Since generally
condensation of the key element into dust is not complete, the extinction
coefficient
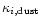 has to be multiplied by the fraction fi of
the key element, which really is condensed into dust species i (see Eq. (15)). This fi is determined by the calculation of dust
condensation.
has to be multiplied by the fraction fi of
the key element, which really is condensed into dust species i (see Eq. (15)). This fi is determined by the calculation of dust
condensation.
The mass extinction coefficients 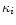 for the different dust species are
calculated from optical constants as described in Paper I and in Gail
(1998). For calculating the extinction by amorphous pyroxene we take
data for the complex index of refraction from Henning & Mutschke (1997)
for pyroxene with 30% iron content. The result for the Rosseland mean
extinction coefficient can be approximated quite accurately by
for the different dust species are
calculated from optical constants as described in Paper I and in Gail
(1998). For calculating the extinction by amorphous pyroxene we take
data for the complex index of refraction from Henning & Mutschke (1997)
for pyroxene with 30% iron content. The result for the Rosseland mean
extinction coefficient can be approximated quite accurately by
![\begin{displaymath}\kappa_{\rm py}=
\Biggl[\left(3.773\,10^{-5}~T^{2.017}\right)...
...}\,T^{2.272}\right)^4
}
\biggr\}^{-1}
\Biggr]^{-{1\over2}}.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img86.gif) |
(16) |
Similar expression for the other dust components are given in Paper I.
The temperature structure in the dust shell is calculated in the approximation
of Lucy (1971,1976)
![$\displaystyle T^4(r)=\frac12T_{\rm eff}^4\,\left[\,1-\sqrt{1-{R_*^2\over r^2}}+\frac32\tau_
{\mbox{\scriptsize L}}
\right].$](/articles/aa/full/2001/19/aah2570/img87.gif) |
|
|
(17) |
The optical depth
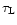 is determined by
is determined by
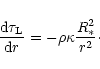 |
(18) |
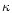 is the Rosseland mean mass extinction coefficient given by
(15). The differential equation for
is the Rosseland mean mass extinction coefficient given by
(15). The differential equation for
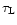 has to be solved
with the boundary condition
has to be solved
with the boundary condition
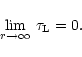 |
(19) |
This approximation assumes that there are no differences between the
gas temperature and any of the internal lattice temperatures of the different
dust species.
Dust condensation generally is a two-step process which starts with the
formation of tiny seed nuclei (probably of sizes of the order of a few nm),
which serve as growth centres for later growth to macroscopic grains. The
materials from which the seed nuclei are formed may either be the same material
as the material of the final dust grains (homogeneous dust formation), or the
final grains may be formed by growth of some kind of material on seed nuclei of
a different composition (heterogeneous dust formation).
Laboratory investigations of presolar carbon grains from carbon stars on the AGB
showed that these grains probably all grew by heterogeneous growth on TiC (or
ZrC) seed nuclei (Bernatowicz et al. 1996). TiC (ZrC) has an extremely
high equilibrium condensation temperature and is likely to condense prior to
carbon, since carbon growth kinetically is possible only for much lower
temperatures in the region of 900-1000K (cf. Cherchneff 1998),
very different from what chemical equilibrium calculations tell us (
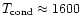 K).
K).
The situation with respect to dust formation in M-stars is unclear. Laboratory
results for presolar grains of the same type, as they are obtained for grains
from C-stars (Bernatowicz et al. 1996), do not exist for grains from
oxygen rich AGB stars. It is known since a long time that homogeneous silicate
dust formation is not possible and requires the formation of some different kind
of seed particle (e.g. Donn 1978; Gail & Sedlmayr 1986). From
theoretical considerations it is proposed by Gail & Sedlmayr (1998a,1998b) that in this case TiO2 seed nuclei are formed first, which then
serve as growth centres for all later condensates.
The detailed calculation of
the properties of TiO2 clusters (structures, bond energies, ...) and its
application to nucleation in a stellar wind by Jeong (2000) has shown,
that this mechanism could really be responsible for dust nucleation in M-stars.
The popular hypothesis that condensation occurs on corundum seed nuclei is
unfounded since small aluminium clusters have low bond energies and form only at
very low temperatures (Chang et al. 1998).
We do not consider in this paper the problem of nucleation but concentrate on
the growth process of dust grains formed from the most abundant refractory
elements. We assume that these grains all grow on some kind of seed particles
which are formed at a temperature above the upper limit temperature of stability
of the abundant dust species. The precise nature of these seed nuclei is not
specified in our calculation, but they might be TiO2 seed particles (cf.
Gail & Sedlmayr 1998b; Jeong 2000).
The basic equations for calculating the growth of dust grains and the
assumptions on which they rest are discussed in Paper I. Since some
modifications are required to treat dust condensation for arbitrary Mg/Si
abundance ratios, we briefly discuss the basic equations in the version used in
the present model calculation.
In chemical equilibrium the iron content of the Mg-Fe silicates is quite small
for temperatures above
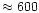 K, at most a few percent (e.g. Saxena &
Ericksson 1986), and can be neglected for the purpose of calculating
equilibrium abundances of the solids. This is no more true if condensation
occurs in a state far from equilibrium. In this case the silicates can take up
a considerable fraction of the iron and we have to consider the possibility that
olivine and pyroxene with a high content of Fe may be formed in the stellar
outflow.
K, at most a few percent (e.g. Saxena &
Ericksson 1986), and can be neglected for the purpose of calculating
equilibrium abundances of the solids. This is no more true if condensation
occurs in a state far from equilibrium. In this case the silicates can take up
a considerable fraction of the iron and we have to consider the possibility that
olivine and pyroxene with a high content of Fe may be formed in the stellar
outflow.
The olivine with composition Mg2xFe2(1-x)SiO4 grows by addition of
SiO, Mg, Fe to the surface of a grain and by oxidation with water vapour from
the gas phase. Other reactive species bearing Si, Mg, Fe, and O have
negligible abundances in the gas phase. The magnesium content, described by
x, can take any value
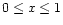 .
The thermally most stable composition
is a magnesium rich olivine with x close to unity (cf. Fig. 1 in Paper I).
The net reaction for olivine formation is
.
The thermally most stable composition
is a magnesium rich olivine with x close to unity (cf. Fig. 1 in Paper I).
The net reaction for olivine formation is
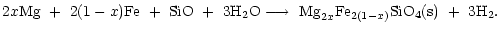 |
|
|
(20) |
The rate determining step for the total growth process may either be the
deposition of a SiO molecule to the surface, if sufficient Mg and Fe are
available to provide totally two Mg2+ and Fe2+ cations per Si atom to
be build into the olivine lattice, or the rate determining step is the addition
of Mg and Fe to a growing grain, if these ingredients are rare in the gas phase.
The deposition rates per unit time and surface area for a particle at rest with
respect to the gas phase are
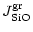 |
= |
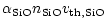 |
(21) |
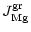 |
= |
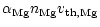 |
(22) |
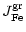 |
= |
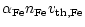 |
(23) |
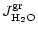 |
= |
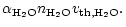 |
(24) |
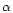 denotes the sticking coefficient, n is the particle density of the
growth species in the gas phase and v is the root mean square thermal velocity
of particles of mass m
denotes the sticking coefficient, n is the particle density of the
growth species in the gas phase and v is the root mean square thermal velocity
of particles of mass m
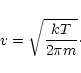 |
(25) |
If the rate determining step for silicate growth is SiO addition all
other deposition rates adjust to this rate and the growth rate for
spherical grains of radius a is
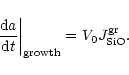 |
(26) |
V0 denotes the volume of the nominal monomer in the solid. This
requires that for each SiO molecule two Mg or Fe atoms (and three H2O
molecules) are deposited from the gas phase, i.e. we must have
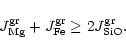 |
(27) |
If the deposition rate of Mg and Fe is less than
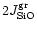 the addition of SiO and H2O to the growing grain adjusts to the
deposition rate of Mg and Fe and we have
the addition of SiO and H2O to the growing grain adjusts to the
deposition rate of Mg and Fe and we have
![\begin{displaymath}\left.\frac{{\rm d}a}{{\rm d}t}\right\vert_{\rm growth}=V_0 \...
...{1}{2}\left[J^{\rm gr}_
{\rm Mg}+J^{\rm gr}_{\rm Fe}\,\right].
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img108.gif) |
(28) |
The vapourisation rate of olivine by thermal decomposition is given by
(see Paper I)
 |
(29) |
where
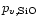 is the partial pressure of SiO molecules in
chemical equilibrium between the gas phase and olivine, corresponding to
reaction (20). The change of particle radius by this process is
is the partial pressure of SiO molecules in
chemical equilibrium between the gas phase and olivine, corresponding to
reaction (20). The change of particle radius by this process is
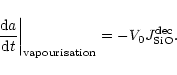 |
(30) |
The total change of particle radius is given by the sum of (26)
and (30) or by the sum of (28) and (30),
depending on whether (27) is satisfied or not, i.e., we have
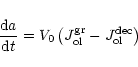 |
(31) |
where the growth rate of olivine is
![\begin{displaymath}J^{\rm gr}_{\rm ol}=\min\left(J^{\rm gr}_{\rm SiO} ,\ \frac{1...
...eft[J^{\rm gr}_
{\rm Mg}+J^{\rm gr}_{\rm Fe}\,\right]\right)
.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img113.gif) |
(32) |
The equation for the magnesium content x of the olivine is as in Paper I
![\begin{displaymath}\frac{{\rm d}x}{{\rm d}t}={3V_0\over a}\,\left[\left(x_g-x\ri...
...\rm ol}+\frac12
\left(J^{\rm ex}_+-J^{\rm ex}_-\right)\right].
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img114.gif) |
(33) |
The rate of exchange of Fe by Mg per unit surface area during collisions of
Mg with the grain surface is
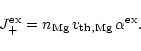 |
(34) |
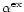 describes the probability of exchange of a Fe lattice atom
at the surface by a Mg atom from the gas phase during the
scattering process. The rate for the reverse reaction is
describes the probability of exchange of a Fe lattice atom
at the surface by a Mg atom from the gas phase during the
scattering process. The rate for the reverse reaction is
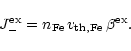 |
(35) |
In chemical equilibrium we have
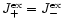 from which it
follows
from which it
follows
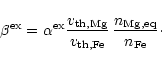 |
(36) |
The effective exchange rate then is
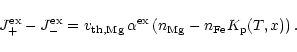 |
(37) |
 is defined by
is defined by
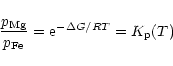 |
(38) |
as in Paper I.
These equations form our model for the growth of olivine grains from the gas
phase. As we have discussed above, we assume that the grains grow on some
kind of pre-formed seed nuclei. We then integrate the coupled system of
equations for the particle radius a of olivine grains and their composition
x starting at that point where
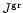 exceeds
exceeds
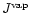 for
olivine.
for
olivine.
The growth of pyroxene has not been considered in Paper I. The equations
determining the growth of this species are obtained in complete analogy to the
case of olivine formation.
The pyroxene with composition MgxFe1-xSiO3 grows by addition of
SiO, Mg, Fe to the surface and by oxidation with water vapour from the gas
phase. The magnesium content, described by x, can take any value
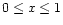 .
The thermally most stable composition is a magnesium rich pyroxene with xclose to unity, as in the case of olivine. The net chemical reaction for
pyroxene formation is
.
The thermally most stable composition is a magnesium rich pyroxene with xclose to unity, as in the case of olivine. The net chemical reaction for
pyroxene formation is
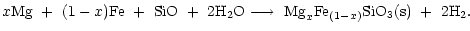 |
|
|
(39) |
If the rate determining step for pyroxene growth is SiO addition, as in the
case of olivine, we have in complete analogy to the previous case
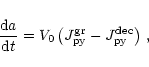 |
(40) |
where the growth rate of pyroxene is
![\begin{displaymath}J^{\rm gr}_{\rm py}=\min\left(J^{\rm gr}_{\rm SiO} ,\ \left[J^{\rm gr}_
{\rm Mg}+J^{\rm gr}_{\rm Fe}\,\right]\right)
.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img127.gif) |
(41) |
The equation for the magnesium content x of pyroxene is
![\begin{displaymath}\frac{{\rm d}x}{{\rm d}t}={3V_0\over a}\,\left[\left(x_g-x\ri...
...m gr}_{\rm py}+
\left(J^{\rm ex}_+-J^{\rm ex}_-\right)\right].
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img128.gif) |
(42) |
The only modification is that now there appears no factor 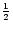 at the
exchange term. The quantities
at the
exchange term. The quantities
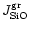 ,
,
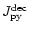 ,
,
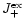 ,
and
,
and
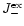 are defined analogously to the case of
olivine.
are defined analogously to the case of
olivine.
These equations form our model for the growth of pyroxene grains from the gas
phase. As we have discussed above, we assume that the grains grow on some kind
of pre-formed seed nuclei. We then integrate the coupled system of equations
for the particle radius a of pyroxene grains and their composition xstarting at that point where for the pyroxene
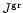 exceeds
exceeds
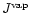 .
.
There exists the possibility that in a Si rich environment, as it is
encountered at the onset of grain growth in the circumstellar shell, the
olivine reacts with molecules from the gas phase and is converted into
pyroxene. Laboratory experiments on conversion of forsterite to enstatite have
shown that this process is likely to be controlled by Mg and Si diffusion
through the enstatite layer formed on top of the forsterite (Imae et al.
1993). The experimentally determined diffusion coefficient is
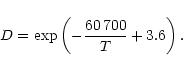 |
(43) |
The characteristic time required to convert a forsterite particle of size ainto an enstatite particle is
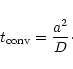 |
(44) |
For a 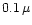 m sized particle one finds at a temperature of T=1000K,
representative for the dust forming layer, a time of
m sized particle one finds at a temperature of T=1000K,
representative for the dust forming layer, a time of
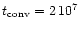 yr.
This is to be compared with the time required for the wind material to traverse
the dust forming layer, which is of the order of at most of one year. This type
of conversion process of olivine into pyroxene by solid diffusion, though in
principle possible, is kinetically strongly forbidden in circumstellar shells.
yr.
This is to be compared with the time required for the wind material to traverse
the dust forming layer, which is of the order of at most of one year. This type
of conversion process of olivine into pyroxene by solid diffusion, though in
principle possible, is kinetically strongly forbidden in circumstellar shells.
The particle growth of these dust components is treated as in Paper I. The
corresponding equations are given in Sect. 5.4 of that paper.
The degree of condensation of Si in olivine is determined by
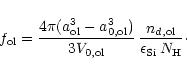 |
(45) |
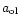 is the particle radius of the olivine grains,
is the particle radius of the olivine grains,
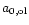 their
initial radius, i.e., the radius of the seed nucleus.
their
initial radius, i.e., the radius of the seed nucleus.
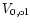 is
the volume of the monomer in the solid and
is
the volume of the monomer in the solid and
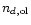 is the number of
olivine grains.
is the number of
olivine grains. 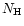 is the number of hydrogen nuclei, which is
determined from the mass density
is the number of hydrogen nuclei, which is
determined from the mass density 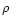 by
by
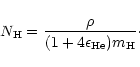 |
(46) |
Correspondingly, the degree of condensation of Si in pyroxene
is given by
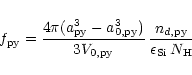 |
(47) |
and the degree of condensation of Si in quartz is
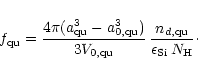 |
(48) |
The degree of condensation of Fe in iron grains is
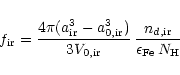 |
(49) |
and the degree of condensation of Mg in periclase (MgO) is
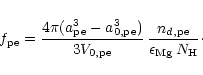 |
(50) |
These condensation degrees fi for the five dust species i considered in
our calculation are used in (15) to calculate the radiation
pressure.
For the growth species SiO, Mg, Fe, and H2O we can assume, that Mg and Fe are
present in the gas phase only as free atoms, that Si is present in the gas phase
only as SiO (we neglect that a small fraction of Si is present as SiS), and that
oxygen is present in the gas phase only as CO, SiO and H2O.
The particle density of H2O molecules in the gas phase then is given by
![$\displaystyle n_{\rm H_2O}=\Bigl[\epsilon_{\rm O}-\epsilon_{\rm C}-\left(1+3f_{...
...\rm qu}\right) \epsilon_{\rm Si}-f_{\rm pe}\epsilon_{\rm Mg}
\Bigr]N_{\rm H}\,,$](/articles/aa/full/2001/19/aah2570/img150.gif) |
|
|
(51) |
the particle density of SiO molecules by
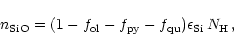 |
(52) |
the particle density of Fe atoms by
![$\displaystyle n_{\rm Fe}=\Bigl[\epsilon_{\rm Fe}(1-f_{\rm ir})-\left(2(1-x_{\rm...
...
f_{\rm ol}+(1-x_{\rm py})f_{\rm py}\right)\epsilon_{\rm Si}\Bigr]
N_{\rm H}\,,$](/articles/aa/full/2001/19/aah2570/img152.gif) |
|
|
(53) |
and the particle density of Mg atoms by
![\begin{displaymath}n_{\rm Mg}=\Bigl[\epsilon_{\rm Mg}(1-f_{\rm pe})-\left(2x_{\r...
...x_{\rm py}f_{\rm py}\right)\epsilon_{\rm Si}\Bigr]\,N_{\rm H}.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img153.gif) |
(54) |
These particle densities are used for calculating the growth rates.
Solving the equations for the growth of dust grains requires the prescription
of initial conditions. Our choice is as follows:
The equations of grain growth are solved from that point on outwards, where the
corresponding bulk condensate becomes stable. Since we assume that the grains
grow on some pre-formed seed nuclei, we prescribe as initial value for the grain
radius the radius of the seed nuclei. This radius is assumed for all dust
species to equal 1 nm. The number density of seed nuclei per H nucleus in the
wind is assumed for all dust species to equal 10-13 since the typical
number densities of grains in the outflow from M-stars observationally has been
determined to be of the order of a few times 10-13 (Knapp 1985).
As initial conditions for solving the Eqs. (33) and (42) for the magnesium content x of olivine and pyroxene,
respectively, we choose as in Paper I the solution of the corresponding
stationary Eqs. (33) and (42) for
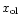 and
and
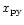 ,
respectively.
,
respectively.
The sticking coefficients 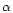 for olivine, iron and MgO are chosen as
described in Paper I. For pyroxene no experimental value for
for olivine, iron and MgO are chosen as
described in Paper I. For pyroxene no experimental value for 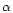 could be
found; for this reason we arbitrarily used the same sticking coefficient as for
olivine, though admittedly there is no special reason why both coefficients
should be equal.
could be
found; for this reason we arbitrarily used the same sticking coefficient as for
olivine, though admittedly there is no special reason why both coefficients
should be equal.
For quartz one finds very low sticking coefficients measured by means of
evaporation experiments. They all are determined from experiments performed at
rather high temperatures (e.g. Hashimoto 1990) and are probably not
applicable to SiO2 vapourisation under circumstellar conditions, where
temperatures are much lower.
More recently, experimental results for SiO2 vapourisation at much lower
temperatures in a H2-CO2 gas mixture have been presented by Mendybaev et al. (1998). The results labeled with IW-3 in their Fig. 2 seem to be
those which are applicable to silica vapourisation under circumstellar
conditions, since these results are consistent with the vapourisation rate for
low pressures (
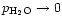 )
in their Fig. 3. We calculated a sticking
coefficient
)
in their Fig. 3. We calculated a sticking
coefficient 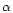 for the vapourisation of solid SiO2 from the relation
(cf. Eq. (29))
for the vapourisation of solid SiO2 from the relation
(cf. Eq. (29))
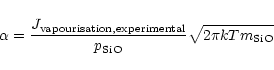 |
(55) |
where
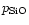 is the partial pressure of the SiO molecule
in chemical equilibrium with the solid. This assumes that ejection of a SiO
molecule from the surface is the rate determining step for vapourisation. From
the three data-points in Fig. 2 of Mendybaev et al. (1998) we obtain
sticking coefficients slightly in excess of 0.2 at temperatures around
1550K. Extrapolating these down to 1000K yields a sticking coefficient
of 0.07, but the extrapolation procedure is very uncertain. As a compromise we
choose in our model calculation for quartz a sticking coefficient of
is the partial pressure of the SiO molecule
in chemical equilibrium with the solid. This assumes that ejection of a SiO
molecule from the surface is the rate determining step for vapourisation. From
the three data-points in Fig. 2 of Mendybaev et al. (1998) we obtain
sticking coefficients slightly in excess of 0.2 at temperatures around
1550K. Extrapolating these down to 1000K yields a sticking coefficient
of 0.07, but the extrapolation procedure is very uncertain. As a compromise we
choose in our model calculation for quartz a sticking coefficient of
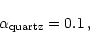 |
(56) |
which, however, can only be considered as a crude estimate.
Element abundances are chosen as in Anders & Grevesse (1989) and
Grevesse & Noels (1993) except for He, C, N, and O for which
AGB abundances according to Table 1 are used. The Mg abundance
is considered to be a free parameter and is varied in the calculations in order
to study the effects of different Mg/Si abundance ratios. No attempt is made to
calculate models for other metallicities.
We have calculated a set models for a stellar wind by solving simultaneously
the set of equations for the stellar wind and for the condensation and growth
of dust as described in the preceding section. We started the outwards
integration at the stability limit where the first of the dust species
condensing at the highest temperature starts to condense. In all cases
considered the first species to condense was found to be olivine. The
calculation then follows the path of a gas parcel on its way out. The initial
value of
 required for solving (18) was determined by a
multiple shooting method until the boundary condition (19) is
satisfied. The integrations were done by an Adams-Bashforth solver of third
order accuracy (e.g. Golub & Ortega 1992) which requires only one
evaluation of the r.h.s. of the equations for each time step. The time step
size was controlled by requiring that the most rapidly varying function changes
by about 3% in each time step.
required for solving (18) was determined by a
multiple shooting method until the boundary condition (19) is
satisfied. The integrations were done by an Adams-Bashforth solver of third
order accuracy (e.g. Golub & Ortega 1992) which requires only one
evaluation of the r.h.s. of the equations for each time step. The time step
size was controlled by requiring that the most rapidly varying function changes
by about 3% in each time step.
The diffusion equation for iron cations in olivine is solved as described in
Paper I.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f3ar.eps}\par\includegr...
...p]{H2570f3br.eps}\par\includegraphics[width=7cm,clip]{H2570f3cr.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg162.gif) |
Figure 3:
Distribution of the elements Si, Mg, and Fe between the solid
condensates and the gas phase. Wind model with standard element abundances and
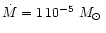 yr-1 yr-1 |
| Open with DEXTER |
First we present some results for a wind model with
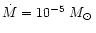 yr-1 and with standard element abundances for M stars on the AGB (cf.
Sect. 2) since the inclusion of pyroxene in calculating
the non-equilibrium dust mixture is new. Figure 3 shows the
degree of condensation of the three most important dust forming elements in M
stars.
yr-1 and with standard element abundances for M stars on the AGB (cf.
Sect. 2) since the inclusion of pyroxene in calculating
the non-equilibrium dust mixture is new. Figure 3 shows the
degree of condensation of the three most important dust forming elements in M
stars.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f4ar.eps}\par\includegr...
...p]{H2570f4br.eps}\par\includegraphics[width=7cm,clip]{H2570f4cr.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg165.gif) |
Figure 4:
Distribution of the elements Si, Mg, and Fe between the solid
condensates and the gas phase. Wind model with standard element abundances and
a high mass loss rate of
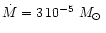 yr-1 yr-1 |
| Open with DEXTER |
Figure 3a shows the distribution of Si between the gas phase
and the three Si bearing condensates considered in this model calculation:
olivine, pyroxene, and quartz. In the standard case with a magnesium to silicon
abundance ratio of
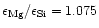 ,
the most
abundant Si bearing species in a non-equilibrium condensation model is olivine
while pyroxene is formed in significantly less quantities. This is in sharp
contrast to the results of chemical equilibrium calculations where for this
element mixture pyroxene would be the dominating condensed silicate species.
The reason for this different condensation behaviour in a stellar wind and in
the idealised case of chemical equilibrium is the result of two circumstances:
,
the most
abundant Si bearing species in a non-equilibrium condensation model is olivine
while pyroxene is formed in significantly less quantities. This is in sharp
contrast to the results of chemical equilibrium calculations where for this
element mixture pyroxene would be the dominating condensed silicate species.
The reason for this different condensation behaviour in a stellar wind and in
the idealised case of chemical equilibrium is the result of two circumstances:
- 1.
- Olivine is the more stable one of the two substances and for
this reason starts to condense first;
- 2.
- Radiation pressure rapidly accelerates the wind material to a highly
supersonic outflow velocity once the first strongly absorbing material has
condensed to such an extent that
 ,
defined by Eq. (11),
exceeds unity (this requires a degree of condensation of the order of f=0.1 in
case of the silicates).
,
defined by Eq. (11),
exceeds unity (this requires a degree of condensation of the order of f=0.1 in
case of the silicates).
Since olivine condenses first, the degree of condensation of pyroxene lags
somewhat behind that of olivine, though the growth conditions for both
substances are similar. The rapid acceleration of the wind, once the degree of
condensation of olivine exceeds the limit
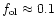 ,
rapidly
expands and dilutes the wind material. The growth conditions for olivine and
pyroxene become unfavourable because of the rapidly decreasing collision rate
with growth species from the gas phase and grain growth effectively ceases
before the condensible material from the gas phase is exhausted. Under these
circumstances pyroxene formation is strongly suppressed. A significant fraction
of the silicon is left over as SiO molecule in the gas phase: in a wind model
with our present choice of parameters nearly 15% of the silicon.
,
rapidly
expands and dilutes the wind material. The growth conditions for olivine and
pyroxene become unfavourable because of the rapidly decreasing collision rate
with growth species from the gas phase and grain growth effectively ceases
before the condensible material from the gas phase is exhausted. Under these
circumstances pyroxene formation is strongly suppressed. A significant fraction
of the silicon is left over as SiO molecule in the gas phase: in a wind model
with our present choice of parameters nearly 15% of the silicon.
A small fraction ( 2% in the present model) condenses as quartz. In
chemical equilibrium this substance would not be formed in a mixture with the
standard Mg/Si abundance ratio since olivine and pyroxene both are more stable
than quartz and since sufficient Mg is available to condense the Si completely
into these two compounds. During the non-equilibrium condensation process in a
stellar wind, however, the quartz first starts to condense at an only slightly
lower temperature than olivine. Since during the early phase of the
condensation and particle growth process sufficient SiO molecules are available
from the gas phase, all silicate compounds grow independently from each other
from the gas phase as long as the gas phase remains strongly supersaturated with
respect the different condensates.
2% in the present model) condenses as quartz. In
chemical equilibrium this substance would not be formed in a mixture with the
standard Mg/Si abundance ratio since olivine and pyroxene both are more stable
than quartz and since sufficient Mg is available to condense the Si completely
into these two compounds. During the non-equilibrium condensation process in a
stellar wind, however, the quartz first starts to condense at an only slightly
lower temperature than olivine. Since during the early phase of the
condensation and particle growth process sufficient SiO molecules are available
from the gas phase, all silicate compounds grow independently from each other
from the gas phase as long as the gas phase remains strongly supersaturated with
respect the different condensates.
![\begin{figure}
\par\mbox{\includegraphics[width=8cm,clip]{H2570f5ar.eps}\hspace{...
....eps}\hspace{1cm}
\includegraphics[width=8cm,clip]{H2570f5dr.eps} }
\end{figure}](/articles/aa/full/2001/19/aah2570/Timg168.gif) |
Figure 5:
Radial variation of the degree of condensation f of the abundant
dust components for different Mg/Si
abundance ratios for a stellar wind model with
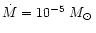 yr-1 yr-1 |
| Open with DEXTER |
If the system would evolve towards a chemical equilibrium state, the silicon
supply from the gas phase finally becomes exhausted. The partial pressure of
SiO in the gas phase drops below the saturation pressure of the least stable
species, in this case quartz, and this species then starts to vapourise until
it finally disappears in favour of the more stable compounds with a lower
saturation pressure of SiO in the gas phase. In this way finally only the most
stable compounds survive if the system approaches the chemical equilibrium
state. However, this is exactly what does not happen in a stellar wind.
The evolution towards a chemical equilibrium state is suppressed in a stellar
wind because of rapid acceleration of the dusty gas by radiation pressure and
the subsequent rapid dilution of the wind material. This freezes some early
transition state reached somewhere during the condensation process before the
growth species become strongly depleted.
For this reason, a small quantity of quartz can be formed in a stellar wind and
this is also the reason why olivine and not pyroxene is the dominating condensed
silicate species. Generally, this means, that the results of chemical
equilibrium calculations cannot be taken too literally with respect to the
existence or non-existence of specific solids, because the dust mixture in
circumstellar shells represents a frozen in transition state!
Figure 3b shows the distribution of Mg between the gas phase
and the three Mg bearing condensates considered in this model calculation:
olivine, pyroxene, and periclase (MgO). According to equilibrium condensation
calculations, no periclase is formed in the standard element mixture. In our
wind model most of the magnesium is consumed in the formation of the silicates.
Periclase is found in the non-equilibrium condensation calculation to be formed
in completely negligible quantities. The reason is, that MgO becomes stable
only at a temperature where already a significant amount of the Si is condensed
in silicates. Growth of significant amounts of solid MgO then is prevented by
the rapid dilution of the wind material.
Figure 3c shows the distribution of Fe between the gas phase
and the three Fe bearing condensates considered in this model calculation:
olivine, pyroxene, and solid iron. The silicates consume only part of the iron,
because iron poor silicates are more stable than iron rich silicates. The iron
content of the non-equilibrium condensates considerably exceeds the iron content
in case of chemical equilibrium, however. Solid iron is formed only in small
quatities, since iron starts to condense at a temperature where already
significant amounts of silicates are condensed. Again the rapid dilution of the
wind material prevents efficient condensation of solid iron.
Figure 4 shows the distribution of elements between
the gas phase and solids for a model with a much higher mass loss rate
of
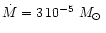 yr-1. In this case only one dust
component forms in significant quantities, and this is olivine. Due to its
early formation and due to rapid grain growth in the high density wind its
formation accelerates the wind material by radiation pressure on grains to
supersonic outflow velocities before any other material had a chance to condense
in significant amounts. This demonstrates how the early formation of an
abundant dust material suppresses any condensation of additional dust species in
a stellar wind. Coexistence of significant amounts of more than one dust
species seems to be possible only for a not too high mass-loss rates or if an
abundant first condensate is only an inefficient absorber for stellar radiation.
yr-1. In this case only one dust
component forms in significant quantities, and this is olivine. Due to its
early formation and due to rapid grain growth in the high density wind its
formation accelerates the wind material by radiation pressure on grains to
supersonic outflow velocities before any other material had a chance to condense
in significant amounts. This demonstrates how the early formation of an
abundant dust material suppresses any condensation of additional dust species in
a stellar wind. Coexistence of significant amounts of more than one dust
species seems to be possible only for a not too high mass-loss rates or if an
abundant first condensate is only an inefficient absorber for stellar radiation.
Next we consider the dependence of the mineral mixture in the dust shell on the
abundance ratio of magnesium to silicon. We concentrate on abundance ratios of
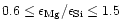 since this is the domain of Mg/Si
ratios which are likely to occur in AGB stars. In the model calculations the Si
abundance is held fixed and the Mg abundance is varied since variations of the
Mg/Si ratio are mainly due to the scattering in Mg abundances (cf. Edvardsson et al. 1993). Figure 1 indicates that also somewhat higher
abundance ratios may be found and for one star a ratio slightly exceeding a value
of two is found, but one may doubt whether such high Mg/Si abundance ratios are
real.
since this is the domain of Mg/Si
ratios which are likely to occur in AGB stars. In the model calculations the Si
abundance is held fixed and the Mg abundance is varied since variations of the
Mg/Si ratio are mainly due to the scattering in Mg abundances (cf. Edvardsson et al. 1993). Figure 1 indicates that also somewhat higher
abundance ratios may be found and for one star a ratio slightly exceeding a value
of two is found, but one may doubt whether such high Mg/Si abundance ratios are
real.
Figure 5 shows the results of model calculations for a set of
wind models with varying Mg/Si abundance ratios and a fixed mass-loss rate of
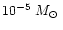 yr-1. The radial variation of the degree of
condensation of the most abundant dust components olivine, pyroxene, solid iron
and quartz is shown for different values of
yr-1. The radial variation of the degree of
condensation of the most abundant dust components olivine, pyroxene, solid iron
and quartz is shown for different values of
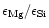 .
The relative abundance of these dust components is quite different from
what is expected from equilibrium calculations.
.
The relative abundance of these dust components is quite different from
what is expected from equilibrium calculations.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f6c.eps}\par\includegra...
...lip]{H2570f6b.eps}\par\includegraphics[width=7cm,clip]{H2570f6a.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg172.gif) |
Figure 6:
Radial variation of the degree of condensation f of the abundant
dust components for a magnesium-poor element mixture with
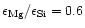 for stellar wind models with three different mass-loss
rates of
for stellar wind models with three different mass-loss
rates of
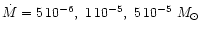 yr-1(from top to bottom) yr-1(from top to bottom) |
| Open with DEXTER |
(a) Considerable amounts of olivine are formed even for
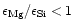 though this mineral according to the results of Sect. 3.3 should exist in a small temperature interval just below its
stability limit only. The high olivine abundance results from the effect
discussed above, that olivine as the most stable silicate is the first of the
silicate minerals to condense and this rapidly accelerates the outflowing gas,
which prevents the system to evolve into the equilibrium state. The quantities
of pyroxene formed increase with decreasing Mg/Si abundance ratio for
though this mineral according to the results of Sect. 3.3 should exist in a small temperature interval just below its
stability limit only. The high olivine abundance results from the effect
discussed above, that olivine as the most stable silicate is the first of the
silicate minerals to condense and this rapidly accelerates the outflowing gas,
which prevents the system to evolve into the equilibrium state. The quantities
of pyroxene formed increase with decreasing Mg/Si abundance ratio for
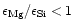 ,
but pyroxene never is the dominating
magnesium-silicate dust species for
,
but pyroxene never is the dominating
magnesium-silicate dust species for
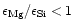 ,
as
suggested by chemical equilibrium calculations, because the early formation of
olivine and the subsequent wind acceleration by radiation pressure on olivine
hampers efficient pyroxene growth.
,
as
suggested by chemical equilibrium calculations, because the early formation of
olivine and the subsequent wind acceleration by radiation pressure on olivine
hampers efficient pyroxene growth.
(b) For
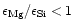 quartz is formed as a
significant dust component, as is to be expected from the results for the chemical
equilibrium condensation. It is, however, not formed in such big quantities as
it is suggested by chemical equilibrium. The reason, again, is the early
condensation of olivine which reduces the efficiency of condensation of the less
stable dust species. In any case, our results show that quartz is formed in
such quantities that this mineral should be a detectable dust component in
objects with low Mg/Si abundance ratios. This is shown in Sect. 6. The condensation of quartz does not vanish for
quartz is formed as a
significant dust component, as is to be expected from the results for the chemical
equilibrium condensation. It is, however, not formed in such big quantities as
it is suggested by chemical equilibrium. The reason, again, is the early
condensation of olivine which reduces the efficiency of condensation of the less
stable dust species. In any case, our results show that quartz is formed in
such quantities that this mineral should be a detectable dust component in
objects with low Mg/Si abundance ratios. This is shown in Sect. 6. The condensation of quartz does not vanish for
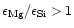 as in the case of chemical equilibrium, but in this
Mg/Si abundance ratio region the quantities of quartz formed in Mg rich objects
is very small. The reason that quartz is formed after all is the
non-equilibrium effect discussed in the preceding section.
as in the case of chemical equilibrium, but in this
Mg/Si abundance ratio region the quantities of quartz formed in Mg rich objects
is very small. The reason that quartz is formed after all is the
non-equilibrium effect discussed in the preceding section.
(c) Considerable amounts of metallic iron are formed as a separate dust
component in our model calculation. Most of the iron, however, is bound in
olivine and pyroxene. Only for the models with lowest Mg/Si abundance ratios
more iron is present in form of iron grains than is bound in
magnesium-iron-silicates. The increase of the degree of condensation of iron
with decreasing
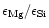 results from the decrease
in the quantities of olivine formed with decreasing
results from the decrease
in the quantities of olivine formed with decreasing
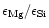 which then less efficiently reduces the efficiency of
condensation of the less stable dust species.
which then less efficiently reduces the efficiency of
condensation of the less stable dust species.
Figure 6 shows the radial variation of the degree of
condensation f of the different minerals for a magnesium-poor element mixture
with
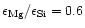 for wind models with three
different mass loss rates. This Mg/Si abundance ratio is at the lowest end of
Mg abundances which might occur in stars with population I and II metallicities
and represents the most extreme case which possibly can be found in
observations.
for wind models with three
different mass loss rates. This Mg/Si abundance ratio is at the lowest end of
Mg abundances which might occur in stars with population I and II metallicities
and represents the most extreme case which possibly can be found in
observations.
The top picture of Fig. 6 shows the mineral mixture for
a wind model with
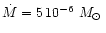 yr-1. In this model the
low density of the outflowing gas results in a rather slow growth of dust. The
wind then is not yet strongly accelerated by radiation pressure on silicate
grains once the outflowing material enters the temperature regime where iron
condensation becomes possible. The high sticking efficiency near unity typical
for growth of metals then results in a much more rapid growth of the iron than
of the other mineral species. As a result, radiation pressure on iron dust and
subsequent strong acceleration of the wind material then hampers the further
growth of the other dust components.
yr-1. In this model the
low density of the outflowing gas results in a rather slow growth of dust. The
wind then is not yet strongly accelerated by radiation pressure on silicate
grains once the outflowing material enters the temperature regime where iron
condensation becomes possible. The high sticking efficiency near unity typical
for growth of metals then results in a much more rapid growth of the iron than
of the other mineral species. As a result, radiation pressure on iron dust and
subsequent strong acceleration of the wind material then hampers the further
growth of the other dust components.
The middle picture of Fig. 6 shows the mineral mixture for a wind model with
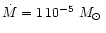 yr-1. It shows in a different way the
mineral mixture also shown in Fig. 5.
yr-1. It shows in a different way the
mineral mixture also shown in Fig. 5.
The bottom picture of Fig. 6c shows the mineral mixture for
a wind model with
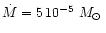 yr-1. The rather
fortunate growth conditions in a high-mass-loss wind favours rapid grain growth
and especially the early growth of olivine. The olivine then is the most
abundant mineral which forms first and hampers efficient growth of the less
stable minerals. Nevertheless pyroxene and quartz are formed in non-negligible
quantities. The formation of iron grains, however, is efficiently suppressed
because of the lower condensation temperature of iron. If the outflowing gas
enters the temperature regime where iron becomes stable, the preceding formation
of the other dust species has accelerated the wind to such an extent, that
efficient dust growth is no more possible.
yr-1. The rather
fortunate growth conditions in a high-mass-loss wind favours rapid grain growth
and especially the early growth of olivine. The olivine then is the most
abundant mineral which forms first and hampers efficient growth of the less
stable minerals. Nevertheless pyroxene and quartz are formed in non-negligible
quantities. The formation of iron grains, however, is efficiently suppressed
because of the lower condensation temperature of iron. If the outflowing gas
enters the temperature regime where iron becomes stable, the preceding formation
of the other dust species has accelerated the wind to such an extent, that
efficient dust growth is no more possible.
These explorative model calculations show that in a certain fraction of giant
stars of spectral type M on the AGB, where magnesium is less abundant than
silicon, one expects quartz grains to be formed besides the two standard
silicate dust components olivine and pyroxene.
A word of warning is appropriate at this place. Our results for the relative
amounts of the different dust species formed in the wind depend to a large
extent on the numerical values accepted for the sticking coefficients, which
are not well known, except perhaps that of iron (for pure metals one generally
has 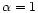 ). Especially we did not succeed in finding experimental
results for the sticking coefficient of pyroxene and, for this reason, assumed
this to equal that of olivine, which may be not true. The relative amounts
of olivine and pyroxene formed in a real dust shell may be different from what
we have found in our model calculation if the two sticking coefficients are
strongly different from each other. The same caveat holds with respect to the
relative amounts of quartz and silicates formed in the wind.
). Especially we did not succeed in finding experimental
results for the sticking coefficient of pyroxene and, for this reason, assumed
this to equal that of olivine, which may be not true. The relative amounts
of olivine and pyroxene formed in a real dust shell may be different from what
we have found in our model calculation if the two sticking coefficients are
strongly different from each other. The same caveat holds with respect to the
relative amounts of quartz and silicates formed in the wind.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H2570f7.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg176.gif) |
Figure 7:
a) Spectral energy distribution of the dust shell for a model with
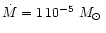 yr-1 for yr-1 for
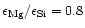 .
Full line: spectral energy distribution including extinction by
quartz. Dashed line: spectral energy distribution neglecting extinction
by quartz. Dotted line; The stellar black-body spectrum. b) .
Full line: spectral energy distribution including extinction by
quartz. Dashed line: spectral energy distribution neglecting extinction
by quartz. Dotted line; The stellar black-body spectrum. b)
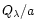 for absorption (full line) and scattering (dashed line) of amorphous quartz, c)
the same for amorphous pyroxene, and d) for amorphous olivine for absorption (full line) and scattering (dashed line) of amorphous quartz, c)
the same for amorphous pyroxene, and d) for amorphous olivine |
| Open with DEXTER |
6 Infrared spectra from the dust shell
In order to study the possibility that quartz grains may be detected by their
characteristic extinction bands from circumstellar spectra in the presence of
other silicates we have calculated IR emission spectra for our wind models.
These are obtained by solving the equation of radiative transfer in a
spherically symmetric dust shell by the p-z-method and the method of
Feautrier as described by Mihalas (1978). The temperature distribution
was taken from the solution of the wind model. This does not consider the
possibility that the dust temperatures may be different for different dust
species and limits to some extent the accuracy of the calculated spectra. It
was not attempted to obtain a completely self consistent solution for the wind
model and the radiative transfer problem. The scattering by grains is included
by a fixed point iteration method and assuming an angular distribution of the
scattered radiation as for dipole scattering (small particle limit).
The radiation of the central star was approximated by a black body of
temperature
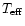 .
At the outer boundary of the shell the influx of
interstellar radiation was chosen as that given by the model of Mathis et al. (1983).
.
At the outer boundary of the shell the influx of
interstellar radiation was chosen as that given by the model of Mathis et al. (1983).
The inner boundary of the dust shell is determined by the condensation
calculation and depends on
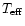 and to some extent on
and to some extent on 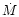 .
For an
assumed
.
For an
assumed
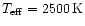 it is located at about 3 R* (cf. Fig. 6). The outer boundary is always assumed to be located at
1000 R*.
it is located at about 3 R* (cf. Fig. 6). The outer boundary is always assumed to be located at
1000 R*.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f8.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg182.gif) |
Figure 8:
Variation of the spectral energy distribution of the dust shell
(in arbitrary units) with varying Mg/Si abundance ratio for a model with
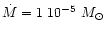 yr-1 and Mg/Si abundance ratios between
0.6 (lowest spectrum) and 1.4 (uppermost spectrum) in steps of 0.1. The
individual spectra are vertically shifted by a factor of 1.5
each. The two spectral features of quartz at yr-1 and Mg/Si abundance ratios between
0.6 (lowest spectrum) and 1.4 (uppermost spectrum) in steps of 0.1. The
individual spectra are vertically shifted by a factor of 1.5
each. The two spectral features of quartz at
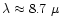 m and m and
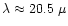 m can clearly be seen in the spectrum for m can clearly be seen in the spectrum for 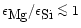 |
| Open with DEXTER |
For calculating the extinction of the dust grains we use optical constants for
amorphous silicate dust grains (cf. Sect. 4.2): (i) for glassy
quartz from Brewster (1992) for the short and from Henning & Mutschke
(1997) for the long wavelength region, (ii) for amorphous olivine from
Dorschner et al. (1995), (iii) for amorphous pyroxene from Henning &
Mutschke (1997), (iv) for iron from Lide (1995) and Pollack et al. (1994). The grain radius used for the calculation of the absorption
and scattering efficiencies 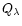 is the grain radius resulting from the
wind model
is the grain radius resulting from the
wind model![[*]](/icons/foot_motif.gif) . Since the grain radii vary with distance
from the star, the extinction efficiencies
. Since the grain radii vary with distance
from the star, the extinction efficiencies 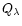 have to be calculated for
each radius in the dust shell and each wavelength grid point used in the model
calculation (
have to be calculated for
each radius in the dust shell and each wavelength grid point used in the model
calculation (
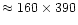 ). For reasons of computational efficiency
these are calculated in the approximation of small grains, which is always valid
in the far IR wavelength region, in which we are interested.
). For reasons of computational efficiency
these are calculated in the approximation of small grains, which is always valid
in the far IR wavelength region, in which we are interested.
Figure 7a shows the resulting spectral energy distribution of
the dust shell for a wind model in the wavelength region
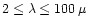 m, where a number of absorption bands of quartz exist. The model is
calculated with a Mg/Si abundance ratio of 0.8 and a mass-loss rate of
m, where a number of absorption bands of quartz exist. The model is
calculated with a Mg/Si abundance ratio of 0.8 and a mass-loss rate of
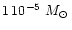 yr-1 for which about 7% of the Si is expected to
condense into quartz (cf. Fig. 5). For this mass-loss rate
the dust absorption bands appear in the spectrum as emission features. The full
line corresponds to the spectral energy distribution of the dust shell including
all dust species, the dashed line is the spectral energy distribution obtained
if the extinction by quartz is omitted. Figs. 7b, 7c, and 7d show for comparison the
absorption and scattering efficiencies
yr-1 for which about 7% of the Si is expected to
condense into quartz (cf. Fig. 5). For this mass-loss rate
the dust absorption bands appear in the spectrum as emission features. The full
line corresponds to the spectral energy distribution of the dust shell including
all dust species, the dashed line is the spectral energy distribution obtained
if the extinction by quartz is omitted. Figs. 7b, 7c, and 7d show for comparison the
absorption and scattering efficiencies 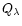 of quartz, pyroxene and
olivine grains with radius
of quartz, pyroxene and
olivine grains with radius 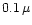 m, respectively. Extinction by quartz
produces two specific signatures in the spectrum:
m, respectively. Extinction by quartz
produces two specific signatures in the spectrum:
- The short wavelength shoulder of the
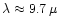 m silicate
emission band is significantly widened and steepened by the contribution of the
m silicate
emission band is significantly widened and steepened by the contribution of the
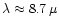 m emission band of quartz;
m emission band of quartz;
- The
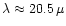 m absorption band of quartz produces a small
emission peak at this wavelength superposed on the long wavelength shoulder of
the
m absorption band of quartz produces a small
emission peak at this wavelength superposed on the long wavelength shoulder of
the
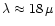 m silicate emission band.
m silicate emission band.
Additionally, the flat trough between the two strong silicate features is
somewhat filled up by quartz emission to the short wavelength side and appears
flatter than without quartz. These modifications of the spectral energy
distribution should be detectable in observed spectra of circumstellar dust
shells, if quartz is present.
Figure 8 shows the spectral energy distributions for a
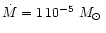 yr-1 model for a set of different abundance
ratios
yr-1 model for a set of different abundance
ratios
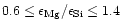 .
For the sake of
clarity the individual spectra each are shifted by a constant factor of
1.5 in
the vertical direction. This figure clearly shows the variation of the strength
of the quartz features with the Mg/Si abundance ratio and how the quartz
features become invisible for
.
For the sake of
clarity the individual spectra each are shifted by a constant factor of
1.5 in
the vertical direction. This figure clearly shows the variation of the strength
of the quartz features with the Mg/Si abundance ratio and how the quartz
features become invisible for
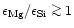 .
.
In this calculation we have not considered that in many of the dust shells
around AGB stars a considerable fraction of the dust is present in a crystalline
state (e.g. Waters & Molster 1999). If crystalline dust is present,
the dust features are more structured and more pronounced than for amorphous
dust. We have calculated spectra for the unfavourable case where dust features
are rather diffuse, which in a certain sense is the worst case for finding
quartz features.
An inspection of a number of ISO spectra of evolved stars (Molster 2000)
shows in some cases weak indications for emission features which might be
associated with quartz dust, especially the feature at 20.67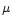 m. Also the
emission band profiles presented by Simpson (1991) seem to show in a few
cases weak indications for the presence of quartz. This suggests, that quartz
could indeed be found as a dust component in circumstellar shells of highly
evolved stars. A definite conclusion can be drawn, however, only on the basis
of detailed model calculations for emission from the dust shell and analysis of
ISO spectra of possible candidate stars. Because of the uncertainties with
respect to the sticking coefficients such calculations should better be done by
conventional radiative transfer models for the dust shell where the relative
abundances of the different dust species are determined by fitting of observed
and synthetic spectra.
m. Also the
emission band profiles presented by Simpson (1991) seem to show in a few
cases weak indications for the presence of quartz. This suggests, that quartz
could indeed be found as a dust component in circumstellar shells of highly
evolved stars. A definite conclusion can be drawn, however, only on the basis
of detailed model calculations for emission from the dust shell and analysis of
ISO spectra of possible candidate stars. Because of the uncertainties with
respect to the sticking coefficients such calculations should better be done by
conventional radiative transfer models for the dust shell where the relative
abundances of the different dust species are determined by fitting of observed
and synthetic spectra.
We have studied in this paper the consequences of star-to-star variations of the
Mg/Si element abundance ratio on the mineral composition of the dust mixture in
dust-shells around AGB stars. For magnesium poor stars with
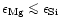 it is expected that quartz is formed as an
additional dust component which, on the other hand, is absent for stars where
it is expected that quartz is formed as an
additional dust component which, on the other hand, is absent for stars where
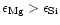 .
We have shown that sufficient amounts
of quartz can be expected to be formed in the Mg-poor stars such that this dust
component can be identified by some characteristic spectral features of quartz
in the IR spectrum from the dust shell.
.
We have shown that sufficient amounts
of quartz can be expected to be formed in the Mg-poor stars such that this dust
component can be identified by some characteristic spectral features of quartz
in the IR spectrum from the dust shell.
The observed element abundances of galactic F and G stars suggest that in a
small fraction of all stars of population I and II metallicity, of the order of
10%, the magnesium abundance is less than the silicon abundance. The majority
of 90% of all stars have magnesium abundances in excess of the silicon
abundance, as it is the case for the sun. For many of these stars, however,
the Mg/Si abundance ratio is higher than that given in the abundance tabulation
of Anders & Grevesse (1989).
If such stars later evolve to the AGB and develop thick circumstellar dust
shells, the Mg-poor stars are likely to form quartz dust grains and a mixture
of mainly pyroxene and a smaller quantity of olivine dust grains (and,
additionally, iron dust grains), while stars with a normal mixture
(
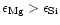 )
form olivine grains and somewhat less
quantities of pyroxene grains, but no quartz grains.
)
form olivine grains and somewhat less
quantities of pyroxene grains, but no quartz grains.
The present day AGB stars inherited their Mg and Si abundances from their
main sequence progenitors. One should expect then that the present days
AGB stars show the same kind of scattering of Mg/Si abundance ratios as the
F and G field dwarf stars, since the average Mg/Si abundance ratio and the
extent of scattering in the Mg/Si abundances seems to be roughly independent of
the metallicity, except for very low metallicities (cf. Edvardsson et al.
1993; Chen et al. 2000). The dust shells of AGB
stars then should show a variable mixture of olivine and pyroxene grains
and in a small fraction of all cases quartz dust should be present.
Only one star of the sample of stars shown in Fig. 1
seems to have a magnesium abundance of about twice the silicon abundance. In
such an element mixture one expects that solid MgO can be formed as a separate
dust component. This high Mg/Si ratio may be an artefact of the errors of
the abundance determinations, but if this high ratio should be correct,
this means that there exist some stars with MgO dust, but in any case,
such objects must be rare.
For very metal poor stars Fig. 1 seems to indicate that
magnesium generally is much less abundant than silicon. This would mean that -
provided dust condensation is possible in such objects - the very first
generations of AGB stars with an oxygen rich chemistry do not form the standard
silicate dust grains; they mainly form quartz grains. We have not performed model
calculations for this case because our model programme is tailored for dust
driven winds, but for very low metallicities mass-loss cannot be driven by dust
condensation.
It should be kept in mind that the quantitative results of the present model
calculation for the relative quantities of the different dust species depend on
the adopted values of the sticking coefficients which generally are badly known.
A better experimental determination of these quantities is urgently required.
Acknowledgements
We acknowledge the constructive criticism of an unknown referee.
This work has been performed as part of a project of the special research
programme SFB 439 "Galaxies in the Young Universe'' which is supported
by the Deutsche Forschungsgemeinschaft (DFG).
-
Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197
In the text
NASA ADS
-
Atkins, P. W. 1994, Physical Chemistry, 5th Ed. (Oxford University Press)
In the text
-
Barin, I. 1992, Thermodynamical Data of Pure Substances (Verlag Chemie, Weinheim)
-
Bernatowicz, T. J., Cowsik, R., Gibbons, P. C., et al. 1996, ApJ, 472, 760
In the text
NASA ADS
-
Bohren, C. F., & Huffman, D. R. 1983, Absorption and Scattering of Light by Small
Particles (John Wiley & Sons, New York)
-
Brewster, M. Q. 1992, Thermal Radiative Transfer and Properties (John Wiley &
Sons, New York etc.)
In the text
-
Chase, M. W. Jr., Davies, C. A., Downey, J. R. Jr., et al. 1985, JANAF Thermodynamic
Tables, National Institute of Standards and Technology, Gaithersburg
In the text
-
Chang, C., Patzer, A. B. C., Sedlmayr, E., & Sülzle, D. 1998, Eur. Phys. J. D, 2, 57
In the text
-
Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141, 491
In the text
NASA ADS
-
Cherchneff, I. 1998, in The
Molecular Astrophysics of Stars and Galaxies, ed. T. W. Hartquist, & D. A. Williams (Clarendon Press, Oxford), 265
In the text
-
Donn, B. 1978, in Protostars & Planets I, ed. T. Gehrels (University of
Arizona Press, Tucson), 100
In the text
-
Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A,
300, 503
In the text
NASA ADS
-
Ebel, D. S., & Grossman, L. 2000, Geoch. Cosmoch. Acta, 64, 339
In the text
-
Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101
In the text
NASA ADS
-
Forestini, M., & Charbonnel, C. 1997, A&AS, 123, 241
In the text
NASA ADS
-
Gail, H.-P. 1998, A&A, 332, 1099
In the text
NASA ADS
-
Gail, H.-P., & Sedlmayr, E. 1986, A&A, 166, 225
In the text
NASA ADS
-
Gail, H.-P., & Sedlmayr, E. 1987, A&A, 171, 197
In the text
NASA ADS
-
Gail, H.-P., & Sedlmayr, E. 1998a, in The
Molecular Astrophysics of Stars and Galaxies, ed. T. W. Hartquist, & D. A. Wiliams (Clarendon Press, Oxford), 285
In the text
-
Gail, H.-P., & Sedlmayr, E. 1998b, Faraday Disc., 109, 303
In the text
-
Gail, H.-P., & Sedlmayr, E. 1999, A&A, 347, 594 (Paper I)
In the text
NASA ADS
-
Golub, G. H., & Ortega, J. M. 1992, Scientific Computing and Differential Equations (Academic Press, Boston etc.)
In the text
-
Gratton, R. G., & Sneden, C. 1988, A&A, 204, 193
In the text
NASA ADS
-
Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, ed. N. Prantzos, E. Vangioni-Flam, & M. Cassé (Cambridge University Press,
Cambridge), 15
In the text
-
Groenewegen, M. A. T., van den Hoek, L. B., & de Jong, T. 1995, A&A, 293, 381
In the text
NASA ADS
-
Grossman, L. 1972, Geochim. Cosmochim. Acta, 36, 597
In the text
-
Hashimoto, A. 1990, Nature, 347, 53
In the text
NASA ADS
-
Henning, Th., & Mutschke, H. 1997, A&A, 327, 743
In the text
NASA ADS
-
Imae, N., Tsuchijama, A., & Kitamura, M. 1993, Earth Planet. Sci. Lett., 118, 21
In the text
NASA ADS
-
Jeong, K. S. 2000, Dust Shells around oxygen-rich Miras and Long-Period
Variables, Thesis, Technical University, Berlin
In the text
-
Knapp, G. R. 1985, ApJ, 293, 273
In the text
NASA ADS
-
Lang, K. R. 1992, Astrophysical Data, Planets and Stars (Springer, New York etc.)
In the text
-
Lattanzio, J., & Forestini, M. 1999, in Asymptotic Giant Branch Stars, ed. T. Le Bertre, A. Lèbre, & C. Waelkens, IAU Symp., 191 (Astronomical Society of
the Pacific), 31
In the text
-
Lattimer, J. M., Schramm, D. N., & Grossman, L. 1978, ApJ, 219, 230
In the text
NASA ADS
-
Le Bertre, T., & Winters, J. M. 1998, A&A, 334, 173
In the text
NASA ADS
-
Lide, R. D. 1995, CRC Handbook of Chemistry and Physics, 76th Ed. (CRC Press,
Boca Raton etc.)
In the text
-
Lodders, K., & Fegley, B., Jr. 1995, Meteoritics, 30, 661
In the text
-
Lodders, K., & Fegley, B. 1999, in ed. T. Le Bertre, A. Lébre, & C. Waelkens,
Asymptotic Giant Stars, IAU Symp., 191, 308
In the text
-
Lucy, L. B. 1971, ApJ, 163, 95
In the text
NASA ADS
-
Lucy, L. B. 1976, ApJ, 205, 482
In the text
NASA ADS
-
Magain, P. 1987, A&A, 179, 176
In the text
NASA ADS
-
Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212
In the text
NASA ADS
-
Mendybaev, R. A., Beckett, J. R., Grossman, L., & Stolper, E. 1998,
Lunar and Planetary Science Conference, 29, 1871
In the text
NASA ADS
-
Mihalas, D. 1978, Stellar Atmospheres 2nd Ed. (Freeman, San Francisco)
In the text
-
Molster, F. J. 2000, Thesis, University of Amsterdam
In the text
-
Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615
In the text
NASA ADS
-
Saxena, S. K., & Eriksson, G. 1986, in Chemistry and Physics of
Terrestrial Planets, ed. S. K. Saxena (Springer, New York etc.), 30
In the text
-
Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
In the text
NASA ADS
-
Sharp, C. M., & Huebner, W. F. 1990, ApJS, 72, 417
In the text
NASA ADS
-
Simpson, J. P. 1991, ApJ, 368, 570
In the text
NASA ADS
-
Smith, V. V., & Lambert, D. L. 1990, ApJS, 72, 387
In the text
NASA ADS
-
Snow, T. P., & Witt, A. 1996, ApJ, 468, L65
In the text
NASA ADS
-
Thielemann, F.-K., Nomoto, K., & Hashimoto, M. 1993, in
Origin and Evolution of the Elements,
ed. N. Prantzos,
E. Vangioni-Flam, & M. Cassé (Cambridge University
Press, Cambridge), 297
In the text
-
Tomkin, J., Edvardsson, B., Lambert, D. L., & Gustafsson, B. 1997, A&A, 327, 587
In the text
NASA ADS
-
Tsuji, T. 1973, A&A, 23, 411
In the text
NASA ADS
-
Waters, L. B. F. M., & Molster, F. J. 1999, in
Asymptotic Giant Branch Stars,
ed. T. Le Bertre, A. Lèbre, & C. Waelkens, IAU Symp., 191, 209
In the text
-
Winters, J. M., Fleischer, A. J., Le Bertre, T., & Sedlmayr, E. 1997, A&A, 326, 305
In the text
NASA ADS
Copyright ESO 2001
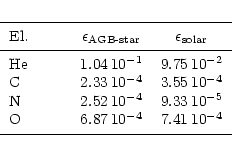
![\begin{figure}
\par\includegraphics[width=8cm,clip]{H2570f2.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg28.gif)
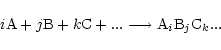
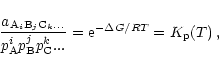
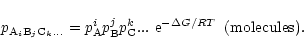
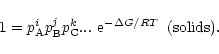
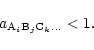
![\begin{figure}
\par\includegraphics[width=12cm,clip]{H2570f1.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg51.gif)
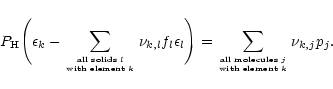
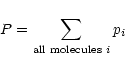
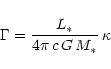
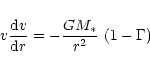
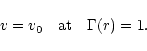
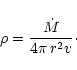
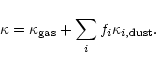
![\begin{displaymath}\kappa_{\rm py}=
\Biggl[\left(3.773\,10^{-5}~T^{2.017}\right)...
...}\,T^{2.272}\right)^4
}
\biggr\}^{-1}
\Biggr]^{-{1\over2}}.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img86.gif)
![$\displaystyle T^4(r)=\frac12T_{\rm eff}^4\,\left[\,1-\sqrt{1-{R_*^2\over r^2}}+\frac32\tau_
{\mbox{\scriptsize L}}
\right].$](/articles/aa/full/2001/19/aah2570/img87.gif)
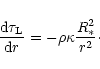
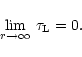
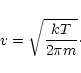
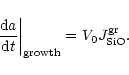
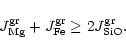
![\begin{displaymath}\left.\frac{{\rm d}a}{{\rm d}t}\right\vert_{\rm growth}=V_0 \...
...{1}{2}\left[J^{\rm gr}_
{\rm Mg}+J^{\rm gr}_{\rm Fe}\,\right].
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img108.gif)

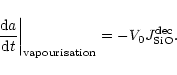
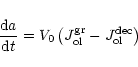
![\begin{displaymath}J^{\rm gr}_{\rm ol}=\min\left(J^{\rm gr}_{\rm SiO} ,\ \frac{1...
...eft[J^{\rm gr}_
{\rm Mg}+J^{\rm gr}_{\rm Fe}\,\right]\right)
.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img113.gif)
![\begin{displaymath}\frac{{\rm d}x}{{\rm d}t}={3V_0\over a}\,\left[\left(x_g-x\ri...
...\rm ol}+\frac12
\left(J^{\rm ex}_+-J^{\rm ex}_-\right)\right].
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img114.gif)
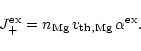
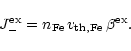
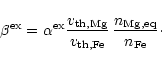
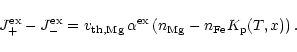
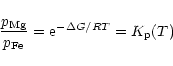
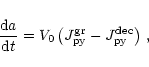
![\begin{displaymath}J^{\rm gr}_{\rm py}=\min\left(J^{\rm gr}_{\rm SiO} ,\ \left[J^{\rm gr}_
{\rm Mg}+J^{\rm gr}_{\rm Fe}\,\right]\right)
.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img127.gif)
![\begin{displaymath}\frac{{\rm d}x}{{\rm d}t}={3V_0\over a}\,\left[\left(x_g-x\ri...
...m gr}_{\rm py}+
\left(J^{\rm ex}_+-J^{\rm ex}_-\right)\right].
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img128.gif)
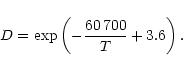
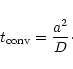
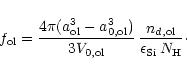
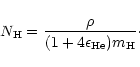
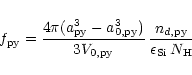
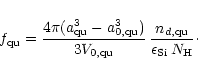
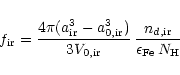
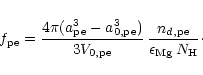
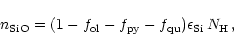
![\begin{displaymath}n_{\rm Mg}=\Bigl[\epsilon_{\rm Mg}(1-f_{\rm pe})-\left(2x_{\r...
...x_{\rm py}f_{\rm py}\right)\epsilon_{\rm Si}\Bigr]\,N_{\rm H}.
\end{displaymath}](/articles/aa/full/2001/19/aah2570/img153.gif)
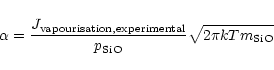
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f3ar.eps}\par\includegr...
...p]{H2570f3br.eps}\par\includegraphics[width=7cm,clip]{H2570f3cr.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg162.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f4ar.eps}\par\includegr...
...p]{H2570f4br.eps}\par\includegraphics[width=7cm,clip]{H2570f4cr.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg165.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=8cm,clip]{H2570f5ar.eps}\hspace{...
....eps}\hspace{1cm}
\includegraphics[width=8cm,clip]{H2570f5dr.eps} }
\end{figure}](/articles/aa/full/2001/19/aah2570/Timg168.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f6c.eps}\par\includegra...
...lip]{H2570f6b.eps}\par\includegraphics[width=7cm,clip]{H2570f6a.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg172.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{H2570f7.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg176.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H2570f8.eps}\end{figure}](/articles/aa/full/2001/19/aah2570/Timg182.gif)