A&A 371, 354-359 (2001)
DOI: 10.1051/0004-6361:20010343

Stark broadening in O III spectrum

A. Sreckovic1 - M. S. Dimitrijevic2 - S. Djenize1


1 - Faculty of Physics1, University of Belgrade, 11001 Belgrade, POBOX 368, Serbia, Yugoslavia
2 - Astronomical Observatory2, 11001 Belgrade, Volgina 7, Serbia, Yugoslavia

Received 18 December 2000 / Accepted 20 February 2001

Abstract
The Stark widths and shifts of 7 doubly ionized oxygen (O III) spectral lines, in five multiplets, have been measured at electron densities between 1.66   1023 m-3 and 2.80   1023 m-3and electron temperatures between 17 000 K and 54 000 K in a linear pulsed-arc discharge in N2 + O2 and CO2 plasmas. The above mentioned species have been calculated using the semiclassical perturbation formalism. Our measured and calculated Stark width and shift values have been compared to the existing calculated and experimental data.

Key words: lines: profiles - atomic data


1 Introduction

Interest for the doubly ionized oxygen (OIII) spectral lines is in recent years increasing in astrophysics because they are found in the spectra emitted by various kinds of cosmic light sources. In a recent publication by Nelson (2000) it was found that a relationship exists between nuclear black hole mass ( $M_{\rm bh}$) and the OIII spectral line widths for active galactic nuclei (AGNs). In their work, Cuesta & Phillips (2000) report on observations of the planetary nebula NGC 2440 in the transition OIII (436.3 nm and 500.7 nm). Sako et al. (2000) present a preliminary analysis of the first high-resolution X-ray spectrum of a Seyfert 2 galaxy (Markarian 3) and notice that the soft X-ray emission is spatially extended along the OIII ionization cone. Measurements of OIII emission in Lyman-break galaxies (LBGs) have been presented by Teplitz et al. (2000) where the 500.7 nm line emission characteristics are used to estimate the star formation rate (SFR) of the LBGs. del Burgo et al. (2000) have discovered OIII (495.9 nm and 500.7 nm) emission in the inner circumnuclear region of the M 31. Furthermore, the OIII spectral line characteristics have been used in order to find nebular chemical abundances (Oey & Shields 2000; Dopita et al. 2000; Dopita & Sutherland 2000).

Therefore, the knowledge of the OIII spectral line widths and shifts is of interest. If the Stark broadening is the principal pressure-broadening mechanism in plasmas, as e.g. for A and B type stars and white dwarfs, it is possible to obtain the other basic plasma parameters (Griem 1974, 1997) essential in the modelling of various plasma compositions and kinetic processes (Lesage 1994; Zeippen 1995) on the basis of the Stark width and shift values.

From the first experimental measurement of displacements of OIII lines (Pretty 1931), Stark broadening parameters of OIII lines have been measured several times (Platisa et al. 1975; Puric et al. 7itePuric88a,b; Blagojevic et al. 2000). Theoretically, Stark broadening of OIII lines has been investigated by Subrahmaniam (1968), Hey & Bryan (1977), Dimitrijevic & Konjevic (1980, 1981, 1987), Hey & Breger (1980, 1981) and Dimitrijevic (1981, 1988a,b).

We have measured and calculated Stark FWHM (full-width at half intensity maximum, W) and shift (d) of 7 OIII spectral lines that belong to the wavelength range of interest for astrophysical observations. These belong to three transitions in 5 multiplets. Stark widths of 3 lines (334.07, 407.39 and 444.78 nm) have not been measured before (Lesage & Fuhr 1999). Stark shift values have been measured in only one experiment (Puric et al. 1988b). Thus, our five d data have not been measured before. We have calculated W and d values using the known semiclassical perturbation formalism (SCPF) (Sahal-Bréchot 1969a,b) updated several times (Sahal-Bréchot 1974; Fleurier et al. 1977; Dimitrijevic & Sahal-Bréchot 1984; Dimitrijevic et al. 1991; Dimitrijevic & Sahal-Bréchot 1996b). It should be pointed out that for the OIII lines Stark shifts no theoretical predictions exist (Lesage & Fuhr 1999 and references therein).

Our measured and calculated W values have been compared with existing theoretical (Hey & Bryan 1977; Dimitrijevic & Konjevic 1981), experimental (Platisa et al. 1975; Puric et al. 1988a; Blagojevic et al. 2000) and estimated values (Djenize et al. 1990; Djenize & Labat 1996; Djenize 2000). Latest values are obtained on the basis of the regularities of the Stark widths found along the oxygen isonuclear sequences.


  \begin{figure} \par\includegraphics[width=8cm,clip]{Fig1.eps}\end{figure} Figure 1: Boltzmann plot in the CO2 plasma
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{Fig2.eps}\end{figure} Figure 2: Temporal evolution of the electron temperature (T) in the two different plasma compositions
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{Fig3.eps}\end{figure} Figure 3: Temporal evolution of the electron density (N) in the two different plasma compositions
Open with DEXTER

2 Experiment

A modified version of the linear-low pressure pulsed arc (Djenize et al. 1992, 1998) has been used as a plasma source at two different discharge conditions. A pulsed discharge was driven in a quartz discharge tube of 5 mm inner diameter and effective plasma lengths of 5.8 cm and 6.3 cm (Fig. 1 in Djenize et al. 1998). The tube has end-on quartz windows. On the opposite side of the electrodes the glass tube was expanded in order to reduce erosion of the glass wall and also sputtering of the electrode material onto the quartz windows. The working gas was a nitrogen-oxygen mixture ($83\%$ N$_2 + 17\%$ O2) at 70 Pa filling pressure (Experiment a) and CO2 at 133 Pa filling pressure (Experiment b) with a constant flux flowing regime. The chosen flux and pressure provide minimal self-absorption of the investigated spectral lines. Spectroscopic observation of isolated spectral lines were made end-on along the axis of the discharge tube. A capacitor of 14 $\mu$F was charged up to 3.0 kV and 2.8 kV, in experiments a and b, respectively. The line profiles were recorded using a step-by-step technique with a photomultiplier (EMI 9789 QB) and a grating spectrograph (Zeiss PGS-2, reciprocal linear dispersion 0.73 nm/mm in the first order) system. The system was calibrated by using the EOA-101 standard lamp. The instrumental FWHM of 0.008 nm was determined by narrow spectral lines emitted from the hollow cathode discharge. The spectrograph exit slit (10 $\mu$m) with the calibrated photomultiplier was micrometrically moved along the spectral plane in small wavelength steps (0.0073 nm). The photomultiplier signal was digitalized and averaged (five shots at each position) using an oscilloscope interfaced to a computer. Total line intensity (I) corresponds to the area under the line profile.

Plasma reproducibility was monitored by the O II and OIII lines and, also, by the discharge current using the Rogowski coil signal (it was found that the signal is reproducible within $\pm 3\%$).

The plasma parameters were determined using standard diagnostic methods (Rompe & Steenbeck 1967). Thus, in the case of the Exp. b, the electron temperature was determined from the Boltzmann plot of twelve O II lines (394.505; 395.437; 407.216; 407.587; 407.886; 408.512; 409.294; 408.716; 413.281; 432.577; 418.546; 418.979 nm) within an energy interval of 5.88 eV for corresponding upper-levels with an estimated error within $\pm 5\%,$ assuming the existence of LTE, according to criterion from Griem (1974). The Boltzmann plot, as an example, obtained at 15 $\mu$s after the beginning of the discharge is presented in Fig. 1. In the case of Exp. a, the electron temperature was determined from the ratios of the relative intensities of 348.49 nm N IV to 393.85 nm N III and the previous N III to the 399.50 nm N II spectral line, assuming the existence of LTE, with an estimated error of $\pm 12\%.$ The necessary atomic data were taken from the available literature (Wiese et al. 1966; Lide 1994; NIST 2000; Kurucz 2000). Forms of the electron temperature decays are presented in Fig 2.

The electron density decay was measured using a well-established single laser interferometry technique (Ashby et al. 1965) for the 632.8 nm He-Ne laser wavelength with an estimated error of $\pm 5\%.$ The electron density decays are presented in Fig. 3.

3 Stark widths and shifts measurements

The measured profiles were of the Voigt type due to the convolutions of the Lorentzian Stark and Gaussian profiles caused by Doppler and instrumental broadening. For the electron density and temperature in our experiments, the Lorentzian fraction was dominant (over 87$\%$). van der Waals (Griem 1974) and resonance (Griem 1974) broadening were estimated to be smaller by more than one order of magnitude in comparison to Stark, Doppler and instrumental broadening. The standard deconvolution procedure (Davies & Vaughan 1963) was computed using the least squares algorithm. The Stark widths were measured with $\pm 12\%$ error. Great care was taken to minimize the influence of self-absorption on Stark width determination. The opacity was checked by measuring relative line intensity ratios within the multiplet No. 2 during the plasma decay. The obtained values were compared with calculated ratios of the products of the spontaneous emission probabilities (A) and the corresponding statistical weights (g) of the upper levels of the lines. The necessary atomic data were taken from Wiese et al. (1966), Lide (1994) and NIST (2000). It turns out that the experimental relative line intensity ratios are constant during the whole plasma decay period, testifying to the absence of self-absorption and agree, within $\pm 11\%$ accuracy, with calculated relative intensity ratio values.

The Stark shifts were measured using the well-known method based on the line center position observations during the whole plasma decay period (Djenize et al. 1998 and references therein). The Stark shift data were corrected for the electron temperature decay (Popovic et al. 1992). Stark shift data are determined with a $\pm$0.0008 nm error at a given N and T.

4 Method of calculation

The semiclassical perturbation formalism, as well as the corresponding computer code (Sahal-Bréchot 1969a,b), have been updated and optimized several times (Sahal-Bréchot 1974; Fleurier et al. 1977; Dimitrijevic & Sahal-Bréchot 1984; Dimitrijevic et al. 1991; Dimitrijevic & Sahal-Bréchot 1996b). The calculation procedure, with the discussion of updatings and validity criteria, has been briefly reviewed e.g. in Dimitrijevic & Sahal-Bréchot (1996a,b) so that only the basic details of calculations will be presented here. Stark full width (W) at the intensity half maximum (FWHM) and shift (d) of an isolated spectral line may be expressed as (Sahal-Bréchot 1996a,b; Fleurier et al. 1977):


W = 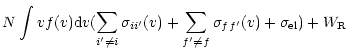$\d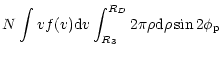isplaystyle N\int vf(v){\rm d}v (\sum_{i'\ne i}\sigma_{ii'}(v) +\sum_{f'\ne f}\sigma_{ff'}(v) + \sigma_{\rm el}) + W_{\rm R}$  
d = $\displaystyle N\int vf(v){\rm d}v\int_{R_3}^{R_D} 2\pi \rho {\rm d}\rho \sin 2\phi_{\rm p}$ (1)

where N is the electron density, f(v) the Maxwellian velocity distribution function for electrons, $\rho $ denotes the impact parameter of the incoming electron, i and f denote the initial and final atomic energy levels, and i', f' their corresponding perturber levels, while $W_{\rm R}$ gives the contribution of the Feshbach resonances (Fleurier et al. 1977). The inelastic cross section $\sigma_{j,j'}(v)$ can be expressed by an integral over the impact parameter of the transition probability $P_{jj'}(\rho ,v)$ as


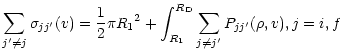$\displaystyle \sum_{j'\ne j}\sigma_{jj'}(v) = {1\over 2}\pi {R_1}^2 +\int_{R_1}^{R_{\rm D}}\sum_{j \ne j'}P_{jj'}(\rho ,v), j=i,f$     (2)

and the elastic cross section is given by


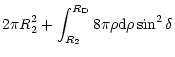$\displaystyle \sigma_{\rm el}$ = $\displaystyle 2\pi R_2^2 + \int_{R_2}^{R_{\rm D}}8\pi \rho {\rm d}\rho\sin^2\delta$  
$\displaystyle \delta$ = $\displaystyle (\phi_{\rm p}^2 + \phi_{\rm q}^2)^{1/2}.$ (3)

The phase shifts $\phi_{\rm p}$ and $\phi_{\rm q}$ due respectively to the polarization potential (r-4) and to the quadrupolar potential (r-3), are given in Sect. 3 of Chap. 2 in Sahal-Bréchot (1969a). $R_{\rm D}$ is the Debye radius. All the cut-offs R1, R2, R3 are described in Sect. 1 of Chap. 3 in Sahal-Bréchot (1969b). For electrons, hyperbolic paths due to the attractive Coulomb force were used, while for perturbing ions the paths are different since the force is repulsive. The formulae for the ion-impact widths and shifts are analogous to Eqs. (1-3), without the resonance contribution to the width. The difference in calculation of the corresponding transition probabilities and phase shifts as functions of the impact parameter in Eqs. (2) and (3) is in the ion perturber trajectories which are influenced by the repulsive Coulomb force, instead of an attractive one as for electrons. Atomic energy levels have been taken from Moore (1985).

The contribution of ion impact widths and shifts to the total line widths and shifts can be neglected since our results for $T=20\,000$ K are two order of magnitude smaller.

5 Results

Our measured Stark FWHM ($W_{\rm m}$) and shift ($d_{\rm m}$) values at various electron temperatures (T) and densities (N) together with other authors data are given in Table 1.


  
Table 1: Measured Stark FWHM ($W_{\rm m}$) and shift ($d_{\rm m}$) values for the OIII spectral lines at observed electron temperatures (T) and densities (N). a, this work; b, Platisa et al. (1975); c, Puric et al. (1988a); d, Puric et al. (1988b) and e, Blagojevic et al. (2000). $W_{\rm m}/W_{\rm th}$represents the ratio between measured and our calculated (SCPF) values taken from Table 2
\begin{table} \includegraphics[width=18cm,clip]{Table1.eps}\end{table}

Our calculated W and d data at 1023 m-3electron density are given in Table 2 for the mean wavelength $<\lambda >$ in the multiplet. The width and shift of each multiplet component can by easily evaluated if one takes into account that the W and d are proportional to $\lambda^2.$


  
Table 2: Electron Stark FWHM (W in pm) and shift (d in pm) calculated by using the semiclassical perturbation formalism (SCPF) (Eqs. (1)-(3)) at 1023 m-3 electron density and various electron temperatures (T in 104 K). $<\lambda >$ is the mean wavelength (in nm) in the multiplet. Negative shift is toward the blue
\begin{table} \includegraphics[width=15cm,clip]{Table2.eps}\end{table}

6 Discussion

In order to compare measured and calculated Stark FWHM and shift values, the theoretical Stark FWHM and shift dependences on the electron temperature, together with the values of other authors and our experimental results, at an electron density of 1023 m-3 are presented graphically in Figs. 4 and 5.


  \begin{figure} \includegraphics[width=6cm,clip]{Fig4.eps} \end{figure} Figure 4: Stark FWHM (W in 0.1 nm) dependence on the electron temperature (T) for the most investigated O III spectral lines belonging to various transitions at 1023 m-3 electron density. SCPF, our calculations by using the semiclassical perturbation formalism. $\bullet $, our experimental results and those of other authors: $\triangle $, Platisa et al. (1975); $\square $, Puric et al. (1988a); $\nabla $, Blagojevic et al. (2000). SE, SEM, G and GM denote theoretical W values (see text). +, calculations by Hey & Bryan (1977). INS denote estimated W values (Djenize et al. 1990; Djenize & Labat 1996; Djenize 2000). The error bars include the uncertanties of the width and electron density measurements. $<\lambda >$ is the mean wavelength in the multiplet
Open with DEXTER

The first O III W values were calculated on the basis of various approximations initiated by Griem (1974); Hey & Bryan (1977) and Dimitrijevic & Konjevic (1980). Thus, SE and SEM denote the results of semi-empirical (Griem 1968) and modified semi-empirical predictions using Eqs. (4), (5) and Eqs. (7)-(10), respectively from Dimitrijevic & Konjevic (1981). G and GM denote W values obtained on the basis of the simplified semiclassical method (Griem 1974). For the GM values the low temperature part is modified (Dimitrijevic & Konjevic 1980). The estimated Wvalues, based on the obtained regularities of the Stark FWHM along an oxygen isonuclear sequences (INS), have been taken from Djenize (1990, 1996, 2000).


  \begin{figure} \par\includegraphics[width=6cm,clip]{Fig5.eps}\end{figure} Figure 5: Stark shift (d in 0.1 nm) dependence on the electron temperature (T) for the OIII spectral lines belonging to various transitions at 1023 m-3electron density. SCPF, our calculations by using the semiclassical perturbation formalism. $\bullet $, our experimental results and those of other authors: $\square ,$ Puric et al. (1988b). The error bars include the uncertanties of the shift and electron density measurements. $<\lambda >$ is the mean wavelength in the multiplet
Open with DEXTER

On the basis of the Tables 1, 2, and Fig. 4 one can conclude that our measured ($W_{\rm m}$) and calculated (SCPF) Stark FWHM values are in satisfactory mutual agreement (within $\pm 13\%$ in average). We notice, also, fair agreement between $W_{\rm m}$ and $W_{\rm G}$ and $W_{\rm INS}$ values. Values W measured earlier (Puric et al. 1988a; Blagojevic et al. 2000) agree, also, with $W_{\rm SCPF}$, $W_{\rm G}$ and $W_{\rm INS}$ calculated values within the accuracy of experiments (up to $\pm 15\%$) and uncertainties of the approximations (up to $\pm 30 \%$).

Our calculated Stark shift values are small and have a negative sign. The measured $d_{\rm m}$ values are, in most of the cases (see Table 2), equal to zero. The only exception is the 408.11 nm OIII line which we have measured and, also, it has a calculated shift different from zero. It turns out that the calculated d values of the particular wavelengths are approximately constant over a wide range of the electron temperatures from 20 000 K up to 500 000 K.

7 Conclusion

We have found very good agreement (within $\pm 10\%$) between measured, calculated and estimated Stark FWHM values in the cases of the OIII wavelengths that belong to the multiplets Nos. 2, 6 and 23. These facts allow us to recommend these lines (375.47 nm, 375.72 nm, 298.38 nm; 407.39 nm and 408.11 nm) for plasma diagnostics as lines with convenient Stark FWHM data. Because the found Stark shift values are very small, and show negligible dependence on the electron temperature, these can be used, also, for diagnostic purposes as data independent of the self-absorption in the optically thick astrophysical plasmas.

Acknowledgements

This work is a part of the project "Astrometrical, Astrodynamical and Astrophysical Investigations'', supported by the Ministry of Science and Technology of the Republic of Serbia.

References

 
Copyright ESO 2001