1 - Space Science & Technology Department, Rutherford Appleton Laboratory, Chilton OX11 0QX, UK
2 - Department of Physics and Applied Physics, University of Strathclyde, Glasgow, Scotland G1 1XQ, UK
3 - School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife, Scotland KY16 9SS, UK

Abstract
Recent images in the radio of UV Ceti show two intense emission regions above the magnetic poles of the star. The emission is overwhelmingly right hand circularly polarized with 100 $\%$ right hand polarization at 3 cm and 6 cm wavelengths during flares. This high degree of polarization rules out gyrosynchrotron emission. In this article we propose that such emission can be produced by a coherent cyclotron maser driven by field aligned electrons moving into an increasing magnetic field. Conservation of the first adiabatic invariant causes the electron beam to increase its pitch angle. This produces a broad region on the distribution function and the possibility of producing a positive slope in the perpendicular velocity space. Such distribution functions are common in magnetic mirror type geometries and are possible sources of free energy leading to electromagnetic emission by a cyclotron maser instability mechanism.

Key words: physical processes: polarization - physical processes: radiation mechanisms: non-thermal - stars: flare - stars: magnetic fields

The first VLBI radio image of a star was recently obtained by Benz et al. (1998). This was for the star UV Ceti - a nearby flare star. The observation was made at a wavelength of 3.6 cm and the radio emission was found to consist of two emission components separated by 4.4 times the radius of the star (i.e. 4.4 $R_\star$ ). The alignment of these two components is actually very similar to the most likely axis of rotation and magnetic field for the star - that is the two emission components apparently lie above the magnetic poles of the star. Benz et al. (1998) interpreted these two structures in terms of two very large magnetic flare loops (magnetic flux tubes). This configuration of magnetic structures overlying the magnetic pole of a star is quite unlike anything ever seen on the Sun.

During the $\sim$ 6.4 hours observation of UV Ceti, no flares were detected although the radio emission of the brighter source ("source 2" in Benz et al. 1998 notation) declined by a factor of 3-6 while the more stable component ("source 1") showed a gradual increase of $\sim$ 50%. The combined radio emission from UV Ceti displayed a net polarization of 10% in the right hand sense. During the observation, the VLA detected 3 radio flares from the binary companion of UV Ceti (UV Ceti A) - the last of these was a "double" flare and was also the brightest. It was unresolved with the VLBI network and Benz et al. (1998) deduced a brightness temperature of greater than 1.2 10¹² K. All the radio flares detected were 100% right hand circular polarized (RCP). This is completely typical for radio flares from either binary component of UV Ceti where the vast majority of radio flares are 60-100% RCP (the degree of polarization being wavelength dependent) (Kellett et al. 2001). Benz et al. (1998) estimated a magnetic field of 15-130 G and an electron density of 10⁶- 10⁸ cm^-3 for "source 2" - based on a gyrosynchrotron emission mechanism origin for the radio emission. The 10% net RCP emission is consistent with gyrosynchrotron emission which is the normal mechanism proposed for stellar radio emission and is also observed on the Sun during flares. However, the polarization and very high brightness temperature of the flare radio emission from UV Ceti argue strongly for a coherent radio emission mechanism (Benz et al. 1998). This was also the conclusion of Kundu et al. (1988). Following earlier work on the loss-cone electron cyclotron maser (Wu & Lee 1979) as the mechanism of auroral kilometric radiation, a number of papers on radio emission from other planets (Zarka 1992), the solar corona (Melrose & Dulk 1982), binary systems (Slee et al. 1984; Trigilio et al. 1998) and dwarf M flare stars (Abada-Simon et al. 1994) have considered the same mechanism.

In this paper we will present a new coherent cyclotron maser instability which can explain the radio flare emission for stars like UV Ceti. The radio emission model builds on earlier work by Kellett et al. (2001) who introduced the concept of dipole magnetic traps to explain a series of radio and X-ray observations from active stars and also the work by Bingham & Cairns (2000) on right hand polarized (R-X) emission by a cyclotron maser instability. The model of radio emission by electron horseshoe distributions (Bingham & Cairn 2000) is now thought to be the mechanism of generation of the Earth's kilometric radiation generated by an electron beam moving into a stronger magnetic field region (Ergun et al. 2000). One of the advantages of maser radiation from the horseshoe type distribution over the traditional loss-cone maser is that emissions are generated high above the stellar surface whereas the loss-cone masers are confined to be near the surface. A problem with the electron-cyclotron maser mechanism is absorption of X-mode radiation in regions where they are at harmonics of the local cyclotron frequency (Melrose & Dulk 1982). However resent studies of auroral emission (Ergun et al. 2000) demonstrate that density cavities such as the auroral cavity efficiently converts the mode to a mode with a substantial $k_{\parallel}$ which is less easily absorbed (Ergun et al. 2000).

2 Background observations

X-ray and radio observations of numerous active late-types stars over the past 20 years have revealed a wide variety of different phenomena. The single most significant is probably the realization of the role played by magnetic fields in driving the activity seen in these stars. However, many of these observations have been studied in isolation and when one tries to bring them together clear contradictions can arise. For example, it is now widely accepted that the X-ray emission from late-type active stars is thermal in nature and probably consists of two or more temperature components in the 1-30 million K temperature range. (This doesn't imply that the mechanism that generates the emission is known.) On the other hand, the radio emission from stars is also widely believed to be non-thermal and as already mentioned above the brightness temperatures observed can be very high indeed (typically in excess of 100 million K). Kellett et al. (2001) summarized six different sets of observations of a wide range of active late-type stars. They then went on to demonstrate that a single model "assumption" could then be used to satisfactorily explain these six varied observational results and in a completely self-consistent way. The one assumption made was that active late-type stars possess a toroidal dipole magnetic field geometry. Such a magnetic configuration forms a natural magnetic trap and is responsible for the Earth's radiation belts and also those of Jupiter. Both these planets also exhibit distinct radio emission in the R-X mode, AKR (auroral kilometric radiation) from the Earth which originates from sources in the northern and southern auroral zones.

UV Ceti itself is actually a binary system (L726-8AB, Gliese 65AB), and it is the "B'' star that is the prototypical flare star UV Ceti. However, both component stars are believed to be essentially identical dwarf M 5.5 emission-line stars (dM5.5e) and both stars are seen to flare in the optical and radio. (X-ray flares are also detected from the system, but the X-ray observations by themselves cannot resolve which of the two stars produced the flare.) The stars are both much smaller and less massive than the Sun (about 1/6th the solar radius in size and 1/10th the solar mass). The rotation period of either star is unknown but based on the levels of activity observed from the stars they are likely to be relatively slow rotators - probably similar to the Sun with periods of 25-35 days.

3 Cyclotron maser emission

The electron cyclotron maser instability is a powerful mechanism for producing non-thermal stimulated radiation in a plasma. The free energy source for producing this type of instability is an anisotropic electron distribution function with a positive slope in perpendicular velocity, which constitutes a population inversion. Such distributions have been used before to explain non-thermal planetary and astrophysical radio emissions (Zarka 1992; Melrose 1986). One of the most common electron distributions used to explain cyclotron maser emission is the loss-cone (Wu & Lee 1979; Melrose 1986). However, in many situations where non-thermal radio emission is observed energetic electron beams are also observed (Delory et al. 1998) or invoked. For the case of planetary radio emission the electron beams are accelerated towards the magnetic poles and into regions of increasing magnetic field. Electron beams moving into stronger magnetic field regions form a crescent or horseshoe distribution as a result of the first adiabatic invariant (Chen 1984). These particular electron distribution functions have been shown by Bingham & Cairns (2000) to be unstable to the generation of R-X mode radio emission. In this article using an energetic electron beam propagating into an increasing magnetic field region we demonstrate the formation of the horseshoe and the instability giving rise to maser emission. The electron cyclotron maser produces stimulated emission with a narrow bandwidth polarized in the R-X mode and occurs in regions where the cold background plasma component is depleted in comparison to the hot component. The beam can arise as a result of flare activity in the equatorial region of the star where the rapidly expanding flare can interact with the dipole field structure creating a shock propagating outwards. Such shock waves have been shown to be responsible for electron beams in solar flares (McClements et al. 1993). This beam will evolve into a horseshoe distribution as it moves into stronger field regions. We examine the stability of a horseshoe type of electron distribution for R-X mode waves propagating perpendicular to the steady magnetic field. To obtain the distribution function we start with a drifting Maxwellian, typically with the drift velocity well above the thermal speed. This is then considered to move into an increasing magnetic field where the distribution function is readily calculated using invariance of the total energy and magnetic moment. The resulting distribution may or may not be taken to move into a background non-drifting plasma. The distribution function is used in a dispersion relation for the R-X mode which is easily obtainable from the susceptibility tensor given by Stix (1992). The frequencies of interest lie below but close to the electron cyclotron frequency. We assume that the Larmor radius is much less than the wavelength for typical electron velocities. This latter condition means that we need only consider the susceptibility to lowest order in $\frac{k_{\perp }v_{\perp }}{\Omega_{\rm e}}.$ If we neglect all but the zero order terms in the susceptibility tensor we get the cold plasma result. To a first approximation we need only take account of the velocity distribution of the electrons in the resonant integral which involves $1/\left(\omega - \Omega_{\rm e}\right)$ where $\Omega_{\rm e}$ is the relativistic electron cyclotron frequency ${eB \over {\gamma m_{\rm e}}}$ with e the electron charge, B the magnetic field $\gamma$ the Lorenz factor and $m_{\rm e}$ the electron rest mass. In this resonant term we must take account of the relativistic shift of the cyclotron frequency, since this picks out a particular group of resonant electrons and produces damping or growth of the wave.

$\begin{figure} \par\includegraphics[width=6cm,clip]{ceti-fig1.ps}\end{figure}$	Figure 1: Contour plot in momentum space of the perpendicular and parallel electron momentum components of the evolved horseshoe or cresecent distribution function. The horseshoe is formed from an initial Maxwellian electron beam of energy 10 keV with thermal spread moving into a magnetic mirror with initial to final magnetic field ratio of 0.1
Open with DEXTER

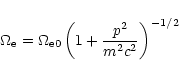$\begin{displaymath}\Omega_{\rm e} =\Omega _{\rm e0}\left(1+\frac{p^{2}}{m^{2}c^{2}}\right)^{-1/2} \end{displaymath}$

(1)

For the real part of the resonant integral we can simply take the cold plasma value. Although this goes as $1/(\omega -\Omega _{\rm e0})$ and appears to be near singular at the resonance, the $1/(\omega -\Omega _{\rm e0})$ factors in the real part of the dispersion relation cancel out, as we shall see, and it behaves quite smoothly in the vicinity of the cyclotron frequency. It is not crucial to include small corrections to the cyclotron frequency in the real part of the dispersion relation. The refractive index n for the R-X mode is given by (Stix 1992).

$\begin{figure} \par\includegraphics[width=6cm,clip]{ceti-fig2.ps}\end{figure}$	Figure 2: Spatial growth rate $Im\ k_{\perp } = \gamma _{\perp }$ of the R-X mode normalized to $\Omega _{\rm ce}/c$ as a function of frequency
Open with DEXTER

$\begin{displaymath}n^{2}=\left(\varepsilon_{\perp}^{2}- \varepsilon _{xy}^{2}\right)/ \varepsilon _{\perp} \end{displaymath}$

(2)

$\displaystyle \varepsilon _{\perp }$	=	$\displaystyle 1-\frac{1}{2}\frac{\omega _{\rm p}^{2}}{\omega (\omega + \Omega _{\rm e0})}+A$	(3)
$\displaystyle \varepsilon _{xy}$	=	$\displaystyle \frac{1}{2}\frac{\omega _{\rm p}^{2}}{\omega (\omega + \Omega _{\rm e0})}+A$	(4)

$\displaystyle A = -\frac{1}{2}\frac{\omega _{\rm p}^{2}}{\omega (\omega- \Omega... ...\rm o} }\int_{1}^{-1} \left(1 - \mu^{2}\right) p_{\rm o}^{2}\gamma_{\rm o}^{2}.$
$\displaystyle \left\{{\partial f_{\rm o} \over {\partial p}} - \frac{\mu}{p_{\r... ... o} \over {\partial_{\mu}}}\right\}\left\vert _{p=p_{\rm o}} \right. {\rm d}\mu$			(5)

Using Eq. (5) in Eqs. (3) and (4) we can analyse the stability of Eq. (2) with respect to induced emission of right hand polarized radiation. We consider the generation of R-X mode radio emission from UV Ceti using an electron beam moving into a strong dipole field in the polar regions. The initial beam is considered to be an isotropic Maxwellian beam with energy 10 keV and a thermal spread of 1 keV. Such beams could result from flare activity described by the model of McClements et al. (1993). The beam is assumed to be formed in the equatorial region and moves into stronger field regions. Figure 1 illustrates the characteristic crescent or horseshoe distribution where the ratio of the final field strength to initial field strength is 10. Using this distribution in Eq. (2) we obtain the growth rate shown in Fig. 2, growth corresponds to negative imaginary $k \left(Im\, k\right)$ . We have assumed a magnetic field ratio of 10 and the ratio of the plasma frequency to cyclotron frequency $\left(\omega_{\rm pe}/\Omega_{\rm ce}\right) = 0.01$ corresponding to low density in the polar regions. A typical convective growth length across the magnetic field is $L_{\rm c} = 2\pi/Im\ k_{\perp}$ of order $10 \lambda$ , where $Im\ k_{\perp}$ is the spatial growth rate obtained from Fig. 2 and $\lambda$ is the wavelength of the R-X mode of order 10 cm for a magnetic field strength of 10³ Gauss, this growth distance is extremely short of order 1 m, allowing many e-foldings within the unstable polar regions of the star. It should be noted that the emission is primarily in the plane perpendicular to the magnetic field and the bandwidth from Fig. 2 is also extremely narrow of order 1 MHz or less.

In the low density regime, the growth rate of the R-X mode is inversely proportional to the density, at least so long as the density is not very low, while the growth rate of the ordinary mode is proportional to the density. This explains why the R-X mode is the dominant feature of radiation in regions where $\omega_{\rm p} \ll \Omega_{\rm e}$ . In the analysis by Benz et al. (1998) they estimated that the plasma density was <10⁸ cm^-3 giving a plasma frequency of 10⁸ Hz, i.e. much less than the frequency used in the observation (8.33 GHz). Our mechanism also explains the fact that the emission is perpendicular to the magnetic field. A parallel component of wavenumber introduces a Doppler shift into the resonance condition, so that the resonant particles no longer lie on a sphere centred on the origin in momentum space. This means, in turn, that for any significant Doppler shift, the resonant particles will no longer all lie in the part of the distribution function where there is a positive slope towards increasing energy. Apart from the density the essential parameters which determine the stability are the initial thermal spread of the beam and the factor by which the magnetic field increases. Together these determine the width of the horseshoe. The frequency range which is unstable is that for which the resonant momentum lies on the low energy side of the horseshoe, where $\partial f_{\rm e}/\partial_{\perp} > 0$ . The higher the beam velocity the more this is shifted below the cyclotron frequency.

The mechanism we have described takes place in a low density region where the electron plasma frequency is much less than the electron cyclotron frequency with the waves being emitted perpendicular to the magnetic field. The problem of absorption can be overcome if we consider the radiation to be produced within a density cavity much like the auroral cavity. Such cavities are a natural result of the dipole model proposed by Kellett et al. (2001). Within the cavity multiple scattering from the edge which contains the right hand cutoff, would produce more parallel propagating R-X mode. As the magnetic field weakens this will occur for outward propagating modes eventually the mode will exceed the right cutoff frequency at which point the waves can freely propagate out into space. An important aspect of our model is that it is driven by a beam moving into a larger magnetic field region and can therefore take place far from the stellar surface unlike the loss-cone mechanism. The observations from UV-Ceti confirm that the mechanism is indeed far from the surface.

4 Conclusions

In this article we have developed an analytical approach describing the cyclotron maser instability convective spatial growth rate, which may produce radio emission of R-X mode radiation from UV Ceti. The instability is sensitive to the ratio of $\Omega_{\rm ce}/\omega_{\rm pe}$ which must be large $\gg$ 1, the opening angle of the tip of the distribution, typically >35 $^{\circ}$ for instability, and the thermal width of the horseshoe distribution.

We suggest that the spreading in parallel velocity as a beam moves into a region of increasing magnetic field may trigger instability and microwave emission. Our results indicate that as the angular width of the beam crosses the instability threshold, a very strong instability rapidly sets in when the density is low. Our model seems to be capable of explaining the strong microwave emission, the narrow bandwidth, the importance of low density regions and coming from regions high in the polar regions of the stellar atmosphere. Future particle-in-cell simulations will investigate self consistently the instability starting with an isotropic beam moving into a stronger magnetic field which will reveal a more realistic comparison with the observations.

The model of radio emission from UV Ceti proposed in this paper differs from the model of Benz et al. (1998). We have shown that a cyclotron maser model can account for the almost 100% right hand polarized high brightness emission. The emission is coming from the polar regions of a dipole type field described by Kellett et al. (2001), with the field strength being close to 10³ Gauss. The radio emission is similar to the new model of the Earth's auroral kilometric radiation proposed by Bingham & Cairns (2000) and Ergun et al. (2000).

Coherent cyclotron maser radiation from UV Ceti

1 Introduction

2 Background observations

3 Cyclotron maser emission

4 Conclusions

References