- In the case of several solar events of the same type associated with a CME, only the nearest event is shown. Speed and acceleration of CME are in
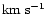 and
and
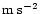 ,
respectively.
,
respectively.
-
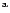
- First appearance time, UT.
-
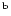
- Maximum time, UT.
-
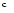
- Start time, UT.
Lists showing the first appearance times and characteristics of CMEs detected in the SOHO LASCO C2/C3 images during January 1997-June 1998 contain 670 records (St. Cyr et al. 2000). In 542 cases it was possible to find polynomial fits to the CME height-time data in the 2-30 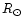 field of view using the data reduction method described by Hundhausen et al. (1994) and St. Cyr et al. (1999). The first order (constant speed) fits are valid in 450 cases. The quadratic (constant acceleration) fits work in 92 ejections. In the latter case both the acceleration value and the final value of the CME speed are listed in the tables. We employ this set of polynomial fits to test a hypothesis that production of SEPs depends not only on the CME velocity, v, but also on the acceleration, a.
field of view using the data reduction method described by Hundhausen et al. (1994) and St. Cyr et al. (1999). The first order (constant speed) fits are valid in 450 cases. The quadratic (constant acceleration) fits work in 92 ejections. In the latter case both the acceleration value and the final value of the CME speed are listed in the tables. We employ this set of polynomial fits to test a hypothesis that production of SEPs depends not only on the CME velocity, v, but also on the acceleration, a.
In the case of function of two arguments, f(a,v), the a-dependence must be studied at a fixed value of v. Otherwise an implicit dependence via the velocity, which is in itself dependent on acceleration, f(v(a)), might be mistaken for the explicit dependence
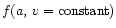 .
This reasoning is equally valid for a statistical study, with the correction that values v and a must be replaced with a set of bins in those variables. Width of the bins is dictated by the statistics available. We adopt
.
This reasoning is equally valid for a statistical study, with the correction that values v and a must be replaced with a set of bins in those variables. Width of the bins is dictated by the statistics available. We adopt 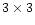 bins in the velocity-acceleration plane. There are three bins in v: (V1) v<300 km s-1; (V2) 300<v<800 km s-1; and (V3) v>800 km s-1. For the three bins in acceleration we employ: (A1) a subclass of accelerating LASCO CMEs with a<10 m s-2 (note that in all registered cases a>2 m s-2); (A2) a subclass of accelerating LASCO CMEs with
bins in the velocity-acceleration plane. There are three bins in v: (V1) v<300 km s-1; (V2) 300<v<800 km s-1; and (V3) v>800 km s-1. For the three bins in acceleration we employ: (A1) a subclass of accelerating LASCO CMEs with a<10 m s-2 (note that in all registered cases a>2 m s-2); (A2) a subclass of accelerating LASCO CMEs with 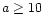 m s-2 (note that in the middle velocity-bin 85% of them have a<20 m s-2); and (A3) constant-speed LASCO CMEs, which experience a strong acceleration below
m s-2 (note that in the middle velocity-bin 85% of them have a<20 m s-2); and (A3) constant-speed LASCO CMEs, which experience a strong acceleration below 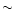 2-4
2-4
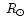 .
The estimated lower limit for the acceleration of the latter group CMEs is
.
The estimated lower limit for the acceleration of the latter group CMEs is
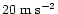 .
A poor statistics of accelerating CMEs in the high velocity range, V3, and the low expectation of SEP production by the low velocity CMEs in the V1 range send us in a search for the a-dependence in the V2 range only
.
A poor statistics of accelerating CMEs in the high velocity range, V3, and the low expectation of SEP production by the low velocity CMEs in the V1 range send us in a search for the a-dependence in the V2 range only![[*]](/icons/foot_motif.gif) .
.
In an effort to observe even not very strong effect of acceleration we initially select CMEs most separated in a, groups A1 and A3. Then the A2 group will be also employed. Thus we start with comparison of the SEP-event occurrences in association with two groups of CMEs: 1) V2_A3, constant speed CMEs with (two digit rounded) speed values in the range from 300 km s-1 through 800 km s-1; and 2) V2_A1, gradually accelerating CMEs in the same speed range with the acceleration value
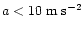 .
We have 253 CMEs of the first type and 43 CMEs of the second type. Hereinafter the first type CMEs are termed impulsive, and the second type CMEs are termed gradual for short, despite this definition of the classes does not exactly coincide with the definition by Sheeley et al. (1999). Figures 1 and 2 show distributions of the impulsive and gradual CMEs over the speed and over the angular width. The SEP-associated impulsive CMEs and all gradual CMEs are listed in Tables 1 and 2, respectively.
.
We have 253 CMEs of the first type and 43 CMEs of the second type. Hereinafter the first type CMEs are termed impulsive, and the second type CMEs are termed gradual for short, despite this definition of the classes does not exactly coincide with the definition by Sheeley et al. (1999). Figures 1 and 2 show distributions of the impulsive and gradual CMEs over the speed and over the angular width. The SEP-associated impulsive CMEs and all gradual CMEs are listed in Tables 1 and 2, respectively.
The CME associated SEP-events were selected using the ERNE
 MeV proton data. In the first stage of selection we find all significant enhancements in the 6.4-12.7 MeV proton channel. Then the neighboring energy channels are used (i) for revealing simultaneous increases in different energy channels, which obviously are of a local origin and should be dropped, and (ii) for refining solar injection time of the first protons observed above the background
MeV proton data. In the first stage of selection we find all significant enhancements in the 6.4-12.7 MeV proton channel. Then the neighboring energy channels are used (i) for revealing simultaneous increases in different energy channels, which obviously are of a local origin and should be dropped, and (ii) for refining solar injection time of the first protons observed above the background![[*]](/icons/foot_motif.gif) .
In the last stage an association of the SEP event with a CME is established, if the first proton injection time does not differ by more than
.
In the last stage an association of the SEP event with a CME is established, if the first proton injection time does not differ by more than
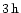 from the first appearance time of a CME. The
from the first appearance time of a CME. The
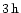 criterion is adopted because the rising phase of the SEP event may extend until the time of the CME arrival at
criterion is adopted because the rising phase of the SEP event may extend until the time of the CME arrival at 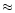 10
10 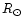 (Kahler 1994), and the pre-event background may be enhanced. The list of CMEs associated with proton events is given in Table 1. It turns out that all 19 SEP-associated CMEs are impulsive. None of gradual CMEs (Table 2) was accompanied by
(Kahler 1994), and the pre-event background may be enhanced. The list of CMEs associated with proton events is given in Table 1. It turns out that all 19 SEP-associated CMEs are impulsive. None of gradual CMEs (Table 2) was accompanied by 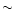 10 MeV proton event in ERNE.
10 MeV proton event in ERNE.
We also studied association of different groups of CMEs with (i) soft X-ray flares, (ii)
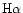 flares, (iii) metric type II radio bursts, and (iv) type IV bursts, using lists available in Solar-Geophysical Data (1997, 1998). The association of a solar event (i-iv) with the CME is established if in the
flares, (iii) metric type II radio bursts, and (iv) type IV bursts, using lists available in Solar-Geophysical Data (1997, 1998). The association of a solar event (i-iv) with the CME is established if in the
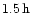 vicinity of the first appearance time of CME we find at least one of the following times of the solar event: start or maximum time of soft X-ray flare, start time of
vicinity of the first appearance time of CME we find at least one of the following times of the solar event: start or maximum time of soft X-ray flare, start time of
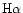 flare, start time of type II/IV radio burst. The CME-associated solar events are also listed in Tables 1 and 2. Different associations are summarized in Fig. 3 for all gradual CMEs, for all impulsive CMEs, and also for the impulsive CMEs associated with proton events (SEP-producing CMEs).
flare, start time of type II/IV radio burst. The CME-associated solar events are also listed in Tables 1 and 2. Different associations are summarized in Fig. 3 for all gradual CMEs, for all impulsive CMEs, and also for the impulsive CMEs associated with proton events (SEP-producing CMEs).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{h2617F01.eps}\end{figure}](/articles/aa/full/2001/18/aah2617/Timg30.gif) |
Figure 1:
Speed distributions of impulsive and gradual (
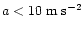 )
CMEs. Total statistics are 253 and 43 CMEs, respectively. The row "6, 5, 1, 2, 5'' shows numbers of SEP events associated with impulsive CMEs in the corresponding sub-bins )
CMEs. Total statistics are 253 and 43 CMEs, respectively. The row "6, 5, 1, 2, 5'' shows numbers of SEP events associated with impulsive CMEs in the corresponding sub-bins |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2617F02.eps}\end{figure}](/articles/aa/full/2001/18/aah2617/Timg31.gif) |
Figure 2:
Width distributions of impulsive and gradual (
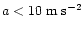 )
CMEs. Total statistics are 253 and 43 CMEs, respectively )
CMEs. Total statistics are 253 and 43 CMEs, respectively |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{h2617F03.eps}\end{figure}](/articles/aa/full/2001/18/aah2617/Timg32.gif) |
Figure 3:
Percentage of CMEs associated with soft X-ray and
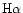 flares, type II and IV radio bursts for the different CME groups. Total statistics are 43, 100, and 19 for the gradual (
flares, type II and IV radio bursts for the different CME groups. Total statistics are 43, 100, and 19 for the gradual (
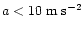 )
CMEs, impulsive CMEs, and SEP-associated CMEs, respectively. The 100 impulsive CMEs have been selected by a random number generator from the total 253 impulsive CMEs )
CMEs, impulsive CMEs, and SEP-associated CMEs, respectively. The 100 impulsive CMEs have been selected by a random number generator from the total 253 impulsive CMEs |
| Open with DEXTER |
Our search revealed
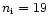 SEP-associated CMEs (Table 1) among the total
SEP-associated CMEs (Table 1) among the total
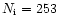 impulsive CMEs, whereas no SEP-associated CMEs (
impulsive CMEs, whereas no SEP-associated CMEs (
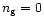 )
were found among
)
were found among
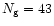 gradual CMEs (Table 2). To check whether this is by a random chance or not, one can employ a statistics
gradual CMEs (Table 2). To check whether this is by a random chance or not, one can employ a statistics
![\begin{displaymath}\chi^2=(n_{\rm i}N_{\rm g}-n_{\rm g}N_{\rm i})^2[N_{\rm i}N_{\rm g}(n_{\rm i}+n_{\rm g})]^{-1}
\end{displaymath}](/articles/aa/full/2001/18/aah2617/img37.gif) |
(1) |
at one degree of freedom (Bolshev & Smirnov
1983). This criterion verifies a conclusion that probabilities to observe SEP events in association with impulsive CMEs and in association with gradual (<10 m s
-2) CMEs are significantly different. The straightforward calculation of
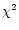
yields at this stage the Estimated Confidence Level
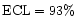
![[*]](/icons/foot_motif.gif)
.
We have compared gradual CMEs with acceleration
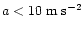 and impulsive CMEs, both in the speed range
and impulsive CMEs, both in the speed range
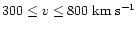 .
The comparison reveals a significant difference in association of the two groups of CMEs with
.
The comparison reveals a significant difference in association of the two groups of CMEs with  10 MeV proton events. The gradually accelerating CMEs did not produce SEP events, while about 8% of impulsive CMEs were associated with SEP events at SOHO. Note that the latter percentage accounts only for the SEP events observable at a given solar longitude. The longitude-integrated probability is significantly higher, most likely above 70%, because the average size of the impulsive CMEs is only 77
10 MeV proton events. The gradually accelerating CMEs did not produce SEP events, while about 8% of impulsive CMEs were associated with SEP events at SOHO. Note that the latter percentage accounts only for the SEP events observable at a given solar longitude. The longitude-integrated probability is significantly higher, most likely above 70%, because the average size of the impulsive CMEs is only 77 .
Note that for gradual CMEs with a<10 m s-2 (15 m s-2) the mean size is 93
.
Note that for gradual CMEs with a<10 m s-2 (15 m s-2) the mean size is 93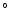 (97
(97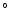 ).
The difference is revealed between frequencies of the SEP-event occurrences in the V2_A1 and V2_A3 CME bins, at the confidence level
).
The difference is revealed between frequencies of the SEP-event occurrences in the V2_A1 and V2_A3 CME bins, at the confidence level
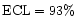 .
In additional set of calculations, we tested sensitivity of the result to the biases in the speed/size distributions, and to the choice of the bin boundaries. Effect of the V2_A2 data-bin employment was also investigated.
.
In additional set of calculations, we tested sensitivity of the result to the biases in the speed/size distributions, and to the choice of the bin boundaries. Effect of the V2_A2 data-bin employment was also investigated.
Previously reported correlation between SEP intensities and CME speeds finds its counterpart in a speed dependence of probability to observe SEP event in association with a given CME. This is evident from comparison of the event statistics in different velocity bins, V1_A3 vs. V2_A3 vs. V3_A3. In the medium velocity bin V2_A3 we find 19 events per 253 CMEs, whereas there are 14 SEP events per 38 CMEs in the high speed bin V3_A3, and only one event per 159 CMEs in the lowest speed bin V1_A3. Thus the percentage of SEP events per one CME rises from less or about 1% for the low speed CMEs,
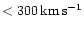 ,
to almost 40% for high speed CMEs,
,
to almost 40% for high speed CMEs,
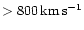 .
Such a tendency, if it holds inside the V2 range, may slightly affect our comparison of different acceleration bins, V2_A1 vs. V2_A3, if velocity distributions inside the bins are biased in respect to one another.
.
Such a tendency, if it holds inside the V2 range, may slightly affect our comparison of different acceleration bins, V2_A1 vs. V2_A3, if velocity distributions inside the bins are biased in respect to one another.
One can note in Fig. 1 approximately three fold excess in the number of impulsive CMEs in the highest speed sub-bin, 700-800 km s-1, as compared to the gradual CMEs. In order to examine whether this bias can affect our result, we dropped three SEP events of five corresponding to this bin, along with the corresponding portion of impulsive 700-800 km s-1 CMEs. Such a manipulation alone shifts the estimated confidence level for the difference between the V2_A1 and V2_A3 CMEs from 93% down to 90%, but it should be also taken into account that on the whole gradual CMEs are wider than the impulsive ejections (Fig. 2). Correspondingly SEPs from gradual CMEs might be more easily detected at a spacecraft. A straightforward correction for the difference in the CME solid angles shifts the ECL value from 90% up to 95%. Hence, accounting for the biases in the speed/size distributions finally rises the confidence level to
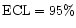 .
.
We have additionally analyzed a possible role of the middle acceleration-bin, V2_A2, which contains accelerating LASCO CMEs with acceleration in excess of 10 m s-2. There are 20 CMEs and 3 SEP events in V2_A2, whereas in the V2_A3 bin we have 253 CMEs and 19 SEP events, and 43 CMEs and no SEP events in V2_A1. Appearance of SEP events in V2_A2 may indicate increase in the SEP-event probability as the CME acceleration increases inside the class of accelerating LASCO CMEs. Comparable frequencies of SEP-events in V2_A2 and V2_A3 bins justify integration of the bins. If one had merged all a>10 m s-2 CMEs into the enlarged bin, V2_A2+V2_A3, and compared a<10 and a>10 m s-2 CMEs, the estimated confidence level would be close to the ECL value for comparison V2_A1 vs. V2_A3. We also employed the bin boundary a=15 m s-2, instead of our basic a=10 m s-2, and compared gradual CMEs with a<15 m s-2 and all a>15 m s-2 CMEs. In this case, 12 more CMEs fall into the slow acceleration group, including a single SEP-event, so that we have 1 SEP-event per 55 slow-acceleration CMEs and 21 SEP-events per 261 fast-acceleration CMEs. At this division, a bias in the speed distributions is absent, but the angular size difference persists, and the resultant
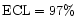 .
.
On the other hand, the merge of bins V2_A2 and V2_A1 a priori removes the acceleration dependence in a very wide region 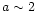 -20 m s-2 and should obscure the general trend observable in the three bin succession. Despite this argument against the merge, one may attempt to compare the enlarged bin V2_A1+V2_A2 and V2_A3, arguing that V2_A1+V2_A2 represents a separate class of LASCO CMEs according to the visual "constant-speed vs. accelerating'' CME classification. Such a comparison, at velocity/width biases
corrected
-20 m s-2 and should obscure the general trend observable in the three bin succession. Despite this argument against the merge, one may attempt to compare the enlarged bin V2_A1+V2_A2 and V2_A3, arguing that V2_A1+V2_A2 represents a separate class of LASCO CMEs according to the visual "constant-speed vs. accelerating'' CME classification. Such a comparison, at velocity/width biases
corrected![[*]](/icons/foot_motif.gif) ,
yields a conclusion that the frequency of SEP-events associated with accelerating CMEs and the frequency of SEP-events associated with constant-speed CMEs are different at
,
yields a conclusion that the frequency of SEP-events associated with accelerating CMEs and the frequency of SEP-events associated with constant-speed CMEs are different at
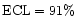 .
A number of tests performed indicate that on the whole our basic result is qualitatively stable and suggests increase in the frequency of SEP events as the CME acceleration increases above
.
A number of tests performed indicate that on the whole our basic result is qualitatively stable and suggests increase in the frequency of SEP events as the CME acceleration increases above 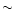 10 m s-2.
10 m s-2.
The 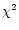 -test revealed significant distinctions also between the CME
-test revealed significant distinctions also between the CME
 flare associations (Fig. 3). Degrees of association in different pairs, gradual/impulsive/SEP-associated CMEs versus X-ray/type II bursts, are significantly different at
flare associations (Fig. 3). Degrees of association in different pairs, gradual/impulsive/SEP-associated CMEs versus X-ray/type II bursts, are significantly different at
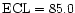 -
-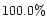 .
We find that the moderate-speed impulsive CMEs associated with SEPs are also highly associated with X-ray flares and type II radio bursts. Thus, the typical SEP-producing CME is that impulsively accelerated at heliocentric distances < 2-
.
We find that the moderate-speed impulsive CMEs associated with SEPs are also highly associated with X-ray flares and type II radio bursts. Thus, the typical SEP-producing CME is that impulsively accelerated at heliocentric distances < 2-
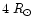 in association with soft X-ray flare and coronal shocks. We would like to stress that we do not examine association of flares and SEPs. Our statistics is related to the association of different groups of CMEs with X-ray flares and type II/IV radio burst. Among others, we have considered a group of CMEs which were accompanied by SEP events at SOHO. It turns out that these SEP-producing CMEs are highly associated with X-ray flares, despite only a small portion of flares is associated with SEP events.
In early 1980s, MacQueen & Fisher (1983) studied 12 CMEs and found that flare-related CMEs moved at constant speeds, whereas prominence-related mass ejections accelerated. A more comprehensive study that determines accelerations for CMEs based on SMM and Mauna Loa observations confirms that conclusion (St. Cyr et al. 1999). Recent investigations with LASCO (Sheeley et al. 1999) suggest two principal types of CMEs: gradually accelerating CMEs and impulsive CMEs. Impulsive CMEs, often associated with flares and Moreton waves, move uniformly across the LASCO field of view. Hence, CMEs of this kind should experience a strong acceleration when getting a full speed during a short period below
in association with soft X-ray flare and coronal shocks. We would like to stress that we do not examine association of flares and SEPs. Our statistics is related to the association of different groups of CMEs with X-ray flares and type II/IV radio burst. Among others, we have considered a group of CMEs which were accompanied by SEP events at SOHO. It turns out that these SEP-producing CMEs are highly associated with X-ray flares, despite only a small portion of flares is associated with SEP events.
In early 1980s, MacQueen & Fisher (1983) studied 12 CMEs and found that flare-related CMEs moved at constant speeds, whereas prominence-related mass ejections accelerated. A more comprehensive study that determines accelerations for CMEs based on SMM and Mauna Loa observations confirms that conclusion (St. Cyr et al. 1999). Recent investigations with LASCO (Sheeley et al. 1999) suggest two principal types of CMEs: gradually accelerating CMEs and impulsive CMEs. Impulsive CMEs, often associated with flares and Moreton waves, move uniformly across the LASCO field of view. Hence, CMEs of this kind should experience a strong acceleration when getting a full speed during a short period below  2-4
2-4
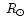 .
.
Kahler et al. (1999) proposed the CME acceleration value as a candidate factor affecting production of >20 MeV protons, because "an accelerating CME may produce a shock later than a CME with a constant speed''. Based on this kinematics-type explanation and on the result of the present statistical study, a question should be raised as to why it is so crucial for shock to appear close to Sun. In this respect two reasons might be considered: (i) a constant-speed shock maintains high Mach numbers predominantly close to Sun, and (ii) a seed particle/wave population for the (moderate-speed) CME-shock acceleration is available only near the Sun. We see no arguments in favour of the first item over the second one, because Alfvén speed does not decrease towards the Sun. On the other hand, Torsti et al. (2001) analyzed the May 9, 1999 SEP event associated with impulsive CME (540 km s-1), X-ray flare, and continuum radio burst in metric band. The case study supports a kind of "closed-chain scenario'': an early rise of CME triggers the X-ray flare that starts a coronal wave, which in its turn initiates proton acceleration apart from the flare site. This first proton acceleration is triggered by the coronal counterparts of CME but followed by the long-term acceleration at the CME-driven shock in the interplanetary medium. It was suggested that the first acceleration may provide a seed population for the second one. Note that in the case of the May 9, 1999 event, neither of the accelerations was identified with the flare-site acceleration. However, presently available case studies are still not sufficient to decide whether such a scenario is typical for the impulsive CMEs of a moderate speed.
We have studied SEP production by the 300-800
 CMEs, and conclude that data in hand support the following
CMEs, and conclude that data in hand support the following
- 1.
- The near-Sun dynamics of CME is a significant factor contributing to the intensities of
 10 MeV proton events;
10 MeV proton events;
- 2.
- A typical SEP-producing CME experiences fast acceleration close to Sun in association with soft X-ray flare and coronal shocks;
- 3.
- The CMEs (very) gradually accelerating across the 2-30
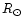 field of view with acceleration 2-10
field of view with acceleration 2-10
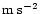 are less likely to produce > 10 MeV SEP events.
are less likely to produce > 10 MeV SEP events.
The conclusions have been drawn with a statistical method at the estimated confidence level of about
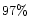
.
These results indicate that at least in the moderate speed range the CME acceleration must be further considered as a significant factor affecting production of solar energetic particles along with the CME speed. The joint analysis of the LASCO and ERNE data-sets brings out one more promising direction for the SEP-CME investigations.
Acknowledgements
The ERNE team thanks Academy of Finland for the grant. The SOHO is an international cooperation project between ESA and NASA.
-
Bolshev, L. N., & Smirnov, N. V. 1983, Tables of mathematical statistics, Nauka, Moscow, 359
In the text
-
Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357
In the text
NASA ADS
-
Cane, H. V., Richardson, I. G., & St. Cyr, O. C. 1998,
GRL, 25, 2517; Correction: 26, 2149
In the text
-
Fox, N. J., Peredo, M., & Thompson, B. J. 1998,
GRL, 25, 2461
In the text
-
Hundhausen, A. J., Burkepile, J. T., & St. Cyr, O. C. 1994,
JGR, 99, 6543
In the text
NASA ADS
-
Kahler, S. W., Sheeley Jr., N. R., Howard, R. A., et al. 1984,
JGR, 89, 9683
In the text
NASA ADS
-
Kahler, S. 1994, ApJ, 428, 837
In the text
NASA ADS
-
Kahler, S., Burkepile, J. T., & Reames, D. V. 1999,
Proc. 26th Internat. Cosmic Ray Conf., Salt Lake City, 6, 248
In the text
-
Laitinen, T., Klein, K.-L., Kocharov, L., et al. 2000, A&A, 360, 729
In the text
NASA ADS
-
MacQueen, R. M., & Fisher, R. R. 1983, Sol. Phys., 89, 89
In the text
NASA ADS
-
Reames, D. V. 1999, Space Sci. Rev., 90, 413
In the text
NASA ADS
-
Reames, D. V. 2000, in 26th Int. Cosmic Ray Conf., ed. B. L. Dingus, D. B. Kieda, & M. H. Salamon, New York: AIP Conf. Proc. 516, 289
In the text
-
Reiner, M. J., Kaiser, M. L., Fainberg, J., et al. 1998,
GRL, 25, 2493
In the text
-
Solar-Geophysical Data 1997 & 1998, NOAA, Space Environment Center, Boulder, Colorado
In the text
-
Sheeley Jr., N. R., Walters, J. H., Wang, Y.-M., & Howard, R. A. 1999, JGR, 104, 24739
In the text
-
St. Cyr, O. C., Burkepile, J. T., Hundhausen, A. J., & Lecinski, A. R. 1999, JGR, 104, 12493
In the text
-
St. Cyr, O. C., Howard, R. A., Sheeley Jr., N. R., et al. 2000, JGR, 105, 18169 In the text
-
Torsti, J., Valtonen, E., Lumme, M., et al. 1995, Sol. Phys., 162, 505
In the text
-
Torsti, J., Anttila, A., Kocharov, L., et al. 1998, GRL, 25, 2525
In the text
-
Torsti, J., Kocharov, L., Teittinen, M., et al. 1999, JGR, 104, NO. A5, 9903
In the text
-
Torsti, J., Kocharov, L., Innes, D. E., et al. 2001, A&A, 365, 198
In the text
NASA ADS
-
Webb, D. F., Cliver, E. W., Gopalswamy, N., Hudson, H. S., & St. Cyr, O. C. 1998,
GRL, 25, 2469
In the text
-
Wu, S. T., Guo, W. P., Michels, D. J., et al. 1997, in Proc. 5th SOHO Workshop, ed. A. Wilson, Noordwijk: ESA SP-404, 739
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{h2617F01.eps}\end{figure}](/articles/aa/full/2001/18/aah2617/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2617F02.eps}\end{figure}](/articles/aa/full/2001/18/aah2617/Timg31.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{h2617F03.eps}\end{figure}](/articles/aa/full/2001/18/aah2617/Timg32.gif)
![\begin{displaymath}\chi^2=(n_{\rm i}N_{\rm g}-n_{\rm g}N_{\rm i})^2[N_{\rm i}N_{\rm g}(n_{\rm i}+n_{\rm g})]^{-1}
\end{displaymath}](/articles/aa/full/2001/18/aah2617/img37.gif)