A&A 370, 923-930 (2001)
DOI: 10.1051/0004-6361:20010304
Radial density and density evolution of radio galaxies
in the Las Campanas redshift survey
J. Machalski - W. Godlowski
Astronomical Observatory, Jagellonian University,
ul. Orla 171, 30244 Cracow, Poland
Received 23 November 2000 / Accepted 27 February 2001
Abstract
The sample of 1157 radio-identified galaxies from the Las Campanas Redshift
Survey (LCRS) (Machalski & Condon 1999) is used to determine the radial density
of both star-forming (starburst) and AGN-type galaxies with the mean redshift of
0.07 and 0.18, respectively. It is shown that the
radial density distribution of these radio galaxies is essentially different
from the respective distribution of optical galaxies in the parent LCRS sample.
While the optical galaxies reveal a systematic decrease of their spatial density
with redshift (which likely is due to some incompleteness of the optical sample
increasing with the apparent isophotal magnitude of galaxies), the radio-emitting
galaxies exhibit evident positive evolution of their radial density with
redshift. Moreover, most of this density evolution is connected to
starburst-type galaxies whose evolution can be parametrized by
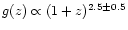 .
No evident density evolution is detected in
LCRS AGN galaxies.
Correcting the 1.4 GHz luminosity function (RLF) (Machalski & Godlowski 2000)
for the above density evolution in starbursts and assuming its lack in AGN, a
pure luminosity evolution
.
No evident density evolution is detected in
LCRS AGN galaxies.
Correcting the 1.4 GHz luminosity function (RLF) (Machalski & Godlowski 2000)
for the above density evolution in starbursts and assuming its lack in AGN, a
pure luminosity evolution
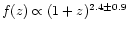 is found for
AGN galaxies after the comparison of the corrected RLF with the local luminosity
function based on nearby UGC galaxies (cf. Condon 1989). Oppositely, no
significant luminosity evolution in starbursts is found.
is found for
AGN galaxies after the comparison of the corrected RLF with the local luminosity
function based on nearby UGC galaxies (cf. Condon 1989). Oppositely, no
significant luminosity evolution in starbursts is found.
Key words: galaxies: active - galaxies: evolution - radio continuum: galaxies
The Las Campanas Redshift Survey of galaxies (Shectman et al. 1996, hereafter
LCRS), containing over 90000 galaxies to a limiting isophotal magnitude of
18.2-18.5, of which over 26000 have spectroscopic redshift measured, is very
useful for a large statistical study of properties of faint radio emission in
the galaxy population lying farther than about 180 Mpc from our Galaxy and the
local space around it. Machalski & Condon (1999; hereafter Paper I) used the
1.4-GHz NRAO-VLA Sky Survey (Condon et al. 1998, hereafter NVSS) to detect radio
emission from LCRS galaxies in the sky area of 0.1438 sr and within a space
volume of about 108 Mpc3. Taking into account a strongly
increasing incompleteness of the LCRS sample with increasing isophotal magnitude
of galaxies (which could be clearly seen in the number-counts of these galaxies),
the radio detection was limited to galaxies with
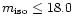 mag.
The optical and radio data, supported by the
IRAS far-infrared (FIR) data, were then used to classify 1157 detected galaxies
by a dominant radio-energy source: starbursts or AGN.
The above sample of 1157 radio galaxies has been used by Machalski & Godlowski
(2000; hereafter Paper II) to derive the 1.4 GHz (radio) luminosity function
(hereafter RLF) of both star-forming galaxies with the mean redshift
mag.
The optical and radio data, supported by the
IRAS far-infrared (FIR) data, were then used to classify 1157 detected galaxies
by a dominant radio-energy source: starbursts or AGN.
The above sample of 1157 radio galaxies has been used by Machalski & Godlowski
(2000; hereafter Paper II) to derive the 1.4 GHz (radio) luminosity function
(hereafter RLF) of both star-forming galaxies with the mean redshift
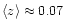 ,
and AGN-type ones with
,
and AGN-type ones with
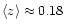 ,
as well as for a direct measure of their
evolution inferred from the evolutionary models of the entire population of
radio sources (e.g. Condon 1984; Dunlop & Peacock 1990). In a result, the
evolution of RLF, in the "translation'' form
,
as well as for a direct measure of their
evolution inferred from the evolutionary models of the entire population of
radio sources (e.g. Condon 1984; Dunlop & Peacock 1990). In a result, the
evolution of RLF, in the "translation'' form
![$\rho_{m}(L,z)=g(z)[L/f(z),z\approx
0]$](/articles/aa/full/2001/18/aah2558/img12.gif) given by Condon (1984), Saunders et al. (1990) and others, has appeared
uncertain at redshifts characteristic for LCRS galaxies. This is caused by a too
large uncertainty of the local luminosity functions determined from bright UGC
galaxies by Condon (1989) and Cotton & Condon (1998) which is of the same order
as an amount of density [g(z)] and/or luminosity [f(z)] evolution expected
from the evolutionary models. However, a direct comparison of the spectral power
density and radial density of UGC and LCRS starburst and AGN galaxies with
1.4-GHz luminosities exceeding 1022.8 W Hz-1 and
1024.0 W Hz-1, respectively (i.e. galaxies from the brighter part of
their RLFs) agreed with a luminosity evolution
given by Condon (1984), Saunders et al. (1990) and others, has appeared
uncertain at redshifts characteristic for LCRS galaxies. This is caused by a too
large uncertainty of the local luminosity functions determined from bright UGC
galaxies by Condon (1989) and Cotton & Condon (1998) which is of the same order
as an amount of density [g(z)] and/or luminosity [f(z)] evolution expected
from the evolutionary models. However, a direct comparison of the spectral power
density and radial density of UGC and LCRS starburst and AGN galaxies with
1.4-GHz luminosities exceeding 1022.8 W Hz-1 and
1024.0 W Hz-1, respectively (i.e. galaxies from the brighter part of
their RLFs) agreed with a luminosity evolution
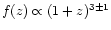 .
An
intriguing fluctuation of the spectral power was noticed if AGN-type galaxies
more luminous than 1024.0 W Hz-1 were divided into three redshift
ranges. Those limited radio data was not sufficient to specify whether that
effect reflected some real clustering of radio galaxies, or was only a
statistical fluctuation of their spatial density.
In this paper we analyse the radial density of starburst-type and AGN-type radio
galaxies in the LCRS sample and compare them with the respective characteristics
of optical galaxies in the parent sample. The principal aim of this investigation
is to look whether the spatial density of radio-emitting galaxies correlates or
not with the respective density of parent optical galaxies, and whether some
density evolution is present in the LCRS sample itself putting aside its
comparison to the density of bright UGC galaxies. Moreover, the data of
Paper I allow to search for such density evolution separately for star-forming
and AGN radio galaxies.
As it was shown in Paper I, in over
60 of 100 cases radio emission has been detected from galaxies not fulfilling
the photometric selection criteria to be observed spectroscopically (cf. Lin et al. 1996). Thus, we cannot confine our analysis only to galaxies with
spectroscopic redshift available, especially if a fraction of galaxies with
known redshift strongly decreases with an increase of their apparent isophotal
magnitude (as in the case of LCRS). On the other hand, presumed effects of
varying radial density or clustering of galaxies can be present at redshifts
corresponding to the faintest magnitudes in the LCRS sample. Therefore, we have
to ascribe a photometric redshift estimate to the remaining optical galaxies,
as it was done for radio-detected galaxies in Papers I and II. This procedure is
summarized in Sect. 2.
The ascribed redshifts are then used to (1) derive the "parent'' radial density
function of optical galaxies taking into account all of them, i.e. those with
spectroscopic redshift and those with its photometric estimate, and (2)
reproduce their optical luminosity function. Comparing this luminosity function
with the original one published by Lin et al., we can test a statistical
correctness of our photometric redshifts. The method of
analysis is described in Sect. 3. First, this method is applied to the entire
optical catalog of LCRS galaxies with the aim to derive their radial density
function to which the respective functions for different types of radio
galaxies can be compared. The resultant radial density and luminosity functions
for the optical galaxies are given in Sect. 4.1. In Sect. 4.2, the same method
is applied to the radio-identified LCRS starburst and AGN galaxies. The radial
densities of optical and radio LCRS galaxies are compared in Sect. 5.
The evident density evolution of starbursts with redshift is shown, and its
consequences for the "translation'' evolution of the RLF are discussed.
The procedure used to evaluate a photometric redshift for radio-identified
LCRS galaxies was described in Paper II. In order to estimate redshift for the
optical galaxies which were not observed spectroscopically, we investigated the
distribution of the absolute isophotal magnitude
.
An
intriguing fluctuation of the spectral power was noticed if AGN-type galaxies
more luminous than 1024.0 W Hz-1 were divided into three redshift
ranges. Those limited radio data was not sufficient to specify whether that
effect reflected some real clustering of radio galaxies, or was only a
statistical fluctuation of their spatial density.
In this paper we analyse the radial density of starburst-type and AGN-type radio
galaxies in the LCRS sample and compare them with the respective characteristics
of optical galaxies in the parent sample. The principal aim of this investigation
is to look whether the spatial density of radio-emitting galaxies correlates or
not with the respective density of parent optical galaxies, and whether some
density evolution is present in the LCRS sample itself putting aside its
comparison to the density of bright UGC galaxies. Moreover, the data of
Paper I allow to search for such density evolution separately for star-forming
and AGN radio galaxies.
As it was shown in Paper I, in over
60 of 100 cases radio emission has been detected from galaxies not fulfilling
the photometric selection criteria to be observed spectroscopically (cf. Lin et al. 1996). Thus, we cannot confine our analysis only to galaxies with
spectroscopic redshift available, especially if a fraction of galaxies with
known redshift strongly decreases with an increase of their apparent isophotal
magnitude (as in the case of LCRS). On the other hand, presumed effects of
varying radial density or clustering of galaxies can be present at redshifts
corresponding to the faintest magnitudes in the LCRS sample. Therefore, we have
to ascribe a photometric redshift estimate to the remaining optical galaxies,
as it was done for radio-detected galaxies in Papers I and II. This procedure is
summarized in Sect. 2.
The ascribed redshifts are then used to (1) derive the "parent'' radial density
function of optical galaxies taking into account all of them, i.e. those with
spectroscopic redshift and those with its photometric estimate, and (2)
reproduce their optical luminosity function. Comparing this luminosity function
with the original one published by Lin et al., we can test a statistical
correctness of our photometric redshifts. The method of
analysis is described in Sect. 3. First, this method is applied to the entire
optical catalog of LCRS galaxies with the aim to derive their radial density
function to which the respective functions for different types of radio
galaxies can be compared. The resultant radial density and luminosity functions
for the optical galaxies are given in Sect. 4.1. In Sect. 4.2, the same method
is applied to the radio-identified LCRS starburst and AGN galaxies. The radial
densities of optical and radio LCRS galaxies are compared in Sect. 5.
The evident density evolution of starbursts with redshift is shown, and its
consequences for the "translation'' evolution of the RLF are discussed.
The procedure used to evaluate a photometric redshift for radio-identified
LCRS galaxies was described in Paper II. In order to estimate redshift for the
optical galaxies which were not observed spectroscopically, we investigated the
distribution of the absolute isophotal magnitude
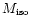 of galaxies from
the original redshift survey of Shectman et al. The equation used to calculate
of galaxies from
the original redshift survey of Shectman et al. The equation used to calculate
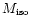 (and
(and 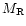 )
is given in Paper I. In that equation the
K-correction is calculated with a constant optical spectral index, and
an eventual correction for the foreground extinction is neglected because
of the high galactic latitudes of the LCRS strips. The distribution of
)
is given in Paper I. In that equation the
K-correction is calculated with a constant optical spectral index, and
an eventual correction for the foreground extinction is neglected because
of the high galactic latitudes of the LCRS strips. The distribution of
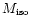 for
5255 galaxies with 14.5
for
5255 galaxies with 14.5
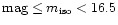 mag and 18 834 with
mag and 18 834 with
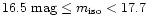 mag are shown in Fig. 1. The mean values and
standard deviations of both distributions are given in the caption of
Fig. 1. Although the means of these two distributions differ only by 0.22 mag,
the Kolmogorov-Smirnov test showed that this difference is very significant
statistically. However, this is a formal difference caused by the simple
calculation of the absolute magnitude of a galaxy with a constant optical
spectral index equivalent to a constant B-R colour. As a matter of fact,
that spectral index evolves with redshift and its evolution can be different for
different
morphological types of galaxies. In general, the above index steepens with
redshift if B-R>1 mag and due to intrinsic evolution of the
stellar content in a galaxy seen at different epochs.
The majority of LCRS galaxies have a redshift in the range 0.05-0.20. If the
evolution of B-R colour within this redshift range for early-type galaxies
(E, S0) (e.g. Bruzual 1983) is taken into account,
mag are shown in Fig. 1. The mean values and
standard deviations of both distributions are given in the caption of
Fig. 1. Although the means of these two distributions differ only by 0.22 mag,
the Kolmogorov-Smirnov test showed that this difference is very significant
statistically. However, this is a formal difference caused by the simple
calculation of the absolute magnitude of a galaxy with a constant optical
spectral index equivalent to a constant B-R colour. As a matter of fact,
that spectral index evolves with redshift and its evolution can be different for
different
morphological types of galaxies. In general, the above index steepens with
redshift if B-R>1 mag and due to intrinsic evolution of the
stellar content in a galaxy seen at different epochs.
The majority of LCRS galaxies have a redshift in the range 0.05-0.20. If the
evolution of B-R colour within this redshift range for early-type galaxies
(E, S0) (e.g. Bruzual 1983) is taken into account,
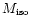 of galaxies
with fainter apparent magnitudes will be enlarged by 0.20 mag, which will
compensate the apparent difference of 0.22 mag. Obviously, the LCRS sample must
contain also a large fraction of spiral galaxies whose spectra are much bluer
in comparison to those in ellipticals, and the difference of 0.22 mag will not
be fully compensated by the spectral evolution. In that view, LCRS galaxies with
fainter
of galaxies
with fainter apparent magnitudes will be enlarged by 0.20 mag, which will
compensate the apparent difference of 0.22 mag. Obviously, the LCRS sample must
contain also a large fraction of spiral galaxies whose spectra are much bluer
in comparison to those in ellipticals, and the difference of 0.22 mag will not
be fully compensated by the spectral evolution. In that view, LCRS galaxies with
fainter
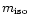 seem to be little less luminous.
seem to be little less luminous.
 |
Figure 1:
Absolute optical magnitude of 24089 LCRS galaxies with 14.5
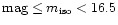 mag (solid line) and with 16.5 mag (solid line) and with 16.5
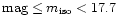 mag
(dashed line). The mean values and standard deviations in these distributions
are -22.11 mag and 0.94 mag, and -21.89 mag and 0.95 mag, respectively mag
(dashed line). The mean values and standard deviations in these distributions
are -22.11 mag and 0.94 mag, and -21.89 mag and 0.95 mag, respectively |
| Open with DEXTER |
Therefore in order to presume a distribution of
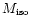 for the
galaxies with
for the
galaxies with
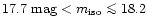 mag, we kept the formal increase of
mag, we kept the formal increase of
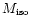 distribution with increasing
distribution with increasing
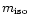 (which resulted from the
calculation of
(which resulted from the
calculation of
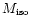 with a constant B-R colour) and found that the
mean of this distribution should be shifted by another 0.1 mag to the value of
about -21.8 mag. Consequently, for each galaxy without spectroscopic redshift
and brighter than 17.7 mag, an absolute magnitude was drawn by chance from the
with a constant B-R colour) and found that the
mean of this distribution should be shifted by another 0.1 mag to the value of
about -21.8 mag. Consequently, for each galaxy without spectroscopic redshift
and brighter than 17.7 mag, an absolute magnitude was drawn by chance from the
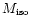 distributions in Fig. 1 whereby, for those fainter than 17.7 mag, +0.10 mag was added to
distributions in Fig. 1 whereby, for those fainter than 17.7 mag, +0.10 mag was added to
![$M_{\rm iso}[16.5\leq m_{\rm iso}<17.7]$](/articles/aa/full/2001/18/aah2558/img20.gif) and used
to calculate the relevant redshift. A statistical error of the radial density
solutions due to uncertain redshift is discussed in Sect. 3.
In order to determine the radial density functions of LCRS galaxies and radio
galaxies, we use the "stepwise maximum likelihood'' (hereafter SWML) method of
Efstathiou et al. (1988) with its modification needed for the
analysis of a sample of objects limited both by the radio and optical flux
densities, as it was shown in Paper II.
As in Saunders et al., we parametrize g(r) as an arbitrary Nz steps
in redshift:
and used
to calculate the relevant redshift. A statistical error of the radial density
solutions due to uncertain redshift is discussed in Sect. 3.
In order to determine the radial density functions of LCRS galaxies and radio
galaxies, we use the "stepwise maximum likelihood'' (hereafter SWML) method of
Efstathiou et al. (1988) with its modification needed for the
analysis of a sample of objects limited both by the radio and optical flux
densities, as it was shown in Paper II.
As in Saunders et al., we parametrize g(r) as an arbitrary Nz steps
in redshift:
 |
(1) |
and maximize the likelihood:
![\begin{displaymath}\ln{\cal L}=\sum_{i=1}^{N}\left\{\ln g(z_{i})-\ln \left[\sum_...
...um_{k=1}^{N_{z}}
g(z_{k})f_{ik}V_{\max,i}\right] +{\rm const},
\end{displaymath}](/articles/aa/full/2001/18/aah2558/img22.gif) |
(2) |
where N is a number of galaxies in the sample,
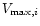 is the maximum
volume determined by the maximum redshift at which the ith galaxy would have
apparent fluxes above both the optical and radio detection limits, and
is the maximum
volume determined by the maximum redshift at which the ith galaxy would have
apparent fluxes above both the optical and radio detection limits, and
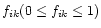 is the fraction of the step volume
contained in the
is the fraction of the step volume
contained in the
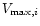 .
Equating the first derivative of the above equation to zero, the maximum
likelihood solution
.
Equating the first derivative of the above equation to zero, the maximum
likelihood solution 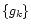 ,
for each k is
,
for each k is
![\begin{displaymath}g_{k}=n_{k}\left\{\sum_{i=1}^{N}\left[f_{ik}V_{k}\left(\sum_{...
...{N_{z}}
g_{j}f_{ij}V_{\max,i}\right)^{-1}\right]\right\}^{-1}.
\end{displaymath}](/articles/aa/full/2001/18/aah2558/img26.gif) |
(3) |
After the differentiation Vk is the volume of the kth redshift bin,
and fik in Eq. (3) is the fraction of the Vk available to the
ith galaxy.
Setting the average density to unity, we arbitrary normalize the radial density
distributions. The radial density function derived as above describes a density
fluctuations of galaxies regardless on their luminosities. In order to stress
its relativity for different type galaxies, hereafter we write the normalized
radial density function by gn(z).
Given the radial density fluctuations, the luminosity function of galaxies can
be reconstructed with the simple binned
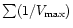 method which (in this
case) accounts for these fluctuations. The application of this method to the
optical LCRS sample allows to check a correctness of the statistical redshift
estimates.
Following the Saunders et al. analysis, we sum reciprocals of the "effective''
volume
method which (in this
case) accounts for these fluctuations. The application of this method to the
optical LCRS sample allows to check a correctness of the statistical redshift
estimates.
Following the Saunders et al. analysis, we sum reciprocals of the "effective''
volume
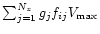 over all galaxies with
absolute magnitude fulfilling
over all galaxies with
absolute magnitude fulfilling
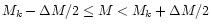 .
That is
.
That is
 |
(4) |
where wik=1 if absolute magnitude of the ith galaxy is within the
kth absolute magnitude bin, otherwise wik=0.
The estimates of gk and 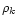 ,
derived as above, are biased by
two statistical errors. The first one is the error of SWML solution which is
mainly dependent on the number of galaxies in a bin. This error is strongly
asymmetric when the numbers are small, and is calculated like that in Efstathiou
et al. and Saunders et al. The second one arises from the redshift error in the
calculation of space volume.
Like in Paper II, we have evaluated the second error, performing a large
number of Monte Carlo simulations in which, for each galaxy without spectroscopic
redshift, a
,
derived as above, are biased by
two statistical errors. The first one is the error of SWML solution which is
mainly dependent on the number of galaxies in a bin. This error is strongly
asymmetric when the numbers are small, and is calculated like that in Efstathiou
et al. and Saunders et al. The second one arises from the redshift error in the
calculation of space volume.
Like in Paper II, we have evaluated the second error, performing a large
number of Monte Carlo simulations in which, for each galaxy without spectroscopic
redshift, a
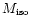 was drawn by chance from the distributions shown in
Fig. 1. The standard deviation of gk and
was drawn by chance from the distributions shown in
Fig. 1. The standard deviation of gk and 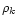 values in the
kth bin, resulted from the above simulations, is taken as the second error.
Thus, the total statistical error is calculated combining both errors quadrically.
The observed numbers in the redshift bins of 0.02 and
the estimates of the normalized gn (z) function for 78 298 optical
galaxies with 12.25
values in the
kth bin, resulted from the above simulations, is taken as the second error.
Thus, the total statistical error is calculated combining both errors quadrically.
The observed numbers in the redshift bins of 0.02 and
the estimates of the normalized gn (z) function for 78 298 optical
galaxies with 12.25
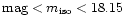 mag selected from the LCRS photometric catalog are tabulated in Cols. 2 and 3 of Table 1, respectively,
and plotted in Fig. 2. Vertical bars indicate the statistical rms uncertainty
(variance) in each of the bin. The gn (z) estimates computed for
the galaxies with spectroscopic redshift only (marked by the dots in Fig. 2)
emphasize the known incompleteness of the LCRS sample due to the original
selection effects dominated by the central surface brightness selection
(cf. Lin et al.).
The derived radial densities systematically decrease with increasing redshift,
at least from
mag selected from the LCRS photometric catalog are tabulated in Cols. 2 and 3 of Table 1, respectively,
and plotted in Fig. 2. Vertical bars indicate the statistical rms uncertainty
(variance) in each of the bin. The gn (z) estimates computed for
the galaxies with spectroscopic redshift only (marked by the dots in Fig. 2)
emphasize the known incompleteness of the LCRS sample due to the original
selection effects dominated by the central surface brightness selection
(cf. Lin et al.).
The derived radial densities systematically decrease with increasing redshift,
at least from
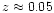 to
to
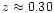 .
This decrease seems to
continue until
.
This decrease seems to
continue until
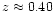 as the most luminous LCRS galaxies, e.g. with
as the most luminous LCRS galaxies, e.g. with
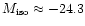 mag, can have
mag, can have
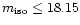 mag at that redshift.
mag at that redshift.
 |
Figure 2:
Arbitrarily normalized radial density of 78 298 optical galaxies with
12.25
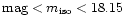 mag. The continuous line indicates the
gn (z) function if these galaxies would be randomly distributed in the
space volume (cf. the text). The dots indicate radial density if only galaxies
with spectroscopic redshift were taken into account, i.e. 25 419 of 78 298
galaxies mag. The continuous line indicates the
gn (z) function if these galaxies would be randomly distributed in the
space volume (cf. the text). The dots indicate radial density if only galaxies
with spectroscopic redshift were taken into account, i.e. 25 419 of 78 298
galaxies |
| Open with DEXTER |
 |
Figure 3:
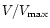 distribution for the same galaxies as in Fig. 2 (open
squares). The statistical rms errors marked by the vertical lines are
comparable to the size of squares. The continuous line indicates the ratio
distribution for the same galaxies as in Fig. 2 (open
squares). The statistical rms errors marked by the vertical lines are
comparable to the size of squares. The continuous line indicates the ratio
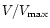 for these galaxies randomly distributed in the space volume
for these galaxies randomly distributed in the space volume |
| Open with DEXTER |
In order to prove that this decrease is not produced by the method, the same
78 298 galaxies with
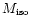 previously drawn by chance (cf. Sect. 2) were
randomly distributed in the space volume limited by the radius equivalent to
z=0.34. The galaxies which then fell out of a limiting
previously drawn by chance (cf. Sect. 2) were
randomly distributed in the space volume limited by the radius equivalent to
z=0.34. The galaxies which then fell out of a limiting
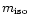 magnitude
(arbitrarily chosen as 18.0 here)
were discarded. The g(z) histogram in the redshift bins of 0.02 for the
remaining galaxies is shown in Fig. 2 by the continuous line. The resultant
density function is fairly uniform; its larger fluctuations at
magnitude
(arbitrarily chosen as 18.0 here)
were discarded. The g(z) histogram in the redshift bins of 0.02 for the
remaining galaxies is shown in Fig. 2 by the continuous line. The resultant
density function is fairly uniform; its larger fluctuations at
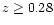 are
caused by much smaller statistics there.
The effect of systematic decrease of the radial density with redshift is
confirmed by the
are
caused by much smaller statistics there.
The effect of systematic decrease of the radial density with redshift is
confirmed by the
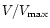 test applied to real LCRS galaxies.
test applied to real LCRS galaxies.
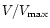 distribution for the same 78 298 galaxies is shown in Fig. 3 and compared with
the respective distribution obtained for randomly distributed galaxies. The
distribution for the same 78 298 galaxies is shown in Fig. 3 and compared with
the respective distribution obtained for randomly distributed galaxies. The
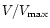 test supports the gn (z) distribution in Fig. 2 which
indicates a maximum of the radial density at
test supports the gn (z) distribution in Fig. 2 which
indicates a maximum of the radial density at 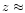 0.05-0.07 and
about 40 per cent decrease of it at
0.05-0.07 and
about 40 per cent decrease of it at
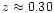 .
The radial density of LCRS galaxies derived here contradicts that originally
published by Lin et al. (1996), which was determined from spectroscopically
observed LCRS galaxies with the use of complicated corrections for the
selection effects. If this discrepancy was caused by
our (uncorrect)
redshift estimates, absolute optical magnitudes of the galaxies without
spectroscopic redshift would have a different distribution than those in Fig. 1.
To check this possibility, we recalculate the optical luminosity function of all
78 298 LCRS galaxies with the prescription given in Sect. 3.2 which takes into
account their density fluctuations. The resultant estimates of
.
The radial density of LCRS galaxies derived here contradicts that originally
published by Lin et al. (1996), which was determined from spectroscopically
observed LCRS galaxies with the use of complicated corrections for the
selection effects. If this discrepancy was caused by
our (uncorrect)
redshift estimates, absolute optical magnitudes of the galaxies without
spectroscopic redshift would have a different distribution than those in Fig. 1.
To check this possibility, we recalculate the optical luminosity function of all
78 298 LCRS galaxies with the prescription given in Sect. 3.2 which takes into
account their density fluctuations. The resultant estimates of
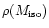 in
in
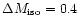 mag bins with their rms errors are plotted in Fig. 4
with the open squares. The solid curve indicates the original luminosity function
fitted with the Schechter form by Lin et al. for their combined North + South
112 sample (cf. their Table 2). The dashed curve is the best-fitted Schechter
function to our estimates. The relevant parameters are:
M*
mag bins with their rms errors are plotted in Fig. 4
with the open squares. The solid curve indicates the original luminosity function
fitted with the Schechter form by Lin et al. for their combined North + South
112 sample (cf. their Table 2). The dashed curve is the best-fitted Schechter
function to our estimates. The relevant parameters are:
M*
![${\rm [mag]}=-20.35\pm 0.05 +
5\log h$](/articles/aa/full/2001/18/aah2558/img61.gif) ,
,
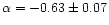 ,
and
,
and 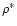 [Mpc
[Mpc
![$^{-3}]=0.023\pm 0.0013$](/articles/aa/full/2001/18/aah2558/img64.gif) ,
where
,
where
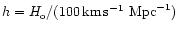 .
A point to note is
that both luminosity functions in the absolute magnitude range
.
A point to note is
that both luminosity functions in the absolute magnitude range
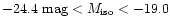 mag are consistent within their combined
mag are consistent within their combined 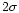 errors.
errors.
 |
Figure 4:
Density-corrected optical luminosity function for 78 298 LCRS galaxies,
67% of which have the redshift estimated (cf. the text). The squares show the
SWML solution plotted with its rms error. The dashed curve shows the
best-fitted Schechter function. The solid curve indicates the original
luminosity function for the combined NS112 sample of Lin et al. |
| Open with DEXTER |
Thus, we can conclude that a systematic redshift error in our analysis is
unlikely, and the decreasing radial density of optical galaxies in the LCRS sample is not caused by erroneous redshift estimates. If not true, this decrease
might be due to an incompleteness of the optical sample increasing with the
apparent magnitude of galaxies and/or a systematic underestimation of this
magnitude in faint galaxies. Our analysis suggests a different weight of these
effects in each of the LCRS declination strips. However, an explanation of the
above effects is not crucial for the purpose to compare the radial densities of
radio-detected galaxies with the respective density of their parent optical
population.
The observed numbers and the normalized gn (z) estimates found for the
radio-detected LCRS galaxies are tabulated in Cols. 4 and 5 of Table 1,
respectively, and plotted in Fig. 5. Again, the vertical bars indicate the
statistical rms error in each of the bin (as given in Table 1). The similar
iterative solutions of the radial density were found separately for the
star-forming and AGN galaxies. The observed numbers and the gn (z)estimates for LCRS starbursts and AGN are tabulated in Cols. 6, 7 and 8, 9 of
Table 1, respectively. In these two distributions we keep the same normalization
as for all radio galaxies. This approach protects an unrealistic increase of
gn (z) e.g. for AGN in respect to its value for all galaxies, i.e.
AGN+starbursts, however some differences due to numerical iterations in the
formal solutions are justified.
Comparing the radial density distributions in Figs. 2 and 5 one can easily
notice that gn (z) for the radio galaxies differs from that for the
optical galaxies. Indeed, the Kolmogorov-Smirnov test indicates that these two
distributions are completely independent (they differ at the significance level
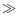 0.9999. This means that the radio-emitting galaxies are not drawn by
chance from their optical population. Dividing
gn (z) estimates in Col. 5 by these in Col. 3, we can correct the
radial density distribution of radio-detected galaxies for the bias introduced
by the density of optical galaxies in the parent LCRS sample.
0.9999. This means that the radio-emitting galaxies are not drawn by
chance from their optical population. Dividing
gn (z) estimates in Col. 5 by these in Col. 3, we can correct the
radial density distribution of radio-detected galaxies for the bias introduced
by the density of optical galaxies in the parent LCRS sample.
 |
Figure 5:
Arbitrarily normalized radial density of radio-detected galaxies;
The statistical rms error in each of the bin is marked by the vertical line.
The continuous (staircase) line indicates gn (z) distribution corrected
for the bias introduced by the respective distribution for optical galaxies in
the parent LCRS sample |
| Open with DEXTER |
The corrected distribution is shown in Fig. 5 by the staircase line. This
histogram clearly has a nonuniform shape and suggests a systematic increase of
gn (z) for radio-detected LCRS galaxies. Our analysis shows that this
increase is caused mostly by the star-forming galaxies. The gn (z)diagrams for starbursts and AGN are plotted in Figs. 6a and b, respectively.
 |
Figure 6:
a) Arbitrarily normalized radial density of Starburst galaxies;
b) the same for AGN galaxies. The vertical line in each of the bin and the
staircase histograms - as in Fig. 5. Symbols in the parenthesis indicate the
density determined by one galaxy only. The solid curve in a) shows the
best-fitted power-law dependence in the redshift range of 0.0 to 0.16:
 |
| Open with DEXTER |
Surprisingly, these two diagrams are essentially different. While the radial
density of starbursts strongly increases with redshift, that for AGN seems to
resemble the gn (z) for optical galaxies. Indeed, the correction of
their radial density estimates for the optical bias gives almost a uniform
distribution indicated by the staircase histogram in Fig. 6b. The above suggest
that LCRS starburst-type and AGN-type galaxies have different radial
distributions.
For the quantitative description of the increase of the radial density with
redshift for starbursts (in Fig. 6a), we have assumed a power-law dependence in
the form
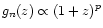 and fitted the best power p using the
and fitted the best power p using the
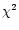 method. For the reason that the enormous increase of
gn (z) at redshifts above 0.15-0.16 results from the detection of few
but very luminous starbursts, we have conservatively fitted p in the redshift
range of
0.0 to 0.16 only, i.e. in the range where the radial density is determined by
at least 30 galaxies in each of the redshift bins. As the result, we found
method. For the reason that the enormous increase of
gn (z) at redshifts above 0.15-0.16 results from the detection of few
but very luminous starbursts, we have conservatively fitted p in the redshift
range of
0.0 to 0.16 only, i.e. in the range where the radial density is determined by
at least 30 galaxies in each of the redshift bins. As the result, we found
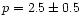 suggesting a systematic density evolution of starburst-type
galaxies. If the radial density of the LCRS starbursts at
suggesting a systematic density evolution of starburst-type
galaxies. If the radial density of the LCRS starbursts at
 was really as high as shown in Fig. 6a, their density
evolution would be even much stronger. The fit in the redshift range
0.12<z<0.24,
was really as high as shown in Fig. 6a, their density
evolution would be even much stronger. The fit in the redshift range
0.12<z<0.24,
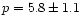 ,
is compatible with
,
is compatible with
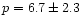 obtained by
Saunders et al. for IRAS galaxies, but disagrees with the result of
Rowan-Robinson et al. (1993) which argued that the density evolution model is
inconsistent with faint radio source counts at 1.4 GHz. Oppositely, we did not
find a noticeable density evolution of LCRS AGN-type galaxies.
Having the radial density distributions of the starburst-type and AGN-type
radio galaxies in the LCRS sample, we have recalculated their 1.4 GHz RLF
accounting for the variable density additionally
corrected for the bias introduced by the respective density distribution of
optical galaxies in their parent sample. This was done by inserting the
corrected values of g(zj) into Eq. (4) and solving it for
obtained by
Saunders et al. for IRAS galaxies, but disagrees with the result of
Rowan-Robinson et al. (1993) which argued that the density evolution model is
inconsistent with faint radio source counts at 1.4 GHz. Oppositely, we did not
find a noticeable density evolution of LCRS AGN-type galaxies.
Having the radial density distributions of the starburst-type and AGN-type
radio galaxies in the LCRS sample, we have recalculated their 1.4 GHz RLF
accounting for the variable density additionally
corrected for the bias introduced by the respective density distribution of
optical galaxies in their parent sample. This was done by inserting the
corrected values of g(zj) into Eq. (4) and solving it for
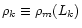 (cf. Paper II).
The solved values of
(cf. Paper II).
The solved values of 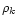 ,
i.e. the comoving space density of galaxies
per "magnitude'' unit
,
i.e. the comoving space density of galaxies
per "magnitude'' unit
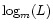 ,
where
m=100.4, can be considered as
the estimates of the 1.4 GHz RLF corrected for the density evolution at the
median redshift of a given sample of LCRS galaxies
,
where
m=100.4, can be considered as
the estimates of the 1.4 GHz RLF corrected for the density evolution at the
median redshift of a given sample of LCRS galaxies
![\begin{displaymath}\rho_{m}(L,z_{\rm med})/g(z_{\rm med})=\rho_{m}[L/f(z_{\rm med}),z\approx 0].
\end{displaymath}](/articles/aa/full/2001/18/aah2558/img80.gif) |
(5) |
Given the RLF which includes the density evolution, its eventual
luminosity evolution can be found by fitting the local luminosity function
(in its logarithmic form) to the
![$\log[\rho_m (\log L,z_{\rm med})]$](/articles/aa/full/2001/18/aah2558/img81.gif) with
a horizontal shift in the
with
a horizontal shift in the 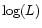 axis
axis
The fitted shift 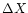 corresponds to
corresponds to
![$\log[f(z_{\rm med})]$](/articles/aa/full/2001/18/aah2558/img85.gif) .
As in Paper II,
the local 1.4 GHz luminosity function was parametrized using the functional form
of Saunders et al. (1990). This form was fitted to the
.
As in Paper II,
the local 1.4 GHz luminosity function was parametrized using the functional form
of Saunders et al. (1990). This form was fitted to the
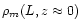 estimates for the starburst-type and AGN-type UGC galaxies taken from Condon
(1989) and Cotton & Condon (1998). In the result,
estimates for the starburst-type and AGN-type UGC galaxies taken from Condon
(1989) and Cotton & Condon (1998). In the result,
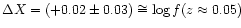 and
and
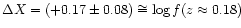 were found for LCRS starbursts and AGN, respectively. For the median
redshift of these two types of galaxies, we have adopted their values corrected
for varying radial density (given in Sect. 5.2). If the luminosity evolution can
be described by
were found for LCRS starbursts and AGN, respectively. For the median
redshift of these two types of galaxies, we have adopted their values corrected
for varying radial density (given in Sect. 5.2). If the luminosity evolution can
be described by
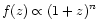 ,
the values of
,
the values of 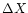 correspond to
correspond to
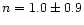 for starbursts and
for starbursts and
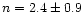 for AGN.
Thus we argue that the LCRS starburst-type galaxies exhibit the strong density
evolution, at least
for AGN.
Thus we argue that the LCRS starburst-type galaxies exhibit the strong density
evolution, at least
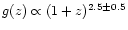 ,
but no certain luminosity
evolution. The LCRS AGN galaxies behave oppositely; they show no sign of a
density evolution, while their luminosities seem to evolve according to
,
but no certain luminosity
evolution. The LCRS AGN galaxies behave oppositely; they show no sign of a
density evolution, while their luminosities seem to evolve according to
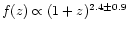 .
The density and luminosity evolution
suggested here
(i) do not contradict with the finding shown in Paper II that luminous
LCRS starburst and AGN galaxies exhibit some evolution of both the spectral-power
density and radial density when compared with the respective local UGC galaxies,
though the statistical significance of those results was low due to the poor
statistics, especially as concerned more luminous UGC starbursts, and
(ii) seems to confirm some predictions of the evolutionary model of Dunlop
& Peacock (1990) where the low-luminosity sources (a population dominated by
normal and star-forming galaxies) and high-luminosity sources (dominated by
powerful AGN) can evolve differently. In particular they concluded that "by
allowing for a slowly evolving population at low luminosities'' all existing
observational data could be fitted "with a model whereby luminous sources
undergo pure luminosity evolution'' if
.
The density and luminosity evolution
suggested here
(i) do not contradict with the finding shown in Paper II that luminous
LCRS starburst and AGN galaxies exhibit some evolution of both the spectral-power
density and radial density when compared with the respective local UGC galaxies,
though the statistical significance of those results was low due to the poor
statistics, especially as concerned more luminous UGC starbursts, and
(ii) seems to confirm some predictions of the evolutionary model of Dunlop
& Peacock (1990) where the low-luminosity sources (a population dominated by
normal and star-forming galaxies) and high-luminosity sources (dominated by
powerful AGN) can evolve differently. In particular they concluded that "by
allowing for a slowly evolving population at low luminosities'' all existing
observational data could be fitted "with a model whereby luminous sources
undergo pure luminosity evolution'' if
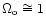 .
It is worth to
emphasize that their and our conclusions are compatible though they are drawn
from the analyses of essentially different samples: high-redshift radio sources
and low-redshift galaxies, respectively.
The effect of varying radial density affects also the observed distributions of
redshift for starburst-type and AGN-type LCRS radio galaxies. Dividing the
observed number of galaxies in a given redshift bin N(z) (cf. Table 1) by the
density distribution derived in Sect. 4, a corrected redshift distribution is
determined
.
It is worth to
emphasize that their and our conclusions are compatible though they are drawn
from the analyses of essentially different samples: high-redshift radio sources
and low-redshift galaxies, respectively.
The effect of varying radial density affects also the observed distributions of
redshift for starburst-type and AGN-type LCRS radio galaxies. Dividing the
observed number of galaxies in a given redshift bin N(z) (cf. Table 1) by the
density distribution derived in Sect. 4, a corrected redshift distribution is
determined
 |
(6) |
The comparison between N(z) and
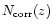 distributions for
starburst-type and AGN-type galaxies is provided in Figs. 7a and b, respectively.
The corrected distributions, shown there by the dashed curves, are smooth as
expected from any model of evolving luminosity function and reveal no trace of
the actual density effects. The median redshifts in the corrected distributions
are
distributions for
starburst-type and AGN-type galaxies is provided in Figs. 7a and b, respectively.
The corrected distributions, shown there by the dashed curves, are smooth as
expected from any model of evolving luminosity function and reveal no trace of
the actual density effects. The median redshifts in the corrected distributions
are
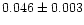 and
and
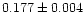 for starbursts and AGN, respectively.
These corrected redshift distributions can be very
useful for a further observational constraint of the existing models of
cosmological evolution of the entire population of radio sources. However this
topic is out of scope of the present paper.
for starbursts and AGN, respectively.
These corrected redshift distributions can be very
useful for a further observational constraint of the existing models of
cosmological evolution of the entire population of radio sources. However this
topic is out of scope of the present paper.
 |
Figure 7:
Histograms of the observed redshift distributions of LCRS galaxies
a) for Starbursts, b) for AGN. The dashed curves indicate underlying
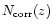 distributions after correction for the gn (z)
functions given in Table 1
distributions after correction for the gn (z)
functions given in Table 1 |
| Open with DEXTER |
Two main conclusions can be drawn from our analysis:
1) The population of starburst-type galaxies seems to be dominated by the
density evolution of a strength at least
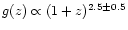 ,
while that of AGN galaxies by the
luminosity evolution
,
while that of AGN galaxies by the
luminosity evolution
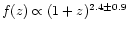 .
The above
conclusion concerning star-forming galaxies fully agrees with that of Mobasher
et al. (1999) that "the faint radio sources (in the Phoenix Deep Survey) are not
affected by luminosity evolution at z<0.3'' [cf. their conclusion (i)].
2) In order to disentangle the effects of density and luminosity evolution at
flux densities below 1 mJy, deep radio detections of, for example,
LCRS galaxies with known redshift would be very fruitful. VLA observations up
to 0.2-0.25 mJy beam-1 at 1.4 GHz, i.e. ten times deeper than the NVSS
survey, would allow to detect starbursts more luminous than
1022.0 W Hz-1 at this frequency up to
.
The above
conclusion concerning star-forming galaxies fully agrees with that of Mobasher
et al. (1999) that "the faint radio sources (in the Phoenix Deep Survey) are not
affected by luminosity evolution at z<0.3'' [cf. their conclusion (i)].
2) In order to disentangle the effects of density and luminosity evolution at
flux densities below 1 mJy, deep radio detections of, for example,
LCRS galaxies with known redshift would be very fruitful. VLA observations up
to 0.2-0.25 mJy beam-1 at 1.4 GHz, i.e. ten times deeper than the NVSS
survey, would allow to detect starbursts more luminous than
1022.0 W Hz-1 at this frequency up to
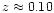 .
While a
maximum of the 1.4 GHz visibility function of starburst-type galaxies is at
.
While a
maximum of the 1.4 GHz visibility function of starburst-type galaxies is at
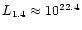 W Hz-1 (cf. Condon 1989; Paper II), suggested
observations would guarantee detections of, at least, one half of the entire
population of this type galaxies. The results of this paper prove that in a
statistically large sample of galaxies, a direct measure of their cosmological
evolution is real even at redshifts as low as 0.05-0.07.
W Hz-1 (cf. Condon 1989; Paper II), suggested
observations would guarantee detections of, at least, one half of the entire
population of this type galaxies. The results of this paper prove that in a
statistically large sample of galaxies, a direct measure of their cosmological
evolution is real even at redshifts as low as 0.05-0.07.
Acknowledgements
This work was supported in part by the State Committee for Scientific Research
(KBN) under the contract PB 0266/PO3/99/17.
- Bruzual, A. G. 1983, ApJ, 273, 105
In the text
NASA ADS
- Condon, J. J. 1984, ApJ, 287, 461
In the text
NASA ADS
- Condon, J. J. 1989, ApJ, 338, 13
In the text
NASA ADS
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998,
AJ, 115, 1693
In the text
NASA ADS
- Cotton, W. D., & Condon, J. J. 1998, in Observational
Cosmology with the NewRadio Surveys, ed. M. N. Bremer, N. Jackson, &
I. Perez-Fournon (Dordrecht: Kluwer), 45
In the text
- Dunlop, J. S., & Peacock, J. A. 1990, MNRAS, 247, 19
In the text
NASA ADS
- Efstathiou, G., Ellis, R. S., & Peterson, B. A. 1988,
MNRAS, 232, 431
In the text
NASA ADS
-
Lin, H., Kirschner, R. P., Shectman, S. A., et al.
1996, ApJ, 464, 60
In the text
NASA ADS
-
Machalski, J., & Condon, J. J. 1999, ApJS, 123, 41 (Paper I)
In the text
NASA ADS
-
Machalski, J., & Godlowski, W. 2000, A&A, 360, 463 (Paper II)
In the text
NASA ADS
-
Mobasher, B., Cram, L., Georgakakis, A., & Hopkins, A. 1999, MNRAS, 308, 45
In the text
NASA ADS
-
Rowan-Robinson, M., Benn, C. R., Lawrence, A., McMahon, R. G., & Broadhurst, T. J. 1993,
MNRAS, 263, 123
In the text
NASA ADS
-
Saunders, W., Rowan-Robinson, M., Lawrence, A., et al.
1990, MNRAS, 242, 318
In the text
NASA ADS
-
Shectman, S. A., Landy, S. D., Oemler, A., et al.
1996, ApJ, 470, 172
In the text
NASA ADS
Copyright ESO 2001


![\begin{displaymath}\ln{\cal L}=\sum_{i=1}^{N}\left\{\ln g(z_{i})-\ln \left[\sum_...
...um_{k=1}^{N_{z}}
g(z_{k})f_{ik}V_{\max,i}\right] +{\rm const},
\end{displaymath}](/articles/aa/full/2001/18/aah2558/img22.gif)
![\begin{displaymath}g_{k}=n_{k}\left\{\sum_{i=1}^{N}\left[f_{ik}V_{k}\left(\sum_{...
...{N_{z}}
g_{j}f_{ij}V_{\max,i}\right)^{-1}\right]\right\}^{-1}.
\end{displaymath}](/articles/aa/full/2001/18/aah2558/img26.gif)






![\begin{displaymath}\rho_{m}(L,z_{\rm med})/g(z_{\rm med})=\rho_{m}[L/f(z_{\rm med}),z\approx 0].
\end{displaymath}](/articles/aa/full/2001/18/aah2558/img80.gif)
![\begin{displaymath}\log[\rho_m(\log L,z_{\rm med})]=\log[\rho_{m}(\log L-\Delta X)].\end{displaymath}](/articles/aa/full/2001/18/aah2558/img83.gif)

