A&A 370, 868-874 (2001)
DOI: 10.1051/0004-6361:20010281

Search for the [CII] 158 micron emission
toward the blue compact dwarf galaxy I Zw 36

K. Mochizuki - T. Onaka

Department of Astronomy, University of Tokyo, Japan

Received 2 August 2000 / Accepted 15 February 2001

Abstract
We observed the blue compact dwarf galaxy I Zw 36 in the [C II] $158\ \mu \rm m$ line with the Infrared Space Observatory obtaining an upper limit for the line flux, $F_{\rm [C{\sc ii}]} \leq 1.1~10^{-20}\ \rm W\ cm^{-2}$($3 \sigma$). A comparison with previous CO observations yields an upper limit for the [C II]/CO J = 1-0 line flux ratio, $F_{\rm [C{\sc ii}]} / F_{\rm CO} \leq 1.3~10^3$($3 \sigma$). This limit indicates that the [C II]/CO J = 1-0 line ratio in I Zw 36 is not higher than those in our Galactic plane ( $I_{\rm [C{\sc ii}]} / I_{\rm CO} = 1.1~10^3$) and is at least one order of magnitude lower than those in irregular galaxies ( $I_{\rm [C{\sc ii}]} / I_{\rm CO} \simeq 2~10^4$) with low metallicities, in spite of the lower metallicity in I Zw 36 ( $\rm 12 + \log[ O / H ] = 7.9$) than in the irregulars. The observed difference in the line ratio between I Zw 36 and the irregulars can be accounted for by a higher gas density ( ) in I Zw 36, because the higher CO-formation rate at the higher density enables CO molecules to survive even against the photodissociation enhanced by the low dust abundance. The expected higher gas density in I Zw 36 may be related to change in large-scale gravitational potential with galactic evolution, if blue compact dwarfs and irregulars have evolutionary links.

Key words: ISM: clouds - dust, extinction - galaxies: abundances - galaxies: dwarf - galaxies: individual: I Zw 36 - infrared: galaxies

1 Introduction

The [C II] 158 $\mu$m fine-structure ( $^2P_{3/2} \rightarrow\, ^2$P_1/2) emission is radiated from interstellar C⁺ ions. The line ratio of the [C II] to the ¹²CO J = 1-0 transitions can be used as a probe of the interstellar ultraviolet (UV) intensity in galaxies (Stacey et al. 1991; Pierini et al. 1999), because the interstellar UV radiation field dissociates CO molecules and ionizes C atoms near the surfaces of molecular clouds. Nevertheless, Stacey et al. (1991) found that even starburst galaxies, which have intense interstellar UV fields, cannot have [C II]/¹²CO J = 1-0 line intensity ratios higher than 5 10³(ratios when the main-beam temperature scale is adopted for the CO intensity instead of the $T_{\rm R}^\ast$ scale). Line ratios exceeding this limit ( $[C{\sc ii}] / {\rm CO} > 10^4$) have been observed on a galactic scale only toward irregular galaxies (Mochizuki et al. 1994; Lord et al. 1995; Madden et al. 1997) and a few spirals in the Virgo cluster (Smith & Madden 1997).

The extremely high [C II]/CO line ratios in the irregulars are accounted for by their lower metallicities; the lower dust abundance due to the lower metallicity allows CO-dissociating UV photons to penetrate deeper into the molecular clouds (Maloney & Black 1988). Low metallicities are also suggested for the spirals with the extremely high [C II]/CO ratios (Smith & Madden 1997), although the metallicities have not been measured in these galaxies.

In the present paper, we report observations of a blue compact dwarf galaxy (BCDG) in the [C II] line. In order to obtain the [C II]/CO line ratio, we selected an object previously detected in the CO J = 1-0 emission: I Zw 36 (Mrk 209; UGCA 281). This nearby ($\simeq$ $4.6\ \rm Mpc$; e.g., Viallefond & Thuan 1983) galaxy has a lower metallicity ( $\rm 12 + \log[ O / H ] = 7.9$ in interstellar oxygen abundance; Viallefond & Thuan 1983) than the irregulars previously observed in the [C II] emission. The comparison of I Zw 36 with the irregulars enables us to investigate the effect of galactic morphology on the C⁺-CO chemical balance in the low-metallicity environments.

 

 

Table 1: Observation parameters of I Zw 36

Parameter	Value	Reference
Object	I Zw 36	1
$\alpha (2000)$ ( $\ \rm ^h\ ^m\ ^s$)	12 26 17.1	2
$\delta (2000)$ ( $\ \hbox{$^\circ$ }\ \hbox{$^\prime$ }\ \hbox{$^{\prime\prime}$ }$)	48 29 37	2
$\rm 12 + \log[ O / H ]$	$7.93 \pm 0.07$	3
$\int T_{\rm A}^\ast (\rm {CO}\ {\it J} = 1{-}0$)  d v $^{\rm a}$ ( $\rm K\ km\ s^{- 1}$)	$0.45 \pm 0.10$	4
$F_{\rm [C\, II]}\, ^{{\rm b}}$ ( $10^{-20}\ \rm W\ cm^{-2}$)	$\leq 1.1$	5
$F_{\rm [C\, II]}/F_{\rm CO}\, ^{{\rm c}}$	$\leq 1.3~10^3$	4, 5

$^{\rm a}$ The $45\hbox{$^{\prime\prime}$ }$ (HPBW) beam was centered on $\rm\alpha (2000) = 12^h 26^m 15 \hbox{$.\!\!^{\rm s}$ }9$ and $\rm\delta (2000) = 48\hbox{$^\circ$ }29\hbox{$^\prime$ }30\hbox{$^{\prime\prime}$ }$.

Open with DEXTER

$^{\rm b}$ The beam size was 68'' in FWHM. The flux calibration uncertainty was taken into account as well as the statistical noise of a $3 \sigma$ level.

$^{\rm c}$ The upper limit results from that in $F_{\rm [C\, II]}$. The main-beam temperature scale is adopted for the CO intensity instead of the $T_{\rm R}^\ast$ scale.

References: 1. Zwicky et al. (1961); 2. Palumbo et al. (1988); 3. Viallefond & Thuan (1983); 4. Young et al. (1995); 5. this work.

   
2 Observations and data reduction

We observed I Zw 36 in the [C II] $158\ \mu \rm m$ line with the Long-Wavelength Spectrometer (LWS; Clegg et al. 1996) on board the Infrared Space Observatory (ISO; Kessler et al. 1996). The observations are two concatenated 3-point raster scans: the Target Dedicated Time (TDT) numbers 19401278 and 19401279. Both the rasters are centered on the optical center of the galaxy, listed in Table 1 with other observational parameters. The other 4 observed positions have offsets of $\pm 3\hbox{$^\prime$ }$ in the north-south (TDT 19401278) and east-west (TDT 19401279) directions, relative to the center position. These off-position observations enable us to evaluate any possible contamination by the foreground Galactic emission. We adopted the Astronomical Observation Template (AOT) LWS02 mode: line observations with a medium-resolution ( $\Delta \lambda = 0.6\ \mu \rm m$) grating spectroscopy. The observations at the galaxy position consisted of 40 grating scans, with 16 seconds of total integration time for each grating position. Twenty grating scans (8 s of total integration) were carried out at each of the off-positions. The grating positions were spaced at 1/4 of the spectral resolution for both the on- and off-position observations. The beam size of the LWS derived from observations of Mars was 68'' in FWHM at the wavelength of the [C II] line (Gry et al. 2000).

We subtracted the detector dark currents from the Standard Processed Data (SPD) of the Off-Line Processing (OLP) version 7 products, using the LWS Interactive Analysis (LIA) version 7.3. The ISO Spectral Analysis Package (ISAP) version 1.6a was used for the data reduction afterwards. The data affected by cosmic-ray hits were manually removed, when they had not been discarded automatically in the SPD. The individual spectra were averaged at each of the observed positions, and then the spectra at the 4 off-positions were averaged resulting in a single off-source spectrum. No difference was seen among the spectra at the off-positions. Finally, we derived the foreground-subtracted spectrum by subtracting the off-source spectrum from the on-source spectrum. We tried to fit the on-source, off-source, and foreground-subtracted spectra with single-Gaussian line profiles and linear baselines. The widths of the Gaussian profiles were assumed to be equal to the instrumental resolution because the ¹²CO J = 1-0 line width of the galaxy was small ( $\Delta v_{\rm CO} = 32\ \rm km\ s^{-1}$; Young et al. 1995) relative to the resolution.

For faint sources, the uncertainty in the LWS flux calibration predominantly results from difficulties in the subtraction of the detector dark currents. These difficulties prevented us from deriving a correct continuum flux density from the LWS02 spectra of I Zw 36. However, line flux is less affected by this problem, especially for brighter emission such as the [C II], which generally have a flux density comparable to that of the continuum on a galactic scale at this wavelength and spectral resolution (Crawford et al. 1985). Thus, for the [C II] line, we adopt the nominal LWS calibration uncertainty of the OLP version 7 products for faint sources, 50%.

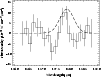Figure 1: Observed flux density (solid curve) of I Zw 36 as a function of wavelength. A linear baseline was subtracted. The vertical bars indicate the uncertainties ($1 \sigma$) based on the scatters among the individual spectral scans. The dashed curve indicates the [C II] line profile expected when the Galactic [C II]/CO J = 1-0 intensity ratio (Nakagawa et al. 1998; Dame et al. 1987) is applied to CO observations (Young et al. 1995) of I Zw 36. The heliocentric radial velocity of the CO emission is $v_{\rm hel} = 288\ \rm km\ s^{-1}$at the line center. The width of the expected line profile is determined predominantly by the instrumental resolution

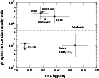Figure 2: Observed [C II]/12CO J = 1-0line intensity ratio of galaxies (filled circles) vs. interstellar oxygen abundance, $\rm 12 + \log[ O / H ]$. The ratio for I Zw 36 indicates the upper limit (Table 1). The horizontal bars indicate the observation uncertainties for I Zw 36 and NGC 1569. For the inner Galaxy, the LMC, and IC 10, the horizontal and vertical bars represent the spatial variations within the galaxies ($1 \sigma$ except the horizontal bar for our Galaxy; see text). The dashed line indicates the upper limit for starburst and normal spirals (Stacey et al. 1991); the main-beam temperature scale is adopted for the CO line in this figure instead of the $T_{\rm R}^\ast$ scale

Open with DEXTER

   
3 Results

The [C II] emission was not detected in any of the on-source, off-source, or foreground-subtracted spectrum. Figure 1 shows the foreground-subtracted spectrum; a linear baseline was also subtracted. An upper limit of $F_{\rm [C{\sc ii}]} \leq 7.2~10^{-21}\ \rm W\ cm^{-2}$ (statistical uncertainty of a $3 \sigma$ level) was derived for the [C II] line flux from this spectrum. Including the LWS calibration uncertainty (Sect. 2), we obtain the final upper limit $F_{\rm [C{\sc ii}]} \leq 1.1~10^{-20}\ \rm W\ cm^{-2}$as listed in Table 1.

The ¹²CO J = 1-0 line emission from I Zw 36 was detected in the Five College Radio Astronomy Observatory (FCRAO) Extragalactic CO Survey (Young et al. 1995). The integrated main-beam intensity of the emission is $\int T_{\rm MB} {\rm d}v = 0.82 \pm 0.18\ \rm K\ km\ s^{-1}$with the uncertainty of a $1 \sigma$ level (including the calibration uncertainty) at a beam size of $45\hbox{$^{\prime\prime}$ }$ (HPBW). This yields a CO J = 1-0 flux of $F_{\rm CO} = (6.9 \pm 1.5)~10^{-24}\ \rm W\ cm^{-2}$in the beam slightly smaller than that of the LWS, under the assumption of a Gaussian profile for the CO beam. Thus, the upper limit ($3 \sigma$) for the [C II]/CO line flux ratio is $F_{\rm [C{\sc ii}]} / F_{\rm CO} \leq 1.3~10^3$. This limit for the flux ratio can also be regarded as an upper limit for the [C II]/CO intensity ratio ( $I_{\rm [C{\sc ii}]} / I_{\rm CO}$) in the CO beam, whose size is close to the optical diameter ( $0\hbox{$.\mkern-4mu^\prime$ }92$; de Vaucouleurs et al. 1991) of the galaxy. Thus, $I_{\rm [C{\sc ii}]} / I_{\rm CO}$ in I Zw 36 is not higher than those observed in the inner Galactic plane, $I_{\rm [C{\sc ii}]} / I_{\rm CO} \simeq 1.1~10^3$(Nakagawa et al. 1998; Dame et al. 1987, corrected as described in Bronfman et al. 1988).

Figure 2 shows the [C II]/¹²CO J = 1-0line intensity ratio observed in galaxies as a function of oxygen abundance, $\rm 12 + \log[ O / H ]$, derived from optical-UV emission line observations of H II regions in the galaxies. The [C II] and CO data are, respectively, from Nakagawa et al. (1998) and Dame et al. (1987) for the Galaxy; Mochizuki et al. (1994) and Cohen et al. (1988) for the Large Magellanic Cloud (LMC); Madden et al. (1997) and Becker (1990) for IC 10. The CO intensity scale of Dame et al. (1987) was corrected as described in Bronfman et al. (1988). The [C II]/CO line ratios for NGC 4449 and NGC 1569 are from Lord et al. (1995). The references for the oxygen abundance are as follows: the inner Galaxy, Deharveng et al. (2000); the LMC, Russell & Dopita (1990); NGC 4449 and IC 10, Hidalgo-Gámez & Olofsson (1998) based on observations of McCall et al. (1985) and Lequeux et al. (1979); NGC 1569, Kobulnicky & Skillman (1997); I Zw 36, Viallefond & Thuan (1983). The radial variation of metallicity in our Galaxy is taken into account; the lower and upper limits in the figure correspond to the abundances at the Galactocentric distance of the Sun and the extrapolation of the relation between the abundance and the Galactocentric distance to the Galactic center, respectively.

Irregular galaxies with low metallicities have [C II]/CO line ratios higher than those in the inner Galaxy and also than the starburst limit obtained by Stacey et al. (1991). These extremely high ratios have been accounted for by the enhanced photodissociation of interstellar CO molecules because of the low dust abundances due to the low metallicities (Maloney & Black 1988). However, the BCDG I Zw 36 does not show a [C II]/CO line ratio higher than those in normal spirals in spite of its low metallicity.

   
4 Discussion

   
4.1 Conditions for extremely high [C II]/CO line ratios

The chemical balance between C⁺ ion and CO molecule depends on dust abundance (Maloney & Black 1988), because interstellar CO molecules are protected from photodissociation mainly by the dust extinction of the incident UV radiation (Wolfire et al. 1989). Accordingly, the high [C II]/CO J = 1-0 intensity ratios observed in irregular galaxies have been attributed to the low dust abundances due to the low metallicities in the galaxies (e.g., Mochizuki et al. 1994). For brief discussions on the C⁺-CO chemical balance, we consider a molecular cloud with a metallicity Xrelative to the solar neighborhood value. The dust abundance is assumed to be proportional to the metallicity. Chemical reaction rates in this cloud can be written as a function of hydrogen column density ($N_{\rm H}$) measured from the cloud surface into the cloud. The total hydrogen (mostly in H atom and H₂ molecule) number density, $n_{\rm H}$, is assumed to be uniform in the cloud.

The conversion of $\rm CO \rightarrow C^+$ is initiated mostly by the dissociation of CO molecule due to UV photons incident on the cloud (e.g., van Dishoeck & Black 1988). Since the photodissociation is followed quite quickly by the photoionization of $\rm C \rightarrow C^+$, the $\rm CO \rightarrow C^+$ conversion rate, $r_{\rm CO} ( N_{\rm H} )$, in the cloud can be written as

$$% r_{\rm CO} ( N_{\rm H} ) = G_0 \alpha_{\rm CO}^0 n_{\rm C... ...ft( - X \frac{ N_{\rm H} }{ N_{\rm H}^{\rm UV} } \right),$$ (1)

where G₀ is the incident UV flux relative to the solar neighborhood value, $\alpha_{\rm CO}^0$ is the CO photodissociation rate under the interstellar radiation field at the solar neighborhood, $n_{\rm CO} ( N_{\rm H} )$ is the number density of CO as a function of $N_{\rm H}$, and $N_{\rm H}^{\rm UV}$ is the hydrogen column density characteristic to the attenuation of the UV radiation effective to the CO dissociation at X = 1.

On the other hand, the conversion of $\rm C^+ \rightarrow CO$consists of two-body reactions in the gas phase. Thus, the $\rm C^+ \rightarrow CO$ conversion rate, $r_{\rm C^+}$, can be approximately written as

$$% r_{\rm C^+} ( N_{\rm H} ) = k_{\rm C^+} n_{\rm H} n_{\rm C^+} ( N_{\rm H} ),$$ (2)

where $k_{\rm C^+}$ is the total rate coefficient of the $\rm C^+ \rightarrow CO$ reactions and $n_{\rm C^+} ( N_{\rm H} )$ is the number density of C⁺ in the cloud. We assume $k_{\rm C^+}$ is constant for the present discussion, although it is actually a function of chemical composition as well as of gas temperature. Its dependence on X through the chemical composition is relatively weak because the $\rm C^+ \rightarrow CO$ conversion rate is often determined by reactions between carbon-bearing species and hydrogen species such as between hydrocarbon anions and hydrogen molecules.

When a steady state $r_{\rm CO} ( N_{\rm H} ) = r_{\rm C^+} ( N_{\rm H} )$ is assumed, the condition $n_{\rm CO} ( N_{\rm H} ) = n_{\rm C^+} ( N_{\rm H} )$ yields a certain value of $N_{\rm H}$, which we define as the transition column density ( $N_{\rm H}^{\rm transit}$) of C⁺-CO. The dominant form of gas-phase carbon is C⁺ at $N_{\rm H} < N_{\rm H}^{\rm transit}$, and CO at $N_{\rm H} > N_{\rm H}^{\rm transit}$. From Eqs. (1) and (2), $N_{\rm H}^{\rm transit}$can be written as

$$% N_{\rm H}^{\rm transit} = \frac{ N_{\rm H}^{\rm UV} }{ X ... ...rm CO}^0 }{ k_{\rm C^+} } \frac{ G_0 }{ n_{\rm H} } \right)$$ (3)

(e.g., Mochizuki et al. 1994).

We estimate $\alpha_{\rm CO}^0 / k_{\rm C^+} \sim 10^4\ \rm cm^{-3}$and $N_{\rm H}^{\rm UV} \simeq 7~10^{20}\ \rm cm^{-2}$according to the chemical network in the models of Hollenbach et al. (1991). Because of the $\ln[ ( \alpha_{\rm CO}^0 / k_{\rm C^+} ) ( G_0 / n_{\rm H} ) ]$dependence, $N_{\rm H}^{\rm transit}$ is insensitive to $G_0 / n_{\rm H}$at $G_0 / n_{\rm H} \gg ( \alpha_{\rm CO}^0 / k_{\rm C^+} )^{-1} \sim 10^{-4}\ \rm cm^3$. According to Eq. (3), $N_{\rm H}^{\rm transit}$ does not exceed $10^{22}\ \rm cm^{-2}$over the wide range of $G_0 / n_{\rm H} \leq 10\ \rm cm^3$. Thus, CO molecules survive inside the clouds with $n_{\rm H} \simeq 10^3\ \rm cm^{-3}$under the realistic conditions of $G_0 \leq 10^4$ ( G₀ = 10²-10⁴ in starbursts; Stacey et al. 1991), if the typical column density ( $N_{\rm H}^{\rm cloud}$) of the clouds is $N_{\rm H}^{\rm cloud} \simeq 2~10^{22}\ \rm cm^{-2}$($\simeq$ $1~10^{22}\ \rm cm^{-2}$ from the surface to the center). This makes the upper limit for the [C II]/CO J = 1-0 line ratios in normal and starburst galaxies (Stacey et al. 1991).

On the other hand, $N_{\rm H}^{\rm transit}$ varies as X^-1. When X = 1/4, typical in the low-metallicity galaxies observed in the [C II] line, $N_{\rm H}^{\rm transit}$ is $10^{22}\ \rm cm^{-2}$at $G_0 / n_{\rm H} \simeq 10^{-2}\ \rm cm^3$. Thus, if $N_{\rm H}^{\rm cloud} \simeq 2~10^{22}\ \rm cm^{-2}$, most of the CO molecules in the clouds are dissociated even at $G_0 \simeq 10$ and $n_{\rm H} \simeq 10^3\ \rm cm^{-3}$in the low-metallicity galaxies. This G₀ is close to the average ( $G_0 \simeq 5$) estimated for the clouds emitting the Galactic [C II] emission (Mochizuki & Nakagawa 2000). Hence, a typical G₀ and $n_{\rm H}$ of galactic molecular clouds can produce the extremely high [C II]/CO line ratios observed in the irregulars, beyond the upper limit for more luminous starbursts.

However, the $\ln[ ( \alpha_{\rm CO}^0 / k_{\rm C^+} ) ( G_0 / n_{\rm H} ) ]$dependence makes $N_{\rm H}^{\rm transit}$ more sensitive to $G_0 / n_{\rm H}$at than at . In the former case, a small $G_0 / n_{\rm H}$ can compensate a small X; (e.g., G₀ = 10 and ) provides $N_{\rm H}^{\rm transit} < 10^{22}\ \rm cm^{-2}$even at X = 1/4. As a result, a low-metallicity galaxy can show a normal [C II]/CO line ratio at a small $G_0 / n_{\rm H}$while a more luminous spiral galaxy cannot show a much higher ratio than the starburst limit even at a large $G_0 / n_{\rm H}$, under the assumption of $N_{\rm H}^{\rm cloud} \simeq 2~10^{22}\ \rm cm^{-2}$.

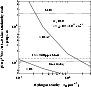Figure 3: The ${\rm [C{\sc ii}]/^{12}CO}\ J = 1$-0 line luminosity ratio (solid curves) of a molecular cloud based on PDR models as a function of the hydrogen number density of the cloud. The relative metallicity and dust abundance are X = 1/4(corresponding to $\rm 12 + \log[ O / H ] = 8.1$) for the low-metallicity models, and X = 1 for the Galactic-abundance models. The incident UV flux and the mean hydrogen column density of the model cloud are G0 = 10and $\langle N_{\rm H} \rangle = 2~10^{22}\ \rm cm^{-2}$, respectively. The mean [C II]/CO J = 1-0 intensity ratios observed in the inner Galaxy and the LMC (dotted lines) and the upper limit obtained for I Zw 36 (dashed line) are also indicated

Open with DEXTER

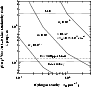	Figure 4: Same as Fig. 3 but with variation in G0 for X = 1/4
Open with DEXTER

   
4.2 Comparison with photon-dominated region models

For more quantitative investigation, we compare the observed [C II]/CO J = 1-0 line ratio with the photon-dominated region (PDR) models by Mochizuki & Nakagawa (2000). In their models, the luminosities of emission lines emergent from the model cloud are derived from a given set of the incident UV flux G₀ (Sect. 4.1), the mean number density of total hydrogen in the cloud $\langle n_{\rm H} \rangle$, and the cloud mass M. We assume a uniform hydrogen density in the cloud for simple discussion of the density dependence of the line ratio, and thus use the hydrogen density $n_{\rm H}$ instead of $\langle n_{\rm H} \rangle$. In addition, the mean hydrogen column density $\langle N_{\rm H} \rangle$ is used as in Mochizuki (2000) instead of M, in accordance with the discussion on $N_{\rm H}^{\rm transit}$in Sect. 4.1.

We can estimate G₀ in I Zw 36 from UV observations with an accuracy limited by the uncertainty (see below) in extinction. The flux density observed toward I Zw 36 is $F_{2000} = 1.0~10^{-13}\ \rm ergs\ s^{-1}\ cm^{-2}$ Å^-1at $\lambda = 2000$ Å after the correction for an extinction of 0.7 mag (Donas et al. 1987). Assuming a uniform distribution of UV sources in a sphere with diameter equal to that in the optical ( $a = 0 \hbox{$.\mkern-4mu^\prime$ }92$; de Vaucouleurs et al. 1991), we obtain the volume-averaged flux density, $\langle F_{2000} \rangle$, in the sphere: $\langle F_{2000} \rangle = 12 F_{2000}^0$, where $F_{2000}^0 = 1.0~10^{-6}\ \rm ergs\ s^{-1}\ cm^{-2}$ Å^-1is the 2000 Å flux density in the solar neighborhood by Mathis et al. (1983). Since a is close to the [C II] and CO beam sizes, we adopt $G_0 \simeq 10$ as an average for I Zw 36 on the scale seen in the [C II]/CO line ratio.

Figure 3 shows the calculated [C II]/CO J = 1-0 line ratios at G₀ = 10plotted as a function of $n_{\rm H}$, along with the observed ratios. The metallicity and the dust abundance in the low-metallicity models are X = 1/4, while X = 1 in the original models (Mochizuki & Nakagawa 2000) for our Galaxy. The former metallicity corresponds to $\rm 12 + \log[ O / H ] = 8.1$, typical in the low-metallicity galaxies observed in the [C II] line. The Galactic-abundance models of X = 1 with the same G₀ are also plotted for comparison. We adopted $\langle N_{\rm H} \rangle = 2~10^{22}\ \rm cm^{-2}$for both the X = 1/4 and X = 1 models, on the basis of the rough estimate (Sect. 4.1) that accounts for the much higher [C II]/CO J = 1-0 line ratios in irregulars than in starbursts (see also below).

At X = 1 and $n_{\rm H} \simeq 10^3\ \rm cm^{-3}$, which represent Galactic molecular clouds, the calculated line ratio is ${\rm [C{\sc ii}]/CO}\ J = 1$- $0 \simeq 1~10^3$, close to those observed in the inner Galactic plane. On the other hand, at X = 1/4, the model with the same $n_{\rm H}$has an extremely high ratio of ${\rm [C{\sc ii}]/CO}\ J = 1$-0 > 10⁴as observed in irregular galaxies. This indicates that the difference in X can account for the observed difference in the [C II]/CO ratio between our Galaxy and the irregulars. With increasing $n_{\rm H}$, the calculated line ratio decreases as expected from Eq. (3). The ratio becomes consistent with the upper limit observed in I Zw 36 at $n_{\rm H} > 10^4\ \rm cm^{-3}$. These calculations indicate that a higher gas density in I Zw 36 is required to reproduce the observed difference in the [C II]/CO ratio between I Zw 36 and the irregular galaxies.

The UV flux of $G_0 \simeq 10$ adopted above was estimated on the basis of the extinction derived from the H I 21 cm line intensity, H I flux divided by a² (Donas et al. 1987). This method can underestimate the extinction by up to 1 mag (Donas et al. 1987) because of oversimplified assumptions on the distribution of H I gas (Donas & Deharveng 1984). By comparison the extinction based on a line ratio toward the dominant H II region (for a smaller aperture of $10\hbox{$^{\prime\prime}$ }\times 20\hbox{$^{\prime\prime}$ }$) in I Zw 36 is 1.4 mag at $\lambda = 1909$ Å (Viallefond & Thuan 1983). Accordingly, we calculated ratios also for G₀ = 10^1.5as well as G₀ = 10^0.5(Fig. 4). At G₀ > 10, the line ratio in the figure is too high compared to the I Zw 36 observations. Thus, G₀ cannot be so large on the galactic scale unless $\langle N_{\rm H} \rangle$ is substantially larger than $2~10^{22}\ \rm cm^{-2}$. On the other hand, at $G_0 \simeq 6$ (no extinction at $\lambda = 2000$ Å), Fig. 4 shows that a high gas density of is still required. As a result, the observed low line ratio in I Zw 36 indicates a high gas density of .

For the above discussions, we assumed $N_{\rm H}^{\rm cloud} \sim 10^{22}\ \rm cm^{-2}$in every galaxy, on the basis of the difference in the line ratios between irregulars and starbursts (Sect. 4.1). However, this assumption is difficult to confirm observationally. When a constant cloud mass is assumed, instead of the constant $N_{\rm H}^{\rm cloud}$ above, $N_{\rm H}^{\rm cloud}$ would increase with $n_{\rm H}$ (e.g., Mochizuki 2000). In addition, Pak et al. (1998) concluded that $N_{\rm H}^{\rm cloud}$ increases with decreasing metallicity, on the basis of large-scale observations of H₂ vib-rotational lines. These suggest that $N_{\rm H}^{\rm cloud}$ may be larger in I Zw 36 than in the irregulars observed in the [C II] emission. Since a larger $N_{\rm H}^{\rm cloud}$ can also contribute to a lower [C II]/CO line ratio, we expect that $n_{\rm H}$ in I Zw 36 is between that in the irregulars and that estimated above for the constant $N_{\rm H}^{\rm cloud}$ case: . Otherwise, a large amount of neutral gas in I Zw 36 would have a very high column density of .

   
4.3 Interstellar medium in I Zw 36

The [C II]/CO J = 1-0 line ratio varies from place to place in a galaxy. For the low ratio of I Zw 36 on the galactic scale, a large fraction of neutral interstellar gas should have a high density. However, the presently available observations do not allow us to investigate density distribution of molecular gas within I Zw 36. Instead we discuss distributions of the starburst (young) stellar population by considering that a starburst results from a high density of molecular gas.

Papaderos et al. (1996a) decomposed the optical spatial profiles of BCDGs into starburst and underlying stellar components, and then derived the area ratios of the starburst components to the underlying components. They found that the area ratio increases with decreasing galactic luminosity (Papaderos et al. 1996b), which is generally correlated with metallicity. A fraction as large as about a half of the optical area is occupied by the starburst component in I Zw 36, which lies close to the low-luminosity end in their sample. Hence, I Zw 36 is likely to have physical conditions producing high-density gas in a larger fraction of its optical area than more luminous BCDGs and irregulars are. This supports a higher average gas density within the optical area in the galaxy.

The present [C II]/CO observations place a limit only for the gas density in the CO beam (Sect. 3), which has a similar size to the optical area of the galaxy. Thus, the proposed high density does not conflict with the presence of a diffuse H I halo (Viallefond & Thuan 1983) extended to a diameter of $\simeq$ $150\hbox{$^{\prime\prime}$ }$, where the gas density is possibly lower.

Since irregular galaxies have extremely high [C II]/CO line ratios generally (Fig. 2), lower [C II]/CO line ratios as well as expected higher gas densities may be distinctive characteristics of a certain class of BCDGs among low-metallicity galaxies: galactic morphology may be one of the crucial factors. This implies that the gravitational potential may change on a large scale with galactic evolution, if BCDGs and irregular galaxies have evolutionary links (e.g., Davies & Phillipps 1988). Such a change is more likely to occur in a dwarf galaxy than in a more massive one, because a dwarf galaxy has a large mass fraction of ISM (Huchtmeier & Richter 1988). For investigation of difference in the ISM properties between BCDGs and irregulars, more samples of BCDGs with variation in metallicity (luminosity) would be helpful.

5 Conclusions

We observed the BCDG I Zw 36 ( $\rm 12 + \log[ O / H ] = 7.9$) in the [C II] $158\ \mu \rm m$ fine-structure line with the ISO/LWS. The conclusions are summarized as follows.

1.

An upper limit for the [C II] flux in the LWS beam (68 $^{\prime\prime}$ in FWHM) was obtained: $F_{\rm [C{\sc ii}]} \leq 1.1~10^{-20}\ \rm W\ cm^{-2}$ ($3 \sigma$).

2.

A comparison with the previous CO observations provides an upper limit for the [C II]/CO J = 1-0 line flux ratio of $F_{\rm [C{\sc ii}]} / F_{\rm CO} \leq 1.3~10^3$. This indicates that the line ratio in I Zw 36 is at least one order of magnitude lower than those observed in irregular galaxies ( $I_{\rm [C{\sc ii}]} / I_{\rm CO} = 2.3~10^4$ in the LMC), in spite of the lower metallicity of I Zw 36.

3.

A comparison with PDR models shows that is required in I Zw 36 to account for the observed difference in the [C II]/CO line ratio between I Zw 36 and irregular galaxies, under the assumption of $N_{\rm H}^{\rm cloud} \sim 10^{22}\ \rm cm^{-2}$in both the types of galaxies. Taking into account a possible larger $N_{\rm H}^{\rm cloud}$ in I Zw 36 than in the previously observed irregulars, we conclude that $n_{\rm H}$ in I Zw 36 is between that in the irregulars and the estimate for the constant $N_{\rm H}^{\rm cloud}$ case: .

Acknowledgements

We are much indebted to I. Yamamura, T. Nakagawa, and T. Tohya for their stimulating discussions at the Institute of Space and Astronautical Science. We are grateful to the members of Japanese ISO Guaranteed Time observation team for constructing the observation plan and supporting the data reduction, especially to H. Okuda, K. Kawara, and Y. Sato. We would also like to thank C. P. Pearson for his helpful comments. K. M. was financially supported by a Research Fellowship of the Japan Society for the Promotion of Science for Young Scientists.

References

 

• Becker, R. 1990, Ph.D. Thesis, Rheinische Friedrich-Wilhelms-Univ. In the text  
• Bronfman, L., Cohen, R. S., Alvarez, H., May, J., & Thaddeus, P. 1988, ApJ, 324, 248 In the text NASA ADS  
• Clegg, P. E., Ade, P. A. R., Armand, C., et al. 1996, A&A, 315, L38 In the text NASA ADS  
• Cohen, R. S., Dame, T. M., Garay, G., et al. 1988, ApJ, 331, L95 In the text NASA ADS  
• Crawford, M. G., Genzel, R., Townes, C. H., & Watson, D. M. 1985, ApJ, 291, 755 In the text NASA ADS  
• Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706 In the text NASA ADS  
• Davies, J. I., & Phillipps, S. 1988, MNRAS, 233, 553 In the text NASA ADS  
• Deharveng, L., Peña, M., Caplan, J., & Costero, R. 2000, MNRAS, 311, 329 In the text NASA ADS  
• de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G. Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Springer-Verlag) In the text  
• Donas, J., & Deharveng, J. M. 1984, A&A, 140, 325 In the text NASA ADS  
• Donas, J., Deharveng, J. M., Laget, M., Milliard, B., & Huguenin, D. 1987, A&A, 180, 12 In the text NASA ADS  
• Gry, C., Swinyard, B., Harwood, A., et al. 2000, The ISO Handbook Volume IV: LWS - The Long-Wavelength Spectrometer, the ISO LWS Consortium In the text  
• Hidalgo-Gámez, A. M., & Olofsson, K. 1998, A&A, 334, 45 In the text NASA ADS  
• Hollenbach, D. J., Takahashi, T., & Tielens, A. G. G. M. 1991, ApJ, 377, 192 In the text NASA ADS  
• Huchtmeier, W. K., & Richter, O.-G. 1988, A&A, 203, 237 In the text NASA ADS  
• Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 In the text NASA ADS  
• Kobulnicky, H. A., & Skillman, E. D. 1997, ApJ, 489, 636 In the text NASA ADS  
• Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 In the text NASA ADS  
• Lord, S. D., Hollenbach, D. J., Colgan, S. W. J., et al. 1995, in ASP Conf. Ser. 73, Airborne Astronomy Symposium on the Galactic Ecosystem: From Gas to Stars to Dust, ed. M. R. Haas, et al., 151 In the text  
• Madden, S. C., Poglitsch, A., Geis, N., Stacey, G. J., & Townes, C. H. 1997, ApJ, 483, 200 In the text NASA ADS  
• Maloney, P., & Black, J. H. 1988, ApJ, 325, 389 In the text NASA ADS  
• Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 In the text NASA ADS  
• McCall, M. L., Rybski, P. M., & Shelds, G. A. 1985, ApJS, 57, 1 In the text NASA ADS  
• Mochizuki, K. 2000, A&A, 363, 1123 In the text NASA ADS  
• Mochizuki, K., & Nakagawa, T. 2000, ApJ, 535, 118 In the text NASA ADS  
• Mochizuki, K., Nakagawa, T., Doi, Y., et al. 1994, ApJ, 430, L37 In the text NASA ADS  
• Nakagawa, T., Yui, Y. Y., Doi, Y., et al. 1998, ApJS, 115, 259 In the text NASA ADS  
• Pak, S., Jaffe, D. T., van Dishoeck, E. F., Johansson, L. E. B., & Booth, R. S. 1998, ApJ, 498, 735 In the text NASA ADS  
• Palumbo, G. G. C., et al. 1988, Accurate positions of Zwicky galaxies, SIMBAD In the text  
• Papaderos, P., Hoose, H.-H., Thuan, T. X., & Fricke, K. J. 1996a, A&AS, 120, 207 In the text NASA ADS  
• Papaderos, P., Hoose, H.-H., Fricke, K. J., & Thuan, T. X. 1996b, A&A, 314, 59 In the text NASA ADS  
• Pierini, D., Leech, K. J., Tuffs, R. J., & Volk, H. J. 1999, MNRAS, 303, L29 In the text NASA ADS  
• Russell, S. C., & Dopita, M. A. 1990, ApJS, 74, 93 In the text NASA ADS  
• Smith, B. J., & Madden, S. C. 1997, AJ, 114, 138 In the text NASA ADS  
• Stacey, G. J., Geis, N., Genzel, R., et al. 1991, ApJ, 373, 423 In the text NASA ADS  
• van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 In the text NASA ADS  
• Viallefond, F., & Thuan, T. X. 1983, ApJ, 269, 444 In the text NASA ADS  
• Wolfire, M. G., Hollenbach, D. J., & Tielens, A. G. G. M. 1989, ApJ, 344, 770 In the text NASA ADS  
• Young, J. S., Xie, S., Tacconi, L., et al. 1995, ApJS, 98, 219 In the text NASA ADS  
• Zwicky, F., Herzog, E., & Wild, P. 1961, Catalogue of galaxies and of clusters of galaxies (Pasadena: California Institute of Technology) In the text