A&A 370, 1030-1043 (2001)
DOI: 10.1051/0004-6361:20010242

The CH out-of-plane bending modes of PAH molecules
in astrophysical environments[*]

S. Hony1 - C. Van Kerckhoven2 - E. Peeters3,4 - A. G. G. M. Tielens3,4 - D. M. Hudgins5 - L. J. Allamandola5

1 - Astronomical Institute `Anton Pannekoek', Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 - Instituut voor Sterrenkunde, K. U. Leuven, Celestijnenlaan 200B, 3001 Heverlee, Belgium
3 - SRON Laboratory for Space Research Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
4 - Kapteyn Astronomical Institute PO Box 800, 9700 AV Groningen, The Netherlands
5 - NASA/Ames Research Center, MS:245-6, Moffett Field, CA 94035-1000, USA

Received 2 August 2000 / Accepted 12 February 2001

Abstract
We present 10-15 $\mu $m spectra of a sample of H  II regions, YSOs and evolved stars that show strong unidentified infrared emission features, obtained with the ISO/SWS spectrograph on-board ISO. These spectra reveal a plethora of emission features with bands at 11.0, 11.2, 12.0, 12.7, 13.5 and 14.2 $\mu $m. These features are observed to vary considerably in relative strength to each-other from source to source. In particular, the 10-15 $\mu $m spectra of the evolved stars are dominated by the 11.2 $\mu $m band while for H  II regions the 12.7 is typically as strong as the 11.2 $\mu $m band. Analysing the ISO data we find a good correlation between the 11.2 $\mu $m band and the 3.3 $\mu $m band, and between the 12.7 $\mu $m and the 6.2 $\mu $m band. There is also a correlation between the ratio of the UIR bands to the total dust emission and the 12.7 over 11.2 $\mu $m ratio. Bands in the 10-15 $\mu $m spectral region are due to CH out-of-plane (OOP) bending modes of polycyclic aromatic hydrocarbons (PAHs). We summarise existing laboratory data and theoretical quantum chemical calculations of these modes for neutral and cationic PAHs. Due to mode coupling, the exact peak position of these bands depends on the number of adjacent CH groups and hence the observed interstellar 10-15 $\mu $m spectra can be used to determine the molecular structure of the interstellar PAHs emitting in the different regions. We conclude that evolved stars predominantly inject compact  100-200 C-atom PAHs into the ISM where they are subsequently processed, resulting in more open and uneven PAH structures.

Key words: circumstellar matter - stars: pre-main sequence - H  II regions - ISM: molecules; - planetary nebulae: general - infrared: ISM: lines and bands


1 Introduction

Many sources show a rich set of emission features at 3.3, 6.2, 7.7, 8.6 and 11.2 $\mu $m commonly called the unidentified infrared (UIR) emission features. These bands dominate the IR spectra of a wide variety of objects, including H  II regions, PNe, post-AGB objects, YSOs, the diffuse ISM, galaxies and galactic nuclei (Cox & Kessler 1999). Understanding these features and the origin and evolution of their carriers has become an important problem in astrophysics. These UIR bands are generally attributed to IR fluorescence of small ($\sim$50 C-atom) polycyclic aromatic hydrocarbons (PAHs) molecules.

Laboratory spectroscopy of PAHs shows that, besides the well known UIR bands, PAHs exhibit many weaker emission bands. In particular, the region from 10 to 15 $\mu $m has a rich spectrum due to the out-of-plane bending vibrations (OOP) of aromatic H-atoms. The peak wavelength of these modes depends on the structure of the molecule; in particular on the number of neighbouring H-atoms per ring (e.g. Bellamy 1958; Hudgins & Allamandola 1999). Here we present data in this region obtained with the Short Wavelength Spectrometer (SWS) (de Graauw et al. 1996) on-board the Infrared Space Observatory (ISO) (Kessler et al. 1996). The sensitivity and medium resolving power of the instrument allows us to detect and resolve several weak features predicted by the PAH hypothesis and to determine the molecular structure of the emitting PAHs and their evolution in space.

In Sect. 2, we present the observations of our sample of H  II regions, YSOs, reflection nebulae (RNe) and evolved objects. The 10-15 $\mu $m regions of these sources are analysed in Sect. 3. The spectral characteristics of PAHs in this wavelength range as measured in the laboratory and calculated by quantum chemical theories are summarised in Sect. 4.1. In Sect. 4.2 the laboratory spectra are compared to the observed spectra. The molecular structures implied by the observed spectra are discussed in Sect. 5 while in Sect. 6 the origin and evolution of these molecular structures are examined. Finally in Sect. 7 our main results are summarised.

   
2 Observations


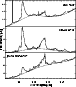  \begin{figure} \psfig{figure=h2367f1.ps,angle=0} \end{figure} Figure 1: Spectra of 3 sources that show features in the region of interest. The dashed lines are the continua mentioned in the text


 

 
Table 1: Source list. Observational details of the sources used in this study
Object Obs.a $\alpha$ $\delta$ TDTb Sp.Type $G_{\rm0}$ Obj.Type
  Mode (J2000) (J2000)     (1.6 10-6 W/m2)
AFGL 437 01(2) 03 07 23.68 +58 30 50.62 86300810 O8.5 1E5 Star forming region
IRAS 03260+3111 01(3) 03 29 10.37 +31 21 58.28 65902719 B9 2E4 Herbig AeBe
NGC 2023 01(3) 05 41 38.30 -02 16 32.59 65602309 B1.5V 3E2 Refl. Nebula
HD 44179 01(4) 06 19 58.20 -10 38 15.22 70201801 B8V 5E6 post-AGB
IRAS 07027-7934 01(2) 06 59 26.30 -79 38 48.01 73501035 WC10 2E7 PN
HD 97048 01(4) 11 08 04.61 -77 39 16.88 61801318 A0 2E4 Herbig AeBe
IRAS 12405-6238 01(3) 12 43 31.93 -62 55 11.39 29400410 O9.5 3E5 H  II
HEN 2-113 $^{\dagger}$         WC10 6E4 PN
- 01(1) 14 59 53.49 -54 18 07.70 07903307      
- 01(2) 14 59 53.49 -54 18 07.70 43400768      
IRAS 15384-5348 01(2) 15 42 17.16 -53 58 31.51 29900661   1E4 H  II
CD-42 11721(off) 01(2) 16 59 05.82 -42 42 14.80 28900461 B0 - Herbig AeBe (off pointing)
CD-42 11721 $^{\dagger}$         B0 - Herbig AeBe
- 01(2) 16 59 06.82 -42 42 07.60 08402527      
- 01(2) 16 59 06.80 -42 42 07.99 64701904      
IRAS 17047-5650 $^{\dagger}$         WC10 5E6 PN
- 01(3) 17 09 00.91 -56 54 47.20 13602083      
- 01(1) 17 09 00.91 -56 54 48.10 27301339      
HB 5 01(3) 17 47 56.11 -29 59 39.70 49400104 120 000$\ddagger$ - PN
NGC 6537 01(3) 18 05 13.14 -19 50 34.51 70300475 A0 - PN
GGD 27-ILL $^{\dagger}$         B1 3E6 Star forming region
- 01(2) 18 19 12.04 -20 47 30.98 14802136      
- 01(2) 18 19 12.03 -20 47 30.59 14900323      
IRAS 18240-0244 01(1) 18 26 40.00 -02 42 56.99 14900804 WC8 - PN
IRAS 18317-0757 01(2) 18 34 24.94 -07 54 47.92 47801040 O8 - H  II
IRAS 18416-0420 01(2) 18 44 15.19 -04 17 56.40 13402168 O5.5 - H  II
IRAS 18502+0051 01(2) 18 52 50.21 +00 55 27.59 15201645 O7 - H  II
TY CRA $^{\dagger}$         B9 6E3 Herbig AeBe
- 01(3) 19 01 40.71 -36 52 32.48 33400603      
- 01(1) 19 01 40.70 -36 52 32.59 34801419      
- 01(3) 19 01 40.71 -36 52 32.48 71502003      
BD +30 3639 01(3) 19 34 45.20 +30 30 58.79 86500540 WC9 1E5 PN
IRAS 19442+2427 01(2) 19 46 20.09 +24 35 29.40 15000444 O7 6E6 H  II
BD+40 4124 01(3) 20 20 28.31 +41 21 51.41 35500693 B2 1E4 Herbig AeBe
S106 IRS4 01(2) 20 27 26.68 +37 22 47.89 33504295 08 1E5 H  II
NGC 7023 $^{\dagger}$         B3 5E2 Refl. Nebula
- 01(4) 21 01 31.90 +68 10 22.12 20700801      
- 01(2) 21 01 30.40 +68 10 22.12 48101804      
NGC 7027 $^{\dagger}$         200 000$\diamond$ 2E5 PN
- 01(4) 21 07 01.71 +42 14 09.10 02401183      
- 01(1) 21 07 01.70 +42 14 09.10 23001356      
- 01(2) 21 07 01.70 +42 14 09.10 23001357      
- 01(3) 21 07 01.70 +42 14 09.10 23001358      
- 06 21 07 01.50 +42 14 10.00 33800505      
- 01(4) 21 07 01.63 +42 14 10.28 55800537      
IRAS 21190+5140 01(2) 21 20 44.85 +51 53 26.59 15901853 - 2E5 H  II
IRAS 21282+5050 $^{\dagger}$         O9 1E5 PN
- 01(2) 21 29 58.42 +51 03 59.80 05602477      
- 01(3) 21 29 58.42 +51 03 59.80 15901777      
- 01(2) 21 29 58.42 +51 03 59.80 36801940      
IRAS 22308+5812 01(2) 22 32 45.95 +58 28 21.00 17701258 O7.5 3E3 H  II
IRAS 23030+5958 01(2) 23 05 10.57 +60 14 40.60 22000961 O6.5 7E3 H  II
IRAS 23133+6050 01(2) 23 15 31.44 +61 07 08.51 22001506 O9.5 7E5 H  II

a SWS observing mode used (see de Graauw et al. 1996). Numbers in brackets correspond to the scanning speed.
bTDT number which uniquely identifies each ISO observation.
$^{\dagger}$These spectra have been obtained by co-adding the separate SWS spectra also listed in the table, see text.
$^{\ddagger}$Effective temperature from Gesicki & Zijlstra (2000). $^{\diamond}$Effective temperature from Latter et al. (2000).

We include 29 high S/N spectra of 16 sources taken from the samples of H  II regions, YSOs, and post-AGB objects. For the trend analysis presented in Sect. 3.4 we have added another 15 sources in which the S/N is such that we cannot reliably measure the weakest features but we determine the intensities of the stronger UIR bands with reasonable accuracy. All spectra presented here have been obtained with the SWS instrument in the AOT01/AOT06 scanning mode at various speeds, with resolving power ( $\lambda/\Delta\lambda$) ranging from 500-1500 (see de Graauw et al. 1996), see Table 1 for details of the observations.

The data were processed using SWS interactive analysis product; IA3(see de Graauw et al. 1996) using calibration files and procedures equivalent to pipeline version 7.0. If a source has been observed multiple times and these observations are of similar quality and of comparable flux-level these data are co-added after the pipeline reduction. Since the features we discuss here are fully resolved in all observing modes, we combine the data obtained in all different modes to maximise the S/N. Further data processing consisted of bad data removal, rebinning on a fixed resolution wavelength grid, removing fringes and splicing of the sub-bands to form a continuous spectrum.

For all spectra the amount of shifting between sub-bands required falls well within the calibration uncertainties in the region of interest: 7 to 16 $\mu $m. Any jumps between bands are due to flux calibration and dark current uncertainties. The effect of dark current is most important in low flux cases while the flux calibration uncertainties will dominate in bright sources. Below 20 Jy we apply offsets to correct for dark current uncertainties. In these low signal cases the typical noise level in the dark current measurements of 1-2 Jy introduces offset uncertainties >5-10 per cent dominating the flux calibration uncertainties. Above 20 Jy we apply scaling factors to correct for flux calibration uncertainties. The splicing introduces little uncertainty in the measured strengths since most features fall completely within one ISO/SWS sub-band. An exception to this is the band strength of the 12.7 $\mu $m feature. This feature is sensitive to the way band 2C (7 to 12.5 $\mu $m) and 3A (12 to 16.5 $\mu $m) are combined. This introduces an extra uncertainty of the band strength of typically 20-30 per cent for the weakest features.

Some SWS data, especially in band 3A, are affected by fringes. We have corrected for fringes in those sources where they occur, using the aarfringe tool of IA3 on the rebinned spectrum. In the method we apply fringes are fitted with sine functions with periods in the range where fringes are known to occur and divided out. Note that the features we study here are much broader than any of fringe periods, therefore the intensities we measure are not directly affected by the fringes. However in some cases after fringe removal the continuum is more easily determined.

SWS spectra of many sources, including stars enshrouded in both carbon-rich and oxygen-rich dust and sources without any circumstellar material show very weak structure around 13.5 and 14.2 $\mu $m at the 3 to 4 per cent level relative to the continuum possibly due to residual instrumental response. The emission features discussed here are all stronger than this with a maximum of 85 per cent of the continuum in the reflection nebula NGC 7023. Near 11.03 $\mu $m there is a residual instrumental feature which coincides with the weak 11.0 $\mu $m feature that we observe in our spectra. We have included the effect of this feature in the uncertainty on the intensities in Table 2.

Many sources in this sample have strong narrow emission lines in their spectrum, in particular the strong [Ne  II] line at 12.81 $\mu $m is perched on top of the 12.7 $\mu $m UIR band. This line and the UIR band are easily separated at the resolution of the SWS instrument. We remove the contribution from this line by fitting a Gaussian profile to the line and subtracting that profile prior to rebinning. The spectrum of NGC 7027 has a very strong [Ne V] emission line at 14.32 $\mu $m. We have removed the part of the spectrum which contains this line. We also include in Table 1 the spectral type of the illuminating source and an estimate of the flux density at the location where the PAH emission originates from in units of the average interstellar UV field (Habing 1968). We have derived these estimates from the observed IR flux ( $I_{\rm IR}$) and the angular size of the PAH emission region (Wolfire et al. 1989). This estimate is based on the assumption that all the UV light is absorbed in a spherical shell with the angular size of the object and re-emitted in the IR. The flux density at the shell is given by:

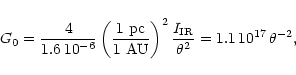\begin{displaymath}G_{\rm0} = \frac{4}{1.6\, 10^{-6}}\left(\frac{1~{\rm pc}}{1~{... ... \frac{I_{\rm IR}}{\theta^2} = 1.1\, 10^{17}\, {\theta}^{-2}, \end{displaymath} (1)

where $G_{\rm0}$ is the UV flux density in 1.6 10-6Watt/m2 and $\theta$ is the angular diameter of the object in arcseconds. We have used for the size of the H  II regions the measured radio sizes. This is reasonable since the PAHs are expected to be destroyed inside the H  II region. For the other objects we estimate the size of the PAH emission region from ISOCAM data (Cesarsky et al. 1996) when available.

   
3 Results


  \begin{figure} \psfig{figure=h2367f2.ps,angle=0} \end{figure} Figure 2: An overview of the observed features. All spectra have been continuum subtracted and are scaled to have the same integrated intensity in the 12.7 $\mu $m feature. The sources are ordered according to their 11.2/12.7 $\mu $m band strength ratio (bottom to top). The ratio of the 11.2 $\mu $m to the 12.7 $\mu $m feature spans a full decade. $^\nabla $ Sources with broad solid CO$_{\rm 2}$ absorption beyond 15 $\mu $m


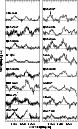  \begin{figure} \psfig{figure=h2367f3.ps,angle=0} \end{figure} Figure 3: An overview of the observed features near 13.5 and 14.2 $\mu $m. $^\nabla $HD 44179 and NGC 7027 have been scaled by a factor of 0.3

3.1 Overview

In Fig. 1 we present spectra of three typical sources to illustrate the spectral detail present and the variety of underlying continua. Even more so than previous IRAS/LRS and ground-based studies suggested (Cohen et al. 1985; Roche et al. 1989; Witteborn et al. 1989), the complete 11-15 $\mu $m spectra reveal an extremely rich collection of emission features with bands at 10.6, 11.0, 11.23, 12.0, 12.7, 13.5, and 14.2 $\mu $m. These features are perched on top of an emission plateau of variable strength, which extends across the entire region.

3.2 Continuum

In order to compare the intrinsic strength of the UIR bands in the different sources, we subtract a continuum, splined through points from 9-10.5 and 14.5-15.5 $\mu $m and through points near 11.8 and 13.1 $\mu $m. Since GGD 27 and IRAS 18416 have broad solid CO$_{\rm 2}$ absorption features beyond 15 $\mu $m, we take 14.7 $\mu $m to be the continuum rather than extending to 15.5 $\mu $m. Typical examples of the continua are included in Fig. 1. Besides the chosen points, the continuum also runs through the local minimum at 10.9, 12.2 and 14.0 $\mu $m with the exception of the Red Rectangle. This object has excess emission around these wavelengths, which could be related to the presence of crystalline silicates in the vicinity of HD 44179 (Waters et al. 1998). For any reasonable choice of continuum points, the underlying plateau ranges from about 10 to 14 $\mu $m, peaking at about 12 $\mu $m. At first sight, the plateau of GGD 27 seems to differ with an onset at about 11 $\mu $m and peaking around 13 $\mu $m. However, this likely reflects the effects of foreground silicate absorption. The PN IRAS 21282+5050 does show a plateau that differs, peaking at 12 $\mu $m but extending all the way to 17 $\mu $m.

3.3 Emission bands


 

 
Table 2: Peak position and strength of the features observed in the 10-15 $\mu $m for the sources shown in Fig. 2
(1) (2) (3) (4) (5) (6) (7) (8) (9)(10)(11)
Source $ {\Delta\lambda_{\rm 11.2}}^\dagger$ $ {I_{\rm 11.2}}^b$ $ {I_{\rm 12.7}}^{b\ddagger}$ $ {\lambda_{\rm c,13.5}}^a$ $ {I_{\rm 13.5}}^b$ $ {\lambda_{\rm c,14.2}}^a$ $ {I_{\rm 14.2}}^b$ $ {I_{\rm 11.0}}^{b}$ $ {I_{\rm 12.0}}^{b\star}$ $ {I_{\rm plateau}}^{b\diamond}$
  $ [10^{-3}\mu {\rm m}] $     $[\mu {\rm m}]$   $[\mu {\rm m}]$      
IRAS 03260 0.9(0.1) 15.8(0.4) 6.4(0.4) 13.57(2) 1.7(0.1) 14.19(2) 0.9(0.1) 0.8(0.1)n22
HD 44179 12.6(0.5) 118.1(6.4) 26.3(1.4) 13.61(2) 13.4(0.5) 14.21(2) 8.6(1.3) 4.8(2.3)5112
HEN 2-113 2.7(0.3) 17.0(1.0) 5.6(1.0) - - 14.26(5) 4.7(1.8) 0.5(0.5)d30
IRAS 15384 0.0(0.6) 14.5(0.8) 13.5(0.6) 13.52(2) 1.5(0.3) 14.30(2) 2.7(0.1) 0.6(0.1)266
CD -42(off) -6.5(0.2) 22.2(0.6) 11.3(0.5) 13.55(2) 1.7(0.5) 14.22(2) 0.8(0.2) 1.0(0.1)225
CD -42 -8.2(0.8) 31.7(1.5) 16.7(1.0) 13.53(2) 1.6(0.6) 14.22(2) 1.6(0.3) 1.9(0.3)158
IRAS 17047 11.8(0.4) 25.1(1.0) 11.6(1.0) 13.50(3) 1.8(1.3) 14.23(3) 2.2(1.0) 1.3(0.8)n145
GGD 27 2.6(0.6) 8.9(0.6) 5.4(0.5) 13.57(2) 2.1(0.2) 14.27(4) 1.5(0.9) 1.4(0.1)d3
IRAS 18317 6.5(0.1) 10.5(0.2) 15.6(0.3) 13.44(2) 2.0(0.3) 14.22(2) 2.2(0.2) 0.2(0.1)183
IRAS 18416 -2.3(0.3) 12.8(0.9) 9.8(0.5) 13.55(2) 2.4(0.4) 14.18(3) 3.1(1.2) 1.2(0.3)n52
TY CRA -5.0(0.3) 15.5(0.1) 4.7(0.2) 13.54(2) 1.3(0.3) 14.21(2) 0.5(0.1) 0.8(0.1)n13
S 106 -4.1(0.1) 19.7(0.9) 15.6(1.0) 13.56(2) 2.7(1.2) 14.19(2) 3.6(0.2) 1.1(0.3)261
NGC 7023 -3.9(0.2) 9.6(0.8) 4.3(0.3) 13.50(2) 1.1(0.2) 14.21(2) 0.7(0.3) 0.5(0.1)n11
NGC 7027 2.8(0.2) 142.7(5.4) 35.9(2.5) 13.52(2) 9.7(1.5) 14.26(2) 11.1(1.5) 4.0(1.7)6451
IRAS 21282 4.2(1.4) 20.4(0.7) 6.2(0.2) 13.40(2) 1.5(0.4) 14.22(2) 1.7(0.6) 0.6(0.3)y104
IRAS 22308 -3.2(0.5) 8.9(0.4) 5.8(0.6) 13.55(4) 1.3(0.6) 14.23(2) 2.1(0.1) 0.7(0.1)n9

The intensities $I_{\rm 11.2}$, $I_{\rm 12.7}$, $I_{\rm 11.0}$, $I_{\rm 12.0}$ and $I_{\rm plateau}$ are the integrated fluxes of the features after continuum subtraction (Cols. 3, 4, 9, 10 and 11). The position of the 11.2 and 12.7 $\mu $m features are determined by fitting the template profile to the spectra in which we allow for a wavelength shift and a scaling of the template (Col. 2). The properties of the features around 13.5 and 14.2 are determined by fitting Gaussian profiles to the data (Cols. 5-8). Numbers in parentheses are uncertainties.
aCentral wavelength of the fitted Gaussian profile, uncertainties are given in parentheses in units of 10$^{-2} \mu$m.
bIntensities and uncertainty units are 10-14 W/m2
$^{\dagger}$Shift of the 11.2 $\mu $m feature relative to the template 11.2 $\mu $m profile. The template profile peaks at 11.229(0.001) $\mu $m.
$^{\ddagger}$No significant shifts of the 12.7 $\mu $m profile are observed with respect to the mean 12.7 $\mu $m profile. The mean profile ranges from 12.2-12.95 $\mu $m with the peak position at 12.804(0.005) $\mu $m. Typical uncertainty in the position determination 0.006 $\mu $m.
$^{\star}$Typical error on $I_{\rm 12.0}$ is 0.5 10-14 W/m2; d means detected but not measured; n means not detected.
$^{\diamond}$Typical error on $I_{\rm plateau}$ is 10 10-14 W/m2.

We show the continuum subtracted spectra of the 16 objects with the highest S/N in Fig. 2. Perusal of the spectra reveals a plethora of weaker features. NGC 7027, HD 44179 and IRAS 21282 have a very weak, broad feature near 10.6 $\mu $m. Almost all these sources show a feature at 11.0 $\mu $m, except for GGD 27, where the feature is possibly present but only at the 1$\sigma$ level. The weak 12.0 $\mu $m band is detected in 10 out of 16 sources. The 13-15 $\mu $m range contains the newly discovered weak 13.5 and 14.2 $\mu $m features (Fig. 3). Structure near 13.5 is present in all sources except HEN 2-113, however for IRAS 21282 and IRAS 18317 the band is replaced by a feature that peaks at a shorter wavelength. A feature near 14.2 $\mu $m is found in all sources although the actual peak position varies considerably (cf., IRAS 03260 and IRAS 15384). This variation in peak position of these two weak bands is quite in contrast with that of the 11.2 and 12.7 $\mu $m bands which almost invariably peak at about the same wavelength (see below). A priori, it is not given that the spectral structure near 14 $\mu $m is actually related in the different sources. Possibly, rather than one molecular vibration with a varying peak position, at this weak level of emission, we are probing different bands whose relative strengths reflect the conditions in the different sources.

In Fig. 2 we show the continuum subtracted spectra after normalising to the integrated strength of the 12.7 $\mu $m feature. The sources are ordered according to the strength of the 11.2 $\mu $m feature relative to the 12.7 $\mu $m band. Relative to the 12.7 $\mu $m band, the sources with the weakest 11.2 $\mu $m feature are the H  II regions (at the bottom of Fig. 2), while the evolved stars show the strongest 11.2 $\mu $m band.

The spectral characteristics of the features are summarised in Table 2. Note that the uncertainties quoted in the table reflect the noise level and the freedom in drawing the continuum within the methodology used to measure these bands. Other ways of decomposing the broad, blended bands and the underlying continuum will give other results (e.g. Boulanger et al. 1998; Uchida et al. 2000; Verstraete et al. 2001). However these differences are systematic differences and do not affect the source-to-source variations we observe. The intensities of the 11.2 and 12.7 $\mu $m features are obtained by direct integration above the chosen continuum. We measure the peak position of the 11.2 and 12.7 $\mu $m bands by fitting them with template spectra of these features. The template spectrum for the 11.2(12.7) $\mu $m feature is constructed by adding the continuum subtracted spectra with each 11.2(12.7) $\mu $m feature normalised to have the same integrated intensity. This way each source has equal contribution to the template spectrum. We use a $\chi^2$-minimisation routine to fit the template to the sources, allowing for both a wavelength shift and scaling in strength. The shifts that we determine for the 11.2 $\mu $m band are very small except for HD 44179 and IRAS 17047 where this band is much broader than the template spectrum (cf., Table 2, see also Peeters et al. 2001, in prep.). Although there are differences between the detailed profiles of the 12.7 $\mu $m band we detect no significant shift of the band as a whole. For the weak features near 13.5 and 14.2 $\mu $m, the parameters have been determined through fitting of Gaussian profiles. We adopted a local linear continuum for the very weak 11.0 $\mu $m feature because of the severe blending of this band with the 11.2 $\mu $m band. The weak 12.0 $\mu $m band is close to both the 11.2 and the 12.7 $\mu $m band. For only a few sources we measure the intensity of this band, for the other sources we refrained from detailed analysis. However Table 2 does note whether we detect this band.

The profile of the 11.2 $\mu $m feature is asymmetric with a sharp blue rise and a more gradual decline to longer wavelengths (Roche et al. 1989; Witteborn et al. 1989). This will be discussed in more detail for this sample by Peeters et al. (2001, in prep.). The 12.7 $\mu $m band is also asymmetric but in the opposite way with a slow blue rise and a sharp red decline between 12.8 and 12.9 $\mu $m. Because of their intrinsic weakness, the profiles of the 10.6, 11.0, 12.0, 13.5, and 14.2 $\mu $m features in the individual sources are not well determined however in the averaged spectrum, these features appear symmetric (cf. Fig. 7).

   
3.4 Trends

Given the large range of band strength ratios in the region of interest and the smooth variations in this ratio, it is of interest to investigate the correlation of the strength of all UIR emission bands with these variations. As a class all the planetary nebulae with a Wolf-Rayet central star (HEN 2-113, BD+30, IRAS 17047, IRAS 07027 and IRAS 18240) as well as the post-AGB star HD 44179 show a distinctly different UIR spectrum characterised by a shift in of the 6.2 and 7.7 $\mu $m bands towards 6.3 and 8 $\mu $m respectively (Peeters et al. 2001, in prep.). Because of these spectral differences we have not included them in the following trend analysis in which they also separate out as a peculiar subgroup. These objects will be discussed in detail in a forthcoming paper (Hony et al. 2001, in prep.).

Because here we want to study variations in the relative strength of the UIR bands to each other, not differences in absolute intensities differences due to intrinsic luminosity and distance of the source, we use 3-feature intensity ratio correlations. Although we observe variations in all ratios, we find only three that correlate and these are shown in Figs. 4-6. First, we find that the CH stretch mode at 3.3 $\mu $m correlates with the 11.2 $\mu $m band (cf. Fig. 4). Note that the slope of the trend is roughly 1, which means that the $I_{\rm 11.2}$/ $I_{\rm 3.3}$ is on the average constant at a value of 3-4.

Second, the 12.7 $\mu $m band correlates with the CC stretch mode at 6.2 $\mu $m, albeit with more scatter (cf. Fig. 5) than the 11.2/3.3 ratio. The 7-9 $\mu $m complex is well correlated with the 6.2 $\mu $m band and similar plots can be made with these interchanged. Inspection of Fig. 2 and Table 2 shows that there is some indication for both the $I_{\rm 13.5}$/ $I_{\rm 11.2}$ and the $I_{\rm 14.2}$/ $I_{\rm 11.2}$ $\mu $m band to be higher in H  II regions, however only about half the sources have such high S/N that these intensities can be reliably measured and this trend is not statistically significant.

Lastly, we show in Fig. 6 the correlation between the ratio of the flux emitted in the PAH bands relative to the total flux emitted in the IR ( $I_{\rm IR}$) and the changing $I_{\rm 12.7}$/ $I_{\rm 11.2}$ ratio. We measure the $I_{\rm IR}$ by integrating the SWS data and Long Wavelength Spectrometer (LWS) data if available. For those sources without LWS data we use a blackbody fitted to IRAS measurements in the wavelength region from 45-200 $\mu $m. We do not apply corrections for aperture differences between the instruments. We estimate an uncertainty of 15 per cent on the $I_{\rm IR}$. Again different classes of objects occupy different parts in this diagram.

We also checked for correlations between band strength ratios and the flux density; $G_{\rm0}$, however we do not detect any correlations.

We emphasise that, while all UIR bands show a loose correlation in the absolute intensity (see also Cohen et al. 1986, 1989), these three are the only tight correlations present in this sample.

  \begin{figure} \psfig{figure=h2367f4.ps,width=8.8cm} \end{figure} Figure 4: Bands strength ratios as derived from the SWS spectra. Hexagons are H  II regions, stars intermediate mass star forming regions, squares RNe and triangles are PNe


  \begin{figure} \psfig{figure=h2367f5.ps,width=8.8cm} \end{figure} Figure 5: Bands strength ratios as derived from the SWS spectra. Plotting symbols are the same as in Fig. 4


  \begin{figure}\psfig{figure=h2367f6.ps,width=8.8cm} \end{figure} Figure 6: The ratio between the flux emitted in the PAH bands over the total amount of IR radiation against the $I_{\rm 12.7}$/ $I_{\rm 11.2}$ ratio. Plotting symbols are the same as in Fig. 4

3.5 Comparison with other studies

It is interesting to compare the result we obtained from the SWS spectra with results by other authors. Studying many locations in the diffuse interstellar medium Chan et al. (2000) find that the relative bands strengths of the 6.2, 7.7 and the 11.2 $\mu $m features do not vary systematically over a wide range of intensities of the incident radiation field. Their observed ratios of $I_{\rm 11.2}$/ $I_{\rm 6.2}$ cluster around 0.8, the value we observe in the RNe and the YSOs. Studying a few RNe at various locations Uchida et al. (2000) with ISO/CAM (Cesarsky et al. 1996) find only small variations in band strength ratios. The $I_{\rm 11.2}$/ $I_{\rm 6.2}$ ratios they derive with the method which is most similar to ours (method 2) are like those we find for the RNe. Their $I_{\rm 12.7}$/ $I_{\rm 11.2}$ ratios are however systematically lower that ours. This is due to the lower spectral resolution of the CAM spectra which results in blending and smearing of the weakish band at 12.7 $\mu $m. The SWS spectra are not affected by smearing since the features are fully resolved. The results of these authors, like the results we present here, demonstrate that similar types of sources show similar PAH band strength ratios. Our results also demonstrate how different classes of objects show systematic differences in their PAH spectra. Observations of the starforming region M 17 have suggested that the 13.5 $\mu $m band is correlated with the mid-IR continuum (Verstraete et al. 1996). Such a correlation is important to establish since it might yield information on the size of the carriers of the 13.5 $\mu $m band. We have examined whether a correlation is also present in the sample of sources we study here. We have therefore compared the 15-16 $\mu $m continuum with the strength of the 13.5 $\mu $m band. We find strong variations, by a factor of $\simeq $100 in the strength of the mid-IR continuum relative to the 13.5 $\mu $m band. These strong variations are not surprising considering the fact that we look at very diverse regions with large differences in dust composition and temperature distributions. For example the evolved object HD 44179 has contributions from crystalline silicates around 15 $\mu $m (Waters et al. 1998). Many H  II regions have a strongly rising continuum due to warm dust. However we would also like to point to the two observations of CD-42 11721 where the 13.5 band is equally strong but the dusty continuum is missing in the off-pointed observation. These two observations show the 15 micron continuum and the 13.5 micron feature to be decoupled even within the same object.

4 The CH out-of-plane bending modes


 

 
Table 3: Wavelength region limits and the integrated absorption cross-sections for the CH out-of-plane bending modes
  ${\lambda_{\rm low}}^\dagger$ ${\lambda_{\rm up}}^\dagger$ $A^\diamond\ddagger$ ${A_{\rm neutral}}^\diamond$ ${A_{\rm cation}}^\diamond$
  $[\mu {\rm m}]$ $[\mu {\rm m}]$[km/mol][km/mol][km/mol]
Solo10.611.424.8(13.5)25.7(14.2)24.1(12.9)
Duo11.3512.84(2.5)4.4(2.4)3.7(2.5)
Trio12.513.39.6(5.9)10.1(5.3)9.0(6.5)
Quartet13.013.912.0(4.8)11.5(5.5)12.6(3.9)

Summary of the laboratory results on CH out-of-plane bending modes for solo, duo, trio and quartet hydrogens on matrix isolated neutral polycyclic aromatic hydrocarbons and their cations. (Adapted from Hudgins et al. 2000b).
$^\dagger\lambda_{\rm low}$ is the lower limit of the region in $\mu $m. $\lambda_{\rm up}$ is the upper limit of the region in $\mu $m.
$^{\diamond}$The cross-section values for the solo, trio, and quartet modes per hydrogen are the averages over the spectra in the database. However, the A values for the duo mode per hydrogen decreases rapidly with size and settles to slightly less than 4 km/mole for PAHs with more than 24 carbon atoms. This value is more appropriate to use in determining the edge structures of PAHs that dominate emission in this wavelength region.
$^{\ddagger}$Total average cross-sections over both neutrals and cations in the database.



  \begin{figure} \psfig{figure=h2367f7.ps,angle=0} \end{figure} Figure 7: A comparison of the average interstellar spectrum (top) with the ranges for the out-of-plane bending modes (bottom). The average spectrum was obtained by co-adding the continuum subtracted spectra after normalisation to the 12.7 $\mu $m band strength. The boxes indicate the wavelength regions associated with the out-of-plane bending vibrations for different types of adjacent hydrogen atoms determined from matrix isolated spectroscopy of neutral and cationic PAHs (see Hudgins et al. 2000b for details). In this comparison it should be kept in mind that the emission process leads to a small ($\simeq $0.1 $\mu $m) wavelength redshift in the peak position

   
4.1 Laboratory spectroscopy of the OOP modes

Chemists have long recognised the diagnostic value of the aromatic CH out-of-plane bending features in the 11 to 15 $\mu $m spectral region for the classification of the aromatic ring edge structures present in a particular sample (e.g. Bellamy 1958). Specifically, the positions of the bands in this spectral region reflect the number of adjacent CH groups on the peripheral rings of the PAH structure (Bellamy 1958; Allamandola et al. 1985; Cohen et al. 1985; Leger et al. 1989; Roche et al. 1989; Witteborn et al. 1989; Allamandola et al. 1999; Hudgins & Allamandola 1999). Traditionally, aromatic rings carrying CH groups which have no neighbouring CH groups (termed "non-adjacent'' or "solo'' CH groups) show IR activity between 11.1 and 11.6 $\mu $m. Likewise, activity between 11.6 and 12.5 $\mu $m is indicative of two adjacent CH groups ("doubly-adjacent'' or "duet'' CH's) on the periphery of the PAH. Three adjacent CH groups ("triply-adjacent'' or "trio'' CH's) are indicated by activity in the 12.4 to 13.3 $\mu $m region, and four adjacent CH groups ("quadruply-adjacent'' or "quartet'' CH's) by activity between 13 and 13.6 $\mu $m. Five adjacent CH groups ("quintuply-adjacent'' or quintet CH's) are indicated by features falling in the 13 to 13.7 $\mu $m range. Trios and quintets also show a weak CCC bending mode in the 14-14.5 range. Other CCC bending modes occur in the 15-20 $\mu $m range and have been discussed in the astrophysical context by Van Kerckhoven et al. (2000) and Moutou et al. (2000). Over the years the reliability of this region to yield insight into the molecular structure and ring sidegroup placement on aromatic samples has been verified again and again (see Hudgins & Allamandola 1999 and references therein). However, most of these chemist's guidelines were based on studies of small PAHs where varying patterns of sidegroup substitution were employed to achieve different degrees of CH adjacency. Furthermore, these chemist's "rules-of-thumb'' are based on spectroscopic studies of aromatic molecules in solution or solid mixtures, environments quite different from that of the emitting aromatic species giving rise to the interstellar features presented here. To obtain infrared data more relevant to the interstellar situation on larger molecules with the spectral details in this region determined by PAH structure rather than side-group substitution pattern, several groups have undertaken new spectroscopic studies of PAHs carried out under more appropriate conditions (e.g. see Szczepanski et al. 1995 and references therein; Hudgins et al. 2000a and references therein). Thanks to this effort, the mid-IR spectra of a few gas phase and many matrix isolated neutral and ionised PAHs are now available. In the Astrochemistry Laboratory at NASA Ames this work has been expanded considerably, including an extensive set of theoretical calculations, aimed to specifically address the questions raised by these new ISO spectra. Since a detailed presentation and analysis of the 11 to 15 $\mu $m region of the expanded dataset of matrix isolated PAH spectra will be published separately (Hudgins et al. 2000b), only the salient points are summarised here and used in the analysis presented below. The IR spectra of matrix isolated PAHs compare favourably with the available spectra of gas phase PAHs, for both neutral PAHs and cationic PAHs (see also Piest et al. 1999) and validates the use of the matrix isolation method to obtain astronomically relevant data.

There are two points that emerge from an analysis of the laboratory database that are of particular importance to the observational data presented here. The first involves the effect of ionisation on the characteristic wavelength regions of the various CH adjacency classes. The second is the intrinsic integrated absorption strengths (A values) which are derived for the various adjacency classes. Together these results provide the tools to not only qualitatively infer the sorts of PAH edge structures present, but also quantitatively determine their relative amounts. As shown below, this allows one to place stringent constraints on the emitting interstellar PAH family.

4.2 OOP modes in the interstellar spectrum

Figure 7 and Table 3 summarise the key points presented in Hudgins et al. (2000b) that are applicable to this work. Figure 7 schematically compares the average UIR spectrum with the wavelength regions associated with different hydrogen type for neutral and ionised isolated PAHs, while Table 3 lists the specific wavelength limits and the integrated band strengths per CH group as a function of hydrogen adjacency for all PAHs in the NASA Ames database. The regions indicated for the neutral PAHs differ slightly from those indicated by Bellamy (1958). We deem our results more astrophysically representative because of the larger set of molecules studied and because no substitution with strongly electro-negative groups were involved. Moreover our data were measured on isolated PAHs in inert matrices, rather than in solid mixtures.

Perusal of Fig. 7 and the wavelength limits listed in Table 3 shows that, while the ranges for neutral PAHs are not modified substantially compared to Bellamy (1958), ionisation causes some important changes in region boundaries. These data expand on the initial report that the PAH cation solo hydrogen position is substantially blue shifted with respect to the wavelength for its neutral counterpart while the domains indicative of the other types of hydrogen are less affected by ionisation (Hudgins & Allamandola 1999). Considering these modified domains and taking into account the roughly 0.1 $\mu $m redshift in the peak position for PAHs emitting at temperatures of $\sim$500-1000 K (Flickinger et al. 1991; Brenner & Barker 1992; Colangeli et al. 1992; Joblin et al. 1995; Cook & Saykally 1998) allows us to draw the following conclusions.

 
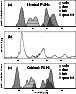  \begin{figure} \psfig{figure=h2367f8.ps} \end{figure} Figure 8: Comparison between the mean interstellar spectrum (panel b)) and synthetic PAH spectra showing the distribution over peak positions of the OOP modes in the Hudgins database (Hudgins et al. 2000b). The shaded surfaces in panels a) and c) represent the contributions per mode for neutral and positively charged PAHs respectively. Each area represents the average absorption cross-section per functional group

The large laboratory database and the high quality of the ISO interstellar spectra allows us to compare the distribution of peak positions of the individual modes with the bands observed in the interstellar spectrum. From the measured peak positions and cross-sections from the Hudgins database we construct a synthetic spectrum of a mixture of PAHs for comparison with the observed interstellar UIR bands. We construct such a spectrum on a mode-per-mode basis. Per mode, we take for each molecule which shows this mode the measured peak position and cross-section per CH bond and convolve this with a Gaussian profile. These contributions we add. The resulting envelopes per mode are normalised to the number of molecules exhibiting this mode and corrected for the number of CH bonds in one functional group. The measured cross-sections for the duo modes show a systematic decrease with increasing PAH size settling to a value of $\simeq $4 km/mol. To be consistent with the cross-section for the largest measured PAHs the contribution of the duo modes have been scaled down by a factor 1/4. This way each envelope shows the distribution over wavelengths, while each area corresponds to the average absorption cross-section per group in the database, see Table 3. Thus the synthetic spectrum for each mode is given by:

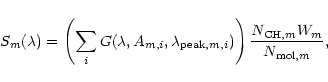\begin{displaymath}S_m(\lambda)=\left(\sum_i G(\lambda,A_{m,i},\lambda_{{\rm peak},m,i})\right) \frac{N_{{\rm CH},m}W_m}{N_{{\rm mol},m}}, \end{displaymath} (2)

where Sm is the synthetic spectrum for mode m, $\lambda$ the wavelength, Am,i the cross-section of the mode m in molecule i and $\lambda_{{\rm peak},m,i}$ the corresponding peak position. $G(\lambda,X,Y)$ is a Gauss function with FWHM=10 cm-1, surface =X, peak position =Y. $N_{{\rm CH},m}$ designates the number of CH bonds in one functional group, $N_{{\rm mol},m}$ the total number of molecules with mode m. Wm is a weighing factor which equals 1, 1/4, 1 and 1 for solo, duo, trio and quartet modes respectively to account for the decrease in strength of the duo modes in larger PAHs. The summation is done over all molecules in the database. The resulting envelopes are shown in Fig. 8 for both the neutral and cationic PAHs.

One should bear in mind, that the measured species are probably smaller than those that dominate the interstellar population and that, for stability reasons, the interstellar PAH family might be skewed to a few of these molecules or the edges structures they represent (cf. Sect. 5). Comparing the interstellar spectrum (Fig. 8b) with these averaged laboratory spectra (Figs. 8a,c) allows us to further refine the discussion:

Summarising the above we find that the overall match between the UIR spectra and the neutral species is best. There are significant differences between the combined laboratory measurements and the interstellar spectra. In particular the precise assignment of the 12.7 $\mu $m feature is uncertain. Given the above observations, we feel that while the assignment with trio modes is attractive, the case in not completely compelling. These issues might be resolved when larger species are measured in the laboratory. However it is clear that the 11.0 and 11.2 $\mu $m feature are due to solo CH bonds in ionised and neutral PAHs respectively, and the bands at longer wavelength are due to multiplets.

It is also immediately clear from Fig. 8 that the interstellar spectrum does not reflect an equal distribution over the different functional groups but is dominated by the contribution of solo modes. This reflects the molecular structure of the emitting PAHs.

   
5 The molecular structures of interstellar PAHs


 

 
Table 4: Relative number of solo,duo,trio and quartet groups in NGC 7027 and IRAS 18317
  s/d s/t s/q
NGC 7207 7.7 4.6 28.5
IRAS 18317 3.4 0.8 10.2

The ratio of the number of solo to duo (s/d), solo to trio (s/t) and solo to quartet (s/q) groups for NGC 7027 and IRAS 18317 as deduced from their 10 to 15 $\mu $m spectra.



  \begin{figure} \par { \psfig{figure=h2367f9.ps,angle=90,height=10cm} } \end{figure} Figure 9: Examples of molecular structures simultaneously satisfying the structural constraints set by the observed band strength ratios of the number of solo, duo and trio modes for different interstellar regions. The number of solo, duo, trio and quartet functional groups are noted s,d,t and q respectively. Solo modes are associated with long straight molecular edges. Duos and trios, on the other hand, correspond to corners. Quartets are due to pendant rings attached to the structure. The numbers in the molecular structures indicate the number of adjacent CH groups per aromatic ring

It is now possible to quantify the relative amounts of the various types of CH groups on the periphery of the interstellar PAHs which dominate the emission in this wavelength range and derive the types and sizes of interstellar PAH structures implied. This is achieved by analysing the peak positions and integrated band strengths listed in Table 2 with the laboratory data summarised in Table 3. In the following we assume that the 11.2 $\mu $m emission band arises from the the solo vibrations, the 12.0 $\mu $m band from duo modes, the 12.7 $\mu $m from trios and the 13.5 $\mu $m from quartets. From the laboratory data we get the intrinsic strength of solos relative to the duos, trios and quartets as 6.2, 2.6 and 2.1 respectively (see Table 3). From the intensities of the individual features listed in Table 2 for NGC 7027 we see that the observed solo to duo, solo to trio and solo to quartet intensity ratios are 23.8, 4.0, 14.7 respectively. We conclude that in NGC 7027 the ratio of the number of solo CH bonds to CH bonds in duo, trio and quartet groups are 3.8, 1.5 and 7.1. Taking into account the number of CH's per functional group there are 7.7, 4.6 and 28.5 solo (groups) relative to the duo, trio and quartet groups. For IRAS 18317 these values are (see also Table 4) 3.4, 0.8 and 10.2 respectively. These two sources represent the extremes in the observed intensity ratio in our sample.

Examples of the types of PAHs which simultaneously satisfy these different structural constraints are shown in Fig. 9. In constructing these structures one should keep in mind that solo H's represent long straight edges, while the corners in the structures give rise to duos or trios. To match the dominance of the 11.2 $\mu $m feature in NGC 7027 one is naturally driven towards rather large molecules with at least $\simeq $100-200 carbon atoms and long straight edges. This is entirely in keeping with previous theoretical calculations of the molecular sizes of the PAH species which account for most of the emission in these features (Schutte et al. 1993). As illustrated in Fig. 9 structure 1 approximates the ratios listed in Table 4 for NGC 7027, these ratios requires a preponderance of solo hydrogens over duos and trios. The extreme quartet to solo group ratio observed for NGC 7027 is not well reproduced even by Fig. 9 structure 1. In order to reproduce that ratio in one single molecule one has to go to even larger molecules. Rather, we surmise the extreme ratio reflects the presence of molecules without any quartet groups. Quartet groups represent pendant rings on the molecule, which can be taken off without altering the other ratios strongly. Of course many other PAH structures that match the observed ratios are possible. However these structures are all very similar to this and the conclusion is the same: in NGC 7027 the PAH family is dominated by large compact PAHs.

In contrast, for IRAS 18317 the situation is very different. The observed ratios force one to include more corners or uneven edges. Structure 4 in Fig. 9 illustrates one way of achieving this. Of course this effect can also be achieved by going to smaller compact structures of the type shown in structure 1 or by breaking up structure 4 in two or more fragments. Structures 2 and 3 shown in Fig. 9 are intermediate between these two extremes and have solo/duo, solo/trio, and solo/quartet ratios consistent with the relative interstellar band intensities shown in Fig. 2 for the objects which lie between the extremes, NGC 7027 and the IRAS 18317. Thus we observe a structural evolution where closed, compact species dominate the emission in some regions, while open, uneven structures are more important in others. We surmise that this structural evolution as revealed by the smooth spectral evolution shown in Fig. 2 reflects the variations in chemical history and excitation environment in these regions.

   
6 Discussion

In this section we will discuss the assignment of 11.2 and 12.7 interstellar bands and observed variations in 11.2/12.7 $\mu $m ratio and their correlation with other UIR bands in view of their underlying physical causes (Sect. 6.1). In the past these variations have been attributed to dehydrogenation. We reconsider this suggestion in Sect. 6.2.

   
6.1 The 11.2,12.7 $\mu $m emission features

Since quantum calculations show that the CH stretch (3.3 $\mu $m band) is inherently very weak in ionized PAHs (Langhoff 1996), the 3.3 $\mu $m emission band is likely a measure of the neutral PAH contribution. Based on both the peak position of the 11.2 $\mu $m band (Sect. 4.2) and its correlation with the 3.3 $\mu $m band (Sect. 3.4) we assign this band to solo CH out-of-plane bending vibrations of neutral PAHs. This result means that in evolved stars the OOP spectrum is dominated by contributions from the neutral PAHs. We already assigned the weak bands at 10.6 and 11.0 $\mu $m to cations (Sect. 4.2). Even though the absorption cross-sections for the OOP modes do not change upon ionisation, we cannot directly derive the ionisation fraction from the measured band strength ratios. This is due to the fact that ionisation does strongly affect the strength of other modes, which in turn influences the fraction of absorbed energy emitted at any wavelength (Bakes et al. 2000).

The spectral identification of the 12.7 band is much less clear and it is not possible at this time to assign this band unambiguously to either neutral or cationic PAHs. In the existing database there is only one species with a strong band that matches well in position, which "happens'' to be a cation. Furthermore the strength of the interstellar 12.7 $\mu $m band correlates with the strength of the 6.2 $\mu $m feature (see Sect. 3.4). The strength of the modes between 6 and 9 $\mu $m are greatly enhanced upon ionisation, and thus, one way to understand this correlation is to assume that the 12.7 is also predominantly carried by cations.

Thus, seemingly, the 11.2 $\mu $m and 12.7 $\mu $m bands represent a dichotomy of interstellar PAHs with the former carried mainly by neutral and the latter by positively charged PAHs. The origin of this interrelation between charge and spectral characteristics in unclear. There is no indication in the laboratory experiments for a causal relation between, for example, charge state and the relative strength of the solo to trio modes. Considering also the discussion on the molecular structures implied by the relative fraction of the solos to duos and trios (Sect. 5; Fig. 9) we are forced to conclude that the good correlation between the 11.2 and 3.3 $\mu $m bands and between the 12.7 and the 6.2 $\mu $m bands reflects a correlation of molecular structure and charge state with environment. Indeed when using PAHs containing some 50 C-atoms (Leger & Puget 1984) the correlation between the $I_{\rm 11.2}$/ $I_{\rm 6.2}$ and $I_{\rm 3.3}$/ $I_{\rm 6.2}$ is well reproduced by model calculations of Bakes et al. (2000) by only varying the degree of ionisation. Thus, those environments which favour large PAHs and the 11.2 $\mu $m band (structure 1 in Fig. 9) also favour neutral PAHs. While in regions where open uneven molecular structures and the 12.7 $\mu $m band (structure 4 in Fig. 9) dominate, PAHs are predominantly charged.

This is probably also the origin of the correlation between the $I_{\rm PAH}$/ $I_{\rm IR}$ ratio and the $I_{\rm 12.7}$/ $I_{\rm 11.2}$ (cf. Fig. 6). The $I_{\rm PAH}$/ $I_{\rm IR}$ measures the PAH/dust abundance ratio. The loose correlation suggests that for the ISM sources the PAH abundance is lower. We recognise that PNe inject freshly synthesised PAHs into the ISM where they are mixed and processed by FUV photons and shocks. This processing will lead to a slow destruction of the PAHs.

The dominant molecular structure reflects the integrated history of the PAH family and we note that all sources with a strong 11.2 $\mu $m band are PNe, which have formed their PAHs within the last some 1000 years. Because open uneven molecular structures are kinetically more reactive to the addition of carbon atoms than compact structures, the predominance of the latter in chemically reactive regions where PAHs have recently formed can be rationalised (Frenklach & Feigelson 1989; Cherchneff et al. 1992). In contrast regions with relatively strong 12.7 $\mu $m bands are all H  II regions where luminous stars illuminate material which has been processed in the ISM for some 109 years. This processing irreversibly leads to a breaking down of the molecular structure because reformation is prohibited by the low temperature of the ISM.

This does not directly explain why the 11.2 $\mu $m band correlates with the neutral PAH indicator while the 12.7 $\mu $m emission feature correlates with bands attributed to ions. The charge state is rapidly set by the charge balance, which is dominated by local physical conditions, or more specifically the ionisation parameter, $(G_{\rm0}\, \sqrt{T_{\rm gas}})/n_{\rm e}$, where $G_{\rm0}$ is the FUV radiation field, $T_{\rm gas}$ is the gas-temperature and $n_{\rm e}$ the electron density. Thus rather than history, ionisation reflects the present. Possibly most of the destruction is occurring presently and is also driven by local physical conditions.

   
6.2 Dehydrogenation

We have argued that the smooth changes in the band strength ratios in the region of interest are caused by variations in the edge-structure of the dominant emitting species. However other effects can also be of influence on the emitted spectra. Most notably dehydrogenation. There has been a long debate in the literature on the effect of dehydrogenation on the spectral characteristics of the 10-15 $\mu $m region. Originally when only the 11.2 UIR band was known, its dominance had been attributed to extreme ($\sim$90%) dehydrogenation of the emitting aromatic species leaving only solo hydrogens (Duley & Williams 1981). However, this question was revisited when IRAS revealed the presence of duos and trios in the interstellar PAH family (Cohen et al. 1985). Theoretical studies of the dehydrogenation of interstellar PAHs have shown that for PAHs larger than about 25 C-atoms hydrogenation through reactions with abundant atomic H is more important than H loss through unimolecular dissociation (Tielens et al. 1987; Allamandola et al. 1989; Jochims et al. 1994; Allain et al. 1996; Jochims et al. 1999). Hence, with a typical PAH size of 50 C-atoms dehydrogenation should have no effect on the UIR spectrum.

Observationally, our analysis also argues against dehydrogenation. First, we observe a constant ratio of the 3.3 $\mu $m band (all CH oscillation) to the 11.2 $\mu $m band (only solo CH oscillation). However, we would expect a non-linear behaviour since, when dehydrogenation commences the number of solo H increases as duos and trios are converted to solo's and only at high dehydrogenation does the relation between the 3.3 and the 11.2 $\mu $m bands become linear (Schutte et al. 1993). Secondly, if the variation in $I_{\rm 12.7}$/ $I_{\rm 11.2}$ reflects dehydrogenation than we would expect that decreasing H coverage (i.e. decreasing $I_{\rm 12.7}$/ $I_{\rm 11.2}$) would correlate with increasing CC/CH mode emission (i.e. $I_{\rm 6.2}$/ $I_{\rm 11.2}$). The opposite is actually observed (cf. Fig. 5). We conclude therefore that dehydrogenation has little influence on the observed interstellar UIR spectrum.

   
7 Summary

We have presented new 10-15 $\mu $m spectra of evolved stars, H  II regions, RNe and YSOs. We observe very rich UIR spectra with strong bands at 11.2 and 12.7 $\mu $m and weaker bands at 10.6, 11.0, 12.0, 13.5 and 14.2 $\mu $m. These spectra show large variations in the band strength ratios between sources, especially in the 11.2 and 12.7 $\mu $m feature ratio. Evolved stars have a dominant 11.2 $\mu $m feature while in H  II regions the 12.7 and 11.2 are typically equally strong. We find that the 11.2 $\mu $m band correlates with the CH stretch band at 3.3 $\mu $m and that the 12.7 $\mu $m band correlates with the CC stretch band at 6.2 $\mu $m.

We have summarised new laboratory spectroscopy results for the CH out-of-plane bending vibrations on isolated neutral and cationic PAHs. Different number of adjacent CH bonds give rise to vibrations in distinctly different wavelength regions. The modes are therefore good diagnostics of the molecular structure of the emitting species. Upon ionisation the solo CH vibrations are shifted to shorter wavelength compared to the solo modes in neutral. The cross-sections per mode are not strongly modified upon ionisation. We attribute the weak bands at 10.6 and 11.0 $\mu $m to solo modes in positively charged PAHs, the strong 11.2 $\mu $m band the solo modes in neutral. The weak 12.0 $\mu $m band we assign to the duo modes, the 12.7 $\mu $m to trio modes and the 13.5 $\mu $m feature to quartet vibrations.

From the average cross-sections per mode we have constrained the relative numbers of solo, duo, trio and quartet CH groups in different sources for the PAH species that effectively emit in this wavelength region. The spectra of PNe with a dominant 11.2 $\mu $m feature arises from large ($\sim$100-150 C-atom) compact PAHs with long straight edges. In contrast the H  II region spectra are due to smaller or more irregular PAHs.

We propose a scenario in which large compact PAHs are formed in the winds around evolved stars. These PAHs are consequently degraded in the ISM. From the correlations between charge indicators, which are set by the local physical conditions, and the 11.2/12.7 $\mu $m band strength ratio, which is determined by the molecular structure, we conclude that much of this degradation happens on a short timescale in the emission objects themselves.

Acknowledgements
The authors wish to thank the referee dr. L. Verstraete whose comments have helped to improve the paper. SH acknowledges the support from an NWO program, grant 616-78-333. EP acknowledges the support from an NWO program, grant 783-70-000. CVK is a Research Assistant of the Fund for Scientific Research. DMH and LJA gratefully acknowledge support under NASA's IR Laboratory Astrophysics (344-02-06-01) and Long Term Space Astrophysics programs (399-20-01). IA3 is a joint development of the SWS consortium. Contributing institutes are SRON, MPE, KUL and the ESA Astrophysics Division. This work was supported by the Dutch ISO Data Analysis Center(DIDAC). The DIDAC is sponsored by SRON, ECAB, ASTRON and the universities of Amsterdam, Groningen, Leiden and Leuven.

References

 
Copyright ESO 2001