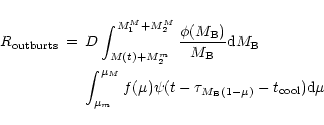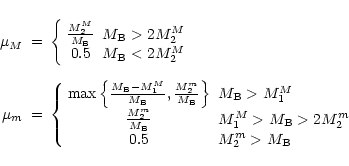A&A 370, 1103-1121 (2001)
DOI: 10.1051/0004-6361:20010296
Galactic chemical abundance evolution in the solar neighborhood up to the iron
peak
A. Alibés1 - J. Labay1 - R. Canal1,2
1 - Departament d'Astronomia i Meteorologia, Universitat de Barcelona,
Martí i Franquès 1, 08028 Barcelona, Spain
2 - Institut d'Estudis Espacials de Catalunya, Edifici Nexus, Gran
Capità 2-4, 08034 Barcelona, Spain
Received 27 December 2000 / Accepted 15 February 2001
Abstract
We have developed a detailed standard chemical evolution model to study the
evolution of all the chemical elements up to the iron peak in the solar vicinity.
We consider that the Galaxy was formed through two episodes of exponentially
decreasing infall, out of extragalactic gas. In a first infall episode, with
a duration of  1 Gyr, the halo and the thick disk were assembled
out of primordial gas, while the thin disk formed in a second episode of infall
of slightly enriched extragalactic gas, with much longer timescale. The model
nicely reproduces the main observational constraints of the solar neighborhood,
and the calculated elemental abundances at the time of the solar birth are in
excellent agreement with the solar abundances. By the inclusion of metallicity-dependent yields for the whole range of stellar masses we follow the evolution
of 76 isotopes of all the chemical elements between hydrogen and zinc. Those
results are compared with a large and recent body of observational data, and
we discuss in detail the implications for stellar nucleosynthesis.
1 Gyr, the halo and the thick disk were assembled
out of primordial gas, while the thin disk formed in a second episode of infall
of slightly enriched extragalactic gas, with much longer timescale. The model
nicely reproduces the main observational constraints of the solar neighborhood,
and the calculated elemental abundances at the time of the solar birth are in
excellent agreement with the solar abundances. By the inclusion of metallicity-dependent yields for the whole range of stellar masses we follow the evolution
of 76 isotopes of all the chemical elements between hydrogen and zinc. Those
results are compared with a large and recent body of observational data, and
we discuss in detail the implications for stellar nucleosynthesis.
Key words: nuclear reactions, nucleosynthesis, abundances - stars: abundances
- Galaxy: abundances - Galaxy: evolution - Galaxy: general
The chemical evolution of our Galaxy has been extensively studied in the
last years. During the last decade a great deal of new data have become available,
revealing in principle the chemical history of the Milky Way and building up
a set of observational constraints that have to be fulfilled by any successful
theoretical model. These observational results concern in particular the age-metallicity
relation (Meussinger et al. 1991; Edvardsson et al. 1993;
Rocha-Pinto et al. 2000), star metallicity distribution (Wyse & Gilmore
1995; Rocha-Pinto & Maciel 1996; Jørgensen 2000),
abundance ratios of an increasing number of chemical elements, both in halo
and local disk stars (Sneden et al. 1994; McWilliam
et al. 1995; Ryan et al. 1996; Chen et al. 2000, among others),
and radial abundance gradients (see Henry & Worthey 1999 for a review).
These observational efforts have been accompanied by the publication of several
theoretical models which try to interpret the data. Most of those works are standard
open chemical evolution models (Carigi 1994; Giovanoli & Tosi 1995;
Prantzos & Aubert 1995; Timmes et al. 1995 (hereafter TWW1995);
Chiappini et al. 1997, 1999; Thomas et al. 1998;
Chang et al. 1999; Goswami & Prantzos 2000 (hereafter GP2000),
etc.) in which the Galaxy is assembled by infall of extragalactic gas and that
use different prescriptions for the main ingredients, i.e. infall rate and composition
of the accreted material, initial mass function (IMF), star formation rate (SFR)
and stellar yields. Chemodynamical models have also been published (Steinmetz
& Müller 1994; Samland et al. 1997; Samland 1998;
Berczik 1999), but due to the numerical complexity they have to introduce
several approximations in the treatment of stellar lifetimes and yields.
As pointed out by GP2000, while the prescriptions for the IMF, the
SFR and the infall rate are just empirical recipes due to our poor understanding
of the physical processes involved, the stellar yields can be determined from
first principles, as they rely upon the much better known theory of stellar
evolution. However, there still remain severe uncertainties in the stellar yields,
especially for massive stars where the treatment of convection, the inclusion
or neglect of mass loss, the explosion mechanisms, etc. could give rise to large
discrepancies in the final yields of several elements.
Most of the available models use metallicity-independent yields and/or concentrate
on a limited number of chemical species. TWW1995 were the first to
consider the evolution of the complete ensemble of light and intermediate-mass
elements (from H to Zn) by including in a simple infall model for the galactic
disk the yields of massive stars with metallicities between Z=0 and
 of Woosley & Weaver (1995), and adopting for the CNO yields of low
and intermediate mass stars the Renzini & Voli (1981) results. Recently,
GP2000 have reanalyzed the evolution of the elements from C to Zn
by means of an infall model that treats separately the halo and the disk, but
they only take into account stellar yields from massive stars, assuming zero
net yields for intermediate mass stars.
of Woosley & Weaver (1995), and adopting for the CNO yields of low
and intermediate mass stars the Renzini & Voli (1981) results. Recently,
GP2000 have reanalyzed the evolution of the elements from C to Zn
by means of an infall model that treats separately the halo and the disk, but
they only take into account stellar yields from massive stars, assuming zero
net yields for intermediate mass stars.
In this paper we present new calculations of the evolution in the solar neighborhood
of all the chemical elements up to Zn, in the framework of a two-infall model
(Chiappini et al. 1997) for the formation of the Galaxy, with metallicity-dependent stellar yields for the whole range of stellar masses considered. Also, we include the contributions from nova nucleosynthesis, since significant
amounts of several isotopes (mainly 7Li, 13C, 15N,
and 17O) could be produced by nova outbursts. The plan of the
paper is as follows: in Sect. 2 we present and discuss the main ingredients of
our model: infall assumptions, SFR, IMF and nucleosynthetic prescriptions. Inspired
by the recent observations of Wakker et al. (1999), who have reported
the detection of a massive cloud with a metallicity 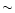 0.09 times solar
falling into the galactic disk, we adopt as our standard model one in which
first the halo and the thick disk of the Milky Way form by accretion of primordial
gas, and then, in a second infall episode lasting up to present, the thin disk
assembles from slightly enriched extragalactic material; however, we have also
considered a popular standard model with infall of primordial gas along the whole
galactic evolution. In Sect. 3 we compare our results with the main observational
constraints in the local disk (G-dwarf distribution, age-metallicity relation,
solar abundances, supernova rates, etc.). The core of the paper is presented
in Sect. 4, where we compare in detail the evolution of the different elements
studied with the available observational data, including the most recent observations.
Finally, in Sect. 5 we give the main conclusions of our work.
0.09 times solar
falling into the galactic disk, we adopt as our standard model one in which
first the halo and the thick disk of the Milky Way form by accretion of primordial
gas, and then, in a second infall episode lasting up to present, the thin disk
assembles from slightly enriched extragalactic material; however, we have also
considered a popular standard model with infall of primordial gas along the whole
galactic evolution. In Sect. 3 we compare our results with the main observational
constraints in the local disk (G-dwarf distribution, age-metallicity relation,
solar abundances, supernova rates, etc.). The core of the paper is presented
in Sect. 4, where we compare in detail the evolution of the different elements
studied with the available observational data, including the most recent observations.
Finally, in Sect. 5 we give the main conclusions of our work.
We have developed a standard open chemical evolution model where the Milky Way
builds up gradually by infall of primordial and, lately, slightly enriched gas.
No outflows are considered. The disk is divided into concentric independent
rings 1 kpc wide, and we neglect any radial flow between them. Inside each zone
we assume instantaneous mixing so that the stellar ejecta are completely mixed
with the interstellar medium as soon as the stars die; in this way, each ring
is made of an homogeneous mixture of gas, stars and stellar remnants, and
the local interstellar medium is characterized at any time by a unique composition;
therefore, the quantities describing the state of each zone, i.e. surface density
of total, gas and stellar masses, chemical abundances, etc., are functions only
of galactocentric radius and time. We relaxed the instantaneous recycling approximation
by treating in detail the delay in chemical enrichment due to the finite stellar
lifetimes, which we adopt from the work of the Geneva group (Schaller et al.
1992; Charbonnel et al. 1996).
The model solves numerically the classical set of nonlinear-integro differential
equations of galactic chemical evolution (Tinsley 1980; Pagel 1997).
In the solar ring we follow the evolution of 76 isotopes from hydrogen to zinc.
For simplicity we use, as in TWW1995, Gaussian quadrature
summation for the mass integrals (Press et al. 1992), and a Cash-Karp
stepper method (Press & Teukolsky 1992) for the explicit time integrations.
In the following subsections we discuss the main ingredients of the model.
Closed box models of galactic evolution face the so-called "G-dwarf problem'',
the formation of too many long lived stars at low metallicities. The most common
way out of this problem is to turn to open models which consider that the Galaxy
forms by continuous infall of extragalactic material. In fact, there are observational
indications of current infall onto the Galactic disk from external regions in
the form of High Velocity Clouds moving towards the Galactic disk, as first
suggested by Larson (1972). Although the interpretation of such clouds
as gas of extragalactic origin has been a matter of debate, the observation
of both High (Mirabel 1981) and Very High Velocity Clouds (Mirabel
& Morras 1984) seemed to confirm the idea of current infall with
rates of the order of 1
 yr-1. Recently, Wakker et al. (1999) have reported the detection of a massive (
yr-1. Recently, Wakker et al. (1999) have reported the detection of a massive (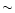 107
107
 )
cloud falling into the disk of the Milky Way, with a metallicity
0.09 times solar, and the authors give strong arguments for the extragalactic
origin of the cloud.
)
cloud falling into the disk of the Milky Way, with a metallicity
0.09 times solar, and the authors give strong arguments for the extragalactic
origin of the cloud.
Different types of infall have been explored in several models, but not all
of them can solve the G-dwarf problem. For instance, constant infall rates just
balancing star formation produce too many stars at high metallicity. Most of
the "successful'' models use simple exponentially decreasing infall rates
(TWW1995; Prantzos & Aubert 1995; Thomas et al. 1998)
for the assembling of the galactic disk, with timescales of the order of 3-4 Gyr at the solar ring, but recent determinations of the metallicity distribution
of disk stars by Wyse & Gilmore (1995) and Rocha-Pinto & Maciel
(1996) require, to be reproduced by the models, longer timescales,
with typical values of 7 Gyr at solar galactocentric distances (Chiappini et al. 1997; Prantzos & Silk 1998; Boissier & Prantzos 1999).
It is worth mentioning that some chemodynamical models also infer long timescales
for the formation of the disk (Samland et al. 1997).
Recently Chiappini et al. (1997), and lately Chang et al. (1999),
have included implicitly the halo phase evolution through models that assume
two subsequent infall episodes. In the first episode the halo and the thick
galactic disk form in a very short time (
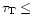 1 Gyr). At the
end of this phase, the thin disk begins to form in a second infall episode characterized
by much longer timescales. In this way, the material that eventually forms the
disk has an extragalactic origin.
1 Gyr). At the
end of this phase, the thin disk begins to form in a second infall episode characterized
by much longer timescales. In this way, the material that eventually forms the
disk has an extragalactic origin.
In the present work, following Chiappini et al. (1997), we adopt the
two-infall exponentially decreasing model. Therefore, the time evolution of
the total surface mass density in the solar ring is given by
where
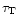 and
and
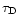 are, respectively, the timescales
for the halo-thick disk and thin disk phases, and
are, respectively, the timescales
for the halo-thick disk and thin disk phases, and 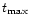 is the time
of maximum mass accretion onto the thin disk, which corresponds to the end of
the halo-thick disk phase. We set
is the time
of maximum mass accretion onto the thin disk, which corresponds to the end of
the halo-thick disk phase. We set
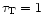 Gyr, and the same value
for
Gyr, and the same value
for 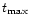 ,
and we take a value of 7 Gyr for
,
and we take a value of 7 Gyr for
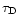 ,
the timescale
for the thin disk formation at the position of the Sun (we adopt a solar galactocentric
distance
,
the timescale
for the thin disk formation at the position of the Sun (we adopt a solar galactocentric
distance
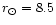 kpc).
kpc).
The coefficients
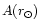 and
and
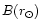 are fixed by imposing
that the current total surface mass densities of the thick and thin disks in
the solar neighborhood are well reproduced by the model
are fixed by imposing
that the current total surface mass densities of the thick and thin disks in
the solar neighborhood are well reproduced by the model
where
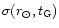 and
and
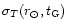 are, respectively, the local surface mass densities of total and thick disk
at the present time,
are, respectively, the local surface mass densities of total and thick disk
at the present time,
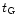 ,
that we take as 13 Gyr. For
,
that we take as 13 Gyr. For
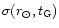 we adopt a value of 54
we adopt a value of 54
 pc-2 (Rana 1991;
Sackett 1997). The local surface mass density of the thick disk is,
in fact, a parameter in this kind of models. Observational estimates can be
obtained from studies of the density ratio of the thick and thin disks, together
with values of their respective scale heights (Kuijken & Gilmore 1989;
Reid & Majewski 1993; Robin et al. 1996; Buser et al. 1998).
Unfortunately, the results obtained in those studies span a rather wide range,
from 4.85 to 14.1
pc-2 (Rana 1991;
Sackett 1997). The local surface mass density of the thick disk is,
in fact, a parameter in this kind of models. Observational estimates can be
obtained from studies of the density ratio of the thick and thin disks, together
with values of their respective scale heights (Kuijken & Gilmore 1989;
Reid & Majewski 1993; Robin et al. 1996; Buser et al. 1998).
Unfortunately, the results obtained in those studies span a rather wide range,
from 4.85 to 14.1
 pc-2. In our calculations we adopt
a value of 10
pc-2. In our calculations we adopt
a value of 10
 pc-2.
pc-2.
Based on the observations of Wakker et al. (1999), we begin accreting
primordial material during the halo-thick disk phase, and then, when the thin disk
initiates its formation, we assume that the infalling material has already being
slightly enriched, with a typical metallicity of
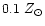 in solar
proportions. By comparison, we have also calculated models that only accrete
primordial matter during the whole evolution. Even if there are not substantial
differences between the results we obtain in both types of models, in agreement
with Tosi (1988) who showed that as long as the metallicity of the
accreted material remains below 0.1
in solar
proportions. By comparison, we have also calculated models that only accrete
primordial matter during the whole evolution. Even if there are not substantial
differences between the results we obtain in both types of models, in agreement
with Tosi (1988) who showed that as long as the metallicity of the
accreted material remains below 0.1
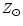 there are little changes
in the model results, we obtain slightly better agreement with the observational
constraints in the solar region for the model that incorporates enriched infall
during the assembling of the thin disk.
there are little changes
in the model results, we obtain slightly better agreement with the observational
constraints in the solar region for the model that incorporates enriched infall
during the assembling of the thin disk.
In view of the difficulties in understanding the rather complicated process of
star formation, standard models for the chemical evolution of the Galaxy adopt
different analytical prescriptions for the star formation rate (SFR) in terms
of intrinsic parameters of spiral galaxies. The simplest and still commonly
used law for star formation is the Schmidt (1959) law:
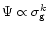 ,
proportional to some power (between 1 and 2) of the surface gas density. Observations
by Kennicutt (1998) of the correlation between average SFR and surface
gas densities (total: atomic plus molecular) in spiral and starburst galaxies
point to a value of the exponent in the Schmidt law of
,
proportional to some power (between 1 and 2) of the surface gas density. Observations
by Kennicutt (1998) of the correlation between average SFR and surface
gas densities (total: atomic plus molecular) in spiral and starburst galaxies
point to a value of the exponent in the Schmidt law of
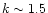 .
Besides this global behaviour, the SFR has also to show dependence on the local
environment, which in turn is typically a function of galactocentric distance.
.
Besides this global behaviour, the SFR has also to show dependence on the local
environment, which in turn is typically a function of galactocentric distance.
The precise radial dependence of the SFR varies according to the scenario considered
for star formation. In theories that describe star formation as a local self-regulating process through the balance between the gravitational settling of the gas onto the disk, that enhances star formation, and the energy injected back into the interstellar medium by massive young stars under the form of winds and supernova explosions, which heat and expand the gas reducing the process of star formation (Talbot & Arnett 1975), the SFR is a function of the local gravitational potential and, therefore, of the total surface mass density, 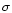 .
In the original Talbot & Arnett (1975) formulation,
.
In the original Talbot & Arnett (1975) formulation,
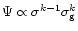 .
We notice that some chemodynamical models (Burkert et al. 1992) find
a similar dependence of the SFR on the total surface mass density.
.
We notice that some chemodynamical models (Burkert et al. 1992) find
a similar dependence of the SFR on the total surface mass density.
Observational support for such star formation law has been obtained by Dopita
& Ryder (1994), who showed the existence in spiral disks of an empirical
link between H
 emission, tracing current star formation,
and the I-band surface brightness, a measure of the contribution of the old
stellar component and, therefore, of the total surface mass density. This observed
relation is well fitted by a SFR law very similar to that of Talbot & Arnett
(1975):
emission, tracing current star formation,
and the I-band surface brightness, a measure of the contribution of the old
stellar component and, therefore, of the total surface mass density. This observed
relation is well fitted by a SFR law very similar to that of Talbot & Arnett
(1975):
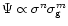 ,
with n=1/3and m=5/3. Moreover, self-regulated star formation can accommodate the
observed correlation between surface brightness and oxygen abundance in late
spiral disks (Edmunds & Pagel 1984; Ryder 1995).
,
with n=1/3and m=5/3. Moreover, self-regulated star formation can accommodate the
observed correlation between surface brightness and oxygen abundance in late
spiral disks (Edmunds & Pagel 1984; Ryder 1995).
We incorporate in our numerical code the star formation law as
where the denominator is introduced as a normalization factor in order to express
the efficiency coefficient 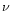 in Gyr-1. Here we adopt
in Gyr-1. Here we adopt 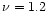 Gyr-1 in order to reproduce the observed current star formation rate and gas surface density in the solar neighborhood.
Gyr-1 in order to reproduce the observed current star formation rate and gas surface density in the solar neighborhood.
The initial mass function (IMF) constitutes another basic input in models of
chemical evolution, since it determines in which proportions stars of different
masses enter into play; that, in turn, fixes the averaged stellar yields and
remnant masses for each generation of stars.
In general, the assumed form of the IMF is a declining function of mass in terms
of a power law:
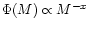 ,
constant in space and time. Salpeter's
(1955) version, with x=1.35 for the whole mass range has been
commonly used. However, recent studies reviewed by Scalo (1998), Kroupa
(1998) and Meyer et al. (2000) indicate, within still rather
large uncertainties, that observations are consistent with an IMF almost flat
at low masses, how flat still being a matter of debate (for instance, Reid &
Gizis 1997 find a unique slope of x=0.05 for
,
constant in space and time. Salpeter's
(1955) version, with x=1.35 for the whole mass range has been
commonly used. However, recent studies reviewed by Scalo (1998), Kroupa
(1998) and Meyer et al. (2000) indicate, within still rather
large uncertainties, that observations are consistent with an IMF almost flat
at low masses, how flat still being a matter of debate (for instance, Reid &
Gizis 1997 find a unique slope of x=0.05 for
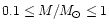 ,
but Kroupa 1998 claims that such slope is only appropriate for
,
but Kroupa 1998 claims that such slope is only appropriate for
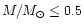 ),
and declining as a power law with a slope similar to the Salpeter's one above
1
),
and declining as a power law with a slope similar to the Salpeter's one above
1
 ,
although there are again discrepancies on the actual value
of x. For instance, Massey et al. (1995) find slopes
,
although there are again discrepancies on the actual value
of x. For instance, Massey et al. (1995) find slopes 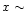 1-1.5
in OB associations, while for massive field stars Massey (1998) obtains
very steep IMFs, with values of
1-1.5
in OB associations, while for massive field stars Massey (1998) obtains
very steep IMFs, with values of 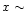 3-4.
3-4.
Another aspect of the IMF that has not yet been satisfactorily settled, neither observationally nor theoretically, is its time behavior. There seems to be a
tendency among observational researchers to favor no variations of the IMF,
although in a recent review Scalo (1998) argues against its universality
in space and time. Besides, an IMF producing more massive stars in the early
Galaxy has been invoked as a solution to the G-dwarf problem. Nevertheless,
in a recent paper, Chiappini et al. (2000) have investigated the effects
on galactic chemical evolution of several time dependent IMFs and conclude that
the combination of infall and a constant IMF is still the best choice to reproduce
the observational constraints in the Milky Way.
In this paper we adopt the constant IMF version of Kroupa et al. (1993),
which consists in a three slope power law. In the range of very low masses the
slope is quite flat, x = 0.3 for
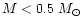 ,
it steepens
to x = 1.2 in the interval
,
it steepens
to x = 1.2 in the interval
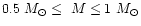 ,
and in
the high mass regime
,
and in
the high mass regime
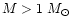 the slope agrees with
the one by Scalo (1986) x = 1.7. As usual, we normalize to unity
this IMF between a minimum stellar mass of 0.08
the slope agrees with
the one by Scalo (1986) x = 1.7. As usual, we normalize to unity
this IMF between a minimum stellar mass of 0.08
 ,
the H-burning
limit, and a maximum of 100
,
the H-burning
limit, and a maximum of 100
 .
.
The chemical yields synthesized by stars in different stellar mass ranges are
a key ingredient when trying to understand the chemical evolution of galaxies,
in particular those corresponding to "massive stars'', stars that end their
lives in Type II supernova explosions, since they are the main responsibles
for the enrichment of the Universe in intermediate and heavy nuclei, through
both hydrostatic burning (elements up to calcium) and explosive nucleosynthesis
(iron peak elements, to which Type Ia supernovae are also important contributors).
Even if the uncertainties in the theory of stellar evolution are far lesser
than those affecting the SFR or the IMF, there still remain serious discrepancies
in the literature about the treatment of crucial aspects of stellar evolution.
For instance, presupernova configurations are affected by the precise formulation
of convection, semi-convection and overshooting, the adopted nuclear reaction
rates (especially for the 12C(
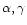 )
16O
reaction), the inclusion or not of mass loss and rotation, etc. A similar situation
holds for the results of core collapse supernova explosions. In fact, in current
calculations the explosion itself is induced rather arbitrarily and the explosion
energy is fixed by imposing a given value for the final kinetic energy. Also,
the ejected mass crucially depends on the degree of "fall-back'', and thus
on the precise details of the explosion. We thus see that the published stellar
yields are yet plagued with severe uncertainties.
)
16O
reaction), the inclusion or not of mass loss and rotation, etc. A similar situation
holds for the results of core collapse supernova explosions. In fact, in current
calculations the explosion itself is induced rather arbitrarily and the explosion
energy is fixed by imposing a given value for the final kinetic energy. Also,
the ejected mass crucially depends on the degree of "fall-back'', and thus
on the precise details of the explosion. We thus see that the published stellar
yields are yet plagued with severe uncertainties.
Although the evolution during the thin disk epoch will be hardly affected by
the slight metallicity dependence shown in the published stellar yields, the
early halo-thick disk phase could be strongly influenced by the material ejected
by stars of different metallicities. Hence, we will consider metallicity dependent
yields for the whole stellar mass range.
We assume that stars in this mass interval end their lifes as core collapse
supernovae. The two major sources in this mass range, widely used in chemical
evolution models, are Woosley & Weaver (1995) (hereafter
WW1995), who calculated full stellar models without mass loss nor
rotation, for stars with masses comprised between 12
 and 40
and 40
 and with different initial metallicities (
and with different initial metallicities (
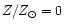 ,
10-4, 10-2, 10-1 and 1), and Thielemann
et al. (1996), who calculated the evolution of He cores corresponding
to stars of solar initial metallicity with masses up to 70
,
10-4, 10-2, 10-1 and 1), and Thielemann
et al. (1996), who calculated the evolution of He cores corresponding
to stars of solar initial metallicity with masses up to 70
 .
There are noticeable
differences between the WW1995 results for Z=0 and
.
There are noticeable
differences between the WW1995 results for Z=0 and 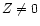 ,
while the yields and stellar remnant masses for nonzero initial metallicities
give more similar results. Solar composition models of WW1995 and
Thielemann et al. (1996) give almost the same values for the yields
of the CNO isotopes, but non-negligible differences exist for other important
elements. For instance, the magnesium yield is systematically lower in WW1995
as a consequence of the different treatments of convection. In the case of the
iron yield, WW1995 give much higher values than Thielemann et al.
(1996) for stars with masses below
,
while the yields and stellar remnant masses for nonzero initial metallicities
give more similar results. Solar composition models of WW1995 and
Thielemann et al. (1996) give almost the same values for the yields
of the CNO isotopes, but non-negligible differences exist for other important
elements. For instance, the magnesium yield is systematically lower in WW1995
as a consequence of the different treatments of convection. In the case of the
iron yield, WW1995 give much higher values than Thielemann et al.
(1996) for stars with masses below 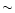 35
35
 ,
since it is very sensitive to the mass cut that separates the ejecta and the
material that falls back onto the compact remnant which, as mentioned above,
depends in turn on the detailed explosion mechanism (see Thomas et al. 1998,
and Chiappini et al. 1999 for a complete discussion).
,
since it is very sensitive to the mass cut that separates the ejecta and the
material that falls back onto the compact remnant which, as mentioned above,
depends in turn on the detailed explosion mechanism (see Thomas et al. 1998,
and Chiappini et al. 1999 for a complete discussion).
Lately, Limongi et al. (2000), from full stellar models, again without
mass loss nor rotation, have also presented yields for massive stars in the range
13-25
 ,
for three metallicities (Z=0, 10-3, and 0.02).
As shown by GP2000, the main difference with respect to WW1995
is a more marked odd-even effect in the case of Limongi et al. (2000)
yields, which translates into systematically lower yields of odd Z elements.
,
for three metallicities (Z=0, 10-3, and 0.02).
As shown by GP2000, the main difference with respect to WW1995
is a more marked odd-even effect in the case of Limongi et al. (2000)
yields, which translates into systematically lower yields of odd Z elements.
In this paper we adopt the metallicity-dependent yields of WW1995
for massive stars between 8 and 100
 .
The reasons for this choice
are twofold: they are the results of full evolutionary calculations and they
consider a wider interval of masses and metallicities as compared with the work
of Limongi et al. (2000). In particular, we take their models A up
to 25
.
The reasons for this choice
are twofold: they are the results of full evolutionary calculations and they
consider a wider interval of masses and metallicities as compared with the work
of Limongi et al. (2000). In particular, we take their models A up
to 25
 ,
and their models B for 30, 35 and 40
,
and their models B for 30, 35 and 40
 (the explosion energy in models B is higher than in models A). Those yields
have been extrapolated up to 100
(the explosion energy in models B is higher than in models A). Those yields
have been extrapolated up to 100
 ,
even though this has just a minor
effect on the final results since the Kroupa et al. (1993) IMF produces
very few stars more massive than 40
,
even though this has just a minor
effect on the final results since the Kroupa et al. (1993) IMF produces
very few stars more massive than 40
 .
.
TWW1995 suggested that a better agreement with most of the observed
evolution of the abundances is obtained if the WW1995 iron yields
are reduced by a factor of two. Observational estimates of the iron synthesized
in SN 1987A (the explosion of a 20
 belonging to a stellar system,
LMC, with an estimated
belonging to a stellar system,
LMC, with an estimated
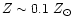 )
and of SN 1993J (whose
progenitor was a 14
)
and of SN 1993J (whose
progenitor was a 14
 star in the galaxy M81, where
star in the galaxy M81, where
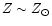 )
also points to such an overestimate (Thomas et al 1998). Therefore,
in view of the uncertainties arising from the flaws in the explosion calculations,
we reduce by a factor of 2 the nominal yields of WW1995.
)
also points to such an overestimate (Thomas et al 1998). Therefore,
in view of the uncertainties arising from the flaws in the explosion calculations,
we reduce by a factor of 2 the nominal yields of WW1995.
As is well known, single stars in this mass range pollute the interstellar
medium through moderate stellar winds and planetary nebula ejection, ending
their lives as white dwarfs. These stars make important contributions to the
He, C and N galactic contents. Here again important uncertainties on the final
yields exist that result from the treatment of mass loss, convection, evolution
on the asymptotic giant branch, etc.
The yields of Renzini & Voli (1981) have been extensively used in
chemical evolution models. However, in the last years several groups have published
new evolutionary calculations for stars belonging to this mass interval and
for different initial metallicities (Marigo et al. 1996; van den Hoek
& Groenewegen 1997). In this work the contribution to the galactic
enrichment by these stars has been taken from van den Hoek & Groenewegen (1997),
who give yields for stars with masses comprised between 0.9 and 8
 and consider five initial metallicities, since the work of Marigo et al. (1996)
is limited to stars with
and consider five initial metallicities, since the work of Marigo et al. (1996)
is limited to stars with
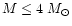 ,
besides taking
into account convective overshooting, which is not considered in WW1995.
,
besides taking
into account convective overshooting, which is not considered in WW1995.
There is a general agreement that Type Ia supernovae are important contributors
to iron and other iron peak elements (in particular 58Ni and 54Cr)
in the late disk evolution, up to the point that they could be responsible for up to 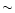 2/3
of the total iron contents (TWW1995). We adopt the conventional view
that Type Ia supernovae are carbon deflagration of massive C-O white dwarfs
in binary systems. The contribution of Type Ia supernovae to the chemical enrichment
of the galaxy, especially the iron content, has been calculated following the
prescriptions of Matteucci & Greggio (1986), where Type Ia supernovae
come from binary systems with a minimum mass of 3
2/3
of the total iron contents (TWW1995). We adopt the conventional view
that Type Ia supernovae are carbon deflagration of massive C-O white dwarfs
in binary systems. The contribution of Type Ia supernovae to the chemical enrichment
of the galaxy, especially the iron content, has been calculated following the
prescriptions of Matteucci & Greggio (1986), where Type Ia supernovae
come from binary systems with a minimum mass of 3
 ,
in order
to ensure that the accreting white dwarf eventually reaches the Chandrasekhar
mass, and a maximum mass of 16
,
in order
to ensure that the accreting white dwarf eventually reaches the Chandrasekhar
mass, and a maximum mass of 16
 ,
if we assume that C-O white
dwarfs come from primaries up to 8
,
if we assume that C-O white
dwarfs come from primaries up to 8
 .
Thus, the amount of isotope
i due to this source is given by
.
Thus, the amount of isotope
i due to this source is given by
where 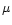 is the mass fraction of the secondary star (
is the mass fraction of the secondary star (
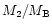 )
and
)
and
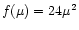 is its distribution function (Greggio & Renzini 1983). The parameter C, which determines the fraction of suitable binary systems
that actually produce Type Ia SN, is set equal to 0.04 in order to fulfill the
restrictions imposed by observational data on supernovae frequency. The chemical
composition of the ejecta is taken from Thielemann et al. (1993)
for the well known model W7 (Nomoto et al. 1984), and we also include
the contribution to the enrichment of the interstellar gas by the secondary
star.
is its distribution function (Greggio & Renzini 1983). The parameter C, which determines the fraction of suitable binary systems
that actually produce Type Ia SN, is set equal to 0.04 in order to fulfill the
restrictions imposed by observational data on supernovae frequency. The chemical
composition of the ejecta is taken from Thielemann et al. (1993)
for the well known model W7 (Nomoto et al. 1984), and we also include
the contribution to the enrichment of the interstellar gas by the secondary
star.
Although classical novae have little or no influence on the evolution of the
abundances of most of the chemical elements included in our calculations, according
to José & Hernanz (1998) they can be significant contributors to
certain isotopes that are strongly overproduced in nova explosions relative
to the solar system abundances (in particular those with overproduction factors
larger than 1000). 7Li, 13C, 15N and
17O are some of the isotopes whose abundances could be affected
by novae.
In order to obtain the nova rates we assume that novae take place in binary
systems made of a white dwarf coming from stars with main sequence masses in
the interval
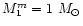 to
to
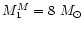 ,
while the secondary stars have masses between
,
while the secondary stars have masses between
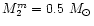 and
and
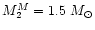 .
The rate of those explosions can
be estimated by a procedure similar to that used by Matteucci & Greggio (1986)
to calculate the rate of SN Ia:
.
The rate of those explosions can
be estimated by a procedure similar to that used by Matteucci & Greggio (1986)
to calculate the rate of SN Ia:
where 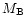 is the total mass of the system and
is the total mass of the system and
In this expression, the value of the free parameter D, which plays a
role similar to the parameter C in the rate of Type Ia supernovae, is
obtained by imposing that the formula reproduces the observed outburst rate
at the present epoch of the Galaxy, of the order of 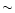 40 yr-1 (Hatano
et al. 1997), and
40 yr-1 (Hatano
et al. 1997), and
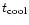 ,
the cooling time for a white dwarf
before it can produce the first nova outburst, is taken as 1 Gyr .
,
the cooling time for a white dwarf
before it can produce the first nova outburst, is taken as 1 Gyr .
The yields for the classical nova outburst are an average of those given by
José & Hernanz (1998). We have considered that 30% of the nova outbursts
come from ONe white dwarf progenitors, while 70% come from CO ones.
As we have discussed in the previous section, there are large uncertainties
in the ingredients of standard chemical evolution models which translate into
a series of more or less free parameters, e.g. infall timescales, efficiency
and exponent of the SFR, slope of the IMF, etc. Fortunately, for the solar neighborhood,
the number of observational constraints is large enough to restrict the space
of variation of these parameters (Boissier & Prantzos 1999). Results
for the whole galactic disk will be the subject of another paper.
First of all, any successful model has to reproduce the present-day surface
density of total mass, gas, star and stellar remnants, the current rate of star
formation, infall and supernovae (both Type Ia and Type II). In Table 1
we show our results for the present values (
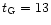 Gyr) of those quantities
compared with the current observational values for the solar vicinity. The time
evolution of the surface densities of total mass (
Gyr) of those quantities
compared with the current observational values for the solar vicinity. The time
evolution of the surface densities of total mass (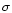 ), stars (
), stars (
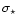 ),
gas (
),
gas (
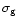 ), and stellar remnants (
), and stellar remnants (
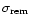 )
are displayed
in the upper panel of Fig. 1, while in the lower panel appear the
star formation rate, and the Type II and Type Ia supernova rates. We see from
Table 1 and Fig. 1 that the model presented in the
previous section nicely fits the observations.
)
are displayed
in the upper panel of Fig. 1, while in the lower panel appear the
star formation rate, and the Type II and Type Ia supernova rates. We see from
Table 1 and Fig. 1 that the model presented in the
previous section nicely fits the observations.
References.-(1) Dickey (1993); Flynn et al. (1999);
(2) Gilmore et al. (1989); (3) Méra et al. (1998); (4) Portinari
et al. (1998) and references therein; (5) Güsten & Mezger (1982);
(6) Tamman et al. (1994); (7) Hatano et al. (1997).
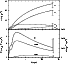 |
Figure 1:
Upper panel: time evolution of the surface densities
of total mass (
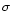 ), visible stars ( ), visible stars (
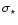 ),
gas ( ),
gas (
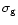 ), and stellar remnants ( ), and stellar remnants (
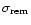 )
for our two-infall model. Lower panel: evolution of the stellar formation
rate, as well as the Type II and Type Ia supernova rates )
for our two-infall model. Lower panel: evolution of the stellar formation
rate, as well as the Type II and Type Ia supernova rates |
| Open with DEXTER |
Our model also fulfills the requisite of producing an age-metallicity relation
in agreement with the observed one. The age-metallicity relation (AMR) shows
the evolution of the ratio [Fe/H], taken as a measure of the metallicity
of the Galaxy, as a function of time. The pioneering work by Twarog (1980)
showed that [Fe/H] rises steeply during the first 2 Gyr up to a value of
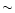 -0.5 dex, and afterwards increases smoothly with time towards
the solar value, although the data presented a large dispersion, and age-bins and
average metallicity per bin were used. Later reexamination of Twarog's data
by Meussinger et al. (1991) found a similar AMR. More recently, Edvardsson
et al. (1993), based on a different sample of nearby F and G stars,
obtained for binned data a good agreement with previous results, but they claimed
that the large dispersion found in their unbinned data was essentially real
and not observational (but see Garnett & Kobulnicky 2000). Finally,
Rocha-Pinto et al. (2000) obtained a chromospheric AMR using a sample
of 552 late-type dwarfs that basically confirms the observed trends, but with
almost half the scatter found by Edvardsson et al. (1993).
-0.5 dex, and afterwards increases smoothly with time towards
the solar value, although the data presented a large dispersion, and age-bins and
average metallicity per bin were used. Later reexamination of Twarog's data
by Meussinger et al. (1991) found a similar AMR. More recently, Edvardsson
et al. (1993), based on a different sample of nearby F and G stars,
obtained for binned data a good agreement with previous results, but they claimed
that the large dispersion found in their unbinned data was essentially real
and not observational (but see Garnett & Kobulnicky 2000). Finally,
Rocha-Pinto et al. (2000) obtained a chromospheric AMR using a sample
of 552 late-type dwarfs that basically confirms the observed trends, but with
almost half the scatter found by Edvardsson et al. (1993).
Models of chemical evolution that adopt the instantaneous mixing approximation,
like ours, cannot produce any dispersion at all, and at most they can only fit
the mean relation. Therefore, the AMR is a less tight constraint than the previous one, even though
the average relation must be fitted by successful models.
We present in the lower panel of Fig. 2 our results for the evolution
with time of [Fe/H] compared with the AMR from Meussinger et al. (1991), Edvardsson et al. (1993), and with the more recent data from Rocha-Pinto
et al. (2000). Just for completeness, in the upper panel we also show
the evolution of the total metallicity in terms of the solar value. Again our
model fits well the averaged trend of the data, although, as stated above, this
is not a really tight constraint, because almost any model can produce a reasonable
AMR.
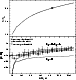 |
Figure 2:
Upper panel: evolution with time of the total metallicity
Z normalized to the solar value
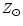 .
Lower
panel: time evolution of the ratio [Fe/H] for contributions from Type II
supernovae (thin line) and for Type II plus Type Ia supernovae (thick
line) .
Lower
panel: time evolution of the ratio [Fe/H] for contributions from Type II
supernovae (thin line) and for Type II plus Type Ia supernovae (thick
line) |
| Open with DEXTER |
Nearly 2/3 of the present total iron contents are made by Type Ia supernovae,
the other third coming from Type II supernovae. We remind here that the iron
yields for Type II supernovae used in this work are half those of WW1995
in order to obtain a better fit to the evolution of the element abundances.
That is also indicated by iron abundance measurements in supernova ejecta. In
any case, as pointed out by TWW1995, whatever contribution to the
present galactic iron contents from Type II supernovae comprised between one and
two thirds is allowed by our current understanding of stellar physics.
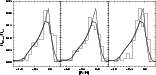 |
Figure 3:
Rough (thin dashed curve) G-dwarf metallicity distributions
and Gaussian convolved distribution (thick solid curve) compared with
observational data by Wyse & Gilmore (1995) (left panel),
Rocha-Pinto & Maciel (1996) (central panel) and by Jørgensen
(2000) (right panel) |
| Open with DEXTER |
The stars of spectral type G have main-sequence lifetimes comparable or even
larger than the estimated age of the Galaxy. Hence, the distribution in metallicity
of a complete sample of these stars in the solar neighborhood carries memory
of the star formation history. This makes the observed G-dwarf distribution
one of the more stringent constraints for models of galactic chemical evolution.
As is well known, the paucity of G-dwarf stars at low metallicities, referred
to as the "G-dwarf problem'', cannot be explained by simple, closed box models.
Several solutions have been proposed to solve this problem, but open models
with progressive infall of primordial or slightly enriched material with long
timescales for the disk formation, like ours, are still the best option (Chiappini
et al. 1997), besides of being compatible with dynamical simulations
of the formation of galactic disks (Burkert et al. 1992), and with
the observation of infall of High and Very High Velocity Clouds.
Figure 3 compares the predicted G-dwarf distribution produced by our
model with the most recent observational data from Wyse & Gilmore (1995)
(left panel), Rocha-Pinto & Maciel (1996) (central
panel) and Jørgensen (2000) (right panel). The direct
results are displayed by thin dashed lines, while the thick solid ones show
the convolution with a Gaussian with a dispersion of 0.15 in order to simulate
observational and intrinsic scatter. Very good agreement is reached, especially
for the rising part of the distribution and the location and height of the peak
when comparing with the two first sets of data. In the case of the distribution
from Jørgensen (2000), the fit is still reasonable, the peak is
again well reproduced, but the model shows a low metallicity tail (around [Fe/H]  -0.5) that is higher than the data. The comparison between theoretical
results and observations could be improved by relaxing the instantaneous mixing
approximation, introducing thus in the models the intrinsic scatter. Our results
confirm once more that infall models with long timescales for the assembling
of the disk are capable of solving the G-dwarf problem.
-0.5) that is higher than the data. The comparison between theoretical
results and observations could be improved by relaxing the instantaneous mixing
approximation, introducing thus in the models the intrinsic scatter. Our results
confirm once more that infall models with long timescales for the assembling
of the disk are capable of solving the G-dwarf problem.
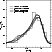 |
Figure 4:
G-dwarf distributions obtained for different types of infall.
The observational data correspond to Rocha-Pinto & Maciel (1996) |
| Open with DEXTER |
As indicated above, our model uses a double exponential infall in order to treat
as separate entities the halo-thick disk and the thin disk, and we consider
accretion of enriched material (
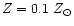 )
during the thin disk
phase. We have also calculated models that incorporate primordial material both
in the halo-thick disk and in the thin disk phases, as well as models that only
consider simple exponential infall of primordial and primordial plus enriched
material which, if not appropriate for the halo and thick disk, are relevant
when making comparisons for the thin disk properties. In all those models we
have adopted the same timescale for the galactic disk, i.e., 7 Gyr. We obtain
in all cases very similar results for the final characteristics of the solar
ring, but slight differences appear for the convolved G-dwarf distributions,
which are displayed in Fig. 4, where for clarity only the observations
by Rocha-Pinto & Maciel (1996) are shown. One and two infall models
with the same composition of the incorporated matter are almost indistinguishable,
but primordial composition models show a moderate excess of stars in the low
metallicity tail and lower maxima than those obtained in enriched models.
)
during the thin disk
phase. We have also calculated models that incorporate primordial material both
in the halo-thick disk and in the thin disk phases, as well as models that only
consider simple exponential infall of primordial and primordial plus enriched
material which, if not appropriate for the halo and thick disk, are relevant
when making comparisons for the thin disk properties. In all those models we
have adopted the same timescale for the galactic disk, i.e., 7 Gyr. We obtain
in all cases very similar results for the final characteristics of the solar
ring, but slight differences appear for the convolved G-dwarf distributions,
which are displayed in Fig. 4, where for clarity only the observations
by Rocha-Pinto & Maciel (1996) are shown. One and two infall models
with the same composition of the incorporated matter are almost indistinguishable,
but primordial composition models show a moderate excess of stars in the low
metallicity tail and lower maxima than those obtained in enriched models.
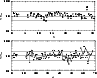 |
Figure 5:
Mass fractions of the calculated elements (upper panel),
from hydrogen to zinc (lithium, beryllium and boron are not shown), and of all
their stables isotopes (lower panel) in the interstellar gas at the
time of solar birth, relative to the solar abundances of Anders & Grevesse
(1989). The isotopes of the same element are connected by solid lines.
The dashed horizontal line would correspond to a perfect agreement, while the
two solid lines correspond to a discrepancy by a factor of 2. We take as successful
those elements and isotopes whose calculated abundances fall within this factor
of 2 of their solar values. The three open circles in the lower panel represent
the relative abundances of 13C, 15N and 17O
when nova yields are excluded from the calculations |
| Open with DEXTER |
We present in Fig. 5 the calculated mass fractions of the elements
(upper panel) and all their stable isotopes (lower panel) studied in this work
(except LiBeB isotopes, whose abundances have important contributions from galactic
cosmic ray nucleosynthesis, not included in the present calculations) in the
interstellar gas at the time of the solar birth, 4.5 Gyr ago, compared with
the observed solar values (Anders & Grevesse 1989), considered as
representative of the composition of the interstellar gas at that epoch. We
must remind here that this last assumption is far from being definitely settled,
since measured abundances in regions of recent star formation, like the Orion
nebula, show metallicities lower than solar (see, for instance, Cardelli &
Federmann 1997).
Due to the uncertainties existing in the observational values, we consider as
good agreement abundances within a factor of 2 of their solar value. As it can
be seen in Fig. 5, all the elemental abundances fulfill this criterion,
nickel excepted, which is clearly oversolar, and the model makes the correct
solar metallicity. The isotopic abundances are also nicely adjusted. The spread
for isotopes below calcium is lower than above it, reflecting the uncertainties
in the present modeling of Type II supernova explosions.
The production factors for hydrogen, helium and the most important CNO isotopes
are nearly equal to unity. In particular, the solar 3He abundance
is almost exactly reproduced by our models without taking into account any partial
destruction by extra-mixing on the RGB (see, however, Romano et al. 2000).
The inclusion of novae worsens our results for 13C and 17O,
which are then a little bit overabundant. On its turn, 15N is
a factor of 3 below its solar value when only nucleosynthesis in massive stars
is considered, and contribution from novae is mandatory to render its abundance
compatible with the solar value.
A few isotopes fall out of the acceptable range. 48Ca, 47Ti,
50Ti and 64Zn are underproduced (especially 48Ca).
In the case of the neutron-rich isotopes 48Ca and 50Ti
there could be a substantial contribution from Type Ia supernovae resulting
from initially slow deflagrations at high density (Woosley & Eastman 1994).
47Ti (and, in lesser extent, 44Ca and 51V)
have been traditionally problematic; these isotopes could have noticeable contributions
from sub-Chandrasekhar explosions of SNeIa (Shigeyama et al. 1992; Woosley
& Weaver 1994). Additional contributions to the abundance of 64Zn
could be obtained, as pointed out by TWW1995, from weak s-process
in massive stars or classical s-process in low-mass AGB stars.
On the other hand, there is a small overproduction of nickel, due to the large
yields of 58Ni in the adopted model for SNeIa and
the high production of 62Ni in current models of
massive star explosions, which reflects the inaccuracies involved in current
supernova modeling.
As noted in previous works (TWW1995; GP2000), the fact that
the solar abundances of all isotopes up to the iron peak, that cover a range
of almost 9 orders of magnitude, are so precisely reproduced by current models
of chemical evolution indicates that the present understanding of stellar nucleosynthesis
is basically correct, at least to first order.
We have calculated the evolution in time of all the stable isotopes of thirty
chemical elements from H to Zn with the nucleosynthetic prescriptions detailed
above. Our results are displayed in Figs. 6 to 15,
where we compare the predicted ratios [X/Fe] as functions of [Fe/H]
with observational data of spectroscopic abundances in nearby stars. Data sources
are detailed in the legends of the figures. As the data normally refer to elemental
abundances, for each element we sum over the calculated isotopic abundances.
We note that following the suggestion of TWW1995 we have reduced the iron yields
of WW1995 by a factor of 2. The reduced iron yields, well within the
current inaccuracies in supernova models, not only give a better agreement with
the observed elemental abundances but they are also consistent with the amount of
iron ejected in recently observed Type II supernovae .
We consider that the calculated abundance evolution is only significant for
[Fe/H] 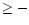 3, a value that our model reaches at
3, a value that our model reaches at 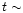 30
Myr, which approximately corresponds to the lifetime of a 8-9
30
Myr, which approximately corresponds to the lifetime of a 8-9
 star. This means that only after reaching such global metallicity the yields
of massive stars are fully averaged over the IMF, therefore reducing the possible
uncertainties in the yields of individual stars.
star. This means that only after reaching such global metallicity the yields
of massive stars are fully averaged over the IMF, therefore reducing the possible
uncertainties in the yields of individual stars.
We present in Fig. 6 the results obtained in our calculations for
the evolution of CNO elemental abundances with respect to iron.
Carbon and iron are primary elements but have different production sites:
carbon is made by the triple-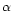 process in hydrostatic helium burning
in massive and, mostly, in intermediate and low-mass stars, while Fe is produced
by explosive burning in Type II and Type Ia supernovae. Observations of carbon abundances in halo and disk dwarfs (field giants are
not reliable indicators of ab initio carbon abundance due to the effects of
the first dredge-up) do actually show that [C/Fe] is almost constant in
time, with a value approximately solar (Laird 1985; Tomkin et al.
1986; Carbon et al. 1987; McWilliam et al. 1995),
although there is an important dispersion in the data at all metallicities.
Those surveys also seem to indicate some trend towards slightly higher values
of [C/Fe] at low [Fe/H], as confirmed to first order by Wheeler et al.
(1989) after reanalyzing the data available at that epoch, although
observational uncertainties counsel to take with some caution this upturn at
low metallicity.
process in hydrostatic helium burning
in massive and, mostly, in intermediate and low-mass stars, while Fe is produced
by explosive burning in Type II and Type Ia supernovae. Observations of carbon abundances in halo and disk dwarfs (field giants are
not reliable indicators of ab initio carbon abundance due to the effects of
the first dredge-up) do actually show that [C/Fe] is almost constant in
time, with a value approximately solar (Laird 1985; Tomkin et al.
1986; Carbon et al. 1987; McWilliam et al. 1995),
although there is an important dispersion in the data at all metallicities.
Those surveys also seem to indicate some trend towards slightly higher values
of [C/Fe] at low [Fe/H], as confirmed to first order by Wheeler et al.
(1989) after reanalyzing the data available at that epoch, although
observational uncertainties counsel to take with some caution this upturn at
low metallicity.
 |
Figure 6:
Evolution of abundances ratios [X/Fe] as a function of
[Fe/H] for the CNO elements. Upper panel: carbon; central
panel: nitrogen; lower panel: oxygen |
| Open with DEXTER |
Our results show that the synthesis of carbon and iron by massive stars suffices
to explain the observations in halo stars. The [C/Fe] ratio shows a slow
decline towards the solar value during the halo-thick disk epoch, which indicates
that intermediate-mass stars, whose lifetimes permit them to evolve during the
late halo phase, do not give very important contributions to the carbon contents.
The bump around [Fe/H] 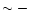 1, at the beginning of the thin
disk phase, results from the contribution of intermediate and, especially, low-mass
stars (
1, at the beginning of the thin
disk phase, results from the contribution of intermediate and, especially, low-mass
stars (
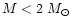 ), which eject important amounts of carbon
but no iron. But the iron ejected by Type Ia supernovae, which start to contribute
around the same epoch, compensates and finally overwhelms the role of the low
mass stars.
), which eject important amounts of carbon
but no iron. But the iron ejected by Type Ia supernovae, which start to contribute
around the same epoch, compensates and finally overwhelms the role of the low
mass stars.
The synthesis of 13C in intermediate and low-mass stars is capable
of building up the solar contents. The inclusion of novae produces a small overabundance
of 13C at the time of the solar birth.
The evolution of the ratio [N/Fe] as a function of [Fe/H] is displayed
in the second graph of Fig. 6. The three observational surveys
shown in the figure present a large scatter and there are no observations below
[Fe/H] 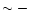 2.5. The data seem to indicate that [N/Fe]
remains more or less constant over the range of metallicities studied, but besides
the large dispersion, there are also uncertainties on the value of the constant,
although the data are compatible with a solar value. Our model predicts a rapid
increase of [N/Fe] at low metallicity, which shows that metal poor massive
stars do not produce primary nitrogen. The ratio [N/Fe] steadily increases
up to [Fe/H]
2.5. The data seem to indicate that [N/Fe]
remains more or less constant over the range of metallicities studied, but besides
the large dispersion, there are also uncertainties on the value of the constant,
although the data are compatible with a solar value. Our model predicts a rapid
increase of [N/Fe] at low metallicity, which shows that metal poor massive
stars do not produce primary nitrogen. The ratio [N/Fe] steadily increases
up to [Fe/H] 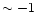 due to the progressive contribution of mostly
secondary nitrogen ejected by intermediate and low-mass stars, until the iron
production by Type Ia supernovae compensates the ejecta of intermediate stars,
flattening the evolution of [N/Fe].
due to the progressive contribution of mostly
secondary nitrogen ejected by intermediate and low-mass stars, until the iron
production by Type Ia supernovae compensates the ejecta of intermediate stars,
flattening the evolution of [N/Fe].
TWW1995 obtained primary nitrogen production by metal poor massive
stars with masses above 30
 by considering enhanced convective
overshooting, but still within the theoretical uncertainties, due to the violent
effects of the penetration of the helium convective burning shell into the hydrogen
shell, although this effect does not occur in more metal-rich massive stars.
This could be a promising mechanism to explain the abundance pattern of damped
Lyman-
by considering enhanced convective
overshooting, but still within the theoretical uncertainties, due to the violent
effects of the penetration of the helium convective burning shell into the hydrogen
shell, although this effect does not occur in more metal-rich massive stars.
This could be a promising mechanism to explain the abundance pattern of damped
Lyman-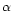 systems (Matteucci et al. 1997). Synthesis of
primary nitrogen due to the injection of protons into helium burning zones could
also happen in stellar models that include rotation (Heger et al. 1999;
Maeder & Meynet 2000). Massive stars produce some 15N but
the dominant contribution in our model comes from novae.
systems (Matteucci et al. 1997). Synthesis of
primary nitrogen due to the injection of protons into helium burning zones could
also happen in stellar models that include rotation (Heger et al. 1999;
Maeder & Meynet 2000). Massive stars produce some 15N but
the dominant contribution in our model comes from novae.
Oxygen is exclusively produced by massive stars and dominates their ejecta.
Until recent years the observational status of the oxygen abundance in dwarfs
and G and K giants showed a nearly constant value of [O/Fe] 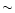 0.5
for [Fe/H]
0.5
for [Fe/H] 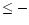 1, and a gradual decline in the disk. In fact,
this is the canonical behavior of the so-called
1, and a gradual decline in the disk. In fact,
this is the canonical behavior of the so-called 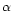 -elements (O,
Mg, Si, S, Ca, Ti): almost flat evolution in the halo, and a gradual decline
in the disk due to the iron production by Type Ia supernovae. However, recent
data by Israelian et al. (1988) and Boesgaard et al. (1999),
which agree with earlier results from Abia & Rebolo (1989), are
in contradiction with the idea of an oxygen plateau, since they find that [O/Fe]
increases between [Fe/H] = -1 and -3, from 0.6 to 1, which means a
slope in this range of
-elements (O,
Mg, Si, S, Ca, Ti): almost flat evolution in the halo, and a gradual decline
in the disk due to the iron production by Type Ia supernovae. However, recent
data by Israelian et al. (1988) and Boesgaard et al. (1999),
which agree with earlier results from Abia & Rebolo (1989), are
in contradiction with the idea of an oxygen plateau, since they find that [O/Fe]
increases between [Fe/H] = -1 and -3, from 0.6 to 1, which means a
slope in this range of
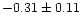 .
.
Our calculations show that [O/Fe] begins with a value of the order of 1
at very low metallicity, and it slowly declines during the thick disk phase,
in part because massive stars of different masses and initial metal contents
produce different O/Fe ratios, and also because Type Ia supernovae begin to
inject iron already in the halo-thick disk phase, though their influence is
stronger during the thin disk epoch, when Type Ia supernovae reach their highest
rate, as it is clearly shown by the steeper decline of [O/Fe] for [Fe/H] 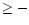 1.
This behaviour is in agreement with previous results by TWW1995 and
Chiappini et al. (1997). We obtain a slope of -0.28, which clearly
indicates a deviation from the traditional oxygen plateau, although a little
bit less pronounced than in the new data. We will see the same kind of evolution,
although less marked, for the rest of the
1.
This behaviour is in agreement with previous results by TWW1995 and
Chiappini et al. (1997). We obtain a slope of -0.28, which clearly
indicates a deviation from the traditional oxygen plateau, although a little
bit less pronounced than in the new data. We will see the same kind of evolution,
although less marked, for the rest of the 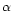 -elements.
-elements.
 |
Figure 7:
Upper panel: evolution of the ratio [F/Fe] as a
function of [Fe/H]. Lower panel: evolution of the ratio
[F/O] as a function of [Fe/H], compared with observational points from
Jorissen et al. (1992) |
| Open with DEXTER |
In our calculations fluorine is synthesized (together with 7Li
and 11B which will not be treated here) by the so-called neutrino-induced
nucleosynthesis in Type II supernova explosions. The amount of fluorine produced
by neutrino spallation of 20Ne is extremely sensitive to the neutrino
fluxes and spectra used in the explosion calculations, which render its yield
very uncertain.
The upper panel of Fig. 7 displays the evolution versus iron abundance
of the ratio [F/Fe]. Our model predicts a practically constant and almost
solar [F/Fe]. In the lower panel of Fig. 7 we present the ratio
[F/O] compared to the only available set of observations in the literature.
In agreement with TWW1995, our model predicts strong subsolar [F/O]
ratios at low metallicity, which is a result of the early efficient oxygen enrichment
by massive stars and not of a deficient production of fluorine, while it fits
the observed abundances of normal K giants.
Most of the plotted data correspond to spectroscopically peculiar giant stars
whose abundances are affected by stellar evolution, although the high ratios
observed in those stars also point to contributions other than from massive
stars. Forestini & Charbonnel (1997) suggest fluorine production
in the helium burning shell of AGB stars, and Meynet & Arnould (2000)
contributions from WR stars. A reliable history of fluorine will only be settled
when we gain new insight into the contributions from different kinds of stars.
Our results for the evolution of the ratios [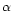 /Fe] for magnesium,
silicon, sulphur and calcium, plotted in Fig. 8, closely follow
the general trends of the data. Chiappini et al. (1999) pointed out
that the so-called "plateau'' for the
/Fe] for magnesium,
silicon, sulphur and calcium, plotted in Fig. 8, closely follow
the general trends of the data. Chiappini et al. (1999) pointed out
that the so-called "plateau'' for the 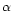 -elements at low metallicities
is not perfectly flat, but instead presents a slight slope. In fact, that is
exactly what we find: the abundance ratios slowly increase with decreasing [Fe/H],
in good agreement with the work of McWilliam et al. (1995) and that
of Ryan et al. (1996) for magnesium, silicon and calcium, although
the slopes are shallower than for oxygen.
-elements at low metallicities
is not perfectly flat, but instead presents a slight slope. In fact, that is
exactly what we find: the abundance ratios slowly increase with decreasing [Fe/H],
in good agreement with the work of McWilliam et al. (1995) and that
of Ryan et al. (1996) for magnesium, silicon and calcium, although
the slopes are shallower than for oxygen.
 |
Figure 8:
Evolution of the abundance ratios to iron of the
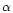 elements Mg, Si, S, and Ca as a function of [Fe/H] elements Mg, Si, S, and Ca as a function of [Fe/H] |
| Open with DEXTER |
The results for silicon and calcium are in excellent agreement with the data.
The evolution of magnesium and sulphur, however, is less satisfactory.
In the case of magnesium, though we begin with typical halo values, the rapid
decline of [Mg/Fe] gives values a little lower than observed in the thick
disk phase, but still marginally compatible with the observations. Later on,
when the thin disk starts, the iron from Type Ia supernovae worsens the problem
and we clearly underestimate the [Mg/Fe] ratio in the disk. In principle,
the metallicity-independent yields for massive stars from Thielemann et al.
(1996) or the WW1995 yields for solar metallicity could
solve this discrepancy (Thomas et al. 1998; Chiappini et al. 1999),
but this type of yields are not appropriate when studying the galactic halo.
Since the magnesium yields of WW1995 increase with the stellar mass,
the use of the rather steep IMF of Kroupa et al. (1993) worsen the
situation. As pointed out by GP2000, the use of the metallicity dependent
yields of Limongi et al. (2000) will probably solve the underproduction
of magnesium but the ratios 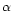 /Mg will not reproduce the observations.
The fact that current yields from massive stars cannot completely explain the
magnesium evolution could indicate the need for a supplementary source of this
element, either in low and intermediate mass stars or by enhancing the magnesium
yield in Type Ia supernovae (TWW1995).
/Mg will not reproduce the observations.
The fact that current yields from massive stars cannot completely explain the
magnesium evolution could indicate the need for a supplementary source of this
element, either in low and intermediate mass stars or by enhancing the magnesium
yield in Type Ia supernovae (TWW1995).
The paucity of data for sulphur at low [Fe/H] does not allow precise comparisons,
but if the points by François (1987, 1988) around and below
[Fe/H] 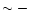 1 adequately represent the main trend, a supplementary
production of sulphur at low metallicity seems necessary. Given our nucleosynthetic
sources, sulphur is only produced by massive stars, and the uncertainties in
the WW1995 yields of metal poor massive stars could be the cause of
the low [S/Fe] at low [Fe/H]. It has been suggested, however, that the
[S/Fe] values measured in the halo stars should be reduced by 0.2 dex (Lambert
1989). If that were the case, our results for sulphur would nicely
fit the corrected data.
1 adequately represent the main trend, a supplementary
production of sulphur at low metallicity seems necessary. Given our nucleosynthetic
sources, sulphur is only produced by massive stars, and the uncertainties in
the WW1995 yields of metal poor massive stars could be the cause of
the low [S/Fe] at low [Fe/H]. It has been suggested, however, that the
[S/Fe] values measured in the halo stars should be reduced by 0.2 dex (Lambert
1989). If that were the case, our results for sulphur would nicely
fit the corrected data.
Unlike most of the chemical elements, in the case of magnesium the evolution
of the isotopic ratios can be compared with observational results.
 |
Figure 9:
Evolution of the magnesium isotopic ratios 25Mg/ 24Mg
(upper panel) and 26Mg/ 24Mg (lower
panel) as a function of metallicity |
| Open with DEXTER |
In the upper panel of Fig. 9 we show our results for the evolution
of the ratio 25Mg/ 24Mg as a function of [Fe/H],
while in the lower panel appears the evolution of the ratio 26Mg/ 24Mg.
The three isotopes are produced during the hydrostatic evolution of massive
stars. Since in the WW1995 yields for massive stars 24Mg
is basically a primary isotope, while the neutron-rich isotopes 25Mg
and 26Mg increase with metallicity (both are affected by the neutron
excess), it is to be expected, indeed, that both ratios decrease towards lower
metallicities.
Our results, similar to those found by TWW1995 and by GP2000,
follow the expected trend, but the model produces isotopic ratios clearly below
the observations in the halo-thick disk phase (i.e., [Fe/H] 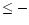 1).
If the WW1995 yields do not underestimate the magnesium isotopic yields,
a supplementary source of 25Mg and 26Mg is needed,
for instance through s-process in AGB stars (Iben & Renzini 1983).
1).
If the WW1995 yields do not underestimate the magnesium isotopic yields,
a supplementary source of 25Mg and 26Mg is needed,
for instance through s-process in AGB stars (Iben & Renzini 1983).
In the thin disk phase ([Fe/H] -1), the model reproduces well
the global trend of the observations, with both ratios systematically increasing
with metallicity. The ratio 25Mg/ 24Mg reaches the
solar value. However, the 26Mg/ 24Mg ratio at [Fe/H] = 0
is  50% higher than solar, again in agreement with the results of
GP2000 who attribute the overabundance of 26Mg at the
solar birth to the effects of the IMF of Kroupa et al. (1993) that
favor the production of 26Mg in front of that of 24Mg.
50% higher than solar, again in agreement with the results of
GP2000 who attribute the overabundance of 26Mg at the
solar birth to the effects of the IMF of Kroupa et al. (1993) that
favor the production of 26Mg in front of that of 24Mg.
Sodium, aluminum and potassium are odd elements (besides, sodium and aluminum
are monoisotopic) mainly produced by massive stars. They are subjected to the
odd-even effect, i.e., stellar yields increasing with metallicity. Therefore,
their galactic abundance ratios to iron must increase with time, although the
evolution of the ratio [element/Fe] could be affected by the iron production
by Type Ia supernovae, especially in the disk. One can eliminate the effects
of Type Ia supernovae on the abundance evolution of odd elements by plotting
the ratio [element/Mg], as in TWW1995, because magnesium is also
nearly exclusively synthesized in massive stars, or by using as metallicity
indicator an element more reliable than iron, which is affected by uncertainties
such as the evolution of Type Ia supernova rates or the mass cut and explosion
energy in Type II supernovae, as done by GP2000 who use calcium instead
of iron as metallicity indicator.
We display in Fig. 10 the calculated [Na/Fe] (upper panel)
and [Al/Fe] (central panel). In Fig. 11 we also show the
ratios [Na/Ca] and [Al/Ca] using [Ca/H] as a measure of the metallicity.
It is worth stressing that the evolution of the calcium abundance obtained in
our model agrees very well with the data (see Fig. 8).
 |
Figure 10:
Evolution of Na, Al and K abundance ratios to iron in terms
of [Fe/H] as metallicity indicator |
| Open with DEXTER |
The observed sodium to iron ratios display a plateau in the disk. The situation
for the halo stars is less clear. The rather old data by Peterson (1981)
indicate a rapid decrease from [Fe/H] = -1 to [Fe/H] =-2.
Recent observations by Stephens (1999) show the same trend, but most
other observations point to a constant [Na/Fe]  0, although with
large dispersion. We obtain an almost constant, but lower than the data, abundance
up to [Fe/H]
0, although with
large dispersion. We obtain an almost constant, but lower than the data, abundance
up to [Fe/H]  2.5, and a steep increase at the beginning of the
thin disk formation that ends in a plateau lower than observed.
2.5, and a steep increase at the beginning of the
thin disk formation that ends in a plateau lower than observed.
The calculated evolution of [Al/Fe] begins almost flat and is clearly higher
than the data from halo stars. Later, it slowly increases at the thick-thin
disk transition, but, as with Na, remains below the disk star observations.
The abundance ratio to calcium of both elements shows now the odd-even effect
(see Fig. 11). We still have low [Na/Ca] in the complete
range of [Ca/H], but the aluminum ratio shows a better agreement with the
observations. We remind that our models underproduce the solar sodium by a factor
of  1.4, and aluminum by a factor of
1.4, and aluminum by a factor of  1.2.
1.2.
As pointed out by TWW1995 and GP2000, intermediate-mass
stars could produce some sodium and aluminum through the Ne-Na and Mg-Al cycles, then
improving the fit to the data.
 |
Figure 11:
Evolution of the ratios [Na/Ca] and [Al/Ca] in
terms of [Ca/H] as metallicity indicator |
| Open with DEXTER |
The potassium abundance is dominated by the odd isotope 39K, and
it is again mainly produced in massive stars through hydrostatic oxygen burning,
so that it should show the odd-even effect. Surprisingly, the observed abundances
display the opposite evolution: the few halo observations give values of [K/Fe]  0.5
with a wide scatter, decreasing to solar values in the disk. Our results, presented
in Fig. 10, show, however, a behavior similar to other odd elements.
We obtain slightly lower than solar values in the halo-thick disk, and a gradual
rise during the thin disk phase towards final solar values, in agreement with
the reduced iron yield evolution of TWW1995.
0.5
with a wide scatter, decreasing to solar values in the disk. Our results, presented
in Fig. 10, show, however, a behavior similar to other odd elements.
We obtain slightly lower than solar values in the halo-thick disk, and a gradual
rise during the thin disk phase towards final solar values, in agreement with
the reduced iron yield evolution of TWW1995.
 |
Figure 12:
Evolution of neon, phosphorus, chlorine and argon abundance
ratios to iron, as a function of [Fe/H] |
| Open with DEXTER |
Although there are no observational data to compare with, we plot in Fig. 12
the calculated evolution of the noble gases neon and argon, as well as those
of phosphorus and chlorine, just for completeness.
Neon abundance is dominated by 20Ne, and the three argon isotopes
are also of even Z. Therefore, both elements should behave as 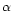 -elements.
The calculations confirm this theoretical expectation. The evolution of neon
in the halo-thick disk shows a clear dependence on metallicity, reminding of
the oxygen behavior. For argon the metallicity effect is less marked, and its
evolution reminds that of intermediate
-elements.
The calculations confirm this theoretical expectation. The evolution of neon
in the halo-thick disk shows a clear dependence on metallicity, reminding of
the oxygen behavior. For argon the metallicity effect is less marked, and its
evolution reminds that of intermediate 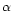 -elements like silicon or
calcium. In the absence of stellar observations for these elements, it is gratifying
that their solar abundances are well reproduced.
-elements like silicon or
calcium. In the absence of stellar observations for these elements, it is gratifying
that their solar abundances are well reproduced.
Both odd-Z elements, phosphorus and chlorine, present solar or slightly subsolar
abundance ratios in the halo-thick disk. When the assembling of the thin disk
begins, their abundances gradually climb towards the solar values due to the
odd-even effect in massive stars (and in a much lesser extent, by contribution
of Type Ia supernovae), until the iron from Type Ia supernovae flattens the
evolution of phosphorus, although it is not the case for chlorine.
 |
Figure 13:
Evolution with metallicity of the iron peak elements scandium,
titanium and vanadium as a function of [Fe/H] |
| Open with DEXTER |
All these elements are basically synthesized through explosive burning in Type
II and/or Type Ia supernova explosions, and some of them can also be produced
by neutron captures during hydrostatic He and C burning. Their stellar yields
are therefore much more uncertain than those of the intermediate-mass elements studied
above, due to our deficient understanding of the parameters that characterize supernova
explosions (energy and mass cut in Type II supernovae, progenitors, burning
propagation and rates of Type Ia supernovae), and of neutron fluxes in hydrostatic
He and C combustion. Isotopes with A 56 are mainly produced in explosive
O and Si burning, and in Nuclear Statistical Equilibrium (NSE), while isotopes
with 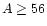 are produced in the alpha-rich freeze-out of NSE, besides contributions
from neutron captures.
are produced in the alpha-rich freeze-out of NSE, besides contributions
from neutron captures.
The calculated history of scandium, titanium and vanadium is displayed in Fig.
13, and that of chromium, manganese, cobalt and nickel appears
in Fig. 14.
The evolution of the [Sc/Fe] ratio agrees reasonably well with the data
for halo stars, characterized by a flat and nearly solar value, although between
[Fe/H] = -2.5 and [Fe/H] = -1 we get a gentle decrease and our results
fall below the observations. At the transition to the thin disk, the abundance
grows slightly, as expected for an odd element, but iron from Type Ia supernovae,
which make little scandium, overwhelms this increase and lowers the ratio [Sc/Fe], which is still below solar, during the disk evolution.
Titanium, dominated by 48Ti, should behave as an 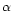 -element.
In fact, the observations point to [Ti/Fe]
-element.
In fact, the observations point to [Ti/Fe] 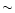 0.3-0.4 in the most
metal-poor halo stars, and to a clear trend towards a declining ratio as metallicity
increases. Loosely speaking, our calculations reproduce such characteristics,
but the abundance is systematically lower than observed for the complete range
of metallicity. At the solar birth all the titanium isotopes except 46Ti
are underabundant (see Fig. 5). TWW1995 and GP2000
found the same problems with titanium. The conclusion that current yields from
massive stars alone fail to explain the titanium history is unavoidable.
0.3-0.4 in the most
metal-poor halo stars, and to a clear trend towards a declining ratio as metallicity
increases. Loosely speaking, our calculations reproduce such characteristics,
but the abundance is systematically lower than observed for the complete range
of metallicity. At the solar birth all the titanium isotopes except 46Ti
are underabundant (see Fig. 5). TWW1995 and GP2000
found the same problems with titanium. The conclusion that current yields from
massive stars alone fail to explain the titanium history is unavoidable.
The isotope 51V is predominant in the total abundance of vanadium.
The few available data show a [V/Fe] flat and solar in population I and
in metal-rich halo stars, and a tendency to increase as [Fe/H] decreases
from -2 to -3. The calculations give a flat [V/Fe] in the halo-thick disk
with a value of 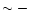 0.3, a moderate and rapid rise at the beginning
of the thin disk formation, and a flat evolution slightly lower than solar during
most of the thin disk phase; here, again, iron from Type Ia supernovae compensates
the vanadium produced by massive stars with
0.3, a moderate and rapid rise at the beginning
of the thin disk formation, and a flat evolution slightly lower than solar during
most of the thin disk phase; here, again, iron from Type Ia supernovae compensates
the vanadium produced by massive stars with
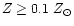 .
.
The observations on the ratio [Cr/Fe] available until mid-nineties showed
a constant and solar value down to [Fe/H] 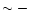 2.5, i.e. the same
behavior as iron, indicating that both elements were produced in the same scenarios.
However, recent observations show that the chromium abundance ratio to iron
decreases as the metallicity goes down from [Fe/H] = -2.5 to [Fe/H] =
-3.5, reaching at the latter metallicity values as low as [Cr/Fe]
2.5, i.e. the same
behavior as iron, indicating that both elements were produced in the same scenarios.
However, recent observations show that the chromium abundance ratio to iron
decreases as the metallicity goes down from [Fe/H] = -2.5 to [Fe/H] =
-3.5, reaching at the latter metallicity values as low as [Cr/Fe] 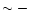 0.7.
The chromium stellar yields of WW1995 are quite insensitive to Z.
Our results, shown in Fig. 14, give an almost flat [Cr/Fe]
in the complete range of metallicities, and thus fail to reproduce the data
at low metallicity. The flatness of the abundance ratio is more marked in the
disk because chromium and iron are produced in the same proportions by Type
Ia supernovae, fitting precisely the solar abundances of the chromium isotopes.
0.7.
The chromium stellar yields of WW1995 are quite insensitive to Z.
Our results, shown in Fig. 14, give an almost flat [Cr/Fe]
in the complete range of metallicities, and thus fail to reproduce the data
at low metallicity. The flatness of the abundance ratio is more marked in the
disk because chromium and iron are produced in the same proportions by Type
Ia supernovae, fitting precisely the solar abundances of the chromium isotopes.
 |
Figure 14:
Evolution of the iron peak elements Cr, Mn, Co and Ni
as a function of [Fe/H] |
| Open with DEXTER |
In the case of manganese, with only one stable and odd-Z isotope ( 55Mn),
the calculated evolution fits well the data for [Fe/H] > -2.5,
although in the thin disk there is an slight overabundance. The roughly linear
increase in the disk reveals the odd-even effect for this element. At very low
metallicities, as for chromium, the calculated abundances lie clearly above
the data.
The observational situation for the ratio [Co/Fe] is rather puzzling. Cobalt
is an odd element and therefore one expects its abundance to diminish with decreasing
metallicity. Instead, the latest data point to a noticeable increase of its
abundance at the lowest metallicities. We find a rough agreement down to [Fe/H]
=-2.5, where [Co/Fe] mildly declines when going to lower metallicities,
although the calculated history appears to lie higher than the observations.
Below [Fe/H] =-2.5, the abundance ratio continues its gentle decline,
just the opposite trend to that observed.
Nickel abundances in halo and disk stars have been obtained in a large number
of surveys. Most of them show a constant and solar value for the ratio [Ni/Fe]
at all metallicities, but the most recent observations seem to indicate an increasing
ratio towards low [Fe/H], although the scatter is really large. The models
give a continuous increase of an overabundant [Ni/Fe] for [Fe/H] > -3.
We obtain higher values than observed due to the combination of a reduction
by a factor of two in the WW1995 iron yields from massive stars, together
with the large amount of 58Ni in the yields of the W7 model of
Type Ia supernovae, the latter being responsible for the positive slope in the
thin disk.
These two elements are produced in significant amounts at different burning
stages in massive stars. As for the iron peak elements, the total ejected amounts
of these nuclei are strongly dependent on the characteristics of the supernova
explosions. Nevertheless, ratios relative to iron could be less affected by
astrophysical uncertainties. For instance, as shown by WW1995, in
the explosion of a solar metallicity 35
 model, variations by
a factor of 2 in the explosion energy give changes in the [Ni/Fe] ratio of
less than 10%. This argument in favor of the relative robustness of the calculated
evolution of the element ratios relative to iron also applies to copper and
zinc. The evolution of both elements is presented in Fig. 15.
model, variations by
a factor of 2 in the explosion energy give changes in the [Ni/Fe] ratio of
less than 10%. This argument in favor of the relative robustness of the calculated
evolution of the element ratios relative to iron also applies to copper and
zinc. The evolution of both elements is presented in Fig. 15.
 |
Figure 15:
Evolution of copper and zinc as a function of [Fe/H] |
| Open with DEXTER |
Observations for these elements are scarce because they do not present enough
suitable transitions. According to the available data, copper behaves like a
typical odd nucleus, with a marked odd-even effect which gives a continuous
growth of [Cu/Fe] with the iron contents. Our model nicely fits the data.
At low metallicities we obtain a flat evolution, and in the thin disk the odd-even
effect is clearly seen. As shown in Fig. 5, the solar abundances
of the two copper isotopes are well adjusted.
The data for the zinc abundance show that this element evolves as iron, with
a constant and solar [Zn/Fe] in the complete interval of observed metallicities.
Here, again, the calculated evolution fits well the data. However, this result
could be misleading since even if we obtain an elemental abundance in almost
perfect agreement with the solar value, the distribution between the four isotopes
of zinc (see Fig. 5) does not agree with the solar isotopic ratios.
As mentioned above, we underproduce by a factor of 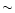 2 the most abundant
isotope, 64Zn, and overproduce 68Zn by the same
factor.
2 the most abundant
isotope, 64Zn, and overproduce 68Zn by the same
factor.
We have analyzed the evolution of all the stable isotopes between hydrogen and
zinc (lithium, beryllium and boron isotopes will be treated in a future paper)
by means of a detailed chemical evolution code. In the framework of standard
chemical evolution models only the works by TWW1995 and by GP2000
have studied such a large number of isotopes. In the first paper, the model
employed was adequate just for the galactic disk evolution, apart from using
the rather old yields of Renzini & Voli (1981) for low- and intermediate-mass
stars. In the second case, even if the halo and the disk were correctly treated,
only yields from massive stars were included
Our model assumes the formation of the Milky Way in two main episodes of exponentially
decreasing infall. The first episode forms the halo and the thick disk from
infall of primordial extragalactic material with an e-folding timescale of 1 Gyr. Then, the thin disk is assembled by infall of metal-rich extragalactic
gas with a global metallicity of
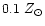 in solar proportions, and
with a relatively long timescale (7 Gyr at the solar ring). We have also calculated
models that accrete material of primordial composition during the complete evolution.
Although the results of the two kind of models are similar, we obtain a better
agreement with the data for the stellar distribution of metallicities in the case
of the model with enriched infall. We have employed an up to date IMF (the version
of Kroupa et al. 1993), and a form for the SFR (the Dopita & Ryder's
1994 law), that relies on observations of the properties of star
formation in spiral galaxies.
in solar proportions, and
with a relatively long timescale (7 Gyr at the solar ring). We have also calculated
models that accrete material of primordial composition during the complete evolution.
Although the results of the two kind of models are similar, we obtain a better
agreement with the data for the stellar distribution of metallicities in the case
of the model with enriched infall. We have employed an up to date IMF (the version
of Kroupa et al. 1993), and a form for the SFR (the Dopita & Ryder's
1994 law), that relies on observations of the properties of star
formation in spiral galaxies.
One important characteristic of our model is that it incorporates metallicity-dependent yields for isolated stars in the whole range of stellar masses. We
use the WW1995 yields for massive stars and van der Hoek & Groenengen
(1997) for low and intermediate-mass stars. Following TWW1995,
in order to obtain a better concordance with observations, we have reduced the
rather uncertain iron yield of WW1995 by a factor of two. We have
not included metallicity effects in the yields of Type Ia supernovae, but GP2000
pointed out that the inclusion of the metallicity dependent yields of Iwamoto
et al. (1999) hardly affects the final results. Finally, we have taken
into account the nucleosynthetic contributions from novae that give important
contributions to isotopes such as 13C, 15N, and
17O.
We have compared in detail the theoretical results with a large ensemble of
observational data. First of all, in Sect. 3 we have shown that our results are
able to reproduce the main characteristics of the solar vicinity, especially
the G-dwarf distribution in the local disk, that we consider the most stringent
restriction. We also obtain close agreement with the solar composition
(both elemental and isotopic) at the time of 8.5 Gyr. It is worth stressing
that:
- All the solar elemental abundances are reproduced within a factor of two, except
for nickel, which is slightly oversolar due to the large production factor of
58Ni in the adopted yields of Type Ia supernovae and of 62Ni
in the yields of exploded massive stars of WW1995;
- The contributions from low and intermediate-mass stars suffice to build up the
abundances of the main CNO isotopes. The inclusion of novae increases the solar
abundances of 13C (by a factor of
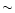 1.6), and noticeably
that of 15N (by a factor of
1.6), and noticeably
that of 15N (by a factor of  4) and 17O
(by a factor of
4) and 17O
(by a factor of  2);
2);
- Massive star yields still encounter difficulties to account for the underproduction
of the neutron-rich isotopes 48Ca and 50Ti, as it
is also the case with 47Ti.
The evolution of the abundance ratios [element/Fe] obtained in our model
has been confronted with a large and updated set of observations. The main conclusions
that result from the comparison are:
- The evolution of the CNO elements is very well reproduced by our model. As it
is well known, massive stars underproduce carbon and nitrogen (TWW1995;
GP2000). However, the inclusion of low and intermediate-mass stars
is enough to reproduce adequately the carbon evolution and its solar abundance.
The behavior of nitrogen is again well reproduced, although some primary nitrogen
from massive stars could be necessary during the halo phase. For oxygen we obtain
a clear deviation of the so-called
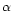 -plateau which is also present,
in a lesser extent, in the rest of the
-plateau which is also present,
in a lesser extent, in the rest of the 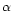 -elements. Our results
show a continuous decrease of the ratio [O/Fe] from the beginning of the
halo-thick disk phase, as pointed out first by TWW1995 and then by
Chiappini et al. (1999). The slope is still shallower than in the
data from Israelian et al. (1988) and Boesgaard et al. (1999),
but the fit with the more recent data of Carretta et al. (2000) is
excellent;
-elements. Our results
show a continuous decrease of the ratio [O/Fe] from the beginning of the
halo-thick disk phase, as pointed out first by TWW1995 and then by
Chiappini et al. (1999). The slope is still shallower than in the
data from Israelian et al. (1988) and Boesgaard et al. (1999),
but the fit with the more recent data of Carretta et al. (2000) is
excellent;
- As with oxygen, most of the
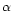 and
and 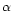 -like elements
show some deviations of the typical
-like elements
show some deviations of the typical 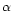 -plateau, in the sense that
their abundance ratios to iron continuously decrease with increasing metallicity
due to the combined effects of stellar yields depending on mass and metallicity
and the contribution to the iron contents from Type Ia supernovae, in agreement
with observations. However, some of these elements are underproduced at all
metallicities by the WW1995 yields (as well as by the yields from
Limongi et al. 2000, according to GP2000), especially
magnesium and titanium;
-plateau, in the sense that
their abundance ratios to iron continuously decrease with increasing metallicity
due to the combined effects of stellar yields depending on mass and metallicity
and the contribution to the iron contents from Type Ia supernovae, in agreement
with observations. However, some of these elements are underproduced at all
metallicities by the WW1995 yields (as well as by the yields from
Limongi et al. 2000, according to GP2000), especially
magnesium and titanium;
- In general, the intermediate odd-Z elements show the expected theoretical behaviour
as a consequence of the marked odd-even effect in the stellar yields. However,
for several of these elements there exist important discrepancies with the observational
data, in particular for sodium and potassium. The same discrepancy appears in
the case of scandium and vanadium which, besides, are underproduced by the model
at all metallicities;
- Although to zero order the evolution of the iron peak elements is consistent
with the data, there are noticeable discrepancies. Chromium and manganese are
overabundant at low metallicities, which may indicate problems with the iron
yields for stars of low metallicity, while nickel is overabundant at moderate
and high metallicity. This last flaw can be attributed to the nickel yields
of model W7 for Type Ia supernovae. However, as mentioned above, the calculations
of massive star explosions are still plagued with severe problems.
- Abia, C., & Rebolo, R. 1989, ApJ, 347, 186
In the text
NASA ADS
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197
In the text
- Barbuy, B. 1985, A&A, 151, 189
NASA ADS
- Barbuy, B. 1987, A&A, 172, 251
NASA ADS
- Barbuy, B., & Erdelyi-Mendes, M. 1989, A&A, 214, 239
NASA ADS
- Barbuy, B., Spite, F., & Spite, M. 1987, A&A, 178, 199
NASA ADS
- Berczik, P. 1999, A&A, 348, 371
In the text
NASA ADS
- Boesgaard, A. M., King, J. R., Deliyannis, C. P., & Vogt, S. S. 1999, AJ, 117, 492
In the text
NASA ADS
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857
In the text
NASA ADS
- Burkert, A., Truran, J. W., & Hensler, G. 1992, ApJ, 391, 651
In the text
NASA ADS
- Buser, R., Rong, J., & Karaali, S. 1998, A&A, 331, 934
In the text
NASA ADS
- Carbon, D. F., Barbuy, B., Kraft, R. P., Friel, E. D., & Suntzeff, N. B. 1987, PASP, 99, 335
In the text
NASA ADS
- Cardelli, J., & Federman, S. 1997, in Nuclei in the Cosmos IV, ed. J. Gorres et al. (Amsterdam: Elsevier), 31
In the text
- Carigi, L. 1994, ApJ, 424,181
In the text
NASA ADS
- Carretta, E., Gratton, R. G., & Sneden, C. 2000, A&A, 356, 238
In the text
NASA ADS
- Chang, R. X., Hou, J. L., Shu, C. G., & Fu, C. Q. 1999, A&A, 350, 38
In the text
NASA ADS
- Charbonnel, C., Meynet, G., Maeder, A., & Schaerer, D. 1996, A&AS, 115, 339
In the text
NASA ADS
- Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141, 491
In the text
NASA ADS
- Chiappini, C., Matteucci, F., & Gratton, G. 1997, ApJ, 477, 765
In the text
NASA ADS
- Chiappini, C., Matteucci, F., Beers, T. C., & Nomoto, K. 1999, ApJ, 515, 226
In the text
NASA ADS
- Chiappini, C., Matteucci, F., & Padoan, P. 2000, ApJ, 528, 711
In the text
NASA ADS
- Clegg, R. E. S., Tomkin, J., & Lambert, D. L. 1981, ApJ, 250, 262
NASA ADS
- Dickey, J. M. 1993, in ASP Conf. Ser. 39, The Minnesota Lectures on the Structure and Dynamics of the Milky Way, ed. R. M. Humphreys (San Francisco: ASP), 93
In the text
- Dopita, M. A., & Ryder, S. D. 1994, ApJ, 430, 163
In the text
NASA ADS
- Edmunds, M. G., & Pagel, B. E. J. 1984, MNRAS, 211, 507
In the text
NASA ADS
- Edvardsson, B., Anderson, J., Gustafsson, B., et al. 1993, A&A, 275, 101
In the text
NASA ADS
- Flynn, C., Gould, A., & Bahcall, J. N. 1999, in ASP Conf. Ser. 165, The Third Stromlo Symposium: The Galactic Halo, ed. B. K. Gibson, T. S. Axelrod, & M. E. Putman (San Francisco: ASP), 387
In the text
- Forestini, M., Charbonnel, C. 1997, A&AS, 123, 241
In the text
NASA ADS
- François, P. 1987, A&A, 176, 294
In the text
NASA ADS
- François, P. 1988, A&A, 195, 226
In the text
NASA ADS
- Garnett, D. R., & Kobulnicky, H. A. 2000, ApJ, 532, 1192
In the text
NASA ADS
- Gay, P. L., Lambert, D. L. 2000, ApJ, 533, 260
NASA ADS
- Gilmore, G., Wyse, R., & Kuijen, K. 1989, in Evolutionary Phenomena in Galaxies, ed. J. Beckman, & B. Pagel (Cambridge University Press), 172
In the text
- Giovanoli, A., & Tosi, M. 1995, MNRAS, 273, 499
In the text
NASA ADS
- Goswami, A., & Prantzos, N. 2000, A&A, 359, 191 (GP2000)
In the text
NASA ADS
- Gratton, R. G. 1985, A&A, 148, 105
NASA ADS
- Gratton, R. G. 1989, A&A, 208, 171
NASA ADS
- Gratton, R. G., & Ortolani, S. 1986, A&A, 169, 201
NASA ADS
- Gratton, R. G., & Sneden, C. 1987, A&A, 178, 179
NASA ADS
- Gratton, R. G., & Sneden, C. 1988, A&A, 204, 193
NASA ADS
- Gratton, R. G., & Sneden, C. 1991, A&A, 241, 501
NASA ADS
- Greggio, L., & Renzini, A. 1983, A&A, 118, 217
In the text
NASA ADS
- Güsten, R., & Mezger, M. 1982, Vistas in Astr., 26, 159
In the text
NASA ADS
- Hartmann, K., & Gehren, T. 1988, A&A, 199, 269
NASA ADS
- Hatano, K., Branch, D., Fisher, A., & Starrfield, S. 1997, MNRAS, 290, 113
In the text
NASA ADS
- Heger, A., Langer, N., & Woosley, S. E. 1999, ApJ, 528, 368
In the text
NASA ADS
- Henry, R. B. C., & Worthey, G. 1999, PASP, 111, 919
In the text
NASA ADS
- Iben, I., & Renzini, A. 1983, ARA&A, 21, 271
In the text
NASA ADS
- Israelian, G., García López, R., & Rebolo, R. 1998, ApJ, 507, 805
In the text
NASA ADS
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al.
1999, ApJS, 125, 439
In the text
NASA ADS
- Jørgensen, B. R. 2000, A&A, 363, 947
In the text
NASA ADS
- Jorissen, A., Smith, V. V., & Lambert, D. L. 1992, A&A, 261, 164
In the text
NASA ADS
- José, J., & Hernanz, M. 1998, ApJ, 494, 680
In the text
NASA ADS
- Kennicutt, R. 1998, ApJ, 498, 541
In the text
NASA ADS
- Kroupa, P. 1998, in Brown Dwarfs and Extrasolar Planets, ed. R. Rebolo et al.,
ASP Conf. 134, 483
In the text
- Kroupa, P., Tout, C., & Gilmore, G. 1993, MNRAS, 262, 545
In the text
NASA ADS
- Kuijken, K., & Gilmore, G. 1989, MNRAS, 239, 605
In the text
NASA ADS
- Laird, J. B. 1985, ApJ, 289, 556
In the text
NASA ADS
- Lambert, D. L. 1989, in Cosmic Abundances of Matter, ed. C. J. Waddington, AIP
Conf., 183, 168
In the text
- Larson, R. B. 1972, Nature, 236, 21
In the text
- Limongi, M., Straniero, O., & Chieffi, A. 2000, ApJS, 129, 625
In the text
NASA ADS
- Luck, R. E., & Bond, H. E. 1985, ApJS, 59, 249
NASA ADS
- Maeder, A., & Meynet, G. 2000, ARA&A, in press
In the text
- Magain, P. 1987, A&A, 179, 176
NASA ADS
- Magain, P. 1989, A&A, 209, 211
NASA ADS
- Marigo, P., Bressan, A., & Chiosi, C. 1996, A&A, 313, 545
In the text
NASA ADS
- Massey, P. 1998, in The Stellar Initial Mass Function, ed. G. Gilmore, & D. Howell, ASP Conf. Ser., 142, 17
In the text
- Massey, P., Johnson, K., & Degioia-Eastwood, K. 1995, ApJ, 454, 151
NASA ADS
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279
In the text
NASA ADS
- Matteucci, F., Molaro, P., & Vladilo, G. 1997, A&A, 321, 45
In the text
NASA ADS
- McWilliam, A., & Lambert, D. L. 1988, MNRAS, 230, 573
NASA ADS
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757
In the text
NASA ADS
- Méra, D., Chabrier, G., & Schaeffer, R. 1998, A&A, 330, 937
In the text
NASA ADS
- Meusinger, H., Reimann, H. G., & Stecklum, B. 1991, A&A, 245, 57
In the text
NASA ADS
- Meyer, M. R., Adams, F. C., Hillenbrand, L. A., Carpenter, J. M., & Larson, R. B. 2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Book - Tucson: University of Arizona Press) 121
In the text
- Meynet, G., & Arnould, M. 2000, A&A, 355, 176
In the text
NASA ADS
- Mirabel, I. F. 1981, Rev. Mex. Astron. & Astrofis., 6, 245
In the text
NASA ADS
- Mirabel, I. F., & Morras, R. 1984, ApJ, 279, 86
In the text
NASA ADS
- Mishenina, T. V., Korotin, S. A., Klochkova, V. G., & Panchuk, V. E. 2000, A&A, 353, 978
NASA ADS
- Nissen, P. E., Gustafsson, B., Edvardsson, B., & Gilmore, G. 1994, A&A, 285, 440
NASA ADS
- Nissen, P. E., Chen, Y. Q., Schuster, W. J., & Zhao, G. 2000, A&A, 353, 722
NASA ADS
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644
In the text
NASA ADS
- Pagel, B. 1997, Nucleosynthesis and Galactic Chemical Evolution (Cambridge University Press)
In the text
- Peterson, R. C. 1981, ApJ, 244, 989
In the text
NASA ADS
- Peterson, R. C., Kurucz, R. L., & Carney, B. W. 1990, ApJ, 350, 173
NASA ADS
- Portinari, L., & Chiosi, C. 1999, A&A, 350, 827
NASA ADS
- Portinari, L., Chiosi, C., & Bressan, A. 1998, A&A, 334, 505
In the text
NASA ADS
- Prantzos, N., & Aubert, O. 1995, A&A, 302, 69
In the text
NASA ADS
- Prantzos, N., & Silk, J. 1998, ApJ, 507, 229
In the text
NASA ADS
- Press, W. H., & Teukolsky, S. A. 1992, Comput. Phys., 6, 188
In the text
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipies in FORTRAN. The art of scientific computing (Cambridge University Press)
In the text
- Rana, N. C. 1991, ARA&A, 29, 129
In the text
NASA ADS
- Reid, I. N., & Gizis, J. 1997, AJ, 113, 2246
In the text
NASA ADS
- Reid, I. N., & Majewski, S. R. 1993, ApJ, 409, 635
In the text
NASA ADS
- Renzini, A., & Voli, M. 1981, A&A, 94, 175
In the text
NASA ADS
- Robin, A. C., Haywood, M., Creze, M., Ojha, D. K., & Bienayme, O. 1996, A&A, 305, 125
In the text
NASA ADS
- Rocha-Pinto, H. J., & Maciel, W. J. 1996, MNRAS, 279, 447
In the text
NASA ADS
- Rocha-Pinto, H. J., Maciel, W. J., Scalo, J., & Flynn, C. 2000, A&A, 358, 850
In the text
NASA ADS
- Romano, D., Matteucci, F., Salucci, P., & Chiappini, C. 2000, ApJ, 539, 235
In the text
NASA ADS
- Ryan, S. G., Norris, J. E., & Beers, T. C. 1996, ApJ, 471, 254
In the text
NASA ADS
- Ryder, S. D. 1995, ApJ, 444, 610
In the text
NASA ADS
- Sackett, P. 1997, ApJ, 483, 103
In the text
NASA ADS
- Salpeter, E. 1955, ApJ, 121, 161
In the text
NASA ADS
- Samland, M. 1998, ApJ, 496, 155
In the text
NASA ADS
- Samland, M., Hensler, G., & Theis, Ch. 1997, ApJ, 476, 544
In the text
NASA ADS
- Scalo, J. M. 1986, FCPhys, 11, 1
In the text
- Scalo, J. M. 1998, in The Stellar Initial Mass Function, ed. G. Gilmore & D.
Howell, ASP Conf. Ser., 142, 201
In the text
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
In the text
NASA ADS
- Schmidt, M. 1959, ApJ, 129, 243
In the text
NASA ADS
- Shigeyama, T., Nomoto, K., Yamahoka, H., & Thielemann, F.-K. 1992, ApJ, 386, L13
In the text
NASA ADS
- Sneden, C., & Crocker, D. A. 1988, ApJ, 335, 406
NASA ADS
- Sneden, C., Gratton, R. G., & Crocker, D. A. 1991, A&A, 246, 354
NASA ADS
- Sneden, C., Preston, G. W., McWilliam, A., & Searle, L. 1994, ApJ, 431, L27
In the text
NASA ADS
- Steinmetz, M., & Müller, E. 1994, A&A, 281, L97
In the text
NASA ADS
- Stephens, A. 1999, AJ, 117, 1771
In the text
NASA ADS
- Talbot, R. J., & Arnett, W. D. 1975, ApJ, 197, 551
In the text
NASA ADS
- Tamman, G., Loefler, W., & Schroder, A. 1994, ApJS, 92, 487
In the text
NASA ADS
- Thielemann, F.-K., Nomoto, K., & Hashimoto, M. 1993, in Origin and Evolution of the Elements, ed. N. Prantzos, E. Vangioni-Flam, & M. Cassé (Cambridge: Cambridge
Univ. Press), 297
In the text
- Thielemann, F.-K., Nomoto, K., & Hashimoto, M. 1996, ApJ, 460, 408
In the text
NASA ADS
- Thomas, D., Greggio, L., & Bender, R. 1998, MNRAS, 296, 119
In the text
NASA ADS
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 (TWW1995)
In the text
NASA ADS
- Tinsley, B. M. 1980, FCPh, 5, 287
In the text
NASA ADS
- Tomkin, J., Sneden, C., & Lambert, D. L. 1986, ApJ, 302, 415
In the text
NASA ADS
- Tosi, M. 1988, A&A, 197, 47
In the text
NASA ADS
- Twarog, B. A. 1980, ApJ, 242, 242
In the text
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305
In the text
NASA ADS
- Wakker, B. P., Howk, J. C., Savage, B. D., et al. Nature, 402,
388
In the text
- Wheeler, J. C., Sneden, C., & Truran, J. W. 1989, ARA&A, 27, 289
In the text
- Woosley, S. E., & Eastman, R. G. 1994, in Proc. Menorca Summer School on Supernovae, ed. E. Bravo, R. Canal, J. M. Ibañez, & J. Isern, 105
In the text
- Woosley, S. E., & Weaver, T. A. 1994, ApJ, 423, 371
In the text
NASA ADS
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 (WW1995)
In the text
NASA ADS
- Wyse, R. F. G, & Gilmore, G. 1995, AJ, 110, 2771
In the text
NASA ADS
- Zhao, G., & Magain, P. 1990, A&A, 238, 242
NASA ADS
Copyright ESO 2001
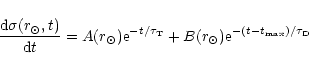
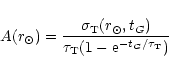
![\begin{displaymath}B(r_{\odot })=\frac{[\sigma (r_{\odot },t_{\rm G})-\sigma _{\...
...\tau _{\rm D}[1-{\rm e}^{-(t_{\rm G}-t_{\max})/\tau _{\rm D}}]}\end{displaymath}](/articles/aa/full/2001/18/aa10620/img22.gif)
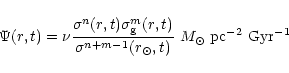
![\begin{displaymath}C\int ^{16}_{3}\Phi (M_{\rm B})\left[ \int ^{0.5}_{\mu _{m}}f...
... B}})\frac{Y_{i}}{M_{\rm B}}{\rm d}\mu \right] {\rm d}M_{\rm B}\end{displaymath}](/articles/aa/full/2001/18/aa10620/img50.gif)