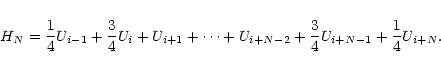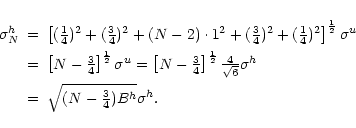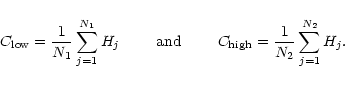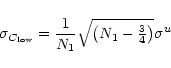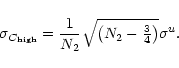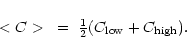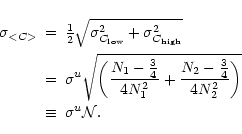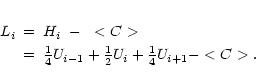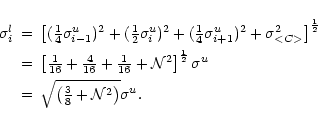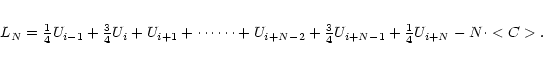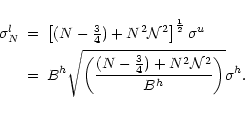Up: The Ursa Major cluster
This Appendix explains how the noise in a total HI map can be
calculated. A total HI map is usually constructed from a 3 dimensional
datacube containing a number of so called channelmaps. Each channelmap
shows an HI image of the galaxy at a certain velocity. A total HI map
is made by adding those channelmaps which contain the HI signal. Before
adding the channel maps the signal in each channelmap should be
isolated. When the signal is not isolated one merely adds noise to the
total HI map because the location of the signal in a channel map varies
with velocity due to the galactic rotation. The signals can be isolated
interactively by blotting away the surrounding noise or in a more
objective way by taking a certain contour level in the smoothed maps as a
mask. As a consequence of adding channel maps with isolated regions, the
noise in the total HI map is not constant but varies from pixel to
pixel. The noise at a certain pixel in the total HI map depends on the
number N of non-blank pixels at the same position in the individual
channel maps that were added.
In case the data cube was obtained with an uniform taper during the
observation, the noise
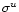 in two channelmaps will be
independent. The noise equivalent bandwidth Bu in a uniform
tapered spectrum is equal to the channel separation b. When adding Nuniform tapered channelmaps at a certain pixel the noise
in two channelmaps will be
independent. The noise equivalent bandwidth Bu in a uniform
tapered spectrum is equal to the channel separation b. When adding Nuniform tapered channelmaps at a certain pixel the noise
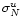 at the same pixel position in the total HI map will be
increased by a factor
at the same pixel position in the total HI map will be
increased by a factor 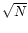 :
:
Usually, the observations are made using a hanning taper in which case the
noise in two adjacent channelmaps is no longer independent. A hanning
taper effectively smooths the data in velocity by convolving the velocity
profile at each pixel. If Ui is the pixel value in the ith
uniform tapered channel map, the value Hi in the ith hanning
tapered channelmap is given by
Since the
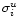 's are independent and all equal to
's are independent and all equal to
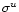 ,
the noise
,
the noise
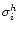 in the ith hanning tapered channelmap
can be calculated according to
in the ith hanning tapered channelmap
can be calculated according to
In this case the noise equivalent bandwidth Bh for a
hanning tapered spectrum is given by
As a consequence, the noise in two hanning tapered channelmaps may be
correlated depending on their separation. Two channelmaps separated by
one channelmap are correlated because both contain a quarter of the flux
from the channel map between them. Only channel maps separated by more
than one channel are independent. This will be shown in the following
three cases in which two hanning tapered channel maps at different
separations will be added.
- 1.
- Adding two adjacent hanning tapered channelmaps i and (i+1) gives
a signal
H(i)+(i+1) of
and the noise
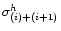 in that map will be
in that map will be
- 2.
- Adding the hanning tapered channels i and (i+2) gives
and the noise becomes
- 3.
- Adding the hanning tapered channels i and (i+3) gives
with a resulting noise of
So, channelmaps i and (i+3) are independent.
Because the noise is correlated, adding N adjacent
hanning tapered channelmaps does not give an increase of the noise with
a factor 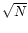 but with a factor
but with a factor
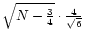 as is shown below. First the total signal HN is
calculated.
as is shown below. First the total signal HN is
calculated.
| Channel |
Ui-1 |
Ui |
Ui+1 |
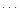 |
Ui+N-2 |
Ui+N-1 |
Ui+N |
|
| i |
1/4 |
1/2 |
1/4 |
|
|
|
|
|
| i+1 |
|
1/4 |
1/2 |
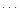 |
|
|
|
|
| i+2 |
|
|
1/4 |
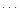 |
|
|
|
|
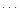 |
|
|
|
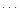 |
|
|
|
|
| i+N-3 |
|
|
|
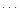 |
1/4 |
|
|
|
| i+N-2 |
|
|
|
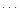 |
1/2 |
1/4 |
|
|
| i+N-1 |
|
|
|
|
1/4 |
1/2 |
1/4 |
+ |
| |
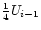 |
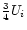 |
Ui+1 |
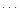 |
Ui+N-2 |
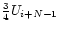 |
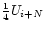 |
|
and thus
From this it follows that the noise
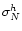 is given by
is given by
However, before the hanning tapered channelmaps are added to form a
total HI map, the continuum must be subtracted. This operation
introduces extra noise in the channelmaps which doesn't behave like a
hanning tapered correlation. Here, it will be assumed that the average
continuum map is formed by averaging N1 line free channels at the low
velocity end of the datacube and N2 channels at the high velocity end
which gives
Since all channels are hanning tapered the noise in these maps can be calculated according to
and
The average continuum map to be subtracted is then formed by
Since
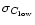 and
and
 are
independent it follows that the noise
are
independent it follows that the noise
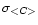 in the finally
averaged continuum map is given by
in the finally
averaged continuum map is given by
After subtraction of the continuum the channelmaps only
contain signal from the HI emission line. The signal in the channelmaps
containing the line emission is now given by
Because
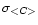 is independent from
is independent from
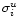 in
the velocity range which is not used to form the averaged continuum map,
it can be written
in
the velocity range which is not used to form the averaged continuum map,
it can be written
When adding N adjacent hanning tapered and continuum subtracted channelmaps containing the line
emission, the signal LN will be
The noise
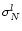 at each pixel in the final map can be derived
analogous to the calculation of
at each pixel in the final map can be derived
analogous to the calculation of
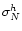 and is given by
and is given by


Up: The Ursa Major cluster
Copyright ESO 2001
![]() in two channelmaps will be
independent. The noise equivalent bandwidth Bu in a uniform
tapered spectrum is equal to the channel separation b. When adding Nuniform tapered channelmaps at a certain pixel the noise
in two channelmaps will be
independent. The noise equivalent bandwidth Bu in a uniform
tapered spectrum is equal to the channel separation b. When adding Nuniform tapered channelmaps at a certain pixel the noise
![]() at the same pixel position in the total HI map will be
increased by a factor
at the same pixel position in the total HI map will be
increased by a factor ![]() :
:
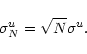
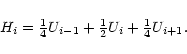
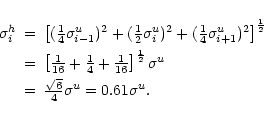
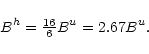
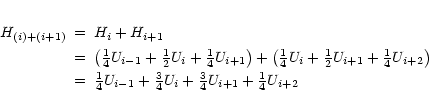
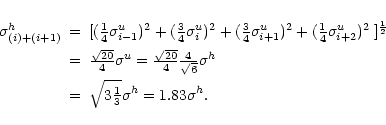
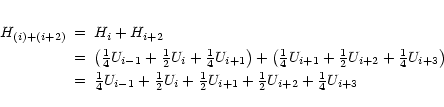
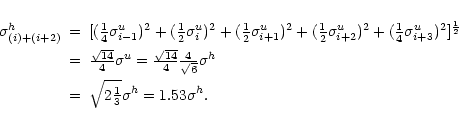
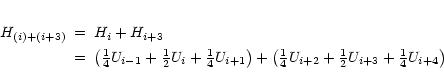
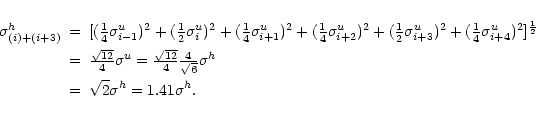
![]() but with a factor
but with a factor
![]() as is shown below. First the total signal HN is
calculated.
as is shown below. First the total signal HN is
calculated.