The Las Campanas Redshift Survey data are used to investigate structures ofthe galaxy number distribution. We construct two volume-limited samples with sizes of
A&A 370, 358-364 (2001)
DOI: 10.1051/0004-6361:20010249
T. Kurokawa1,2 - M. Morikawa1 - H. Mouri3
1 - Department of Physics, Ochanomizu University, 2-2-1 Otsuka,
Bunkyo, Tokyo 112-8610, Japan
2 -
Institute for Gender Studies, Ochanomizu University, 2-2-1 Otsuka,
Bunkyo, Tokyo 112-8610, Japan
3 -
Meteorological Research Institute, 1-1 Nagamine, Tsukuba 305-0052, Japan
Received 14 December 1999 / Accepted 23 November 2000
Abstract
The Las Campanas Redshift Survey data are used to investigate
structures ofthe galaxy number distribution. We construct two
volume-limited samples with sizes of
![]() and
and
![]() h-1 Mpc,
and calculate the second- to ninth-order moments with the count-in-cell
method. The galaxy distribution at
h-1 Mpc,
and calculate the second- to ninth-order moments with the count-in-cell
method. The galaxy distribution at ![]() 30 h-1 Mpc is found
to be statistically homogeneous. On the other hand, we find a multifractal
scaling at <30 h-1 Mpc. From the scaling exponent, we
obtain the generalized dimension, which decreases from 2 toward 1 as the
order is increased from 2 to 9. Galaxies are known to lie, around voids, in
planar structures with filamentary dense regions. The present result
indicates that these void-filament structures are predominant up to 30 h-1 Mpc. Statistically, they appear to be the largest-scale
significant structures in the Universe.
30 h-1 Mpc is found
to be statistically homogeneous. On the other hand, we find a multifractal
scaling at <30 h-1 Mpc. From the scaling exponent, we
obtain the generalized dimension, which decreases from 2 toward 1 as the
order is increased from 2 to 9. Galaxies are known to lie, around voids, in
planar structures with filamentary dense regions. The present result
indicates that these void-filament structures are predominant up to 30 h-1 Mpc. Statistically, they appear to be the largest-scale
significant structures in the Universe.
Key words: cosmology: observations - large-scale structure of Universe - methods: statistical
The galaxy number distribution at large scales (![]() 10 Mpc) is
expected to be homogeneous. For example, the X-ray background emission,
which originates in distant active galactic nuclei, is isotropic on the sky
(e.g. Peebles 1993). Recently, several deep redshift surveys were
carried out. The two-point correlation function and power spectrum based on
these data indicate that the galaxy distribution actually becomes
homogeneous at large scales (e.g. Wu et al. 1999; Martínez 1999). On
the other hand, at small scales, the distribution is not homogeneous.
Galaxies are distributed roughly on the walls of spherical voids, and show
various spatial patterns such as groups, clusters, filaments, and sheets
(e.g. Geller & Huchra 1989). At what scale are these structures
predominant? Is there any other structure greater in scale? To answer these
questions, we have to study the galaxy distribution in detail.
10 Mpc) is
expected to be homogeneous. For example, the X-ray background emission,
which originates in distant active galactic nuclei, is isotropic on the sky
(e.g. Peebles 1993). Recently, several deep redshift surveys were
carried out. The two-point correlation function and power spectrum based on
these data indicate that the galaxy distribution actually becomes
homogeneous at large scales (e.g. Wu et al. 1999; Martínez 1999). On
the other hand, at small scales, the distribution is not homogeneous.
Galaxies are distributed roughly on the walls of spherical voids, and show
various spatial patterns such as groups, clusters, filaments, and sheets
(e.g. Geller & Huchra 1989). At what scale are these structures
predominant? Is there any other structure greater in scale? To answer these
questions, we have to study the galaxy distribution in detail.
One promising approach to statistically describe the galaxy distribution is
a "multifractal'' analysis, which characterizes scaling properties of
moments at all the
orders (Parisi & Frisch 1985; Jensen et al. 1985; Halsey
et al. 1986; Sect. 3). The distribution is described more precisely
than by the standard tools such as the two-point correlation function and
power spectrum, which are based on the second-order moment alone. Kurokawa
et al. (1999) studied galaxy data obtained from the CfA2 survey
(Huchra et al. 1999), and found a multifractal scaling at ![]() 20
Mpc (see also, e.g., Domínguez-Tenreiro et al. 1994; Martínez &
Coles 1994). However, because of limitation of the volume size of the
CfA2 survey, Kurokawa et al. (1999) were unable to determine the
entire scaling range. Of great interest is an analysis of the scaling
property at >20 Mpc.
20
Mpc (see also, e.g., Domínguez-Tenreiro et al. 1994; Martínez &
Coles 1994). However, because of limitation of the volume size of the
CfA2 survey, Kurokawa et al. (1999) were unable to determine the
entire scaling range. Of great interest is an analysis of the scaling
property at >20 Mpc.
We analyze galaxy data of the Las Campanas Redshift Survey (LCRS).
This is the largest complete survey carried out so far and is expected to
reach the scale of homogeneity (Shectman et al. 1996, Sect. 2). The volume
size of the LCRS data is greater than those in the previous
multifractal analyses. Since, however, the LCRS consists of
two-dimensional slices, we newly define a multifractal analysis on a
two-dimensional section of the three-dimensional distribution (Sect. 3). We
demonstrate that the galaxy distribution exhibits a multifractal scaling at <30 Mpc and is homogeneous at ![]() 30 Mpc (Sect. 4). This
result is used to discuss the galaxy distribution as a function of scale (Sect. 5).
Finally we discuss potential problems of our approach and future prospects (Sect. 6).
30 Mpc (Sect. 4). This
result is used to discuss the galaxy distribution as a function of scale (Sect. 5).
Finally we discuss potential problems of our approach and future prospects (Sect. 6).
Throughout this paper, we use the Hubble constant H0 = 100 h kms-1Mpc-1 and the deceleration parameter q0 = 0.5. With these parameters, the distance to a galaxy is estimated from its recession velocity in the Local Group frame. We ignore the peculiar velocities of the individual galaxies. They are typically 300 km s-1(Davis & Peebles 1983), which corresponds to 3 h-1 Mpc. This scale is less than the scales of our interest (>5 h-1 Mpc), where we find a multifractal distribution.
The LCRS provides the largest galaxy sample which has been obtained
so far (Shectman et al. 1996). This survey consists of six thin strips on
the sky, each of which is
![]() in declination,
in declination,
![]() in
right ascension, and made of
in
right ascension, and made of
![]() beams. Thus,
the survey volumes are essentially two-dimensional slices. There are 26418 galaxies,
which were selected from photometry in the R-band. Their
average redshift is
beams. Thus,
the survey volumes are essentially two-dimensional slices. There are 26418 galaxies,
which were selected from photometry in the R-band. Their
average redshift is
![]() .
The most distant galaxy lies at
.
The most distant galaxy lies at
![]() .
.
When we analyze the LCRS data, we encounter two problems. First, the LCRS has both upper and lower magnitude limits. They vary from beam to beam. To avoid the effect of this variation, our samples are constructed by applying the narrowest magnitude range to all the beams. Second, in the individual beams, redshifts of some galaxies were not measured. This was due to mechanical constraints of the spectrometer. Since the observed galaxies were selected randomly in the beam, we assigned the inverse of the number fraction of the observed galaxies as a statistical weight to each of the beams.
We extracted volume-limited samples, where the luminosities of the galaxies
are above certain thresholds. The K-correction term was set to be K
![]() ,
which provides a good approximation to the R-band data
of LCRS galaxies (Lin et al. 1996a). We used the LCRS slices
,
which provides a good approximation to the R-band data
of LCRS galaxies (Lin et al. 1996a). We used the LCRS slices
![]() and
and
![]() .
The other slices do not generate
samples with sufficient numbers of galaxies. Our volume-limited samples
contain the largest numbers of galaxies among those with thickness of 4 h-1 Mpc. The sample from the slice
.
The other slices do not generate
samples with sufficient numbers of galaxies. Our volume-limited samples
contain the largest numbers of galaxies among those with thickness of 4 h-1 Mpc. The sample from the slice
![]() is
complete in
is
complete in
![]() and
and
![]() ,
contains 173 galaxies, and is
,
contains 173 galaxies, and is
![]() Mpc in size. Here mR and MR are the apparent and absolute magnitudes
in the R-band. The sample from the slice
Mpc in size. Here mR and MR are the apparent and absolute magnitudes
in the R-band. The sample from the slice
![]() is
complete in
is
complete in
![]() and
and
![]() ,
contains 291 galaxies, and is
,
contains 291 galaxies, and is
![]() Mpc in size. We underline that the volume sizes of these samples are
greater than those used in previous multifractal analyses.
Mpc in size. We underline that the volume sizes of these samples are
greater than those used in previous multifractal analyses.
In the thickness direction, we applied a Gaussian window function in order
to use the samples as two-dimensional cuts of the three-dimensional galaxy
distribution (e.g. Landy et al. 1996). The full widths at half maximum
of the window function are 0.6 and 0.5 h-1 Mpc, respectively,
in the samples for
![]() and
and
![]() .
These widths
are very small compared to the sample size,
.
These widths
are very small compared to the sample size, ![]() 100 h-1 Mpc, and have been determined so
as to reproduce most clearly the scaling properties
of artificial fractal samples with the same number of discrete points as
the LCRS data (Sect. 3).
100 h-1 Mpc, and have been determined so
as to reproduce most clearly the scaling properties
of artificial fractal samples with the same number of discrete points as
the LCRS data (Sect. 3).
We also studied the three-dimensional CfA2 sample (Huchra et al. 1999). Kurokawa et al. (1999) conducted a multifractal analysis of
volume-limited samples with
![]() and -20.00, which
contain 358 and 194 galaxies and are
and -20.00, which
contain 358 and 194 galaxies and are
![]() and
and
![]() Mpc in size. Their result for the
CfA2 galaxies is compared with ours for the LCRS galaxies
(Sect. 4). The LCRS and CfA2 observations were made in the
R- and B(0)-bands. A typical LCRS galaxy is fainter in the B(0)-band by 1.8 mag that it is in the R-band (Lin et al. 1996a). That is, galaxies in our LCRS samples are less luminous than those in the CfA2 samples. Nevertheless, the luminosity difference does not adversely affect our analysis, because there are no gross differences in the distribution of galaxies at different luminosities (Huchra et al. 1990; Park et al. 1994).
Mpc in size. Their result for the
CfA2 galaxies is compared with ours for the LCRS galaxies
(Sect. 4). The LCRS and CfA2 observations were made in the
R- and B(0)-bands. A typical LCRS galaxy is fainter in the B(0)-band by 1.8 mag that it is in the R-band (Lin et al. 1996a). That is, galaxies in our LCRS samples are less luminous than those in the CfA2 samples. Nevertheless, the luminosity difference does not adversely affect our analysis, because there are no gross differences in the distribution of galaxies at different luminosities (Huchra et al. 1990; Park et al. 1994).
The formal definition of multifractal is not applicable to discrete sets. Hence, for analyses of the galaxy distribution, several different techniques have been proposed. They are reviewed and compared to each other in Ueda (1995). We employ the "count-in-cell'' method, which appears to be more straightforward than other methods. Since the LCRS samples are two-dimensional (Sect. 2), the present method is to infer a multifractal distribution in three-dimensional space from the distribution on a two-dimensional section.
Suppose that there are N galaxies on a square of size L. This square is
divided into cells of size r. The qth moment
![]() at the
scale r is defined as
at the
scale r is defined as
We plot
![]() against
against ![]() .
If the local slope is
nearly constant over some range, there is said to be a scaling for that range:
.
If the local slope is
nearly constant over some range, there is said to be a scaling for that range:
| |
Figure 1:
The fifth-order moments
|
To justify our approach, we analyzed artificial monofractal samples, i.e.,
"Lévy flight'' sets with
Df = 1.5 and 2.0 (e.g. Mandelbrot 1982). The number of the points and the shape of the volume are the same as
those of our LCRS sample for
![]() .
We applied the
same Gaussian window as the LCRS sample, and calculated the moments
.
We applied the
same Gaussian window as the LCRS sample, and calculated the moments
![]() .
The average and standard deviation over 100 such samples
are shown in Fig. 1. The moments
.
The average and standard deviation over 100 such samples
are shown in Fig. 1. The moments
![]() follow the dotted lines,
which represent the relation (2) with
Dq(2) = Df -1. The
same result is obtained if the point number, volume shape, and Gaussian
window are the same as our LCRS sample for
follow the dotted lines,
which represent the relation (2) with
Dq(2) = Df -1. The
same result is obtained if the point number, volume shape, and Gaussian
window are the same as our LCRS sample for ![]() =
=
![]() .
Since the generalized dimensions
.
Since the generalized dimensions
![]() were obtained in previous three-dimensional analyses of the galaxy distribution (e.g. Kurokawa et al. 1999), our method is expected to work well in the following
analysis of the LCRS data.
were obtained in previous three-dimensional analyses of the galaxy distribution (e.g. Kurokawa et al. 1999), our method is expected to work well in the following
analysis of the LCRS data.
However, in Fig. 1, the moments
![]() at
at
![]() tend to
lie above the dotted lines. They suffer from the finiteness of the point
number. When the scale is very small and the number of cells is very
large, every cell contains a single point at most. Even if the scale
becomes smaller, the number of filled cells remains constant. The
moments at these scales are simply proportional to the value N1-q.
This effect is less significant in the sample with
Df = 1.5. The reason
is that a fractal structure has local clusters of points. The effective
mean distance among the points is smaller in a fractal set with a smaller
Df value (Kurokawa et al. 1999).
tend to
lie above the dotted lines. They suffer from the finiteness of the point
number. When the scale is very small and the number of cells is very
large, every cell contains a single point at most. Even if the scale
becomes smaller, the number of filled cells remains constant. The
moments at these scales are simply proportional to the value N1-q.
This effect is less significant in the sample with
Df = 1.5. The reason
is that a fractal structure has local clusters of points. The effective
mean distance among the points is smaller in a fractal set with a smaller
Df value (Kurokawa et al. 1999).
The moments
![]() of the two LCRS samples for
of the two LCRS samples for ![]() =
=
![]() and
and
![]() are computed with q = 2-9 and
r/L =
1/64-1/2. The results for
are computed with q = 2-9 and
r/L =
1/64-1/2. The results for
![]() with q = 2, 5, and 9
are shown in Fig. 2 (filled squares). The scale r in units of h-1 Mpc
is indicated on the upper axes. The vertical bars on the
moments represent the 1
with q = 2, 5, and 9
are shown in Fig. 2 (filled squares). The scale r in units of h-1 Mpc
is indicated on the upper axes. The vertical bars on the
moments represent the 1![]() statistical errors evaluated with the
"bootstrap resampling'' method (Efron 1982; Barrow et al. 1984).
statistical errors evaluated with the
"bootstrap resampling'' method (Efron 1982; Barrow et al. 1984).
Two scaling ranges are evident in Fig. 2. The transition from the one range
to the other occurs within the scale interval of our analysis, which is
roughly 0.5 in logarithms. The moments at ![]() 28 h-1 Mpc lie
on the dotted line, which represents the relation expected for a
homogeneous distribution. The moments at <28 h-1 Mpc
exhibit another scaling. We apply the least-squares fit to the moments at
the scales 7, 9, 14, and 19 h-1 Mpc (
r/L = 1/16, 1/12, 1/8,
and 1/6). The results are shown by solid lines. Below the scale 5 h-1 Mpc,
the moments do not follow the scaling relation. They suffer
from the finiteness of the galaxy number (Sect. 3). The same results have
been obtained for the other moments which are not shown in Fig. 2. We have
also found a homogeneous distribution at r
28 h-1 Mpc lie
on the dotted line, which represents the relation expected for a
homogeneous distribution. The moments at <28 h-1 Mpc
exhibit another scaling. We apply the least-squares fit to the moments at
the scales 7, 9, 14, and 19 h-1 Mpc (
r/L = 1/16, 1/12, 1/8,
and 1/6). The results are shown by solid lines. Below the scale 5 h-1 Mpc,
the moments do not follow the scaling relation. They suffer
from the finiteness of the galaxy number (Sect. 3). The same results have
been obtained for the other moments which are not shown in Fig. 2. We have
also found a homogeneous distribution at r ![]() 32 h-1 and another
scaling relation at
5 < r < 32 h-1 Mpc in the
LCRS sample for
32 h-1 and another
scaling relation at
5 < r < 32 h-1 Mpc in the
LCRS sample for
![]() .
.
The generalized dimensions Dq(2) for the moments at r< 28-32 h-1 Mpc are derived from their scaling exponents, i.e., the
slopes of the solid lines in Fig. 2. The values of
Dq(3) = Dq(2)
+ 1 for
![]() (filled squares) and
(filled squares) and
![]() (filled circles) are plotted as a function of q in Fig. 3.
We also show the generalized dimensions Dq(3) of the CfA2
samples by open circles and squares (Kurokawa et al. 1999). The vertical bars on the data points represent the 1
(filled circles) are plotted as a function of q in Fig. 3.
We also show the generalized dimensions Dq(3) of the CfA2
samples by open circles and squares (Kurokawa et al. 1999). The vertical bars on the data points represent the 1![]() uncertainties associated
with the least-squares fit, which incorporate the statistical errors of the
individual moments. Within the 1
uncertainties associated
with the least-squares fit, which incorporate the statistical errors of the
individual moments. Within the 1![]() uncertainties, the results for the
four samples are consistent with each other. The Dq(3) value
decreases as q increases. Therefore, over the scale and order ranges
considered here, the distribution of the LCRS galaxies satisfies
the requirement for multifractal scaling.
uncertainties, the results for the
four samples are consistent with each other. The Dq(3) value
decreases as q increases. Therefore, over the scale and order ranges
considered here, the distribution of the LCRS galaxies satisfies
the requirement for multifractal scaling.
We have presented only the galaxy moments
![]() with
with ![]() .
The statistical errors of the higher-order moments are quite large. With an
increase of q above 10, the generalized dimension
Dq(3) =
Dq(2)+1 seems to converge to
.
The statistical errors of the higher-order moments are quite large. With an
increase of q above 10, the generalized dimension
Dq(3) =
Dq(2)+1 seems to converge to
![]() in both
the samples for
in both
the samples for
![]() and
and
![]() .
Their scaling
ranges seem to be the same as those for
.
Their scaling
ranges seem to be the same as those for ![]() .
This result is again
consistent with that for the CfA2 data, which exhibit
.
This result is again
consistent with that for the CfA2 data, which exhibit
![]() (Kurokawa et al. 1999).
(Kurokawa et al. 1999).
In summary, we have found a multifractal distribution at <30 h-1 Mpc and a homogeneous distribution at ![]() 30 h-1 Mpc. This result has been
obtained from both the LCRS samples for
30 h-1 Mpc. This result has been
obtained from both the LCRS samples for
![]() and
and
![]() ,
agrees with the result for the
CfA2 samples, and hence is expected to be general
,
agrees with the result for the
CfA2 samples, and hence is expected to be general![]() .
Hereafter we separately discuss the multifractal and homogeneous distributions.
.
Hereafter we separately discuss the multifractal and homogeneous distributions.
By using the two-point correlation function ![]() ,
power spectrum
p(k), or other multifractal techniques, it is possible to estimate the
D2(3) value (e.g. Guzzo et al. 1991;
Martínez & Coles 1994):
,
power spectrum
p(k), or other multifractal techniques, it is possible to estimate the
D2(3) value (e.g. Guzzo et al. 1991;
Martínez & Coles 1994):
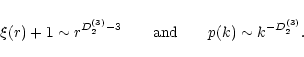 |
(3) |
With increasing the order q, the Dq(3) value decreases from 2.0 to 1.5 (Fig. 3). This decrease might be considered small, but it is
significant. Since the higher-order moments give more weight to the dense
regions, those Dq(3) values are obtained if there are filament-like
dense regions within sheet-like structures.
The former has Dq(3)![]() 1 while the latter has Dq(3)
1 while the latter has Dq(3) ![]() 2. Galaxies are known
to lie roughly on the walls of spherical voids (e.g. Geller & Huchra
1989). From the topology of isodensity contours of CfA2 galaxies, Vogeley et al. (1994) found that their distribution forms "walls with holes'' or a "filamentary net''. Kurokawa et al. (1999)
interpreted the multifractal distribution of the CfA2 data as originating in these
void-filament structures. If this interpretation is correct, the present
result indicates that the void-filament structures are important up to 30
h-1 Mpc. The typical size of voids is actually known to be
about 30 h-1 Mpc (e.g. Peebles 1993).
2. Galaxies are known
to lie roughly on the walls of spherical voids (e.g. Geller & Huchra
1989). From the topology of isodensity contours of CfA2 galaxies, Vogeley et al. (1994) found that their distribution forms "walls with holes'' or a "filamentary net''. Kurokawa et al. (1999)
interpreted the multifractal distribution of the CfA2 data as originating in these
void-filament structures. If this interpretation is correct, the present
result indicates that the void-filament structures are important up to 30
h-1 Mpc. The typical size of voids is actually known to be
about 30 h-1 Mpc (e.g. Peebles 1993).
The above structures can be generated via gravitational instability from primordial random fluctuations (e.g. Jenkins et al. 1998). With N-body simulations of cold dark matter models, Doroshkevich et al. (1999) showed richness of sheet-like structures with sizes of 20-30 h-1 Mpc. To discriminate between different cosmological models, a comparison of the observed scaling with those of model predictions would be useful.
The observed multifractal scaling is unlikely to extend to the smaller
scales (![]()
![]() Mpc). The value
Mpc). The value
![]() estimated for
estimated for
![]() h-1 Mpc is different from the
value D2(3)
h-1 Mpc is different from the
value D2(3) ![]() 1.2 obtained by Guzzo et al. (1991) for
1.2 obtained by Guzzo et al. (1991) for ![]() h-1 Mpc (Table 1). These small scales correspond to a typical size of galaxy clusters. They are virialized systems, which originate in processes different to those for the void-filament structures. It is therefore natural to expect different scaling laws between scales above and below
h-1 Mpc (Table 1). These small scales correspond to a typical size of galaxy clusters. They are virialized systems, which originate in processes different to those for the void-filament structures. It is therefore natural to expect different scaling laws between scales above and below ![]() 3.5 h-1 Mpc.
3.5 h-1 Mpc.
We have found Dq(3) ![]() 3 at
3 at ![]() 30 h-1 Mpc. This result is consistent with those in Table 1. Thus, we conclude that the galaxy distribution at
30 h-1 Mpc. This result is consistent with those in Table 1. Thus, we conclude that the galaxy distribution at ![]() 30 h-1 Mpc is homogeneous (e.g. Wu et al. 1999). The void-filament structures in
Sect. 5.1 are the largest-scale spatial structure of the galaxy distribution. Here it should be noted that this
conclusion is statistical. The largest void size in the CfA sample is
30 h-1 Mpc is homogeneous (e.g. Wu et al. 1999). The void-filament structures in
Sect. 5.1 are the largest-scale spatial structure of the galaxy distribution. Here it should be noted that this
conclusion is statistical. The largest void size in the CfA sample is
![]() 50 h-1 Mpc. The CfA sample also contains sheet-like
structures such as the Great Wall and the Perseus-Pisces Supercluster, which
are greater than 100 h-1 Mpc in size (e.g. Geller & Huchra
1989). Such large-scale structures exist in our LCRS samples (Landy et al. 1996). However, the large-scale structures seem to be exceptional or of low amplitude and hence statistically unimportant in the present analyses. The LCRS
data yield
50 h-1 Mpc. The CfA sample also contains sheet-like
structures such as the Great Wall and the Perseus-Pisces Supercluster, which
are greater than 100 h-1 Mpc in size (e.g. Geller & Huchra
1989). Such large-scale structures exist in our LCRS samples (Landy et al. 1996). However, the large-scale structures seem to be exceptional or of low amplitude and hence statistically unimportant in the present analyses. The LCRS
data yield ![]()
![]() 0 at r
0 at r ![]() 30-250 h-1
Mpc (Tucker et al. 1997; see also Martínez 1999).
Kurokawa et al. (1999) studied CfA2 samples containing
and not containing the Perseus-Pisces Supercluster, and found no significant diference
in the multifractal statistics.
30-250 h-1
Mpc (Tucker et al. 1997; see also Martínez 1999).
Kurokawa et al. (1999) studied CfA2 samples containing
and not containing the Perseus-Pisces Supercluster, and found no significant diference
in the multifractal statistics.
Sylos-Labini et al. (1998) claimed that the galaxy distribution has
D2(3) ![]() 2 up to 500
2 up to 500 ![]() Mpc. They ignored
the
K-correction. Scaramella et al. (1998) re-analyzed the same sample
with the K-correction, and found a cross-over to homogeneity at several tens of
h-1 Mpc. When the K-correction is ignored, high-redshift
galaxies are estimated to be less luminous. Their number density is
underestimated in a volume-limited sample with a certain luminosity
threshold. Even if the galaxy distribution is homogeneous, the neglect of
the K-correction introduces a spurious structure in the redshift
direction. To obtain the D2(3) value, both Sylos-Labini et al. (1998) and Scaramella et al. (1998) used the number of galaxies within the distance d: N(<d)
Mpc. They ignored
the
K-correction. Scaramella et al. (1998) re-analyzed the same sample
with the K-correction, and found a cross-over to homogeneity at several tens of
h-1 Mpc. When the K-correction is ignored, high-redshift
galaxies are estimated to be less luminous. Their number density is
underestimated in a volume-limited sample with a certain luminosity
threshold. Even if the galaxy distribution is homogeneous, the neglect of
the K-correction introduces a spurious structure in the redshift
direction. To obtain the D2(3) value, both Sylos-Labini et al. (1998) and Scaramella et al. (1998) used the number of galaxies within the distance d: N(<d) ![]() d3-D2(3). This quantity depends directly on the galaxy distribution in the redshift direction, and hence is sensitive to the K-correction (Joyce et al. 1999).
d3-D2(3). This quantity depends directly on the galaxy distribution in the redshift direction, and hence is sensitive to the K-correction (Joyce et al. 1999).
We, on the other hand, have divided a volume-limited sample into square
cells, and investigated the number of galaxies in those cells. That is, we
have studied the galaxy distribution not only in the redshift direction but
also in the perpendicular direction. We expect that our analysis depends
only weakly on the K-correction. To demonstrate this, we analyzed the
LCRS data for ![]() =
=
![]() with different K-correction
terms. From spectral energy distributions of nearby galaxies, Fukugita et
al. (1995) obtained relations between z and the K-correction as a function of morphological type. For spiral to elliptical galaxies, the
K-correction term in the R-band is (1.3-5.0)
with different K-correction
terms. From spectral energy distributions of nearby galaxies, Fukugita et
al. (1995) obtained relations between z and the K-correction as a function of morphological type. For spiral to elliptical galaxies, the
K-correction term in the R-band is (1.3-5.0) ![]()
![]() .
We
changed the K-correction term in this range, and calculated the moments
.
We
changed the K-correction term in this range, and calculated the moments
![]() .
The results are shown in Fig. 4 (filled and open diamonds).
They are consistent with reference lines, which are the same as in Fig. 2,
at least in the multifractal and homogeneous regimes (r > 5 h-1 Mpc).
.
The results are shown in Fig. 4 (filled and open diamonds).
They are consistent with reference lines, which are the same as in Fig. 2,
at least in the multifractal and homogeneous regimes (r > 5 h-1 Mpc).
| sample | D2(3) | scale rangea | methodb | reference |
| h-1 Mpc | ||||
| Perseus-Pisces |
|
|
1 | |
| CfA1 |
|
|
2 | |
| Perseus-Pisces |
|
|
1 | |
| CfA1 |
|
|
3 | |
| CfA1 |
|
multifractalc | 4 | |
| CfA2 (
|
|
|
multifractald | 5 |
| CfA2 (
|
|
|
multifractald | 5 |
| IRAS QDOT | 2.25 |
|
multifractalc | 6 |
| LCRS | 5 < r < 30 | p(k) | 7 | |
| LCRS |
|
8 | ||
| LCRS ( |
|
(5) < r < 28 | multifractald | 9 |
| LCRS ( |
|
(5) < r < 32 | multifractald | 9 |
| Perseus-Pisces | 25-
|
1 | ||
| CfA1 | 20-
|
multifractalc | 4 | |
| IRAS QDOT | 2.77 |
|
multifractalc | 6 |
| LCRS ( |
|
multifractald | 9 | |
| LCRS ( |
|
multifractald | 9 | |
| Abell Clusters |
|
|
N(<d) | 10 |
| ESO Slice Project |
|
|
N(<d) | 10 |
Notes. (a) the value in parentheses is the analysis limit,
which is determined by the volume or galaxy number of the sample; (b)
![]() is the two-point correlation function, n is the mean number
density, p(k) is the power spectrum, and N(<d) is the number of
galaxies within the distance d; (c) the density reconstruction method;
(d) the count-in-cell method.
is the two-point correlation function, n is the mean number
density, p(k) is the power spectrum, and N(<d) is the number of
galaxies within the distance d; (c) the density reconstruction method;
(d) the count-in-cell method.
References. (1) Guzzo et al. 1991; (2) Davis & Peebles
1983; (3) Lemson & Sanders 1991; (4) Domínguez-Tenreiro
et al. 1994; (5) Kurokawa et al. 1999; (6) Martínez &
Coles 1994; (7) Lin et al. 1996b; (8) Amendola & Palladino
1999; (9) this work; (10) Scaramella et al. 1998.
The scaling property of the galaxy number density has been explored through
a multifractal analysis of the LCRS data. Since the LCRS is
the largest complete survey carried out so far, our analysis is statistically more significant than the previous multifractal analyses. From the
survey slices
![]() and
and
![]() ,
we have
constructed two volume-limited samples. The former is complete in -21.4
,
we have
constructed two volume-limited samples. The former is complete in -21.4![]() MR
MR ![]() -20.3, contains 173 galaxies, and is 113
-20.3, contains 173 galaxies, and is 113 ![]() 113
h-1 Mpc in size. The latter is complete in -21.7
113
h-1 Mpc in size. The latter is complete in -21.7 ![]() MR
MR![]() -20.6, contains 291 galaxies, and is 126
-20.6, contains 291 galaxies, and is 126 ![]() 126 h-1 Mpc in size. The count-in-cell method on a two-dimensional section
has been employed. At
126 h-1 Mpc in size. The count-in-cell method on a two-dimensional section
has been employed. At ![]() 30 h-1 Mpc, the moments
30 h-1 Mpc, the moments
![]() follow the scaling expected for a homogeneous
distribution. On the other hand, from 5 to 30 h-1 Mpc, we have
found a multifractal scaling. The measured generalized dimensions
Dq(3) =
Dq(2)+1 are consistent with those for the
three-dimensional CfA2 galaxy samples. The results for
D2(3) are also consistent with those obtained so far from various galaxy catalogues with
follow the scaling expected for a homogeneous
distribution. On the other hand, from 5 to 30 h-1 Mpc, we have
found a multifractal scaling. The measured generalized dimensions
Dq(3) =
Dq(2)+1 are consistent with those for the
three-dimensional CfA2 galaxy samples. The results for
D2(3) are also consistent with those obtained so far from various galaxy catalogues with ![]() and p(k).
and p(k).
| |
Figure 3:
The fifth-order moments
|
These results are interpreted as follows. The galaxy distribution at ![]() 30 h-1 Mpc
is homogeneous. From 5 to 30 h-1 Mpc,
void-filament structures are predominant. Statistically, they are the
largest-scale spatial structures of galaxy distribution. The
multifractal scaling is unlikely to extend to small scales (
30 h-1 Mpc
is homogeneous. From 5 to 30 h-1 Mpc,
void-filament structures are predominant. Statistically, they are the
largest-scale spatial structures of galaxy distribution. The
multifractal scaling is unlikely to extend to small scales (![]() 5 h-1 Mpc), where the structures are expected to be virialized.
5 h-1 Mpc), where the structures are expected to be virialized.
Since the LCRS samples are two-dimensional, we have been unable to apply a three-dimensional analysis. The galaxy distribution in three-dimensional space has been inferred from the distribution in two-dimensional sections. However, the relation Dq(3) =
Dq(2)+1 is not applicable to all cases, although this relation is valid for Lévy flight sets that have nearly the same distribution as the galaxies. Moreover, there are structures much larger than 30 h-1 Mpc in size. Our two-dimensional LCRS samples might have missed such structures by chance, or our multifractal method might be unable to detect them. For example, the two-dimensional power spectrum of the LCRS data exhibits a strong peak at ![]() 100 h-1 Mpc (Landy et al. 1996). We have ascertained that the present results for the two-dimensional LCRS data are consistent with previous analyses for the three-dimensional data (e.g. the CfA2 sample; Kurokawa et al. 1999), but it is important to confirm our results by analyzing a three-dimensional galaxy sample that is as deep as the present LCRS samples with various statistical methods. We hope that on-going redshift surveys such as the Sloan Digital Sky Survey will soon provide such galaxy data.
100 h-1 Mpc (Landy et al. 1996). We have ascertained that the present results for the two-dimensional LCRS data are consistent with previous analyses for the three-dimensional data (e.g. the CfA2 sample; Kurokawa et al. 1999), but it is important to confirm our results by analyzing a three-dimensional galaxy sample that is as deep as the present LCRS samples with various statistical methods. We hope that on-going redshift surveys such as the Sloan Digital Sky Survey will soon provide such galaxy data.
Acknowledgements
This paper is in part the result of research of T. Kurokawa toward fulfillment of the requirements of the Ph. D. degree at the Ochanomizu University. T. Kurokawa thanks O. Iguchi, I. Joichi, M. Obara, T. Okamura, Y. Sota, E. Takayama, and A. Yoshisato for interesting discussion. We also thank M. Lachièze-Ray for useful comments.