NGC 4449 is an active star-forming dwarf galaxy of Magellanic type. From radio observations, van Woerden et al. (1975) found an extended HI-halo around NGC 4449 which is at least a factor of 10 larger than the optical diameter
A&A 370, 365-383 (2001)
DOI: 10.1051/0004-6361:20010198
Ch. Theis1 - S. Kohle2,3
1 -
Institut für Theoretische Physik und Astrophysik der
Universität Kiel, Olshausenstr. 40, 24098 Kiel, Germany
2 -
Radioastronomisches Institut der Universität Bonn, Auf dem Hügel 71,
53121 Bonn, Germany
3 -
Center for Medical Diagnostic Systems and Visualization MeVis GmbH at University
of Bremen,
Universitätsallee 29, 28359 Bremen, Germany
Received 9 July 1999 / Accepted 3 January 2001
Abstract
NGC 4449 is an active star-forming dwarf galaxy of Magellanic type.
From radio observations, van Woerden et al. (1975)
found an extended
HI-halo around NGC 4449 which is at least a factor of 10 larger than the
optical diameter
![]() kpc. Recently,
Hunter et al. (1998) discerned details
in the HI-halo: a disc-like feature around the center of NGC 4449 and
a lopsided arm structure.
We combined several N-body methods in order to investigate
the interaction scenario between NGC 4449 and DDO 125, a close companion
in projected space.
In a first step fast restricted N-body models are used
to confine a region in parameter space reproducing the main
observational features. In a second step a genetic algorithm
is applied for a uniqueness test of our preferred parameter set.
We show that our genetic algorithm reliably recovers
orbital parameters, provided that the data are sufficiently
accurate, i.e. all the key features are included.
In the third step the results of the restricted N-body models
are compared with self-consistent N-body simulations.
In the case of NGC 4449, the applicability of the simple
restricted N-body calculations is demonstrated. Additionally,
it is shown that the HI gas can be modeled here by a purely stellar
dynamical approach.
In a series of simulations, we demonstrate
that the observed features of the extended HI disc can be explained
by a gravitational interaction
between NGC 4449 and DDO 125. According to
these calculations the closest approach between both galaxies
happened
kpc. Recently,
Hunter et al. (1998) discerned details
in the HI-halo: a disc-like feature around the center of NGC 4449 and
a lopsided arm structure.
We combined several N-body methods in order to investigate
the interaction scenario between NGC 4449 and DDO 125, a close companion
in projected space.
In a first step fast restricted N-body models are used
to confine a region in parameter space reproducing the main
observational features. In a second step a genetic algorithm
is applied for a uniqueness test of our preferred parameter set.
We show that our genetic algorithm reliably recovers
orbital parameters, provided that the data are sufficiently
accurate, i.e. all the key features are included.
In the third step the results of the restricted N-body models
are compared with self-consistent N-body simulations.
In the case of NGC 4449, the applicability of the simple
restricted N-body calculations is demonstrated. Additionally,
it is shown that the HI gas can be modeled here by a purely stellar
dynamical approach.
In a series of simulations, we demonstrate
that the observed features of the extended HI disc can be explained
by a gravitational interaction
between NGC 4449 and DDO 125. According to
these calculations the closest approach between both galaxies
happened ![]() 4-6 108 yr ago at a minimum distance of
4-6 108 yr ago at a minimum distance of ![]() 25 kpc on a parabolic or slightly elliptic orbit.
In the case of an encounter scenario,
the dynamical mass of DDO 125 should not be smaller than 10% of NGC 4449's
mass. Before the encounter, the observed HI gas
was arranged in a disc with a radius of
35-40 kpc around the center of NGC 4449. It had the same
orientation as the central ellipsoidal HI structure.
The origin of this disc is still unclear, but it might have been caused by a
previous interaction.
25 kpc on a parabolic or slightly elliptic orbit.
In the case of an encounter scenario,
the dynamical mass of DDO 125 should not be smaller than 10% of NGC 4449's
mass. Before the encounter, the observed HI gas
was arranged in a disc with a radius of
35-40 kpc around the center of NGC 4449. It had the same
orientation as the central ellipsoidal HI structure.
The origin of this disc is still unclear, but it might have been caused by a
previous interaction.
Key words: galaxies: interactions - galaxies: kinematics and dynamics - individual: NGC 4449, DDO 125 - methods: N-body simulations - methods: data analysis
During the last decades the classical picture of galaxies being Weltinseln (e.g. Kant 1755; von Humboldt 1850), i.e. island universes, has completely changed. In the 1920s, galaxies were thought to be in general islands, i.e. isolated stellar systems, with just a few obvious exceptions like the M 51 system. Systems not fitting the Hubble classification have been neglected - by definition - as peculiar. Interest in these systems has increased strongly since the new catalogues by Vorontsov-Velyaminov (1959) and Arp (1966) became available. They demonstrated that even peculiar objects have common features like bridges, tails, or rings. Better observational instruments allowing for deeper images and new wavelength ranges have revealed more complex structures. Galaxies formerly classified as non-interacting may have had some gravitational interaction in the past which is still reflected in e.g. warps, flares, or thick discs. Especially useful are HI observations which can cover a much larger radial extension than the optical images. Therefore, HI is a very good tracer for tidal interactions.
The theoretical understanding of interacting galaxies suffered for a long time from the lack of computational power allowing for a numerical solution of the gravitational N-body problem. After a remarkable treatment by Holmberg (1941) who built an analogue computer (consisting of light bulbs and photo cells) to determine the gravitational force, it took 20 years until N-body simulations were performed on a general purpose computer (Pfleiderer & Siedentopf 1961): the basic idea of these restricted N-body simulations is the assumption that the potential of interacting galaxies can be adequately modeled by two particles which represent the galactic masses and move under their mutual gravitation, i.e. on Keplerian orbits. With these assumptions all the other particles are just test particles, and the complete N-body problem is reduced to N single body problems for a time-dependent potential. In a remarkable series of simulations Toomre & Toomre (1972) applied this technique to determine the parameters of some well-studied interacting systems like Arp 295, M 51 + NGC 5195, or NGC 4038/39.
New N-body techniques have been developed which increased the accessible
particle number by many orders of magnitude. E.g. the TREE-method (Barnes & Hut 1986;
Hernquist 1987, 1990)
in which the organization of the force calculation - the most time-consuming part
of N-body calculations - adapts to clumpy mass distributions for a moderate
computational price (![]() O
O
![]() )
compared to direct simulations
(
)
compared to direct simulations
(![]() O(N2)). By this, Barnes (1988)
was able to simulate encounters
of disc galaxies including all dynamical components, i.e. the disc,
the bulge, and the halo as N-body systems.
Compared to faster grid-based methods (e.g. Sellwood 1980)
or expansion methods (e.g. Hernquist & Ostriker 1992)
direct N-body
simulations (or semi-direct methods like TREEs) are more flexible
with respect to strongly varying geometries and scalelengths.
An alternative to these techniques are special-purpose computers
(such as the machines of the GRAPE project,
Sugimoto et al. 1990). They implemented Newton's law of gravity
(modified for gravitational softening) in the hardware which allows for
a very fast direct determination of the gravitational forces (however,
there still exists the N2 bottleneck). E.g. for simulations with
N=105 particles a GRAPE3af (with 8 GRAPE processors) is
competitive with a TREE-code running on a CRAY T90.
O(N2)). By this, Barnes (1988)
was able to simulate encounters
of disc galaxies including all dynamical components, i.e. the disc,
the bulge, and the halo as N-body systems.
Compared to faster grid-based methods (e.g. Sellwood 1980)
or expansion methods (e.g. Hernquist & Ostriker 1992)
direct N-body
simulations (or semi-direct methods like TREEs) are more flexible
with respect to strongly varying geometries and scalelengths.
An alternative to these techniques are special-purpose computers
(such as the machines of the GRAPE project,
Sugimoto et al. 1990). They implemented Newton's law of gravity
(modified for gravitational softening) in the hardware which allows for
a very fast direct determination of the gravitational forces (however,
there still exists the N2 bottleneck). E.g. for simulations with
N=105 particles a GRAPE3af (with 8 GRAPE processors) is
competitive with a TREE-code running on a CRAY T90.
Two main methods (based on particles) to treat a dissipative, star-forming gas have been applied: the smoothed particle hydrodynamics scheme (SPH) solves the gasdynamical equations, by this emphasizing the diffuse nature of the interstellar medium (ISM) (e.g. Hernquist & Katz 1989). An alternative approach focuses on the clumpiness of the ISM treated as sticky particles: without physical collisions or close encounters of clouds they move in ballistic orbits like stars. However, in the case of a collision the clouds might merge or lose kinetic energy depending on the adopted microphysics (e.g. Casoli & Combes 1982; Palous et al. 1993; Theis & Hensler 1993).
Relatively few papers exist modeling special objects. This deficiency is the result of two factors: first high resolution data in configuration and velocity space are required, covering a large fraction of the space between the interacting galaxies. In principle, HI would be suitable, however, there are just a few observational sites which give data of sufficient quality.
The second problem is the large parameter space for a galactic interaction resulting in two connected difficulties: finding a good fit and determining its uniqueness (or other acceptable parameter sets). Observationally, only three kinematical quantities - the projected position on the sky and the line-of-sight velocity - can be measured. Another parameter, the galactic mass, depends on the availability of velocity data, the determination of the distance, and the reliability of the conversion from velocity to masses. Neglecting the center-of-mass data of the interacting system these 14 parameters reduce to 7 parameters containing the relative positions and velocities. These 7 values just fix the orbit in the case of a two-body interaction. Moreover, one has to specify the parameters that characterize both stellar systems, e.g. characteristic scales, orientation, or rotation. The final result is a high-dimensional parameter space which is in general too large for a standard search method. For instance, the interaction of a galactic disc with a point-mass galaxy is described at least by 7 parameters. A regular grid with a poor coverage of 10 grid points per dimension demands 107 models or 3400 years GRAPE simulation time (assuming 3 CPU-hours for a single simulation) or still about a year with a restricted N-body program (assuming 3 CPU-seconds per simulation).
An alternative approach to investigate large
parameter spaces is a genetic algorithm (Holland 1975;
Goldberg 1989). This applies an evolutionary mechanism
on a population (i.e. a set of parameters), from which members
are selected for parenthood according to their fitness. Fitness is determined
by the ability of the parameters to match the observations,
whereas the reproduction within the genetic algorithm
is done by cross-over of the parental
parameters and applying a mutation operator.
Although genetic algorithms (GA)
have been used in many branches of science, there are just a few
applications in astrophysics, e.g. for fitting rotation curves or
analysis of Doppler velocities in ![]() Scuti stars (for a review see
Charbonneau 1995). Recently, Wahde (1998)
demonstrated the ability of genetic algorithms to recover orbital parameters for artificial
data generated by N-body simulations of strongly interacting galaxies.
He stressed that in these systems the positional information can be
already sufficient to determine the orbital elements.
Scuti stars (for a review see
Charbonneau 1995). Recently, Wahde (1998)
demonstrated the ability of genetic algorithms to recover orbital parameters for artificial
data generated by N-body simulations of strongly interacting galaxies.
He stressed that in these systems the positional information can be
already sufficient to determine the orbital elements.
In this paper we combine different N-body techniques in order to create a model for the dynamics of interacting galaxies. In a first step, restricted N-body simulations are performed to constrain the model parameters: if a sufficiently accurate data set is available, the genetic algorithm can be used to find the orbital parameters and to check the uniqueness of the result. Additionally, the sensitivity of the solution can be checked by an extended parameter study. Alternatively, in the case of insufficient data, one can use the restricted N-body models to obtain a first guess of the parameters, creating an artificial intensity map and then apply the genetic algorithm to check its uniqueness. In the second step, self-consistent models are necessary in order to tune the parameters and to check the applicability of the restricted N-body method. These checks must address two questions: is the neglection of self-gravity acceptable? Does gas dynamics alter the results significantly? Technically this means that self-consistent simulations with and without gas have to be performed.
The numerical models of this paper are performed on NGC 4449 which is a prototype actively star-forming galaxy similar in size and mass to the Large Magellanic Cloud. NGC 4449 is surrounded by an extended HI halo which shows some distortion (van Woerden et al. 1975; Bajaja et al. 1994). Hunter et al. (1998) published high resolution HI images showing a large scale lopsided structure. Though there seems to be a close dwarf companion, DDO 125, it is not clear whether the observed streamers are tidal tails caused by an interaction with DDO 125 (Hunter et al. 1998). For example, tidal distortions are missing in the optical image of both galaxies and no clear bridge has been detected. Theis & Kohle (1998) demonstrated qualitatively by N-body simulations that the main HI features could stem from a face-on encounter provided the mass of DDO 125 exceeds 10% of the mass of NGC 4449. An alternative scenario assumes that the HI structure is an ongoing infall of gas onto NGC 4449, possibly caused by the encounter with DDO 125 followed by a compression and cooling of the gas (Silk et al. 1987). However, it is puzzling that the observed large-scale, lopsided and regular structure in NGC 4449 can be maintained over timescales such as the orbital period which is longer than 1 Gyr for the outer streamer. The high internal velocity dispersion of 10 kms-1 would destroy the streamers on a timescale of 2 108 yr (Hunter et al. 1998). In this paper we investigate this interaction scenario, addressing the question of whether the observed structures can actually be formed by tidal interaction and which constraints on the mass distribution or the orbits of both galaxies can be derived.
Section 2 summarizes the observational data of NGC 4449 and DDO 125 relevant for the models of this paper. The different modeling techniques and the numerical results are described in Sect. 3 (the restricted N-body method is introduced (Sect. 3.1) and a set of first results is shown in Sects. 3.2 and 3.3). The genetic algorithm approach is briefly introduced in Sect. 3.4 and explained in more detail in the Appendix. Its results are shown in Sect. 3.5. Finally, the restricted N-body simulations are compared with self-consistent models with (Sect. 3.7) and without gas (Sect. 3.6). The results of these different approaches are summarized and discussed in Sect. 4.
When optical images of NGC 4449 and the Large Magellanic
Cloud are compared, many similarities like the presence of
a bar, the size or the total luminosity are found.
However, unlike the LMC
NGC 4449 is a candidate for studies of the properties of a
Magellanic-type irregular unaffected by the tidal field of a
large galaxy. Its distance of
2.9-5.6 Mpc![]() allows for detailed investigations, performed in the
visual (e.g. Crillon & Monnet 1969;
Hunter & Gallagher 1997), in the radio band
(e.g. van Woerden et al. 1975; Klein et al. 1996),
in the HI emission line (e.g. Bajaja et al. 1994;
Hunter & Gallagher 1997; Hunter et al. 1998),
in the CO emission line (e.g. Sasaki et al. 1990;
Hunter & Thronson 1996; Kohle et al. 1998),
in the infrared (e.g. Hunter et al. 1986),
in the FUV (e.g. Hill et al. 1994) and in
X-rays (e.g. della Ceca et al. 1997;
Bomans & Chu 1997). Inside the Holmberg diameter of 11 kpc,
NGC 4449 shows ongoing strong star formation along a bar-like
structure (Hill et al. 1994). This activity seems to induce a
variety of morphological features like filaments, arcs, or loops which have
a size of several kpc (Hunter & Gallagher 1997).
allows for detailed investigations, performed in the
visual (e.g. Crillon & Monnet 1969;
Hunter & Gallagher 1997), in the radio band
(e.g. van Woerden et al. 1975; Klein et al. 1996),
in the HI emission line (e.g. Bajaja et al. 1994;
Hunter & Gallagher 1997; Hunter et al. 1998),
in the CO emission line (e.g. Sasaki et al. 1990;
Hunter & Thronson 1996; Kohle et al. 1998),
in the infrared (e.g. Hunter et al. 1986),
in the FUV (e.g. Hill et al. 1994) and in
X-rays (e.g. della Ceca et al. 1997;
Bomans & Chu 1997). Inside the Holmberg diameter of 11 kpc,
NGC 4449 shows ongoing strong star formation along a bar-like
structure (Hill et al. 1994). This activity seems to induce a
variety of morphological features like filaments, arcs, or loops which have
a size of several kpc (Hunter & Gallagher 1997).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{fig1.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg21.gif) |
Figure 1: Contour map of the integrated HI-intensity of NGC 4449. NGC 4449 is at the center of the image and DDO 125 is located at the almost circular contours in the South. Details are given in Hunter et al. (1998). This image was kindly provided by Deidre Hunter |
| Open with DEXTER | |
Early radio observations
of van Woerden et al. (1975) exhibited a large HI structure
exceeding the Holmberg diameter of 11 kpc by a factor of 7.5.
Recent observations by Bajaja et al. (1994)
with the Effelsberg telescope
and by Hunter et al. (1998) with
the VLA revealed a complex structure of several components (Fig. 1):
an elongated ellipse of HI gas centered on NGC 4449 has a total mass
of ![]()
![]() .
This gas rotates rigidly inside
11 kpc, reaching a level of 97 kms-1 in the deprojected velocity.
Outside 11 kpc, the rotation curve is flat. Bajaja et al. (1994)
derived a dynamical mass of
.
This gas rotates rigidly inside
11 kpc, reaching a level of 97 kms-1 in the deprojected velocity.
Outside 11 kpc, the rotation curve is flat. Bajaja et al. (1994)
derived a dynamical mass of
![]() inside 32 kpc and a HI
gas mass fraction of 3.3%. Within 11 kpc the dynamical mass
is
inside 32 kpc and a HI
gas mass fraction of 3.3%. Within 11 kpc the dynamical mass
is
![]() and the mass inside the optical radius
of about 5.6 kpc is
and the mass inside the optical radius
of about 5.6 kpc is
![]() .
Applying single dish data for
a
.
Applying single dish data for
a ![]() beamwidth, Hunter et al. (1998)
derived about
beamwidth, Hunter et al. (1998)
derived about
![]() .
The HI gas inside the optical part of
NGC 4449 counterrotates with respect to the outer regions.
For the central ellipse, Hunter et al. (1998) determined a
position angle of
.
The HI gas inside the optical part of
NGC 4449 counterrotates with respect to the outer regions.
For the central ellipse, Hunter et al. (1998) determined a
position angle of
![]() and an inclination of
and an inclination of
![]() .
.
South of the galactic center, a streamlike
structure of 25 kpc emanates which abruptly splits into two parts:
a small spur (5 kpc) which points towards DDO 125, a close irregular
galaxy, and a long extended stream.
The latter first points 24 kpc to the
north (in the following: vertical streamer),
then 49 kpc north-east and, finally, 27 kpc to the south-east
(together called the northeastern streamer),
covering 180![]() around NGC 4449. The long
straight sections are notable, as are the rather abrupt changes of direction.
The total mass of the streamers measured by the VLA observations
is about
around NGC 4449. The long
straight sections are notable, as are the rather abrupt changes of direction.
The total mass of the streamers measured by the VLA observations
is about
![]() .
Hunter et al. (1998) point
out that compared to the Effelsberg data there is an additional
diffuse HI mass not detected in the VLA observations which amounts to
two-thirds of the HI in the extended structures.
.
Hunter et al. (1998) point
out that compared to the Effelsberg data there is an additional
diffuse HI mass not detected in the VLA observations which amounts to
two-thirds of the HI in the extended structures.
DDO 125 is located in the south-east of NGC 4449 at a projected
distance of 41 kpc. The line-of-sight velocity difference between DDO 125
and NGC 4449 is only about 10 kms-1. Tully et al. (1978) found
rigid rotation inside the optical radius of DDO 125 and an inclination of the
adopted disc of ![]() .
From this they derived a total mass of
.
From this they derived a total mass of
![]() (corrected for a distance of 3.9 Mpc) which is
in agreement with single dish observations (
(corrected for a distance of 3.9 Mpc) which is
in agreement with single dish observations (![]() beamwidth)
of Fisher & Tully (1981). However, Ebneter et al.
(1987) reported VLA-observations which show a linear
increase of the rotation curve out to the largest radii where HI
has been detected, i.e. out to twice the optical radius. This already
allows for an estimate of a lower mass limit for DDO 125
which is a factor 8 larger than
the value of Tully et al. (1978), i.e.
beamwidth)
of Fisher & Tully (1981). However, Ebneter et al.
(1987) reported VLA-observations which show a linear
increase of the rotation curve out to the largest radii where HI
has been detected, i.e. out to twice the optical radius. This already
allows for an estimate of a lower mass limit for DDO 125
which is a factor 8 larger than
the value of Tully et al. (1978), i.e.
![]() .
Since
neither flattening of the rotation curve nor any decline has been observed,
this value is only a lower limit. If one compares that mass with the
total mass of NGC 4449 derived by Bajaja et al. (1994)
one gets a mass ratio of about
.
Since
neither flattening of the rotation curve nor any decline has been observed,
this value is only a lower limit. If one compares that mass with the
total mass of NGC 4449 derived by Bajaja et al. (1994)
one gets a mass ratio of about
![]() which is, however, just a lower limit.
Comparison of the masses inside the range of rigid rotation gives
a higher mass ratio of
which is, however, just a lower limit.
Comparison of the masses inside the range of rigid rotation gives
a higher mass ratio of
![]() .
.
For the simulations described in this paper three different N-body approaches have been applied: the method of restricted N-body simulations (Pfleiderer & Siedentopf 1961; Toomre & Toomre 1972) is described in Sect. 3.1. The self-gravitating models are split into calculations without gas (Sect. 3.6) and simulations which include gas by means of sticky particles (Sect. 3.7).
The advantage of the first method is twofold: the reduction of the full
N-body problem to N single body problems and the use of particles as
test particles which gives high spatial resolution at the
places of interest for almost no computational cost. As a direct consequence,
restricted N-body calculations can be performed with fewer particles
than self-consistent simulations which strongly suffer from
two-body relaxation in case of small particle numbers. Furthermore,
the CPU-time scales linearily with particle number which is
superior to almost all N-body codes. E.g. a restricted N-body simulation
sufficiently reproduces tidal features with only 1000 particles,
whereas a direct self-consistent calculation
needs an (optimistic) minimum of 10000 particles to reproduce a
stable galactic disc on the interaction timescale. Comparing the CPU-times
of such a self-consistent simulation performed on a GRAPE3 board with the values of a
restricted N-body simulation we get a time saving of at least a factor of
1000![]() .
Hence, the restricted N-body calculation
is at the moment the only method which allows about 104simulations in a couple of CPU-hours. Such a fast computation is a
prerequisite for all systematic searches in parameter space such as the
genetic algorithm described in Sect. 3.4.
.
Hence, the restricted N-body calculation
is at the moment the only method which allows about 104simulations in a couple of CPU-hours. Such a fast computation is a
prerequisite for all systematic searches in parameter space such as the
genetic algorithm described in Sect. 3.4.
However, the simplified treatment of the galactic potential in restricted N-body simulations prohibits any feedback of the tidal interaction on the orbits of both galaxies, e.g. no transfer of orbital angular momentum into galactic spin is possible (i.e. no merging). To overcome this problem, the results of restricted N-body models and genetic algorithms must be compared with detailed self-consistent simulations. In a first step the stellar dynamical applicability of the restricted models is checked by a comparison with self-gravitating systems calculated with a GRAPE3af special purpose computer (Sugimoto et al. 1990; see Sect. 3.6).
So far the dynamics of the system have been investigated in terms of stellar dynamics, though in many cases (such as the case of NGC 4449) HI gas is observed. In general, the effects of neglecting gas dynamics are not clear. E.g. a purely stellar dynamical ansatz was successfully applied for the system M 81 and NGC 3077 (Thomasson & Donner 1993), whereas in other systems the dynamics of the gas can deviate strongly from the behaviour of the stars (e.g. Noguchi 1988; Barnes & Hernquist 1996). Therefore, one has to compare stellar and gas dynamical results which is done in this paper by a sticky particle method (Sect. 3.7).
The units are chosen as 1 kpc,
![]() (the dynamical mass of NGC 4449) and G=1. This results
in a time unit of 1.78 Myr and a velocity of 549 kms-1.
(the dynamical mass of NGC 4449) and G=1. This results
in a time unit of 1.78 Myr and a velocity of 549 kms-1.
Restricted N-body simulations aim to reduce the N-body problem to N 1-body problems by assuming that the gravitational potential is given by a simple relation. E.g. two- or a few-body problems have known (semi-)analytical solutions or can be solved by fast standard methods. Here we assume that the gravitational forces on each particle are given by the superposition of the forces exerted by two point-like objects (the galaxies) moving on Keplerian orbits. Thus, for the orbits one has to specify 14 parameters which reduce to 7 in the center-of-mass frame (relative coordinates/velocities and the mass ratio): the orbital plane is fixed by the inclination angle and the argument of the ascending node. The orbit itself is characterized by its eccentricity and the location of the pericenter, i.e. the pericentric distance and the argument of the pericenter. Finally, mass and initial location of the reduced particle (or the time of pericentric passage) have to be specified to fix the phase. For a comparison with the observations, the phase of the observation also must be supplied. Three of the seven orbital parameters can be fixed by the observed location of both galaxies on the plane of sky (x-y plane) and the line-of-sight velocity. The masses (and thus the mass ratio) can be estimated by the velocity profiles of both galaxies, provided the distance to them is known.
In this paper, the time of pericentric passage is set to zero. As input,
the orbital eccentricity and inclination and the minimum distance are
given. Furthermore, the directly
observable parameters, i.e. the masses of the galaxies, the projection of
the relative positions of both galaxies onto the plane of sky, and their
line-of-sight velocity difference, are supplied. They are used to
determine the argument of the pericenter, the phase (or time since
pericentric passage) of the observed system and the argument of
the ascending node of the orbital plane. Additionally, the initial distance
or phase has to be specified: in the case of parabolic and hyperbolic
encounters, the distance was set to 100 kpc, which guarantees a sufficiently
low tidal influence at the start of the simulation. In the case of an elliptical
encounter, the situation is more difficult, because the apocentric distance
might be small, especially if the eccentricity is low. Thus, the system
might be tidally affected all the time or by a series of
repeated encounters which makes the applicability of the restricted N-body
method doubtful. For these elliptical orbits, the initial azimuthal angle of
the orbit was set to 120![]() (0
(0![]() corresponds to pericenter).
corresponds to pericenter).
The test particles are arranged in a flat disc moving on circular orbits. The disc itself is characterized by its orientation, i.e. its inclination and position angle, the scalelength and the outer edge. Additionally, an inner edge can be specified in order to avoid a waste of computational time by integrating tidally unaffected orbits well inside the tidal radius of the galaxy. In most of the restricted N-body simulations the test particles are distributed in 30 to 60 equidistant rings of 125 particles, i.e. a total of N=3750 to 7500 particles. The typical spacing of the rings is 0.7 to 1.5 kpc depending on the outer edge of the disc. The time integration of the equations of motion is performed by a Cash-Karp Runge-Kutta integrator of fifth order with adaptive timestep control (Press et al. 1992). In order to prevent a vanishingly small timestep by an accidental infall of a test particle to the galactic center, the gravitational force is softened on a length scale of 1 kpc. In order to speed-up the calculation the galactic positions are tabulated by cubic splines and the integrator uses these look-up tables. On a SPARC10 with a 150 MHz CPU a typical 7500-particle encounter takes 23 CPU seconds, which can be reduced by a factor of 2-3 by applying an inner edge of 10 kpc.
In a series of simulations the orbital parameters
(minimum distance
![]() ,
the eccentricity
,
the eccentricity ![]() ,
the mass
ratio q and the orientation of the orbital plane) as well as the
disc parameters (size
,
the mass
ratio q and the orientation of the orbital plane) as well as the
disc parameters (size
![]() of the disc,
its position angle
of the disc,
its position angle ![]() and inclination i)
are varied (see Table 1).
and inclination i)
are varied (see Table 1).
The evolution of the primary galaxy (NGC 4449) in the reference model A is displayed in Fig. 2. At the beginning, both galaxies have a distance of 100 kpc corresponding to 995 Myr before closest approach. The particles inside 10 kpc are omitted for an easier identification of the evolving structure. This does not alter the results, since the related particles are only weakly affected by the interaction, as the persistence of the elliptical shape of the central hole demonstrates. At the moment of closest approach (t=0), only the outer region of NGC 4449's disc reacts on the intruder. 71 Myr later (i.e. system time 40), a dense outer rim, starting at the projected position of DDO 125 and pointing to the north, begins to form. Secondly, a weak bridge-like feature seems to connect both galaxies. Both features are more pronounced after 178 Myr. At that time an additional tidal feature begins to evolve north of the center. When DDO 125 has a projected distance of 41 kpc (362 Myr after closest approach), three features are discernible: the remnant of the former bridge starts south of the center of NGC 4449 pointing to the south-west. The vertical feature starts at the end of the first structure and points to the north. The third structure is a long tidal arm which starts west of NGC 4449 pointing to north-east before turning back to the south-east.
A comparison of the intensity map of model A (lower right diagram in
Fig. 2) with the observations (Fig. 1)
demonstrates that the main observational features
can be reproduced qualitatively by the reference model A, i.e. a
parabolic orbit, a mass ratio q=0.2 and a minimum distance
![]() kpc. The parameters for the disc orientation are chosen in agreement
with Hunter et al.'s suggestion of
kpc. The parameters for the disc orientation are chosen in agreement
with Hunter et al.'s suggestion of
![]() ,
,
![]() ,
whereas the disc radius was set to
,
whereas the disc radius was set to
![]() kpc.
Although this numerical model is not a detailed fit of the data,
the characteristic sizes and locations of the streamers as well
as the unaffected disc can be found. The material located between the
streamer and the disc, which is not seen in Hunter's data,
corresponds to the extended HI mass detected in the single dish
observations by van Woerden et al. (1975).
In the following sections
we will discuss the influence of the individual parameters. The global
uniqueness of the reference model is investigated in
Sect. 3.5.
kpc.
Although this numerical model is not a detailed fit of the data,
the characteristic sizes and locations of the streamers as well
as the unaffected disc can be found. The material located between the
streamer and the disc, which is not seen in Hunter's data,
corresponds to the extended HI mass detected in the single dish
observations by van Woerden et al. (1975).
In the following sections
we will discuss the influence of the individual parameters. The global
uniqueness of the reference model is investigated in
Sect. 3.5.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{fig2.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg39.gif) |
Figure 2:
Temporal evolution of the particle positions
around NGC 4449 projected onto the plane-of-sky for different times.
The perturber DDO 125 is shown by the star. Closest approach is at
t=0. The final diagram corresponds to a projected distance of
41 kpc. The mass ratio of both galaxies is set to q=0.2. The original
HI disc has an inclination of
|
| Open with DEXTER | |
In this section the influence of the basic parameters,
i.e. the orientation of the orbital plane, the orbital eccentricity
and the minimum distance, the mass ratio of both galaxies, and the orientation
of the HI disc and its extent are discussed (see Table 1).
In the following simulations, all parameters except the one of interest
are kept constant with respect to model A. Thus, the vicinity of the
reference model in parameter space is studied.
Model parameters of the restricted N-body simulations
| model | q |
|
i |
|
|
comment | ||
| A | 1.0 | 0.2 | 25 | 40 | 60 | 230 | 40 | reference model |
B1 |
0.5 | 0.2 | 25 | 40 | 60 | 230 | 40 | eccentricity |
| B2 | 0.8 | 0.2 | 25 | 40 | 60 | 230 | 40 | |
| B3 | 1.5 | 0.2 | 25 | 40 | 60 | 230 | 40 | |
| B4 | 5.0 | 0.2 | 25 | 40 | 60 | 230 | 40 | |
C1 |
1.0 | 0.01 | 25 | 40 | 60 | 230 | 40 | mass ratio |
| C2 | 1.0 | 0.05 | 25 | 40 | 60 | 230 | 40 | |
| C3 | 1.0 | 0.1 | 25 | 40 | 60 | 230 | 40 | |
| C4 | 1.0 | 0.3 | 25 | 40 | 60 | 230 | 40 | |
| C5 | 1.0 | 0.4 | 25 | 40 | 60 | 230 | 40 | |
D1 |
1.0 | 0.2 | 15 | 40 | 60 | 230 | 40 | minimum distance |
| D2 | 1.0 | 0.2 | 20 | 40 | 60 | 230 | 40 | |
| D3 | 1.0 | 0.2 | 30 | 40 | 60 | 230 | 40 | |
| D4 | 1.0 | 0.2 | 35 | 40 | 60 | 230 | 40 | |
| D5 | 1.0 | 0.2 | 40 | 40 | 60 | 230 | 40 | |
E1 |
1.0 | 0.2 | 25 | 10 | 60 | 230 | 40 | orbital inclination |
| E2 | 1.0 | 0.2 | 25 | 20 | 60 | 230 | 40 | |
| E3 | 1.0 | 0.2 | 25 | 30 | 60 | 230 | 40 | |
| E4 | 1.0 | 0.2 | 25 | 50 | 60 | 230 | 40 | |
| E5 | 1.0 | 0.2 | 25 | 70 | 60 | 230 | 40 | |
F1 |
1.0 | 0.2 | 25 | 40 | 40 | 230 | 40 | disc inclination |
| F2 | 1.0 | 0.2 | 25 | 40 | 50 | 230 | 40 | |
| F3 | 1.0 | 0.2 | 25 | 40 | 70 | 230 | 40 | |
G1 |
1.0 | 0.2 | 25 | 40 | 60 | 210 | 40 | pos. angle of disc |
| G2 | 1.0 | 0.2 | 25 | 40 | 60 | 250 | 40 | |
H1 |
1.0 | 0.2 | 25 | 40 | 60 | 230 | 25 | outer edge of disc |
| H2 | 1.0 | 0.2 | 25 | 40 | 60 | 230 | 30 | |
| H3 | 1.0 | 0.2 | 25 | 40 | 60 | 230 | 35 | |
| H4 | 1.0 | 0.2 | 25 | 40 | 60 | 230 | 50 |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{fig3.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg40.gif) |
Figure 3: Dependence on the eccentricity. Projection of the particle positions onto the plane-of-sky at the moment of a projected distance of 41 kpc. The eccentricities of the models are 0.5 (upper left, model B1), 0.8 (upper right, B2), 1.0 (A, reference model), 1.5 (B3) and 5.0 (B4) |
| Open with DEXTER | |
Eccentricity. The eccentricity mainly influences the interaction
timescale which is defined here as the time between maximum approach and
a projected distance of 41 kpc, i.e. the moment of observation.
An eccentricity of 5.0 (corresponding to a hyperbolic encounter)
decreases the interaction time by
a factor 2.6 resulting in less structural changes of the primary galaxy
(Fig. 3): only the remnant of the bridge feature can be
discerned, whereas the other two streamers found in the reference model
are missing completely. With decreasing eccentricity, the north-eastern
streamer becomes pronounced before the vertical structure arises. The latter
is weakly expressed for
![]() .
Reducing
.
Reducing ![]() further
to bound orbits makes the features even more prominent. In the case
of
further
to bound orbits makes the features even more prominent. In the case
of
![]() the north-eastern and the vertical streamer form
a single structure clearly detached from the center.
However, due to the strength of the interaction, a second broad tidal arm
is ejected from NGC 4449, leaving a low-density region south to the
northern tip of the north-eastern streamer.
the north-eastern and the vertical streamer form
a single structure clearly detached from the center.
However, due to the strength of the interaction, a second broad tidal arm
is ejected from NGC 4449, leaving a low-density region south to the
northern tip of the north-eastern streamer.
In order to compare the
![]() model with observations,
we reran model B1, but with
model with observations,
we reran model B1, but with ![]() ,
in order to derive
intensity and velocity maps. This model reproduces several
observed features very well (Fig. 4):
first, the intensity map shows the three observed abrupt changes:
at the lower tip of the vertical streamer, at the transition from the
vertical streamer to the north-eastern streamer and at the northern tip
of the north-eastern streamer. Second, the spatial extent of the streamers
is in agreement with the observations. Third, we find a bridge
between the north-eastern streamer and the central tidally-unaffected
part of NGC 4449. Fourth, during the encounter, material is ejected south
to NGC 4449. The latter two features can be found in deeper images of
NGC 4449 (cf. Fig. 1 of Hunter et al. 1998).
However, there are also some remarkable differences:
first, both model and observation show a spur at the lower tip of the
vertical streamer. However, their directions differ by about 90
,
in order to derive
intensity and velocity maps. This model reproduces several
observed features very well (Fig. 4):
first, the intensity map shows the three observed abrupt changes:
at the lower tip of the vertical streamer, at the transition from the
vertical streamer to the north-eastern streamer and at the northern tip
of the north-eastern streamer. Second, the spatial extent of the streamers
is in agreement with the observations. Third, we find a bridge
between the north-eastern streamer and the central tidally-unaffected
part of NGC 4449. Fourth, during the encounter, material is ejected south
to NGC 4449. The latter two features can be found in deeper images of
NGC 4449 (cf. Fig. 1 of Hunter et al. 1998).
However, there are also some remarkable differences:
first, both model and observation show a spur at the lower tip of the
vertical streamer. However, their directions differ by about 90![]() .
Second, the position of the northern tip of the north-eastern streamer (or
the angle between vertical and the north-eastern streamer) differ.
.
Second, the position of the northern tip of the north-eastern streamer (or
the angle between vertical and the north-eastern streamer) differ.
Looking at the velocity map, we find Keplerian rotation in the central
region of the simulations, whereas the observations show rigid rotation.
The velocities in the streamers reach about 80-100 kms-1, which
is in agreement with the observed values. Additionally, the velocity
field in the simulations shows a small, but significant V-shape,
south of NGC 4449 which is also observed (cf. Fig. 3 of Hunter et al.
1998). The main discrepancies between the observed and
numerical velocity maps comes from the point mass approximation of the
galactic potential used for the numerical model. Although this
approximation must fail for the central region, it should be sufficient
for the outer regions which are most affected by tides
and which contain almost the entire dynamical mass of NGC 4449.
![\begin{figure}
\includegraphics[width=7.9cm,clip]{fig4.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg43.gif) |
Figure 4:
Projected particle positions (upper left),
velocity map (upper right) and intensity map (lower left)
for model B1 (
|
| Open with DEXTER | |
Mass ratio. The variation of the mass ratio gives a lower limit of
about 10% in order to create a sufficient tidal response (Fig. 5).
If the mass ratio exceeds 0.3, the vertical feature becomes less vertical
and the north-eastern streamer is more diffuse, both due to the enhanced
tidal pull of the intruder.
![\begin{figure}
\includegraphics[width=7.2cm,clip]{fig5.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg44.gif) |
Figure 5: Dependence on the mass ratio. Projection of the particle positions onto the plane-of-sky at the moment of a projected distance of 41 kpc. The mass ratios are - starting with the upper left diagram - 0.01 (model C1), 0.05 (C2), 0.1 (C3), 0.2 (A, reference model), 0.3 (C4) and 0.4 (C5) |
| Open with DEXTER | |
Minimum distance. Although the interaction time is not strongly
influenced by the minimum distance
![]() ,
it determines the maximum
strength of the tidal field (Fig. 6):
for small separations, the structures become more
diffuse and the primary is much more affected.
The vertical feature is more
extended, creating an additional tidal arm
(similar to the model with an orbital eccentricity
,
it determines the maximum
strength of the tidal field (Fig. 6):
for small separations, the structures become more
diffuse and the primary is much more affected.
The vertical feature is more
extended, creating an additional tidal arm
(similar to the model with an orbital eccentricity
![]() ).
If the distance of closest approach exceeds 30 kpc, almost no streamers
are formed.
).
If the distance of closest approach exceeds 30 kpc, almost no streamers
are formed.
![\begin{figure}
\includegraphics[width=7.2cm,clip]{fig6.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg45.gif) |
Figure 6: Dependence on the minimum distance during the encounter. Projection of the particle positions onto the plane-of-sky at the moment of a projected distance of 41 kpc. The minimum distances are - starting with the upper left diagram - 15 kpc (model D1), 20 kpc (D2), 25 kpc (A, reference model), 30 kpc (D3), 35 kpc (D4) and 40 kpc (D5) |
| Open with DEXTER | |
Orbital plane. The orientation of the orbital plane characterizes
the observer's location or the line-of-sight, which is fixed
by two parameters. For the models here only the orbital inclination
is a free parameter, since the second parameter, the
position angle of the orbital plane, is fixed by the
observed relative line-of-sight velocity of both galaxies.
The models show that the inclination affects mainly
the orientation of the vertical streamer (Fig. 7):
an inclination outside the range
![]() gives too
much deviation from the south-north direction of the vertical
feature.
gives too
much deviation from the south-north direction of the vertical
feature.
![\begin{figure}
\includegraphics[width=7.2cm,clip]{fig7.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg47.gif) |
Figure 7:
Dependence on the inclination angle of the orbital plane.
Projection of the particle positions onto the plane-of-sky at the
moment of a projected distance of 41 kpc. The inclinations are
10 |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=7.2cm,clip]{fig8.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg48.gif) |
Figure 8: Dependence on the extension of the HI distribution in NGC 4449. Projection of the particle positions onto the plane-of-sky at the moment of a projected distance of 41 kpc. The radial extensions are 25 kpc (upper left, model H1), 30 kpc (upper right, H2), 35 kpc (H3), 40 kpc (A, reference model) and 50 kpc (H4) |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=7.2cm,clip]{fig9.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg49.gif) |
Figure 9:
Dependence on the orientation of the HI disc in NGC 4449.
Projection of the particle positions onto the plane-of-sky at the
moment of a projected distance of 41 kpc. The orientation is characterized
by the inclination |
| Open with DEXTER | |
HI distribution in NGC 4449. A specification of the mass- and especially the HI distribution is a more difficult task, because, contrary to the well-known two-body problem, the number of free parameters characterizing the structure and internal dynamics of the interacting galaxies is unknown and a matter of investigation itself. For example, it is not a priori clear how the HI is distributed. To reduce the number of free parameters, we will assume here that the observed inner elongated ellipse is the remnant of an original exponential HI disc, which can be specified by its orientation, its scale length and radial extent. The inclination of the disc can roughly be determined from the HI map, whereas its sign is not unambiguous. Placing the south-eastern side of the HI disc into the foreground means that the orbital plane of the companion and the plane of the HI disc are nearly orthogonal. We performed several simulations with geometries of this kind, but these show almost no strong tidal responses and they all result in situations completely different to that observed (Kohle 1999). However, placing the north-western side of the HI disc into the foreground and considering the HI velocity field, we now have the companion on a prograde orbit.
Since the particles are treated as test particles, a variation of the scale length does not change the final location of a particle, but rather its mass, which is required for the calculation of the intensity map. A small scale length (e.g. 5 kpc) would confine too much HI in the center which is unaffected by the encounter. Since the observations show a large fraction of HI outside 20 kpc, we have chosen a large scale length of 30 kpc which gives only a weak radial decline of the HI surface density and, by this, a sufficient amount of HI in the outer regions.
DISC SIZE.
The influence of the maximum radius
![]() of the disc is
shown in Fig. 8. If
of the disc is
shown in Fig. 8. If
![]() is smaller than 35 kpc, the
vertical streamer has not been formed at all, indicating that this feature
stems from the HI gas far outside the center. The north-eastern
arm and the bridge, however, are already built up for
is smaller than 35 kpc, the
vertical streamer has not been formed at all, indicating that this feature
stems from the HI gas far outside the center. The north-eastern
arm and the bridge, however, are already built up for
![]() kpc.
With increasing disc size the vertical streamer becomes more
pronounced and more extended, which excludes disc sizes larger than 45 kpc.
kpc.
With increasing disc size the vertical streamer becomes more
pronounced and more extended, which excludes disc sizes larger than 45 kpc.
DISC ORIENTATION.
The orientation of the HI disc also strongly affects the appearance
of the primary galaxy. Variation of the position angle ![]() by 20
by 20![]() gives HI distributions which are incompatible
with the observations (Fig. 9).
If
gives HI distributions which are incompatible
with the observations (Fig. 9).
If ![]() is decreased, the vertical streamer
is more extended and diffuse. On the other hand, if
is decreased, the vertical streamer
is more extended and diffuse. On the other hand, if ![]() is increased,
the north-eastern arm becomes too long and the vertical feature vanishes
almost completely. Similarly, the results depend strongly on the inclination i:
inclinations below
is increased,
the north-eastern arm becomes too long and the vertical feature vanishes
almost completely. Similarly, the results depend strongly on the inclination i:
inclinations below ![]() give only a weak bridge and a weak vertical
streamer, whereas the orientation of the vertical streamer deviates
strongly from the northern direction for inclinations exceeding 70
give only a weak bridge and a weak vertical
streamer, whereas the orientation of the vertical streamer deviates
strongly from the northern direction for inclinations exceeding 70![]() .
.
The performed parameter study demonstrates that even close to the parameters of model A, the final particle distribution shows significant variations which are not in agreement with the observations. Thus, the reference model might be a good and locally unique candidate describing the dynamics of NGC 4449 and DDO 125. The confidence in this encounter scenario is especially enhanced by the strong dependence on the orientation of the HI disc of NGC 4449. Qualitatively good models are only found if the disc orientation agrees well with the values determined independently by observations. On the other hand, the former parameter study only investigates a small fraction of parameter space and, thus, the uniqueness of the solution is not confirmed. Moreover, in general, it is very tedious to find a good model by hand, i.e. by an unsystematic non-automated search in parameter space. Thus, the probability of accepting the first solution found seems to be very high (especially, if CPU-intensive simulations are performed), by this neglecting other regions in parameter space which might also give sufficient fits. In the next section an automatic search in parameter space by means of a genetic algorithm is introduced. This allows in principle for an ab initio determination of acceptable parameter sets (if data sets of sufficient quality are available) or at least for a uniqueness test of a favoured scenario like the reference model described above.
The idea of applying models of organic evolution for optimization problems dates back to the 1960s and 1970s (e.g. Rechenberg 1965; Schwefel 1977). Unlike standard deterministic gradient techniques for optimization (e.g. the downhill simplex method, Press et al. 1992) Rechenberg's Evolutionsstrategie is probabilistic: starting with a more or less random parent, i.e. a single point in parameter space, a child is generated by a random mutation of the parameter set characterizing the parent. The quality of both individuals with respect to the optimization problem (i.e. their fitness) determines the parent of the next generation. Repeating this process of mutation and selection improves the quality of the individual monotonously. This special implementation of evolutionary algorithms (EAs) in general, has certain advantages: compared to complete grids in parameter space, the probabilistic but oriented nature of the evolutionary search strategy allows for an efficient check of a high-dimensional parameter space. Compared to gradient methods which are very fast near the optimum, EAs do not need any gradient information which might be computationally expensive. They depend only weakly on the starting point and - most important - they are able to leave local optima. The price for these features is a large number of fitness evaluations or test points in parameter space before converging to a good solution.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{fig10.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg51.gif) |
Figure 10: Best fit model during the course of a GA fitting procedure. The projection of the particles in x-y-plane and the corresponding grid for the intensity evaluation are displayed: the original data (upper left), the best fit of the GA after initialization (upper middle), after the first breeding (upper right), after 11 generations (lower left) and at the end of the fitting procedure after 100 generations (lower middle). The evolution of the maximum fitness is shown in the lower right diagram. The number of test particles per simulation is 900 |
| Open with DEXTER | |
Holland (1975) extended the Evolutionsstrategie of Rechenberg by abandoning asexual reproduction: he used a population of individuals instead of a single individual (and its offspring). From the population two individuals were selected according to their fitness to become parents. These parents represent two points (chromosomes) in parameter space and the corresponding coordinates are treated like genes on a chromosome. These chromosomes are subject to a cross-over and a mutation operation resulting in a new individual which is a member of the next generation. Such a breeding is repeated until the next generation has been formed. Finally, the whole process of sexual reproduction is repeated iteratively until the individuals representing a set of points in parameter space confine sufficiently one or several regions of high fitness. Despite many differences in the detailed implementations of genetic algorithms (GAs), the basic concept of an iterated application of randomized processes like recombination, mutation, and selection on a population of individuals remains in all GAs (Goldberg 1989; Bäck 1996).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{fig11.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg52.gif) |
Figure 11: Development of six parameters of the best fit model during a GA run. The parameters are the mass of the secondary galaxy (upper left), the minimum distance (upper right), the inclination (middle left) and position angle (middle right) of the orbital plane, and the inclination (lower left) and position angle (lower right) of the disc of the primary galaxy. The filled squares show the parameters of the fitted artificial reference model |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.9cm,clip]{fig12.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg53.gif) |
Figure 12:
Test of the capability of the GA (lower row)
to recover original data
when these data (upper row) are of low quality or incomplete.
Shown are runs with low resolution, i.e. a discretization on a
|
| Open with DEXTER | |
In order to check the uniqueness of the reference model A, several runs
with different parameter sets encoded in genes were performed. Figure 10 shows a typical run of the GA operating on a population of
100 members. The reference model![]() - displayed in the upper left diagram -
as well as the GA models were calculated with 900 test particles.
This makes the streamers less
prominent, but still discernible. The next plots show the GA status
at different generations: at generation 1, the best model is
created out of the randomly chosen initial parameter sets. However,
already by the second generation, i.e. after the first application of the
reproduction operator, the best model clearly exhibits the north-eastern
streamer. At generation 11, even the weaker vertical feature and the
bridge feature appear. At the end of this GA run the particle distribution
of the original model A and the best fit of the GA are almost identical,
at least compared by eye. The fitness of the best fit has strongly
increased from 0.04 to 0.14 where values above 0.1 indicate
a very good fit. Most of the improvements were found during the first
50 generations, i.e. analyzing 5000 models. After that generation,
the homogeneity of the population led to inbreeding which strongly
prohibits the appearance and spread of new (better) parameters. However,
this is not a problem for the models here, because a very good fit to
all parameters was already found after 40 generations (Fig. 11).
The relative deviation of the derived
parameters from the original values is less than 15% in all cases,
and for many is better than 5%.
- displayed in the upper left diagram -
as well as the GA models were calculated with 900 test particles.
This makes the streamers less
prominent, but still discernible. The next plots show the GA status
at different generations: at generation 1, the best model is
created out of the randomly chosen initial parameter sets. However,
already by the second generation, i.e. after the first application of the
reproduction operator, the best model clearly exhibits the north-eastern
streamer. At generation 11, even the weaker vertical feature and the
bridge feature appear. At the end of this GA run the particle distribution
of the original model A and the best fit of the GA are almost identical,
at least compared by eye. The fitness of the best fit has strongly
increased from 0.04 to 0.14 where values above 0.1 indicate
a very good fit. Most of the improvements were found during the first
50 generations, i.e. analyzing 5000 models. After that generation,
the homogeneity of the population led to inbreeding which strongly
prohibits the appearance and spread of new (better) parameters. However,
this is not a problem for the models here, because a very good fit to
all parameters was already found after 40 generations (Fig. 11).
The relative deviation of the derived
parameters from the original values is less than 15% in all cases,
and for many is better than 5%.
In a series of different GA runs, we varied the population size, the number of generations or particles, the parameter combination encoded on chromosomes, the fitness function, and the random initial population. In almost all of them the best fit gave an acceptable fit of the reference model which demonstrates the capability of GAs to recover the parameters, even for weak encounters. The models which failed suffered from inbreeding or from a fitness function which did not discriminate sufficiently between high and low quality fits. Moreover, a different region in parameter space producing a good fit (f>0.1) was never found. Thus, the model A - or more exact the corresponding intensity map - seems to result from a unique parameter set. However, this is only a motivated guess, not a mathematical proof!
Another interesting question is how strongly do the
GA results depend on the completeness or accuracy of the
data. We studied this in two ways: first, we used
a coarser grid (![]() )
in order to mimic a lower resolution of
observational data (left column in Fig. 12).
The GA is then only qualitatively able to
reproduce the reference model. Obviously, too much
information is lost when the resolution becomes
too small. On the other hand, an increase of the number of cells to
)
in order to mimic a lower resolution of
observational data (left column in Fig. 12).
The GA is then only qualitatively able to
reproduce the reference model. Obviously, too much
information is lost when the resolution becomes
too small. On the other hand, an increase of the number of cells to
![]() did not improve the fit found on a
did not improve the fit found on a ![]() grid, but introduced
more noise into the intensity maps. In the second test
we discarded one or several grid cells from the fitness
calculation (middle and right column in Fig. 12).
Omitting one cell does not affect the final fit,
independent of the location of the cell (here, the center).
However, if a whole feature, such as the vertical streamer,
is neglected, the GA is unable to recover the original
data.
grid, but introduced
more noise into the intensity maps. In the second test
we discarded one or several grid cells from the fitness
calculation (middle and right column in Fig. 12).
Omitting one cell does not affect the final fit,
independent of the location of the cell (here, the center).
However, if a whole feature, such as the vertical streamer,
is neglected, the GA is unable to recover the original
data.
The self-consistent models in this paper were performed by a direct N-body integration using the GRAPE3af board in Kiel for the calculation of the gravitational forces and the potentials. The time integration was done by a leap-frog scheme with a fixed timestep of 1.78 Myr. The GRAPE board uses intrinsically a Plummer softening, the softening length was chosen to be 0.2 kpc. These choices give a total energy conservation of better than 1% for the whole simulation.
Different to the restricted N-body models, the set-up of the initial particle configuration for self-gravitating systems is far from being trivial. In principle, any stable stationary stellar system fulfills the collisionless Boltzmann equation. Thus, a solution of the latter could be used as a trial galactic system. From observations of the Milky Way it is known, however, that even if the Galaxy is axisymmetric, three integrals of motion are required to construct a stationary model (e.g. Binney & Tremaine 1987). Unfortunately, only two are known analytically (the energy and the z-component of the angular momentum). Additionally, even if a particle configuration is generated from a distribution function depending on the integrals of motion, it is unclear whether it is stable against perturbations which might lead to e.g. the Toomre instability or the bar instability. Thus, on the timescale of interest one has to check the stability by numerical simulations.
In this paper we use the models of Kuijken & Dubinski (1995) consisting of three components which are determined self-consistently from the Boltzmann equation: the bulge follows a King model and the halo a lowered Evans model. For the disc the third integral is approximated by the z-energy, i.e. the energy in vertical oscillations. The advantage of Kuijken & Dubinski's method is the possibility to specify parameters like scale length or scale height of the disc directly, whereas many other methods (e.g. Barnes 1988) not starting in exact virial equilibrium readjust the mass distribution on a dynamical timescale, which means less control on the structural parameters.
Our initial model of NGC 4449 is derived from the observational data of
Bajaja et al. (1994) and Hunter et al. (1998).
The total mass is set according to the dynamical mass of
![]() within 32 kpc. 90% of this mass is
attributed to the dark halo, 3% to the disc and
7% to the bulge component. The radial extent of the halo was set to
32 kpc. The disc modelled here should not be confused
with the optical disc of the galaxy. Since we are interested in the
tidal response of the outer regions, especially the formation of the
streamers, we did not model the inner (optical) region of NGC 4449,
i.e. the stellar disc. The missing signatures of any tidal features in
the optical image demonstrate that the stellar body of NGC 4449 is
not affected by the interaction. For the same reason we did not consider
the counter-rotation of the inner region. However, its gravity is taken
into account by means of the bulge and halo contributions to the
overall rotation curve. The radial extension of the bulge is 3 kpc.
The scale length of the extended (HI) disc was varied
between 10 and 30 kpc, the outer edge was set to 40 kpc.
within 32 kpc. 90% of this mass is
attributed to the dark halo, 3% to the disc and
7% to the bulge component. The radial extent of the halo was set to
32 kpc. The disc modelled here should not be confused
with the optical disc of the galaxy. Since we are interested in the
tidal response of the outer regions, especially the formation of the
streamers, we did not model the inner (optical) region of NGC 4449,
i.e. the stellar disc. The missing signatures of any tidal features in
the optical image demonstrate that the stellar body of NGC 4449 is
not affected by the interaction. For the same reason we did not consider
the counter-rotation of the inner region. However, its gravity is taken
into account by means of the bulge and halo contributions to the
overall rotation curve. The radial extension of the bulge is 3 kpc.
The scale length of the extended (HI) disc was varied
between 10 and 30 kpc, the outer edge was set to 40 kpc.
The long-term stability was checked by simulations of an isolated
disc with ![]() particles (8000 for the disc, 4000 for the bulge
and 6000 for the halo). Within 1.5 Gyr the Lagrange radii at 10% and
90% mass vary only by 2-4%. They show no systematic trend except for a
small expansion during the first 100 Myr which is probably caused by
gravitational softening. Due to two-body relaxation the scale height of
the disc increases by almost a factor of 2 within 1.5 Gyr. However, this
heating is not expected to alter the result of the dominant interaction
significantly. The Fourier amplitude C2, defined by
particles (8000 for the disc, 4000 for the bulge
and 6000 for the halo). Within 1.5 Gyr the Lagrange radii at 10% and
90% mass vary only by 2-4%. They show no systematic trend except for a
small expansion during the first 100 Myr which is probably caused by
gravitational softening. Due to two-body relaxation the scale height of
the disc increases by almost a factor of 2 within 1.5 Gyr. However, this
heating is not expected to alter the result of the dominant interaction
significantly. The Fourier amplitude C2, defined by
![]() (with the
surface density
(with the
surface density ![]() ), is always less than 5%, in agreement
with no significant bar or spiral pattern built up during the simulation.
), is always less than 5%, in agreement
with no significant bar or spiral pattern built up during the simulation.
Figure 13 shows a comparison of restricted N-body
simulations with self-consistent models. Except for
the more diffuse structure in the
latter, the large-scale features are very similar in both simulations.
The streamer structure can be found in both self-consistent
simulations, as the surface plots demonstrate. The fact that the streamers
are better resolved in the simulation with an eccentricity
![]() ,
is partly due to the increased number of particles
(80000) used for this simulation. The simulations for the parabolic orbits
were performed with 8000 (disk) particles for both, the restricted
and the self-consistent simulations. The latter clearly demonstrates
the ability of the restricted N-body models to resolve structures, even
when a small number of particles is used. It is remarkable that the
extended dark halo which has been applied for the self-consistent models
does not strongly affect the results as the comparison
of the
,
is partly due to the increased number of particles
(80000) used for this simulation. The simulations for the parabolic orbits
were performed with 8000 (disk) particles for both, the restricted
and the self-consistent simulations. The latter clearly demonstrates
the ability of the restricted N-body models to resolve structures, even
when a small number of particles is used. It is remarkable that the
extended dark halo which has been applied for the self-consistent models
does not strongly affect the results as the comparison
of the
![]() -models shows: the vertical and the north-eastern
streamer, the mass ejected to north of the north-eastern streamer,
the small bridge between the central region and the eastern tip of the
streamer, the extent of the HI distribution south and south-east to
the center show up in both simulations at almost the same locations.
The only significant difference is that the north-eastern streamer is less
straight in the self-consistent model than in the restricted N-body
simulation. This very good agreement confirms the applicability of the
restricted N-body method here. Another interesting aspect
concerns the response of the halo
to the intruder. Unlike to the disc, the halo remains almost
unchanged by the encounter (Fig. 14). This
behaviour allows the application of a rigid galactic potential
which has been used in the restricted N-body simulations.
-models shows: the vertical and the north-eastern
streamer, the mass ejected to north of the north-eastern streamer,
the small bridge between the central region and the eastern tip of the
streamer, the extent of the HI distribution south and south-east to
the center show up in both simulations at almost the same locations.
The only significant difference is that the north-eastern streamer is less
straight in the self-consistent model than in the restricted N-body
simulation. This very good agreement confirms the applicability of the
restricted N-body method here. Another interesting aspect
concerns the response of the halo
to the intruder. Unlike to the disc, the halo remains almost
unchanged by the encounter (Fig. 14). This
behaviour allows the application of a rigid galactic potential
which has been used in the restricted N-body simulations.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{fig13.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg59.gif) |
Figure 13:
Comparison of restricted N-body models (left)
with self-consistent simulations (right) for a parabolic encounter
(upper row) and an eccentricity of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{fig14.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg60.gif) |
Figure 14: Self-consistent N-body simulation "sin gas'': projection of the particle positions onto the plane-of-sky at different times: initially (upper row), at closest approach (middle row) and at the projected distance of 41 kpc (lower row). The left column shows the disc particles, whereas the right column displays the halo particles |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig15.ps}
\end{figure}](/articles/aa/full/2001/17/aa9045/Timg61.gif) |
Figure 15: Projection of the particle positions onto the plane-of-sky at different times: at closest approach (upper row), at the projected distance of 41 kpc (middle row) and at the end of the simulation (lower row). Both models include self-gravity. The left column shows a purely stellar simulation, whereas the right column includes gas dynamics by means of sticky particles |
| Open with DEXTER | |
For the gasdynamical models we use a sticky particle scheme which
treats each particle of the HI disc as a gaseous cloud. The radius of
these clouds is assumed to follow
![]() which is derived from
the mass-radius relation of Rivolo & Solomon (1987) corrected
for glancing collisions (
which is derived from
the mass-radius relation of Rivolo & Solomon (1987) corrected
for glancing collisions (
![]() is the mass of a gas cloud).
When the distance of two clouds falls below
the sum of their radii, merging
of the clouds is allowed, if their relative orbital angular momentum
is smaller than the maximum angular momentum a merged cloud
can acquire before break-up. If this angular momentum criterion prevents
a merger, the clouds keep their kinematical data, i.e. no energy is
dissipated. Star formation is only qualitatively included by adopting
an upper mass limit of
is the mass of a gas cloud).
When the distance of two clouds falls below
the sum of their radii, merging
of the clouds is allowed, if their relative orbital angular momentum
is smaller than the maximum angular momentum a merged cloud
can acquire before break-up. If this angular momentum criterion prevents
a merger, the clouds keep their kinematical data, i.e. no energy is
dissipated. Star formation is only qualitatively included by adopting
an upper mass limit of
![]() for clouds. If they
exceed this limit no further merging is allowed, i.e. they are treated
as stars. However, the star formation criterion is not important
for the models of this paper. (For details of the cloud model or the
merging mechanism see Theis & Hensler 1993). This dissipative
scheme has been successfully applied to collapsing systems reproducing
many observed properties of spiral and elliptical galaxies. For the
long-term evolution of barred disc galaxies, a comparison of this scheme with
that of Palous et al. (1993) for their standard coefficients
of restitution of
for clouds. If they
exceed this limit no further merging is allowed, i.e. they are treated
as stars. However, the star formation criterion is not important
for the models of this paper. (For details of the cloud model or the
merging mechanism see Theis & Hensler 1993). This dissipative
scheme has been successfully applied to collapsing systems reproducing
many observed properties of spiral and elliptical galaxies. For the
long-term evolution of barred disc galaxies, a comparison of this scheme with
that of Palous et al. (1993) for their standard coefficients
of restitution of
![]() gives
basically the same results (Jungwiert, private communication).
Thus, the chosen model
should be applicable for a reliable determination of the difference
between gas dynamical and purely stellar dynamical models.
gives
basically the same results (Jungwiert, private communication).
Thus, the chosen model
should be applicable for a reliable determination of the difference
between gas dynamical and purely stellar dynamical models.
A comparison of gaseous models with dissipationless models shows no significant difference (Fig. 15). Due to the low gas densities only about 20-30% of the clouds undergo inelastic collisions which mainly occur in the denser central regions. Thus, the outer HI halo is only very weakly influenced by (sticky particle) gas dynamics and the application of purely stellar simulations for the HI is possible.
The previous simulations demonstrate that models based on an encounter scenario are able to reproduce the morphology of the three streamers. Furthermore, the interaction puts gas to the south-west of NGC 4449, where a clumpy HI distribution is observed (Hunter et al. 1998). Though its detailed patchy structure has not been recovered by the models, an initial gas distribution less regular than the smooth disc-like one used for the numerical models might be responsible for this deviation.
The parameter study showed that small variations
in the parameters give HI distributions which are not in agreement
with the observations. Especially, the strong dependence of the
final structure on the initial orientation of the HI disc
confines its inclination and position angle within 10![]() to the values derived independently from the observations.
This remarkable coincidence would occur necessarily in the
encounter scenario, whereas in the infall scenario it happens
just by chance. A second critical feature is the abrupt direction
change of the streamers. In the infall scenario they mark
the path of the perturbed gas which
collapses to the galactic center. However, it is hard to
imagine how a realistic static potential could create orbits
with such strong direction changes as e.g. the one from the vertical to the bridge
feature. Moreover, due to the large distance of these
features from the galactic center the potential should
be more or less spheroidal or already spherical, which makes
it even more difficult to produce such orbits.
to the values derived independently from the observations.
This remarkable coincidence would occur necessarily in the
encounter scenario, whereas in the infall scenario it happens
just by chance. A second critical feature is the abrupt direction
change of the streamers. In the infall scenario they mark
the path of the perturbed gas which
collapses to the galactic center. However, it is hard to
imagine how a realistic static potential could create orbits
with such strong direction changes as e.g. the one from the vertical to the bridge
feature. Moreover, due to the large distance of these
features from the galactic center the potential should
be more or less spheroidal or already spherical, which makes
it even more difficult to produce such orbits.
The most critical parameter for the interaction scenario is the
mass ratio q of DDO 125 and NGC 4449. The simulations demonstrate that
a mass ratio smaller than 10% cannot reproduce the streamer structure.
In order to determine q, both galactic masses have to be
known. In Bajaja et al.'s (1994) estimate for the mass of NGC 4449
they assumed that the HI is in rotational equilibrium even at a
distance of 32 kpc. However, in the case of an interaction with DDO 125
the velocities at large distances are strongly affected by
the interaction and they are definitely not in rotational equilibrium
(as the ejection of the tidal arms in a continuation of the simulations
demonstrates). Hence, the derived mass of
![]() is
at best an upper mass limit of NGC 4449. A better guess
is the dynamical mass inside the central gaseous ellipse
which seems to be unaffected by interaction. E.g. the dynamical
mass inside 11 kpc would be a factor 3 smaller than Bajaja's value.
is
at best an upper mass limit of NGC 4449. A better guess
is the dynamical mass inside the central gaseous ellipse
which seems to be unaffected by interaction. E.g. the dynamical
mass inside 11 kpc would be a factor 3 smaller than Bajaja's value.
Even more difficult is the mass determination
of DDO 125. Observations by Tully et al. (1978) gave a dynamical
mass of
![]() inside the optical radius of DDO 125.
However, Ebneter et al. (1987) reported a linear increase
in the rotation curve exceeding the range observed by Tully et al.
by a factor of two. Moreover, they found no hint of a flattening
or turn-over in DDO 125's rotation curve. This gives a lower mass
limit of
inside the optical radius of DDO 125.
However, Ebneter et al. (1987) reported a linear increase
in the rotation curve exceeding the range observed by Tully et al.
by a factor of two. Moreover, they found no hint of a flattening
or turn-over in DDO 125's rotation curve. This gives a lower mass
limit of
![]() .
Combining the mass estimates yields
a lower limit of the mass ratio of 6% when using Bajaja's mass
determination of NGC 4449. A more realistic mass ratio might be
derived from the ranges of rigid rotation resulting
in
.
Combining the mass estimates yields
a lower limit of the mass ratio of 6% when using Bajaja's mass
determination of NGC 4449. A more realistic mass ratio might be
derived from the ranges of rigid rotation resulting
in
![]() .
Thus, observationally it cannot be excluded that
the mass ratio is below the critical one for the interaction
scenario, however, the more realistic estimates seem to be in
agreement with the values found in the simulations. The situation
could be clarified when a reliable mass determination of DDO 125
is available.
.
Thus, observationally it cannot be excluded that
the mass ratio is below the critical one for the interaction
scenario, however, the more realistic estimates seem to be in
agreement with the values found in the simulations. The situation
could be clarified when a reliable mass determination of DDO 125
is available.
Another important question is related to the initial conditions of the previous simulations, i.e. the origin of the extended HI distribution. In principle, there are several possibilities:
Idea 1. The HI comes from DDO 125.
In a previous encounter (
![]() )
the gas was stripped off
from DDO 125. Due to the long orbital period of e.g. 3.6 Gyr for
)
the gas was stripped off
from DDO 125. Due to the long orbital period of e.g. 3.6 Gyr for
![]() the gas has enough time to settle down in a regular
disc-like structure. However, the amount of HI gas in DDO 125 is much
smaller than the gas seen around NGC 4449. It seems unlikely that
DDO 125 could have survived the loss of such a large fraction of its
gas content without disruption.
the gas has enough time to settle down in a regular
disc-like structure. However, the amount of HI gas in DDO 125 is much
smaller than the gas seen around NGC 4449. It seems unlikely that
DDO 125 could have survived the loss of such a large fraction of its
gas content without disruption.
Idea 2. The HI comes from NGC 4449. Though a star forming dwarf galaxy drives a galactic wind e.g. by means of type II supernovae, a detailed fine-tuning of the energy injection would be required to prevent a blow-out of the HI gas, especially if it acquired enough energy to form such an extended system. Moreover, the counter-rotation of the HI outside and inside the optical radius of NGC 4449 makes this scenario not very appealing.
Idea 3. The HI gas stems from a previous minor merger with NGC 4449. Though a satellite galaxy can be disrupted by the tidal field of NGC 4449, it is very unlikely that it is already disrupted far outside the galactic center where the HI gas is detected.
Idea 4. The HI originates from the collapse of a dwarf companion. A dwarf galaxy forms in the vicinity of NGC 4449 similar to the formation scenario of compact ellipticals suggested by Burkert (1994). By this it undergoes a strong collapse which leads to mass ejection due to violent relaxation. In principle, a mass loss of up to 40% of the companion could occur, providing enough gas to explain the HI. However, where is the dwarf today? Excluding an unlikely radial orbit, the dwarf's orbit could in principle decay by dynamical friction. However, due to the large distance to NGC 4449 the decay time should be at least several orbital periods, which exceeds the Hubble time.
Idea 5. Another major encounter. Although NGC 4449 is a member
of the loose Canes Venatici group, there seems to be
no close galaxy which has a radial velocity in agreement with
the rotational sense of the gaseous disc in NGC 4449. The only candidate is
the ringed Sab-type galaxy NGC 4736, located about 5.5 degrees south-east of
NGC 4449. The projected distance of 350 kpc and the differential radial
velocity of
![]() km s-1 (NED) is compatible with a
scenario in which both galaxies experienced a close encounter about
3.5 109 years ago on a hyperbolic orbit (Kohle 1999).
Placing NGC 4736 at a distance of 4.4 Mpc, its total HI mass is
km s-1 (NED) is compatible with a
scenario in which both galaxies experienced a close encounter about
3.5 109 years ago on a hyperbolic orbit (Kohle 1999).
Placing NGC 4736 at a distance of 4.4 Mpc, its total HI mass is
![]() (Bosma et al. 1977;
Mulder & van Driel 1993), which is quite low for Sab-type galaxies
(Solanes et al. 1996). Might it be that NGC 4449 formed its
halo out of gas stripped from another galaxy?
(Bosma et al. 1977;
Mulder & van Driel 1993), which is quite low for Sab-type galaxies
(Solanes et al. 1996). Might it be that NGC 4449 formed its
halo out of gas stripped from another galaxy?
Several N-body methods are combined in order to develop a method for the determination of the parameters of interacting galaxies. This method is applied to the HI distribution of NGC 4449. In a first step, the fast restricted N-body method is used to confine a region in parameter space which reproduces the main observed features. In a second step, a genetic algorithm (also using restricted N-body calculations) is employed which allows, in principle for both, an automatic fit of observational data even in a high-dimensional parameter space and/or a uniqueness test of a favoured parameter combination (only the latter has been done in this paper). For a genetic algorithm one typically has to follow a population of (at least) 100 members for 100 generations in order to get a good fit, provided the data are sufficiently accurate. Missing single pixels do not inhibit the parameter determination, as long as the key features are included in the data. Since a typical restricted N-body simulation takes a few CPU-seconds on a Sparc workstation, the whole fitting procedure is finished after 3-6 CPU-hours.
In the third step, the results of the previous steps are compared with detailed self-consistent N-body simulations. In the case of NGC 4449, they show that the restricted N-body calculations are reliable models for this encounter. The comparison with the sticky particle models demonstrates that the HI gas can be modeled without any restriction by a purely stellar dynamical approach, provided the encounter is weak, as in the case of NGC 4449 and DDO 125.
From the previous simulations, we conclude that the extended
HI features observed in NGC 4449 are created by an encounter
with DDO 125. Prior to the encounter, the HI gas formed
an extended, almost homogenous disc with a large scale length
of about 30 kpc and a radial extension of 40 (![]() ) kpc.
The orientation of the disc is in agreement with the
orientation of the inner ellipsoidal HI distribution.
The orbital plane has an inclination
angle of about 40
) kpc.
The orientation of the disc is in agreement with the
orientation of the inner ellipsoidal HI distribution.
The orbital plane has an inclination
angle of about 40![]() (
(
![]() ). The eccentricity
is in the vicinity of a parabolic encounter, but favouring the region
of elliptical orbits (
). The eccentricity
is in the vicinity of a parabolic encounter, but favouring the region
of elliptical orbits (
![]() ).
The apocenter distance of the galaxies is about
25 (
).
The apocenter distance of the galaxies is about
25 (![]() ) kpc. The closest approach happened
3.5-6.2 108 yr ago
(depending on eccentricity). The mass ratio of both galaxies must
be approximately 0.2 (and cannot be smaller than 0.1).
) kpc. The closest approach happened
3.5-6.2 108 yr ago
(depending on eccentricity). The mass ratio of both galaxies must
be approximately 0.2 (and cannot be smaller than 0.1).
Acknowledgements
The simulations were partly performed with the GRAPE3af special purpose computer in Kiel (DFG Sp345/5). The authors are grateful to Deidre Hunter, Jay Gallagher, Uli Klein and Hugo van Woerden for stimulating discussions about NGC 4449. We are also greatly indebted to Konrad Kuijken and John Dubinski who made their program for the generation of initial particle distributions available to the public, and Paul Charbonneau and Barry Knapp for providing their PIKAIA code. S.K. acknowledges DFG grant III GK-GRK 118/2. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Finally, we thank the language editor of A&A for a careful reading (and improving) of the manuscript.
In the following sections we briefly describe the main ingredients of our genetic algorithm. The GA used here is a slightly modified version of P. Charbonneau's code PIKAIA (for details see Charbonneau 1995). The interface between the GA and the simulations, i.e. the fitness determinations, is performed in a similar way as in Wahde (1998), however the coding of genes as well as the choice of parameters used as genes differ from Wahde's approach.
In order to determine the fitness of an individual (i.e. a special parameter
set), the N-body simulation has to be performed and compared with the
observation. Generally, this is done by mapping the particles on a Cartesian
grid. However, here a quadratic grid of size 60 kpc centered on NGC 4449
is used. The resolution
of the grid was set to ![]() in order to allow for a better resolution of the
tidal features of an encounter. For each grid cell the intensity was
calculated by summing the masses of the individual particles in that
cell. The conversion to observed intensities can be performed by assuming
a mass-to-light ratio for the particles (or treating it as another free
parameter) or by normalizing the intensities. Here the intensities are
normalized to the total intensity of the whole grid. The quality can be
measured by the relative deviation
in order to allow for a better resolution of the
tidal features of an encounter. For each grid cell the intensity was
calculated by summing the masses of the individual particles in that
cell. The conversion to observed intensities can be performed by assuming
a mass-to-light ratio for the particles (or treating it as another free
parameter) or by normalizing the intensities. Here the intensities are
normalized to the total intensity of the whole grid. The quality can be
measured by the relative deviation ![]() of the intensities in both
maps:
of the intensities in both
maps:
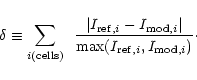 |
(A.1) |
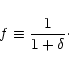 |
(A.2) |
In the case of an impossible parameter configuration (e.g. a circular orbit with a distance less than the observed projected distance) or any convergence problems the fitness of that point in parameter space is set to zero, prohibiting any offspring. Typically, only a few models in 104 parameter sets fail, most of them in the first few generations before the system starts to approach the parameter space region of interest.
In order to determine the parents of the next generation, the members of the actual generation are ranked by their fitness. The parents are then selected randomly, whereas the probability of being chosen is proportional to the rank (roulette-wheel selection).
In organic systems the information is coded in genes in the form of sequences of the four nucleotide bases where a triplet of them (a codon) encodes one amino acid, the building block of proteins. The genes themselves are arranged in one or several chromosomes which contain all the genetic information (or the genotype). The phenotype which is subject to the selection process is the result of the genetic information and the interaction with its environment.
Translated to our fitting problem, the
phenotype is the final intensity map created by a special choice of
parameters or initial conditions. The latter correspond to the proteins
which physically express the genetic information. The mapping between
the parameters and the genes or the number of chromosomes is not fixed in GAs.
Many GAs apply a binary alphabet to encode the parameters
(e.g. Holland 1975; Goldberg 1989).
In Charbonneau's program
PIKAIA a decimal encoding is implemented. For our calculations we
combined four decimal digits giving a number between zero and one.
This gene has been mapped to a real parameter by a linear or logarithmic
transformation, e.g. the orbital inclination is mapped
linearily to the range [![]() ,
180
,
180![]() ]
(Fig. A.2).
In general, the linear mapping of parameter x, which is allowed to vary
between
]
(Fig. A.2).
In general, the linear mapping of parameter x, which is allowed to vary
between
![]() and
and
![]() ,
is performed by
,
is performed by
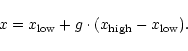 |
(A.3) |
The main difference between evolutionary strategies and genetic algorithms is the sexual reproduction in the framework of GAs. This means that the chromosomes of the parents are combined in a new manner by means of a cross-over mechanism in addition to mutation. The principle idea is illustrated in Fig. A.3: after determining the two parents a random position on the chromosomes is selected. At this position the chromosomes are split into two fragments which are exchanged among the chromosomes resulting in two new ones.
In order to introduce completely new information into a genepool
a mutation process, i.e. a random change of the information on the
chromosomes is introduced (Fig. A.4). For each position
on a chromosome, mutation is applied with a small probability
(typ.
![]() ). After selecting a position for
mutation, an integer random number in the range [0,9] replaces
the original value at that position. Thus, a real change in the genetic
information takes place with a probability of 90%, even if
that position of a gene is subject to mutation. The overall probability
for at least one real mutation on a chromosome coding 6
parameters by 4 digits is about 11%. Thus, cross-over is the most
important process introducing diversity into the population, whereas
mutation affects only each 9th member of the population. In principle,
the mutation rate can be increased, but the price would be a more
or less random search in parameter space which is already after a
few generations inferior to the oriented search of a GA method
(Wahde 1998).
). After selecting a position for
mutation, an integer random number in the range [0,9] replaces
the original value at that position. Thus, a real change in the genetic
information takes place with a probability of 90%, even if
that position of a gene is subject to mutation. The overall probability
for at least one real mutation on a chromosome coding 6
parameters by 4 digits is about 11%. Thus, cross-over is the most
important process introducing diversity into the population, whereas
mutation affects only each 9th member of the population. In principle,
the mutation rate can be increased, but the price would be a more
or less random search in parameter space which is already after a
few generations inferior to the oriented search of a GA method
(Wahde 1998).
A principal danger of GAs is inbreeding, i.e. the homogenization of the genepool by one or a few dominant
genes. If they successfully replace other genes, cross-over does not
introduce sufficient (or - if inbreeding is complete - any) diversity
into the population and thus any further improvement of the
chromosomes is prohibited. The only way to overcome this situation
is to introduce more diversity by mutation. Therefore, PIKAIA
allows for a variable mutation rate which increases the mutation
probability
![]() whenever the fitness distribution becomes narrow,
i.e. inbreeding is suspected to operate.
On the other hand,
whenever the fitness distribution becomes narrow,
i.e. inbreeding is suspected to operate.
On the other hand,
![]() is decreased if the fitness distribution
becomes very broad, i.e. the randomization is dominant.
is decreased if the fitness distribution
becomes very broad, i.e. the randomization is dominant.
After
![]() children have been created, the old
generation is completely replaced by the next generation (full
generational replacement). The only exception is the survival of the fittest
member of the parent generation, if it is fitter than the child which
would replace it (elitism). This mechanism prevents the
system from forgetting successful solutions.
children have been created, the old
generation is completely replaced by the next generation (full
generational replacement). The only exception is the survival of the fittest
member of the parent generation, if it is fitter than the child which
would replace it (elitism). This mechanism prevents the
system from forgetting successful solutions.
The initial population is randomly chosen in the accessible
parameter space. A standard population size is about
![]() members. The GA converges typically after
about
members. The GA converges typically after
about
![]() generations. Thus, 104 or a few 104N-body simulations are required for a single GA fit. For a
genetic algorithm simulation with 900 particles (and no offset for an inner
edge) 2 CPU-seconds are required per simulation compared to 3 CPU-hours
on a GRAPE3. Thus, self-consistent
N-body models, such as the mentioned GRAPE models, would still need
3.4 years, whereas the restricted N-body models reduce the
CPU-requirement to 5.6 hours on a 150 MHz-Sparc10.
generations. Thus, 104 or a few 104N-body simulations are required for a single GA fit. For a
genetic algorithm simulation with 900 particles (and no offset for an inner
edge) 2 CPU-seconds are required per simulation compared to 3 CPU-hours
on a GRAPE3. Thus, self-consistent
N-body models, such as the mentioned GRAPE models, would still need
3.4 years, whereas the restricted N-body models reduce the
CPU-requirement to 5.6 hours on a 150 MHz-Sparc10.