A&A 370, 436-446 (2001)
DOI: 10.1051/0004-6361:20010258

Open clusters in the third galactic quadrant

I. Photometry

A. Moitinho[*]


1 - Observatorio Astronómico Nacional, UNAM, Apdo. Postal 877, CP 22800, Ensenada B.C., México
2 - Instituto de Astrofísica de Andalucía (CSIC), Apdo. 3004, 18080 Granada, Spain

Received 13 December 2000 / Accepted 14 February 2001

Abstract
We have performed a photometric survey of open clusters in the third Galactic quadrant in order to study the star formation history and spatial structure in the Canis Major-Puppis-Vela region. In this paper we describe a catalogue of CCD $U\!BV\!RI$ photometry of approximately 65000 stars in the fields of 30 open clusters. The data were obtained and reduced using the same telescope, the same reduction procedures, and the same standard photometric system, which makes this catalogue the largest homogeneous source of open cluster photometry so far. In subsequent papers of this series, colour-colour and colour-magnitude diagrams will be presented which, amongst other uses, will allow the determination of an homogeneous set of cluster reddenings, distances, and ages that will constitute the observational basis for our studies of the spatial structure and star formation history in the third Galactic quadrant.

Key words: techniques: photometric - stars: fundamental parameters - Galaxy: open clusters and associations: general - Galaxy: structure - ISM: dust, extinction


1 Introduction

Open clusters are ideal objects for the investigation of several astrophysical problems, since they are groups of stars placed at a common distance, which were formed under the same conditions, in most cases at approximately the same time, and spanning a broad range in mass. These properties allow open cluster distances and ages to be better determined than in the case of isolated stars. Indeed, there is a virtually endless list of literature on stellar clusters used as tests for stellar evolution theories, and as probes of Galactic structure and evolution.

In the case of Galactic structure studies the existing compilations of open cluster parameters have allowed some understanding of the structure and development of the Galactic disc (Vogt & Moffat 1972; Janes & Adler 1982; Alfaro et al. 1991; Twarog et al. 1997; Carraro et al. 1998). However, many of the conclusions drawn from open cluster data have been if not controversial, at least affected by considerable uncertainty. Among the reasons for this situation are the lack of homogeneity of derived open cluster fundamental parameters (reddening, distances, ages, metalicities), as well as the small number of studies of certain kinds of clusters (e.g. old clusters and distant clusters).

The Catalogue of Open Cluster Data (COCD) (Lyngå 1981, 1987), which includes information for 1151 clusters (distances for 422) has been the observational basis for many Galactic structure studies. However, the parameters presented in the COCD were derived by different authors using a variety of instrumentation, techniques, calibrations, and analytic criteria, and therefore result in a rather inhomogeneous set. An analysis of the precision expected due to the effects of these inhomogeneities has been performed by Janes & Adler (1982) who have found a typical difference of 0.55 mag in distance moduli determined in different $U\!BV$ photometric studies. But even this large scatter in distance modulus determinations might be underestimated since several clusters have much larger ranges in their estimated distances. Cases like NGC 2453 which has distance estimates from 1500 to 5900 pc are not rare. These problems have been known to the astronomical community for a long time and have led to several attempts to produce more consistent sets of open cluster parameters. Loktin & Matkin (1994) reanalysed UBV photometry of 330 clusters and obtained a more homogeneous, although less numerous, catalogue of open cluster reddenings, distances and ages. However, Loktin & Matkin (1994) used three different sets of isochrones in their age and distance determinations which is likely to affect the internal precision of the catalogue. More recently, Dambis (1998) has given another contribution towards an homogeneous set of cluster parameters by redetermining the reddenings, distances and ages of 203 open clusters, younger than $\log t < 8.2$ to avoid chemical composition effects, using a single set of isochrones and an empirical ZAMS.

Although the works of Loktin & Matkin (1994) and Dambis (1998) have generated improved sets of cluster parameters by using the same kind of data ($U\!BV$ photometry), and were analysed in an homogeneous fashion, at least two effects still contribute to degrade the precision of their results. The first one is that both works used $U\!BV$ data from different sources, nominally on the $U\!BV$ system but in fact were calibrated using various sets of standard stars which can produce considerably different photometry (see Table 8 in this paper, and also Bessel 1995 for a detailed comparison of some versions of the $U\!BV\!RI$ system). The second and perhaps most important factor is the effect of photometric depth. Photoelectric photometry is usually limited to $V \sim 16$ mag, which in many cases is not enough for reliable distance determinations: evolutionary effects will produce redder colours and lead to underestimated distances. Also, for the younger clusters, the nearly vertical shape of the upper main sequence will introduce large uncertainties in distance determinations via ZAMS fitting.

In the light of the above mentioned problems with the current open cluster parameter compilations and of our interest in studying the star formation history and spatial structure of the Canis Major-Puppis-Vela region, we have performed a deep CCD $U\!BV\!RI$ photometric survey of open clusters using the same instruments, reduction methods and standard stars. In this paper we describe the photometric database. Reddenings, distances and ages will be determined in forthcoming papers using the same Zero Age Main Sequence (ZAMS) and evolutionary models.

In the next sections we describe the observations and data reductions, and present the photometric database. Later, in Sect. 6 a comparison with previously published photometry is shown. Finally, Sect. 7 is a discussion of the interstellar extinction law in the direction of our sample.

2 Observations

Open clusters in the galactic range $217^{\circ}< l <260^{\circ}$and $-5^{\circ} < b < 5^{\circ}$, with angular diameters of approximately $5^{\prime}$ and with estimated ages lesser than 1.3 108 yr ( $\log (age) \sim 8.1$) were selected from the COCD. 24 objects were selected following these criteria. To extend the sample, another 9 open clusters were selected in the same coordinate range but with no previous age estimates.

Data were acquired during five nights in Jan. 1994 and ten nights in Jan. 1998 at the CTIO 0.9 m telescope. Due to technical difficulties (focus), and to some non photometric nights, only 30 clusters were observed. The typical seeing during both runs was about $1.2\hbox{$^{\prime\prime}$ }$ although a few images presented higher values ($\sim$ $2.0\hbox{$^{\prime\prime}$ }$). The cluster names, coordinates and observing run are presented in Table 1.

 

 
Table 1: Observed open clusters
Name l b $\alpha (2000)$ $\delta(2000)$ Run
Bo 5 $232\hbox{$.\!\!^\circ$ }57$ $+00\hbox{$.\!\!^\circ$ }69$ $07^{\rm h}30\hbox{$.\!\!^{\rm m}$ }9$ $-17^{\circ}04^{\prime}$ 1998
Cz 29 $230\hbox{$.\!\!^\circ$ }80$ $+00\hbox{$.\!\!^\circ$ }93$ $07^{\rm h}28\hbox{$.\!\!^{\rm m}$ }3$ $-15^{\circ}24^{\prime}$ 1998
Haf 10 $230\hbox{$.\!\!^\circ$ }82$ $+01\hbox{$.\!\!^\circ$ }00$ $07^{\rm h}28\hbox{$.\!\!^{\rm m}$ }6$ $-15^{\circ}23^{\prime}$ 1998
Haf 16 $242\hbox{$.\!\!^\circ$ }07$ $+00\hbox{$.\!\!^\circ$ }47$ $07^{\rm h}50\hbox{$.\!\!^{\rm m}$ }3$ $-25^{\circ}27^{\prime}$ 1994
Haf 18 $243\hbox{$.\!\!^\circ$ }11$ $+00\hbox{$.\!\!^\circ$ }42$ $07^{\rm h}52\hbox{$.\!\!^{\rm m}$ }5$ $-26^{\circ}22^{\prime}$ 1994
Haf 19 $243\hbox{$.\!\!^\circ$ }04$ $+00\hbox{$.\!\!^\circ$ }52$ $07^{\rm h}52\hbox{$.\!\!^{\rm m}$ }7$ $-26^{\circ}15^{\prime}$ 1994
NGC 2302 $219\hbox{$.\!\!^\circ$ }28$ $-03\hbox{$.\!\!^\circ$ }10$ $06^{\rm h}51\hbox{$.\!\!^{\rm m}$ }9$ $-07^{\circ}04^{\prime}$ 1998
NGC 2309 $219\hbox{$.\!\!^\circ$ }89$ $-02\hbox{$.\!\!^\circ$ }22$ $06^{\rm h}56\hbox{$.\!\!^{\rm m}$ }2$ $-07^{\circ}12^{\prime}$ 1998
NGC 2311 $217\hbox{$.\!\!^\circ$ }73$ $-00\hbox{$.\!\!^\circ$ }68$ $06^{\rm h}57\hbox{$.\!\!^{\rm m}$ }8$ $-04^{\circ}35^{\prime}$ 1998
NGC 2335 $223\hbox{$.\!\!^\circ$ }62$ $-01\hbox{$.\!\!^\circ$ }26$ $07^{\rm h}06\hbox{$.\!\!^{\rm m}$ }6$ $-10^{\circ}05^{\prime}$ 1998
NGC 2343 $224\hbox{$.\!\!^\circ$ }31$ $-01\hbox{$.\!\!^\circ$ }15$ $07^{\rm h}08\hbox{$.\!\!^{\rm m}$ }3$ $-10^{\circ}39^{\prime}$ 1998
NGC 2353 $224\hbox{$.\!\!^\circ$ }73$ $+00\hbox{$.\!\!^\circ$ }38$ $07^{\rm h}14\hbox{$.\!\!^{\rm m}$ }6$ $-10^{\circ}18^{\prime}$ 1994
NGC 2367 $235\hbox{$.\!\!^\circ$ }64$ $-03\hbox{$.\!\!^\circ$ }85$ $07^{\rm h}20\hbox{$.\!\!^{\rm m}$ }1$ $-21^{\circ}56^{\prime}$ 1994
NGC 2383 $235\hbox{$.\!\!^\circ$ }27$ $-02\hbox{$.\!\!^\circ$ }43$ $07^{\rm h}24\hbox{$.\!\!^{\rm m}$ }8$ $-20^{\circ}56^{\prime}$ 1998
NGC 2384 $235\hbox{$.\!\!^\circ$ }39$ $-02\hbox{$.\!\!^\circ$ }42$ $07^{\rm h}25\hbox{$.\!\!^{\rm m}$ }1$ $-21^{\circ}02^{\prime}$ 1998
NGC 2401 $229\hbox{$.\!\!^\circ$ }67$ $+01\hbox{$.\!\!^\circ$ }85$ $07^{\rm h}29\hbox{$.\!\!^{\rm m}$ }4$ $-13^{\circ}58^{\prime}$ 1998
NGC 2414 $231\hbox{$.\!\!^\circ$ }41$ $+01\hbox{$.\!\!^\circ$ }97$ $07^{\rm h}33\hbox{$.\!\!^{\rm m}$ }3$ $-15^{\circ}27^{\prime}$ 1998
NGC 2425 $231\hbox{$.\!\!^\circ$ }49$ $+03\hbox{$.\!\!^\circ$ }31$ $07^{\rm h}38\hbox{$.\!\!^{\rm m}$ }3$ $-14^{\circ}52^{\prime}$ 1998
NGC 2432 $235\hbox{$.\!\!^\circ$ }48$ $+01\hbox{$.\!\!^\circ$ }78$ $07^{\rm h}40\hbox{$.\!\!^{\rm m}$ }9$ $-19^{\circ}05^{\prime}$ 1998
NGC 2439 $246\hbox{$.\!\!^\circ$ }41$ $-04\hbox{$.\!\!^\circ$ }43$ $07^{\rm h}40\hbox{$.\!\!^{\rm m}$ }8$ $-31^{\circ}39^{\prime}$ 1994
NGC 2453 $243\hbox{$.\!\!^\circ$ }33$ $-00\hbox{$.\!\!^\circ$ }93$ $07^{\rm h}47\hbox{$.\!\!^{\rm m}$ }8$ $-27^{\circ}14^{\prime}$ 1998
NGC 2533 $247\hbox{$.\!\!^\circ$ }80$ $+01\hbox{$.\!\!^\circ$ }29$ $08^{\rm h}07\hbox{$.\!\!^{\rm m}$ }0$ $-29^{\circ}54^{\prime}$ 1998
NGC 2571 $249\hbox{$.\!\!^\circ$ }10$ $+03\hbox{$.\!\!^\circ$ }54$ $08^{\rm h}18\hbox{$.\!\!^{\rm m}$ }9$ $-29^{\circ}44^{\prime}$ 1998
NGC 2588 $252\hbox{$.\!\!^\circ$ }28$ $+02\hbox{$.\!\!^\circ$ }45$ $08^{\rm h}23\hbox{$.\!\!^{\rm m}$ }2$ $-32^{\circ}59^{\prime}$ 1998
NGC 2635 $255\hbox{$.\!\!^\circ$ }60$ $+03\hbox{$.\!\!^\circ$ }97$ $08^{\rm h}38\hbox{$.\!\!^{\rm m}$ }5$ $-34^{\circ}46^{\prime}$ 1998
Rup 18 $239\hbox{$.\!\!^\circ$ }94$ $-04\hbox{$.\!\!^\circ$ }92$ $07^{\rm h}24\hbox{$.\!\!^{\rm m}$ }8$ $-26^{\circ}13^{\prime}$ 1998
Rup 55 $250\hbox{$.\!\!^\circ$ }68$ $+00\hbox{$.\!\!^\circ$ }76$ $08^{\rm h}12\hbox{$.\!\!^{\rm m}$ }3$ $-32^{\circ}36^{\prime}$ 94/98
Rup 72 $259\hbox{$.\!\!^\circ$ }55$ $+04\hbox{$.\!\!^\circ$ }37$ $08^{\rm h}52\hbox{$.\!\!^{\rm m}$ }1$ $-37^{\circ}36^{\prime}$ 1998
Rup 158 $259\hbox{$.\!\!^\circ$ }55$ $+04\hbox{$.\!\!^\circ$ }42$ $08^{\rm h}52\hbox{$.\!\!^{\rm m}$ }3$ $-37^{\circ}34^{\prime}$ 1998
Tr 7 $238\hbox{$.\!\!^\circ$ }28$ $-03\hbox{$.\!\!^\circ$ }39$ $07^{\rm h}27\hbox{$.\!\!^{\rm m}$ }3$ $-24^{\circ}02^{\prime}$ 94/98


In both runs, images were taken with a $2048 \times 2048$ Tek CCD and the standard set of $U\!BV\!RI$ filters available at CTIO. The $0.39^{\prime \prime}$/pixel plate scale resulted in a field of view of $13^{\prime}\times 13^{\prime}$. Images were acquired using the CTIO ARCON operating in Quad mode (http://www.ctio.noao.edu/instruments/arcon/ arcon.html). The gain was set at 3.2 e-/adu and the readout noise was determined to be 4.0 e-.

Besides the cluster fields, a number of standard star fields (Landolt 1983, 1992) were observed for calibration purposes. For the bias level and flat field corrections, zero second exposures and blank sky exposures in all filters were acquired each night. In the 1998 run, several short and long dome exposures were obtained with the purpose of creating a mask for the correction of shutter effects.

3 Data reduction

   
3.1 Photometry

Images were processed using IRAF. All images were subjected to the usual overscan, bias, and flatfield corrections. In the case of the 1998 run, a shutter mask was built and used to correct both flatfield and object frames from shutter timing effects, prior to flatfield division. The shutter mask was built and used following a variation of the recipe given by Stetson (Stetson 1989) using six series of one twenty sec exposures and twenty one sec exposures. In the 1994 run no shutter images were acquired, so these data were not corrected from shutter effects. To quantify the effect of the shutter on the 1994 data we have analysed our photometry of Ruprecht 55 and Trumpler 7, which were observed on both runs, and found no significant trends.

Photometry was performed using the IRAF/ DAOPHOT (Stetson et al. 1990) package. Standard stars were measured via aperture photometry with the APPHOT task. A 26 pix ( $10\hbox{$^{\prime\prime}$ }$) radius aperture was adopted since it included virtually all the stellar flux in all images as indicated by a growth curve analysis (Howell 1989). Magnitudes in the cluster fields were obtained following the standard procedures for PSF determination and fitting within IRAF/DAOPHOT. Due to the large size of the CCD chip, a quadratically variable PSF had to be used. About 60-70 well distributed PSF stars were selected by hand in each frame and were also used in the aperture correction determinations. The variable PSF was not able to adequately model the external regions of the images, so measurements for stars separated less than 150 pix from the edges were not used, which limited the useful field of view to $11^{\prime}\times 11^{\prime}$. Stars with a goodness of fit parameter, $\chi$, greater that 2.5 and with error estimates greater than 0.1, as output from ALLSTAR, were also dropped out. At the end of this process a list of aperture corrected PSF photometry was obtained for each image. In total, 4.095 standard star aperture measurements and 2.096.414 cluster field PSF measurements were performed.

  
3.2 Atmospheric extinction 

Although there are good reasons to determine the extinction and transformation coefficients simultaneously through a multilinear regression (Harris et al. 1981), our experience has shown us that the presence of a larger number of free parameters in each equation can affect the robustness of the method, thus leading to unphysical coefficients (such as negative extinction coefficients when airmass-colour cross terms are included). Therefore, we have decided to determine the extinction and transformation coefficients separately.

Traditionally, extinction is determined assuming Bouguer's law, Mi=Mi0 + KiX, where Mi is the i band magnitude measured at airmass X, Mi0 is the magnitude one would measure outside the atmosphere, and Ki is the extinction coefficient for band i. Following this model, the extinction coefficient is usually determined as the slope yielded by a simple linear least squares fit of Mi vs. X. Ignoring the contribution of higher order extinction coefficients (Young 1974), the main inconvenience of this approach is that the slope determination should be based on many measurements of a single star. Since Mi0 will be different from star to star one can not use different stars on a simultaneous determination of Ki in a direct manner. The use of an average Ki value determined from a few measurements of different stars is not a good alternative because the errors of individual determinations can be very large, producing an uncertain Ki. One way to use different stars in a simultaneous determination of the extinction coefficients is to employ Bouguer's law in a modified fashion. If we consider two measurements of a star at two different airmasses, we can write $\Delta M = K \Delta X$, were $\Delta M$ is the difference of the star's magnitudes measured at different airmasses and $\Delta X$ is the difference of the airmasses (the i index is dropped for simplicity). Since the M0 term is no longer present, this equation is independent of the star under consideration and therefore measurements from different stars can be used in a simultaneous determination of the extinction coefficient. When there are N measurements at different airmasses for a certain star the question of which of the possible N(N-1)/2 differences, $\Delta M$ and $\Delta X$, should be used arises, since only N-1 of them are independent. One of the most natural solutions would be to use the lowest airmass measurement as a reference to be subtracted from all the other measurements so that the range in $\Delta X$ would be maximised. The drawback of this choice is that any error in the reference's measurements will be introduced in a systematic way in all the differences. Since in principle any of the possible $\Delta M$ and $\Delta X$ could be used to determine the extinction coefficient, we have decided to use all the possible differences together in the same plot expecting that a bad measurement should produce outliers distinguishable from the dense cloud of good points.

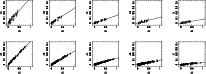  \begin{figure} \par\resizebox{18cm}{!}{\includegraphics{ms10557f1.eps}}\end{figure} Figure 1: Top: linear fits for the 1994 run extinction determinations. Bottom: the same for the 1998 run
Open with DEXTER

Figure 1 shows the linear fits of the extinction determinations for the 1994 and 1998 runs. The fits were performed with the origin fixed to zero. A per night analysis showed that within each run the extinction coefficients remained constant (with a precision better that 0.01 mag), and therefore data from different nights were used together to determine average extinction coefficients for each run. The results are summarised in Table 2, where a noticeable decrease in extinction of about 0.03 mag is appreciated from 1994 to 1998.

 

 
Table 2: Extinction coefficients and rms residuals of the fits
Run KU $\sigma_U$ KB $\sigma_B$ KV $\sigma_V$ KR $\sigma_R$ KI $\sigma_I$
1994 0.484 0.029 0.273 0.015 0.146 0.009 0.110 0.013 0.072 0.012
1998 0.444 0.012 0.248 0.011 0.122 0.008 0.083 0.010 0.037 0.009


3.3 Transformation to the standard system

Once the instrumental magnitudes were corrected from extinction, night to night variations in the instrumental zero point were determined, for each band, relative to a reference night (in the same observing run) using stars that were observed across several nights. These displacements were used to transform observations from different nights onto the system of the reference night.

As previously mentioned, photometry for several stars from Landolt (1992) was obtained in order to determine the transformations between the instrumental and the standard system. We assume that the instrumentation was stable enough so that besides zero point variations, the transformation coefficients did not change within an observing run. The photometric relations between the reference night and the standard system were taken to be of the form of Eqs. (1) to (5).

     
v-V = $\displaystyle \alpha_{0} + \alpha_{1} (B-V)$ (1)
(b-v) = $\displaystyle \beta_{0} + \beta_{1} (B-V)$ (2)
(u-b) = $\displaystyle \gamma_{0} + \gamma_{1} (B-V) + \gamma_{2} (U-B)$ (3)
(v-i) = $\displaystyle \delta_{0} + \delta_{1} (V-I)$ (4)
(v-r) = $\displaystyle \varepsilon_{0} + \varepsilon_{1} (V-R).$ (5)

In these equations, the upper case letters refer to the standard indexes, the lower case letters are the instrumental magnitudes and colours (corrected from atmospheric extinction and on the system of the reference night). The $\alpha_{i}$, $\beta_{i}$, $\gamma_{i}$, $\delta_{i}$, and $\varepsilon_{i}$ were determined through least squares fits. In the 1998 data the residuals of the (u-b)transformation (Eq. (3)) showed some dependence on (B-V)2, so for this run Eq. (3) was modified to

 \begin{displaymath}% (u-b) = \gamma_{0} + \gamma_{1} (B-V) + \gamma_{2} (U-B) + \gamma_{3} (B-V)^{2}. \end{displaymath} (6)

Because the B photometry was not as deep as the V photometry, Eq. (7) was used in the determination of the V magnitudes when B photometry was not available.

 \begin{displaymath}v-V = \zeta_{0} + \zeta_{1} (V-I). \end{displaymath} (7)


 

 
Table 3: Transformation coefficients
Run Night $\alpha_{0}$ $\alpha_{1}$ $\beta_{0} $ $\beta_{1}$ $\gamma_{0}$ $\gamma_{1}$ $\gamma_{2}$ $\gamma_{3}$ $\delta_{0}$ $\delta_{1}$ $\varepsilon_{0}$ $\varepsilon_{1}$ $\zeta_{0}$ $\zeta_{1}$
1994 1 2.821 -0.013 0.148 1.106 1.625 0.076 0.757 0.000 -1.000 0.997 -0.128 0.963 2.821 -0.012
  2 2.801 -0.013 0.162 1.106 1.559 0.076 0.757 0.000 -1.015 0.997 -0.126 0.963 2.801 -0.012
  3 2.832 -0.013 0.185 1.106 1.635 0.076 0.757 0.000 -0.995 0.997 -0.121 0.963 2.832 -0.012
  4* 2.839 -0.013 0.180 1.106 1.614 0.076 0.757 0.000 -0.976 0.997 -0.111 0.963 2.840 -0.012
  5 2.844 -0.013 0.180 1.106 1.597 0.076 0.757 0.000 -0.950 0.997 -0.100 0.963 2.845 -0.012
1998 1 2.826 -0.015 0.185 1.096 1.480 -0.013 0.772 0.144 -0.994 0.999 -0.124 0.964 2.830 -0.017
  2 2.821 -0.015 0.167 1.096 1.503 -0.013 0.772 0.144 -1.004 0.999 -0.115 0.964 2.825 -0.017
  3* 2.825 -0.015 0.175 1.096 1.500 -0.013 0.772 0.144 -1.003 0.999 -0.115 0.964 2.828 -0.017
  4 2.815 -0.015 0.174 1.096 1.497 -0.013 0.772 0.144 -1.008 0.999 -0.122 0.964 2.819 -0.017
  5 2.811 -0.015 0.175 1.096 1.506 -0.013 0.772 0.144 -1.009 0.999 -0.115 0.964 2.815 -0.017
  8 2.767 -0.015 0.166 1.096 1.491 -0.013 0.772 0.144 -1.009 0.999 -0.119 0.964 2.770 -0.017
  9 2.754 -0.015 0.176 1.096 1.485 -0.013 0.772 0.144 -1.021 0.999 -0.112 0.964 2.758 -0.017


The transformation coefficients obtained from the linear fits of Eqs. (1) to (7) are presented in Table 3. This table also presents the zero point coefficients for each night corrected from the displacements relative to the reference night. The reference night for each run is marked with an asterisk. Coefficients for nights 6, 7 and 10 of the 1998 run are not presented since these were considered to be non photometric due to occasional cloud coverage. The rms deviations of the fits are shown in Table 4. In the 1994 run, typically 14 standard stars were observed each night, resulting in a total of 17 standards for the whole run. In the 1998 run about 30 standard stars were observed each night, yielding a total of 60 standards.
 

 
Table 4: Rms residuals of the transformations to the standard system
Run $\Delta V$ $\Delta (B-V)$ $\Delta (U-B)$ $\Delta (V-I)$ $\Delta (V-R)$ $\Delta V$
  (Eq. (1)) (Eq. (2)) (Eq. (3)) (Eq. (4)) (Eq. (5)) (Eq. (7))
1994 0.011 0.012 0.024 0.016 0.011 0.011
1998 0.012 0.008 0.010 0.007 0.007 0.012


4 Construction of the photometric catalogue

The photometry lists obtained as described in Sect. 3.1 were corrected from atmospheric extinction using the coefficients in Table 2 and transformed to the system of the reference night. Since several measurements per band were available for each cluster, the final instrumental photometry is an average of the individual measurements weighted by the internal errors output by the ALLSTAR task. The final internal errors assigned to each star were taken to be the error of the average. When only one measurement was available the error was taken to be the one output by ALLSTAR. The average magnitudes were then transformed to the standard system using the coefficients from Table 3.

As previously mentioned, nights 6, 7 and 10 of the 1998 run were considered non photometric due to occasional cloud coverage. During the clear periods of these nights, long exposures of several open clusters were acquired (NGC 2571, NGC 2311, NGC 2343, NGC 2432, NGC 2635, and Rup 18). The photometry for these frames was then transformed to the instrumental system by comparison with shorter exposures taken on photometric nights.

The final catalogue of calibrated data which includes photometry and error estimates for 64.619 stars in at least three of the five $U\!BV\!RI$bands will be made available electronically at the CDS. Table 5 summarises the contribution in number of measurements, photometric depth and field of view of this study relative to previous works. In Table 5, N is the number of stars measured in this work, $N_{\rm O}$, $V_{\rm lim}$ and Field are the number of stars, limiting magnitude and the field of view covered in previous works that used the technique presented in the Data column (pe - photoelectric; pgr - photographic; ccd - CCD). The column Other indicates the existence of other studies performed using other techniques that, due their lower precision or number of stars, were not included in the comparison. For this work the limiting magnitude is $V_{\rm lim} \sim 21$ (except for Haf 18 and Haf 19 where $V_{\rm lim} \sim 20$) and the field of view is approximately $11\hbox {$^\prime $ }\times 11\hbox {$^\prime $ }$. In Table 5, the clusters marked with the same symbol have small angular separations and appear in the same image. For these clusters the number of stars refers to the whole image and is indicated only once. All the other empty fields represent unavailable data. The data from previous studies was obtained from the WEBDA (http://obswww.unige.ch/webda/) open cluster database of Mermilliod (1988, 1992). The WEBDA database has allowed this and other analysis throughout this work to be performed in a reasonable time.

 

 
Table 5: Contribution of this study relative to previous work. For this study $V_{\rm lim} \sim 21$ and the field of view is $11\hbox {$^\prime $ }\times 11\hbox {$^\prime $ }$
Cluster N $N_{\rm O}$ $V_{\rm lim}$ Field Data Other
        ($^{\prime}$)    
Bo 5 861 16 12.5 $10\times 5$ pe  
Cz 29a 3018 18 15 $3\times 3$ pgr  
Haf 10a   9 15 $3\times 3$ pgr  
Haf 16 4522 15 15 $4\times 4$ pe  
Haf 18b 2304 50 17 $2\times 3$ ccd pe, pgr
Haf 19b   70 18 $2\times 3$ ccd pe, pgr
NGC 2302 1521 16 15 $4\times 4$ pe  
NGC 2309 1767   21 $6\times 6$ ccd  
NGC 2311 1191          
NGC 2335 1332 60 14 $20\times 20$ pe  
NGC 2343 1319 55 15 $16\times 16$ pe  
NGC 2353 2199 53 15 $17\times 17$ pe pgr
NGC 2367 2571 15 14 $3\times 4$ pe  
NGC 2383c 2682 722 20.5 $5\times 5$ ccd pe
NGC 2384c   304 20 $5\times 5$ ccd pe
NGC 2401 1892          
NGC 2414 1992 12 14 $4\times 3$ pe pgr
NGC 2425 2397          
NGC 2432 2901          
NGC 2439 3477 120 18.5 $2\times 3$ ccd pe, pgr
NGC 2453 2605 356 19 $4\times 6$ ccd pe, pgr
NGC 2533 3121 122 14.5 $11\times 11$ pgr pe
NGC 2571 2723 144 14.5 $16\times 16$ pgr pe
NGC 2588 2904          
NGC 2635 3198 6 14 $2\times 2$ pe  
Rup 18 2068 20 14 $2\times 7$ pe  
Rup 55 4534 29 16 $4\times 4$ pe pgr
Rup 72d 2951          
Rup 158d            
Tr 7 2569 16 14 $3\times 5$ pe  


5 Photometric errors

The path that leads from the observations to the final calibrated photometry is composed of several steps, each one affected by some error that contributes to the total uncertainty of the final results. To estimate the errors we have split the problem in two parts. In the first place are all the processes involved in obtaining the instrumental magnitudes, which are mainly affecting the photometric precision. In the second place is the transformation to the standard system, which mainly affects the final photometric accuracy.

In the process of arriving to the instrumental magnitudes, CCD images were processed, PSFs were fit, aperture and extinction corrections were applied, and night to night photometric zero point offsets were also applied. The whole process is highly complex and full of subjective decisions, which makes any formal step by step error treatment virtually impossible. Nevertheless, we can analyse how the these processes affect the photometric precision by analysing the dispersion of measurements.

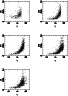  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10557f2.eps}}\end{figure} Figure 2: Standard deviation of the instrumental magnitudes for stars of NGC 2571 observed 10 times or more
Open with DEXTER

Figure 2 shows the standard deviation (not the error of the mean value) of the instrumental magnitudes for stars in the field of NGC 2571 which have 10 or more measurements and therefore represent the error of an individual measurement. Table 6 summarises the data in Fig. 2 for a number of magnitude ranges.

 

 
Table 6: Typical precision of an individual measurement
V $\sigma_U$ $\sigma_B$ $\sigma_V$ $\sigma_R$ $\sigma_I$
$\leq$14 0.026 0.015 0.011 0.012 0.012
14 - 16 0.033 0.021 0.017 0.016 0.018
16 - 18 0.042 0.038 0.032 0.026 0.031
>18 -- 0.054 0.053 0.046 0.043


Because NGC 2571 was observed in four different nights, the dispersion also includes the effects of uncertainties in the night to night variations of the transformation zero point. The errors of the averaged data are represented by the error of the mean which are smaller than values in Table 6, depending on the number of measurements used. Most stars in the catalogue have three measurements per band, although there are cases like NGC 2571 and Rup 18 that have been observed up to seventeen times per band and whose errors are considerably smaller (about one fourth of the tabulated values).

 

 
Table 7: Total errors for individual measurements
V $\sigma_V$ $\sigma_{(B-V)}$ $\sigma_{(U-B)}$ $\sigma_{(V-R)}$ $\sigma_{(V-I)}$
$\leq$14 0.016 0.020 0.032 0.018 0.018
14- 16 0.021 0.028 0.040 0.024 0.026
16- 18 0.034 0.050 0.058 0.042 0.045
>18 0.054 0.076 -- 0.071 0.069


The total photometric errors for a single measurement have been estimated by quadratically adding the internal errors from Table 6 to obtain the errors in each colour and then quadratically adding these errors to the residuals of the standard transformation from Table 3. The total errors are presented in Table 7. The values in this table should be regarded as upper error limits for our photometry since they refer to individual measurements. Also, when constructing the colour indexes some contributions to the magnitude errors tend to cancel out instead of increasing the uncertainty, as we have assumed by quadratically adding the errors in each band. Finally, because only one long exposure per band was acquired for NGC 2571, the error analysis has been performed using photometry from short exposure frames, therefore leading to overestimated errors in the faint end.

   
6 Comparison with photometry from other studies

Several of the observed cluster fields have been the subject of previous photometric studies. Most of them, however, have been performed by different authors using different kinds of detectors, filters, and sets of standard stars. The comparison of these data to the homogeneous photometry from this study can provide a common photometric scale therefore making the discussion of the different results more meaningful. In the search of photometry and finding charts from previous studies we have made extensive use of the WEBDA database. The result of the comparisons is summarised in Table 8 where only studies with more than five stars in common were considered.

In Tables 8a and 8b, $\Delta$ is the difference between our photometry and previous one in the sense of $\Delta = $ this work - previous work, $\sigma$ is the standard deviation of $\Delta$, N is the number of stars used in the comparison, and Data is the kind of compared data: Pe - photoelectric, Pgr - photographic, and CCD - CCD. Because of the large number of studies involved, we have limited the analysis to the average differences and their dispersions. Some stars that presented large discrepancies possibly due to bad identifications, variability, or contamination from neighbouring stars (affecting non-psf studies) were not used.

The comparisons in Tables 8a and 8b show that in general our photometry does agree with the one from other studies. Cases were the agreement is not so good usually correspond to comparisons with photographic data (ex. Cz 29 and Haf 10). There are significative differences relative to the photoelectric photometry of Seggewiss (Seggewiss 1971), but there is good agreement with other data for the same clusters.

 

 
Table 8: a) Comparison with previous $U\!BV$ photometry
Cluster $\Delta V$ $\sigma$ N $\Delta (B-V)$ $\sigma$ N $\Delta (U-B)$ $\sigma$ N Data Ref
Bo 5 0.025 0.017 11 0.000 0.025 14 -0.006 0.038 9 pe 1
Cz 29 0.179 0.142 18 0.073 0.056 14 -0.025 0.104 15 pgr 2
Haf 10 0.284 0.244 9 0.087 0.142 8 -0.046 0.183 7 pgr 2
Haf 16 0.030 0.090 12 0.020 0.054 11 0.087 0.041 11 pe 3
Haf 18 0.030 0.090 20 0.075 0.050 20 0.022 0.154 22 pgr 4
Haf 18 0.047 0.048 14 0.000 0.038 13 -0.044 0.046 11 pe 5
Haf 18 -0.002 0.016 50 -0.042 0.017 51 0.046 0.091 10 ccd 6
Haf 18 -0.012 0.029 26 -0.035 0.030 23 -- -- -- ccd 7
Haf 19 0.024 0.015 50 -0.092 0.017 52 -0.308 0.045 11 ccd 8
Haf 19 0.027 0.063 16 0.056 0.077 20 -0.042 0.108 16 pe 5
Haf 19 -0.010 0.073 17 0.099 0.081 19 0.042 0.146 20 pgr 4
Haf 19 -0.015 0.018 31 -0.048 0.021 31 -- -- -- ccd 7
NGC 2302 0.061 0.062 15 -0.005 0.014 13 0.032 0.049 14 pe 1
NGC 2335 0.027 0.022 24 -0.013 0.016 24 -0.005 0.046 24 pe 9
NGC 2335 0.163 0.087 5 0.029 0.030 5 -0.075 0.069 5 pe 10
NGC 2343 0.055 0.034 32 -0.011 0.015 33 -0.005 0.040 36 pe 11
NGC 2343 0.164 0.116 7 0.000 0.026 6 0.010 0.143 7 pe 10
NGC 2353 -0.028 0.031 23 -0.003 0.026 25 -0.027 0.093 26 pe 12
NGC 2353 -0.026 0.071 57 0.000 0.069 59 0.006 0.105 53 pgr 13
NGC 2353 -0.061 0.043 5 0.030 0.062 5 -0.006 0.089 5 pe 13
NGC 2353 -0.031 0.145 4 0.008 0.020 4 -0.028 0.147 4 pe 14
NGC 2367 0.013 0.032 12 -0.010 0.011 11 -0.065 0.041 12 pe 3
NGC 2367 -0.033 0.012 6 -0.009 0.043 8 -0.035 0.013 5 pe 15
NGC 2383 -0.014 0.018 8 0.035 0.038 11 -0.009 0.068 9 pe 3
NGC 2383 0.000 0.054 579 -0.014 0.066 487 -- -- -- ccd 16
NGC 2384 0.033 0.025 10 0.036 0.020 10 0.000 0.021 10 pe 3
NGC 2384 0.052 0.051 19 0.021 0.034 20 -0.009 0.031 14 pgr 17
NGC 2384 0.041 0.060 215 0.006 0.066 185 -- -- -- ccd 16
NGC 2414 0.019 0.035 7 -0.007 0.016 7 -- -- -- pe 3
NGC 2439 -0.007 0.041 98 0.004 0.029 95 0.026 0.107 92 pgr 18
NGC 2439 0.002 0.027 96 -0.022 0.042 89 -0.032 0.061 33 ccd 19
NGC 2439 -0.003 0.027 38 -0.013 0.022 39 0.031 0.047 34 pe 18
NGC 2439 -0.060 0.106 48 -0.024 0.059 47 -- -- -- pgr 20
NGC 2453 0.001 0.056 44 0.061 0.069 43 -0.108 0.060 36 pgr 21
NGC 2453 0.016 0.042 16 -0.004 0.026 16 -0.046 0.054 20 pe 22
NGC 2453 0.037 0.039 292 0.028 0.046 180 -- -- -- ccd 23
NGC 2453 0.105 0.125 5 0.059 0.045 6 -0.060 0.078 6 pe 10
NGC 2533 -0.004 0.090 93 0.120 0.092 93 0.192 0.074 37 pgr 24
NGC 2533 0.020 0.084 5 -0.024 0.047 4 0.011 0.042 4 pe 25
NGC 2533 0.054 0.034 7 -0.038 0.034 7 0.030 0.022 6 pe 26
NGC 2533 -0.041 0.041 11 -0.021 0.039 13 -0.080 0.061 12 pe 27
NGC 2571 0.002 0.025 37 -0.013 0.015 38 -0.007 0.038 39 pe 28
NGC 2571 0.098 0.069 73 -0.011 0.068 70 -0.014 0.072 71 pgr 29
NGC 2571 -0.008 0.099 76 0.050 0.150 84 -0.048 0.131 40 pgr 24
NGC 2635 0.159 0.114 6 0.029 0.077 5 -0.097 0.233 6 pe 3
Rup 18 0.011 0.042 19 0.023 0.017 16 -0.135 0.094 18 pe 1
Rup 55 0.009 0.032 13 -0.020 0.031 14 -0.035 0.058 13 pe 1
Tr 7 0.029 0.021 6 0.016 0.020 6 -0.034 0.048 6 pe 3



 
Table 8: b) Comparison with previous $V\!RI$ photometry
Cluster $\Delta (V-R)$ $\sigma$ N $\Delta (V-I)$ $\sigma$ N Data Ref
Haf 18 -0.001 0.012 35 0.033 0.027 33 ccd 6
Haf 19 0.028 0.020 57 0.015 0.019 55 ccd 8
NGC 2383 0.003 0.052 591 -0.095 0.061 564 ccd 16
NGC 2384 0.021 0.057 223 -0.103 0.080 224 ccd 16
NGC 2453 -- -- -- 0.061 0.056 287 ccd 23
NGC 2533 -0.118 0.204 11 -0.289 0.318 15 pe 27

References for Tables 8a and 8b  
1 -- Moffat & Vogt (Moffat & Vogt 1975) 16 -- Subramaniam & Sagar (Subramaniam & Sagar 1999)
2 -- FitzGerald & Moffat (FitzGerald & Moffat 1980) 17 -- Hassan (Hassan 1984)
3 -- Vogt & Moffat (1972) 18 -- White (White 1975)
4 -- FitzGerald & Moffat (FitzGerald & Moffat 1974) 19 -- Ramsay & Pollaco (Ramsay & Pollacco 1992)
5 -- Moffat & FitzGerald (Moffat & FitzGerald 1974) 20 -- Becker et al. (Becker et al.(1976)Becker, Svolopoulos, & Fang)
6 -- Munari et al. (Munari et al. 1998) 21 -- Moffat & FitzGerald (Moffat & FitzGerald 1974)
7 -- Labhart et al. (Labhart et al. 1992) 22 -- Moffat & FitzGerald (Moffat & FitzGerald 1974)
8 -- Munari & Carraro (Munari & Carraro 1996) 23 -- Mallik et al. (Mallik et al. 1995)
9 -- Clariá (Clariá 1973) 24 -- Lindoff (Lindoff 1968)
10 -- Seggewiss (Seggewiss 1971) 25 -- Eggen (Eggen 1974)
11 -- Clariá (Clariá 1972) 26 -- Havlen (Havlen 1976)
12 -- FitzGerald et al. (FitzGerald et al. 1990) 27 -- Jorgensen & Westerlund (Jorgensen & Westerlund 1988)
13 -- Hoag et al. (Hoag et al. 1961) 28 -- Clariá (Clariá1976)
14 -- Clariá (Clariá1974) 29 -- Kilambi (Kilambi 1978)
15 -- Pedreros (Pedreros(1984))    


In the case of Haf 19 we find a great difference in (U-B) relative to the values of Munari & Carraro (Munari & Carraro 1996) ( $\Delta(U-B) \sim -0.3$). On the other hand we find that our (U-B) photometry is comprised between the data of Moffat & FitzGerald (Moffat & FitzGerald 1974) and FitzGerald & Moffat (FitzGerald & Moffat 1974), although the dispersion in these comparisons is quite large ( $\sigma \sim 0.1$). The photometry of NGC 2635 also presents large deviations from the one obtained by Vogt & Moffat (1972). However the comparison was performed with only five stars, and three of them have very close bright neighbours, which could be the explanation of the higher brightness of the photoelectric data of Vogt & Moffat (1972) relative to our PSF magnitudes.

Regarding the $V\!RI$ comparisons, we find good agreement with the CCD photometry of Munari & Carraro (Munari & Carraro 1996) and Munari et al. (Munari et al. 1998), and somewhat large deviations with respect to the (V-I) colours from the other CCD studies. The largest deviations occur with the photoelectric data of Jorgensen & Westerlund (Jorgensen & Westerlund 1988) where the difference is better described by a significative colour term ( $\Delta (V-R)_{\rm pe}=0.009 - 0.621\times (V-R)_{\rm CCD}$ with $\sigma \sim 0.052$; and $\Delta (V-I)_{\rm pe}=0.008 - 0.437\times (V-I)_{\rm CCD}$ with $\sigma \sim 0.194$).

   
7 Interstellar extinction

In this section we discuss the extinction law in the direction of our open cluster sample. We find that the typical Galactic values for the reddening slope, E(U-B)/E(B-V) = 0.72, and for the ratio of total to selective absorption, $R_V \sim 3.1$, are consistent with our data. The adopted values for the reddening slope, the ratio of total to selective absorption will be used in the subsequent papers of this series to correct our data from the effects of interstellar extinction.

7.1 The reddening slope

Determining the amount of interstellar reddening from photometry alone using techniques such as ZAMS main sequence fitting in a colour-colour diagram, or Johnson & Morgan's (Johnson & Morgan 1953) Q Method, requires the knowledge of the slope of the reddening line. It is well known (Mathis 1990; Turner 1994) that there are variations in the reddening law throughout the Galaxy, although a mean reddening slope of E(U-B)/E(B-V) = 0.72 is found for most Galactic longitudes.

Turner (Turner 1989) in an empirical study of the fields of six open clusters determined a mean value of $E(U-B)/E(B-V) = 0.724\, \pm\, 0.005$ for the reddening slope, although values ranging from at least 0.62 to 0.80 were found from one region to another. One of the regions analysed by Turner (Turner 1989) was the field of NGC 2439, which is also one of the clusters in our sample, and for which he finds a value of E(U-B)/E(B-V) = 0.75.

To investigate the reddening law in the region of our open cluster sample we have searched the WEBDA database for MK spectral types of O, B, A dwarfs observed in this study in order to derive their intrinsic colours. The intrinsic colours were determined by interpolation over the tables given by Schmidt-Kaler (Schmidt-Kaler 1982) which relate MK types to the $U\!BV$ indexes and were then used to compute the colour excesses.

Figure 3 shows the linear fit to the slope of the colour excess data. The fit yielded a value of $(E(U-B)/E(B-V)=0.69 \pm 0.03$ with an 0.07 rms dispersion of the residuals, which despite its low accuracy is in excellent agreement with the standard slope of 0.72. The relatively high dispersion in the residuals may be due to errors in the spectral classifications (as suggested by the dispersion of the NGC 2453 data) and do not necessarily reflect to cluster to cluster variations of the reddening law. In view of these results we find that the reddening law in the direction of our sample follows the mean Galactic law and we therefore adopt the standard value E(U-B)/E(B-V)=0.72 for subsequent reddening analysis. For the other colour-colour combinations, the standard slopes given by Straizys (Straizys 1992) were adopted. We do note however that the available data is not sufficient for a rigorous analysis, so that cluster to cluster variations up to $\sim$0.07 in the reddening slope cannot be discarded.

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms10557f3.eps}}\end{figure} Figure 3: Reddening slope defined by the data of the 1998 run. The straight line is a fit of $E(U-B)/E(B-V)=0.69 \pm 0.03$ with an 0.07 rms dispersion of the residuals
Open with DEXTER

7.2 The ratio of total to selective absorption

As in the case of the reddening slope, it is not possible to perform a rigorous study of the ratio of total to selective absorption, RV=AV/E(B-V), where AV is the absorption in the V band. The same kind of proportionality is also defined for the other combinations of bands and colours. Several authors (Sherwood 1975; Crawford & Mandwewala 1976; Turner 1976) have shown that the ratio of total to selective absorption has a typical value of $R_V \sim 3.1$ for a diffuse interstellar medium. Denser molecular clouds can give rise to higher values of RV around 4 - 6 (Mathis 1990; Turner 1994).

For cases in which there is evidence of variable extinction across a cluster field, where all cluster members are assumed to be at a common distance, a plot of V - MV versus E(B-V) should show a correlation of slope RV. Evidently, this method commonly known as the variable extinction method requires the knowledge of the absolute magnitude, MV, and the colour excess, E(B-V), for each star. Both MV and E(B-V) can be derived from spectral types. Turner (1976) applied this method to determine RV for 51 open clusters and obtained an average value of $R_V = 3.08 \pm 0.03$. Three of the open clusters studied by Turner (1976) were NGC 2323, NGC 2343 and Trumpler 9, which lie in the same Galactic longitude range of our sample, and for which he obtained the values 2.85, 3.09 and 2.75 respectively.

  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms10557f4.eps}}\end{figure} Figure 4: The linear least squares fit of the slope yields $R_V=2.71 \pm 0.70$. If the deviated point of NGC 2453 (marked with a circle) is eliminated the fit yields $R_V=3.06 \pm 0.75$
Open with DEXTER

We have also investigated the ratio of total to selective absorption using the same photometric and spectroscopic data as in the study of the reddening slope. Because there are not enough stars with known spectral types in each cluster, the variable extinction method cannot be used in a direct form. Instead, a differential approach, similar to the one in Sect. 3.2 for the determination of the extinction coefficients, was followed. If a certain cluster has at least two stars with known spectral types we can write $\Delta(V-M_V)=R_V\Delta(E-B)$ which is distance independent and where RV is the only unknown. Another advantage of this approach is that a greater range in E(B-V) may be achieved than in the traditional one-cluster method. However, the sensitivity to cluster-to-cluster variations is lost and only an average value can be determined.

Figure 4 shows a plot of $\Delta(V-M_V)$ versus $\Delta(E-B)$. A value of $R_V=2.71 \pm 0.70$ was found from a linear least squares fit of the slope (i.e. $\Delta(V-M_V)=0$ for $\Delta(E-B)=0$) which despite its large uncertainly is consistent with the standard RV=3.1. Furthermore, if the deviating point of NGC 2453 in the lower left of Fig. 4 is eliminated, then the fit yields $R_V=3.06 \pm 0.75$ which is practically identical to the mean value of RV=3.08 given by Turner (1976). Once again, we take the value obtained in this analysis more as an indication that the region under study follows a standard extinction law than that an actual determination of RV, and will use the standard RV=3.1 value in the upcoming analysis of our open cluster photometry.

8 Conclusions

We have obtained homogeneous $U\!BV\!RI$ photometry in the fields of 30 open clusters between $217^{\circ}< l <260^{\circ}$and $-5^{\circ} < b < 5^{\circ}$ using data gathered at the same telescope, following the same reduction procedures, and calibrating all the data to the same $U\!BV\!RI$ standard system. These data have resulted in a precise and deep (up to $V \sim 21$), photometric catalogue of approximately 65000 stars.

We have compared our data to photometry from other sources finding that in general there is good agreement (at a 0.03 mag level) although some studies present large deviations. The differences between our photometry and that from other studies have been presented in a table which can be used to put all the measurements on the common scale defined by this study.

Since we intend to use this catalogue for cluster reddening, distance and age determinations, we have performed a rough analysis of the reddening slope and of the ratio of total to selective absorption for this region of the Galaxy and found that the typical Galactic values E(U-B)/E(B-V) = 0.72 and $R_V \sim 3.1$are consistent with our data.

Acknowledgements
The author wishes to thank E. J. Alfaro and A. J. Delgado for providing the 1994 images. The author would also like to thank J.-C. Mermilliod and J. Alves for many useful comments and help. This work was financially supported by FCT (Portugal) through the grant PRAXIS XXI BD/3895/94 and the YALO project. Most of the work was done at the IAA-CSIC (Spain) as part of the author's Ph.D. research. This research made use of the NASA Astrophysics Data System, and of the Simbad database operated at the Centre de Données Stellaires - Strasbourg, France.

References

 
Copyright ESO 2001