A&A 370, 586-590 (2001)
DOI: 10.1051/0004-6361:20010274
1 - Raman Research Institute, Bangalore 560 080, India
2 -
Stichting ASTRON, Postbus 2, 7990 AA Dwingeloo, The Netherlands
Received 24 November 2000 / Accepted 7 February 2001
Abstract
We have measured the scatter broadening of pulsars in the direction of
the Gum nebula. For the first time, our observations show clear variations of
scattering properties across the Gum nebula. The IRAS-Vela shell is shown to be
a high scattering region. Our revised estimations of distances to these pulsars
are consistently less by a factor of 2-3, which has very important consequences
for the deduced values of radio luminosity and transverse velocity of pulsars.
Key words: ISM: Gum nebula - stars: pulsars: general
The Gum Nebula appears extremely diffuse and faint in
![]() thus
making it extremely difficult to estimate its size. One of the earliest
measurements gave its size to be as large as
thus
making it extremely difficult to estimate its size. One of the earliest
measurements gave its size to be as large as
![]() (Brandt et al. 1971). Refined estimates of the size of the nebula using wide
field H
(Brandt et al. 1971). Refined estimates of the size of the nebula using wide
field H![]() imaging is given by Sivan (1974), which restricts the size to
imaging is given by Sivan (1974), which restricts the size to
![]()
![]() .
Based on a spectroscopic study of ionized gas, Reynolds
(1976a,b) proposed that the Nebula is a one million year old expanding gas
shell, originally produced by a supernova explosion, which is now being heated
and ionized by the massive stars
.
Based on a spectroscopic study of ionized gas, Reynolds
(1976a,b) proposed that the Nebula is a one million year old expanding gas
shell, originally produced by a supernova explosion, which is now being heated
and ionized by the massive stars ![]() Puppis and
Puppis and
![]() Velorum. According to Reynolds, the average density of the nebula is as large as
about 2 cm-3. Assuming a diameter of about 250 pc, we can see that the
nebula can potentially introduce a dispersion measure of about 500 pccm-3.
Velorum. According to Reynolds, the average density of the nebula is as large as
about 2 cm-3. Assuming a diameter of about 250 pc, we can see that the
nebula can potentially introduce a dispersion measure of about 500 pccm-3.
According to Weaver et al. (1977), the stellar wind
from ![]() Puppis could be
strong enough to produce the observed Nebula, which is a shell. The shell is
formed by the interaction of the stellar winds from
Puppis could be
strong enough to produce the observed Nebula, which is a shell. The shell is
formed by the interaction of the stellar winds from ![]() Puppis and
Puppis and
![]() Velorum with the ambient interstellar medium. They also predict
soft X-rays from the hot interior, which is at a temperature of about
106 K. Wallerstein et al. (1980), from a study of the interstellar gas
towards stars in the direction of the nebula, came to the conclusion that the
nebula is consistent with a model of the Gum Nebula as an HII region ionized by
OB stars and stirred up by multiple stellar winds. Chanot & Sivan (1983), on
the basis of
Velorum with the ambient interstellar medium. They also predict
soft X-rays from the hot interior, which is at a temperature of about
106 K. Wallerstein et al. (1980), from a study of the interstellar gas
towards stars in the direction of the nebula, came to the conclusion that the
nebula is consistent with a model of the Gum Nebula as an HII region ionized by
OB stars and stirred up by multiple stellar winds. Chanot & Sivan (1983), on
the basis of
![]() -field
-field
![]() photographs, suggested that the
Gum Nebula is composed of two regions, one which is a circular main body with a
typical ring-like appearance of diameter of 36
photographs, suggested that the
Gum Nebula is composed of two regions, one which is a circular main body with a
typical ring-like appearance of diameter of 36![]() ,
and the other which
consists of faint diffuse and filamentary extensions which merge with the faint
,
and the other which
consists of faint diffuse and filamentary extensions which merge with the faint
![]() background. This idea supports the model of Reynolds (1976a) for
an expanding
background. This idea supports the model of Reynolds (1976a) for
an expanding
![]() shell ionized by UV flux of
shell ionized by UV flux of ![]() Puppis and
Puppis and
![]() Velorum. The origin of the shell structure is, however, uncertain.
Velorum. The origin of the shell structure is, however, uncertain.
From a detailed study of the Gum Nebula, Sahu (1992) came to the conclusion that
the nebula is a shell-like structure surrounding the Vela R2 association which
is at a distance of about 800 pc, while the shell-like structure near the Vela
OB2 association known as the IRAS Vela shell is at a distance of about 450 Kpc. This hypothesis crucially depended on the distance to ![]() Puppis, as
this star is believed to be the primary source of ionization of the Gum Nebula,
which Sahu (1992) found to be
Puppis, as
this star is believed to be the primary source of ionization of the Gum Nebula,
which Sahu (1992) found to be ![]() 800 pc. However the Hipparcos distance
estimates to
800 pc. However the Hipparcos distance
estimates to ![]() Puppis rules out the above scenario. Rajagopal (1999)
showed from the kinematics of the IRAS Vela shell that the Gum Nebula is either
inside or overlapping with the shell.
Puppis rules out the above scenario. Rajagopal (1999)
showed from the kinematics of the IRAS Vela shell that the Gum Nebula is either
inside or overlapping with the shell.
The various possible alternative scenarios as discussed above has left several
open ends in our understanding of the Gum Nebula. The electron density estimates
inside the Gum Nebula, as shown by Reynolds (1976a), and Wallerstein
et al. (1980), show large variations from 0.1 to 100
![]() .
The
complicated structure of the nebula is also evident from the
.
The
complicated structure of the nebula is also evident from the
![]() images available (e.g. Chanot & Sivan 1983).
images available (e.g. Chanot & Sivan 1983).
Taylor & Cordes (1993, hereafter TC93), as part of their galactic free electron density distribution model, considered the Gum nebula as a separate component, with an angular diameter of 30 degrees. They assumed that the number density of free electrons is uniform all over this component (0.2 cm-3). They also assumed that the fluctuation parameter, which determines the amount of scattering introduced by the medium, is zero. Though this is a drastic assumption (as, for example, demonstrated by the scattering properties of the Vela pulsar), as they state, this is mainly due to very poor constraints available. In this work, we have done a systematic survey across the Gum Nebula to measure the scatter broadening of pulsars due to the electron density fluctuations, which should eventually help to model the scattering properties of this region in more detail.
We have observed 40 pulsars located in the galactic coordinate range
![]() and
and
![]() with the Ooty Radio Telescope during March 1997. The Ooty Radio Telescope is a
semi-parabolic cylinderical array, whose dimensions are about 500 m in
North-South, and 30 m in East-West. It operates at a fixed centre frequency
of 327 MHz. It has 1056 dipoles arranged North-South along the focal line of the
semi parabolic cylinder, and as the result of which it is not sensitive to the
other (East-West) component of polarization (for further details
refer Swarup et al. 1971; Sarma et al. 1975a, 1975b; Kapahi et al. 1975).
with the Ooty Radio Telescope during March 1997. The Ooty Radio Telescope is a
semi-parabolic cylinderical array, whose dimensions are about 500 m in
North-South, and 30 m in East-West. It operates at a fixed centre frequency
of 327 MHz. It has 1056 dipoles arranged North-South along the focal line of the
semi parabolic cylinder, and as the result of which it is not sensitive to the
other (East-West) component of polarization (for further details
refer Swarup et al. 1971; Sarma et al. 1975a, 1975b; Kapahi et al. 1975).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10502_f1.ps}
\end{figure}](/articles/aa/full/2001/17/aa10502/Timg33.gif) |
Figure 1:
Observed scatter broadening (
|
| Open with DEXTER | |
Although there are in total 48 known pulsars in this range, we selected only those above a flux (at 400 MHz) of 5 mJy. The dispersion measures (DM) of these pulsars are in the range 30-306 pccm-3. Our sample also includes pulsars for which scatter broadening measurements at other frequencies exist in the literature.
To carry out these observations, we have used a pulsar receiver that was mainly
built for pulsar searches (Ramkumar et al. 1994). The pulsar receiver consists
of a 4-bit sampler (Analog-to-digital converter), which samples the incoming
signal voltage of bandwidth 8 MHz. The output of this is fed to an FFT
engine. The FFT produces 256-point complex spectra which are converted to power
spectra using look-up tables. The resultant power spectra are pre-integrated
over successive spans of ![]() 0.5 msec, which is the final time resolution in
recorded data. A block integration is done over a number of pre-integrated
samples for calculation of the running mean for each of the 256 frequency
channels. The running mean is finally subtracted from the pre-integrated data to
remove the effects of receiver gain variations. The mean subtracted
pre-integrated data are then represented as a one-bit signal by recording the
sign bit and stored on magnetic tape. We observed each pulsar for 20 min, and
compensated for the interstellar dispersion by offline analysis. The integrated
pulse profiles were obtained by folding the time series with the correct
rotation period of the pulsar.
0.5 msec, which is the final time resolution in
recorded data. A block integration is done over a number of pre-integrated
samples for calculation of the running mean for each of the 256 frequency
channels. The running mean is finally subtracted from the pre-integrated data to
remove the effects of receiver gain variations. The mean subtracted
pre-integrated data are then represented as a one-bit signal by recording the
sign bit and stored on magnetic tape. We observed each pulsar for 20 min, and
compensated for the interstellar dispersion by offline analysis. The integrated
pulse profiles were obtained by folding the time series with the correct
rotation period of the pulsar.
Out of the 40 pulsars in our sample, only 21 were above our detection limit. For each observed pulsar, we compensate for the interstellar dispersion by offline software, and fold the time series with the exact expected rotation period, to produce average pulse profiles.
The scatter broadening was then estimated by a least-square-fit to the average
pulse profile with the following model: the observed pulse profile function
P(t) is the convolution of the intrinsic pulse profile (which is emitted by
the pulsar)
![]() with (1) the impulse response characterising the scatter
broadening in the ISM T(t), (2) the dispersion smearing function across the
spectral channel in the receiver S(t), and (3) the instrumental response
function I(t).
with (1) the impulse response characterising the scatter
broadening in the ISM T(t), (2) the dispersion smearing function across the
spectral channel in the receiver S(t), and (3) the instrumental response
function I(t).
The results of the fit are given in Table 1. In
Table 1, PSRs J0742-2822, J0745-5351 and J0835-4510 were not
observed by us; we have used the scattering measurements listed in the
literature (Roberts & Ables 1982; Alukar et al. 1986). For those measurements not done at 327 MHz, we have used the frequency scaling law
![]() (where
(where ![]() is the observing frequency) to obtain the
scatter broadening value at 327 MHz. PSRs J0809-4753, J0837-4145 and J0840-5332
in Table 1 have had their scatter broadening reported earlier at
frequencies other than 327 MHz, but we have reobserved them. The values listed
for them in the table are from our measurements.
is the observing frequency) to obtain the
scatter broadening value at 327 MHz. PSRs J0809-4753, J0837-4145 and J0840-5332
in Table 1 have had their scatter broadening reported earlier at
frequencies other than 327 MHz, but we have reobserved them. The values listed
for them in the table are from our measurements.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{10502_f2.ps}
\end{figure}](/articles/aa/full/2001/17/aa10502/Timg40.gif) |
Figure 2:
A plot of
|
| Open with DEXTER | |
Figure 1 gives the spatial distribution of the pulsars across the
Gum nebula as a function of the galactic coordinates. Note that the distribution
is skewed to one side (mostly lying in the longitude range of 255![]() to
to
![]() )
of the nebula marked by the large circle in the figure. This must
be primarily due to the fact that pulsars are mostly concentrated in the
galactic disk and at such galactic longitudes toward the Galactic anti-center
one does have significant contribution from the disk. Pulsars with high
)
of the nebula marked by the large circle in the figure. This must
be primarily due to the fact that pulsars are mostly concentrated in the
galactic disk and at such galactic longitudes toward the Galactic anti-center
one does have significant contribution from the disk. Pulsars with high
![]() appear to lie behind the IRAS vela shell, as marked by the small
circle in the figure.
appear to lie behind the IRAS vela shell, as marked by the small
circle in the figure.
In Fig. 2 we plotted the values of scatter broadening
![]() for the whole pulsar population including our new results as a
function of dispersion measure (DM). A function of the form as given by
for the whole pulsar population including our new results as a
function of dispersion measure (DM). A function of the form as given by
![]() msec, as
discussed by Ramachandran et al. (1997), is shown as a fit to the data points,
where
msec, as
discussed by Ramachandran et al. (1997), is shown as a fit to the data points,
where ![]() is the wavelength in meters.
On inclusion of our new
measurements the fit does not seem to change significantly. The dotted curve in
the figure corresponds to
A = 4.5 10-5,
B = 3.1 10-5,
is the wavelength in meters.
On inclusion of our new
measurements the fit does not seem to change significantly. The dotted curve in
the figure corresponds to
A = 4.5 10-5,
B = 3.1 10-5,
![]() ,
,
![]() .
The solid curve is modelled by fixing
.
The solid curve is modelled by fixing
![]() which is the expected
dependence from Kolmogorov spectrum, thus giving
A = 8.4 10-6,
B =
8.3 10-5 and
which is the expected
dependence from Kolmogorov spectrum, thus giving
A = 8.4 10-6,
B =
8.3 10-5 and
![]() .
The term
.
The term
![]() should
provide a useful description of the apparent mean dependence of the turbulence
level on DM. The scatter around the mean trend may be understood as due to
possible existance of isolated regions of enhanced scattering in the line of
sight, and consequent failure of the assumption that the scatterer is half way
down the line of sight.
should
provide a useful description of the apparent mean dependence of the turbulence
level on DM. The scatter around the mean trend may be understood as due to
possible existance of isolated regions of enhanced scattering in the line of
sight, and consequent failure of the assumption that the scatterer is half way
down the line of sight.
Though PSR J0924-5814 seems to have a large deviation compared to the mean
Kolmogorov line, the error in the estimate of
![]() for this pulsar is
more than 100% (refer Table 1) due to poor signal-to-noise ratio
of the integrated pulse profile.
for this pulsar is
more than 100% (refer Table 1) due to poor signal-to-noise ratio
of the integrated pulse profile.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{10502_f3.ps}
\end{figure}](/articles/aa/full/2001/17/aa10502/Timg49.gif) |
Figure 3:
A comparison between the distance
|
| Open with DEXTER | |
| Name | DM |
|
|
|
|
|
F | Distance |
|
| (pc cm-3) | (msec) | (msec) | (msec) | (kpc) | (kpc) | ||||
|
|
160.8 | 76 |
6.3 | 4.5 | >11.03 | ||||
|
|
73.7 | 1 | 0.8 | 0.65 | 1.89 | ||||
| J0745-53511 | 122.3 | 60 | 7.0 | 4.11 | >7.14 | ||||
| J0809-47532 | 228.3 | 79 |
9 |
8 | 697 | 1.03 | 5.9 | >12.65 | >12.72 |
| J0820-4114 | 113.4 | 30 |
42 |
9 | 216 | 1.23 | 6.6 | 0.64 | 2.83 |
|
|
68.2 | 8 | 6.3 | 0.50 | 0.50 | ||||
| J0837-41352 | 147.6 | 1 |
9 |
2 | 597 | 3 | 0.0 | 1.89 | 4.24 |
| J0840-53322 | 156.5 | 57 |
13 |
10 | 218 | 1.1 | 5.3 | 4.25 | 7.78 |
| J0846-3533 | 91.1 | 4 |
44 |
5 | 135 | 2.1 | 1.7 | 0.58 | 1.31 |
| J0855-3331 | 87.7 | 1 |
24 |
1 | 595 | 1.3 | 0.0 | 0.57 | 1.27 |
| J0904-4246 | 189 | 8 |
21 |
3 | 397 | 0.99 | 0.8 | 4.6 | 4.40 |
| J0905-5127 | 189 | 4 |
11 |
5 | 218 | 0.88 | 0.5 | 5.54 | 8.35 |
| J0907-5157 | 104 | 1 |
32 |
10 | 228 | 0.9 | 0.15 | 0.88 | 2.65 |
| J0924-5302 | 152.9 | 1 |
6 |
1 | 195 | 1.1 | 0.15 | 4.02 | 5.61 |
| J0924-5814 | 60.0 | 55 |
1 |
45 | 238 | 1.0 | 2.01 | ||
| J0934-5249 | 99.4 | 7 |
21 |
5 | 197 | 1.1 | 1.3 | 1.66 | 2.90 |
| J0942-5552 | 180.2 | 5 |
7 |
2 | 237 | 1.1 | 0.3 | 5.28 | 6.35 |
| J0952-3839 | 167 | 2 |
48 |
8 | 227 | 0.91 | 0.25 | >8.46 | >8.44 |
| J0955-5304 | 156.9 | 3 |
5 |
1 | 122 | 1.2 | 0.67 | 4.25 | 4.86 |
| J1001-5507 | 130.6 | 15 |
13 |
2 | 197 | 1.1 | 10.7 | 3.44 | 3.59 |
| J1003-4747 | 98.1 | 0 |
9 |
3 | 197 | 1.2 | 3.44 | ||
| J1017-5621 | 439.1 | 16 |
8 |
25 | 228 | 0.97 | 11.77 | ||
| J1042-5521 | 306 | 7 |
29 |
10 | 238 | 1.1 | 6.95 | ||
| J1046-5813 | 240.2 | 43 |
2 |
50 | 238 | 1.03 | 4.8 | ||
| J1059-5742 | 107.9 | 2 |
20 |
5 | 237 | 1.2 | 2.74 |
The presence of the Gum nebula has been invoked explicitly in models estimating
pulsar distances and free electron density distribution in the Galaxy (e.g.
Bhattacharya et al. 1992, TC93 and references therein). TC93 modelled the Gum
nebula as a sphere of 130 pc radius at a distance of 500 pc, with a uniform
electron density of 0.25 cm-3, and the density falls off as an one-sided
Gaussian with an rms of 50 pc. They also assumed that the fluctuation
parameter, which is defined as
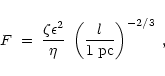 |
(2) |
From our observation, it is obvious that many parts of the nebula significantly
contribute to enhanced scattering of pulsar signals. This issue was addressed by
Deshpande & Ramachandran (1998) in detail, where they explicitly showed that in
order to explain the enhanced scattering observed for PSR J0738-4042, which is
a pulsar in the Gum Nebula (refer Table 1), one has to increase
![]() ,
and adopt values of fluctuation parameter almost equal to that of the
spiral arm. We have used a similar method as suggested by Deshpande &
Ramachandran (1998), and have obtained the distances and the fluctuation
parameters for the pulsars behind the Gum Nebula under the framework of the TC93
model. which we briefly describe below.
,
and adopt values of fluctuation parameter almost equal to that of the
spiral arm. We have used a similar method as suggested by Deshpande &
Ramachandran (1998), and have obtained the distances and the fluctuation
parameters for the pulsars behind the Gum Nebula under the framework of the TC93
model. which we briefly describe below.
Deshpande & Ramachandran (1998) showed that if the distance to a dominant
discrete scatterer is known, then it is possible to use only the DM and the
![]() measurements to constrain F and distances to pulsars lying
behind the scattering region. With the available data on the Vela pulsar and
J0738-4042, they find similar values of
measurements to constrain F and distances to pulsars lying
behind the scattering region. With the available data on the Vela pulsar and
J0738-4042, they find similar values of ![]() and F, of about 0.32 cm-3 and 6.3, respectively. This helped constrain the distance of
J0738-4042 to 4.5 kpc (as opposed to >11 kpc by TC93). As they suggest, it
seems reasonable to characterise a major part of the Gum nebula with
and F, of about 0.32 cm-3 and 6.3, respectively. This helped constrain the distance of
J0738-4042 to 4.5 kpc (as opposed to >11 kpc by TC93). As they suggest, it
seems reasonable to characterise a major part of the Gum nebula with
![]() and a fluctuation parameter F = 6.3. In a simple exercise,
for various lines-of-sight in the Gum Nebula we have applied the above technique
to obtain F and distances to pulsars, keeping
and a fluctuation parameter F = 6.3. In a simple exercise,
for various lines-of-sight in the Gum Nebula we have applied the above technique
to obtain F and distances to pulsars, keeping ![]() fixed at 0.32. The
values of F and distances (in kpc) obtained is given in
Table 1. Though these values are not unique (as different
combinations of
fixed at 0.32. The
values of F and distances (in kpc) obtained is given in
Table 1. Though these values are not unique (as different
combinations of ![]() and F can match the observed values of DM and
and F can match the observed values of DM and
![]() ), as Deshpande & Ramachandran (1997) show, it is not
unreasonable. It is interesting to note that most of the pulsars lying in the
IRAS Vela shell seems to be consistent with a fluctuation parameter of
), as Deshpande & Ramachandran (1997) show, it is not
unreasonable. It is interesting to note that most of the pulsars lying in the
IRAS Vela shell seems to be consistent with a fluctuation parameter of ![]() 6.5, while the other regions in the Gum Nebula have an F of only
6.5, while the other regions in the Gum Nebula have an F of only
![]() 0.5. This, at least intuitively, indicates that the IRAS-Vela shell is a
different entity with different fluctuation properties. Note that we have not
attempted any modelling of the region outside the Gum Nebula. The value of Ffor PSR J1001-5507 is 10.7, which we believe is too high to be associated with
the nebula. For PSR J0924-5814, we get a value of 25 which is unreasonable, and
this is due to the poor estimation of
0.5. This, at least intuitively, indicates that the IRAS-Vela shell is a
different entity with different fluctuation properties. Note that we have not
attempted any modelling of the region outside the Gum Nebula. The value of Ffor PSR J1001-5507 is 10.7, which we believe is too high to be associated with
the nebula. For PSR J0924-5814, we get a value of 25 which is unreasonable, and
this is due to the poor estimation of
![]() .
Thus, we reject this
pulsar in our analysis.
.
Thus, we reject this
pulsar in our analysis.
The distances we obtain from our procedure seem to be consistently different
from the values obtained by the TC93 model (as shown in Fig. 3).
It is worth noting that out of this list in the table, proper motion
measurements are already available for those pulsars marked with a dagger
(![]() ). For them, on the average, our analysis makes a difference of 2-3
in the estimated value of transverse velocity.
). For them, on the average, our analysis makes a difference of 2-3
in the estimated value of transverse velocity.
As an extension of the present study to a more detailed one, it would be
interesting to establish the electron density variation of the Gum Nebula along
the various lines-of-sight of these pulsars. As found by Reynolds (1976b), the
number density in the Gum nebula can in principle vary by many times, with an
average density of about 2 cm-3. This can potentially introduce dispersion
measures of the order of 500 pccm-3. Estimates of density variations can
be obtained from detailed H![]() studies, which involves measuring emission
measures in the line-of-sight to pulsars. The ratio of the emission measure and
the DM can be used to estimate the electron densities. Although such estimates
are available (Reynolds 1976a), they are not sufficient for the entire set of
lines-of-sight observed. Further, as we have estimated the scatter broadening of
only a subset of pulsars in this region, there remains a significant fraction of
pulsars for which such measurements are not available (as clearly seen in
Fig. 1). With a more sensitive instrument, it should be possible to
enlarge the sample of scatter broadening measurements, giving further clues
about the electron density distribution.
studies, which involves measuring emission
measures in the line-of-sight to pulsars. The ratio of the emission measure and
the DM can be used to estimate the electron densities. Although such estimates
are available (Reynolds 1976a), they are not sufficient for the entire set of
lines-of-sight observed. Further, as we have estimated the scatter broadening of
only a subset of pulsars in this region, there remains a significant fraction of
pulsars for which such measurements are not available (as clearly seen in
Fig. 1). With a more sensitive instrument, it should be possible to
enlarge the sample of scatter broadening measurements, giving further clues
about the electron density distribution.
Acknowledgements
We would like to thank Dr. A. A. Deshpande of the Raman Research Institute for his invaluable help and stimulating discussions. We would also like to thank V. Balasubramanium for providing us with telescope time and help during the observations in Ooty. We would like to thank Bilal and Mangesh for their kind help during the observations.