Without attempting to provide a review of the available techniques in
the literature, we briefly describe here the procedures we have
tested. They are summarized in Table 3.
| Procedure | Implementation | Version | Method |
| EMLDETECT | XMM-SAS v5.0 | 3.7.2 | Cell detection + Maximum likelihood |
| VTPDETECT | Chandra CIAO | 2.0.2 | Voronoi Tessellation and percolation |
| WAVDETECT | Chandra CIAO | 2.0.2 | Wavelet |
| EWAVELET | XMM-SAS v5.0 | 2.4 | Wavelet |
| G+SE | Gauss + SExtractor | 2.1.6 | Mixed - Gauss convolution followed by SExtractor detection |
| MR/1+SE | MR/1 + SExtractor | 2.1.6 | Mixed - multi-resolution filtering followed by SExtractor detection |
Historically, the sliding cell detection method was first used for Einstein Observatory observations (e.g. EMSS - Gioia et al. 1990). It is included in ROSAT, Chandra and XMM-Newton data analysis tools and a good description can be found in the specific documentation for each of those missions.
The X-ray image is scanned by a sliding square box and if the signal-to-noise of the source centered in the box is greater than the specified threshold value it is marked as an object. The signal is derived from the pixel values inside the cell and noise is estimated from the neighboring pixels. Secondly, the objects and some zone around them are removed from the image forming the so-called "cheese'' image which is interpolated later by a suitable function (generally a spline) to create a smooth background image. The original image is scanned again but this time using a threshold from the estimated background inside the running cell to give the map detection object list.
The procedure is fast and robust and does not rely on a priori assumptions. However it has difficulties, especially in detecting extended features, close objects and sources near the detection limit. Many refinements are now implemented improving the sliding cell method: (1) consecutive runs with increasing cell size, (2) matched filter detection cell where the cell size depends on the off-axis angle. However, the most important improvement was the addition of the maximum likelihood (ML) technique to further analyze the detected sources.
The ML technique was first applied to analyze ROSAT observations (Cruddace et al. 1988, 1991; Hasinger et al. 1993). It was used to produce all general X-ray surveys from ROSAT mission (e.g. RASS - Voges et al. 1999, WARPS survey - Ebeling et al. 2000). The two lists from local and map detection passes can be merged to form the input objects list for the ML pass. It is useful to feed the ML procedure with as many candidate objects as possible, having in mind that large numbers of objects could be very CPU-expensive. The spatial distribution of an input source is compared to the PSF model - the likelihood that both distributions are the same - is calculated with varying the input source parameters (position, extent, counts) and the corresponding confidence limits can be naturally computed. A multi-PSF fit is also implemented which helps in deblending and reconstructing the parameters of close sources. In the output list, only sources with a likelihood above a threshold are kept.
The ML method performs well and has many valuable features, however, it has some drawbacks - it needs a PSF model to perform the likelihood calculation and thus favours point-like source analysis, extent likelihood could be reliably taken only for bright sources, it cannot detect objects which are not already presented in the input list (e.g. missing detections in the local or map passes).
Here we have used EMLDETECT - an implementation of the method
specifically adapted for XMM-SAS (Brunner 1996). In the map mode
sliding cell pass we used a low signal-to-noise ratio (![]()
![]() )
above the background in order to have as many as possible input
objects for the ML pass. The likelihood limit (given by
)
above the background in order to have as many as possible input
objects for the ML pass. The likelihood limit (given by
![]() ,
where P is the probability of finding an excess above the
background) was taken to be 10, which corresponds roughly to
,
where P is the probability of finding an excess above the
background) was taken to be 10, which corresponds roughly to ![]() detection. A multi-PSF fitting mode with the maximum of 6 simultaneous
PSF profile fits was used.
detection. A multi-PSF fitting mode with the maximum of 6 simultaneous
PSF profile fits was used.
VTP - the Voronoi Tessellation and Percolation method (Ebeling & Wiedenmann 1993; Ebeling 1993) is a general method for detecting structures in a distribution of points (photons in our case) by choosing regions with enhanced surface density with respect to an underlying distribution (Poissonian in X-ray images). It treats the raw photon distribution directly without any recourse to a PSF model or a geometrical shape of the objects it finds. Each photon defines a centre of a polygon in the Voronoi tessellation image and the surface brightness is simply the inverse area of the polygon (assuming one single photon per cell). The distribution function of the inverse areas of all photons is compared to that expected from a Poisson distribution and all the cells above a given threshold are flagged and percolated, i.e. connected to form an object. This method was successfully used with ROSAT data (Scharf et al. 1997) and is currently incorporated in the Chandra DETECT package (Dobrzycki et al. 1999).
Apart from these advantages, VTP has some drawbacks which are especially important for XMM-Newton observations: (1) because of the telescope's high sensitivity and rather large PSF with strong tails, the percolation procedure tends to link nearby objects; (2) excessive CPU time for images with relatively large number of photons; (3) there is no simple way to estimate the extension of objects.
In the past few years a new approach has been extensively used: the
wavelet technique (WT). This method consists in convolving an image
with a wavelet function:
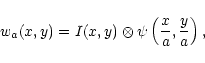 |
(1) |
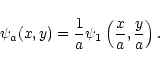 |
(2) |
The WT procedure consists of decomposing the original image into a given number of wavelet coefficient images, wa, within the chosen set of scales a. In each wavelet image, features with characteristic sizes close to the scale are magnified and the problem is to mark the significant ones, i.e. those which are not due to noise. In most cases, this selection of significant wavelet coefficients cannot be performed analytically because of the redundancy of the WT introducing cross-correlation between pixels. For Gaussian white noise, wa are distributed normally, allowing easy thresholding. This is not the case for X-ray images which are in the Poissonian photon noise regime.
Various techniques were developed for selecting the significant wavelet coefficients in X-ray images. In Vikhlinin et al. (1997) a local Gaussian noise was assumed; Slezak et al. (1994) used the Ascombe transformation to transform an image with Poissonian noise into an image with Gaussian noise; in Slezak et al. (1993), Starck & Pierre (1998) a histogram of the wavelet function is used. In recent years a technique based on Monte Carlo simulations is used successfully (e.g. Grebenev et al. 1995; Damiani et al. 1997; Lazzati et al. 1999).
Once the significant coefficients at each scale are chosen, the local maxima at all scales are collected and cross-identified to define objects. Different characteristics, such as centroids, light distribution etc., can be computed, as well as an indication of the source size at the scale where the object wavelet coefficient is maximal.
WT has many advantages - the multiresolution approach is well suited both for point-like and extended sources but favours circularly symmetric ones. Because of the properties of the wavelet function a smoothly varying background is automatically removed. Extensive description of wavelet transform and its different applications can be found in Starck et al. (1998).
In this work we have tested two WT procedures:
The use of such a mixed approach is motivated by the fact that procedures for source detection in astronomical images have been developed for many years and the steps and problems of deblending, photometry, classification of objects are now quite well understood. The raw photon image manipulations can be performed with very simple smoothing procedures (for example a Gaussian convolution) or with more sophisticated methods like the "matching filter'' technique, adaptive smoothing or multiresolution (wavelet) filtering.
We have used two different types of raw image filtering:
Copyright ESO 2001