A&A 370, 447-455 (2001)
DOI: 10.1051/0004-6361:20010199

Dynamical modeling of large scale asymmetries in the $\beta$Pictoris dust disk

J. C. Augereau¹ - R. P. Nelson² - A. M. Lagrange¹ - J. C. B. Papaloizou² - D. Mouillet¹

1 - Laboratoire d'Astrophysique de l'Observatoire de Grenoble, Université J. Fourier, CNRS, BP 53, 38041 Grenoble Cedex 9, France
2 - Astronomy Unit, School of Mathematical Sciences, Queen Mary & Westfield College, Mile End Road, London E1 4NS, UK

Received 27 October 2000 / Accepted 19 January 2001

Abstract
We report a new and complete model of the $\beta$Pictoris disk, which succeeds in accounting for both the surface brightness distribution, warp characteristics, the outer ``butterfly'' asymmetry as observed by HST/STIS in scattered light, as well as the infrared emission. Our model includes the presence of a disk of planetesimals extending out to 120-150AU, perturbed gravitationally by a giant planet on an inclined orbit, following the approach of Mouillet et al. (1997b). At any time, the planetesimal disk is assumed to be the source of a distribution of grains produced through collisional evolution, with the same initial orbital parameter distribution. The steady state spatial grain distribution is found incorporating the effects of radiation pressure which can cause the distribution of the smallest particles to become very distended. With realistic assumptions about the grains' chemical properties, the modeling confirms the previously evident need for an additional population of hot grains close to the star, to account for the 12$\mu$m fluxes at short distances from the star. It also indicates that this population cannot explain the outer 12$\mu$m flux distribution when the effects of gravity and radiation pressure determine the distribution. Very small grains, produced by collisions among aggregates, are tentatively proposed to account for this 12$\mu$m outer emission.

Key words: stars: circumstellar matter - stars: $\beta$Pictoris

1 Introduction

The $\beta$Pictoris gaseous and dusty disk has been extensively studied for 15 years. The dust disk, seen nearly edge-on, extends to at least a distance of 100AU from the central star, with a sharp decrease in the surface brightness distribution of scattered light beyond about 120AU. The dynamics of the small grains producing the scattered light is determined by radiation pressure, collisions with other grains and/or evaporation and to a lesser extent, Poynting-Robertson drag. The images at 12$\mu$m show that the maximum of the dust surface density distribution is located between 80AU and 100AU (Pantin et al. 1997, assuming the Hipparcos distance of 19.28pc from Crifo et al. 1997 for $\beta$Pictoris). The total dust mass, as measured from sub-millimeter data, ranges between a few and a few tens of lunar masses (Zuckerman & Becklin 1993; Holland et al. 1998; Dent et al. 2000).

The 10$\mu$m silicate spectrum (Knacke et al. 1993) appears to mimic that of Halley's comet but not that of comet Hale-Bopp (Lagage et al. 1999). The 10$\mu$m features are best fitted by the emission of small (submicronic) crystalline silicates (Knacke et al. 1993; Li & Greenberg 1998). It was suggested that these grains could result from comet evaporation, a scenario that had already been proposed to explain the very peculiar spectroscopic activity (Lagrange et al. 1987; Ferlet et al. 1987). Furthermore, Lecavelier des Etangs et al. (1996) proposed that the appearance of the entire disk, as seen in scattered light, could be explained by grains released from evaporating comets at distances of 15-30AU and subsequently pushed out by radiation pressure.

1.1 Asymmetries in the dust disk

The Northeast and Southwest extensions of the dust disk have been found to be asymmetric in scattered light as well as in thermal emission. At visual wavelength, Kalas & Jewitt (1995) noticed five radial or vertical asymmetries beyond 150AU. In the Northeast extension for example, the vertical brightness distribution in scattered light is asymmetric with respect to the disk mid-plane out to hundreds of AU and this situation is reversed in the Southwest extension (``butterfly'' asymmetry). Kalas et al. (2000) and Larwood et al. (2001) recently proposed that this asymmetry is produced by a close encounter with a M0V star in the last 10⁵ years.

In the inner part of the disk (at about 60-70AU) the 12$\mu$m images reveal a factor of 3 side to side brightness asymmetry (Pantin et al. 1997) which is much smaller at optical and near-infrared wavelengths (Mouillet et al. 1997a, at most a factor of 1.5). Orbiting evaporating bodies on eccentric orbits with the same longitude of periastron can produce such axial asymmetries (Lecavelier des Etangs et al. 1996; Lecavelier des Etangs 1998).

Adaptive optics (Mouillet et al. 1997b) and HST observations (Burrows et al. 1995; Heap et al. 2000) revealed the inner warping of its dust disk at about 70AU and in the same direction as the ``butterfly'' asymmetry. Mouillet et al. (1997b) modeled this warp as being due to grains which followed the distribution of a parent body planetesimal disk which was perturbed by the gravitational influence of a Jupiter-like planet on an orbit inclined at 3 degrees to the disk mid-plane.

1.2 Propagation of the warp

The important effect of perturbation by the giant planet is to cause the parent body disk to precess differentially. The more rapid precession in the inner regions causes the parent body disk to become coplanar with the planetary orbit. At large distances the inclination of the parent body disk retains its initial value. The warp is located in the transition region where the local orbital precession timescale is comparable to the age of the system. The location of the warp accordingly propagates outwards with time.

Mouillet et al. (1997b) found an approximate relationship between the position of the warp, the mass ratio of planet to star, its orbital (assumed circular) radius and the age of the system in the form:

  $$\begin{eqnarray*}\log\left(\frac{R_{\rm w}}{10{\rm AU}}\right)= 0.29\,\log\left(... ...rac{D}{10~{\rm AU}}\right)^2 \frac{t}{t_{\rm unit}}\right)-0.2 . \end{eqnarray*}$$

Here $M_*, M, R_{\rm w}, D$, t and $t_{\rm unit}$ are the mass of the star, the mass of the planet, the radius of the warp in the parent body disk, the planetary orbital radius, the age of the system and the time unit $\sqrt{(10~{\rm AU})^3/(GM_*)} \sim 5.2\,y$ respectively. For example, to obtain $R_{\rm w} =70~{\rm AU},$ M/M_* =10^-3 and D=10AU requires the age of the system to be $\sim$ $2.1~ 10^7\,y.$ Such orbital parameters for the proposed perturbing planet allow the spectroscopic activity to be successfully reproduced (Beust & Morbidelli 2000, and references therein).

Note that when, as assumed here, the warp location is significantly larger than the orbital radius, that location depends only on the product of the age of the system, the square of the orbital radius and the planetary mass ratio. We comment that, because it does not incorporate a non axisymmetric perturbation, the model proposed by Lecavelier des Etangs et al. (1996) cannot account for the inner warp, but the influence of radiation pressure, clearly revealed by their study, is certainly of great importance.

1.3 Aims of the present modeling

Complete modeling of the disk has not been performed so far. In this paper we formulate a model of the disk which reproduces both the scattered light images, in particular the warped disk and the ``butterfly'' asymmetry, and also the infrared (IR) images and fluxes. In Sect. 2, we outline the basis of this model and Sect. 3 presents the scattered light images which can be compared with the recent HST/STIS data (Heap et al. 2000). In Sect. 4, we synthesize the IR 12$\mu$m image and compare with the observations. In Sect. 5 we summarize and discuss the proposed model in a more general context.

   
2 The basic model

2.1 The parent body disk

The short lifetime of the grains, in comparison to the age of the system, as a result of the action of collisions and radiation pressure leads to the hypothesis of the existence of a parent body disk consisting of planetesimals with sizes larger than 1m which acts as a source for the grains as collision products (see for example the discussion in Mouillet et al. 1997b, and references therein).

As in Mouillet et al. (1997b) we suppose that the physical collision time in the parent body disk is sufficiently long compared to the age of the system that it can be approximated as a collisionless disk lying between 1.5D and 15D. The disk aspect ratio H/r is taken to be 0.1. Through our modeling procedure we are able to construct arbitrary surface density profiles. This is done by constructing parent body disks consisting of weighted contributions from 100 elementary rings composed of 10⁴ particles and with a ratio of inner and outer radii equal to $10^{1/99}\sim 1.0235$. This is possible because the particles are collisionless.

2.2 Orbital parameters of the perturbing planet

For working parameters we adopt $D= 10~{\rm AU},$ being also the model unit of distance, planet to star mass ratio M/M_* = 10^-3,planetary orbital eccentricity of zero with an inclination of 3$\hbox{$^\circ$ }$with respect to the initial mid-plane of the parent body disk. However, as above, we note that the important parameter is MD²rather than M and D separately. Mouillet et al. (1997b) also show that the propagation of the warp is unaffected for eccentricities of the planetary orbit up to 0.5. However, large eccentricities may lead to side to side (radial) asymmetries of the parent body disc which in turn may lead to some asymmetries in the generation of small dust particles. The study of asymmetries produced in this way is beyond the scope of this paper.

2.3 Parent body disk precession

The parent body disks are modeled here using 10⁶ particles. It is not possible to carry out orbital integrations over the system lifetime for such a number of particles. Instead, after realizing the parent body disk by allocating particles a random inclination and eccentricity consistent with the aspect ratio, the system was allowed to phase mix by integrating for 20 outer orbital periods. At this stage the orbital plane of each particle was precessed at the local rate for the age of the system while each particle retained its orbital phase. Finally the system was phase mixed again. This procedure is equivalent to evolving the orbits using the time averaged potential of the planet and its validity has been checked by comparison with complete integrations over time spans where these were feasible. The local precession rate for near circular orbits was taken to be (Mouillet et al. 1997b):

$$\begin{eqnarray*}\vert\omega_{\rm p}\vert ={3GM D^2\over 4 \Omega r^5}\cdot \end{eqnarray*}$$

Here r is the orbital radius and $\Omega= \sqrt{GM_*/r^3}$ is the local Keplerian frequency. The age of the system adopted here, corresponding to the mass ratio M/M_* =10^-3, was 2.6 10⁷ y consistent with the recent estimated age of $\beta$Pictoris from Barrado y Navascués et al. (1999) and which yields $R_{\rm w}\simeq 75\,$AU. But note as above that the significant parameter is the product of the age and the mass ratio.

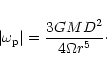
The configuration of the warped parent body disk, obtained using the above procedures, with the surface density we adopted is illustrated in Fig. 1.

	Figure 1: Vertical position of the mean PB disk mass assuming the surface density distribution of Fig. 2. The vertical and radial scales are not the same in this figure. The warped disk extends out to 140-150AU with a maximum close to 75AU from the star and a vertical extension of $\sim$4AU to the initial mid-plane of the PB disk
Open with DEXTER

2.4 Simulation of the dust disk

We assume that each planetesimal (parent body or hereafter PB) is the progenitor of small particles (produced for instance by collisions) that are significantly affected by the radiation pressure of the central star. We assume no initial relative velocity between the PB and the smallest particles produced. A consequence of this assumption and the near circular motion of the PB is that the periastron of a dust particle equals that of the PB. The effect of radiation pressure is quantified by the ratio of the force due to radiation pressure to that due to the gravity of the central star, $\beta_{\rm pr} = F_{\rm rad}/F_{\rm grav}.$ The case $\beta_{\rm pr} = 0$ corresponds to a bound dust particle with the same motion as its PB. When $\beta_{\rm pr} = 0.5$, particles have zero energy and so are just unbound. We consider 11 values of $\beta_{\rm pr}$ equally spaced between and including 0.45 and 0.001. For each value of $\beta_{\rm pr}$, a dust distribution is generated from the PB by phase mixing 10⁶ particles for 20 orbital periods measured at the outer radius of the disk. The time-scales required for phase mixing are always short compared to the time-scale for propagating the warp. Also the optical depth of the disk is large enough that the timescale for destruction of the dust by collisions is shorter than any drag timescale due to the Poynting-Robertson effect (see also Mouillet et al. 1997b). The Poynting-Robertson effect then is neglected here.

2.5 Modeling of the scattered light and thermal images

2.5.1 Efficient modeling of the PB surface density distribution

To construct the final image of the disk in scattered light or in thermal emission arising from any PB surface density distribution in practice, a radial weight function is applied to the contribution from each dust particle depending on the elementary ring between 1.5D and 15D from which it originated (the distance to this ring also corresponds to the periastron distance of the dust particle). Several $\Sigma(r)$ distributions can therefore be investigated using this technique in a reasonable amount of time.

2.5.2 Grain properties

The image of the disk also depends on the physical properties of the grains. Here we have adopted the comet dust model proposed by Li & Greenberg (1998, and references therein) to reproduce the $\beta$Pictoris spectral energy distribution (SED). In this model, the dust consists of porous aggregates made from a silicate core coated with organic refractories (see also Pantin et al. 1997). A more detailed account of the grain model used here is given in Augereau et al. (1999). Initially, we fix the porosity of the grains to be 0.95 and assume that most are amorphous (Li & Greenberg 1998; Lagage et al. 1999).

2.5.3 Presence of ice

Water ice may be present on the surfaces of the elementary submicronic particles that compose an aggregate (Greenberg & Hage 1990, and references therein). The amount of ice is quantified by a volume percentage in addition to that of vacuum (due to the porosity). A grain is assumed icy if it is produced further than the ice sublimation distance. That distance depends on the grain size and amount of ice (typically between 20AU for grains larger than $\sim$100$\mu$m and 100AU for grains smaller than $\sim$1$\mu$m). Due to the effect of radiation pressure, non-icy grains can be present at very large distances as well as icy grains, possibly mixing two dust chemical compositions at a given distance from the star.

2.5.4 Grain sizes

For the range of $\beta_{\rm pr}$ values we consider, there is a one-to-one relationship between the value of $\beta_{\rm pr}$ and the grain size a which can be expressed in the form $a=K\beta_{\rm pr}^{-1}$ (Artymowicz 1988, for instance), where Kdepends on the optical properties of the grain which are computed using the Mie theory (Bohren & Huffman 1983). Some examples of K values for different amounts of ice and porosities can be derived from the values of $a_{\rm\beta_{\rm pr}=0.5}$ given in Table 1. A grain size distribution with ${\rm d}n(a)/{\rm d}a \propto a^{-3.5}$ is assumed to take into account the relative number n(a) of grains with radius greater than a produced in the disk by collision processes. For each $\beta_{\rm pr}$ value (or grain size), the appropriate relative number density and thus the contribution to a scattered light or thermal emission image is computed. The 11 independent images then are correctly superimposed with appropriate weight factors so as to produce a final image of the disk for any required PB surface density distribution or wavelength of interest.

2.5.5 Orientation of the disk to the line of sight

In order to complete the above procedure, the disk orientation with respect to the observer has to be specified. This introduces two additional parameters: the line of nodes of the perturbing planet and the disk inclination with respect to a plane normal to the line of sight.

   
3 Scattered light images

3.1 PB surface density distribution

The first stage in the modeling procedure is to find a surface density distribution for the PB disk that leads to consistent results with both scattered light observations and thermal emission data.

Figure 2: Surface density of the PB disk (bold-dashed line) that gives a good fit to the observed surface brightness distribution in scattered light. The resulting dust surface density integrated over the grain size (or $\beta_{\rm pr}$) distribution is displayed with a bold-solid line. Both profiles are normalized to 100 at their maximum. The relative grain surface densities (thin lines) for five values of $\beta_{\rm pr}$ ranging between 0.135 and 0.45 are also superimposed for comparison

Open with DEXTER

The range of possible surface density distributions can be restricted using the following observational constraints: 1/ Both the resolved 12$\mu$m images (Pantin et al. 1997) and SED modeling (Li & Greenberg 1998) indicate that little dust lies inside $\sim$50AU; 2/ Beyond about 120AU, the radial surface brightness profile in scattered light revealed by STIS is roughly proportional to r^-5(Heap et al. 2000). For an edge-on disk like the $\beta$Pictoris one, this is in very good agreement with the profile expected from small dust particles produced by colliding large bodies confined within 120AU and blown out by radiation pressure (Lecavelier des Etangs et al. 1996). Because dust particles trace the distribution of the PB disk (Mouillet et al. 1997b), qualitatively, these remarks imply that most of the PB disk mass is contained within an annulus lying between $\sim$50AU and 120AU.

3.2 Surface brightness distribution

Applying the observational constraints described above, we tried several PB body surface density distributions. We were able to find a solution (Fig. 2) that gives a fit to the scattered light images (Fig. 3).

In this solution, the distribution of PB is confined inside $\sim$150AU. Due to the radiation pressure acting on the grains, the outer part of the disk is filled with small particles. This can be seen in Fig. 2, where we have plotted the resulting surface density distributions for grains of different sizes. The final surface density of the grains averaged over the grain size distribution peaks at about 110-120AU from the star, close to the assumed outer edge of the parent disk (Fig. 2).

   

Table 1: Thermal emission in IRAS bands for different dust models. According to Li & Greenberg (1998), dust models with P=0.98 and P=0.95 assuming icy grains give a satisfactory fit to the overall SED. The percentages of ice have been adjusted to respect the ice to silicate core-organic refractory mantle mass ratio of 1 from Li & Greenberg (1998). Dust grains with P=0.5 have a mass ratio of 0.25. Dust models with non-icy grains are also given for comparison. In each case, the dust surface density has been normalized in order to reproduce the scattered light profile and then the integrated thermal emission computed. With this procedure, the computed IR fluxes then also depend indirectly on the grain anisotropic scattering properties. There, we assume isotropic scattering properties, but the fluxes are increased by a factor of about 1.4 if the asymmetry factor |g| increases to 0.5 and the ratio of the observed to computed flux is accordingly decreased by the same amount

	IRAS	$\begin{array}{c} P=0.98 \\ 0\textrm{\% ice} \end{array}$	$\begin{array}{c} P=0.98 \\ 4\textrm{\% ice} \end{array}$	$\begin{array}{c} P=0.95 \\ 0\textrm{\% ice} \end{array}$	$\begin{array}{c} P=0.95 \\ 10\textrm{\% ice} \end{array}$	$\begin{array}{c} P=0.5 \\ 0\textrm{\% ice} \end{array}$	$\begin{array}{c} P=0.5 \\ 50\textrm{\% ice} \end{array}$
Flux at 12$\mu$m [Jy]	$1.64 \pm 0.1$	0.040	0.056	0.037	0.047	0.017	0.017
Flux at 25$\mu$m [Jy]	$10.1 \pm 0.5$	3.5	2.1	3.4	1.9	2.4	1.6
Flux at 60$\mu$m [Jy]	$18.8 \pm 1$	12.5	16.3	12.4	16.3	11.9	13.6
Flux at 100$\mu$m [Jy]	$11.2 \pm 1$	10.4	10.2	10.3	10.2	9.8	9.7
$a_{\beta_{\rm pr}=0.5}=2$ K [$\mu$m] $\left\{\begin{array}{l} \textrm{no ice} \\ \textrm{ice} \end{array}\right.$		$\begin{array}{c} 92.7 \\ \, \end{array}$	$\begin{array}{c} 92.7 \\ 46.5 \end{array}$	$\begin{array}{c} 37.1 \\ \, \end{array}$	$\begin{array}{c} 37.1 \\ 18.9 \end{array}$	$\begin{array}{c} 3.7 \\ \, \end{array}$	$\begin{array}{c} 3.7 \\ 3.0 \end{array}$
$\begin{array}{c} \textrm{Ratio of observed to} \\ \textrm{computed flux at 12\,$\mu$ m} \\ \textrm{further than $\sim$ 30\,AU (NE side)} \end{array}$		6	12	7	15	16	26

At distances greater than about 30AU, the main shape of the mid-plane surface brightness distribution in scattered light from Heap et al. (2000) is well matched depending somewhat on the precise anisotropic scattering properties (Fig. 3).

Figure 3: Surface brightness distributions in mag$\;$arcsec-2 along the mid-plane of the disk in scattered light (R band) assuming the PB surface density shown in Fig. 2. The solid line assumes isotropic scattering properties whereas the dash-dotted line assumes a Henyey & Greenstein (1941) phase function with an asymmetry factor |g| of 0.5. The two dashed lines represent radial power laws with indices -1.1 and -5.5 as measured on the HST/STIS images

Open with DEXTER

A radial power law index between -5 and -5.5 is measured at distances larger than 120AU when the dust disk is seen almost edge-on as predicted by Lecavelier des Etangs et al. (1996) and indeed observed with the HST/STIS instrument.

Importantly, due to the effect of radiation pressure, the distribution of the grain sizes is a function of the distance from the star as shown in Figs. 2 and 4.

Figure 4: Upper panel: grain size distribution at different distances from the star. In each case the distribution is normalized such that the integral over a has been normalized to 1. Lower panel: N index assuming that the grain size distribution $\vert{\rm d}n(a)/{\rm d}a\vert$ is proportional to: $(1-x^{-1})^M\times x^{-N}$ with $x=a/a_{\rm min}$ and $a_{\rm min}=a_{\beta_{\rm pr}=0.5}=2~$K (see Table 1). In this example, M is between 1.4 and 2 inside $\sim$150AU and up to 4 at larger distances

Open with DEXTER

3.3 Small scale vertical asymmetry (the warp)

Due to the effect of the assumed perturbing planet, the precession of the orbital planes of PB within 70-80AU results in a distribution with average inclination coincident with the planetary orbit. Beyond 70-80AU and up to the assumed outer edge of the PB disk (close to 140-150AU), the PB orbits have undergone only partial precession. Therefore, the mean inclination of their orbital planes to that of the initial disk ranges between 3 $\hbox{$^\circ$ }$ and about 0.5 $\hbox{$^\circ$ }$.

Mouillet et al. (1997b) showed that the warp, or the short scale asymmetry of the vertical position of the maximum surface brightness, can be reproduced assuming all particles followed the distribution of the parent body disk. Adding the effects of radiation pressure acting on grains with a given size distribution to the model of Mouillet et al. (1997b) causes a modest shift of the warp position, and so does not affect the conclusions on the propagation and observability of the warp as seen in Fig. 5, which can be directly compared to the HST/STIS images (Heap et al. 2000).

3.4 The large scale vertical (``butterfly'') asymmetry

We now investigate whether our model can account for the ``butterfly'' asymmetry. Basically, radiation pressure greatly extends the surface density distribution of the smallest particles, i.e. those which have the larger $\beta_{\rm pr}$ values, beyond that of the PB disk (Fig. 2). Accordingly, the asymmetry in the vertical location of the surface brightness maximum originating in the PB disk can be transmitted outwards as illustrated in Fig. 6. The result is a flared-like disk, with the so-called butterfly asymmetry.

	Figure 5: The warped disk normalized for each vertical cut to its maximum surface brightness. To compare with Fig. 10 from Heap et al. (2000) and to emphasize the vertical asymmetry, contours at 99%, 50% and 10% of the maximum surface brightness have been superimposed
Open with DEXTER

For illustrative purpose, we focus on the particular case for which the line of nodes of the planetary orbit and the line of sight are aligned (the observability of the warp as a function of the location of the line of nodes is discussed in Mouillet et al. 1997b). The simulated disk in scattered light then convincingly exhibits a large scale asymmetry as observed in STIS data up to 200AU (Fig. 5).

It is worth noticing that this asymmetry is present much further out than 200AU (Fig. 7), in agreement with the large scale images of Kalas & Jewitt (1995) for instance. Figure 8 quantifies the radial dependence of the asymmetry by the ratio of half widths at half maximum above and below the observed mid-plane. The ratio evidences the position of the warp at 70-80AU and shows that the disk remains asymmetric up to at least 500AU as observed. In other words, the asymmetric distribution of PB responsible for the observed warp at 70-80AU, and assumed to result from the perturbation of an inclined planet, leads naturally to a large scale asymmetry very similar to the ``butterfly'' asymmetry. Therefore, the observability of the ``butterfly'' asymmetry depends as well on the inclination of the planet to the PB disk mid-plane (3 $\hbox{$^\circ$ }$ in this model), and on the line of nodes of the planet to the line of sight.

Figure 6: The location of the maximum surface brightness for a vertical cut as a function of distance, for disks composed of grains with a single size as indicated, seen in scattered light. The line for $\beta_{\rm pr}=0.001$ traces the PB disk. The line for $\beta_{\rm pr}=0.45$ indicates the way the small scale asymmetry (warp) can be extended outwards as a result of radiation pressure. The position of the observed mid-plane to the original mid-plane of the PB disk is superimposed in this particular case (line of nodes of the planet aligned with the line of sight and disk seen edge-on)

Open with DEXTER

3.5 Summary

The dynamical approach we have followed allows us to reproduce in a consistent way most observations in scattered light, namely: the surface brightness distribution, the small scale (warp) and large scale (``butterfly'') asymmetries, assuming a planetary perturber and taking into account the effects of radiation pressure acting on the grains. But as expected, the model does not explain the NE-SW asymmetries.

   
4 Thermal emission data

4.1 IRAS fluxes

A fully consistent disk model should reproduce both the scattered light images and thermal data. Our aim is to estimate the thermal IR (12, 25, 60 and 100$\mu$m) fluxes produced by the distribution found in Sect. 3. Table 1 summarizes the computed fluxes assuming the dust model proposed by Li & Greenberg (1998) for different porosities and amounts of ice.

The 100$\mu$m and 60$\mu$m emissions (the latter slightly depending on the amount of ice) are correctly matched by the dust ring made of grains at the blow-out size limit that reproduces the scattered light profile.

	Figure 7: Modeled disk at large distances from the star. A large scale asymmetry with respect to the mid-plane is found, similar to the observed ``butterfly'' asymmetry
Open with DEXTER

	Figure 8: Ratio of half widths at half maximum above and below the observed mid-plane for a vertical cut as a function of distance and for the extension of the disk seen in Fig. 7
Open with DEXTER

Such a consistency strongly supports our dynamical approach.

On the other hand, the simulated 12$\mu$m and 25$\mu$m fluxes are smaller than observed. This shows that an additional population of hotter grains is required, in total agreement with previous works showing that most of the 12$\mu$m emission comes from a region close to the star (see for example Knacke et al. 1993), which is also confirmed by the resolved images from Pantin et al. (1997). This close population also certainly contributes to the integrated 25$\mu$m flux.

4.2 The 12 $\mu$m resolved images

Most of the 12$\mu$m flux originates within $\sim$20AU from the star as seen before. However, as shown by Pantin et al. (1997), a small part of the 12$\mu$m flux comes from regions up to $\sim$100AU. Our aim is here to see whether our model accounts for this ``outer'' 12$\mu$m emission.

Figure 9: Linear brightness distribution in thermal emission at $\lambda=12\,\mu$m assuming the PB surface density distribution shown in Fig. 2 and non-icy grains larger than 2 K with P=0.95. At each distance from the star, this linear brightness has been computed by multiplying the maximum of flux along the vertical axis by the vertical thickness (in arcsec) of the disk at $12\,\mu$m given by the Fig. 4 from Pantin et al. (1997) and available for distances smaller than 70AU. To compare with the Pantin et al. (1997) resolved emission, the predicted fluxes have also been multiplied by a factor of 7, indicating that most of the grains that contribute to the $12\,\mu$m emission at distances larger than 20-30AU are not taken into account

Open with DEXTER

Simulated and observed 12$\mu$m images compare well in terms of radial shape down to about 20-30AU (and especially when the most porous grains are not too icy, Fig. 9) but not in terms of flux. The ratio of observed to computed flux is given in the last line of the Table 1 for different dust properties. This shows that an additional population of efficient 12$\mu$m emitters, and at the same time bad scatterers at near IR wavelengths, is needed between 20-30AU and 100AU. Very small, typically submicronic, grains are a priori good candidates. For example, the emission/absorption at 12$\mu$m to scattering at 1$\mu$m efficiency ratio is a few hundred for $0.1\,\mu$m grains with porosity P=0.95 and 3 orders of magnitude larger if the grains are only $10^{-2}\,\mu$m in size.

4.3 Possible scenarios to account for the 12 $\mu$m missing flux at large distances

Core-mantle grains smaller than $a_{\beta_{\rm pr}=0.5}=2$ K have $\beta_{\rm pr}$ ratios larger than 0.5. A close inspection of Fig. 2 indicates that particles with $\beta_{\rm pr}$ratios larger than typically 0.4 have quite similar surface densities and tend to mimic that of the $\beta_{\rm pr}=0.45$ grains which are almost just unbound. In the following, we will use this property to simulate a dust disk with very small particles.

We propose hereafter possible scenarios a priori able to explain the presence of very small grains at large distances, and we check whether or not they may quantitatively reproduce the 12$\mu$m flux at large distances under reasonable assumptions.

4.3.1 First scenario: Small grains produced by cometary evaporation

A first possibility is that the submicronic grains produced close to the star, for instance by comet evaporation, responsible for most of the integrated 12$\mu$m flux and required to explain the 10$\mu$m silicate spectroscopic features, also supply the disk beyond $\sim$30AU with enough small dust particles through radiation pressure. This would give an attractive solution to the lack of 12$\mu$m emission at distances larger than $\sim$30AU in our model.

We therefore assumed a population of very small grains close to the star and let them evolve under radiation pressure. It appears that, whatever the assumptions on the surface density distribution of the inner population, the radial shape of the 12$\mu$m flux distribution does not match the one found by Pantin et al. (1997) beyond $\sim$30AU. This is mainly due to the radial decrease of the grain temperature with distance from the star which tends to result in most of the emission at 12 $\mu$m coming from close to the star leading either to very to small contributions further than $\sim$30AU or to radial profiles for the emission not consistent with the resolved observations.

A population of submicronic grains certainly exists close to the star but our modeling indicates that additional grains produced further than $\sim$30AU should be present to account for the radial shape of the 12$\mu$m emission.

4.3.2 Second scenario: Small unbound grains below the blow-out limit

We will now consider the dust disk that reproduces the scattered light data and extrapolate the initial a^-3.5 grain size distribution to grains with $\beta_{\rm pr}$ ratios larger than 0.5. We consider non-icy grains for simplicity and P=0.95 which gives good fits to the large wavelength fluxes.

In other terms, we simply extend the grain size distribution that successfully fitted the scattered light images in Sect. 3 to a minimum grain size of about 0.1$\mu$m instead of a few tens of micrometers. This actually allows us to fit the 12$\mu$m emission further than $\sim$20AU. The 60 $\mu$m and 100$\mu$m integrated fluxes are unchanged as well as the scattered light profile inside 120AU because the amount of large grains is not affected by the reduction in minimum grain size. However, beyond 120AU, the scattered light surface brightness profile changes: it follows now a r^-3.5 radial power law (instead of r^-5). r^-3.5 is not consistent with STIS data, but is in better agreement with previous data (e.g. Golimowski et al. 1993; Kalas & Jewitt 1995; Mouillet et al. 1997b).

It is therefore premature to conclude whether or not this extrapolation is correct on the sole basis of the surface brightness distribution at large distances. Moreover, the rate of production of such small grains must be continuous and more efficient than indicated by a simple extrapolation from the larger grains, since being unbound, their life-time in the disk is very short, in fact 1 to 10³ times shorter than grains with sizes just above the blow out limit. The mass loss rate from the system due to the blow out of these grains is also correspondingly larger.

4.3.3 Third scenario: Small compact bound grains produced by collisions

The physics of aggregates, present in circumstellar environments, is complex and not well understood. Catastrophic disruption of an aggregate can occur if the impact velocity is high enough (typically a few tenths of kms^-1, Dominik & Tielens 1997, for instance), producing nearly compact submicronic grains. In the vicinity of $\beta$Pictoris, such grains smaller than $\sim$10 $^{-2}\,\mu$m may have $\beta_{\rm pr}$ ratios smaller than 0.5 depending on their precise chemical composition, i.e. if they are not too refractory (e.g. Artymowicz 1988). This leads ultimately to a discontinuity in the grain size distribution which could appear depleted in grains of sizes ranging between $\sim$10 $^{-2}\,\mu$m and 2 K.

We tested this scenario by assuming an additional population of $10^{-2}\,\mu$m compact silicate grains with a surface density distribution that corresponds to that of the $\beta_{\rm pr}=0.45$particles. The 12$\mu$m resolved emission is very well matched in terms of shape and flux $\sim$20-30AU with a mass of $10^{-2}\,\mu$m grains of the same order of magnitude as the mass contained in the particles of size 2 K. The far-IR emission and the scattered light images, in particular the r^-5 radial shape of the surface brightness distribution further than 120AU, are not affected by the presence of such very small grains since they are very poor scatterers. The presence of such very small grains, and if so, their chemical composition as well as their size distribution, remain open issues.

   
5 Summary and conclusions

As in Mouillet et al. (1997b), we assumed a disk of planetesimals orbiting around $\beta$Pictoris and subject to the gravitational perturbation of a planet on an inclined orbit.

Assuming that collisions among these planetesimals produce grains with a size distribution proportional to a^-3.5 between the blow out limit and millimeter sizes, and assuming that these grains are subject to radiation pressure in addition to gravitational forces, and using plausible chemical composition and optical properties for the grains, we are able to reproduce the scattered light images (intensity, radial distribution, warp, ``butterfly'' asymmetry) as well as the far IR integrated fluxes. The PB are located between 20 and 150AU with a peak at $\sim$100-120AU. Due to radiation pressure, the grain radial distribution strongly depends on their size and the resulting dust disk extends very far from the star. The ``butterfly'' asymmetry is nothing more than the mirror of the warp of PB disk at larger distances due to radiation pressure.

The 12$\mu$m images require an additional population of small grains close to the star as was evident several years ago and attributed to comet evaporation. We have shown that radiation pressure acting on these grains does not produce a distribution that can account for the observed radial shape of the 12$\mu$m emission as found by Pantin et al. (1997) at distances larger than $\sim$20-30AU. A population of grains smaller than (or comparable to) the blow-out limit in addition to the population necessary to reproduce the scattered light images may account for this >30AU 12$\mu$m emission. It is found that the extrapolation of the a^-3.5 distribution down to such small sizes is somewhat problematic. A tentative alternative could be that there is a discrete population of grains with size less than $10^{-2}\,\mu$m in addition to the main population of grains. This is plausible as we assume that the main population of grains is made of porous aggregates ultimately breaking down and producing <10 $^{-2}\,\mu$m grains that could be responsible for the emission further than 30AU at 12$\mu$m, without affecting the scattered light images and the 60-100$\mu$m integrated fluxes. As another alternative, it is also possible to argue that the a^-3.5 law is unlikely close to the blow-out limit: grains close to the blow-out size may be over-abundant simply because of the lack of smaller grains able to efficiently destroy them. In this latter scenario, a larger number of small grains is explained as a result of collisions, without involving additional processes.

Finally, our consistent modeling of the $\beta$Pictoris disk, combining the various available observations has the following limitations: 1) the solution found is probably not unique as various parameters (optical properties, size distribution, spatial distribution, grain production mechanisms) are intricately involved; 2) the application of the a^-3.5 size distribution all the way between blow-out size and parent bodies is questionable; 3) the side-to-side asymmetry in the 12$\mu$m and 20$\mu$m images has not yet been explained. Obviously, this asymmetry originates close to the star and might be due to the evaporating comets as was proposed by Lecavelier des Etangs et al. (1996).

Further investigations will be able to benefit from new direct constraints on the spatial distribution of grains, as observed at various wavelengths (scattered light and thermal emission high angular resolution images), for the inner disk ($\!<$50 AU), and optical properties of the grains.

Acknowledgements

We wish to thank Philippe Thébault, Alain Lecavelier, Hervé Beust for fruitful discussions. J. C. Augereau and A. M. Lagrange acknowledge visitor support at QMWC through PPARC grant: PPARC GR/J88357.

References

 
• Artymowicz, P. 1988, ApJL, 335, 79 In the text  
• Augereau, J. C., Lagrange, A. M., Mouillet, D., Papaloizou, J. C. B., & Grorod, P. A. 1999, A&A, 348, 557 In the text NASA ADS  
• Barrado y Navascués, D., Stauffer, J. R., Song, I., & Caillault, J. 1999, ApJL, 520, 123 In the text  
• Beust, H., & Morbidelli, A. 2000, Icarus, 143, 170 In the text NASA ADS  
• Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light by small particles (Wiley, New-York) In the text  
• Burrows, C. J., Krist, J. E., & Stapelfeldt, K. R. 1995, WFPC2 Investigation Definition Team, Amer. Astron. Soc. Meet., 187, 3205 In the text NASA ADS  
• Crifo, F., Vidal-Madjar, A., Lallement, R., Ferlet, R., & Gerbaldi, M. 1997, A&A, 320, L29 In the text NASA ADS  
• Dent, W. R. F., Walker, H. J., Holland, W. S., & Greaves, J. S. 2000, MNRAS, 314, 702 In the text NASA ADS  
• Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 In the text NASA ADS  
• Ferlet, R., Vidal-Madjar, A., & Hobbs, L. M. 1987, A&A, 185, 267 In the text NASA ADS  
• Golimowski, D. A., Durrance, S. T., & Clampin, M. 1993, ApJL, 411, 41 In the text  
• Greenberg, J. M., & Hage, J. I. 1990, ApJ, 361, 260 In the text NASA ADS  
• Heap, S. R., Lindler, D. J., Lanz, T. M., et al. 2000, ApJ, 530 In the text  
• Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 In the text NASA ADS  
• Holland, W. S., Greaves, J. S., Zuckerman, B., et al. 1998, Nature, 392, 788 In the text NASA ADS  
• Kalas, P., & Jewitt, D. 1995, AJ, 110, 794 In the text NASA ADS  
• Kalas, P., Larwood, J., Smith, B. A., & Schultz, A. 2000, ApJL, 530, 133 In the text NASA ADS  
• Knacke, R. F., Fajardo-Acosta, S. B., Telesco, C. M., et al. 1993, ApJ, 418, 440 In the text NASA ADS  
• Lagage, P. O., de Boula, O., Cesarsky, C. J., et al. 1999, The Universe as Seen by ISO, ed. P. Cox, & M. F. Kessler, ESA-SP 427, 207 In the text  
• Lagrange, A. M., Ferlet, R., & Vidal-Madjar, A. 1987, A&A, 173, L289 In the text  
• Lecavelier des Etangs, A., Vidal-Madjar, A., & Ferlet, R. 1996, A&A, 307, 542 In the text NASA ADS  
• Lecavelier des Etangs, A. 1998, A&A, 337, 501 In the text NASA ADS  
• Larwood, J., & Kalas, P., MNRAS, accepted In the text  
• Li, A., & Greenberg, J. M. 1998, A&A, 331, 291 In the text NASA ADS  
• Mouillet, D., Lagrange, A. M., & Beuzit, J.-L. 1997a, A&A, 324, 1083 In the text NASA ADS  
• Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A.-M. 1997b, MNRAS, 292, 896 In the text NASA ADS  
• Pantin, E., Lagage, P.-O., & Artymowicz, P. 1997, A&A, 327, 1123 In the text NASA ADS  
• Zuckerman, B., & Becklin, E. E. 1993, ApJ, 414, 793 In the text NASA ADS