A&A 370, 672-679 (2001)
DOI: 10.1051/0004-6361:20010257
Lund Observatory, Box 43, SE-22100 Lund, Sweden
Received 26 October 2000 / Accepted 7 February 2001
Abstract
Observations with the planned astrometry satellite GAIA are modeled in order
to determine the detection probabilities for systems consisting of a main-sequence
star and a companion of sub-stellar mass.
Among the stars within 100 pc from the Sun,
most systems having a companion greater than 0.01 solar masses and with periods
between 0.25 and 25 yr will be detected. For
these systems with periods longer than 10-15 yr, statistical information about orbits
is obtained through the curved proper motions. Shorter periods usually result in
orbital solutions. For nearly all systems with periods less than five years,
accurate orbital elements are obtained from which companion masses can be
estimated. For systems having 0.001 solar mass companions, the detection probability exceeds 0.1
in the 1.2-10 yr range. Many of these systems will result in orbital solutions.
Key words: methods: data analysis - space vehicles - astrometry - binaries: general - stars: low-mass, brown dwarfs - planetary systems
The space astrometry satellite GAIA (Gilmore et al. 1998) is planned as a
cornerstone mission within the European Space Agency's (ESA) Horizon 2000+
programme. The current baseline is
a scanning instrument capable of determining positions, annual
proper motions and parallaxes to
![]()
![]() as (micro-arcsec) accuracy
for all stars brighter than 15 mag and to
as (micro-arcsec) accuracy
for all stars brighter than 15 mag and to
![]()
![]() as for the stars
brighter than 20 mag.
GAIA will dramatically improve our understanding of the dynamics of the
Milky Way, star formation processes, binary statistics, stellar astrophysics,
distance scales and more.
as for the stars
brighter than 20 mag.
GAIA will dramatically improve our understanding of the dynamics of the
Milky Way, star formation processes, binary statistics, stellar astrophysics,
distance scales and more.
GAIA will detect many large planets through the astrometric wobble of the parent star (Lattanzi et al. 1997). In the present work, GAIA's ability to detect sub-stellar mass companions ranging from 0.08 solar masses down to 0.001 solar masses, viz. the upper brown dwarf limit and Jupiter sized planets, is studied. It is shown that GAIA will provide large-number statistics of the nearby brown dwarf and large planet populations.
Attempts have been made to differentiate between brown dwarfs and planets through their orbital element distributions (Heacox 1999; Mayor et al. 1998). Planets are thought to have circular orbits, via planetary disks, while brown dwarfs should have a distribution similar to stellar binaries, via fracturing of molecular clouds. The currently available results, however, show no discernible differences in the distributions of orbital elements between planets, brown dwarfs and stellar binary systems. The detection and classification of sub-stellar companions is also important for testing stellar formation theories, as they provide direct information about the initial mass function (IMF) below the hydrogen burning limit.
Field brown dwarfs seem to be quite common (Kirkpatrick et al. 1999), while few brown dwarfs are found in binaries (Halbwachs et al. 2000). For instance, less than one percent of the stars in the Doppler surveys have a brown dwarf companion within 3 AU (Marcy & Butler 2000). This leads to obvious questions about star formation and orbital evolution. Are brown dwarfs generally formed as single objects, or are they formed in binary systems and then, through some type of orbital evolution, systematically ejected? In contrast to the paucity of brown dwarf companions, there seems to be a large number of Jupiter-sized planets (Heacox 1999, his Fig. 12), which suggests two different formation processes. It has been suggested that brown dwarfs and/or planets could perhaps make up a significant percentage of the halo dark matter (Kerins & Carr 1994). Microlensing searches for brown dwarfs in the halo are on-going but to date there has been no confirmed brown dwarf detection.
Quist & Lindegren (2000) used a synthetic star catalogue and a model of the Hipparcos observations and data reductions to study binary statistics from Hipparcos. One important result was that the observed frequency of curved proper motions (acceleration solutions) gives useful constraints on real binary frequencies especially in the period range 1 to 30 yr. It is therefore natural to extend this model to the proposed GAIA mission and the astrometric detection of sub-stellar mass companions.
A "concept and technology study" of the GAIA mission was completed by ESA and Matra Marconi Space in 1999. Based on that study, the sky scanning and observational errors can be accurately modeled in realistic simulations.
GAIA will have two astrometric telescopes separated by a basic angle of 106 degrees. The satellite will scan the sky, completing one rotation every 120 min. The spin axis, which is perpendicular to the two telescopes, will precess around the Sun, maintaining a constant Sun-spin angle of 55 degrees. This scanning law results in observations that are more uniformly distributed in time and scanning angle compared to Hipparcos.
GAIA will be located at the Earth-Sun L2 Lagrange point, giving a thermally stable environment, as well as eliminating occultations by the Earth and Moon. GAIA is planned as a 5 years mission, resulting in an average of about 170 scans per object. GAIA will survey all point sources down to 20th magnitude, approximately 1 billion stars. A small patch of the sky, approximately one arcsec in diameter, is mapped around each detected point source, and within this patch it is possible to find companions considerably fainter than 20th magnitude. Other characteristics of the mission are summarized in Table 1.
| Magnitude limit | 20-21 mag |
| Completeness | |
| Brightness limit | |
| Number of stars | 26 million to V = 15 |
| 250 million to V = 18 | |
| 1000 million to V = 20 | |
| Number of quasars | |
| Number of galaxies | >107 |
| Astrometric accuracy | 4 |
| (parallaxes) | 11 |
| 160 |
|
| Broad-band photometry | 4-colour to V = 20 |
| Medium-band photometry | 11-colour to V = 20 |
| Radial velocities | 1-10 kms-1 to V = 16-17 |
| Observing programme | On-board detection |
All astrometric measurements will be made in a single wide photometric band
defined by the quantum efficiency of the CCDs, i.e. unfiltered white light
convolved with the CCD's wavelength dependent sensitivity. With
current detector assumptions, the corresponding wide-band magnitude
m has the following relation to the standard V and I mag:
A non-dynamical galaxy model was used to create a synthetic star catalogue.
The galaxy model was made up of three components; disk, thick disk and halo. The scale
heights for each component were
based on Hipparcos observations (Holmberg et al. 1997). The luminosity
function for brighter stars (
![]() )
was also based on the model by
Holmberg et al. (1997).
This luminosity function was extended down to the faint end of the
HR diagram (Gould et al. 1997). Interstellar extinction was based on
Hakkila et al. (1997).
)
was also based on the model by
Holmberg et al. (1997).
This luminosity function was extended down to the faint end of the
HR diagram (Gould et al. 1997). Interstellar extinction was based on
Hakkila et al. (1997).
The synthetic catalogue contains for each star the heliocentric coordinates
(r, l, b), apparent and absolute magnitudes (m and MV), and colour
indices (![]() ). As seen in Eq. (1),
the colour was needed for the observational standard errors and galactic
coordinates were needed for the scanning law.
). As seen in Eq. (1),
the colour was needed for the observational standard errors and galactic
coordinates were needed for the scanning law.
Only main-sequence primaries were considered in this study. This allows
a single mass-luminosity relation to be assumed, which was based on Andersen (1991)
for masses above 0.59
![]() and on Chabrier et al. (1996)
for smaller masses. The Chabrier mass-luminosity (M-L) relation was extended
down to the smallest masses considered, 0.001
and on Chabrier et al. (1996)
for smaller masses. The Chabrier mass-luminosity (M-L) relation was extended
down to the smallest masses considered, 0.001
![]() .
This may be
far from the true M-L relations for brown dwarfs and planets, which depend
strongly on age. This is of little consequence for the present
work because the magnitude differences for the smaller objects will, in virtually all cases, be larger than
.
This may be
far from the true M-L relations for brown dwarfs and planets, which depend
strongly on age. This is of little consequence for the present
work because the magnitude differences for the smaller objects will, in virtually all cases, be larger than
![]() mag, so that few systems will actually be resolved (Sect. 4).
These systems could still be detected through the motion of the photocentre about the mass centre.
mag, so that few systems will actually be resolved (Sect. 4).
These systems could still be detected through the motion of the photocentre about the mass centre.
The galactic model gave about 280000 main-sequence stars within 100 pc of the Sun brighter than the GAIA detection limit (V = 20).
To determine the detection probabilities, all stars in the synthetic catalogue were
assumed to have a sub-stellar companion. The distributions of orbital parameters
were based on the results for nearby binaries with solar-type primaries (Duquennoy & Mayor 1991).
In particular, circular orbits were assumed for semi-major axis
a < 0.1 AU. For a>2 AU, the assumed distribution was
![]() .
In the intermediate range,
.
In the intermediate range,
![]() was assumed (Quist & Lindegren 2000).
was assumed (Quist & Lindegren 2000).
The mass of the primary was determined by the M-L relation described above.
The mass of the companion was assumed to be 0.08
![]() ,
0.01
,
0.01
![]() or 0.001
or 0.001
![]() .
Since the stellar luminosity function extends into the
brown-dwarf region, the primary and secondary masses were compared in order to assure
that the mass ratio q<1. The larger mass was always defined to be the primary.
For a fixed mass-luminosity relation,
this also assured a positive magnitude difference.
.
Since the stellar luminosity function extends into the
brown-dwarf region, the primary and secondary masses were compared in order to assure
that the mass ratio q<1. The larger mass was always defined to be the primary.
For a fixed mass-luminosity relation,
this also assured a positive magnitude difference.
The individual masses and semi-major axis determine the orbital period (P) through Kepler's third law. The time of periastron passage was then randomly chosen between 0 and P. The orbital plane was randomly oriented in space. Since the distance to the object was known from the Galaxy model, the component positions in the apparent orbits on the sky plane could be calculated for each observational epoch defined by the scanning law.
Since the model was non-dynamical, the centre-of-mass motion was assumed to be zero. The parallax was also assumed to be zero. Any non-zero proper motion and parallax in the solution must therefore come from orbital motion of the binary and/or observational errors.
The astrometric reduction of scan data for single stars is fairly straightforward. As for Hipparcos, a standard model of stellar motion (ESA 1997, Vol. 1, Sect. 1.2.8) was fitted to the observations, resulting in the five standard astrometric parameters for position (2 parameters), proper motion (2 parameters) and parallax. Double-star solutions contained in the Hipparcos Catalogue (ESA 1997) required much more effort (Mignard et al. 1992) and resulted in five different categories designated C, G, O, V and X (Lindegren et al. 1997; Quist & Lindegren 2000). In the present model, a simplified companion detection scheme was assumed with the categories described below. For each of the 280000 assumed binary systems, a series of tests were applied. Once a system passed a given test, the system was classified according to that test and no further tests were applied. Sections 4.1 to 4.5 reflect the sequence of tests applied.
Systems having mean separations greater than 0.5 arcsec were completely resolved by GAIA and individually detected, provided both components were brighter than the survey limit (20th magnitude). Nominally, each component would then receive the standard five parameter solution. Binarity could still be detected through common parallax and proper motion. These are the "Wide" binaries in Fig. 1. A wide binary with a companion fainter than 20 mag would not be detected (Sect. 4.3).
Binaries having a magnitude difference
![]() and a separation
between
and a separation
between
![]() arcsec, where
arcsec, where
![]() is the mean separation during the mission, were
considered resolved systems.
An additional condition was that the apparent
magnitude of the companion must be brighter than 22nd magnitude.
In these cases, the point spread functions cannot be completely isolated
and the astrometric parameters need to be solved simultaneously,
usually assuming a common parallax.
is the mean separation during the mission, were
considered resolved systems.
An additional condition was that the apparent
magnitude of the companion must be brighter than 22nd magnitude.
In these cases, the point spread functions cannot be completely isolated
and the astrometric parameters need to be solved simultaneously,
usually assuming a common parallax.
Some of the resolved systems will have periods less than 5-10 years, see Fig. 1. In these cases, orbital elements and individual component masses can be determined.
Binaries not meeting the above criteria could still be
detected through the astrometric motion of the photocentre about the
centre of mass. In these cases, the photocentre describes an orbit
with semi-major axis a0, where
To test whether there was significant non-linear motion of the photocentre,
the angular separations ![]() computed from the relative orbit were
multiplied by the ratio a0/a. This gave the angular separations
of the photocentre from the mass centre.
Observational errors from Eq. (2) were then added to
each observation, based on the total magnitude of the system.
Finally, a standard five-parameter model was fitted to the data.
If the fit was acceptable, the star was classified as a "non-detected"
binary and the five standard astrometric parameters were adopted for
the photocentre.
A fit was accepted if the residual chi-square was less than
the 99.87th percentile (corresponding to a
computed from the relative orbit were
multiplied by the ratio a0/a. This gave the angular separations
of the photocentre from the mass centre.
Observational errors from Eq. (2) were then added to
each observation, based on the total magnitude of the system.
Finally, a standard five-parameter model was fitted to the data.
If the fit was acceptable, the star was classified as a "non-detected"
binary and the five standard astrometric parameters were adopted for
the photocentre.
A fit was accepted if the residual chi-square was less than
the 99.87th percentile (corresponding to a ![]() limit for a
normal distribution).
limit for a
normal distribution).
The non-curved motion of the photocentre implies either a long orbital period (giving near linear motion), or a very short period (giving a small amplitude of the photocentre). Other "non-detected" binaries could consist of systems for which the secondary was fainter than 20 mag (Sect. 4.1). In all these cases, standard five parameter solutions were adopted.
If the system failed the five-parameter test, two or four extra parameters were added to the model, viz. the quadratic and cubic terms in time for each coordinate. These are called acceleration solutions (analogous to the Hipparcos G solutions) since the extra terms correspond to non-linear motion of the photocentre, or an apparent curvature of the proper motion. Acceleration solutions typically apply when only a fraction of the orbit is covered over the mission lifetime.
First, a seven-parameter model, with quadratic polynomials in time, was fitted to the data. The same chi-square criterion as above was used to accept or reject the fit. Acceptable quadratic solutions could have orbital periods ranging from about 8 years up to a few thousand years, see Figs. 1-3.
If the seven-parameter fit was not accepted, a nine-parameter model, with cubic polynomials in time, was then tested. Cubic solutions may apply to orbital periods from 5 years up to a hundred years. In Figs. 1-3, the acceleration solutions are labeled "Quadratic" and "Cubic" according to the accepted fits.
Having failed all of the previous models, the system was classified as "orbital" even though an orbit was not (yet) fitted. Since there was significant non-linear motion which could not be represented by simple polynomials, it was reasonable to assume that orbital elements could be determined. This is further investigated in Sect. 5.2.
A simplified version of the Hipparcos double star data reductions was used for this study. There were, however, a small number of multiple systems observed by Hipparcos. Of the main sequence survey stars, there were fewer than 40 triple systems and only one quadruple star. Most of these were known prior to the Hipparcos mission. The data reductions for these objects were performed on a "case by case'' basis, i.e. there were no standard data reduction routines for multiple systems.
GAIA will surely detect many new multiple systems but the modeling of such systems is of course more difficult. N-body simulations are required for accurate orbital determination. We know, however, that multiple stellar systems tend to be in stable, hierarchical systems. One can imagine a "Wide" or "Resolved" system, where one component is a close double star. This closer binary could possibly receive an "Orbital'' solution.
Multiple planetary systems have also been discovered (Butler et al. 1999),
where the companions have orbital periods of 4.6, 242 and 1269 days.
The minimum (![]() )
masses are estimated to be 1.0, 2.0 and 4.1
Jupiter masses respectively. This triple system could be a test
case for future data reductions. New automated methods
for detecting multiple systems need to be developed if the GAIA mission is to
maximize its scientific output. Such methods are already being considered
at several institutes involved in the GAIA mission.
)
masses are estimated to be 1.0, 2.0 and 4.1
Jupiter masses respectively. This triple system could be a test
case for future data reductions. New automated methods
for detecting multiple systems need to be developed if the GAIA mission is to
maximize its scientific output. Such methods are already being considered
at several institutes involved in the GAIA mission.
In Figs. 1-3,
the detection probabilities are shown
for the different solution categories as functions of orbital period.
These three figures are divided according to the companions mass, 0.08
![]() ,
0.01
,
0.01
![]() or
0.001
or
0.001
![]() respectively.
Each figure is further divided into different
absolute magnitudes (MV) ranges.
respectively.
Each figure is further divided into different
absolute magnitudes (MV) ranges.
In Fig. 1A, it can be seen that virtually all companions with periods less than 100 yr will be detected. For longer period binaries, the companions will be directly imaged ("Wide") when the companion has an apparent magnitudes greater than 20. Most systems having periods from about the mission lifetime (5 years) up to a few hundred years will be detected through the non-linear motion of the photocentre. These systems are labeled "Cubic" and "Quadratic". Short period binaries receive further analyses in order to determine orbital elements, see Sect. 5.2. The lack of resolved systems in Frame A is expected and is due to the large magnitude differences caused by the bright primaries, see Sect. 4.2.
In the next frame, a large percent of resolved systems are found, i.e. fainter primaries. "Resolved" systems having periods less than the mission lifetime can have individual orbits determined and therefore their masses. Virtually all systems less than a few hundred years will be detected as "Orbital", "Cubic", "Quadratic" or "Resolved". The number of resolved binaries in the last frame increases to nearly 100% for periods between 5 and 500 years, decreasing the number of allowed "Cubic" and "Quadratic" solutions.
In Figs. 2 and 3, the apparent magnitudes of the companions are too faint to be imaged directly. Therefore, there are no "Wide" or "Resolved" systems in the figures. On the other hand, the "Cubic" and "Quadratic" solutions are found, reaching to more than a 60% detection probability for periods of around 10 years in Fig. 2 and more than 20% in Fig. 3 for periods of around 6 years. Furthermore, many systems will receive "Orbital" solutions.
Broadly speaking, the detection probability for companions greater than 0.01
![]() (by the sum of methods described above)
exceeds 0.5 for periods between 0.25 yr and 25 yr.
In about half of this interval, the detection probability is close to 100%.
For orbital solutions, the detection probability exceeds 0.5 for periods between
0.25 and 6.5 yr.
(by the sum of methods described above)
exceeds 0.5 for periods between 0.25 yr and 25 yr.
In about half of this interval, the detection probability is close to 100%.
For orbital solutions, the detection probability exceeds 0.5 for periods between
0.25 and 6.5 yr.
For Jupiter-size companions, there is a greater than 0.1 detection probability for periods between 1.2 yr and 10 yr. This increases for brighter primaries where the observational errors are smallest. Many systems with Jupiter-sized companions will also have their orbital elements determined.
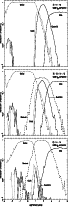 |
Figure 1:
Detection probabilities for 0.08
|
| Open with DEXTER | |
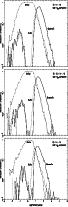 |
Figure 2:
Similar to Fig. 1 but for 0.01
|
| Open with DEXTER | |
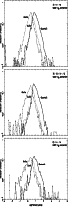 |
Figure 3:
Similar to Fig. 1 but for 0.001
|
| Open with DEXTER | |
As described above, the criterion for an orbital solution was that a cubic solution was not sufficient to represent the observed photocentre motion. This does not automatically imply that a good determination of the orbital elements can be found. Among the orbital solutions there are many for which only part of the orbit is covered by the mission lifetime of 5 years, which may result in a poor determination of the orbital elements. For the short-period systems, the (irregular) sampling of the orbit could lead to aliasing problems, i.e. that a completely wrong period is found.
To investigate this, a random sample of 800 cases having a 0.01 solar mass companion was selected from the approximately 55000 orbital solutions for further analysis. That only a small fraction of the cases was analyzed was mainly due to practical constraints on computing. The full orbit determination (especially the search for orbital period) is very time consuming, where one sample of 800 stars required about 2.5 days using ten parallel, 250 MHz Intel Pentium II CPU's running under Linux. However, the random sub-sample gives sufficient confidence in the statistics of the orbit determination.
The number of orbital solutions given above, 55000, and the predicted number of brown dwarf detections, see Sect. 6, are strongly dependent on the assumed distribution of the semi-major axis, which was that of Duquennoy & Mayor (1991). The assumed distribution does not, however, affect any of the figures shown in this work, as they represent only detection probabilities and a random sample of orbital element solutions.
When determining orbital elements, a total of 12 parameters are needed, viz. the five standard astrometric parameters for the mass centre, plus seven orbital elements for the photocentre about the mass centre.
Thiele-Innes elements were used for the geometric representation
of the orbit (equivalent to semi-major axis a0, inclination i,
position angle of the node ![]() and argument of periastron
and argument of periastron ![]() ).
The three remaining orbital elements were period (P), eccentricity (e)
and time of periastron passage (T). If P, e and T were known,
the Thiele-Innes elements and the five astrometric parameters for the
mass centre could be determined by a direct linear least-squares
solution, which is computationally very fast. However, P, e, and T enter the
observation equations in a highly non-linear way, making a direct
solution of these elements difficult. To find the global minimum of the
chi-square, the linear least-squares solution was therefore combined
with a discrete search of the three-dimensional (P, e, T) space.
The step sizes used were 0.05 yr-1 in frequency (1/P),
0.1 in e and 0.05P in T. The period interval 0.01 to 20 yr
was searched.
).
The three remaining orbital elements were period (P), eccentricity (e)
and time of periastron passage (T). If P, e and T were known,
the Thiele-Innes elements and the five astrometric parameters for the
mass centre could be determined by a direct linear least-squares
solution, which is computationally very fast. However, P, e, and T enter the
observation equations in a highly non-linear way, making a direct
solution of these elements difficult. To find the global minimum of the
chi-square, the linear least-squares solution was therefore combined
with a discrete search of the three-dimensional (P, e, T) space.
The step sizes used were 0.05 yr-1 in frequency (1/P),
0.1 in e and 0.05P in T. The period interval 0.01 to 20 yr
was searched.
In Fig. 4, the resulting periods are plotted against the true periods. For periods between 0.01 and 5 yr, virtually 100% of the systems have correctly determined orbital periods. For the few systems with incorrect periods, perhaps these periods could be found by using a global minimization algorithm, such as simulated annealing. For true periods longer than 5 yr, the period determination becomes increasingly uncertain. In general, one can have good confidence in the period determination if the calculated period is less than 4.8 yr, which is the average time span of observations per object defined by the scanning law.
The true and calculated eccentricities are compared in Fig. 5. There is a significant spread in this diagram, especially for true periods greater than 5 yr (open circles and crosses). For periods between 0.01 and 5 yr, the error in e is less than 0.1 in 65% of the cases.
The true and calculated angular semi-major axes for the absolute orbit of
the photocentre are compared in Fig. 6. In spite of the
often rather large eccentricity errors, the semi-major axis is usually
well determined, at least for periods less than 5 yr (filled circles).
For
![]() yr, the relative error in a0 is below
10% in three quarters of the cases.
yr, the relative error in a0 is below
10% in three quarters of the cases.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{10398f4.ps} \end{figure}](/articles/aa/full/2001/17/aa10398/Timg33.gif) |
Figure 4:
The calculated periods for primaries with a 0.01
|
| Open with DEXTER | |
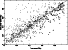 |
Figure 5:
The calculated eccentricities are plotted against true
values. Filled circles are for periods |
| Open with DEXTER | |
 |
Figure 6: The calculated semi-major axes of the photocentre (a0) plotted against the true values. The symbols are the same as in Fig. 5. The majority of stars with periods less than 5 yr (filled circles) have well-determined photocentre axes |
| Open with DEXTER | |
Using a model of the GAIA observations, the detection of sub-stellar
companions to main-sequence stars within 100 pc has been studied.
It is found that many companions with periods from 0.01 to 200 yr
will be detected through the non-linear proper motion of the primary
star or photocentre. Orbital solutions can be obtained for periods
![]() 15 yr. Solutions with periods less than
the mission lifetime (5 yr) generally give orbital elements in
good agreement with the true values.
15 yr. Solutions with periods less than
the mission lifetime (5 yr) generally give orbital elements in
good agreement with the true values.
The orbital solutions are usually unresolved systems. As such, it is the
semi-major axis of the photocentre, a0, that is determined.
If the magnitude difference is large, the second term on the right
hand side of Eq. (3) can be neglected. Using Kepler's
third law, the observations then give the quantity
![]() .
If the mass of the primary star (
.
If the mass of the primary star (
![]() )
can be estimated,
e.g. from its luminosity, then the companion mass (
)
can be estimated,
e.g. from its luminosity, then the companion mass (
![]() )
can be determined.
A small percentage of the resolved binaries have periods less than
five years, see Fig. 1.
These objects can be used to determine the individual masses of
the components without additional assumptions, as well as their
luminosities. They are therefore very interesting
for the calibration of the faint end of the mass-luminosity relation,
which is poorly known.
)
can be determined.
A small percentage of the resolved binaries have periods less than
five years, see Fig. 1.
These objects can be used to determine the individual masses of
the components without additional assumptions, as well as their
luminosities. They are therefore very interesting
for the calibration of the faint end of the mass-luminosity relation,
which is poorly known.
GAIA will directly observe many field brown dwarfs as well as brown dwarfs in "Wide" systems, see Fig. 1. The assumed mass-luminosity relation shows that brown dwarfs near the hydrogen burning limit could be as bright as 15th magnitude in V. Such objects could be directly detected out to about 75 pc. The smallest brown dwarfs that might be directly observed will have masses of around 0.06 solar masses. The galaxy model predicts on the order of 3500 field brown dwarfs will be detected by GAIA.
The total frequency of brown dwarf companions and their period distribution
are not known, and therefore it is difficult to estimate how many of them
would be detected by GAIA. From spectroscopic surveys it appears that
perhaps 0.5% of the late-type stars have a brown-dwarf companion within
3 AU (Marcy & Butler 2000). If the period distribution is similar to that of
nearby solar-type binaries (Duquennoy & Mayor 1991), i.e. log-normal with median
period 180 yr and
![]() ,
then the total frequency
would be around 2%. Half of these would have P<200 yr and could be
detected by GAIA through the astrometric wobble of the photocentre.
The total number of detections within 100 pc, and
a sample size of 280000 primaries, would
then be of the order of 3000. Almost half of these would get
accurate photocentric orbits. Clearly,
GAIA will be very powerful, not only for detecting brown dwarfs and large
planets, but also for determining their orbital characteristics and masses.
,
then the total frequency
would be around 2%. Half of these would have P<200 yr and could be
detected by GAIA through the astrometric wobble of the photocentre.
The total number of detections within 100 pc, and
a sample size of 280000 primaries, would
then be of the order of 3000. Almost half of these would get
accurate photocentric orbits. Clearly,
GAIA will be very powerful, not only for detecting brown dwarfs and large
planets, but also for determining their orbital characteristics and masses.
Acknowledgements
This work was supported by the Royal Physiographic Society in Lund. Dr. Lennart Lindegren (Lund) supplied data on the expected GAIA performance. I would like to thank Dr. Mario Lattanzi (Torino) for encouraging me to start this project and the referee for making prompt and useful remarks.