A&A 370, 602-609 (2001)
DOI: 10.1051/0004-6361:20010222
Mass and density of asteroids (4) Vesta and (11) Parthenope
B. Viateau - M. Rapaport
Observatoire de Bordeaux, UMR 5804, CNRS, BP 89, 33270 Floirac, France
Received 29 August 2000 / Accepted 7 February 2001
Abstract
As mentioned in a previous paper (Viateau & Rapaport 1997), the orbit of asteroid (17) Thetis is strongly
perturbed by two large minor planets, (4) Vesta and (11) Parthenope.
These strong gravitational perturbations enabled us to determine both the
mass of Vesta and the mass of Parthenope. We also independently derived
the mass of Vesta from observations of (197) Arete. The weighted mean of the two results
gives the value
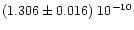
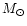 (solar mass) for the mass of Vesta,
and its derived mean density is (
(solar mass) for the mass of Vesta,
and its derived mean density is (
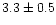 )
g/cm3. For (11)
Parthenope, the values
)
g/cm3. For (11)
Parthenope, the values
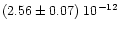
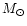 and
and
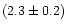 g/cm3
were obtained, respectively for its mass and its mean density.
g/cm3
were obtained, respectively for its mass and its mean density.
Key words: minor planets, asteroids - astrometry - ephemerides
1 Introduction
Large asteroids induce significant gravitational perturbations on the
orbits of other solar system bodies. The uncertainties on their mass
are a problem for the calculation of
accurate planetary ephemerides
(Standish et al. 1995; Hilton et al. 1996).
As an example, these uncertainties cause
problems in improving the determination of the relativistic precession of the
perihelion of Mars' orbit, because of long-period resonances
between the planet and some large asteroids (Eubanks 1996). (4) Vesta
is one of the strongest perturbers of Mars' orbit and one of those
causing the largest uncertainties on its ephemeris. Vesta also induces
strong gravitational perturbations on the orbits of many other
asteroids. For example, Bange (1998) showed that the mass of asteroid (20)
Massalia obtained from perturbations on (44) Nysa was strongly
correlated with the mass of Vesta. Thus, a very accurate
value of the mass of Vesta is needed.
The mass of a large asteroid can directly be determined from its
gravitational perturbations on other bodies, named "target" bodies.
Most of the time, the target bodies are other asteroids.
In a previous paper (Viateau & Rapaport 1997), hereafter referred to as Paper I, we pointed
out that recent very close encounters occurred between asteroid (17) Thetis and
two larger minor planets, (4) Vesta and (11) Parthenope, respectively
in 1996 and 1997. In that paper, a first value of the mass of Parthenope
was obtained from the analysis of the observations of Thetis,
thanks to a previous very close encounter in 1968. We also pointed out that, due
to the very strong perturbation of Vesta on the orbit of Thetis, only a few years
of additional ground-based observations of the latter asteroid would be sufficient to
obtain a very precise determination of the mass of Vesta, which is a rare phenomenon
in asteroid mass determination.
This determination of the mass of Vesta from observations of Thetis is now possible.
In order to improve the accuracy of the determination of this mass, we also used
the observations of a second target asteroid, (197) Arete. Arete was the first
asteroid used for the determination of the mass of Vesta, by Hertz (1966). A few other
determinations of this mass have been made since, most of them from perturbations on
Arete (Table 1), which now appears to be the second-best target
asteroid after Thetis for the determination of the mass of Vesta. The
final result presented in this paper is obtained from the resolution of the
equations associated with the observations of Thetis and Arete. These
equations are treated as a single system, and solved by the
Gauss-Seidel iterative method, so that the masses of Vesta and
Parthenope are determined together, with their correlation coefficient.
Table 1:
Status of the mass determination of Vesta, before the
work presented here
| Author |
perturbed |
mass |
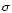 |
| |
bodies |
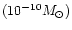 |
| Hertz (1966) |
(197) Arete |
1.17 |
0.10 |
| Hertz (1968) |
(197) Arete |
1.2 |
0.08 |
| Schubart & Matson (1979) |
(197) Arete |
1.38 |
0.12 |
| Standish & Hellings (1989) |
Mars |
1.5 |
0.3 |
| Goffin (1991) |
(197) Arete |
1.33 |
|
| Sitarski (1995) |
(197) & (486) |
1.396 |
0.043 |
| Standish et al. (1995) |
DE403 solution |
1.34 |
|
| Standish et al. (1998) |
DE405 solution |
1.3 |
|
| Hilton (1999) |
(1) & (2) |
1.69 |
0.11 |
| Michalak (2000) |
25 asteroids |
1.36 |
0.05 |
The evolution with time of the distance between Thetis and
Vesta is shown in Fig. 1a. It can be seen that both asteroids
come close to each other every 55 years. The last encounter in 1996 was unusual,
because both asteroids had almost the same osculating elements and
consequently the distance between the asteroids remained
smaller than 0.4 AU from March 1995 to June 1998 (Fig. 1b).
The
minimum was 0.0194 AU in June 1996, with a relative velocity of 1.2 kms-1.
A much smaller relative velocity of 0.2 kms-1 was reached in
March 1997. Since Vesta is the second most massive asteroid of the main
belt, with a mass equal to about 30% of the mass of Ceres
(Table 2), such an encounter induced a very strong gravitational
perturbation on the orbit of Thetis, up to 1
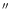 per year on average (Fig. 2).
Since the best ground-based asteroid observations
currently have an accuracy better than 0.1
per year on average (Fig. 2).
Since the best ground-based asteroid observations
currently have an accuracy better than 0.1
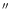 ,
a few years of such data
are sufficient to obtain the value of the mass of Vesta with a very
small standard deviation.
,
a few years of such data
are sufficient to obtain the value of the mass of Vesta with a very
small standard deviation.
Reciprocally, Thetis, with an assumed mass of
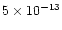
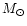 (its diameter measured by the IRAS satellite is 93 km and its mean density was
assumed to be 2.4 g/cm3), is almost 300 times less massive than Vesta, and
its perturbation on the orbit of Vesta is always less than 0.2
(its diameter measured by the IRAS satellite is 93 km and its mean density was
assumed to be 2.4 g/cm3), is almost 300 times less massive than Vesta, and
its perturbation on the orbit of Vesta is always less than 0.2
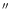 in right ascension,
too small for its mass to be determined.
in right ascension,
too small for its mass to be determined.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10233f1.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/Timg12.gif) |
Figure 1:
Distance between (17) Thetis and (4) Vesta. a) From 1850 to
2023. b) From 1995 to 1999 |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10233f2.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/Timg13.gif) |
Figure 2:
Effect of the gravitational perturbation of (4) Vesta on the orbit
of (17) Thetis in right ascension, starting forward numerical integration
at epoch JD 2450000.5 = 1995 Oct. 10.0 TT and assuming a mass of 1.35 10-10
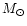 for Vesta
for Vesta |
| Open with DEXTER |
2.2 (11) Parthenope-(17) Thetis
Since its discovery in 1852, Thetis has experienced two close encounters
with (11) Parthenope (Fig. 3). The first one, in February 1968, was
extremely close, with a minimal distance of 0.0016 AU (i.e. about 240000 km)
and a relative velocity of
2.3 kms-1. This is this encounter that allows the mass
of Parthenope to be determined, with a gravitational perturbation up to 15
 in right
ascension (Fig. 4). The second encounter took place in January 1997 with
a minimal distance of 0.0054 AU and a relative
velocity of 2.4 kms-1.
This recent encounter was not yet effective
when the first determination of the mass of Parthenope
was made (Paper I), and allows now suppress
a more precise determination
of this mass.
in right
ascension (Fig. 4). The second encounter took place in January 1997 with
a minimal distance of 0.0054 AU and a relative
velocity of 2.4 kms-1.
This recent encounter was not yet effective
when the first determination of the mass of Parthenope
was made (Paper I), and allows now suppress
a more precise determination
of this mass.
0.0016 AU is the smallest minimal distance
between two asteroids
we had to deal with
in asteroid mass determination. Moreover, both
asteroids are not very different in size: the IRAS diameter of Parthenope
is 162 km, and the diameter of Thetis is 93 km. The closer two
asteroids come to each other, the more accurately their mutual
distance must be calculated. The necessity of taking into account the reciprocal
perturbation of Thetis when the orbit of
Parthenope was computed by numerical
integration was considered. However, the maximal deviation of the orbit of
Parthenope caused by Thetis was about 2
 ,
which caused
a too small relative change
on the mutual distance for the determination of the mass
of Parthenope to be affected. We therefore neglected this effect.
The deviation of 2
,
which caused
a too small relative change
on the mutual distance for the determination of the mass
of Parthenope to be affected. We therefore neglected this effect.
The deviation of 2
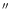 of the orbit of Parthenope was also too small for
the mass of Thetis to be determined.
of the orbit of Parthenope was also too small for
the mass of Thetis to be determined.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10233f3.ps} \end{figure}](/articles/aa/full/2001/17/aa10233/Timg14.gif) |
Figure 3:
Distance between (11) Parthenope and (17) Thetis from 1800
to 2050 |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10233f4.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/Timg15.gif) |
Figure 4:
Effect of the gravitational perturbation of (11) Parthenope on the orbit
of (17) Thetis in right ascension, backward numerical integration
at epoch JED 2450000.5 = 1995 Oct. 10.0 TT and assuming a mass of 2.6 10-12
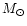 for Parthenope
for Parthenope |
| Open with DEXTER |
Vesta and Arete come close to each other every 18 years (Fig. 5).
Among the 7 close encounters experienced by the two
asteroids in the period 1879-1999, the first one in May 1885 was the closest,
with a minimal distance of 0.018 AU and a relative velocity of 2.2 kms-1.
Since that date, the minimal distance tends to increase at each
encounter. The last encounter between the two asteroids occurred in
March 1994 with a minimal distance of 0.042 AU. This series of encounters
induced a strong perturbation on the orbit of Arete, up to 60
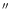 in 100 years,
which allows the mass of Vesta to be obtained with good
accuracy. On the other hand, the determination of the mass of Arete
from this encounter is not possible, because its gravitational
pertubation on the orbit of Vesta is too small (the IRAS diameter of
Arete is only 32 km).
in 100 years,
which allows the mass of Vesta to be obtained with good
accuracy. On the other hand, the determination of the mass of Arete
from this encounter is not possible, because its gravitational
pertubation on the orbit of Vesta is too small (the IRAS diameter of
Arete is only 32 km).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10233f5.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/Timg16.gif) |
Figure 5:
Distance between (4) Vesta and (197) Arete from 1875
to 2050 |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10233f6.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/Timg17.gif) |
Figure 6:
Effect of the gravitational perturbation of (4) Vesta on the orbit
of (197) Arete in right ascension, starting backward numerical integration
at epoch JED 2450000.5 = 1995 Oct. 10.0 TT and assuming a mass of
1.35 10-10 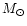 for Vesta
for Vesta |
| Open with DEXTER |
3.1 System resolution
The unknowns to be determined are the masses of Vesta and Parthenope,
and the orbital elements of Thetis and Arete, from astrometrical
observations of the two latter asteroids. The equation matrix M has the
following structure:
where A1 and A2 are 6-columns blocks and correspond to
the orbital elements of Thetis and Arete, respectively. Blocks B1 and
B2 have 2 columns, each of these columns respectively
corresponds to the masses of Vesta and Parthenope.
Calculation of singular values of M shows that the problem is
well conditioned, the condition number being equal to 440.
The equation system is solved by using the Gauss-Seidel iterative
algorithm. In this algorithm, the global system is partitioned in
blocks and solved by an iterative process, each block being solved independently.
The interest of this method is that it converges to the solution of
the global system, whatever the starting point, if the matrix of this
system is positive definite (e.g. Ralston & Rabinowitz 1978;
Jefferys 1963).
This condition is satisfied in our case because
the normal equation matrix
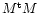 is symmetric and regular.
That result allows us to choose as initial values for masses and
orbits estimates from previous works, which are expected to be close
to the solution, so that convergence can be accelerated.
is symmetric and regular.
That result allows us to choose as initial values for masses and
orbits estimates from previous works, which are expected to be close
to the solution, so that convergence can be accelerated.
In our case, the chosen initial values were the mass of Parthenope
determined in Paper I,
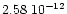
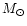 ,
the
corresponding orbital data of Thetis, a value of the mass of
Vesta estimated from previous works by other authors,
,
the
corresponding orbital data of Thetis, a value of the mass of
Vesta estimated from previous works by other authors,
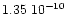
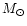 ,
and orbital elements of Arete taken in
the "Ephemerides of Minor Planets for 1995'' (Batrakov 1994).
,
and orbital elements of Arete taken in
the "Ephemerides of Minor Planets for 1995'' (Batrakov 1994).
The small blocks to be separately solved here are the classical
systems including one mass and six orbital elements. In the first
step, the mass of Vesta was separately determined from observations of
Thetis and then from observations of Arete, each time with the orbital
elements of the test asteroid, and a weighting mean of the two values
of the mass was calculated. Gravitational perturbations on the orbits
of Thetis and Arete from other asteroids including Parthenope were
taken into account, as will be detailed in Sect. 3.2.
In the next step, the mass of Parthenope was determined from
observations of Thetis. Results from the previous step were used, in
particular new orbital elements of Thetis and the new value of the mass of
Vesta to take into account its gravitational perturbation on the
orbit of Thetis. The global process was iterated and convergence was
reached in two iterations.
The following sections describe the orbit
computation and data
selection procedures used for each mass
determination.
3.2 Orbit computation
The procedures presented in this section and in the next one are similar
to those used in Paper I. The theoretical positions of asteroids (17) Thetis and
(197) Arete were calculated for a given date with the Bulirsh and Stoer numerical
integration method (Bulirsh & Stoer 1966). The osculating elements used as initial
conditions for Thetis were the ones obtained in Paper I, and expressed
for the initial date JD 2450000.5 TT. The orbital elements of Arete were
taken in the "Ephemerides of Minor Planets for 1995'' (Batrakov 1994,
initial date JD = 2450000.5 TT). As discussed in Sect. 3.1, in the case
of (17) Thetis, only one mass (Vesta or Parthenope) was determined at a time.
The integration of the motion of Thetis and Arete took into account,
as a standard procedure, the gravitational perturbations of the nine major
planets but Pluto (VSOP82 theory, Bretagnon 1982), the perturbations of Vesta
and Parthenope and, in addition, the perturbations of 6 other massive asteroids.
These asteroids are listed in Table 2 with the assumed value for
their mass, and the resulting maximal perturbation on the orbits of Thetis and Arete.
The values of the masses were taken from the literature when possible, or, if not,
were deduced from the mean diameter of the asteroids and an estimation of their mean
density. For (1) Ceres, the assumed initial value of
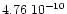
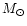 (solar mass) is the value obtained by Viateau & Rapaport (1998). For (2) Pallas, (4) Vesta and
(704) Interamnia, the values assumed are close to the mean of all mass determinations
for these asteroids. The value used for (10) Hygiea is the result found by Scholl et al.
(1987).
For (11) Parthenope, the value used was the result found in Paper I.
For (52) Europa and (511) Davida, which are respectively CF and C-class asteroids,
and for which no direct mass determination has ever been made, the mass was
calculated from the diameter of those asteroids given by IRAS, and an assumed mean
density of 1.8 g/cm3.
(solar mass) is the value obtained by Viateau & Rapaport (1998). For (2) Pallas, (4) Vesta and
(704) Interamnia, the values assumed are close to the mean of all mass determinations
for these asteroids. The value used for (10) Hygiea is the result found by Scholl et al.
(1987).
For (11) Parthenope, the value used was the result found in Paper I.
For (52) Europa and (511) Davida, which are respectively CF and C-class asteroids,
and for which no direct mass determination has ever been made, the mass was
calculated from the diameter of those asteroids given by IRAS, and an assumed mean
density of 1.8 g/cm3.
Most of the data used in this work were provided by the Minor Planet Center (USA),
through their Extended Computer Service. The MPC data used contained 1170
observations of (17) Thetis, covering the period 1852-1999, and 396
observations of (197) Arete, for the period 1879-1999. Tables 3
and 4 give the characteristics of these data. About 10% of the
observations of Thetis are photoelectric observations made with the Bordeaux
meridian circle from 1984 to 1994, which are presented in detail in Paper I.
156 new observations of Thetis were made between 1996 and 1999, since
Paper I was written. 29 of them were made with the Bordeaux and
the São Paulo CCD meridian circles as part of a collaboration
between Bordeaux Observatory and Instituto Astronomico e Geofisico of
São Paulo, Brazil (Viateau et al. 1999). As a standard procedure, all the data
were expressed in the ICRF (International Celestial Reference Frame). Since all
the observations do not have the same accuracy, a procedure of data selection and
weighting, similar to the one described in Paper I, was applied.
First, all the observations provided with a precision worse than 0.1 s
of time in right ascension and 1 arcsec in declination were eliminated.
Then, an iterative procedure was used. At the first iteration, the residuals
of the observations were calculated using the initial conditions mentioned
in Sect. 3.2. Since there were observations of very different
epochs and, thus, of different accuracies among the data used, these data
were separated into several groups with respect to the epoch of the observations.
Each group was made up of observations showing residuals of about the
same visual dispersion.
At every iteration, the standard deviation 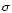 of the residuals was
calculated for each group, and the observations giving residuals over
of the residuals was
calculated for each group, and the observations giving residuals over
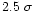 were eliminated. Weights corresponding to
were eliminated. Weights corresponding to 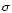 were
applied to the observations. Corrections for the mass of the
perturbing asteroid and the six osculating elements of the perturbed
body were calculated by a classical least-squares method, and gave a new
solution that was used as initial conditions for the next iteration. In the
case of photographic or CCD observations, since right ascension and
declination are not independent of each other in the reduction procedure,
both coordinates were rejected if one of them gives a residual over
were
applied to the observations. Corrections for the mass of the
perturbing asteroid and the six osculating elements of the perturbed
body were calculated by a classical least-squares method, and gave a new
solution that was used as initial conditions for the next iteration. In the
case of photographic or CCD observations, since right ascension and
declination are not independent of each other in the reduction procedure,
both coordinates were rejected if one of them gives a residual over
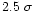 .
Iterations were made until convergence.
.
Iterations were made until convergence.
The new value found for the mass of Parthenope is
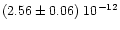
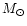 ,
and is very close to the value
,
and is very close to the value
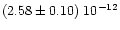
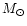 obtained in Paper I.
The main difference between the two results is the smaller standard deviation
on the value of the mass, due to the effect of the second close encounter between
Thetis and Parthenope in 1997, as explained in Sect. 2.2. Assuming
the mean diameter of Parthenope to be the IRAS value (
obtained in Paper I.
The main difference between the two results is the smaller standard deviation
on the value of the mass, due to the effect of the second close encounter between
Thetis and Parthenope in 1997, as explained in Sect. 2.2. Assuming
the mean diameter of Parthenope to be the IRAS value (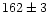 km)
gives a mean density of
km)
gives a mean density of
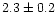 g/cm3 for this S-class
asteroid (see Fig. 7 for comparison with other asteroids).
g/cm3 for this S-class
asteroid (see Fig. 7 for comparison with other asteroids).
After convergence, the value of the mass of Vesta obtained from perturbations on
Thetis was
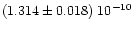
 ,
and the result obtained from
perturbations on Arete was
,
and the result obtained from
perturbations on Arete was
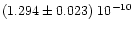
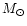 .
Tables 5 and 6 present the corresponding new orbital elements
obtained for Thetis and Arete. It can be noted that the two results
found for the mass of Vesta are very close to each other: the difference between them,
.
Tables 5 and 6 present the corresponding new orbital elements
obtained for Thetis and Arete. It can be noted that the two results
found for the mass of Vesta are very close to each other: the difference between them,
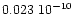
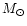 ,
is less than 2%, and approximately corresponds
to the standard deviation on both results. This agreement enhances the confidence in
the results. The weighting mean of the two values gives the final
value
,
is less than 2%, and approximately corresponds
to the standard deviation on both results. This agreement enhances the confidence in
the results. The weighting mean of the two values gives the final
value
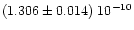
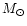 .
.
The correlation coefficient between the masses of Vesta and
Parthenope, calculated from the global matrix M (Sect. 3.1), is
0.41. This is a reasonable value that is explained by the fact that the
mass of Vesta is determined using two test asteroids (the correlation
coefficient is 0.60 if the data from Arete are omitted) and also by
the fact that the major close encounter between Parthenope and
Thetis and the close encounter between Vesta and Thetis are separated
by 27 years (1968 versus 1995).
Along with the correlation coefficient, matrix M provides the
standard deviations of the masses determined, that take into account
the correlation between both masses. These standard deviations are
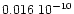
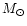 for Vesta and
for Vesta and
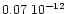
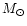 for Parthenope, which represents a slight increase from the values
that do not take into account the correlation between the two masses.
for Parthenope, which represents a slight increase from the values
that do not take into account the correlation between the two masses.
It can be noted that our final result for the mass of Vesta is very close to
the initial value assumed for this mass (
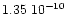
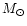 ), and
legitimate this choice. We assumed the same a-priori value of the mass of
Vesta in our previous papers, and in particular in
Paper I for the first determination of the mass of Parthenope, when we took into
account the perturbation of Vesta on the orbit of Thetis. In such mass determinations
where gravitational perturbations from other asteroids influence the
result found for the mass, it is necessary to use a good estimate of the
masses of those perturbing asteroids.
), and
legitimate this choice. We assumed the same a-priori value of the mass of
Vesta in our previous papers, and in particular in
Paper I for the first determination of the mass of Parthenope, when we took into
account the perturbation of Vesta on the orbit of Thetis. In such mass determinations
where gravitational perturbations from other asteroids influence the
result found for the mass, it is necessary to use a good estimate of the
masses of those perturbing asteroids.
It can also be noted that our final result for the mass of Vesta is in good agreement
with most of other authors' (see Table 1), and in
particular with Standish et al. (1998) and Michalak (2000), whose
results were obtained using other test objets (planets and other
test asteroids).
The accuracy of the mean density of Vesta is strongly dependent on
the accuracy of its mean diameter, or its "effective" diameter
(Bowell et al. 1989), that is, the diameter of the equal volume sphere. For
asteroids having the shape of a triaxial ellipsoid like Vesta, the
effective diameter
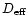 is given by
is given by
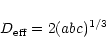 |
(1) |
where 2a, 2b and 2c are the ellipsoid axis (Müller & Lagerros 1998).
Determining an accurate effective diameter of Vesta is not
the purpose of this paper, however we tried to find a good estimate from
the literature. A summary of diameter determinations of Vesta is given in
Table 7.
Table 7:
Summary of diameter determinations of Vesta. Part of these
results were taken in Tedesco (1994). "3e" (resp. "2e") means that the shape was
assumed to be a triaxial (resp.biaxial) ellipsoid
| Author |
Technique |
Result |
| |
|
(km) |
| Barnard (1900) |
filar microm. |
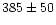 |
| Allen (1971) |
radiometry |
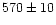 |
| TRIAD (1979) |
polarimetry |
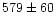 |
| TRIAD (1979) |
radiometry |
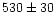 |
| IRAS (1986) |
radiometry |
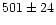 |
| Drummond et al. (1988) |
speckle interf. |
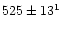 |
| Drummond & Hege (1989) |
speckle interf. |
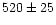 |
| Stamm (1989) |
occultation |
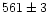 |
| Dunham (1991) |
occultation |
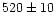 |
| IMPS (1992)2 |
radiometry |
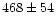 |
| McCarthy et al. (1994) |
IR speckle, 3e |
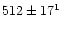 |
| McCarthy et al. (1994) |
IR speckle, 2e |
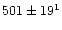 |
| Thomas et al. (1997) |
HST3, 3e |
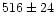 |
| Müller & Lagerros (1998) |
HST |
530.4 |
| Müller & Lagerros (1998) |
radiometry |
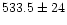 |
| Müller & Lagerros (1998) |
radiom., STM4 |
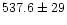 |
| 1 Calculated with Eq. (1).
|
| 2 IRAS Minor Planet Survey. |
|
3 Hubble Space Telescope. |
|
4 Standard Thermal Model. |
The diameter used to calculate Vesta's mean density was determined
by averaging the values given in Table 7, and their scattering
was used to calculate the standard deviation. Barnard's result and
the IMPS value, both much smaller than other results, were rejected.
The effective diameter found is 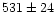 km, which is logically
very close to many results (TRIAD, Drummond et al. 1988; Müller &
Lagerros 1998,...). It gives a mean density of
km, which is logically
very close to many results (TRIAD, Drummond et al. 1988; Müller &
Lagerros 1998,...). It gives a mean density of
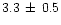 g/cm3
for Vesta, to be compared to other authors' results (Table 8).
This table summarizes the density determinations explicitely published,
but it must be pointed out that most of the diameters listed in
Table 7 give a mean density for Vesta between 3 and 4 g/cm3 when
associated with most of the mass determinations given in Table 1.
This is a rather high value compared to other asteroids for which density
determinations have been made, since most of them show densities close
to 2 g/cm3 (Fig. 7). Our result therefore confirms a
high density for Vesta, but we point out that this conclusion is
strongly dependent on the effective diameter adopted for this asteroid.
g/cm3
for Vesta, to be compared to other authors' results (Table 8).
This table summarizes the density determinations explicitely published,
but it must be pointed out that most of the diameters listed in
Table 7 give a mean density for Vesta between 3 and 4 g/cm3 when
associated with most of the mass determinations given in Table 1.
This is a rather high value compared to other asteroids for which density
determinations have been made, since most of them show densities close
to 2 g/cm3 (Fig. 7). Our result therefore confirms a
high density for Vesta, but we point out that this conclusion is
strongly dependent on the effective diameter adopted for this asteroid.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10233f7.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/T10233f7.gif) |
Figure 7:
Mean density of each of the 16 asteroids for which a mass
has already been determined, sorted by class; references of
the masses used (in brackets is
given the asteroid number): [1] Viateau & Rapaport (1998), [2] Standish et al.
(1995), [4] this work, [10] Scholl et al. (1987), [11] this work,
[15] Hilton (1997), [16] Viateau (2000), [20] Bange (1998),
[24] López García et al. (1997), [45] Merline et al. (1999),
[121] Viateau (2000), [243] Belton et al. (1995),
[253] Yeomans et al. (1997), [433] Yeomans et al. (1999), [704 and 804] Landgraf (1992) |
| Open with DEXTER |
New values of mass and density were determined for two large
asteroids, (4) Vesta and (11) Parthenope. The value found for the
mass of Parthenope,
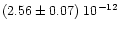
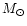 ,
confirmed
and improved the result obtained in a previous paper. It gives a mean
density of
,
confirmed
and improved the result obtained in a previous paper. It gives a mean
density of
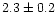 g/cm3, consistent with most of other S-class
asteroids. The value obtained for the mass of Vesta is
g/cm3, consistent with most of other S-class
asteroids. The value obtained for the mass of Vesta is
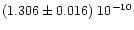
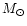 and gives
a mean density of
and gives
a mean density of
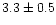 g/cm3, higher than most of other
asteroids. The masses of Vesta and Parthenope are obtained with small standard
deviations, but it is well known that the actual uncertainty of the
results is higher due to observational bias and physical systematic
effects, in particular gravitational effects of asteroids not yet taken into account
in the physical model of the test asteroids used for the mass
determination. A good point, however, is that our result for the mass
of Vesta is in good agreement with recent results from authors who used other test
objects to determine this mass, and also that Arete and Thetis, the two test
asteroids used in this paper to determine the mass of Vesta, gave two
very close results.
g/cm3, higher than most of other
asteroids. The masses of Vesta and Parthenope are obtained with small standard
deviations, but it is well known that the actual uncertainty of the
results is higher due to observational bias and physical systematic
effects, in particular gravitational effects of asteroids not yet taken into account
in the physical model of the test asteroids used for the mass
determination. A good point, however, is that our result for the mass
of Vesta is in good agreement with recent results from authors who used other test
objects to determine this mass, and also that Arete and Thetis, the two test
asteroids used in this paper to determine the mass of Vesta, gave two
very close results.
This is the first time asteroid
(17) Thetis has been used to determine the mass of Vesta. Thetis is now the
best target for this, and further observations of this asteroid, if made
regularly, will help a lot to improve the knowledge of the mass of Vesta.
A very good level of accuracy is needed for this mass, since Vesta
is the second most massive asteroid and induces important gravitational
perturbations on the orbits of many other solar system objects,
including the planet Mars. Improvement of the mean densities of Vesta and
Parthenope will be obtained only if the effective diameters of these asteroids
can be known with a better accuracy, for example from star occultations.
Observations of these phenomena are very useful, since our
knowledge of sizes of asteroids is currently insufficient
for most of the large asteroids.
Acknowledgements
The authors would like to thank the people from the meridian teams of
Bordeaux and Valinhos (São Paulo) observatories, as well as
Bill Owen, from the Jet Propulsion Laboratory, and Ronald C. Stone, from
US Naval Observatory. All of these people contributed to
the present work by making new and accurate observations of (17) Thetis.
The authors also thank the referee, J. L. Hilton, for his helpful
comments and suggestions.
-
Allen, D. A. 1971, In Physical Studies of Minor Planets, ed. T. Gehrels,
NASA SP-267, 41
In the text
-
Bange, J. F. 1998, A&A, 340, L1
In the text
NASA ADS
-
Barnard, E. E. 1900, MNRAS, 60, 261
In the text
NASA ADS
-
Batrakov, Y. V. 1994, Ephemerides of Minor Planets for 1995,
Institute of Theoretical Astronomy, S
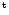 Petersburg
In the text
Petersburg
In the text
-
Belton, M. J. S., Chapman, C. R., Thomas, P. C., et al. 1995, Nature, 374, 785
In the text
NASA ADS
-
Bowell, E., Hapke, B., Domingue, D., et al. 1989, in ed. R. P. Binzel,
T. Gehrels, & M. S. Matthews, Asteroids II (Univ. of Arizona
Press, Tucson), 524
In the text
-
Bretagnon, P. 1982, A&A, 114, 278
In the text
NASA ADS
-
Bulirsh, R., & Stoer, J. 1966, Num. Math., 8, 1
In the text
-
Cellino, A., Zappalà, V., Di Martino, M., et al. 1987, Icarus, 70, 546
In the text
NASA ADS
-
Drummond, J., Eckart, A., & Hege, E. K. 1988, Icarus, 73, 1
In the text
NASA ADS
-
Drummond, J. D., & Hege, E. K. 1989, in ed. R. P. Binzel,
T. Gehrels, & M. S. Matthews, Asteroids II (Univ. of Arizona
Press, Tucson), 171
In the text
-
Dunham, D. W. 1991, Occultation Newsletter, 5, 93
In the text
-
Eubanks, T. M. 1996, e-mails to "Friends of Mars Pathfinder"
In the text
-
Goffin, E. 1991, A&A, 249, 563
In the text
NASA ADS
-
Hertz, H. G. 1966, IAU Circ., 1983
In the text
-
Hertz, H. G. 1968, Science, 160, 299
In the text
NASA ADS
-
Hilton, J. L., Seidelmann, P. K., & Middour, J. 1996, AJ, 112, 2319
In the text
NASA ADS
-
Hilton, J. L. 1997, AJ, 114, 402
In the text
NASA ADS
-
Hilton, J. L. 1999, AJ, 117, 1077
In the text
NASA ADS
-
Infrared Astronomical Satellite Asteroid and Comet Survey;
Preprint Version No. 1, 1986, ed. D. L. Matson, JPL Internal
Document NO. D-3698, Jet Propulsion Laboratory, Pasadena
In the text
-
IRAS Minor Planet Survey, 1992, ed. E. F. Tedesco, PL-TR-92-2049,
Phillips Laboratory, Hanscom Air Force Base, MA
In the text
-
Jefferys, W. H. 1963, AJ, 68, 111
In the text
NASA ADS
-
Landgraf, W. 1992, in Proc. IAU Symp. 152,
Chaos, resonance and collective dynamical phenomena in the Solar
System, ed. S. Ferraz-Mello (Kluwer Academic Publishers, Dordrecht), 179
In the text
-
López García, A., Medvedev, Yu. D., & Mora
 o Fernández,
J. A. 1997, in
Dynamics and Astrometry of Natural and Artificial
Celestial Bodies, ed. I. M. Wytrzyszczak, J. H. Lieske, & R. A. Feldman
(Kluwer Academic Publishers, The Netherlands), 199
In the text
o Fernández,
J. A. 1997, in
Dynamics and Astrometry of Natural and Artificial
Celestial Bodies, ed. I. M. Wytrzyszczak, J. H. Lieske, & R. A. Feldman
(Kluwer Academic Publishers, The Netherlands), 199
In the text
-
McCarthy, D. W., Freeman, J. D., & Drummond, J. D. 1994, Icarus, 108, 285
In the text
NASA ADS
-
Merline, W. J., Close, L. M., Dumas, C., et al.
1999, Nature, 401, 565
In the text
NASA ADS
-
Michalak, G. 2000, A&A, 360, 363
In the text
NASA ADS
-
Müller, T. G., & Lagerros, J. S. V. 1998, A&A, 338, 340
In the text
NASA ADS
-
Ralston, A., & Rabinowitz, P. 1978, A first course in numerical analysis
(International Student Editions), 444
In the text
-
Scholl, H., Schmadel, L. D., & Röser, S. 1987, A&A, 179, 311
In the text
NASA ADS
-
Schubart, J., & Matson, D. L. 1979, in Asteroids, ed. T. Gehrels
(University of Arizona Press, Tucson), 84
In the text
-
Sitarski, G. 1995, Acta Astron., 45, 673
In the text
NASA ADS
-
Stamm, J. 1989, Reports of asteroidal appulses and occultations, Occultation
Newsletter, 5, 327
In the text
-
Standish, E. M., & Hellings, R. W. 1989, Icarus, 80, 326
In the text
NASA ADS
-
Standish, E. M., Newhall, XX, Williams, J. G., & Folkner, W. M. 1995,
IOM 314.10-127, Jet Propulsion Laboratory, Pasadena, USA
In the text
-
Standish, E. M., Newhall, XX, Williams, J. G., et al. 1998,
IOM 312.F-98-048, Jet Propulsion Laboratory, Pasadena, USA
In the text
-
Tedesco, E. F. 1994, in Asteroids, Comets, Meteors 1993,
ed. A. Milani et al., 55
In the text
-
Thomas, P. C., Binzel, R. P., Gaffey, M. J., et al. 1997, Icarus, 128, 88
In the text
NASA ADS
-
Viateau, B. 2000, A&A, 354, 725
In the text
NASA ADS
-
Viateau, B., & Rapaport, M. 1997, A&A, 320, 652
In the text
NASA ADS
-
Viateau, B., & Rapaport, M. 1998, A&A, 334, 729
In the text
NASA ADS
-
Viateau, B., Réquième, Y., Le Campion, J. F., Benevides-Soares, P., Teixeira,
R., et al. 1999, A&AS, 134, 173
In the text
NASA ADS
-
Yeomans, D. K., Barriot, J. P., Dunham, D. W., Farquhar, R. W., Giorgini, J. D., et al. 1997, Science, 278, 2106
In the text
NASA ADS
-
Yeomans, D. K., Antreasian, P. G., Cheng, A.,
et al. 1999, Science, 285, 560
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10233f1.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/Timg12.gif)
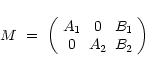
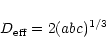
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10233f7.eps} \end{figure}](/articles/aa/full/2001/17/aa10233/T10233f7.gif)