A&A 370, 157-169 (2001)
DOI: 10.1051/0004-6361:20010197

ROSAT all-sky survey of W Ursae Majoris stars and the problem of supersaturation

K. Stepien1 - J. H. M. M. Schmitt2 - W. Voges3


1 - Warsaw University Observatory, Al. Ujazdowskie 4, 00-478 Warszawa, Poland
2 - Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
3 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstr. 1, 85741 Garching, Germany

Received 30 November 2000 / Accepted 31 January 2001

Abstract
From ROSAT all-sky survey (RASS) data we obtained X-ray fluxes for 57 W UMa type contact systems. In our sample we detected three stars which are the shortest period main sequence binaries ever found as X-ray sources. For stars with (B-V)0 < 0.6 the normalized X-ray flux decreases with a decreasing color index but for (B-V)0 > 0.6 a plateau is reached, similar to the saturation level observed for single, rapidly rotating stars. The X-ray flux of W UMa stars is about 4-5 times weaker than that of the fastest rotating single stars. Because early type, low activity variables have longer periods, an apparent period-activity relation is seen among our stars, while cool stars with (B-V)0 > 0.6 and rotation periods between 0.23 and 0.45 days do not show any such relation. The lower X-ray emission of the single, ultra fast rotators (UFRs) and W UMa stars is interpreted as the result of a decreased coronal filling factor. The physical mechanisms responsible for the decreased surface coverage differs for UFRs and W UMa systems. For UFRs we propose strong polar updrafts within a convection zone, driven by nonuniform heating from below. The updrafts should be accompanied by large scale poleward flows near the bottom of the convective layer and equatorward flows in the surface layers. The flows drag dynamo generated fields toward the poles and create a field-free equatorial region with a width depending on the stellar rotation rate. For W UMa stars we propose that a large scale horizontal flow embracing both stars will prevent the magnetic field from producing long-lived structures filled with hot X-ray emitting plasma. The decreased activity of the fastest rotating UFRs increases the angular momentum loss time scale of stars in a supersaturated state. Thus the existence of a period cutoff and a limiting mass of W UMa stars can be naturally explained.

Key words: stars: activity - (stars:) binaries: eclipsing - stars: coronae - stars: late type - stars: rotation - X-rays: stars


1 Introduction

W Ursae Majoris type variables are eclipsing contact binaries with spectral types between F and K, and orbital periods extending from 0.2 to 1.5 days (Rucinski 1998a) but strongly peaked between 0.25-0.6 days. Because of their extremely rapid rotation rates, which are only very rarely encountered in single stars, W UMa systems are expected to show also extremely high levels of chromospheric and coronal emission. These expectations are confirmed by observations both at UV and X-ray wavelengths (Rucinski 1985; Rucinski et al. 1985; Cruddace & Dupree 1984). In the Einstein Observatory IPC survey of WUma systems Cruddace & Dupree (1984) detected X-ray emission from 14 W UMa systems (out of 17 observed) with typical activity levels in the range $L_{\rm x}/L_{\rm bol} \approx 10^{-4}$. Schmitt et al. (1990) discussed the (low-resolution) observed X-ray spectra of 44i Boo and VW Cep and showed them to be consistent with a two-temperature thermal emission model. More recently, McGale et al. (1996) published the results of a spectral survey of 8 W UMa systems, based on the ROSAT PSPC observations and again found two-temperature models, with temperatures of around 2 106 K and 107 K, consistent with the data. X-ray eclipses of W Uma systems have not been reported, although small amplitude variations below 20% on the time scales (roughly) of the orbital period are observed. The most extensive space observations of a W UMa system were carried out by Brickhouse & Dupree (1998), who recently published the results of a very long contiguous (nearly 130 hours) observation of 44i Boo with the spectrometers and the Deep Survey (DS) instrument on-board of Extreme Ultraviolet Explorer (EUVE). The observations, albeit with rather low SNR, showed a sinusoidal variation of the EUV flux with a period close to the orbital period. These variations are interpreted as an indication of the presence of an active region on the primary component of the binary. The EUV light curve does not follow the variations of the transition region lines and therefore the X-ray emission should come from a different region. In addition, the same authors argue that line ratio diagnostics indicate extremely high electron densities in the corona, of 2 1013 cm-3.

Because of their high rotation rates W UMa stars should show X-ray activity close to the saturation level (Vilhu 1984; Vilhu & Walter 1987). However, Cruddace & Dupree (1984) show that these stars have a significantly lower level of X-ray activity than other rapidly rotating stars and suggest that this may be a sign of a turn over of a rotation-activity relation for extremely short rotation periods. Indeed, the recent observations of ultra fast rotating (UFR) stars in young clusters also show this surprising behavior of the X-ray flux: for stars with rotation periods less than about 0.4 days the ratio $L_{\rm x}/L_{\rm bol}$ appears to decrease with decreasing period. This phenomenon has been termed "supersaturation'' (for the most recent review of the supersaturation phenomenon see Randich 1998). The individual components of W UMa systems belong to the fastest rotating main sequence stars with many stars having periods below 0.3 days. Thus W UMa systems are ideally suited to study the still poorly understood phenomenon of supersaturation. We therefore used the ROSAT all-sky survey (RASS; Voges et al. 1999) data to study the X-ray properties of W UMa stars and to present the results of our studies in this paper.

2 Observations and data reduction

2.1 Sample selection and definition

From their optical light curves two subtypes of the W UMa variables are usually distinguished, based on the relative depths of the optical minima: those with the deeper minimum corresponding to an eclipse of the more massive component (primary) are called A-type variables, whereas W-type variables have shallower minima (Rucinski 1993). The A-type variables are hotter, with spectral types earlier than about F7-F8 (Lipari & Sistero 1988) whereas the W-type variables have later spectral types. It is important to realize that there is no clear separation between these two types. Quite a few stars exchange the relative depths of the minima with time, so an analysis of different light curves results in different classification. The whole class of W UMa stars is also not well bounded at the hot end. Many eclipsing binaries with periods below one day and spectral types of early F or even late A have been recently identified with masses substantially exceeding the masses of components of the classical W UMa systems. The analysis of their light curves produces contradictory classifications: some of such stars (e.g. BK And, AG Vir, RV Crv, BV Eri, RU Eri) have been included in the group of contact binaries of the W UMa type by some authors (e.g. Lipari & Sistero 1988) but to a group of nearly contact close binaries by others (e.g. Shaw et al. 1996). Niarchos et al. (1991) analyzed the light curve of GK Per and obtained $2.8~M_{\odot}$ and 2.6 $M_{\odot}$ for masses of the components, yet they call the variable a W UMa type star. The problem of the ill-defined boundary between A-type variables and the more massive, early type contact, or near-contact binaries was recognized by Maceroni & van't Veer (1996), who suggest a subdivision of A-type variables into low- and high-mass variables. Fortunately, the problem of exact location of the hot boundary of the W UMa stars is not critical for our work, since the X-ray emission of contact binaries decreases rapidly between late F and early F spectral types.

2.2 Input data

Our input list of W UMa variables was compiled mostly from two extensive, recently published surveys of W UMa systems. Maceroni & van't Veer (1996) listed all the W UMa stars with a reliable photometric and/or spectroscopic solution so that the basic parameters of both components are known. Rucinski & Duerbeck (1997) published a list of all nearby W UMa systems with reliable Hipparcos parallaxes (ESA 1998). The list was used to improve an existing calibration between the absolute magnitude, color and period of the variables. The authors collected or, if necessary, determined the V-magnitudes of the stars at maximum light, their B-V and E(B-V). The same parameters are also listed for several stars by Maceroni & van't Veer (1996), but for others no data are given. In order to produce a list as complete as possible other recent sources of data on the W UMa stars were checked including Hilditch et al. (1988), Al-Naimy et al. (1989), Rovithis-Livaniou et al. (1992), Lipari & Sistero (1988) and Pantazis & Niarchos (1998). In addition the current literature was searched. Altogether 7 additional stars were found with useful data. One further star, EL Aqr, was also added, although no orbital solution exists for it; it has been detected quite a while ago as a W UMa type star by one of us (Stepien 1968). The total input list consists of 102 objects.


 

 
Table 1: Input data for W UMa stars

Name

 P (days) V B-V E(B-V) ref. Par (mas)   cts error HR

CC Com

 0.2210 11.30 1.24   2 12.5 p      
V523 Cas 0.2337 10.62 1.05   2, 5 12.4 p 0.097 0.017 0.20
RW Com 0.2373 11.07 0.88 0.00 1 11.45   0.043 0.003 -0.28
BI Vul 0.2518 13.17 1.00 0.13 1, 6 4.0 p      
VZ Psc 0.2612 10.15 1.14 0.00 1 16.77   0.181 0.024 0.03
V803 Aql 0.2634 12.7 1.36 0.08 2, 16 6.3 p      
FS CrA 0.2636 12.7 1.13 0.13 2, 7 4.7 p      
44i Boo 0.2678 5.80 0.85 0.00 1 78.39   3.414 0.076 -0.16
FG Sct 0.2705 12.59 1.07 0.14 2, 16 4.5 p      
VW Cep 0.2783 7.30 0.86 0.00 1 36.16   1.416 0.039 -0.05
BX Peg 0.2804 10.80 0.78   8 6.7 p 0.042 0.018 -0.42
AD Cnc 0.2827 13.13 0.93   7 2.8 p      
XY Leo 0.2841 9.55 0.99 0.02 1 15.86   0.368 0.032 0.01
RW Dor 0.2854 10.9 0.89 0.00 1 8.91   0.052 0.005 -0.01
ER Cep 0.2857 15.67 0.82 0.07 2 0.74 p      
BW Dra 0.2923 8.61 0.63 0.01 1 15.32   0.660 0.029 0.03
EH Hya 0.2969 14.37 0.83 0.06 2, 9 1.3 p      
TZ Boo 0.2972 10.48 0.64 0.03 1 6.76        
CE Leo 0.3034 11.88 0.90 0.00 2, 10 4.5 p      
SY Hor 0.3117 11.40 0.83 0.00 2 5.0 p      
TW Cet 0.3117 10.43 0.69   2 9.91   0.073 0.015 -0.10
SX Crv 0.3166 8.98 0.54 0.02 1 10.90   0.188 0.044 0.38
TY Boo 0.3171 10.81 0.76   2 5.8 p      
CW Cas 0.3188 11.20 0.74   2, 16 4.7 p 0.026 0.010 0.29
GW Cep 0.3188 11.4 0.65   2, 16 3.8 p      
SW Lac 0.3207 8.54 0.75 0.01 1 12.30   0.491 0.031 0.15
YY Eri 0.3215 8.16 0.66 0.00 1 17.96   0.317 0.033 -0.02
TU Boo 0.3243 11.4 0.69   3 3.9 p      
V677 Cen 0.3251 10.80 0.61   5 4.6 p      
FG Hya 0.3278 9.90 0.61 0.02 2 2.92   0.056 0.017 -0.01
AO Cam 0.3299 9.5 0.68   16 9.2 p 0.035 0.010 1.63
DF Hya 0.3306 11.03 0.59   5 4.0 p      
AB And 0.3318 9.49 0.88 0.01 1 8.34   0.128 0.017 0.12
W UMa 0.3336 7.76 0.66 0.00 1 20.17   0.460 0.040 -0.13
RZ Com 0.3385 10.42 0.57 0.04 2 1.51   0.008 0.002 0.00
V700 Cyg 0.3400 11.2 0.74   3 3.1 p      
VY Cet 0.3408 11.10 0.69 0.00 2 4.5 p      
VW Boo 0.3422 10.41 0.81   4 3.44   0.053 0.015 0.09
V757 Cen 0.3432 8.40 0.65 0.03 1 14.18   0.235 0.033 0.01
V508 Oph 0.3448 10.60 0.73   2 7.68   0.025 0.008 0.79
V781 Tau 0.3449 8.55 0.58 0.05 1 12.31   0.155 0.020 -0.09
GR Vir 0.3470 7.80 0.57 0.00 1 18.83   0.303 0.043 -0.07
BV Dra 0.3501 7.89 0.54 0.01 1 14.86   0.660 0.029 0.03
AC Boo 0.3524 9.96 0.62 0.00 1 7.58   0.034 0.009 0.54
TY UMa 0.3545 11.50 0.69   11 3.5 p      
CK Boo 0.3552 8.99 0.55 0.01 1 6.38   0.081 0.018 0.28
AH Cnc 0.3604 13.31 0.53 0.06 2 1.2 p 0.0021 0.0004 1.11
RW PsA 0.3604 11.50 0.75   2 3.7 p 0.035 0.017 0.11
BB Peg 0.3615 11.6 0.52   16 3.02        
AE Phe 0.3624 7.56 0.64   1 20.49   0.492 0.044 -0.06
LS Del 0.3638 8.61 0.68   2, 16 12.6 p 0.096 0.021 -0.06
AM Leo 0.3658 9.25 0.53 0.00 2 13.03   0.062 0.015 0.06
V752 Cen 0.3702 9.17 0.60 0.02 1 9.51   0.098 0.022 0.32
XY Boo 0.3706 10.30 0.49   2 2.94   0.026 0.013 -0.30
U Peg 0.3748 9.47 0.62 0.02 1 7.18   0.063 0.014 0.26
RT LMi 0.3749 10.8 0.60   16 4.0 p 0.004 0.003 -0.37
AD Phe 0.3799 10.27 0.59   2 5.85        
TX Cnc 0.3829 10.00 0.61 0.02 2 5.8 p 0.037 0.017 0.21



 
Table 1: continued

Name

 P (days) V B-V E(B-V) ref. Par (mas)   cts error HR
BI CVn 0.3841 10.26 0.62   2, 4 5.31        
AU Ser 0.3865 10.9 0.87 0.05 2 5.4 p 0.038 0.009 0.71
W Crv 0.3881 11.16 0.71   2 3.9 p 0.017 0.009 3.58
EM Lac 0.3891 12.50 0.68   2 2.0 p      
V759 Cen 0.3939 7.44 0.59 0.02 1 15.88   0.501 0.045 0.38
ST Ind 0.4019 11.3 0.50   12 2.6 p      
SS Ari 0.4060 10.37 0.62   2 4.7 p 0.029 0.013 0.76
AH Vir 0.4075 8.89 0.78 0.02 2 10.86   0.218 0.027 0.02
V839 Oph 0.4090 8.82 0.63 0.09 1 8.09   0.119 0.019 0.88
V566 Oph 0.4096 7.45 0.43 0.01 1 13.98   0.120 0.020 0.08
UV Lyn 0.4150 9.42 0.67 0.00 1 8.16   0.063 0.019 -0.22
RZ Tau 0.4157 10.00 0.59 0.10 3, 2 5.74        
WZ Cep 0.4174 9.72 0.47   16 5.0 p 0.017 0.006 2.81
Y Sex 0.4198 9.80 0.45   3 9.02        
AK Her 0.4215 8.29 0.53 0.00 2 10.47   0.064 0.012 0.68
ER Ori 0.4234 9.28 0.54 0.05 2 6.7 p* 0.032 0.011 0.02
AP Dor 0.4272 9.26 0.44 0.00 1 4.66   0.045 0.011 0.06
AP Leo 0.4304 9.30 0.62 0.00 1 8.26   0.062 0.015 0.30
HI Pup 0.4326 10.33 0.60 0.07 1 5.36        
AW UMa 0.4387 6.84 0.35 0.00 1 15.13        
UX Eri 0.4453 10.50 0.67   3 6.57   0.060 0.027 2.90
TV Mus 0.4457 10.50 0.82 0.23 13, 2 5.4 p      
V502 Oph 0.4534 8.34 0.64 0.01 1 11.84   0.156 0.018 0.37
TY Men 0.4617 8.11 0.29 0.03 1 5.93        
CN And 0.4628 9.70 0.45   2 4.5 p 0.081 0.017 0.77
AA UMa 0.4681 10.88 0.60   2 3.2 p      
DK Cyg 0.4707 10.37 0.37 0.09 2 4.42        
AQ Psc 0.4756 8.60 0.50 0.03 1 8.03   0.125 0.018 0.37
EL Aqr 0.4814 10.37 0.42   14 4.71        
XZ Leo 0.4877 10.20 0.38   4 0.62        
OO Aql 0.5068 9.20 0.61 0.15 2 6.4 p 0.167 0.022 0.32
BU Vel 0.5163 10.49 0.29   2 2.3 p      
eps CrA 0.5914 4.74 0.41 0.00 1 33.43   0.088 0.023 -0.17
AQ Tuc 0.5948 9.91 0.41 0.03 2 0.9        
RR Cen 0.6057 7.27 0.36 0.02 1 9.76        
UZ Leo 0.6180 9.69 0.37 0.00 15 6.27        
V535 Ara 0.6293 7.17 0.34 0.02 1 8.87        
S Ant 0.6483 6.28 0.33 0.05 1 13.30        
RS Col 0.6724 9.52 0.59 0.02 1 5.50   0.029 0.009 0.90
V1073 Cyg 0.7859 8.24 0.42 0.08 1 5.44        
MW Pav 0.7950 8.53 0.36 0.05 1 4.80        
TY Pup 0.8192 8.40 0.41   2, 4 1.97        
CV Cyg 0.9834 10.80 0.55 0.00 15 1.6 p      
UZ Oct 1.1494 9.03 0.54 0.03 1 3.79        
(1) Rucinski & Duerbeck (1997), (2) Maceroni & van't Veer (1996), (3) Eggen (1967), (4) Hipparcos catalogue, (5) Tycho catalogue, (6) Bradstreet (1985), (7) Samec et al. (1989), (8) Samec (1990), (9) Samec et al. (1991), (10) Samec et al. (1993), (11) Broglia & Conconi (1983), (12) Zola et al. (1997), (13) Hilditch et al. (1989), (14) Stepien (1968), (15) Vinko et al. (1996), (16) taken from Simbad or estimated from photographic photometry and/or spectral type, * the Hipparcos parallax is negative.


For several stars no published UBV photometry or only contradictory data exists in the literature. We did not attempt to critically evaluate all the existing sources. Instead, we accepted the following simple rule for selecting the numbers given in Table 1: the highest priority was given to the photometric data from Rucinski & Duerbeck (1997) and they are copied for all the stars from their sample. The second priority was given to the data by Maceroni & van't Veer (1996). In a few cases with obvious errors (e.g. the value for maximum magnitude is higher than for minimum light) other sources were used. For stars in neither of the two previous sources the magnitudes and colors were taken from Eggen (1967) whenever available. However, his listed V-magnitudes were not always measured during maximum light and no correction for this effect was applied. For stars missing also from the list of Eggen the V-magnitudes from Hipparcos were taken. The average difference between $V_{\rm max}$ and V(Hip), determined from 56 stars for which both magnitudes are available, is -0.16 of a magnitude. V-magnitudes from Hipparcos were corrected by this value before entering them into Table 1 whereas Hipparcos B-V values were adopted at face value. In a few cases no V(Hip) exists and only V(Tycho) is given. Here the uncertainty is much larger - the cataloged Tycho V-values for some stars are even brighter than $V_{\rm max}$. Tycho B-V values also deviate from good ground based data by an amount up to 0.1 of a magnitude. In lack of anything better we adopted the Tycho values at face value for a couple of stars. They should be considered as uncertain within about 0.3 of a magnitude (V band) and 0.1 of a magnitude (B-V color). The data from the recent literature, SIMBAD database or crudely estimated from the photographic magnitudes and spectral types are listed for the remaining stars. The final data for our input stars therefore have a highly nonuniform quality.

Table 1 gives our input list of variables, together with the results of the RASS search. The first seven columns give name of a star, period, the adopted V-magnitude at maximum light, B-V, E(B-V), source of photometric data, and a parallax, either taken from the Hipparcos Catalogue or, if not available (or negative, as in case of ER Ori), calculated using the calibration given by Rucinski & Duerbeck (1997). The latter parallaxes are called photometric and are flagged with ``p'' in Table 1. No distinction between W-type and A-type variables is given because of the ambiguities discussed above.

2.3 X-ray observations

The ROSAT all-sky survey (RASS) was carried out using the ROSAT observatory during the second half of 1990 and the beginning of 1991. Some small areas of the sky not covered during the main phase of the all-sky survey were covered during later "survey repair'' observations, which made the RASS a complete all-sky survey. Each point on the sky was observed several times as the scan path of 2 degrees width progressed along ecliptic with an angular velocity of 1$^{\circ}$ per day. Towards the ecliptic poles the cumulated exposure time increases due to a large number of scans covering a particular position. Details on the ROSAT observatory and the RASS can be found in Trümper et al. (1991) and Voges et al. (1999). The RASS data were checked for the existence of X-ray sources at the positions of our input stars (Table 1) by using a search radius of 90 arcsec. All but three identified sources lie closer than 60 arcsec from the respective star positions. The three more distant sources lie: 74 arcsec from V523 Cas, 81 arcsec from BX Peg and 82 arcsec from RW PsA. For sources detected with a maximum-likelihood source detection algorithm as coincident with the star positions the number of counts in two energy bands was retrieved together with their errors. From this the so-called hardness ratio

HR = (H-S)/(H+S), (1)

where H and S denote the source counts in the hard (0.5-2.0 keV) and soft (0.1-0.4 keV) passbands of ROSAT can be computed. For each point at the sky the exposure time is known, and hence the effective count rate can be determined. The last three columns of Table 1 list the effective count rate, its error and the hardness ratio for each detected star. In order to convert count rates, CR, into X-ray flux, $f_{\rm X}$, we multiplied CR by an energy-conversion factor as determined by Hünsch et al. (1996)

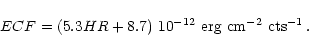\begin{displaymath}ECF=(5.3HR + 8.7)\ 10^{-12}\ \mathrm{erg~cm}^{-2}\ \mathrm{cts}^{-1}\,. \end{displaymath} (2)

The dependence of ECF on the hardness ratio compensates partially for differences in the X-ray spectral energy distributions; it should, however, be borne in mind that the above formula for ECF is not appropriate for highly absorbed sources. Due to relative proximity of our sources none falls into this category. The X-ray luminosity was then calculated from

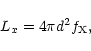\begin{displaymath}L_x = 4\pi d^2f_{\rm X}, \end{displaymath} (3)

where d is the distance to the star. Two stars, BV Dra and BW Dra, form a very close pair in the sky with an angular separation of 16 arcsec, which cannot be resolved with the ROSAT PSPC. The derived count rate was divided between both stars in the proportion determined by McGale et al. (1996) who used the High Resolution Imager (HRI) on board of ROSAT to resolve the two stars. We assumed that 0.386 cts was due to BW Dra and 0.271 cts was due to BV Dra.

Hipparcos parallaxes were used to calculate distances to the detected stars unless the parallax was less than 3 times its error. This was the case for TW Cet, RZ Com, VW Boo, ER Ori (a negative Hipparcos parallax), FG Hya, XY Boo and UX Eri. Photometrically determined parallaxes were used for these stars similarly as for those without Hipparcos parallaxes. Following Rucinski & Duerbeck (1997) a single parallax was adopted for two stars, BV Dra and BW Dra, corresponding to the Hipparcos parallax of BV Dra, which was determined with a higher accuracy. In case of AH Cnc, a member of M 67, a distance of 720 pc was adopted, and for TX Cnc, a member of Praesepe, a distance of 180 pc was adopted. The absolute visual magnitudes were converted into bolometric using the bolometric corrections given by Flower (1996). For stars with unknown E(B-V)a value 0 was adopted for distances less than 100 pc and 0.02 for more distant stars when calculating their absolute magnitudes.

All the results are summarized in Table 2, whose columns are self-explanatory (1RXS refers to ROSAT name designation).


 

 
Table 2: Basic physical and coronal parameters of the detected stars

Star

 1RXS P(days) (B-V)0 d(pc) $M_{\rm bol}$(mag) $\log L_x$(erg s-1) $\log (L_x/L_{\rm bol})$
V523 Cas J004005.0+501414 0.2337 1.05 81 5.65 29.87 -3.35
RW Com J123301.4+264255 0.2373 0.88 87 6.10 29.45 -3.60
VZ Psc J232748.5+045126 0.2612 1.14 60 5.74 29.83 -3.35
44i Boo J150348.3+473924 0.2678 0.85 13 5.03 29.72 -3.75
VW Cep J203719.4+753554 0.2783 0.86 28 4.84 30.04 -3.51
BX Peg J213849.2+264121 0.2804 0.76 149 4.70 29.86 -3.75
XY Leo J100140.5+172436 0.2841 0.97 63 5.14 30.19 -3.24
RW Dor J051833.2-681328 0.2854 0.89 112 5.37 29.83 -3.50
BW Dra J151150.4+615134 0.2923 0.62 67 4.37 30.27 -3.46
TW Cet J014852.7-205340 0.3117 0.67 156 4.29 30.24 -3.53
SX Crv J124014.6-184806 0.3166 0.52 92 4.09 30.31 -3.54
CW Cas J004552.1+630456 0.3188 0.72 213 4.35 30.16 -3.58
SW Lac J225341.8+375617 0.3207 0.74 81 3.81 30.57 -3.39
YY Eri J041208.5-102800 0.3215 0.66 56 4.34 30.00 -3.74
FG Hya J082702.6+033050 0.3278 0.59 147 3.99 30.10 -3.79
AO Cam J042812.5+530308 0.3299 0.66 109 4.15 29.94 -3.88
AB And J231131.8+365331 0.3318 0.87 120 3.79 30.31 -3.65
W UMa J094344.9+555724 0.3336 0.66 50 4.19 30.04 -3.77
RZ Com J123504.8+232005 0.3385 0.53 208 3.78 29.57 -4.40
VW Boo J141726.6+123354 0.3422 0.79 143 4.37 30.08 -3.66
V757 Cen J135155.7-363726 0.3432 0.62 71 4.00 30.09 -3.80
V508 Oph J175847.8+132928 0.3448 0.71 130 4.19 29.82 -3.99
V781 Tau J055013.3+265738 0.3449 0.53 81 3.81 30.00 -3.96
GR Vir J144520.1-064402 0.3470 0.57 53 4.12 29.93 -3.90
BV Dra J151150.4+615134 0.3501 0.53 67 3.69 30.11 -3.89
AC Boo J145627.9+462146 0.3524 0.62 132 4.29 29.91 -3.85
CK Boo J143503.8+090647 0.3552 0.54 157 2.96 30.39 -3.91
AH Cnc J085137.7+115048 0.3604 0.47 720 3.86 30.28 -3.66
RW PsA J220951.1-270342 0.3604 0.73 270 4.14 30.45 -3.38
AE Phe J013232.8-493138 0.3624 0.64 49 4.03 30.07 -3.80
LS Del J205710.3+193855 0.3638 0.68 79 4.01 29.78 -4.10
AM Leo J110211.4+095345 0.3658 0.53 77 3.63 29.59 -4.44
V752 Cen J114247.8-354832 0.3702 0.58 105 3.95 30.13 -3.78
XY Boo J134908.2+201118 0.3706 0.47 227 3.50 30.05 -4.03
U Peg J235800.0+155704 0.3748 0.60 139 3.63 30.17 -3.86
RT LMi J094947.8+342733 0.3749 0.58 250 3.70 29.36 -4.65
TX Cnc J084002.3+190017 0.3829 0.59 179 3.69 30.14 -3.87
AU Ser J155650.6+221602 0.3865 0.82 196 4.21 30.34 -3.46
W Crv J120733.0-130853 0.3881 0.69 256 3.92 30.57 -3.35
V759 Cen J141041.5-474608 0.3939 0.57 63 3.33 30.41 -3.74
SS Ari J020418.9+235959 0.4060 0.60 213 3.60 30.31 -3.74
AH Vir J121420.7+114912 0.4075 0.76 92 3.98 30.29 -3.60
V839 Oph J180920.6+090907 0.4090 0.54 124 3.05 30.47 -3.80
V566 Oph J175652.8+045907 0.4096 0.42 72 3.17 29.83 -4.39
UV Lyn J090324.6+380602 0.4150 0.67 123 3.89 29.93 -3.99
WZ Cep J232216.6+725505 0.4174 0.45 200 3.18 30.29 -3.92
AK Her J171358.0+162051 0.4215 0.53 96 3.36 29.94 -4.20
ER Ori J051114.9-083318 0.4234 0.49 149 3.40 29.87 -4.25
AP Dor J050644.2-590319 0.4272 0.44 215 2.63 30.36 -4.08
AP Leo J110504.2+050914 0.4304 0.62 121 3.83 30.05 -3.90
UX Eri J030952.6-065327 0.4453 0.65 227 3.55 30.95 -3.12
V502 Oph J164120.8+003019 0.4534 0.63 85 3.59 30.15 -3.89
CN And J002031.3+401323 0.4628 0.43 222 2.92 30.78 -3.53
AQ Psc J012103.7+073629 0.4756 0.47 125 3.02 30.40 -3.88
OO Aql J194812.9+091826 0.5068 0.46 192 2.79 30.88 -3.48
eps Cra J185843.5-370618 0.5914 0.41 30 2.38 28.87 -5.66
RS Col J051531.2-284510 0.6724 0.57 182 3.11 30.19 -4.04



  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H2566F1.eps}}\end{figure} Figure 1: Cumulative number of W UMa systems as a function of distance (stepped curve) and $N = 3.6~10^{-5}d_{\rm pc}^3$ (straight line)
Open with DEXTER

3 Results and discussion

3.1 Sample completeness

The sample of W UMa systems given in Table 1 has been compiled from various sources. The question arises to what extent this sample can be considered to be statistically complete. For a population homogeneously distributed in space one expects the total number of sources N to linearly increase with the sampled volume. In Fig. 1 we plot the cumulative number of W UMa systems as a function of distance (stepped curve) as well as the curve $N = 3.6~10^{-5}d_{\rm pc}^3$, which clearly provides a good fit to the observed number counts out to a distances $\approx$80 pc. In other words, our sample should be (statistically) complete out to that distance. The chosen normalization corresponds to a space density of 8.6 10-6systems per pc3.

3.2 Detection rates

In the RASS data X-ray emission from 54 out of 102 stars in our input catalog was detected. Three more stars, RW Com, RZ Com and AH CnC, were added using their pointed observations obtained by chance within the fields of other targets. This brings the total number of detections to 57. Among the detections there are three binaries which are the shortest period MS binaries ever observed in X-rays. The detection rate is - not surprisingly - distance dependent. Of 31 stars with parallaxes larger than 9 mas, i.e. lying closer than about 100 pc, 26 were detected. The four undetected stars from this sample are early type variables with $B-V \le 0.45$ (among them S Ant, see Table 3), the fifth star is CC Com - a W UMa type star with the shortest known period and with the faintest absolute magnitude. Only an upper limit could be determined which unfortunately is not very sensitive due to the relatively short RASS exposure of this region. The high detection rate among the closest W UMa variables confirms that they are strong sources of coronal X-ray emission and - coupled with the completeness properties of our sample - leads us to suspect that all of these systems exhibit X-ray emission.

There exist, of course, more sensitive X-ray data than the RASS data, however, these data are incomplete in sky coverage. Specifically, for stars not detected by RASS, we found X-ray data for four more W UMa stars, which are listed in Table 3; the stars EV Cnc and QX And are members of M 67 and NGC 752, respectively and for BH Cas a distance of 370 pc was adopted following its photometric parallax.


 

 
Table 3: The photometric and X-ray data from literature for W UMa stars not detected by RASS

Star

 P(days) B-V $\log (L_x/L_{\rm bol})$ ref.
BH Cas 0.4059 0.93 -3.90 1, 2
QX And 0.4181 0.44 -4.44 3, 4
EV Cnc 0.4576 0.52 -3.92 5, 6
S Ant 0.6483 0.27 -5.28 7
(1) Metcalfe (1999), (2) Brandt et al. (1997).
(3) Rucinski (1998b), (4) Belloni & Verbunt (1996).
(5) Gilliland et al. (1991), (6) Belloni et al. (1998).
(7) Cruddace & Dupree (1984).


3.3 X-ray luminosities and contribution to X-ray background

For distances out to $\approx$80 pc our sample is statistically complete and the detection rate is almost 100%, implying that the observed X-ray luminosity distribution is identical to the actual X-ray luminosity distribution function (XLDF). In Fig. 2 we plot the observed XLDF (stepped curve) together with a analytical fit assuming a log-normal distribution (continuous curve); the median of the distribution function is log $L_{\rm X,median}$ = 30.04 with $\sigma$ = 0.347. These numbers yield a logarithmic mean X-ray luminosity of 1030.18 erg/s, which results with the above derived space densities in a volume emissivity $j_{\rm W\, Uma} = 1.3~10^{25}$ erg/s/pc3. This is at least one order of magnitude smaller than the contribution of M dwarfs (cf., Schmitt & Snowden 1990), and we thus conclude that W Uma systems do not provide any significant contribution to the galactic X-ray background.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H2566F2.eps}}\end{figure} Figure 2: Observed X-ray luminosity distribution function for W Uma systems within 100 pc (stepped curve) and best-fit log-normal distribution (continuous curve)
Open with DEXTER

3.4 Color dependence of X-ray activity


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H2566F3.eps}}\end{figure} Figure 3: Dependence of the X-ray flux of W UMa stars on their color index. Open and filled circles denote hotter ( $(B-V)_0 \leq 0.6$) and cool ( (B-V)0 > 0.6) variables, respectively. Errors in ordinate are dominated by the count errors (see Table 1)
Open with DEXTER

Figure 3 shows the dependence of the X-ray flux of W UMa stars, normalized by the bolometric flux, on color index; early type stars with $B-V \le 0.60$ are plotted with open circles, late type stars with B-V > 0.60 with filled circles. The scaled X-ray flux of the hotter stars decreases with a decreasing color index, similarly as is observed among single field stars or members of clusters (Schmitt et al. 1985; Prosser et al. 1996). For cool stars the X-ray flux of single, rapidly rotating stars reaches the saturation value of about -3 for B-V approaching 0.6 and remaining at that level through G and K spectral types, except for the scatter of individual values. The saturated value of the X-ray flux may slightly increase for M-type stars. The X-ray flux of cool W UMa stars reaches a level of only $\approx$-3.6. This corresponds to a normalized X-ray flux about four-five times lower than in single stars, or detached binaries of RS CVn and BY Dra type. Contrary to the W UMa stars the detached binaries do not show significant differences in the X-ray activity level, compared to single stars (Dempsey et al. 1993; Dempsey et al. 1997). It is not possible to decide from the present data whether the X-ray activity level of cool W UMa stars increases with the increasing color index. There are too few stars detected with B-V > 1.

3.5 Period dependence of X-ray activity


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H2566F4.eps}}\end{figure} Figure 4: Dependence of the X-ray flux of W UMa stars on period. Open and filled circles denote hotter ( $(B-V)_0 \leq 0.6$) and cool ( (B-V)0 > 0.6) variables, respectively
Open with DEXTER

A diagram showing the dependence of $\log (L_x/L_{\rm bol})$ on period of the W UMa stars is shown in Fig. 4. A clear dependence of the normalized X-ray flux on period is apparent: variables with longer periods have weaker X-ray emission. One should, however, be careful in interpreting this dependence in a similar fashion as for single MS stars, for which a well-known activity-period relation exists. In the latter case it is possible to demonstrate that the X-ray flux decreases with the rotation period for stars of a given spectral type, i.e. for stars with the same global parameters and differing only by their rotation rate (Walter 1983; Stepien 1994; Wichmann et al. 1998). In case of W UMa stars there exists a strong period-color correlation (Rucinski 1993; Rucinski & Duerbeck 1997) in the sense that hotter stars tend to have longer periods. Indeed, as Fig. 4 demonstrates, the apparent activity-period relation is due to hotter stars with longer periods and lower activity level (compare Fig. 3). This behavior was also noted by Cruddace & Dupree (1984). Cool W UMa stars alone do not show any unquestionable period-activity relation.

4 W UMa systems and the phenomenon of supersaturation

4.1 Supersaturation in ultra fast rotators

Recent X-ray measurements of several UFRs with $v\sin i$ of the order of 100 kms-1 or more showed an unexpected behavior among $\alpha$ Persei members: the normalized X-ray flux decreased with an increasing $v\sin i$ (Randich et al. 1996; Prosser et al. 1996). Stars from other clusters followed this pattern. Photometric observations of UFRs confirmed that they have very short rotation periods of the order of 1 day or less. About 60 such stars are presently known with periods between 0.2 and 1 days. The star with the shortest known rotation period of 0.183 days is AP 124, a member of $\alpha$ Persei cluster. In a diagram X-ray flux versus rotation period stars with rotation periods above 0.4 days show the normalized X-ray flux at the saturation level ($\approx -$3), but stars with shorter periods show progressively weaker X-ray emission. This effect has been termed supersaturation (Prosser et al. 1996). The effect becomes more pronounced when the hotter UFRs are omitted - they have lower X-ray fluxes due to their early spectral types hence they confuse the picture. The effect is also present among pre-MS stars (Wichmann et al. 1998).


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{H2566F5.eps}}\end{figure} Figure 5: Dependence of the X-ray flux of UFRs (crosses) and cool W UMa stars (filled circles) on period. Broken horizontal lines denote a median value of the X-ray flux of UFRs from period intervals 0.2 to 0.3, 0.3 to 0.4 and longer than 0.4. Solid line denotes a median value of all plotted W UMa stars
Open with DEXTER

We have collected literature data on about 50 cool UFRs (i.e. single stars with B-V > 0.6) with reliably determined rotation periods and measured X-ray fluxes. These stars are members from IC 2602 (Barnes et al. 1999), IC 2391 (Patten & Simon 1996), $\alpha$ Per (Randich et al. 1996; Prosser et al. 1996; O'Dell et al. 1995) and the Pleiades (Stauffer et al. 1994; O'Dell et al. 1995; Micela et al. 1996; Micela et al. 1999; Krishnamurthi et al. 1998). Some authors (e.g. Stauffer et al. 1997) prefer using the Rossby number instead of period to study the supersaturation. However, the plot of activity-rotation diagram for UFRs of different spectral types does not show any systematic difference from one spectral type to another as in the case of slow rotating stars. Further, the published turnover times, used for the Rossby number determination, do not differ much for G and K type stars, while substantial differences exist for M type stars among different authors (Stepien 1994; Gunn et al. 1998). Depending on the adopted values of turnover times the Rossby numbers of M stars may differ by a factor of two, relative to early G stars. In addition, it is not clear whether turnover times determined for single stars can be used for contact binaries. We therefore decided to discuss a period-activity, rather than Rossby number-activity diagram.

Figure 5 shows a plot of the normalized X-ray flux versus period for cool UFRs from young clusters (crosses). A sharp decrease of the X-ray flux is visible for $P_{\rm rot} < 0.4$day. Broken horizontal lines give median values of $\log (L_x/L_{\rm bol})$ for single stars with rotation periods in the range 0.2-0.3, 0.3-0.4 and >0.4 day, respectively. For the last interval a value of -3 was adpoted. An upper limit on $\log (L_x/L_{\rm bol}) < -3.51$ published for AP 124 is in agreement with the observed trend. Filled circles correspond to cool W UMa stars. A solid horizontal line gives a median value of $\log (L_x/L_{\rm bol})$ for all the plotted W UMa stars. Apart from a few individual values falling within the region occupied by single stars, most of them lie much lower and the median value for all the binaries is significantly lower than the value for the most rapid single rotators.

4.2 Decreased X-ray emission of UFRs

Our basic assumption is that X-ray coronae have a geometrical thickness much smaller than the stellar radius, hence the total X-ray flux is proportional to a fraction of the stellar surface covered by X-ray emitting regions. The coefficient of proportionality (i.e. the local surface flux) may vary, depending e.g. on the particular heating mechanism and/or geometry of the magnetic field but we assume the primary reason for different X-ray fluxes produced by different stars to be different X-ray filling factors. The problem of X-ray loop lengths, and the vertical extent of X-ray emitting regions has recently been reviewed by Schmitt (1998), where our basic assumption is more thoroughly justified.

The average X-ray surface flux reaches a maximum value for saturated stars with rotation periods of 2-3 days. Such stars presumably have filling factors close to 1. Stars with still faster rotation do not show any increase in X-ray flux suggesting that the vertical extent of X-ray producing regions is bounded and the star is unable to increase it. The total X-ray flux of a saturated star is strictly proportional to its surface area; this would not be the case if the vertical extents of the coronae were comparable to or greater than the stellar radius and variable from one star to another. This may not fully apply to detached close binaries of RS CVn and BY Dra type with two active components. In such systems an additional source of energy exists compared to single, or contact stars, i.e., the energy of the orbital motion which can be converted directly into magnetic energy by any relative motion of surfaces of both stars if they are connected by the magnetic field lines.

Following our assumption we interpret the decrease of the X-ray surface flux observed in UFRs with rotation periods less than 0.4 day as the result of a decrease of the filling factor of these stars. We conjecture that in such stars an increasingly broader equatorial region, free of magnetic surface flux and of coronal X-ray emission, appears due to a strong concentration of the magnetic flux toward the rotational poles. Such a concentration has already been invoked to explain an ubiquitous occurrence of polar spots on very active stars observed with the Doppler imaging technique (e.g. Strassmeier & Rice 1998a, 1998b).

Magnetic flux ropes emerging over the rotating stellar surface are subjected to Coriolis forces. For fast enough rotation the flux ropes should move through the convection zone nearly parallel to the rotation axis (Schüssler et al. 1996). However, according to detailed computations the Coriolis force alone is insufficient. Only a shift of the flux emergence belt toward higher latitudes is predicted, but no strong concentration of the field around the poles (Strassmeier & Rice 1998a, 1998b). A further increase of the rotation rate does not change the dynamics of the magnetic ropes, and a need for an additional mechanism dragging the magnetic fields towards the poles, e.g. in a form of a strong poleward circulation flow near the bottom of the convection zone, has been invoked.

We suggest such a poleward circulation mechanism as the consequence of the nonuniform heating of the convective envelope from below. Because the stellar core of a cool star is in radiative equilibrium the emergent energy flux $F(\theta)$is given by the well-known von Zeipel theorem which states that F is proportional to the local effective gravity. For a rotating core the local value of effective gravity is given by

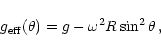\begin{displaymath}g_{\rm eff}(\theta) = g - {\omega}^2R\sin^2\theta\,, \end{displaymath} (4)

where g denotes gravitational acceleration, $\omega$ the angular velocity of the core, R the radius and $\theta$ polar angle; the energy flux leaving the core is thus largest at the poles and is monotonically decreasing towards the equator. This effect is well studied for hot stars with radiative envelopes (Pérez Hernández et al. 1999), for cool stars it has however been neglected. For a one solar mass star with a core radius of 0.7 $R_{\odot}$ the polar energy flux at poles exceeds the equatorial energy flux by 10% for the rotation period of 0.23 days, and by 30% for a period of 0.15 days. Therefore pronounced consequences for the dynamics of the convective envelope are expected for sufficiently rapid rotation. As to the reaction of a convection zone heated from below by a nonuniform flux, two-dimensional numerical simulations show that the excess radiative flux is quickly converted into an excess convective flux. A strong updraft appears near the maximum flux entering the convection zone (Stepien et al. 1998), but in addition to producing an intense vertical updraft the excess energy flux is also distributed horizontally so that the energy flux emerging from the stellar surface is more uniform compared to the purely radiative case. According to Lucy (1967) the energy flux emerging from a deep convection zone is proportional to $g_{\rm eff}^{0.32}$, while for shallow zones with a significant radiative transport the index is between 0.32 and 1 (Pérez Hernández et al. 1999). The updrafts in the polar regions must be accompanied by poleward circulation flows in the lower part of the convection zone and corresponding equator-ward surface return flows. The flows would then sweep magnetic flux tubes in the deep interior toward the poles where they can rise to the surface, and a more or less field-free zone near equator is formed.

The important point now is that the efficiency of this mechanism increases as $\omega^2$, while the Coriolis force increases only as $\omega$. We therefore conjecture that the effect is negligible for solar-like rotation rates, for rotation rates $\omega \sim 10\ \omega_{\odot}$ it becomes noticeable, and it dominates the dynamics of the magnetic fields inside a convection zone for $\omega \sim 100\ \omega_{\odot}$ in qualitative agreement with observations. Measurements of the surface velocity field on the Sun and theoretical models show the flows in the solar convection zone to be dominated by a poleward surface circulation accompanied by the equator-ward return flow near the bottom of the convection zone (Wang 1998; Kitchatinov & Rüdiger 1999). The dynamics is driven by Reynolds stresses and anisotropic heat conductivity, but the models do not take into account the nonuniformity of the energy flux entering the convection zone which is expected to be extremely small ($\approx$10-5). For an ultrafast rotator this nonuniformity reaches $\approx$30% and the convection zone flow pattern has to essentially reverse.

The stars with rotation periods between 0.2 and 0.3 days radiate on average slightly less than a half of X-ray energy compared to the saturation level (Fig. 5). It then follows from our assumption that they have only roughly 40% of their surface covered with X-ray emitting regions, which corresponds to an equatorial field-free region extending to about $\pm 35\hbox{$^\circ$ }$ latitude. By the same assumption, stars with rotation periods between 0.3 and 0.4 day should have about 2/3 of their surface covered with X-ray emitting regions, i.e. the field-free region extends up to about $\pm 22\hbox{$^\circ$ }$ latitude.

4.3 Decreased emission from W UMa systems

So far we have concentrated only on rapidly rotating single stars. How do W UMa binaries fit into this picture? Similarly to the case of single UFRs, we assume that the decreased X-ray emission level of W UMa stars is a result of only a partial coverage of the stellar surface by X-ray emitting regions. In the present case, however, we suggest that this is a result of a strong surface horizontal flow encircling both components. Such a flow is expected to develop when two stars with different specific entropies overflow their respective critical Roche lobes. They cannot be in hydrostatic equilibrium because the dependence of pressure on the vertical coordinate, perpendicular to the equipotential surface, is different for both stars (this also applies to early type contact binaries). A horizontal pressure gradient develops, driving matter from a primary to a secondary component on the dynamical time scale. Due to the Coriolis force the flow will be declined toward one side of the secondary. The matter will flow around the secondary and return to the parent star. If the sheet of the flowing matter has the thermal time scale much longer than the dynamical time scale, a uniform photospheric temperature will develop on both components. Evolutionary effects make the secondary slowly expand whereas its Roche lobe shrinks due to a permanent loss of angular momentum. This forces the secondary to lose matter to the primary. Because its matter has a lower specific entropy, it will flow through the central part of the neck, carrying most, or all nuclear energy of the secondary with it.

Such a pattern of flow was described by Martin & Davey (1995) who also carried out the corresponding hydrodynamic calculations. The results confirmed the predictions, except that the flow around the secondary could not freely return to the primary due to a counterflow consisting mostly of the matter from the secondary. It is possible that this is a result of the boundary conditions chosen for the computations. In reality, the relatively cool and dense matter from the secondary should sink into the primary star and not appear on the surface to perturb the return flow. A more or less laminar flow should develop embracing both stars. But even if the results of Martin & Davey (1995) do correctly describe the interaction of matter from both components, large scale horizontal flows around both stars were obtained from the calculations. It seems improbable that coronal loops will persist long enough to be filled with a hot matter emitting X-rays in the presence of such flows. The magnetic field will more likely develop a strong azimuthal component with low-lying, short-living loops appearing from time to time above the surface and then be quickly drawn back, beneath the photosphere. Weak, or no coronal activity is expected from regions covered by the flow i.e. from the whole surface of the secondary and a broad equatorial region on the primary. However, the magnetic field can produce long lived loops in the polar regions of the primary.

This picture of activity of a W UMa star is in a good qualitative agreement with observations. Several pieces of evidence indicate that the primary is the dominant active component. Many photometric observations indicate that in many stars the secondary has a higher surface brightness than the primary heating it (the W phenomenon). This paradox was explained in terms of dark spots on the surface of the primary (Binnendijk 1970). Multicolor observations of W UMa and SW Lac confirmed this supposition (Eaton et al. 1980; Stepien 1980). As to coronal activity, Brickhouse & Dupree (1998) conclude that the active region, responsible for the variability of the observed flux, must be located near a pole of the primary of 44i Boo. The recent results of the analysis of an X-ray flare observed on VW Cep with ASCA (Choi & Dotani 1998) also indicate that the primary was a site of the flare. The X-ray light curve of the flare shows a presence of an eclipse when the primary was behind the secondary. The authors concluded that the flare developed close to the eclipsed pole of the primary. Contrary to coronal and spot activity, chromospheric activity can easily be produced on both components by an interaction of the (partly turbulent) flow with the intermittent magnetic fields, in agreement with the observations (Vilhu & Walter 1987) although its level may also decrease with decreasing period (Rucinski 1985).

The median value of the $\log (L_x/L_{\rm bol})$ of the W UMa stars is 0.63 less than the saturated value for single stars. If interpreted in terms of the surface fraction covered with X-ray emitting regions it corresponds to only about 23% of the stellar surface being coronally active. The large scale equatorial flow should therefore extend to about $\pm 50\hbox{$^\circ$ }$ in latitude.

4.4 The cut-off period of W UMa systems

The W UMa type star with the shortest known period (0.221 days) is CC Com; a number of stars with periods only slightly longer are known (Table 1). The total mass of the least massive W UMa systems is about 1-1.1 $M_{\odot}$ (Hilditch et al. 1988; Rovithis-Livaniou et al. 1992; Maceroni & van't Veer 1996). The latest spectral type of a W UMa system is around K5, in agreement with these data. There seems to exist a sharp lower period limit (or, equivalently, spectral type or mass) of the late type contact binary as noted by Rucinski (1992). He tried to explain the existence of this limit on physical grounds, but his "full convection limit'' applies only to significantly less massive stars. Why do we not find contact binaries with a total mass significantly below 1 $M_{\odot}$? Why do binaries, like CM Dra, with masses of both components close to 0.2 $M_{\odot}$, not form contact systems? For a while the intrinsic faintness of and thus the difficulty to find late K and M stars was blamed for the apparent lack of such systems among the known variables. However, the recent statistical analysis of a large sample of W UMa stars detected during the OGLE microlensing experiment showed this sample to be complete out to a distance of 3 kpc (Rucinski 1997), and yet none of the newly detected W UMa stars had a period shorter than CC Com. The eclipsing binary BW3 V38 with a period of 0.198 days was first classified as a contact system (Udalski et al. 1995), but later Maceroni & Rucinski (1997) showed it to be a detached binary. Therefore it appears that the observed period cutoff of 0.22 days is in fact real and hence a physical explanation is called for.

Contact binaries are believed to form from short period detached binaries. These systems lose angular momentum via a magnetized wind, approach each other and spin up until they overflow their critical Roche lobes (Vilhu 1982; Stepien 1995). This process takes several Gigayears even when both stars are in a saturated state. More massive stars with $\sim$ $1~M_{\odot}$ components reach a contact configuration already when their periods are of the order of 0.4 days. Such systems never reach a supersaturation state and lose angular momentum all the time with full efficiency. Instead, a binary with 0.5 $M_{\odot}$ components must spin up to about 0.2 days to form a contact system. As a consequence its components are in a supersaturated state for a substantial fraction of the spin up process. If our conjecture is correct and the supersaturated stars develop field-free equatorial regions, the angular momentum loss rate drops significantly compared to the saturated state. It takes now much longer to lose enough angular momentum. A binary similar to CM Dra would form a contact system only for $P_{\rm rot} \approx 0.1$ days. Due to the supersaturation effect the time to reach such a short period may be longer than the age of the Universe. Accurate computations of the evolution of close binaries with different component masses are needed to obtain the necessary time scales which permit to determine a quantitative lower mass limit for contact binaries in our Galaxy. Angular momentum loss rates for stars of different masses and ages are necessary to carry out such computations. Nevertheless, our explanation of the phenomenon of the supersaturation leads in a natural way to an existence of such a limit.

5 Conclusions

The high percentage of RASS detections among W UMa type stars lying within a distance of 100 pc from the Sun confirms that the stars are strong X-ray emitters. The X-ray emission decreases rapidly for hotter stars of early F spectral type. G and K type stars do not show any significant color-activity dependence. We confirm the earlier conclusion by Cruddace & Dupree (1984) that, on average, the X-ray flux of W UMa stars, normalized to the bolometric flux, is considerably lower (by a factor of 4-5) than that of single, rapidly rotating stars of the same spectral types. W UMa stars do show a dependence of X-ray luminosity on orbital period but this is a result of a period-color relation obeyed by the stars (Rucinski 1993).

We compared the X-ray emission of W UMa stars with that of the cool, rapid single rotators (UFRs) with periods shorter than 0.4 days. The majority of G and K type W UMa stars have periods within this range, but they do not follow the trend shown by single stars. Instead, their average X-ray flux is significantly lower than the flux of even the fastest known single rotators. We suggest a common explanation for the decreased X-ray flux observed in single stars in a state of supersaturation and in W UMa binaries via a decreased coverage of a stellar surface by X-ray emitting regions. The physical mechanisms leading to such a decreased coverage are, however, different for both kinds of stars.

We conjecture that the nonuniform heating of a convection zone from the underlying radiative core results in strong convective updrafts along the rotational axis. For rapidly rotating core the energy flux at the poles is significantly larger than at equator due to a decrease of equatorial effective gravity by a centrifugal force. This should drive a large scale flow within the convection zone with polar updrafts and poleward flows near the bottom of the convective zone. Because this effect increases as $\omega^2$ it can very likely be neglected for slowly rotating stars ( $\omega \sim \omega_{\odot}$), but it may be strong enough to influence the dynamics within a convection zone of a star with $\omega \sim 100\ \omega_{\odot}$ i.e. a star in a state of supersaturation. We suggest that the poleward flows drag magnetic ropes toward the poles and create a field-free equatorial region. If the observed decrease of X-ray emission is interpreted as resulting from the existence of such field-free regions, they should extend to latitudes $\pm 35\hbox{$^\circ$ }$ for stars with $0.2 < P_{\rm rot} < 0.3$ days and to latitudes $\pm 22\hbox{$^\circ$ }$ for stars with $0.3 < P_{\rm rot} < 0.4$.

In case of W UMa stars we suggest that the broad, equatorial region of a primary and the whole surface of a secondary star are covered by a surface azimuthal flow encircling both components. The flow results from a lack of hydrostatic equilibrium between two stars with different specific entropies overflowing the critical Roche surface (Martin & Davey 1995). The flow inhibits the magnetic field from producing long lived coronal loops filled with hot, X-ray emitting plasma.

Our suggestion of a decreased activity of stars in a supersaturated state leads to a natural explanation for the observed minimum cut-off period of W UMa stars within the generally accepted scenario for their origin from cool, close detached binaries losing orbital angular momentum. Detached binaries with more massive components, of the order of 1 $M_{\hbox{$\odot$ }}$, reach contact when the orbital period is close to 0.4 days. During the approach lasting several Gyr (Stepien 1995) they remain in a saturated state, losing angular momentum with a maximum efficiency. For components with masses of the order of 0.5-0.6 $M_{\hbox{$\odot$ }}$ (which is close to the least massive primaries of W UMa systems) contact is established when the period reaches $\sim$0.2days. The components are now in a supersaturated state with ensuing reduced angular momentum loss and increased formation time. Still less massive stars have not yet had enough time, according to our assumption, to reach contact even within the age of the Universe. The picture is in qualitative agreement with the observed period cutoff of W Uma systems, but accurate model computations are necessary to also provide quantitative agreement between the predicted minimum mass for a contact binary and observations.

Acknowledgements
This work was carried out when one of us (KS) held an Alexander von Humboldt Foundation follow-up fellowship. He thanks the Foundation for support and Jürgen Schmitt for hospitality during his stay at the Hamburger Sternwarte. We acknowledge discussions with Dr. H. Kähler on contact binary systems. An extensive use of the SIMBAD database operated by the CDS, Strasbourg, is acknowledged. A partial support for this work came from the grant KBN 2 P03D 010 12.

References

 
Copyright ESO 2001