A&A 370, 311-319 (2001)
DOI: 10.1051/0004-6361:20010191

Asteroid candidates for mass determination

A. Galád

Astronomical Institute, Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava,
Slovak Republic

Received 17 July 2000 / Accepted 31 January 2001

Abstract
The first 9511 numbered asteroids are studied in terms of their mutual closest approaches and encounter velocities during the period from November 6, 1967, to September 13, 2023. Several large asteroids (diameter $200 \,{\rm km}$ and above) were (will be) encountered by smaller counterparts within a distance of $0.0200 \,{\rm AU}$. Thus, they are possible candidates for mass determination by the astrometrical method. Similarly, the search for effective perturbers is extended to even smaller asteroids for the much closer separation distance of $0.0020 \,{\rm AU}$ and below. Only the simplified method for evaluation of observable effects on a perturbed body is used. Asteroid masses alone are not computed here. But a stronger criterion to reveal pairs for this purpose in comparison to some specially devoted papers should compensate for the difference and act as a reliable test. The best candidates for mass determination at present are asteroids (1), (2), (4), (10), (11), (24), (52) and (65). This list may be extended by at least (29) in the next 5 years and by many others in the next two decades. Several other strong perturbers from the last three decades are not included in the list, while there is still only a limited number of (or no) precise and reliable observations of perturbed asteroids before a close encounter. It seems that a perturbation by (10) is at least as effective as that by (2) and could be included in asteroid orbit determination in the future. Except for their bulk density determinations (knowing the size), the masses of perturbers could occasionally be used to improve the precision of the computed orbit for perturbed large-numbered and unnumbered asteroids as well.

Key words: minor planets, asteroids - astrometry - ephemerides


1 Introduction

Asteroid observations have a long history. Larger telescopes, more sensitive detectors and different techniques were used to increase the number of known bodies. Due to observational effects large and close asteroids were discovered at first. Most of the known asteroids orbit the Sun at a distance of $\approx$2-4 AU - in the main belt.

The orbits of asteroids are usually computed by numerical integration. This takes into account the perturbations by the eight planets (Mercury to Neptune) and, in addition, by the three largest minor planets (1) Ceres, (2) Pallas and (4) Vesta from the main belt of asteroids (Marsden 1995). The last three of these perturbers contain about half the mass of the belt. The Earth-Moon system may be considered as one body with the sum of their masses or, in the case of Earth-approaching asteroids, perturbations by both bodies are taken separatedly.

It is known that the collisions of known objects are extremely rare even in the main belt. Thus, it is expected that sufficiently high accuracy of orbit solutions for a long time period should be reached for numbered asteroids. However, from time to time interasteroidal close encounters occur. Then, some of the larger asteroids may cause deflection from the ephemeris position of their smaller counterparts. Knowledge of the encounter geometry enables us to compute the masses (and densities, if the size and shape is also evaluated) of new perturbers while the perturbed body residuals (observed minus computed positions) should decrease. Precise astrometric positions of the perturbing and perturbed bodies are needed over several years before and after their close encounter. The observations from the period closer to the encounter are helpful, as well.

The astrometrical method was used not only for the mass determination of the three largest main-belt asteroids mentioned above. Many times it was used even for the smaller ones (see e.g. Hoffmann 1989; Kuzmanoski & Knezevic 1994; Viateau 2000 and references therein). A deflection as small as $1 \hbox{$^{\prime\prime}$ }$ from the ephemeris position of the perturbed body can be measured several (say $\approx$10-20) years after an encounter by optical telescopes from the ground. Subarcsecond measurements by meridian circles (Viateau & Rapaport 1997) and astrometric satellites like Hipparcos (Bange 1998) are the most precise and valuable - they reduce the time needed for deflection measurements.

Mass is an important physical characteristic. The rapid increase in new asteroid discoveries and the improvement (in precision) of poorly determined orbits in recent years challenge as to determine it for many objects. The first step is to provide a database of suitable close encounters. Such searching was recently done by Hilton et al. (1996) in quite a large set of asteroids. They integrated 4583 orbits for 57 years. The subject of this paper is to recognize the best candidates from the main belt for asteroid mass determination in a larger database.

2 Data

The asteroid orbital elements used in this paper were taken from the CD Guide 7.0 (Gray 1998). In this software the orbital elements for various epochs are included due to the need of rapid drawing of asteroids in star charts for any time in the recent past and near future. Only a little programming is needed to convert them from a compressed form to a readable format.

The initial osculating elements for epoch October 14, 1998 (JD 2451100.5) were based on observations and were taken from Bowell et al. (1994). All perturbations mentioned above were taken into account. However, orbital elements for the other epochs derived on the CD are adjusted for planetary perturbations only. Asteroidal perturbations were not included at all. The asteroid positions between adjacent epochs can be computed as a two-body problem at first approximation. Thus, it is possible to study the whole sample of asteroids for mutual approaches without an additional numerical integration. But we should bear in mind that the computations of orbital elements excluding the perturbations by large asteroids is a source of inaccuracy in the estimation of the close encounter's effect on these asteroids. The actual positions of asteroids may differ from their computed ones far from the initial epoch. These can be checked by examining observations from the past. According to the CD's manual this comparison was done for some asteroids, and the difference in position was less than 1 arcsec.

By the release of the CD (October 1998) there were 9511 numbered asteroids and thousands of multiopposition and singleopposition unnumbered asteroids known. In this paper only numbered asteroids were studied during the period from November 6, 1967 (JD 2439800.5) to September 13, 2023 (JD 2460200.5). In general, their orbits are much better determined in comparison to multiopposition unnumbered asteroids. Only (719) Albert was lost at the time of the CD's release. Increasing the number of items (unnumbered asteroids) and choosing a longer time period would affect not only the time needed to process the data but also the reliability of data.


 

 
Table 1: The parameter P for the perturbers (the first column) and perturbed bodies (the second column) mentioned in the Hoffmann's list (1989). P is a measure of the change in the mean motion
  N1   N2 date r v P
        yr/m/d ${\rm [AU]}$ ${\rm [km\, s^{-1}]}$ ${\rm [km\, s]}$
(1) Ceres (91) Aegina 1973/09/13 0.03312 3.285 47.3
(3) Juno (1767) Lampland 1982/12/31 0.00548 4.536 4.1
(10) Hygiea (1725) CrAO 1984/03/07 0.09685 3.761 $ 1.2^{{\rm a}}$
(65) Cybele (526) Jena 1984/06/24 0.00586 3.330 6.6
(92) Undina (2950) Rousseau 1985/12/03 0.00270 3.087 2.4
(324) Bamberga (1939) Loretta 1988/08/18 0.00714 7.973 1.7
(704) Interamnia (993) Moultona 1973/11/23 0.01414 5.718 3.4
(804) Hispania (1002) Olbersia 1982/03/23 0.00467 1.306 4.9

$^{{\rm a}}$
Assumed pair instead of (16) (1725) written in original list.

3 Selection process

According to Carpino & Knezevic (1996) the magnitude of the change in the mean motion $\Delta{n}$of the perturbed body depends on several quantities during the encounter. Neglecting the orbital eccentricity of the scattered asteroid, they obtained

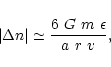\begin{displaymath}\vert\Delta{n}\vert \simeq \frac {6 ~G ~m ~\epsilon}{a ~r ~v},\nonumber \end{displaymath}  

where G is the universal constant of gravitation, m is the mass of the perturber, $\epsilon$ is the energy efficiency of the close approach (the fraction of the change in the heliocentric velocity, which occurs in the tangential direction), a is the semimajor axis of the perturbed asteroid, r is the minimum separation distance, v is the encounter velocity. In fact, authors assumed that the mass of the perturbed asteroid is much smaller than that of the perturber (they used the equation for mass determination of (1) Ceres). More precisely, the sum of the masses should be written instead.

To find out possible candidates for mass determinaton, the mass of the perturber should be assessed from asteroid diameter D and the evaluated value of its bulk density $\rho$, as it is not known in advance. Three quantities (D, r and v) out of six that characterize $\Delta{n}$may differ by several orders of magnitude (in different pairs). An auxiliary P parameter can be defined by them so that P is a measure of $\Delta{n}$. In this paper the search for possible candidates for mass determination is focused on the search for largest values of P. It is computed from the equation

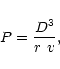\begin{displaymath}P = \frac {D^{3}}{r ~v},\nonumber \end{displaymath}  

where D is the asteroid diameter in ${\rm km}$(as the mass depends on D3), r is the minimum separation distance in ${\rm km}$, v is the encounter velocity in ${\rm km\, s^{-1}}$. It is possible to replace r with the impact parameter b and at the same time v with the relative velocity of the scattered asteroid at infinity $v_{\infty}$ ( $r ~v = b ~v_{\infty}$). To be punctual, b and $v_{\infty}$ are really computed here, but they are designated by the letters r and v, respectively. D is assessed from known albedos directly (Tedesco 1989), or indirectly through taxonomic class (Tholen 1989). The latter usually determines the narrow range of possible values for albedo. If neither albedo, nor taxonomic class data are available, only the upper limit of the size is taken into account, with the albedo value set to 0.04.

It must be noted that neither the P parameter nor $\Delta{n}$ are valid outside the sphere of action of the perturber. But the computation of the P parameter is just an approximation allowing comparisons between the encounters.

The following steps were taken to gain and process the data in chronological order:

1.
Database of osculating orbital elements for 9511 numbered asteroids for 51 epochs was obtained. Adjacent epochs differed by 400 days (the first epoch was JD 2440000.5, the last JD 2460000.5).
2.
Using the orbital elements from the nearest epoch, rectangular positions in the heliocentric reference system were computed for each asteroid as a two-body problem for each day during the period from November 6, 1967 (JD 2439800.5), to September 13, 2023 (JD 2460200.5). (The ephemerides of asteroids are always computed within 200 days of the epoch.) Pairs with a separation distance less than $0.0200 \,{\rm AU}$ on a given day were stored.
3.
The minimum separation distance r, encounter velocity v, and time of minimum encounter for a given pair can be computed from stored data but only if at least three items are available on a day-by-day basis. (After several months members of a given pair can meet closely again. They are considered as a new pair, then.) For each possible pair even sizes of its members should be computed to determine P parameters. At first, P parameters are computed for some pairs successfully used (or at least intended to be used) for mass determination. From published data a short Hoffmann's list (1989) was chosen for this purpose (Table 1). Only eight pairs were accepted, since they occured after 1967 and could be found in computed data (previous step). The largest value of P reached $\approx$47 $\,{\rm km\,s}$when the largest asteroid (1) Ceres was encountered by (91) Aegina in 1973. An extra computation was added in that case, since $r > 0.02 \,{\rm AU}$. For the rest of seven pairs P was an order of magnitude lower ( $1 \,{\rm km\, s} < P < 7 \,{\rm km\, s}$). In fact, one pair seems to be incorrectly written in the original list. In 1984, the perturber for (1725) CrAO could be perhaps (10) Hygiea instead of (16) Psyche. But even this is questionable, since $r \approx 0.10 \,{\rm AU}$for (10) and $\approx$0.15 $\,{\rm AU}$ for (16)!
4.
Larger database of pairs that Hilton et al. (1996) consider to be useful for mass determination was used partly. In three tables authors list significant encounters involving large asteroids, the same for small asteroids, and pairs with the largest quality factor for 34 asteroids, respectively. It must be mentioned that their first table is much larger than the others despite of the fact that only a small fraction was published. (Their method is discussed in next section.) Table 2, which is divided into three parts that correspond to their three tables, contains computed P values for some pairs. Namely pairs for which $r < 0.02 \,{\rm AU}$, and some others, mainly in the third part. (Some pairs in the third part would be the same as in two previous and were not repeatedly written.) Encounters before 1968 were rejected, as in step 3. P values for the rest of pairs ( $r > 0.02 \,{\rm AU}$) are, in general, smaller. The sizes of (19) Fortuna and (24) Themis were underestimated here in comparison to Hilton et al. (1996) due to larger albedo. As (19) belongs to G taxonomic type its albedo is assumed to be 0.09 here. The albedo of 0.061 for (24) was found in Bowell et al. (1989). The determination of the time of minimum separation for a slow encounter is not precise, as is the case of (720) Bohlinia and (1029) La Plata ( $v \approx 0.3 \,{\rm km\, s^{-1}}$). However, dates are given without fractional numbers in tables.
5.
As the process of P determination for all pairs from step 2 (several tens of thousands in number) is time consuming and a majority of pairs are not important for mass determination, some selection criteria should be applied to pick up only pairs with the largest P. Small asteroids may become possible candidates for mass determination under special circumstances only. They include small v and, at the same time, small r. All close approaches with $r \le 0.0020 \,{\rm AU}$ were stored to find them. This reduced the number of possible pairs by $\approx$2 orders of magnitude. The total of 1072 pairs remained. The largest P exceeded $5 \,{\rm km\, s}$ even though perturbers are mostly much smaller than is usually considered (none was larger than $100 \,{\rm km}$).
6.
Large asteroids are effective perturbers to larger distances than $0.002 \,{\rm AU}$. Bright asteroids with absolute magnitude H < 8should include all (even the darkest) asteroids of $D > 200 \,{\rm km}$and many smaller ones (even below $100 \,{\rm km}$). (There is still a lack of information about the size for some of them. Moreover, some asteroids may be binaries or of the bifurcated shape (e.g. Merline et al. 2000; Marchis et al. 1999), which means that effective diameter induced from absolute magnitude and albedo can be wrong.) In the inner part of the Solar System 142 such bodies were selected and considered as perturbers for the rest of the smaller asteroids. The P parameter was computed for all of 2205 encounters within a distance of $0.02 \,{\rm AU}$. As expected, (1) Ceres and (4) Vesta are responsible for the highest values of P exceeding even $60 \,{\rm km\, s}$ in several pairs.
7.
The largest asteroids (1), (2), and (4) are effective perturbers to distances even larger than $0.02 \,{\rm AU}$. As in step 2, rectangular positions for all asteroids were computed anew, but they were compared with the positions of 15 largest asteroids only. Pairs with a separation distance <0.05 $\,{\rm AU}$ on a given day were stored. P was computed for all these pairs.


 

 
Table 2: The parameter P for some perturbers (N1) and perturbed bodies (N2) mentioned in the Hilton et al. (1996). Large perturbers are in the first, small ones in the second, and pairs with largest quality factor for some asteroids in the third part, respectively
  N1   N2 date r v P P/v
        yr/m/d ${\rm [AU]}$ ${\rm [km\, s^{-1}]}$ ${\rm [km\, s]}$ ${\rm [s^{2}]}$
(1) Ceres (2377) Shcheglov 1994/06/21 0.04636 4.153 26.7 6.4
(1) Ceres (2933) Amber 1996/01/14 0.01963 2.965 88.3 29.8
(2) Pallas (2995) Taratuta 2014/05/14 0.04925 7.627 2.7 0.4
(3) Juno (1767) Lampland 1982/12/31 0.00548 4.534 4.1 0.9
(4) Vesta (113) Amalthea 1994/07/12 0.04022 1.874 11.2 6.0
(4) Vesta (17) Thetis 1996/06/16 0.01938 1.168 37.2 31.8
(7) Iris (1825) Klare 1979/02/02 0.01144 1.632 4.5 2.8
(10) Hygiea (3946) Shor 1998/03/30 0.01439 0.920 33.3 36.2
(19) Fortuna (2198) Ceplecha 2013/08/04 0.01214 1.013 $ 2.6^{{\rm a}}$ 2.6
(24) Themis (2296) Kugultinov 1975/12/23 0.01570 0.436 9.0 20.6
(45) Eugenia (308) Polyxo 1985/11/27 0.01338 1.768 2.2 1.2
(65) Cybele (1668) Hanna 1987/12/17 0.01459 2.366 3.7 1.6
(87) Sylvia (2246) Bowell 1989/08/18 0.01363 3.940 2.6 0.6
(451) Patientia (3286) Anatoliya 2017/04/13 0.01499 2.009 2.8 1.4
                 
(12) Victoria (1110) Jaroslawa 2013/11/03 0.00464 1.222 2.0 1.6
(14) Irene (1078) Mentha 2013/09/19 0.00619 1.376 $ 5.0^{{\rm b}}$ 3.6
(20) Massalia (356) Liguria 1983/07/10 0.00952 3.482 0.8 0.2
(28) Bellona (4056) Timwarner 2002/01/01 0.00519 1.496 2.0 1.3
(70) Panopaea (4410) Kamuimintara 2011/09/17 0.00534 1.457 1.6 1.1
(111) Ate (2455) Somville 2003/11/22 0.00601 1.620 1.6 1.0
(720) Bohlinia (1029) La Plata 1989/02/25 0.00662 0.277 0.2 0.7
(804) Hispania (1002) Olbersia 1982/03/23 0.00467 1.304 4.9 3.8
(1669) Dagmar (2248) Kanda 1993/11/04 0.00613 0.659 0.1 0.2
(1686) De Sitter (2918) Salazar 2005/10/10 0.00756 0.644 0.1 0.2
                 
(1) Ceres (348) May 1984/09/02 0.04242 0.909 133.3 146.6
(2) Pallas (2495) Noviomagum 1991/01/01 0.03227 7.373 4.4 0.6
(4) Vesta (3002) Delasalle 1994/07/16 0.03904 0.722 29.9 41.4
(7) Iris (836) Jole 1989/02/14 0.04772 2.531 0.7 0.3
(13) Egeria (3489) Lottie 2014/03/22 0.04005 3.605 0.3 0.1
(16) Psyche (2589) Daniel 1981/09/13 0.04284 0.934 3.7 4.0
(19) Fortuna (827) Wolfiana 2010/06/11 0.04928 0.944 $ 0.7^{{\rm a}}$ 0.7
(31) Euphrosyne (109) Felicitas 1969/05/03 0.04293 5.254 0.4 0.1
(45) Eugenia (4374) Tadamori 2014/11/15 0.04686 2.096 0.5 0.2
(52) Europa (3019) Kulin 1988/11/18 0.04806 1.678 2.5 1.5
(65) Cybele (3071) Nesterov 2016/04/03 0.04794 1.559 1.7 1.1
(107) Camilla (670) Ottegebe 2014/05/06 0.04115 1.999 0.8 0.4
(165) Loreley (1913) Sekanina 1981/07/01 0.04163 3.483 0.2 0.1
(216) Kleopatra (3976) Lise 1986/11/04 0.04193 4.061 0.2 0.0
(511) Davida (1847) Stobbe 1974/09/20 0.04858 2.304 2.2 1.0
(704) Interamnia (445) Edna 1995/11/29 0.03857 1.988 3.6 1.8

$^{{\rm a}}$
Assumed albedo of 0.09 due to G type.
$^{{\rm b}}$
Assumed albedo of 0.16 due to S type.

4 Results and comparison

As can be seen in Tables 1 and 2, the lowest values of the P parameter for pairs considered to be significant for the mass determination are as small as $\approx$1 $\,{\rm km\,s}$. These need at least some comment. Hilton et al. (1996) searched for convenient close approaches using a scattering formula. But according to Carpino & Knezevic (1996) the use of only angular deflection of the trajectory produced by the close approach ($\theta$) may lead to overestimating the importance of low-velocity encounters, since, in fact, we are interested in the change in relative velocity $\Delta{v}$ that is proportional to $\vert\Delta{n}\vert$:

$\displaystyle \vert\Delta{n}\vert$ $\textstyle \simeq$ $\displaystyle \frac {3 ~\epsilon ~\Delta{v}}{a},$  
$\displaystyle \Delta{v}$ = $\displaystyle \frac {2 ~G ~m}{r ~v} \simeq v ~\theta,$  

where G is the universal constant of gravitation, m is the mass of the perturber, r is the minimum separation distance, v is the encounter velocity.

Contrary to $\theta$, the P parameter directly represents $\Delta{v}$ and could better serve as a measure of observable effects on a perturbed body:

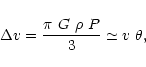\begin{displaymath}\Delta{v} = \frac { \pi ~G ~\rho ~P}{3} \simeq v ~\theta,\nonumber \end{displaymath}  

where $\rho$ is the asteroid bulk density (asteroid is considered to be spherical). $\theta$ may be represented by P/v ratio. For comparison Table 2 (the last two columns) contains both P along with P/v values, respectively. On the other hand, even P is not a sufficient criterion for finding possible candidates for the mass determination,

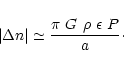\begin{displaymath}\vert\Delta{n}\vert \simeq \frac {\pi ~G ~\rho ~\epsilon ~P}{a}\cdot\nonumber \end{displaymath}  

The energy efficiency $\epsilon$ is not a constant and may be crucial for some pairs. It was not computed here, but can be assessed from the values in Carpino & Knezevic (1996). It varied from 0.15 to 0.99. One way to compensate for the difference between the simplified form used here and special computation is choosing a relatively strong limit for P. The remaining quantities are of minor importance. The deflection from the ephemeris is larger, if a is small and $\rho$ is large. In the main belt they vary within a factor of three in different asteroids.

The main results of this paper are summarized in Tables 3 and 4. These contain pairs with the largest values of their Pparameter encountered within $0.02 \,{\rm AU}$. Only pairs with $P \ge 6 \,{\rm km\, s}$ were chosen. These are higher than most of the P values in pairs suspected to use for mass determination according to both Hoffmann (1989) or Hilton et al. (1996), respectively. In fact, these references served to set a low limit for the values of parameter P due to an unknown $\epsilon$ needed. As this paper is not focused on (1), (2), and (4) perturbations, the comparison of the results is restricted. For example, only one pair from the former (and much shorter) list - (65) Cybele and (526) Jena - really passed the chosen criterion.

Table 5 contains additional pairs with $P > 6 \,{\rm km\, s}$encountered at a mutual distance of $0.05 \,{\rm AU} > r > 0.02 \,{\rm AU}$. Pairs with (1) and (4) were removed. Otherwise, this table would contain 107 extra items with (1) and 98 with (4). The largest P value would be $\approx$133 $\,{\rm km\,s}$ here, but it is mentioned in the third part of the Table 2 - since it was recognized by Hilton et al. (1996). Only six pairs were left - one pair with (2) and five with (10). These are really strong perturbators, but much less effective than (1) and (4) are, if one judge by the numbers of pairs as indicators of effectiveness of encounters. Although (2) is large, its orbit is highly inclined to the ecliptic. It means that effective encounters are rare and even v is large.

P has a large uncertainty (of the order of 0.1-1 $\,{\rm km\,s}$) mainly due to the uncertainty in diameter D (and albedo). The uncertainty of the separation distance r is mostly not so crucial until an extremely close encounter occurs (e.g. in a distance below $\approx$0.0001 $\,{\rm AU}$). In such cases the uncertainty in P may exceed even $1 \,{\rm km\, s}$. Only two such pairs were significant in that manner (from step 5). In 2014 (1961) will be encountered by (5569) at a distance of $0.00011 \,{\rm AU}$ and (445) by (1764) at a distance of $0.00007 \,{\rm AU}$, respectively. The uncertainties are more than $0.00005 \,{\rm AU}$ and actual values of P may not pass the chosen limit. The sizes of these perturbers are far below $200 \,{\rm km}$. The diameter of (1961) may be overestimated due to extremely low albedo of 0.019 used here. An additional uncertainty for P comes from the computed asteroid orbit alone that affects the encounter geometry. In general, this one increases with the time separation from the 1998 (encounters both back to the past and into the future), as the asteroid perturbations are not taking into account from this starting year of integration. For example, the orbital elements used for (17) in 1968, when it encountered (11), were not precise due to a strong perturbation by (4) in 1996 ( $P = 37.2 \,{\rm km\, s}$). One should determine its orbit from precise observations before 1996 only or take the perturbation by (4) into account, but this was realized by Viateau & Rapaport (1997), who used the (11)-(17) encounter for mass determination. In this special case even (17) as a large asteroid contributes to the total P. Its actual value in Table 3 should be $9.6 \,{\rm km\, s}$. (These asteroids met each other even in 1997, but related P was below $6 \,{\rm km\, s}$.)

The largest P ( $ > 300 \,{\rm km\, s}$) was computed for the pair (1) and (5303) in 1996 (Table 3). Neglecting the perturbation by (1) the ephemeris position of (5303) would be more than $1 \hbox{$^{\prime\prime}$ }$ off from its real position after 3.5 years! Such a large perturbation alone may improve the mass determination of the largest asteroid. Improvements can be reached from approaches of others, as well. Similarly, the mass determination of (4) Vesta can be improved from several large perturbations. The masses of smaller preliminary candidates could be specially computed including other quantities that may cause deflection from the ephemeris. However, the most crucial element for mass determination of smaller perturbers is the time period covered by reliable and precise observations.

The P parameter may be used to evaluate the deflection from the ephemeris $\Delta{n}$ under some assumptions only, namely the perturbers's density and energy efficiency. Assuming the density of the perturber is $2000 \,{\rm kg\, m^{-3}}$, the semimajor axis of perturbed body $2.8 \,{\rm AU}$, and the energy efficiency $\epsilon = 1$, the correction factor of 0.0065 may be used to convert the values between the $P / {\rm [km \,s]}$parameter and $\Delta{n} / {\rm [\hbox{$^{\prime\prime}$ }\, yr^{-1}]}$. This means, that the perturbed body deflection of $\approx$ $1 \hbox{$^{\prime\prime}$ }$ could be revealed after two to three decades (in the main belt), if $P = 6 \,{\rm km \,s}$. Smaller P may be used only if precise observations are available during much longer time period (for low-numbered asteroids) or astrometric measurements reached subarcsecond precision during several years. The latter are relatively new and still do not cover the period of more than a decade for most objects.

The last column of Tables 3-5 contains the year from which astrometric positions for both members of a given pair are known. It helps to recognize if that pair can be used for mass determination. But it is not always a reliable indicator due to the low precision of some measurements (mostly the very earliest) in the past and the long intervals between them. Perturbers that are emphasized in Tables 3 and 5 have convenient conditions for mass determination at present. Several asteroids (perturbers) were not emphasized due to poor (e.g. less than 10 observations, positions above $1 \hbox{$^{\prime\prime}$ }$ precision) or no observations of related perturbed bodies before an encounter. For example, (511) was encountered by (7191) in 1969, but the latter has only 4 observations before the approach, although 2 of them are from 1949 - 20 years to the encounter. The first astrometric observations for the perturbed bodies by (121) and (704) in 1982 and 1997 come from only 12 and 13 years to the encounter, respectively. Almost all pairs in Table 4 could probably be used for mass determination in the future. The only exception is probably (104)-(9049), as the latter will have 13 years period of observations before an encounter with in 2004. On the other hand, the development of milliarcsecond astrometry may enlarge the number of observations that are very accurate. The limit put on the P parameter ( $P \ge 6 \,{\rm km\, s}$) in Table 4 may become too conservative then.

The Tables 3-5 cannot be viewed as a complete list of pairs with $P \ge 6 \,{\rm km\, s}$, even excluding those with (1) or (4). Several large asteroids may be larger than assumed here (from taxonomic class or assumed albedo), or some dark asteroids with absolute magnitude slightly above 8 (the limit in step 6) are so large that if encountered very slowly by a counterpart ( $v \approx 1 \,{\rm km\, s^{-1}}$) at a distance just above $0.002 \,{\rm AU}$ (the limit in step 5) P could exceed a given threshold.


 

 
Table 3: List of the effective perturbers (N1) along with perturbed bodies (N2) encountered within $0.02 \,{\rm AU}$among the first 9511 numbered asteroids before January, 1998. Emphasized numbers and names denote asteroids, masses of which can be determined at present. The last column (obs) denotes the year from which astrometric observations for both encountered bodies are available
  N1   N2 date r v P obs
        yr/m/d ${\rm [AU]}$ ${\rm [km\, s^{-1}]}$ ${\rm [km\, s]}$ year
(1) Ceres (2572) Annschnell 1971/03/26 0.01201 4.784 89.5 1950
(1) Ceres (7381) Mamontov 1971/12/07 0.00712 4.478 161.3 1981
(1) Ceres (3643) Tienchanglin 1972/09/11 0.00828 2.767 224.4 1937
(1) Ceres (6010) Lyzenga 1973/04/27 0.01145 8.060 55.7 1953
(1) Ceres (2660) Wasserman 1980/04/14 0.01354 7.307 52.0 1924
(1) Ceres (6594) Tasman 1982/05/16 0.01304 6.715 58.7 1954
(1) Ceres (6325) 1991 EA1 1983/09/18 0.01559 3.602 91.6 1955
(1) Ceres (2933) Amber 1996/01/14 0.01963 2.965 88.3 1917
(1) Ceres (5303) Parijskij 1996/09/11 0.00554 2.737 339.1 1971
(2) Pallas (6995) 1996 BZ1 1968/04/04 0.00924 14.678 7.7 1978
(2) Pallas (7671) Albis 1977/06/05 0.00352 12.441 23.8 1969
(2) Pallas (5470) 1988 BK5 1979/12/13 0.00650 12.837 12.5 1977
(2) Pallas (3131) Mason-Dixon 1984/12/04 0.01189 10.838 8.1 1922
(3) Juno (6817) Pest 1970/04/19 0.00157 5.441 11.8 1982
(4) Vesta (4295) Wisse 1967/11/06 0.01126 4.905 15.2 1960
(4) Vesta (8311) Zhangdaning 1971/02/23 0.01890 2.335 19.1 1982
(4) Vesta (5482) 1990 DX 1975/02/13 0.01818 4.624 10.0 1984
(4) Vesta (5205) 1988 CU7 1977/05/12 0.00285 3.729 79.2 1954
(4) Vesta (8688) 1992 PV1 1978/05/09 0.00739 3.725 30.6 1992
(4) Vesta (4416) Ramses 1982/03/17 0.01811 4.984 9.3 1954
(4) Vesta (7990) 1981 SN1 1987/09/15 0.01680 6.649 7.5 1949
(4) Vesta (8331) Dawkins 1988/01/19 0.00796 1.477 71.6 1982
(4) Vesta (413) Edburga 1991/06/26 0.01057 8.213 9.7 1917
(4) Vesta (8114) Lafcadio 1993/01/19 0.01995 1.895 21.9 1986
(4) Vesta (17) Thetis 1996/06/16 0.01938 1.168 37.2 1852
(4) Vesta (5166) Olson 1996/07/07 0.01757 2.331 20.6 1974
(9) Metis (7684) Marioferrero 1989/02/15 0.00249 2.753 $6.4^{{\rm a}}$ 1983
(9) Metis (9362) 1992 FE1 1989/07/26 0.00589 1.175 $6.3^{{\rm a}}$ 1992
(10) Hygiea (6143) Pythagoras 1983/12/19 0.01876 2.452 9.6 1951
(10) Hygiea (6006) Anaximandros 1995/02/07 0.00924 2.668 17.9 1972
(11) Parthenope (17) Thetis 1968/02/18 0.00179 2.296 8.1 1852
(15) Eunomia (3591) Vladimirskij 1989/02/27 0.00380 5.554 6.4 1932
(16) Psyche (6852) 1985 CN2 1979/09/10 0.00683 1.958 11.2 1952
(16) Psyche (9473) Ghent 1984/05/17 0.00974 2.119 7.3 1993
(19) Fortuna (3486) Fulchignoni 1996/05/14 0.00213 2.303 $6.5^{{\rm b}}$ 1952
(24) Themis (2296) Kugultinov 1975/12/23 0.01570 0.436 9.0 1941
(24) Themis (8700) 1993 JL1 1981/02/01 0.00874 0.622 11.3 1975
(29) Amphitrite (6904) 1990 QW1 1985/06/15 0.00933 0.571 14.9 1990
(29) Amphitrite (987) Wallia 1994/03/03 0.00245 3.199 10.1 1899
(52) Europa (1023) Thomana 1971/05/31 0.00653 3.761 8.0 1924
(52) Europa (124) Alkeste 1993/10/17 0.01243 2.589 6.1 1872
(65) Cybele (526) Jena 1984/06/24 0.00586 3.331 6.6 1901
(76) Freia (3766) Junepatterson 1982/06/21 0.01116 0.875 6.2 1915
(121) Hermione (5750) Kandatai 1982/06/09 0.00113 4.543 15.3 1970
(409) Aspasia (9347) 1991 RY21 1970/05/12 0.00061 4.270 12.4 1979
(511) Davida (7191) 1993 MA1 1969/07/16 0.00431 5.980 9.7 1949
(704) Interamnia (7461) Kachmokiam 1997/05/31 0.00747 5.288 7.0 1984

$^{{\rm a}}$
Assumed albedo of 0.16 due to S type.
$^{{\rm b}}$
Assumed albedo of 0.09 due to G type.


 

 
Table 4: The same as in previous table for the period after January, 1998
  N1   N2 date r v P obs
        yr/m/d ${\rm [AU]}$ ${\rm [km\, s^{-1}]}$ ${\rm [km\, s]}$ year
(1) Ceres (7738) Heyman 1999/04/08 0.01014 3.229 157.0 1981
(1) Ceres (8231) Tetsujiyamada 2005/11/12 0.01620 2.746 115.6 1975
(1) Ceres (8363) 1990 RV 2008/02/29 0.01787 2.941 97.8 1990
(1) Ceres (6813) 1978 VV9 2014/12/28 0.01647 4.318 72.3 1978
(1) Ceres (1393) Sofala 2022/05/19 0.00692 2.202 337.4 1928
(2) Pallas (6752) Ashley 2000/06/25 0.01503 8.086 8.6 1971
(2) Pallas (3219) Komaki 2021/08/16 0.01111 11.267 8.3 1934
(2) Pallas (99) Dike 2022/01/07 0.01164 14.320 6.3 1915
(4) Vesta (3184) Raab 1998/05/14 0.01668 4.905 10.3 1949
(4) Vesta (6900) 1988 XD1 2008/01/16 0.00930 5.233 17.3 1958
(4) Vesta (6685) Boitsov 2012/12/02 0.00547 2.924 52.7 1978
(4) Vesta (1549) Mikko 2015/06/04 0.01917 3.458 12.7 1935
(4) Vesta (5675) Evgenilebedev 2016/08/05 0.01745 4.150 11.6 1950
(4) Vesta (6507) 1982 QD 2018/08/24 0.01678 7.122 7.0 1982
(4) Vesta (3359) Purcari 2018/12/26 0.00937 4.893 18.4 1951
(4) Vesta (9017) 1986 TW9 2020/08/05 0.00469 6.694 26.8 1953
(4) Vesta (6465) Zvezdotchet 2021/02/03 0.00384 6.405 34.2 1938
(4) Vesta (8947) 1997 CH26 2022/09/16 0.00424 4.895 40.6 1986
(10) Hygiea (3946) Shor 1998/03/30 0.01439 0.920 33.3 1950
(10) Hygiea (2061) Anza 1999/04/04 0.00646 9.417 7.3 1960
(10) Hygiea (5941) Valencia 2001/02/15 0.01795 2.977 8.3 1972
(10) Hygiea (5957) Irina 2007/01/03 0.00656 7.620 8.8 1988
(10) Hygiea (4803) Birkle 2017/04/05 0.01193 2.064 17.9 1950
(15) Eunomia (765) Mattiaca 2010/06/04 0.00344 2.726 14.3 1913
(15) Eunomia (5199) Dortmund 2015/06/17 0.00271 5.688 8.7 1934
(16) Psyche (6442) Salzburg 2014/10/16 0.00550 2.472 11.0 1987
(52) Europa (8269) Calandrelli 2011/07/02 0.00931 2.459 8.6 1964
(52) Europa (8660) 1990 TM1 2019/10/19 0.00478 2.633 15.7 1979
(87) Sylvia (8976) Leucura 2009/08/24 0.00515 3.698 7.4 1973
(87) Sylvia (1227) Geranium 2020/08/09 0.00389 4.403 8.2 1931
(104) Klymene (9049) 1991 RQ27 2004/09/09 0.00042 3.828 9.2 1991
(120) Lachesis (1755) Lorbach 2006/07/14 0.00087 5.162 8.6 1924
(190) Ismene (8626) 1981 EC18 2014/04/16 0.00281 2.716 $7.5^{{\rm c}}$ 1981
(203) Pompeja (908) Buda 2014/06/16 0.00057 4.503 7.2 1918
(324) Bamberga (5766) 1986 QR3 2017/10/11 0.00165 7.700 7.7 1955
(445) Edna (1764) Cogshall 2014/10/31 0.00007 8.232 $ 7^{{\rm d}}$ 1935
(704) Interamnia (1467) Mashona 1999/02/04 0.00647 4.675 9.1 1923
(704) Interamnia (651) Antikleia 2016/04/21 0.00542 6.790 7.5 1910
(1961) Dufour (5569) 1974 FO 2014/08/28 0.00011 2.916 8.5 1974

$^{{\rm c}}$  Assumed albedo of 0.04 due to P type.
$^{{\rm d}}$ Large uncertainty due to r <<.


 

 
Table 5: The P parameter for the largest perturbers except (1) and (4) with $r > 0.02 \,{\rm AU}$. Symbols are as in previous tables
  N1   N2 date r v P obs
        yr/m/d ${\rm [AU]}$ ${\rm [km\, s^{-1}]}$ ${\rm [km\, s]}$ year
(2) Pallas (2204) Lyyli 1968/05/03 0.02320 6.779 6.6 1943
(10) Hygiea (9268) 1978 VZ2 1972/12/15 0.02591 2.461 6.9 1978
(10) Hygiea (1259) Ógyalla 1984/02/11 0.03452 2.063 6.2 1928
(10) Hygiea (2619) Skalnaté Pleso 1989/12/11 0.02238 1.709 11.5 1975
(10) Hygiea (465) Alekto 1995/12/26 0.03804 1.512 7.7 1901
(10) Hygiea (1965) van de Kamp 2000/10/15 0.02141 3.296 6.3 1927


5 Discussion and conclusion

The parameter P is defined to reveal the effective perturbers for some asteroids. It is connected to the change in relative velocity and mean motion of the perturbed body. These quantities are sensitive to the mass of the perturbing body and to the closeness and mutual velocity of the perturbed body. Asteroid masses alone are not computed here.

There are several pairs with a large value of P among the first 9511 numbered asteroids. Larger members of these are good candidates for mass determination by the astrometric method, if precise measurements (for both) are known long before their mutual encounter. Unlike computations that use only angular deflection of the perturbed body trajectory as a criterion in searching for the effective perturbators, the P parameter should not overestimate low-velocity encounters.

Special attention has been paid to finding smaller perturbers in addition to the three largest ones (from the main belt) that are usually taken into account for orbit determination. Thus, the search for pairs is limited mainly to mutual encounter distance of $0.02 \,{\rm AU}$. It is found that at present the masses of asteroids (1) Ceres, (2) Pallas, (4) Vesta, (11) Parthenope, (24) Themis, (52) Europa, and (65) Cybele could be best evaluated from encounters by other asteroids within such a distance. In Table 3 they are in bold type in pairs that could be used for this purpose. Astrometric observations of related perturbed bodies are available for several years (or decades) before an encounter. In the next 5 years at least (10) Hygiea and (29) Amphitrite could be added to the list due to recent encounters with smaller asteroids in 1998 and 1994, respectively. Table 4 summarizes pairs, the majority of which can be used for mass determination during the next decades.

Asteroid approaches to the fifteen largest main belt asteroids were studied up to a distance of $0.05 \,{\rm AU}$. It was found that except for (1), (2) and (4), even (10) as a fourth largest asteroid is an effective pertuber above $0.02 \,{\rm AU}$ limit. Moreover, its mass could be determined at present from one such distant encounter (emphasized in Table 5), in contrast to recent encounters by several asteroids within a distance of $r < 0.02 \,{\rm AU}$ (Table 3) whose preencounter positions are probably not sufficient to reveal deflection from ephemeris yet. In the total number of significant encounters it can displace even (2), since the latter has a highly inclined orbit! Thus, its mass could be included in orbit determination in the future as a standard as well (at least for the outer part of the main belt).

In addition to these candidates, the list of large perturbers will rapidly increase due to new discoveries (by the end of 2000 the number of numbered asteroids doubled), due to longer period covered by observation (recent discoveries scarcely have observations back to the 1970s, but observations from the 1990s are evenly covered for lot of asteroids which allow to rely on observations and make the orbit more precise) and due to observations of better precision (astrometric satellites, meridian circles, radar), respectively. The chosen selection process should guarantee to list (nearly) all pairs of $P \ge 6 \,{\rm km\, s}$. This large value of P enable to reveal possible candidates for mass determination quickly. Within $\approx$3 decades the deflection from the ephemeris of perturbed asteroid can be >1 $\hbox{$^{\prime\prime}$ }$. Some significant perturbers can't be used for mass determination at present while preencounter astrometric observations of perturbed bodies are missing. However, they may be recorded on older plates, e.g., from the sky surveys from the 1960s. In the near future, encounters with smaller values of P may become of great interest. This could be done next - e.g., after new version of CD GUIDE is released (encounters with smaller P values are far from completeness at this point - only some of them are available by request).

Multiopposition asteroids become numbered after a reliable orbit is computed. Standard orbit determination may not be sufficient to cover all precise observations with small residuals in extremely rare occasions over a very long time period (several decades). There are two possible ways to decrease the orbit uncertainty.

1.
Computing the orbit from the shorter (more recent) period;
2.
Recognizing all possible significant close encounters and individually including the perturbations by new perturbers in orbit computation.
For these reasons it is more difficult to reveal new perturbers among numbered asteroids during their well-observed period in the past. But recognizing future encounters in advance will help to avoid a possible increase in residuals (taking all precise observations into account), especially if we are interested in subarcsecond precision. Over a too-long period, however, there are also other perturbers that may cancel out the previous perturbations.

Acknowledgements
This work was supported by the Slovak Grant Agency for Science, VEGA, (grant No. 1/7157/20). The author would like to thank Bill Gray from Project Pluto, Bowdoinham, ME, USA, for his kind advice and allowing me to use orbital elements from the CD GUIDE 7.0.

References

 

Copyright ESO 2001