A&A 370, 121-135 (2001)
DOI: 10.1051/0004-6361:20010221
H. Sana - G. Rauw![]() ,
,
![]() - E. Gosset
- E. Gosset![]() ,
,![]()
Institut d'Astrophysique et de Géophysique, Université de Liège, 5 avenue de Cointe, 4000 Liège, Belgium
Received 18 December 2000 / Accepted 7 February 2001
Abstract
We present the results of a four year spectroscopic campaign on the early-type binary system HD152248. Our analysis yields a new classification as O7.5III(f) + O7III(f), in contradiction with previous classifications of the components as supergiants. We derive improved orbital elements and the corresponding masses (
![]() and
and
![]() )
are somewhat larger than previously reported in the literature, although they are still significantly lower than the ones expected from evolutionary tracks. Both components of the system are close to filling their Roche lobe at periastron passage. We also investigate the equivalent width variations of the lines of the two components and we discuss their relation to the Struve-Sahade effect.
Finally, we show that the line profile variability of the He II
)
are somewhat larger than previously reported in the literature, although they are still significantly lower than the ones expected from evolutionary tracks. Both components of the system are close to filling their Roche lobe at periastron passage. We also investigate the equivalent width variations of the lines of the two components and we discuss their relation to the Struve-Sahade effect.
Finally, we show that the line profile variability of the He II![]() 4686 and H
4686 and H![]() lines is consistent with a strong wind interaction between the two stars, quite as predicted by current colliding wind models.
lines is consistent with a strong wind interaction between the two stars, quite as predicted by current colliding wind models.
Key words: binaries: close - binaries: spectroscopic - stars: early-type - stars: fundamental parameters - stars: individual: HD152248 - stars: winds, outflows
Over the last twenty years, the interest in wind interaction has grown, and numerous studies both from theoretical (e.g. Stevens et al. 1992; Walder 1998; Pittard 2000) and observational (e.g. Corcoran 1996; Rauw et al. 1999; Hill et al. 2000) points of view have been undertaken. These studies demonstrate that considerable insight into the mass loss process can be gained from a detailed investigation of the wind interaction phenomenon. In addition, binary systems provide precious astrophysical laboratories allowing a direct determination of the fundamental parameters of the stars that are crucial in order to test evolutionary models and to probe the impact of binarity on the evolution of the components of the system.
HD152248 is an O+O binary system that belongs to the young open cluster NGC6231 which is considered to be the nucleus of the rich SCOOB1 association. Situated at a distance of 1.99 kpc (Baume et al. 1999), this cluster contains a number of interesting single O stars as well as O binaries and a WR+O system (WR79). Not only is the HD152248 system one of the brightest objects of the cluster (V=6.06, Baume et al. 1999) but it also appears from ROSAT X-ray observations to be the brightest X-ray source in NGC6231. Corcoran (1996) has further shown that the ROSAT X-ray flux from HD152248 displays phase-locked variations, though the poor phase coverage of the ROSAT data did not allow elucidation of their origin. On these grounds, NGC6231 has been selected as a target for the XMM X-ray observatory as part of the Liège project for guaranteed time. The pointings will be centered on HD152248 for a total duration of 180 ksec, consisting of six 30 ksec exposures in order to adequately sample the orbital variations.
In this context, we have undertaken a spectroscopic campaign to monitor the optical counterpart of most of the ROSAT X-ray sources of the NGC6231 cluster. Some preliminary results have already been presented by Sana et al. (2001). The present paper is the first of a series devoted to the O stars in NGC6231. We present here a complete and detailed spectroscopic study of the HD152248 system (the main target of our campaign) in the optical domain. One aim is to derive accurate, contemporaneous ephemerides required to correctly interpret the forthcoming XMM data and to clarify the evolutionary status of both components of the system. Another objective of this study is the search for the optical signature of a wind interaction which is suspected to exist within the system because of its high and variable X-ray luminosity.
This paper is organised as follows. The next section is devoted to a review of the main results already published about this object in the literature. In the third section, we describe our spectroscopic observing campaign, the data we collected and the data reduction techniques we applied. The determination of the orbital parameters is presented in the fourth section. The fifth one is devoted to the study of the variations of the equivalent widths of the absorption lines and their link to the Struve-Sahade effect (S-S effect). We next turn to the emission lines displayed by the spectrum of this system. Particular attention is paid to the He II![]() 4686 and H
4686 and H![]() lines and to their phase-locked variability. Section 7 is devoted to the discussion of the evolutionary status of the system, and, among other things, we re-investigate its spectral and luminosity classification.
Finally, we present a wind-wind interaction model that is consistent with most of the observational features of the emission lines. The last section is devoted to a brief summary of our main results.
lines and to their phase-locked variability. Section 7 is devoted to the discussion of the evolutionary status of the system, and, among other things, we re-investigate its spectral and luminosity classification.
Finally, we present a wind-wind interaction model that is consistent with most of the observational features of the emission lines. The last section is devoted to a brief summary of our main results.
Based on the same set of IUE data and using a tomographic reconstruction algorithm to separate primary and secondary spectra, Penny et al. (1999, PGB hereafter) derived a spectral type of O7I+O7I. They also re-analysed the light curve of the system, complementing the Mayer et al. (1992) data set with Hipparcos observations. PGB showed that the system displays ellipsoidal light variations due to tidal deformations. They derived an inclination of
![]() for the orbit of the system and polar radii of
for the orbit of the system and polar radii of
![]() and
and
![]() for the primary and secondary respectively. Combining spectroscopic and photometric results, they computed masses of
for the primary and secondary respectively. Combining spectroscopic and photometric results, they computed masses of
![]() and
and
![]() .
Howarth et al. (1997) reported that HD152248 is displaying the Struve-Sahade effect, i.e. that the secondary lines seem to be stronger when the secondary is approaching. However, this result was not confirmed by PGB, who found no evidence for this effect in the strength of the cross-correlation function of the IUE spectra of HD152248 with their standard star, HD34078.
.
Howarth et al. (1997) reported that HD152248 is displaying the Struve-Sahade effect, i.e. that the secondary lines seem to be stronger when the secondary is approaching. However, this result was not confirmed by PGB, who found no evidence for this effect in the strength of the cross-correlation function of the IUE spectra of HD152248 with their standard star, HD34078.
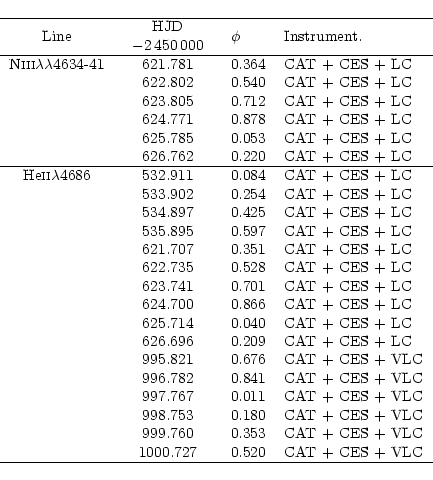
| HJD | He I |
|
n | Instrument. | |||
|
|
RV1 | RV2 | RV1 | RV2 | |||
| 205.859 | 0.851 | 207.4 | -208.0 | 212.7 | -214.0 | 6 | ESO 1.5 m + B&C |
| 206.852 | 0.022 | -11.6 | -11.6 | -56.3 | 38.1 | 6 | ESO 1.5 m + B&C |
| 207.816 | 0.188 | -207.2 | 203.6 | -200.8 | 204.2 | 6 | ESO 1.5 m + B&C |
| 208.795 | 0.356 | -156.1 | 155.8 | -166.8 | 164.4 | 6 | ESO 1.5 m + B&C |
| 208.879 | 0.370 | -150.4 | 136.7 | -148.9 | 164.1 | 6 | ESO 1.5 m + B&C |
| 209.789 | 0.527 | -7.5 | -7.5 | 1.7 | 1.7 | 6 | ESO 1.5 m + B&C |
| 209.903 | 0.546 | -7.0 | -7.0 | -10.4 | -8.6 | 6 | ESO 1.5 m + B&C |
| 210.782 | 0.698 | 167.3 | -173.9 | 184.7 | -167.2 | 6 | ESO 1.5 m + B&C |
| 210.910 | 0.720 | 187.2 | -196.4 | 183.8 | -199.2 | 6 | ESO 1.5 m + B&C |
| 211.777 | 0.869 | 186.7 | -187.8 | 203.2 | -180.6 | 6 | ESO 1.5 m + B&C |
| 211.912 | 0.892 | 175.0 | -177.9 | 194.8 | -178.9 | 6 | ESO 1.5 m + B&C |
| 534.902 | 0.426 | -75.7 | 129.5 | -110.3 | 95.9 | 6 | ESO 1.5 m + B&C |
| 535.904 | 0.599 | 70.7 | -110.5 | 91.1 | -114.9 | 6 | ESO 1.5 m + B&C |
| 536.888 | 0.768 | 213.2 | -208.9 | 209.1 | -210.1 | 6 | ESO 1.5 m + B&C |
| 537.897 | 0.941 | 98.7 | -73.8 | 116.9 | -121.8 | 6 | ESO 1.5 m + B&C |
| 538.889 | 0.112 | -165.6 | 135.6 | -163.5 | 156.3 | 6 | ESO 1.5 m + B&C |
| 539.907 | 0.287 | -201.4 | 191.8 | -200.0 | 191.5 | 6 | ESO 1.5 m + B&C |
| 531.908 | 0.912 | 160.2 | -155.2 | 160.2 | -155.2 | 1 | CAT + CES + LC |
| 532.881 | 0.079 | -97.9 | 122.7 | -97.9 | 122.7 | 1 | CAT + CES + LC |
| 533.859 | 0.247 | -206.7 | 219.7 | -206.7 | 219.7 | 1 | CAT + CES + LC |
| 534.844 | 0.416 | -99.7 | 108.2 | -99.7 | 108.2 | 1 | CAT + CES + LC |
| 535.859 | 0.591 | 48.7 | -85.6 | 48.7 | -85.6 | 1 | CAT + CES + LC |
| 536.856 | 0.762 | 219.0 | -201.2 | 219.0 | -201.2 | 1 | CAT + CES + LC |
| 622.604 | 0.506 | -4.9 | 1.9 | -4.9 | 1.9 | 1 | CAT + CES + LC |
| 623.628 | 0.682 | 154.2 | -170.8 | 154.2 | -170.8 | 1 | CAT + CES + LC |
| 624.554 | 0.841 | 215.8 | -211.1 | 215.8 | -211.1 | 1 | CAT + CES + LC |
| 625.607 | 0.022 | -2.2 | -2.2 | -2.2 | -2.2 | 1 | CAT + CES + LC |
| 626.571 | 0.188 | -202.0 | 214.9 | -202.0 | 214.9 | 1 | CAT + CES + LC |
| 1000.668 | 0.509 | 0.3 | 3.1 | 0.3 | 3.1 | 1 | CAT + CES + VLC |
| 1299.817 | 0.945 | 136.7 | -91.8 | 130.4 | -103.7 | 11 | ESO 1.5 m + FEROS |
| 1300.809 | 0.115 | -147.8 | 163.4 | -150.5 | 166.8 | 11 | ESO 1.5 m + FEROS |
| 1301.815 | 0.288 | -204.3 | 202.5 | -202.4 | 194.7 | 11 | ESO 1.5 m + FEROS |
| 1302.808 | 0.459 | -12.9 | -12.9 | -50.1 | 42.6 | 11 | ESO 1.5 m + FEROS |
| 1304.889 | 0.817 | 223.2 | -213.0 | 213.0 | -210.3 | 11 | ESO 1.5 m + FEROS |
| 1323.740 | 0.058 | -88.6 | 49.4 | -86.8 | 76.5 | 11 | ESO 1.5 m + FEROS |
| 1327.780 | 0.753 | 199.2 | -202.4 | 200.7 | -202.9 | 11 | ESO 1.5 m + FEROS |
| 1328.734 | 0.917 | 151.8 | -150.2 | 158.2 | -144.5 | 6 | CTIO 1.5 m + BME |
| 1329.738 | 0.089 | -130.2 | 117.9 | -122.6 | 136.2 | 6 | CTIO 1.5 m + BME |
| 1330.739 | 0.261 | -215.9 | 194.0 | -212.9 | 184.1 | 6 | CTIO 1.5 m + BME |
| 1331.771 | 0.439 | -81.4 | 36.7 | -91.5 | 60.6 | 6 | CTIO 1.5 m + BME |
| 1332.798 | 0.615 | 84.8 | -108.4 | 94.7 | -107.2 | 6 | CTIO 1.5 m + BME |
| 1668.832 | 0.393 | -108.1 | 131.5 | -120.5 | 125.2 | 11 | ESO 1.5 m + FEROS |
| 1669.853 | 0.568 | 36.0 | -42.3 | 37.2 | -51.4 | 11 | ESO 1.5 m + FEROS |
| 1670.836 | 0.737 | 206.7 | -190.0 | 204.2 | -188.4 | 11 | ESO 1.5 m + FEROS |
| 1671.839 | 0.910 | 157.9 | -158.6 | 163.2 | -159.3 | 11 | ESO 1.5 m + FEROS |
| 1672.828 | 0.080 | -122.7 | 102.1 | -120.9 | 111.4 | 11 | ESO 1.5 m + FEROS |
| 1673.809 | 0.248 | -203.6 | 217.2 | -206.4 | 207.6 | 11 | ESO 1.5 m + FEROS |
During two runs in May 1996 and March 1997, a set of medium resolution spectra was obtained with the Boller & Chivens spectrograph (B&C) fed by the ESO 1.5 m telescope. The detector was a 2k ![]() 2k UV flooded Loral-Lesser CCD. The pixel size is
2k UV flooded Loral-Lesser CCD. The pixel size is
![]() m. We used the holographic grating (ESO grating #32) with
2400 lines/mm, providing a spectral resolution of 1.2 Å as measured from the FWHM of the lines of the HeAr comparison spectrum. The covered spectral range extends from
m. We used the holographic grating (ESO grating #32) with
2400 lines/mm, providing a spectral resolution of 1.2 Å as measured from the FWHM of the lines of the HeAr comparison spectrum. The covered spectral range extends from ![]() 3790 to
3790 to ![]() 4765 Å.
4765 Å.
High resolution spectra of the He I![]() 4471, N III
4471, N III![]()
![]() 4634-4641 and He II
4634-4641 and He II![]() 4686 lines were obtained with ESO's 1.4m Coudé Auxiliary Telescope (CAT) at La Silla, using the Coudé Echelle Spectrometer (CES) equipped with the Long Camera (LC, before March 1998) or the Very Long Camera (VLC, after March 1998). The detector used was ESO CCD#38, a Loral
4686 lines were obtained with ESO's 1.4m Coudé Auxiliary Telescope (CAT) at La Silla, using the Coudé Echelle Spectrometer (CES) equipped with the Long Camera (LC, before March 1998) or the Very Long Camera (VLC, after March 1998). The detector used was ESO CCD#38, a Loral
![]() pixel CCD with a pixel size of
pixel CCD with a pixel size of
![]() m. The slit width was chosen to achieve a nominal resolving power of 70000-80000. The effective resolving power as derived from the FWHM of the lines of the ThAr calibration exposures is 65000-75000. Typical exposure times were of the order of 20 min and the average S/N ratio is above 150. The wavelength domain is centered on the He I
m. The slit width was chosen to achieve a nominal resolving power of 70000-80000. The effective resolving power as derived from the FWHM of the lines of the ThAr calibration exposures is 65000-75000. Typical exposure times were of the order of 20 min and the average S/N ratio is above 150. The wavelength domain is centered on the He I ![]() 4471, N III
4471, N III![]() 4641 or He II
4641 or He II ![]() 4686 lines and is
4686 lines and is ![]() 40Å and
40Å and ![]() 20Å wide for spectra taken with the LC and the VLC respectively.
20Å wide for spectra taken with the LC and the VLC respectively.
During three observing runs in April - May 1999, end of May 1999 and May 2000, a set of echelle spectra was taken with the Fiber-fed Extended Range Optical Spectrograph (FEROS) attached to the ESO 1.5m telescope at La Silla. Thirty seven orders corresponding to a wavelength domain from 3650 to 9200Å were observed. Typical exposure times were of the order of 6 min and the average S/N ratio is about 100, 220 and 150 at 4050, 6000 and 7500Å respectively. The spectral resolving power of the FEROS instrument is 48000. The detector was an EEV CCD with
![]() pixels of
pixels of
![]()
![]() m.
Finally, another set of echelle spectra over the range 3850 to 5790Å was obtained with the Bench-Mounted Echelle Spectrograph (BME) attached to the 1.5m CTIO Ritchey-Chrétien Telescope, during a 5 night run in June 1999. Forty nine orders were observed using the KPGL2 316linesmm-1 grating as a cross-disperser. The detector was a Tek2048 CCD with 24
m.
Finally, another set of echelle spectra over the range 3850 to 5790Å was obtained with the Bench-Mounted Echelle Spectrograph (BME) attached to the 1.5m CTIO Ritchey-Chrétien Telescope, during a 5 night run in June 1999. Forty nine orders were observed using the KPGL2 316linesmm-1 grating as a cross-disperser. The detector was a Tek2048 CCD with 24![]() m pixels. The slit width was set to 70
m pixels. The slit width was set to 70 ![]() m corresponding to a resolving power of 45 000. Exposure times were of the order of 45 min and the average S/N ratio in the continuum is about 100.
m corresponding to a resolving power of 45 000. Exposure times were of the order of 45 min and the average S/N ratio in the continuum is about 100.
The B&C and CAT observations were reduced in a standard way using the MIDAS package provided by ESO. Whenever possible, the spectra were rectified using a reference star observed under the same conditions. When such a spectrum was not available the spectra were normalized by fitting a polynomial to the continuum.
We used the FEROS context working under the MIDAS environment to reduce the FEROS echelle spectra. The reduction was performed using the standard option. Most of the unavoidable strong fringes that affect the red part of the spectrum (above 6600Å) are simply corrected by flat-fielding. There are however a few residual fringes near 6670, 7140, 7385 and 7930Å.
Finally, the spectra were normalized over a range of a few hundred Å at once by fitting a polynomial of degree 4 or 5 to the continuum. Whenever doubt existed about the quality of the automatic merging between the different orders, we checked our results using the unmerged spectrum. Good agreement between both methods was generally observed.
The BME data were reduced using the IRAF![]() package and following the recommendations of the BME User's Manual. The pixel to pixel variations were removed using flat field exposures taken with a very bright light source and a diffusing screen placed inside the spectrograph (so-called milky flats). A first rectification of the extracted echelle orders was carried out with the projector flat exposures. The spectra were then normalized by fitting a low-order polynomial to the continuum.
package and following the recommendations of the BME User's Manual. The pixel to pixel variations were removed using flat field exposures taken with a very bright light source and a diffusing screen placed inside the spectrograph (so-called milky flats). A first rectification of the extracted echelle orders was carried out with the projector flat exposures. The spectra were then normalized by fitting a low-order polynomial to the continuum.
The inspection of our data reveals that the spectra of the primary and secondary are very similar and that every absorption line detected is present in both spectra. Several lines are further present in emission and we will discuss them later in this paper.
|
|
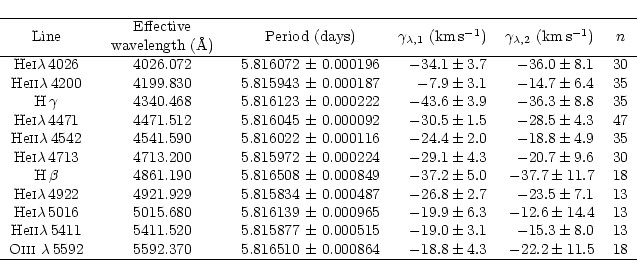
We selected eleven pure absorption lines in the spectrum of HD152248 to compute the orbital elements of the system. These lines were chosen according to the following criteria: the intensity of the line, the fact that they do not suffer a heavy blend with another neighbouring line at large RV separation phases (e.g. H![]() ,
C IV
,
C IV
![]() 5801-12) and the requirement that they should be free from pollution by any ISM lines (e.g. H
5801-12) and the requirement that they should be free from pollution by any ISM lines (e.g. H![]() )
or telluric lines (e.g. He I
)
or telluric lines (e.g. He I![]() 7065). The selected lines are listed in Table 2. We measured the Doppler shifts by fitting two Gaussians at phases where the separation between the lines of both stars was sufficient. We then used the cross-correlation like method described in Rauw et al. (2000) to attempt to disentangle the blended lines. As HD152248 is an eclipsing binary, we used the light curve of PGB to achieve a rough first order correction of the relative line intensity at eclipsing phases. The observed lines are further affected by slight intensity and/or profile variations; we assumed, from our experience, that the errors on Doppler shifts measured in this way are about 2.5 times larger than the errors on the two-Gaussian fit results. For those phases where the lines were too heavily blended for the latter method to give reliable results, we adopted the RV obtained with a single Gaussian fit. We estimated, from the FWHM of the blend, that the accuracy on the line position in this latter case could be ten times lower than the one reached at large separation phases (i.e. with the two-Gaussian fit method). While computing the orbital solution, we thus attributed a relative weight of 1.0, 0.15 and 0.01 to the RVs respectively measured with the two-Gaussian fit, the cross-correlation like and the single Gaussian fit methods. Ruling out the single Gaussian fit points provides orbital parameters that are only marginally different.
7065). The selected lines are listed in Table 2. We measured the Doppler shifts by fitting two Gaussians at phases where the separation between the lines of both stars was sufficient. We then used the cross-correlation like method described in Rauw et al. (2000) to attempt to disentangle the blended lines. As HD152248 is an eclipsing binary, we used the light curve of PGB to achieve a rough first order correction of the relative line intensity at eclipsing phases. The observed lines are further affected by slight intensity and/or profile variations; we assumed, from our experience, that the errors on Doppler shifts measured in this way are about 2.5 times larger than the errors on the two-Gaussian fit results. For those phases where the lines were too heavily blended for the latter method to give reliable results, we adopted the RV obtained with a single Gaussian fit. We estimated, from the FWHM of the blend, that the accuracy on the line position in this latter case could be ten times lower than the one reached at large separation phases (i.e. with the two-Gaussian fit method). While computing the orbital solution, we thus attributed a relative weight of 1.0, 0.15 and 0.01 to the RVs respectively measured with the two-Gaussian fit, the cross-correlation like and the single Gaussian fit methods. Ruling out the single Gaussian fit points provides orbital parameters that are only marginally different.
We adopted the effective wavelengths for O stars listed in Table 2 to compute the barycentric RVs. These effective wavelengths are from Conti et al. (1977) below 5000 Å, and from Underhill (1994) above. As our spectra taken with different instruments cover different wavelength ranges, the number of RV points associated with the different lines is variable. We report this number in
Col. 6 of Table 2. The He I![]() 4471 line provides the largest data set with 47 RV points. These measurements are listed in Table 1.
4471 line provides the largest data set with 47 RV points. These measurements are listed in Table 1.
As a first step, we computed an orbital solution for each of the 11 absorption line data sets. Accounting for the error bars, the computed orbital elements do agree with each other, except for the apparent systemic velocities ![]() and
and ![]() (respectively associated with the primary and secondary star). Though the
(respectively associated with the primary and secondary star). Though the ![]() and
and ![]() values are in
acceptable agreement with each other for the same line (see Table 2), their values as deduced from the different lines are indeed significantly different. This illustrates the well-known effect that different lines might reflect different systemic velocities. This might stem from the fact that these lines are formed at different depths in the atmosphere and thus at different outward velocities, resulting in slightly different apparent systemic velocities.
values are in
acceptable agreement with each other for the same line (see Table 2), their values as deduced from the different lines are indeed significantly different. This illustrates the well-known effect that different lines might reflect different systemic velocities. This might stem from the fact that these lines are formed at different depths in the atmosphere and thus at different outward velocities, resulting in slightly different apparent systemic velocities.
In order to combine the RVs obtained from the different lines, we had to refer all the RV measurements to a ``zero systemic velocity'' reference frame. For this purpose, we simply subtracted the corresponding weighted mean between ![]() and
and ![]() from the individual RVs of the considered line. We then computed a weighted RV mean from all the RV data obtained at the same observing date.
These mean RVs in the zero systemic velocity reference frame are listed in Cols. 5 and 6 of Table 1.
from the individual RVs of the considered line. We then computed a weighted RV mean from all the RV data obtained at the same observing date.
These mean RVs in the zero systemic velocity reference frame are listed in Cols. 5 and 6 of Table 1.
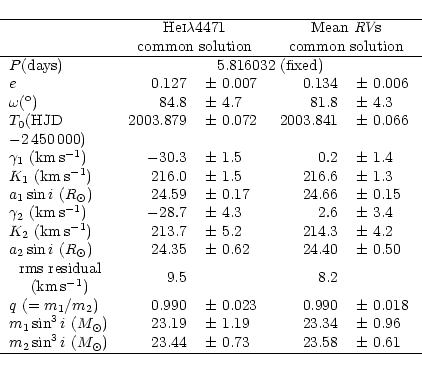
The computed orbital solutions from the He I![]() 4471 RV and the mean RV sets are both presented in Table 3. These two solutions are in excellent agreement with each other. Our way of combining the RVs from the different lines is further justified by the fact that the apparent systemic velocities computed from the mean data lie well within 1
4471 RV and the mean RV sets are both presented in Table 3. These two solutions are in excellent agreement with each other. Our way of combining the RVs from the different lines is further justified by the fact that the apparent systemic velocities computed from the mean data lie well within 1![]() of the zero velocity. We also tested the value of the period found by ST96. This does not affect the rms residual by more than a few tenths of kms-1 and the difference between the computed orbital elements is not significant.
of the zero velocity. We also tested the value of the period found by ST96. This does not affect the rms residual by more than a few tenths of kms-1 and the difference between the computed orbital elements is not significant.
|
|
![\begin{figure}
\par\includegraphics[height=7.5cm,width=7.9cm,clip]{MS10575f1.ps}\end{figure}](/articles/aa/full/2001/16/aa10575/Timg58.gif) |
Figure 1:
Radial velocity curve of the HD152248 binary system as computed from the He I |
| Open with DEXTER | |
|
|
![\begin{figure}
\par\includegraphics[width=6.6cm,height=6.4cm,clip]{MS10575f2.ps}\end{figure}](/articles/aa/full/2001/16/aa10575/Timg72.gif) |
Figure 2:
Illustration of the variation of the He I |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=6.3cm,clip]{MS10575f3.ps}\end{figure}](/articles/aa/full/2001/16/aa10575/Timg73.gif) |
Figure 3:
Primary to secondary ratios of the mean EWs of the He I lines in each quadrant. Downwards triangles = He I |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=6.3cm,clip]{MS10575f4.ps}\end{figure}](/articles/aa/full/2001/16/aa10575/Timg74.gif) |
Figure 4:
Primary to secondary ratios of the mean EWs of the Balmer and the O III (upper panel) lines and of the He II (lower panel) lines in each quadrant. Upper panel: circles = H |
| Open with DEXTER | |
Using a two-Gaussian fit, we measured the EWs of the primary and secondary absorption lines listed in Table 2, except near conjunction. Particular attention has been paid to the normalization process to avoid systematic deviations. We estimate that our continuum determination is self-consistent with an accuracy better than 0.5%. For the strongest lines, this corresponds to a maximum contribution to the error on the EW measurements of about 0.05 Å. We further estimate that the mean contribution of the continuum determination to the error is about 0.02 Å and that the intrinsic error related to the measurement process is of the same order of magnitude.
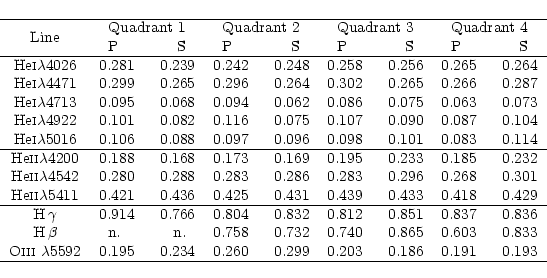
Several clear tendencies appear from these measurements and are presented below. First of all, let us divide the orbital cycle into four parts which we call quadrants, each of them corresponding to an interval of 90![]() in true anomaly. The first quadrant ranges then from the primary eclipse to the first quadrature; the second, from the first quadrature to the secondary eclipse and so on for the third and fourth quadrants. Due to the blend near conjunction, the effective corresponding phase intervals are, respectively for 1st to 4th interval, [0.06-0.22], [0.22-0.40], [0.66-0.80] and [0.80-0.95]. To limit the uncertainties and outline the observed trends, we computed the mean EWs over each of the quadrants. These are listed in Table 5. The primary to secondary ratios of the mean EWs in each quadrant are further plotted in Figs. 3 and 4.
in true anomaly. The first quadrant ranges then from the primary eclipse to the first quadrature; the second, from the first quadrature to the secondary eclipse and so on for the third and fourth quadrants. Due to the blend near conjunction, the effective corresponding phase intervals are, respectively for 1st to 4th interval, [0.06-0.22], [0.22-0.40], [0.66-0.80] and [0.80-0.95]. To limit the uncertainties and outline the observed trends, we computed the mean EWs over each of the quadrants. These are listed in Table 5. The primary to secondary ratios of the mean EWs in each quadrant are further plotted in Figs. 3 and 4.
|
|
From these figures, we can identify the following trends:
Strictly speaking, only H![]() and two of the three studied He II lines display the S-S effect. Indeed, the variation of the He I line intensity does not match the ``classical'' definition of the S-S effect, as the strengthening of the secondary lines and the corresponding weakening of the primary ones occur between the 3rd and the 4th quadrants. A detailed investigation of the intrinsic variations of the EWs related to each star would further require correcting them for the relative contribution of the primary and secondary fluxes to the continuum. However, we have to defer this task to future works as we do not have at our disposal, at this stage, the appropriate photometric information required to properly carry out this study.
and two of the three studied He II lines display the S-S effect. Indeed, the variation of the He I line intensity does not match the ``classical'' definition of the S-S effect, as the strengthening of the secondary lines and the corresponding weakening of the primary ones occur between the 3rd and the 4th quadrants. A detailed investigation of the intrinsic variations of the EWs related to each star would further require correcting them for the relative contribution of the primary and secondary fluxes to the continuum. However, we have to defer this task to future works as we do not have at our disposal, at this stage, the appropriate photometric information required to properly carry out this study.
Finally, Gayley (2001) has recently suggested that the S-S effect might be due to surface flows generated by the irradiation of the stellar surface by the companion. This could modify the rotational broadening of the lines and might break down the approaching/receding symmetry, resulting in shallower or deeper absorption lines according to the line of sight. However, no influence on the intensity of the line is expected due to surface flows. The maximum projected velocity of such surface flows predicted in the case of the components of HD152248 lies near 110 kms-1. The measured FWHMs of the absorption lines in the spectrum of HD152248 present a scatter of about 0.3-0.4 Å around the mean value, though no clear correlation with the phase is observed. This corresponds to a variation of the broadening velocity of about 25 kms-1. The exact contribution of surface flows induced by irradiation to these slight profile variations is unknown. Clearly, detailed numerical modelling as well as more observations combining very high S/N and high resolution are needed to clarify this question.
![\begin{figure}
\par\mbox{\includegraphics[width=7.8cm,height=4.6cm,clip]{MS10575...
...m}
\includegraphics[width=7.3cm,height=4.8cm,clip]{MS10575f5b.ps} }
\end{figure}](/articles/aa/full/2001/16/aa10575/Timg76.gif) |
Figure 5:
Left: dynamical spectrum of the C III |
| Open with DEXTER | |
As mentioned earlier in this paper, the HD152248 spectrum presents several emission features. These include the He II![]() 4686 and H
4686 and H![]() lines that consist of a mixture of absorption and emission lines, the heavily blended N III
lines that consist of a mixture of absorption and emission lines, the heavily blended N III![]()
![]() 4634-4641 features, the C III
4634-4641 features, the C III![]() 5696 line and the faint unidentified of emissions at
5696 line and the faint unidentified of emissions at ![]() 4486 and
4486 and ![]() 4504.
4504.
As it clearly appears from Fig. 5, the C III![]() 5696 emission line turns out to be double peaked around quadrature and the peaks seem to move in phase with the RV curves of the absorption lines. In order to measure the RVs associated with these peaks, we first modelled the diffuse interstellar band (DIB) at
5696 emission line turns out to be double peaked around quadrature and the peaks seem to move in phase with the RV curves of the absorption lines. In order to measure the RVs associated with these peaks, we first modelled the diffuse interstellar band (DIB) at
![]() Å (
Å (
![]() Å) on a spectrum where it was well separated from the C III line (HJD2451669.853). We then subtracted the modelled DIB from all spectra and fitted two Gaussians to the C III emission line whenever the separation between the components was large enough; at other phases, we used the cross-correlation like method. The measured RVs are plotted together with the He I
Å) on a spectrum where it was well separated from the C III line (HJD2451669.853). We then subtracted the modelled DIB from all spectra and fitted two Gaussians to the C III emission line whenever the separation between the components was large enough; at other phases, we used the cross-correlation like method. The measured RVs are plotted together with the He I![]() 4471 RV curve on the right panel of Fig. 5. The left panel presents a grey scale image around the C III line; the He I
4471 RV curve on the right panel of Fig. 5. The left panel presents a grey scale image around the C III line; the He I![]() 4471 line orbital solution has been overplotted. It is clear from the two panels of Fig. 5 that the C III
4471 line orbital solution has been overplotted. It is clear from the two panels of Fig. 5 that the C III![]() 5696 lines closely follow the orbital motion. As we already pointed out in the case of HD93403 (Rauw et al. 2000), this is a strong argument in favour of a photospheric origin of the C III
5696 lines closely follow the orbital motion. As we already pointed out in the case of HD93403 (Rauw et al. 2000), this is a strong argument in favour of a photospheric origin of the C III
![]() line as suggested by Nussbaumer (1971) and Cardona-Núnez (1978).
Finally, unlike the case of HD93403 (see Rauw et al. 2001), the C III
line as suggested by Nussbaumer (1971) and Cardona-Núnez (1978).
Finally, unlike the case of HD93403 (see Rauw et al. 2001), the C III![]() 5696 line in the spectrum of HD152248 does not seem to display a reversal of the intensity ratio due to the Struve-Sahade
effect.
5696 line in the spectrum of HD152248 does not seem to display a reversal of the intensity ratio due to the Struve-Sahade
effect.
The HD152248 spectrum presents a highly complex emission structure between about
![]() Å and
Å and
![]() Å, which displays important phase-locked profile variations. In this region of the spectrum, the N III
Å, which displays important phase-locked profile variations. In this region of the spectrum, the N III![]()
![]() 4634 and 4641 lines are heavily blended with each other as well as with the neighbouring Si IV
4634 and 4641 lines are heavily blended with each other as well as with the neighbouring Si IV![]() 4631 and C III
4631 and C III![]()
![]() 4647-4650 lines at all phases. Due to their lower resolution, we excluded the B&C spectra from our study. Similarly we did not consider the CTIO spectra because of their relatively lower S/N ratio. A complementary journal of the CAT N III
4647-4650 lines at all phases. Due to their lower resolution, we excluded the B&C spectra from our study. Similarly we did not consider the CTIO spectra because of their relatively lower S/N ratio. A complementary journal of the CAT N III![]()
![]() 4634-4641 observations is given in Table 6. A careful comparison of the CAT and FEROS N III
4634-4641 observations is given in Table 6. A careful comparison of the CAT and FEROS N III![]()
![]() 4634-4641 spectra with the predicted line positions computed from our ephemerides and our orbital solution allows us to identify the components of the blend. Both stars of the HD152248 system present the N III
4634-4641 spectra with the predicted line positions computed from our ephemerides and our orbital solution allows us to identify the components of the blend. Both stars of the HD152248 system present the N III![]()
![]() 4634-4641 lines in emission in their spectra. Following e.g. Mathys (1988), an (f) tag should then be added to their spectral classification. The Si IV
4634-4641 lines in emission in their spectra. Following e.g. Mathys (1988), an (f) tag should then be added to their spectral classification. The Si IV![]() 4631 and C III
4631 and C III![]()
![]() 4647-4650 lines are in absorption in both spectra.
4647-4650 lines are in absorption in both spectra.
The two ![]()
![]() 4486, 4504 emission lines are related to the Of phenomenon and still remain unidentified, although they have been known for several decades now. These two lines are rather faint in the spectra of HD152248 and their peak intensities reach maxima of respectively 2.5% and 2% of the continuum level at conjunction phases. The stellar Mg II
4486, 4504 emission lines are related to the Of phenomenon and still remain unidentified, although they have been known for several decades now. These two lines are rather faint in the spectra of HD152248 and their peak intensities reach maxima of respectively 2.5% and 2% of the continuum level at conjunction phases. The stellar Mg II![]() 4481 lines, the DIB near
4481 lines, the DIB near ![]() 4502 and the probable presence of the N III
4502 and the probable presence of the N III![]()
![]() 4510-4514 absorption lines render this region of the spectrum very crowded and prevent us from performing a detailed analysis. It seems however clear that the
4510-4514 absorption lines render this region of the spectrum very crowded and prevent us from performing a detailed analysis. It seems however clear that the ![]() 4486 line is double peaked with the two components closely following the orbital motion. The situation is less clear concerning the
4486 line is double peaked with the two components closely following the orbital motion. The situation is less clear concerning the ![]() 4504 line, because of the DIB that affects the blue side of the line. A careful inspection of the spectra however suggests that the
4504 line, because of the DIB that affects the blue side of the line. A careful inspection of the spectra however suggests that the ![]() 4504 line might also be double peaked according to the orbital motion.
4504 line might also be double peaked according to the orbital motion.
|
|
| Line | EW (He II |
EW (H |
| component | (Å) | (Å) |
| Primary absorption | 0.245 | 0.590 |
| Secondary absorption | 0.178 | 0.400 |
| Emission | -0.630 | -2.588 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10575f6.ps}
\end{figure}](/articles/aa/full/2001/16/aa10575/Timg83.gif) |
Figure 6:
Two superimposed spectra of the He II |
| Open with DEXTER | |
We have a total of 51 He II![]() 4686 line spectra (17 B&C, 16 CES, 5 BME and 13 FEROS) at our disposal that provide a very good phase coverage. The journal of the CAT observations of He II
4686 line spectra (17 B&C, 16 CES, 5 BME and 13 FEROS) at our disposal that provide a very good phase coverage. The journal of the CAT observations of He II![]() 4686 is given in Table 6. Our H
4686 is given in Table 6. Our H![]() line data set is much more limited and consists of only 13 FEROS spectra. The normalization of the FEROS spectra around these two lines turned out to be a rather difficult task. Indeed, both lines are situated at the junction of two echelle orders and we had to normalize the spectra locally. To compare the B&C spectra with the echelle spectra, we also had to apply a local normalization around He II
line data set is much more limited and consists of only 13 FEROS spectra. The normalization of the FEROS spectra around these two lines turned out to be a rather difficult task. Indeed, both lines are situated at the junction of two echelle orders and we had to normalize the spectra locally. To compare the B&C spectra with the echelle spectra, we also had to apply a local normalization around He II![]() 4686 on the B&C spectra, in order to account for the broad underlying emission extending from 4600 to 4720 Å.
4686 on the B&C spectra, in order to account for the broad underlying emission extending from 4600 to 4720 Å.
![\begin{figure}
\par\includegraphics[width=7.3cm,height=4.6cm,clip]{MS10575f7a.ps...
...{8mm}
\includegraphics[width=7.3cm,height=4.6cm,clip]{MS10575f7b.ps}\end{figure}](/articles/aa/full/2001/16/aa10575/Timg84.gif) |
Figure 7:
Dynamical spectra of the He II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.1cm,height=4.9cm,clip]{MS10575f8a.ps...
...mm}
\includegraphics[width=7.1cm,height=4.9cm,clip]{MS10575f8b.ps}
\end{figure}](/articles/aa/full/2001/16/aa10575/Timg85.gif) |
Figure 8:
Equivalent widths of the He II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.1cm,height=4.9cm,clip]{MS10575f9a.ps...
...mm}
\includegraphics[width=7.1cm,height=4.9cm,clip]{MS10575f9b.ps}
\end{figure}](/articles/aa/full/2001/16/aa10575/Timg86.gif) |
Figure 9:
Full widths of the base of the emission component of the He II |
| Open with DEXTER | |
It is clear from these two diagrams and from Fig. 6 that the He II![]() 4686 and H
4686 and H![]() line profiles are strongly variable. For both lines, we can identify two absorption components at RVs that closely match the orbital motion. These absorptions are thus most probably formed in the atmosphere of the stars of the system. These two absorption features are superimposed on a broader emission component. The width of this latter emission varies with orbital phase (see e.g. Fig. 6).
line profiles are strongly variable. For both lines, we can identify two absorption components at RVs that closely match the orbital motion. These absorptions are thus most probably formed in the atmosphere of the stars of the system. These two absorption features are superimposed on a broader emission component. The width of this latter emission varies with orbital phase (see e.g. Fig. 6).
To quantify these variations, we first measured the total EW of the lines. The results for both lines are plotted against the phase in Fig. 8. Concerning the He II![]() 4686 line, we notice that the absorption is clearly dominating near phase
4686 line, we notice that the absorption is clearly dominating near phase ![]() and in a less prominent way near
and in a less prominent way near ![]() .
On the other side, the emission is overwhelming at phase
.
On the other side, the emission is overwhelming at phase
![]() (and to some extent at
(and to some extent at
![]() ).
).
We next attempted to restore the emission component. To this aim, in order to model the three line components, we fitted three Gaussians to the line profile on a spectrum where the two absorption contributions are well separated. The EWs of all three components as obtained from the fit are reported in Table 7. These results should however be considered with caution since the EWs of the three components are most probably undergoing some variation with phase. For each observed spectrum, we then shifted the template of the absorption components according to our He I![]() 4471 orbital solution and the observation phase, and we subtracted the shifted fake lines from the observed profile. This ``restoration'' process is a very crude method. In fact, the apparent systemic velocities of the He II
4471 orbital solution and the observation phase, and we subtracted the shifted fake lines from the observed profile. This ``restoration'' process is a very crude method. In fact, the apparent systemic velocities of the He II![]() 4686 and H
4686 and H![]() absorption components are unknown and could be different from that of the He I
absorption components are unknown and could be different from that of the He I![]() 4471 line, though Fig. 7 suggests that this difference should be small. In addition, HD152248 displays both ellipsoidal variations and photometric eclipses. As a consequence, the EWs of the lines are most probably varying with phase, and it is almost impossible to correctly account for this effect without the exact knowledge of the amount of light originating from the primary and from the secondary at each orbital phase. However, we used the eclipse depths from PGB to derive a first order correction for the line intensities of the absorbing components. We then measured the full width at the base of the restored emission components. To this aim, we defined the limits of the emission at a normalized intensity of 1.01, i.e. we considered the emission above 1% of the continuum. Results are displayed in Fig. 9 and show a strong phase-locked variation of the full width at the base of the emission components. Similar measurements have been carried out on the raw observed spectra to check that our restoration method does not bias the results. Only slight differences of the order of 20 kms-1 for the start and end positions of the He II
4471 line, though Fig. 7 suggests that this difference should be small. In addition, HD152248 displays both ellipsoidal variations and photometric eclipses. As a consequence, the EWs of the lines are most probably varying with phase, and it is almost impossible to correctly account for this effect without the exact knowledge of the amount of light originating from the primary and from the secondary at each orbital phase. However, we used the eclipse depths from PGB to derive a first order correction for the line intensities of the absorbing components. We then measured the full width at the base of the restored emission components. To this aim, we defined the limits of the emission at a normalized intensity of 1.01, i.e. we considered the emission above 1% of the continuum. Results are displayed in Fig. 9 and show a strong phase-locked variation of the full width at the base of the emission components. Similar measurements have been carried out on the raw observed spectra to check that our restoration method does not bias the results. Only slight differences of the order of 20 kms-1 for the start and end positions of the He II![]() 4686 emission component were detected. The H
4686 emission component were detected. The H![]() emission component being much more intense, no significant difference could be detected for this line.
emission component being much more intense, no significant difference could be detected for this line.
In summary, the He II![]() 4686 and H
4686 and H![]() lines behave similarly in many points. A common interpretation of the observed phase-locked modulation of both
lines will be provided in Sect. 8, within the framework of a colliding wind model. However, we first need to discuss the evolutionary
status of the components of HD 152248.
lines behave similarly in many points. A common interpretation of the observed phase-locked modulation of both
lines will be provided in Sect. 8, within the framework of a colliding wind model. However, we first need to discuss the evolutionary
status of the components of HD 152248.
Following the criterion of Conti (1973), we use the logarithm of the EW ratio of He I![]() 4471 and He II
4471 and He II![]() 4542 to determine the spectral types of both components of the system. We get for the mean ratio:
4542 to determine the spectral types of both components of the system. We get for the mean ratio:
![\begin{eqnarray*}&&\log W'_{\rm prim}(\lambda4471/\lambda4542) = 0.013\ [-0.035,...
...g W'_{\rm sec}(\lambda4471/\lambda4542) = -0.044\ [-0.101,0.006].\end{eqnarray*}](/articles/aa/full/2001/16/aa10575/img91.gif)
Walborn (1972) quoted a supergiant luminosity class for the composite spectrum of HD152248 though he noted that his classification could be vitiated because of the peculiar He II![]() 4686 profile.
PGB also adopted a supergiant luminosity class for both components of the system. However, the presence of He II
4686 profile.
PGB also adopted a supergiant luminosity class for both components of the system. However, the presence of He II![]() 4686 and H
4686 and H![]() in absorption in the spectrum of both stars argues against such a classification. In fact, PGB's assertion was based on the following UV criteria: a very strong emission in the Si IV
in absorption in the spectrum of both stars argues against such a classification. In fact, PGB's assertion was based on the following UV criteria: a very strong emission in the Si IV![]()
![]() 1394-1403 lines in all the IUE composite spectra and a blue asymmetry and red emission in the N IV
1394-1403 lines in all the IUE composite spectra and a blue asymmetry and red emission in the N IV![]() 1718 line in both primary and secondary spectra. However, as these authors mentioned in Penny et al. (1996), the Si IV
1718 line in both primary and secondary spectra. However, as these authors mentioned in Penny et al. (1996), the Si IV![]()
![]() 1394-1403 doublet is a wind feature that might not be associated with the photosphere. Furthermore, the dependence of the N IV
1394-1403 doublet is a wind feature that might not be associated with the photosphere. Furthermore, the dependence of the N IV![]() 1718 line on wind strength might lead to a more luminous classification in the case of a star with an unusually strong wind. We believe that previous confusion about the luminosity class of this system arises mainly from the fact that the lines adopted as luminosity classification criteria are probably affected by a wind interaction process occurring within the HD152248 system (see below).
1718 line on wind strength might lead to a more luminous classification in the case of a star with an unusually strong wind. We believe that previous confusion about the luminosity class of this system arises mainly from the fact that the lines adopted as luminosity classification criteria are probably affected by a wind interaction process occurring within the HD152248 system (see below).
Based on the presence of He II![]() 4686 and H
4686 and H![]() in absorption in the spectrum of both components, we follow Mathys (1988) recommendation and, according to a rough determination of the EW of the He II
in absorption in the spectrum of both components, we follow Mathys (1988) recommendation and, according to a rough determination of the EW of the He II![]() 4686 absorption components (from Table 7), we adopt a giant luminosity class for both stars of the HD152248 system. Morrell et al. (1991) further showed that the unidentified
4686 absorption components (from Table 7), we adopt a giant luminosity class for both stars of the HD152248 system. Morrell et al. (1991) further showed that the unidentified ![]()
![]() 4486, 4504 lines display a clear luminosity dependence. An estimate of the intensity of the
4486, 4504 lines display a clear luminosity dependence. An estimate of the intensity of the ![]() 4486 line in the spectrum of HD152248 also suggests that the stars of HD152248 are giants.
4486 line in the spectrum of HD152248 also suggests that the stars of HD152248 are giants.
Finally both stars present N III![]()
![]() 4634-4641 in emission so that, associated with weak He II
4634-4641 in emission so that, associated with weak He II![]() 4686 absorption, an (f) tag should be added to the spectral classification. The new classification for this system is thus: O7.5III(f) + O7III(f).
4686 absorption, an (f) tag should be added to the spectral classification. The new classification for this system is thus: O7.5III(f) + O7III(f).
![\begin{figure}
\par\includegraphics[width=7.3cm,height=7.3cm,clip]{MS10575f10.ps}
\end{figure}](/articles/aa/full/2001/16/aa10575/Timg93.gif) |
Figure 10: Hertzsprung-Russell diagram of the HD152248 system. The open and filled symbols stand for the primary and secondary respectively. Evolutionary tracks are from Schaller et al. (1992) for Z=0.020 and adopting `standard' mass loss rates |
| Open with DEXTER | |
Adopting the effective temperature calibration of Chlebowski & Garmany (1991), the spectral types derived above yield
![]() K and
K and
![]() K for the primary and the secondary respectively. The quoted uncertainty corresponds to half a spectral subtype.
K for the primary and the secondary respectively. The quoted uncertainty corresponds to half a spectral subtype.
Howarth et al. (1997) and Penny et al. (1999) quote a luminosity ratio in the UV and in the visible of
![]() .
Raboud et al. (1997) reported V = 6.09 and
E(B-V) = 0.46 for HD152248. The photometry of HD152248 is affected by the presence of a nearby visual companion that is about 2.0 mag fainter than the close binary (Mason et al. 1998). The values of the distance modulus of the NGC6231 cluster range from 10.7 to 11.6. In the following, we will adopt the value DM = 11.2 derived by Raboud et al. (1997). We thus obtain
.
Raboud et al. (1997) reported V = 6.09 and
E(B-V) = 0.46 for HD152248. The photometry of HD152248 is affected by the presence of a nearby visual companion that is about 2.0 mag fainter than the close binary (Mason et al. 1998). The values of the distance modulus of the NGC6231 cluster range from 10.7 to 11.6. In the following, we will adopt the value DM = 11.2 derived by Raboud et al. (1997). We thus obtain
![]() and
and
![]() for the primary and secondary respectively. The uncertainties on the quoted luminosities correspond to the sole
uncertainty (0.5 dex) on the distance modulus of NGC6231.
for the primary and secondary respectively. The uncertainties on the quoted luminosities correspond to the sole
uncertainty (0.5 dex) on the distance modulus of NGC6231.
The locations of the components of HD152248 are plotted in a H-R diagram in Fig. 10 together with the evolutionary tracks of Schaller et al. (1992). From the above results, we can infer radii of
![]() and
and
![]() .
These radii overlap within the errors with the values derived by PGB (13.4 and 12.9
.
These radii overlap within the errors with the values derived by PGB (13.4 and 12.9![]() for the primary and secondary respectively) and Mayer et al. (15.6 and 17.1
for the primary and secondary respectively) and Mayer et al. (15.6 and 17.1![]() for the primary and secondary respectively). Our values of the radii are slightly larger than the typical radii of O7-O7.5 giants as listed by Howarth & Prinja (1989), but they are definitely smaller than the radii of luminosity class I stars of same spectral type (Howarth & Prinja 1989) lending further support to our assertion that the components in HD152248 are giants rather than supergiants.
for the primary and secondary respectively). Our values of the radii are slightly larger than the typical radii of O7-O7.5 giants as listed by Howarth & Prinja (1989), but they are definitely smaller than the radii of luminosity class I stars of same spectral type (Howarth & Prinja 1989) lending further support to our assertion that the components in HD152248 are giants rather than supergiants.
From a crude interpolation between the evolutionary tracks of Schaller et al. (1992), we derive ``theoretical'' masses of
![]() and
and
![]() .
If we adopt the inclination of 67.2
.
If we adopt the inclination of 67.2![]() as determined by Mayer et al. (2001), the minimal masses reported in Table 3 yield observed masses of 29.6 and 29.9
as determined by Mayer et al. (2001), the minimal masses reported in Table 3 yield observed masses of 29.6 and 29.9![]() for the primary and the secondary respectively. These latter values are significantly smaller than the masses predicted from the theoretical models for stars at the same location in the HR diagram. This problem was already pointed out by PGB. Improved stellar evolution models including the effects of rotation (Meynet & Maeder 2000) might provide a solution for this mass discrepancy. In fact, the new models discussed by Meynet & Maeder (2000) predict a large scatter in the mass-luminosity relation that can amount to a difference of 30% in mass. However, we caution that the components of HD152248 do not show an exceptionally large projected equatorial rotational velocity (see Howarth et al. 1997).
for the primary and the secondary respectively. These latter values are significantly smaller than the masses predicted from the theoretical models for stars at the same location in the HR diagram. This problem was already pointed out by PGB. Improved stellar evolution models including the effects of rotation (Meynet & Maeder 2000) might provide a solution for this mass discrepancy. In fact, the new models discussed by Meynet & Maeder (2000) predict a large scatter in the mass-luminosity relation that can amount to a difference of 30% in mass. However, we caution that the components of HD152248 do not show an exceptionally large projected equatorial rotational velocity (see Howarth et al. 1997).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{MS10575f11.ps}
\end{figure}](/articles/aa/full/2001/16/aa10575/Timg106.gif) |
Figure 11:
Schematic view of the wind-wind interaction process occurring within the HD152248 system. The shaded area represents the high density, emitting region. The P and S letters refer respectively to the primary and secondary components of the system. Conjunction and quadrature phases have been indicated. The adopted value for the separation between the two components is 53.1 |
| Open with DEXTER | |
We now attempt to provide a consistent explanation to all our observations. It is obvious, from the results presented above, that both components of the HD152248 system are very similar. They indeed have similar polar radii, masses, luminosities and spectral types. Therefore, we can expect that the stars also have similar wind properties (mass loss rates and asymptotic velocities).
Howarth et al. (1997) derived terminal velocities of
![]() kms-1 and
kms-1 and
![]() kms-1 for the primary and secondary respectively. We can use the stellar parameters derived above in conjunction with the theoretical mass loss recipe of Vink et al. (2000) to estimate the mass-loss rates of the two components. In this way, we obtain
kms-1 for the primary and secondary respectively. We can use the stellar parameters derived above in conjunction with the theoretical mass loss recipe of Vink et al. (2000) to estimate the mass-loss rates of the two components. In this way, we obtain
![]() and
and
![]() (
(![]() yr-1) yielding a wind momentum ratio (Stevens et al. 1992) of
yr-1) yielding a wind momentum ratio (Stevens et al. 1992) of
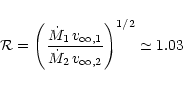 |
(1) |
A very simple model that can match most of the observations consists therefore in assuming the existence of a wind-wind interaction region located mid-way between both stars and limited by two roughly planar hydrodynamic shocks. This high density region, where the He II![]() 4686 and H
4686 and H![]() emission components are assumed to be produced, would (partly) be occulted at conjunction phases (
emission components are assumed to be produced, would (partly) be occulted at conjunction phases (![]() and 0.52) which explains why the absorption is overwhelming near these phases. Similarly, this simple scenario also accounts for the phase-locked variations of the width of the emission component. Indeed, we expect from our model that the inner shock region would be almost perpendicular to the axis of the system, so that the distribution of the radial velocities of the particles escaping from the wind interaction region should be broader when our line of sight is aligned with the interaction zone (i.e. around
and 0.52) which explains why the absorption is overwhelming near these phases. Similarly, this simple scenario also accounts for the phase-locked variations of the width of the emission component. Indeed, we expect from our model that the inner shock region would be almost perpendicular to the axis of the system, so that the distribution of the radial velocities of the particles escaping from the wind interaction region should be broader when our line of sight is aligned with the interaction zone (i.e. around ![]() and 0.80). On the other hand, this velocity distribution should be narrower at conjunction phases when our line of sight is forming an angle of about
and 0.80). On the other hand, this velocity distribution should be narrower at conjunction phases when our line of sight is forming an angle of about
![]() with the interaction region. Near conjunction, we thus expect to observe a narrower emission line than around quadrature.
with the interaction region. Near conjunction, we thus expect to observe a narrower emission line than around quadrature.
Part of the difference of the relative strengthening of the emission near quadrature phases might be explained by assuming that the emission process is depending of the separation D between the two stars following some power of 1/D. Indeed this distance is slightly larger at ![]() than at
than at ![]() .
The difference between the two absorption peaks at conjunction phases might also result from a difference in the separation between the two stars since the phases
.
The difference between the two absorption peaks at conjunction phases might also result from a difference in the separation between the two stars since the phases
![]() and
and ![]() respectively coincide with the periastron and the apastron passage. The unequal depths of the primary and secondary eclipses might also account for part of this difference, as the continuum level is lower at primary eclipse and the dilution of the emission is thus weaker.
We might expect that the forthcoming X-ray observations will help to address those questions and will further allow us to refine the wind-wind interaction model of the HD152248 system.
respectively coincide with the periastron and the apastron passage. The unequal depths of the primary and secondary eclipses might also account for part of this difference, as the continuum level is lower at primary eclipse and the dilution of the emission is thus weaker.
We might expect that the forthcoming X-ray observations will help to address those questions and will further allow us to refine the wind-wind interaction model of the HD152248 system.
We presented the results of an optical spectroscopic campaign on the HD152248 O+O binary system. Based on a large set of medium and high resolution spectra which provides a very good phase coverage, we derived improved orbital parameters. Combining literature data with our observations, we detected the presence of an apsidal motion with a rate of about 3.4![]() yr-1. As this system is going to be observed with the XMM X-ray observatory, the new contemporaneous ephemerides we derived are of major importance to correctly interpret the X-ray observation of the HD152248 binary.
yr-1. As this system is going to be observed with the XMM X-ray observatory, the new contemporaneous ephemerides we derived are of major importance to correctly interpret the X-ray observation of the HD152248 binary.
We found that the previous classification of both components as supergiants is most probably erroneous and we provide a new classification as O7.5III(f) + O7III(f) for the system. This leads to a better agreement between the observed radii and masses of the components and the typical values for O7-O7.5 giants. The masses we derived are, however, still significantly lower than the ones predicted by the evolutionary tracks.
Finally, we demonstrated that the He II![]() 4686 and H
4686 and H![]() line profiles result from a blend of two absorption components, associated with the stars of the system, with a broader and more intense emission component. We further showed that their profile and intensity variations are consistent with a wind-wind collision process within the system, assuming that the He II
line profiles result from a blend of two absorption components, associated with the stars of the system, with a broader and more intense emission component. We further showed that their profile and intensity variations are consistent with a wind-wind collision process within the system, assuming that the He II![]() 4686 and H
4686 and H![]() emissions are produced within the interaction region through the recombination process.
emissions are produced within the interaction region through the recombination process.
The probable existence of a wind-wind interaction within the HD152248 system makes this object an even more attractive target for XMM X-ray observations. The XMM pointings are scheduled to properly cover the orbital cycle and will further allow to investigate the different time scales of the wind interaction process. Detailed comparison of these data with recent theoretical hydrodynamical simulations (e.g. Stevens et al. 1992; Pittard 2000) will provide an important test for these models. It will further help to improve our understanding of the wind-wind collision process, and more widely of the winds of hot stars in general.
Acknowledgements
We wish to thank Dr. O. Stahl and Dr. A. Kaufer for their efficient help in adapting the FEROS reduction package to our data and the referee Dr. Stahl for his suggestions that improve our manuscript. We are grateful to Y. Nazé and Dr. J. Manfroid for their help in the reduction of the BME data. We thank Dr. J.-M. Vreux for many helpful comments and stimulating discussions. We are also grateful to Drs. P. Harmanec and P. Eenens for discussion about HD152248 and for communicating their results prior to publication. We are greatly indebted to the Fonds National de la Recherche Scientifique (Belgium) for multiple support. This research is also supported in part by contract P4/05 ``Pôle d'Attraction Interuniversitaire'' (SSTC-Belgium). Partial support through the PRODEX XMM-OM and INTEGRAL Projects is also gratefully acknowledged. The SIMBAD database was consulted for the bibliography.