4 Observations versus models

We first analyze diagnostic diagrams involving the H$\beta$ equivalent width. The classical, pure emission line ratio diagnostic diagrams will be discussed subsequently.

4.1 Diagnostic diagrams with equivalent widths

The observed samples of H  II galaxies, and giant H  II regions in general, are characterized by a very narrow range in ionization parameters. This was already noted before from a comparison of observed diagrams with model grids (McCall et al. 1985; Dopita & Evans 1986; García-Vargas & Díaz 1994; García-Vargas et al. 1995; Stasinska & Leitherer 1996; Bresolin et al. 1999; Dopita et al. 2000). We show in Fig. 12 the values of [O  III]/[O  II] as a function of $EW({\rm H}\beta )$ for models with $M_\star$ = 1, 10³, 10⁶ and 10⁹ $M_\odot$ and metallicity 0.2 $Z_\odot$ (corresponding to a range of a factor 10 in U between each curve) superimposed on the Terlevich data. For $EW({\rm H}\beta )$ > 100 Å, the observed dispersion in [O  III]/[O  II] suggests a range in ionization parameters of about a factor 10. Most of the data are bracketed by the series with $M_\star$ = 10³ and 10⁶ $M_\odot$ (corresponding roughly U $\sim$ 1-2 10^-3 and to U $\sim$ 1-2 10^-2, for the first 5 Myr). At lower equivalent widths, the observations fall outside the predicted values, apparently indicating a much higher U. As we will show below, this would be a premature conclusion.

If H  II galaxies are powered by coeval star clusters, one expects the [O  III] $\lambda$5007/H$\beta$ ratio to decrease as time goes by and $EW({\rm H}\beta )$ decreases. Panels a in Figs. 6-11 show the predictions for [O  III] $\lambda$5007/H$\beta$ as a function of $EW({\rm H}\beta )$. All the sequences show a steep decline of [O  III] $\lambda$5007/H$\beta$ at an $EW({\rm H}\beta )$ around 20 Å, irrespective of metallicity. A similar effect was predicted by the models of SL96. This is due to the average effective temperature of the exciting stars (as roughly expressed by $Q_{\rm He^0}/Q_{\rm H}$) dropping much more rapidly than the total number of ionizing photons, once the most massive stars have disappeared. The rise in the curves in Figs. 6-11 prior to the final steep decline for the Z=2 $Z_\odot$ and $Z_\odot$ models is due to the appearance of Wolf-Rayet stars. The sequences of models with $M_{\rm up}$ = 30 $M_\odot$ show a strong accumulation of points at early ages since it takes stars with masses below 30 $M_\odot$ more than 4 Myr to evolve off the main-sequence. The drop in [O  III] $\lambda$5007/H$\beta$ at $EW({\rm H}\beta )$ smaller than 20 Å is of course the same as for the $M_{\rm up}$ = 120 $M_\odot$ sequences. The sample of H  II galaxies in the SL96 study had $EW({\rm H}\beta )$ too large to show this drop, as a consequence of the requirement on [O  III] $\lambda$4363, as stated in the introduction. Since no such restriction was applied here, the values of $EW({\rm H}\beta )$ go down to a few Angströms. The data in each sample have a tendency to a decrease of [O  III] $\lambda$5007/H$\beta$ with decreasing $EW({\rm H}\beta )$. This decrease, however, is rather mild and the scatter in [O  III] $\lambda$5007/H$\beta$ increases for lower $EW({\rm H}\beta )$. One might think that extending the star formation over a longer period would help to reconcile the predicted trends with the observations. However, Fig. 9 suggests that even considering a constant star formation during 10 Myr is not sufficient to produce the large [O  III]/H$\beta$ observed at $EW({\rm H}\beta )$ of 20 Å or smaller.

A similar effect is seen in the He  I $\lambda$5876/H$\beta$ versus $EW({\rm H}\beta )$ diagrams (panels b). In contrast to [O  III]/H$\beta$ which, for a given stellar radiation field depends on U and Z, He  I $\lambda$5876/H$\beta$ is independent of the ionization parameter and depends only weakly on metallicity (in the sense that at larger metallicities a lower electron temperature increases He  I $\lambda$5876/H$\beta$). Instantaneous starburst models predict a sharp drop in He  I $\lambda$5876/H$\beta$ at $EW({\rm H}\beta )$ around 20 Å. This is not seen in any of the observed samples. The observed He  I $\lambda$5876/H$\beta$ ratio in the Terlevich sample remains remarkably constant around a value of 0.1. The slight rise and the increasing dispersion at low $EW({\rm H}\beta )$ could be due to observational errors, He  I $\lambda$5876 being a weak line. Unfortunately, this line is measured in only 98 out of 305 objects, and one might argue that the remaining objects have a much lower He  I $\lambda$5876/H$\beta$ ratio. All the objects in the Izotov sample have the He  I $\lambda$5876 intensity measured with very good accuracy, and all except one are of the order of 0.1. Although the statistics are very poor, since only 10 objects in the Izotov sample have $EW({\rm H}\beta )$ of the order of 20 Å or smaller, there seems to be no drop of He  I $\lambda$5876/H$\beta$ at this $EW({\rm H}\beta )$. The Popescu & Hopp sample shows the same behavior as the Terlevich sample.

Figure 12: Objects from the Terlevich sample superimposed on sequences of instantaneous burst models ( $M_{\rm up}$ = 120 $M_\odot$, $M_\star$ = 1, 103, 106 and 109 $M_\odot$), full sphere geometry, n = 10 cm-3 metallicity $Z/{Z_\odot } = 0.2$

The presence of an older underlying stellar component in H  II galaxies, as supported by many studies based on infrared colors and stellar features, changes the interpretation of the diagrams. It would decrease the H$\beta$ equivalent width of the young, ionizing population ("dilution'' effect), and also lead to an underestimate of the nebular H$\beta$ luminosity due to underlying stellar absorption. Qualitatively, these effects work in the direction required to reconcile models and observations. Such an explanation is suggested by a recent study of Raimann et al. (2000a). These authors grouped 185 spectra from the Terlevich et al. (1991) paper into 19 templates in order to increase the signal-to-noise and to allow a population synthesis analysis from the absorption features. They found that H  II galaxies are age-composite stellar systems, and that they can contain a significant population of stars with ages larger than 10 Myr. In Fig. 13 we plotted the same quantities as in Figs. 1-3 for the spectral groups defined by Raiman et al. (2000a) (excluding the 3 groups corresponding to Seyferts which are not discussed in the present paper). Open circles represent the averaged observed spectra. Each open circle is linked by a straight line with a filled circle representing the data after correction for an underlying stellar population (line and continuum) and for internal reddening. The same trends with $EW({\rm H}\beta )$ are seen for the filled circles as for the data shown in Figs. 1-3, but with larger slopes. The drop in [O  III]/H$\beta$ starts at much higher values of $EW({\rm H}\beta )$. This is much more compatible with our models than the uncorrected data. The steep decline starts immediately, which seems to be in better agreement with our models with $M_{\rm up}$ = 30 $M_\odot$ (Fig. 10) than with 120 $M_\odot$. However, the distribution of the open circles in the [O  III]/H$\beta$ versus $EW({\rm H}\beta )$ diagram of Fig. 13 is quite different from the distribution of the individual galaxies from the Terlevich sample (Fig. 1); therefore this averaged sample is unsuitable for describing the general properties of H  II galaxies. The important point is that the work of Raimann et al. (2000a,b) demonstrates that signatures of older underlying stellar populations are present in the spectra of H  II galaxies and can explain the observed trend in the uncorrected [O  III]/H$\beta$ versus $EW({\rm H}\beta )$ diagrams of Figs. 1-3. The multiwavelength analysis of 17 H  II galaxies by Mas-Hesse & Kunth (1999) reached a similar conclusion. Using indicators of young stellar populations (the UV continuum, the stellar + interstellar W(Si  IV)/W(C  IV) ratio, the strength of the Wolf-Rayet bump), these authors conclude that the majority of these galaxies have experienced recent nearly instantaneous star formation dominating the ultraviolet light. Yet their synthetic spectra are often below the observed visible continuum, indicating the presence of an older stellar population.

Other causes may contribute to the behavior of [O  III]/H$\beta$ and He  I $\lambda$5876/H$\beta$ as a function of $EW({\rm H}\beta )$ as well. For example, H  II regions may become gradually density bounded or the covering factor may decrease with time. A lower covering factor decreases the H$\beta$ luminosity and thus $EW({\rm H}\beta )$. Allowing for leakage of ionizing photons from the outskirts of the emitting region maintains [O  III]/H$\beta$ and He  I $\lambda$5876/H$\beta$ at a high level. This is an attractive possibility, since as nebulae expand, they become less and less opaque to ionizing photons (for a homogeneous gas sphere, the mass that can be ionized changes as $Q_{\rm H}/n$). Alternatively, it is possible that most of the giant H  II regions in the samples are density bounded or have a covering factor smaller than 1, regardless of their evolutionary state. Another possibility is that the spectroscopic data encompass only part of the nebula (for simplicity, we will refer to these explanations as the "aperture effect''). Such "aperture effects'' are likely to occur in our H  II galaxy samples. A detailed study of the H  II galaxy I Zw 18 indicates that the brightest H  II region, which dominates the spectrum, is density bounded, at least in some directions (Stasinska & Schaerer 1999). This could be a general property since diffuse or filamentary ionized gas has been observed at large distances in a number of H  II galaxies (e.g., Hoopes et al. 1996; Martin 1997; Hunter & Gallagher 1997), implying that the data in this paper may be missing part of the distant low-ionization gas.

High values of [O  III]/H$\beta$ and He  I $\lambda$5876/H$\beta$ at low $EW({\rm H}\beta )$ could also result if the extinction of the ionized gas is systematically higher than that of the stellar light, as found in several studies of H  II galaxies and starbursts (e.g. Fanelli et al. 1988; Calzetti 1997; Mas-Hesse & Kunth 1999; Schaerer et al. 2000).

To summarize, simple photoionization models of H  II galaxies as pure evolving starbursts cannot entirely account for the observed diagrams involving $EW({\rm H}\beta )$ (panels a-d) of Figs. 1-3. One or more of these effects are likely explanations: (i) an older stellar population; (ii) starlight systematically suffering a smaller extinction than ionized gas; or (iii) an aperture effect where the observed spectra correspond to density bounded nebulae or nebulae with a covering factor smaller than 1. These interpretations explain in a natural way the absence of H  II galaxies with $EW({\rm H}\beta )$ larger than 400 Å in objective prism surveys, whereas starburst models for ionization bounded H  II regions predict values of up to 700 Å (see also discussion in SL96). This also implies that such surveys are biased against galaxies where the latest starbursting episode is older than about 5 Myr, as such objects would tend to have too weak H$\beta$ and H$\alpha$ emission lines to be detected.

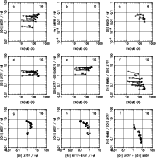Figure 13: Groups of H  II galaxies as defined by Raimann et al. (2000a) from the Terlevich et al. (1991) catalogue. Open circles: the averaged spectra as used by Raiman et al. (2000a); filled circles: the same after correction for underlying stellar population and internal reddening

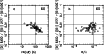Figure 14: Comparison of the trends for [O  I]/([O  II]+[O  III]) as a function of $EW({\rm H}\beta )$ and O/H for the 60 objects with measured [O  III] $\lambda$4363 of the Izotov sample

How can these explanations be reconciled with the increase of [O  I]/H$\beta$ as $EW({\rm H}\beta )$ decreases (panels c in Figs. 1-3)? This trend is also present in the corrected template spectra from Raimann et al. (Fig. 13), but the number of points is small and confirmation on a larger sample is required. One could argue that the old underlying population is stronger in higher metallicity objects, so that the increase in [O  I]/H$\beta$ with decreasing $EW({\rm H}\beta )$ could be attributed to a metallicity effect. We can test this idea by plotting [O  I]/([O  II]+[O  III]) as a function of O/H for the 60 objects with measured [O  III] $\lambda$4363 of the Izotov sample. This is done in panel b of Fig. 14. Panel a of this figure shows the same objects in the [O  I]/([O  II]+[O  III]) vs. $EW({\rm H}\beta )$ plane. Clearly, the metallicity effect is not a good explanation. Also, the behavior of [O  I] cannot be explained by the "aperture effect'' discussed above. Reducing the covering factor while keeping the nebulae ionization bounded does not change the [O  II]/H$\beta$ and [O  I]/H$\beta$ ratios. Making the nebulae density bounded reduces the ratios. Note that the observed behavior of [O  I]/H$\beta$ with $EW({\rm H}\beta )$ argues in favor of $EW({\rm H}\beta )$ remaining a statistical age indicator (although the age cannot be obtained by a direct comparison with photoionization models for pure starbursts). As pointed out by by Stasinska & Schaerer (1999) in the case of I Zw 18, strong [O  I] emission is easily produced by photoionization models in dense filaments which may contribute only marginally to the total emission in the other lines. Possibly, giant H  II regions are globally density bounded but contain high density filaments. Such filaments could be produced by shock-wave compression or instabilities, induced by stellar winds and supernovae whose effects are expected to increase with time.

4.2 On the strong line method to derive oxygen abundances

An important consequence of these observational selection effects in H  II galaxy samples is that the age of the ionizing population has little influence on the observed ([O  III]+[O  II])/H$\beta$ ratio (see panel e in Figs. 6-9). Combined with the narrow range of U in giant H  II galaxies (cf. panels a of Figs. 1-3 and  6-11), this explains a posteriori why strong line methods based on ([O  III]+[O  II])/H$\beta$ and methods utilizing the electron temperature lead to similar oxygen abundance estimates in these objects (Pilyugin 2000). A priori one would have expected large differences induced by the temporal variation of the ionizing radiation field during the evolution of a starburst.

Figure 15 shows how the [O  III]/[O  II] vs. ([O  III]+[O  II])/H$\beta$ diagram (introduced by McGaugh 1991, 1994 to derive O/H and U at the same time) changes over a period of 4 Myr. Continuous lines join models with equal metallicities (the thickest lines correspond to the most metal rich cases), dotted lines join models with equal M_*. Panels a, b, c correspond to starburst ages of .01, 2.01 and 4.01 Myr, respectively. The objects from the Terlevich sample are overlaid in the three panels. We see that the theoretical diagrams at metallicities lower than half solar evolve little over this period, demonstrating the applicability of the strong line method at these metallicities. In practice, it is however preferable to calibrate the method not on models but empirically with a sample of high signal-to-noise observations of H  II galaxies, as done by Pilyugin (2000).

Figure 15: Evolution of the McGaugh (1991) diagram over a period of 4 Myr for our instantaneous burst models ( $M_{\rm up}$ = 120 $M_\odot$), full sphere geometry, n = 10 cm-3. Models with equal metallicities are linked by full lines (whose thickness is proportional to the metallicity). Models with equal M* are linked with dotted lines. Panels a), b), c) correspond to starburst ages of .01, 2.01 and 4.01 Myr, respectively Superimposed are the objects from the Terlevich sample

Interestingly, as already pointed out by Stasinska (1999), rapid evolution of the McGaugh (1991) diagram is, however, predicted at metallicities solar, due to important changes in the hardness of the stellar radiation field at such metallicities, and due to the strong impact on optical line ratios. This behavior of the stellar radiation field at large metallicity is due to the fact that the overall main sequence is shifted toward lower temperatures, and thus the temperature of the stars falls below 40 kK earlier, as the hardness measured by $Q_{\rm He}/Q_{\rm H}$ decreases rapidly. This explains the more rapid decrease of the hardness of the ionizing flux of stellar populations at high metallicity (cf. Schaerer & Vacca 1998; Leitherer et al. 1999). Therefore at metallicities around solar or above (where electron temperature based methods cannot be used), the results from strong line methods to derive the oxygen abundance are likely to be rather inaccurate.

We also emphasize that strong line methods are statistical, as compared to electron temperature methods. They should be used with caution in cases when a systematic variation in the starburst properties or the gas density distribution is expected. This applies to studies of environmental effects on metallicities, e.g., such as those of giant H  II regions seen in tidal tails of galaxies (Duc & Mirabel 1998) or H  II galaxies in the core of galaxy clusters (Vílchez 1995) as compared to isolated H  II galaxies.

4.3 Pure emission line ratio diagnostic diagrams

Next we consider classical diagnostic diagrams which exclusively rely on line ratios. To a first approximation, such diagrams depend only on the population of the most massive stars which produce the ionization. They have been extensively studied for giant H  II regions in spiral galaxies and, as mentioned in Sect. 2.4, it has been found that [O  III]/H$\beta$ versus [O  II]/H$\beta$, or [O  III]/H$\beta$ versus [O  II]/[O  III] define a very narrow sequence, called the H  II region sequence. This sequence was analyzed with the help of photoionization models and has been interpreted as a sequence in metallicity with effective temperature/ionization parameter varying in line with metallicity (McCall et al. 1985; Dopita & Evans 1986; Dopita et al. 2000).

Since H  II galaxy samples are believed to contain mostly low-metallicity objects, it is not surprising that the H  II galaxy sequences shown in Figs. 1-3 a are less populated at the low [O  III]/H$\beta$ end than the McCall et al. (1985) or van Zee et al. (1998) sequences, and that they extend to high [O  III]/H$\beta$.

Although some of the observed trends are met by the predictions, it is, nevertheless, apparent from Figs. 6-11 that our models do not reproduce the sequence very well. Compared to other classical diagnostic diagrams, the [O  III]/H$\beta$ vs. [O  II]/H$\beta$ diagram has the advantage of being independent of the abundances ratios of O/N or O/S. Therefore we will focus our discussion on this diagram, but the conclusions are similar for the [O  III]/H$\beta$ vs. [S  II]/H$\beta$ diagram. Diagrams involving [N  II] are discussed in Sect. 4.4.

Excluding the 2 $Z_\odot$ and $Z_\odot$ sequences (models represented by squares and circles), which are not representative of the bulk of the objects in our samples, the parameter space occupied by the models in the diagram does not exactly match the observations. First, our model sequences predict an almost vertical drop in the [O  III]/H$\beta$ vs. [O  II]/H$\beta$ diagram, and the maximum [O  II]/H$\beta$ is almost independent of the ionization parameter. This is due to oxygen mainly being in the form of O⁺when the most massive stars have disappeared. Since we have argued above that our H  II galaxies sample should contain few, if any, galaxies with the most recent starburst older than 5 Myr, our observational diagrams should be compared to the model sequences until 5 Myr only (roughly corresponding to $EW({\rm H}\beta )$ 50 Å in Figs. 6-11).

Even with that restriction, our photoionization models are unable to reproduce [O  II]/H$\beta$ ratios larger than 4 and the kink at [O  III]/H$\beta$ > 4 and [O  II]/H$\beta$ > 2. Moreover, the problem may become even worse if the model spectra used for the Wolf-Rayet phase were too hard (cf. Sect. 3.1). We have computed supplementary photoionization models especially for this purpose (including depletion of metals on grains or heating by X-rays), but without success. The disagreement becomes even larger if we assume that H  II galaxies are density bounded, as argued above. Whether additional heating sources (shocks, conduction, turbulence) may solve the problem is an open question.

Dopita et al. (2000) compared an observed sample of giant regions in spiral galaxies with photoionization models and found that their models could not reproduce the high [O  I]/H$\beta$ and [S  II]/H$\beta$ ratios seen in some objects, invoking shocks as an explanation. Our models use a different prescription for the density structure than those of Dopita et al. and differ also in other respects, such as numerical aspects and the N/O vs. O/H prescription. Still, we find that the problems exists not only for [O  I]/H$\beta$ and [S  II]/H$\beta$ but also for [O  II]/H$\beta$. Of course, the observed [O  II]/H$\beta$ ratio is largely affected by the dereddening procedure, while this is much less the case for the other two ratios. Since strong line diagnostics heavily rely on [O  II], and since this line is becoming increasingly important for the study of galaxies at high redshift, it would be useful to better constrain the problem by a detailed observational and theoretical study of those few H  II galaxies with a firm indication of shock excitation.

McCall et al. (1985) argued that giant H  II regions must be mostly ionization bounded, otherwise one would not observe such a tight sequence in emission line ratio diagrams. This is at variance with the fact that we now know that a fair portion of Lyman continuum radiation is leaking out of H  II regions (Martin 1997; Stasinska & Schaerer 1999; Beckman et al. 2000). However, if the density structure of giant H  II regions were driven by the mechanical action of winds and supernovae explosions from their embedded stellar populations, one could understand why there is so little dispersion among giant H  II regions in such diagrams, even if they are partially density bounded, since the driving parameter would boil down to the stellar population itself. In this respect, hydrodynamic modelling of the ionization structure of giant H  II regions (the follow-up of the single star H  II region modelling performed by Rodriguez-Gaspar & Tenorio-Tagle 1998) would be extremely important.

   
4.4 The N/O ratio

Among others, Kunth & Sargent (1986), Pagel et al. (1986, 1992), Olofsson (1995b) suggested that gas might be chemically enriched in, e.g., helium and nitrogen from the winds of Wolf-Rayet stars during the evolution of giant H  II regions. Traces of such a local pollution have been found in the irregular galaxy NGC 5253 from imaging spectroscopy (Walsh & Roy 1987, 1989; Kobulnicky et al. 1997), but other attempts to detect local N/O enhancement in Wolf-Rayet galaxies have failed (Kobulnicky & Skillman 1996, 1998; Kobulnicky 1999). Moreover, Izotov et al. (1997) and Kobulnicky & Skillman (1996) analyzed observational data on H  II galaxies in the literature and found that galaxies with strong Wolf-Rayet features in their integrated spectra exhibited the same N/O ratios as the remaining galaxies at identical O/H ratios, contrary to the claim of Pagel et al. (1986, 1992).

In the light of these previous studies, the [N  II]/[O  II] vs. $EW({\rm H}\beta )$ diagram is revealing. There is a definite trend of [N  II]/[O  II] strongly increasing as $EW({\rm H}\beta )$ decreases in all our H  II galaxy samples. If we take [N  II]/[O  II] as an indicator of N/O, it is tempting to attribute this trend to an increase in N/O as the ionizing starburst gets older. However, several biases must be examined first. Could the observed relation be the result of a selection effect? While the absence of low [N  II]/[O  II] ratios at small equivalent widths could be attributed to selection effects against the weakest lines, at large H$\beta$ equivalent widths, values of [N  II]/[O  II] larger than $\sim$0.2-2 should be observed if such objects exist. Moreover, there is no selection effect in the Izotov sample since all the objects appear in Fig. 2f, and the relation is seen there as well. The trend is less distinct than in the other samples, probably because the sample is weighted towards the most metal poor galaxies. Finally, as mentioned in Sect. 2.4, if a complete subsample is extracted from the Terlevich sample, the observed relation between [N  II]/[O  II] and $EW({\rm H}\beta )$ remains. Therefore, the observed relation cannot be attributed to a simple selection effect.

Turning to an interpretation, it is important bearing in mind that [N  II]/[O  II] does not only depend on N/O but also on the electron temperature. It is larger at lower electron temperatures and therefore at higher O/H for a given N/O. Second, at metallicities above solar, the [N  II] and [O  II] lines are produced by recombination rather than by collisional excitation (if the N⁺⁺/N⁺ and O⁺⁺/O⁺ratios in the nebula are not close to zero). Our models (panels f in Figs. 6-11) do account for that. We have already argued that models with ages 5 Myr may not be relevant to our samples of H  II galaxies, but that $EW({\rm H}\beta )$ is an indicator of the age of the ionizing starburst (in the sense that smaller $EW({\rm H}\beta )$ correspond to larger ages). We have also argued that one should perhaps consider density bounded rather than ionization bounded models. However, the [N  II]/[O  II] ratio would remain unchanged in a density bounded model. The large values of [N  II]/[O  II] ( 0.3) seen in some of the H  II regions of our samples therefore indicate a N/O ratio larger than the largest predicted by our models (0.1 at $Z = 2\ {Z_\odot}$).

If the metallicities (i.e., O/H ratios) in our samples have identical distributions in each age bin, the observed trend could be explained if the two following conditions hold at the same time: (i) the relation between N/O and O/H is steeper than the relation based on McGaugh (1991) adopted in our models and (ii) the most metal rich objects are those whose $EW({\rm H}\beta )$ values are the most affected by the contribution of an old stellar population. The first hypothesis might indeed be true. There are indirect indications, from studies of giant H  II regions in spiral galaxies, that at high metallicities N/O increases more rapidly than N/O $\alpha$ (O/H)^0.5 adopted in our models (cf. van Zee et al. 1998; Henry et al. 2000). The second hypothesis appears quite reasonable. Earlier generations of stars are necessary to produce the bulk of presently observed O/H in more metal rich H  II galaxies, and these earlier generations still contribute to the continuum. Qualitatively, the results of Raimann et al. (2000b) support this picture. We note however that the anticorrelation between [N  II]/[O  II] and $EW({\rm H}\beta )$ subsists in the Raimann et al. templates even after correction for the old stellar population (Fig. 13f). If this effect is real, it calls for an additional explanation.

N/O might be increasing with time. Such an explanation would be more compatible with the observed [N  II]/[O  II] versus ([O  II]+[O  III])/H$\beta$ diagram in Figs. 1-3i, in which the scatter in ([O  II]+[O  III])/H$\beta$ at a given [N  II]/[O  II] is extremely small. Models with ages smaller than 5 Myr (panels i in Figs. 6-11) show about the same scatter, but in order to compare with observations a convolution of the theoretical scatter with observational errors, and a correction for reddening and underlying H$\beta$ absorption is first required. With N/O increasing with time, the theoretical scatter at a given [N  II]/[O  II] becomes smaller. The hypothesis of N/O increasing with time can in principle be checked directly by plotting the N/O determined by electron temperature based methods as a function of $EW({\rm H}\beta )$. We performed this test. No obvious trend is seen, but none of the objects with large observed [N  II]/[O  II] in our samples has [O  III] $\lambda$4363 measured, so this test is not conclusive.

Deep spectroscopy for a detailed analysis of the stellar populations in the objects showing high [N  II]/[O  II] ratios should be obtained. High resolution emission line imaging and tailored photoionization modeling should also be undertaken, in order to put the strongest possible constraints on O/H and N/O in these objects.