A&A 370, 1-22 (2001)
DOI: 10.1051/0004-6361:20010232

The evolution of emission lines in H II galaxies

G. Stasinska¹ - D. Schaerer² - C. Leitherer³

1 - DAEC, Observatoire de Paris-Meudon, 92195 Meudon Cedex, France
2 - Laboratoire d'Astrophysique, Observatoire Midi-Pyrénées, 14 Av. E. Belin, 31400 Toulouse, France
3 - Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA

Received 27 October 2000 / Accepted 22 January 2001

Abstract
We constructed diagnostic diagrams using emission line ratios and equivalent widths observed in several independent samples of H  II galaxies. Significant trends are seen, both in the line ratio diagrams, and in diagrams relating line ratios to the equivalent width of H$\beta$. The diagrams are compared to predictions from photoionization models for evolving starbursts. This study extends the work of Stasinska & Leitherer (1996) by including objects with no direct determination of the metallicities, and by using updated synthesis models with more recent stellar tracks and atmospheres. We find that H  II galaxies from objective-prism surveys are not satisfactorily reproduced by simple models of instantaneous starbursts surrounded by constant density, ionization bounded H  II regions. The observed relations between emission line ratios and H$\beta$ equivalent width can be understood if older stellar populations generally contribute to the observed optical continuum in H  II galaxies. In addition, different dust obscuration for stars and gas and leakage of Lyman continuum photons from the observed H  II regions can be important. As a result, H  II galaxies selected from objective-prism surveys are not likely to contain significant numbers of objects in which the most recent starburst is older than about 5 Myr. This explains the success of the strong line method to derive oxygen abundances, at least in metal poor H  II galaxies. The observed increase of [O  I]/H$\beta$ with decreasing H$\beta$ equivalent width can result from the dynamical effects of winds and supernovae. This interpretation provides at the same time a natural explanation of the small range of ionization parameters in giant H  II regions. The classical diagnostic diagram [O  III]/H$\beta$ vs. [O  II]/H$\beta$ cannot be fully understood in terms of pure photoionization models. The largest observed [O  II]/H$\beta$ ratios require additional heating. The [N  II]/[O  II] ratio is shown to increase as the H$\beta$ equivalent width decreases. A possible explanation is an N/O increase due to gradual enrichment by winds from Wolf-Rayet stars on a time scale of $\sim$5 Myr. Alternatively, the relation between N/O and O/H could be steeper than N/O $\propto$ O/H^0.5, with a previous stellar generation more important at higher metallicities.

Key words: galaxies: abundances - galaxies: evolution - galaxies: ISM - galaxies: starburst - galaxies: stellar content - ISM: H  II regions - stars: Wolf-Rayet

1 Introduction

Isolated extragalactic H  II regions, which we will simply refer to as H  II galaxies, are powered by clusters of hot, massive stars that ionize their environment. Recent analyses of such objects, comparing the observed nebular emission lines, colors, and stellar features with evolutionary models (Mas-Hesse & Kunth 1991, 1999; Schaerer et al. 1999; Stasinska & Schaerer 1999) found that most have experienced a recent, quasi instantaneous burst of star formation. In addition, there is growing evidence for an older stellar population (Telles & Terlevich 1997; Papaderos et al. 1998; Raimann et al. 2000a). Some clues regarding the evolution of giant H  II regions, their properties and stellar content may be obtained by considering H  II galaxies in different evolutionary stages with respect to the most recent star formation event.

The present paper follows this approach: we compare the emission line properties of a large sample of H  II galaxies with those of photoionization models in which the ionizing continuum is provided by synthetic models of evolving starbursts. In a previous paper (Stasinska & Leitherer 1996, hereinafter SL96), we considered a sample of metal poor galaxies in which the oxygen abundance could be derived directly from observations using the electron temperature sensitive [O  III] $\lambda$4363 line. Thus the derived abundances were unambiguous and model independent. Unfortunately, we were automatically restricted to young starbursts by this requirement. As the most massive stars disappear, the radiation field gradually softens inducing a decrease of the [O  III] emission, and the weak [O  III] $\lambda$4363 becomes undetectable after about 5 Myr. Alternatively, the oxygen abundances can be estimated via strong line methods (Pagel et al. 1979; McGaugh 1991, 1994). The relevance and accuracy of these methods is however still under debate. We address this question in Sect. 4.2.

Lifting the restriction to the youngest starbursts immediately leads to inclusion of objects with a priori unknown metallicities. However, the distribution in metallicities should be the same for old and young objects, permitting an interpretation of diagnostic diagrams based on emission lines. This advantage of a large sample of bona fide young and old H  II galaxies is explored in the present work. With respect to SL96, we also use updated evolutionary synthesis models with more recent stellar tracks and stellar atmospheres as input for our photoionization models.

The study in the present paper is complementary to work on giant H  II regions in spiral galaxies, such as published by García-Vargas & Díaz (1994), García-Vargas et al. (1995), and more recently Bresolin et al. (1999) and Dopita et al. (2000). First, our observational samples are based on extragalactic H  II regions, for which the equivalent width of H$\beta$ can be used as a direct first-order indicator of the age of the latest starburst (Dottori 1981). Second, our samples are biased towards dwarf galaxies with correspondingly low average metallicities.

In Sect. 2 we present the observational samples, discuss possible selection effects, and display a series of observational diagrams. In particular, we show that emission line trends are seen not only in classical emission line ratio diagrams, but also in diagrams relating emission line ratios with the H$\beta$ equivalent width. In Sect. 3 we describe the models, present our model grid, and show theoretical diagrams for evolving starbursts. In Sect. 4 observations and models are compared. The main conclusions are summarized in Sect. 5.

2 Sample selection

2.1 The database

The prerequisites for our observational data base are the following. We require a large sample of objects with uniform observation parameters. The sample must be large since there are several factors determining the line spectra, the most important being metallicity and starburst age. We wish to use information from the He  I $\lambda$5876 line, which is directly related to the mean effective temperature of the ionizing stars (cf. Stasinska 1996). Deep spectroscopy is required for this generally weak line. In addition, we want to make use of a direct estimator of the starburst age, such as provided by the equivalent width of H$\beta$ (hereafter $EW({\rm H}\beta )$). While this estimator has its well-known drawbacks (effects of dust, incomplete absorption of the stellar ionizing photons by the observed nebula), it is relatively independent of the assumed nebular properties, as compared with emission line ratios such as [S  II]  $\lambda\lambda$6717+30/H$\beta$ or [S  II] $\lambda\lambda$6717+30/[S  III] $\lambda$9069 proposed by García-Vargas et al. (1995). However, $EW({\rm H}\beta )$ is difficult to use for giant H  II regions with a strong underlying old stellar component, such as in nuclear starbursts or giant H  II regions in evolved galaxies. Our sample is thus restricted to giant H  II regions in irregular or blue compact galaxies, where the old stellar component is expected to be weaker.

The largest, homogeneous sample meeting these requirements is the spectrophotometric catalogue of H  II galaxies by Terlevich et al. (1991). It contains spectra of 425 emission line galaxies, among which about 80% are classified as genuine H  II galaxies by the authors (as opposed to active galactic nuclei and nuclear starbursts). Further imaging of these objects identified some of these H  II galaxies as giant H  II regions in spiral galaxies (Telles, private communication). Those objects were removed to produce the final sample, hereafter referred to as the Terlevich sample, which consists of 305 objects. Most of the observations for the Terlevich catalogue were made with 2-m class telescopes, and the typical signal-to-noise in the continuum is 5. Note, however, that second-order contamination could affect some of the line ratios for $\lambda >$ 6000 Å (Terlevich et al. 1991).

As a control sample, we consider a much more restricted collection of isolated extragalactic H  II regions with very high quality observational data. These are the blue compact galaxies observed by Izotov and coworkers (Izotov et al. 1994, 1997; Thuan et al. 1995; Izotov & Thuan 1998; Guseva et al. 2000) on 2-m and 4-m class telescopes. Their signal-to-noise in the continuum is typically 20-40. The latter sample, referred to as the Izotov sample, comprises 69 objects.

Recently, another survey of emission line galaxies meeting our requirements has been published. This is the catalogue of Popescu & Hopp (2000) which contains 90 objects, out of which 70 are classified as H  II galaxies. The quality of the data is not as good as for the Izotov sample, but the sample is more homogeneous, as explained below.

2.2 Selection effects

Objective-prism surveys of emission line objects tend to underestimate the true proportion of objects with weak emission line equivalent widths. On the other hand, genuine, isolated giant extragalactic H  II regions will always be discovered in such surveys if they are bright enough. The Terlevich catalogue comprises 75% (25%) of the non-quasar emission line objects identified in the Michigan (Tololo) objective-prism survey, and additional biases are not expected to be important. Therefore, one expects a roughly uniform distribution of ages of the most recent starbursts, and the same distribution of metallicities at each age bin above a certain threshold in H$\beta$ equivalent width in the Terlevich sample.

In the case of the Izotov sample, the objects are mainly blue compact galaxies from the First and Second Byurakan objective-prism surveys. The sample is obtained by merging two sub-samples. One is composed of objects which had been selected for their low metallicities ( $Z < {\rm Z}_\odot/10$) as estimated from low signal-to-noise 6-m telescope spectra. The other subsample (the 39 objects studied by Guseva et al. 2000) is composed of objects selected on the basis of broad Wolf-Rayet features seen in the 6-m telescope spectra. The metallicities in the latter subsample range between $Z_\odot$/40 and $Z_\odot$. The H$\beta$ equivalent widths in the Guseva subsample are, on average, lower than those in the other Izotov et al. subsample, and contamination from old stellar populations is likely present at least for some objects known as nuclear starbursts. Compared to the Terlevich sample, the Izotov sample is affected by strong biases which must be kept in mind when interpreting the diagnostic diagrams shown below.

The Popescu & Hopp sample is a complete subsample of emission line galaxies found on the objective-prism plates for the Hamburg Quasar Survey. The single selection criterion was the location of the galaxies with respect to voids. Therefore, as for the Terlevich sample, we expect a roughly uniform distribution of ages, and the same metallicity distribution at each age bin. The sample is however much smaller than the Terlevich sample; therefore statistical fluctuations may not be negligible.

2.3 Reddening corrections

Izotov and coworkers used an iterative procedure to deredden their sample where the reddening constant and stellar absorption at H$\beta$ are determined simultaneously. Such a procedure was feasible due to the high signal-to-noise of the data. They assumed the Whitford (1958) extinction law and took for the intrinsic H$\alpha$/H$\beta$ ratio the recombination value corresponding to the electron temperature derived from [O  III] 4363/5007, when available. In most cases, the contribution of the stellar absorption in H$\beta$ turns out to be only a few percent, except in some objects from the Guseva sample which includes a few nuclear starbursts (see Guseva et al. 2000; Schaerer et al. 2000).

The line intensities in the Popescu & Hopp (2000) sample are published corrected for reddening. For the galaxies with a strong underlying continuum relative to the H$\beta$ emission ( $EW({\rm H}\beta )$ < 20 Å), they assumed a constant underlying absorption at H$\beta$ of 2 Å. The reddening was computed from H$\alpha$/H$\beta$ assuming an intrinsic ratio of 2.87 and using the Howarth (1983) extinction law.

In the case of the Terlevich sample, the data are published without reddening correction. We have dereddened them adopting the Seaton (1979) reddening law and an intrinsic H$\alpha$/H$\beta$ ratio of 2.87. We assumed a constant underlying stellar absorption of 3 Å for all the spectra in the H$\alpha$ and H$\beta$ lines, which is predicted by models for synthetic absorption line spectra in starburst galaxies (Olofsson 1995a; González Delgado et al. 2000). Unfortunately, spectra in the H$\alpha$ region have second order contamination in many objects (cf. Terlevich et al. 1991), affecting the reddening correction. Alternatively, one could use H$\gamma$/H$\beta$ instead of H$\alpha$/H$\beta$ to determine the reddening correction, but this procedure is plagued by the fact that H$\gamma$ is a much weaker line than H$\alpha$, introducing substantial errors due to the reduced signal-to-noise, and by the lack of published H$\gamma$ equivalent widths. In any event, for objects without published H$\alpha$ data, we used H$\gamma$/H$\beta$ to derive the reddening, assuming that the stellar (negative) contribution to the observed H$\gamma$ line is three times as large as for the H$\beta$ line.

The reddening correction introduces some uncertainties into each sample. Even in the case of the Izotov sample, where dereddening was performed in a completely self-consistent way, the reddening correction may not be perfect. First, departures from the standard reddening law exist (e.g. Mathis & Cardelli 1988 or Stasinska et al. 1992). Second, the intrinsic H$\alpha$/H$\beta$ ratio in a nebula is not necessarily the recombination value. In objects with high electron temperatures, collisional excitation increases H$\alpha$/H$\beta$ with respect to the recombination value, in a proportion that depends on the quantity of neutral hydrogen in the emitting regions (Davidson & Kinman 1985; Stasinska & Schaerer 1999). Adopting the same underlying absorption of 3 or 2 Å at H$\beta$ for all the objects of the Terlevich and Popescu & Hopp samples may not be justified if stellar populations from previous star-forming events contribute significantly to the continuum (see below). Among the line ratios discussed in this paper, the one most affected by reddening is [O  II]/H$\beta$. It is prudent to assume that the [O  II]/H$\beta$ ratios may well be uncertain by up to about 30%, and even more for some objects in the Terlevich sample.

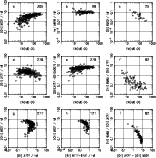	Figure 1: The Terlevich sample of H  II galaxies. On the upper right of each panel is given the total number of the objects appearing in the diagram
Open with DEXTER

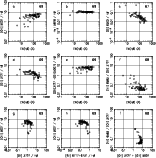	Figure 2: Same as Fig. 1 for the Izotov sample of H  II galaxies
Open with DEXTER

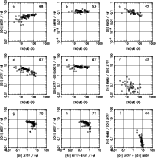	Figure 3: Same as Fig. 1 for the Popescu & Hopp sample of H  II galaxies
Open with DEXTER

2.4 Observed emission line trends

The nine panels of Figs. 1, 2, and 3 are various observational diagrams for the Terlevich, Izotov, and Popescu & Hopp samples, respectively. Panels a through f in these figures show the behavior of various emission line ratios as a function of $EW({\rm H}\beta )$. In spite of some (expected) dispersion, striking line trends are seen. These trends are very similar in the three samples, and are shown for the first time.

Some differences among the samples are likely due to the quality of the data. The smaller dispersion in He  I $\lambda$5876/H$\beta$ in the Izotov sample, for example, is probably due to the better signal-to-noise. We also note that the Terlevich and Popescu & Hopp samples contain some objects with rather large [O  II]/H$\beta$: $\sim$ 20% of the Popescu & Hopp sample and 3% of the Terlevich sample have [O  II]/H$\beta$ $\ge$ 5, while no object of the Izotov sample has such large values for this ratio. However, if we retain only the 50 objects from the Terlevich sample with measurements in the four lines [O  II] $\lambda$3727, [O  III] $\lambda$5007, He  I $\lambda$5876 and [N  II] $\lambda$6584, the diagrams become very similar to those corresponding to the Izotov sample. Therefore, we will ignore the objects with [O  II]/H$\beta$ > 5 since such high ratios may be attributed to poor signal-to-noise and/or to inadequate reddening corrections.

We generally note a gradual increase in the dispersion and a decrease of the average value of [O  III]/H$\beta$ as $EW({\rm H}\beta )$ decreases, while the He  I $\lambda$5876/H$\beta$ ratio remains remarkably constant. The [O  I]/H$\beta$ ratio, on the other hand, steadily increases with decreasing $EW({\rm H}\beta )$, extending the trend already noted by SL96 to lower $EW({\rm H}\beta )$. The [O  II]/H$\beta$ increases and tends to level off at $EW({\rm H}\beta )$ about 30 Å. The ([O  II]+ [O  III])/H$\beta$ ratio is rather constant at the largest $EW({\rm H}\beta )$, and becomes more dispersed with a tendency to decrease as $EW({\rm H}\beta )$ decreases. The [N  II]/[O  II] ratio shows a clear tendency to increase as $EW({\rm H}\beta )$ decreases, although the dispersion is larger than in the remaining diagrams. Overall, all the trends of emission line ratios with H$\beta$ equivalent width are significant and require an explanation.

Finally, panels g, h, and i in Figs. 1-3 show the standard emission line ratio diagrams ([O  III]/H$\beta$ vs. [O  II]/H$\beta$, [O  III]/H$\beta$ vs. [S  II]/H$\beta$ and [N  II]/[O  II] vs. ([O  II]+[O  III])/H$\beta$), similar to those that have been widely used in the literature to distinguish H  II regions from active galaxies (Baldwin et al. 1981; Veilleux & Osterbrock 1987; van Zee et al. 1998; Martin & Friedli 1999) and for studies of abundance ratios in H  II regions (McGaugh 1994; Ryder 1995; Kennicutt & Garnett 1996; van Zee et al. 1998; Bresolin et al. 1999). For comparison, we have plotted in Fig. 4 the same three emission line ratio diagrams for the sample of giant H  II regions in spiral galaxies from McCall et al. (1985).

	Figure 4: Emission line ratio diagrams for the sample of giant H  II regions in spiral galaxies from Mc Call et al. (1985)
Open with DEXTER

The H  II galaxies of our samples clearly appear like an extension of the giant H  II region sequence of McCall et al. toward the high [O  III]/H$\beta$ end and towards the low [N  II]/[O  II] end. Some of the H  II galaxies (mainly in the Terlevich sample) reach values of [N  II]/[O  II] which are as high as those observed in the giant H  II regions of the central parts of spiral galaxies. The true scatter in [O  II]/H$\beta$ is probably smaller than it appears in our figures: as discussed in Sect. 2.3, [O  II]/H$\beta$ is strongly affected by uncertainties in the dereddening procedure. Note the pronounced bending of the [O  III]/H$\beta$ vs. [O  II]/H$\beta$ and [O  III]/H$\beta$ vs. [S  II]/H$\beta$ sequences toward the left at high [O  III]/H$\beta$ in the three H  II galaxies samples. The relation between [N  II]/[O  II] and ([O  II]+[O  III])/H$\beta$ is extremely tight in all the samples we consider. This was also seen in diagrams originally studied by the authors mentioned above. Considering that line ratios in nebulae are determined by several factors (abundance ratios, intensity and spectral distribution of the ionizing radiation field, density distribution of the nebular gas), the question arises as to why the observed sequences are so narrow.

We will try to understand the observational data in the light of the photoionization models described in the next section.

3 The models

   
3.1 Technique and assumptions

The evolutionary synthesis models of Schaerer & Vacca (1998) are used to predict the theoretical spectral energy distributions. They are based on the non-rotating Geneva stellar evolution models, with the high mass-loss tracks of Meynet et al. (1994). The spectral energy distributions for massive main-sequence stars are those given by the CoStar models (Schaerer & de Koter 1997) taking into account the effects of stellar winds, non-LTE, and line blanketing. The pure He models of Schmutz et al. (1992) are used for Wolf-Rayet stars. The spectral energy distributions from the plane-parallel LTE models of Kurucz (1991) are used for the remaining stars which contribute to the continuum.

To illustrate the differences between the ionizing spectra adopted here with the recent Starburst99 models (Leitherer et al. 1999) and the earlier Leitherer & Heckman (1995) models adopted in SL96, we plot the ratio of the He⁰ and He⁺ ionizing photons ( $Q_{\rm He}$, $Q_{\rm He^+}$ respectively) to $Q_{\rm H}$, the number of H ionizing photons issued from various models in Fig. 5. Differences with the Leitherer & Heckman (1995) models (left panel) are mostly due to the updated stellar tracks, which in particular, lead to a shorter Wolf-Rayet (WR) phase in the solar metallicity model shown, and thus to a more rapid decline of the hardness of the ionizing spectrum. From this figure it is also apparent that at solar (and higher) metallicities the changes brought about by recent stellar tracks have a rather important impact on the ionizing fluxes, which affects photoionization models based on the older Leitherer & Heckman (1995) spectra (e.g. SL96, Bresolin et al. 1999). As both the Schaerer & Vacca (1998) and Starburst99 models use the same stellar tracks, the differences (right panel) in the predicted spectra are only due to different treatments of stellar atmospheres. Outside the phases with WR stars (i.e. at ages 3 Myr or 6 Myr), the Schaerer & Vacca spectrum in the He⁰ionizing continuum is somewhat harder due to the use of improved O star model atmospheres (cf. also Schaerer & Vacca 1998, Fig. 5). Differences in the He⁺ ionizing flux (non-negligible during part of the WR phase; cf. Schaerer & Vacca) are due to slightly different assumptions on the link between the stellar evolution and atmosphere models and other numerical differences.

Figure 5: Comparison of the predicted hardness of the ionizing spectra from various evolutionary synthesis models for instantaneous bursts, Salpeter IMF, and different metallicities. Illustrated are the ratios of the He0 and He+ to H ionizing photon fluxes ( $Q_{\rm He}/Q_{\rm H}$ and $Q_{\rm He^+}/Q_{\rm H}$ respectively). a) Schaerer & Vacca (1998, hereafter SV98) models (solid, long-dashed) versus Leitherer & Heckman (1995) models (dashed, dotted) at solar metallicity. b) SV98 models (solid, long-dashed) at 1/5 solar, Leitherer & Heckman (1995) models (dashed, dotted) at 1/4 solar. c) SV98 models (solid, long-dashed) versus Starburst99 models (dashed, dotted) at 1/5 solar. d) Same as c for 1/20 solar metallicity. Discussion in text

Open with DEXTER

As also apparent from Fig. 5, WR stars are predicted to provide a non-negligible fraction of the ionizing flux, especially at high energies during the WR-rich phase, whose duration increases with metallicity (cf. Schaerer & Vacca 1998). The predicted ionizing fluxes are likely more uncertain during these phases, due to 1) the neglect of metals in the WR atmosphere models of Schmutz et al. (1992), and 2) uncertainties in relating the stellar interior and atmosphere models (cf. review by Schaerer 2000). However, while the predicted spectra are possibly too hard at high metallicities (see also Crowther et al. 1999; Bresolin et al. 1999), there are good indications that at low metallicities - of main concern here - the non blanketed WR atmospheres combined with the latest stellar tracks provide a reasonable description of the ionizing spectra (e.g. de Mello et al. 1998; Luridiana et al. 1999; González Delgado & Pérez 2000; Schaerer 2000).

We used the code PHOTO to build the photoionization models, with exactly the same atomic data as in SL96.

3.2 The model grid

We built a wide model grid in order to cover the full parameter space found in our observational samples.

Most models are computed for instantaneous bursts with a Salpeter initial mass function and an upper stellar limit $M_{\rm up}$ = 120 $M_\odot$. The evolution of the burst is followed in time steps of 10⁶ yr, starting from an age of 10⁴ yr. Such a time step may be too long for a detailed description of the Wolf-Rayet stage in the evolution of the burst at metallicities lower than $Z_\odot$/5 (see Schaerer & Vacca 1998), but is a good compromise to cover the evolution until 10 Myr. A second set of models was computed for an upper stellar limit of 30 $M_\odot$ instead of 120 $M_\odot$. Another set of models was built with $M_{\rm up}$ = 120 $M_\odot$ and a Salpeter IMF but for a star formation extended over a period of 10 Myr.

We considered five metallicities: 2, 1, 0.4, 0.2 and 0.02 times the solar metallicity. The metallicities of the stars and the nebular gas are assumed to be the same. As in SL96, the metallicity is defined as the oxygen abundance (oxygen is the main gas coolant). O/H is taken equal to 8.51 10^-4 for the solar abundance set. The abundances of the other elements relative to oxygen are given by the prescription of McGaugh (1991). In particular, He/H = 0.0772 + 15 (O/H) and $\log$ N/O = 0.5 $\log$ (O/H) + 0.4. The ionized gas is assumed to be dust free.

The third main parameter that determines the emission line ratios and equivalent widths of a model is the gas distribution. The photoionization models in our grid are spherically symmetric with constant density, and are ionization bounded. Most models presented in this paper are spheres uniformly filled with gas at a density of n = 10 cm^-3. We also constructed some models represented by hollow spheres with f=3 and n = 200 cm^-3, where f is the inner radius in units of Strömgren radius for a full sphere (see Stasinska & Schaerer 1997). These two extreme cases are intended to highlight the sensitivity of the results on the adopted density distribution. It can easily be shown that such hollow sphere models have the same ionization parameter (averaged over the nebular volume) as the filled sphere models with n = 10 cm^-3 and a total ionizing luminosity 1000 times lower.

Four values of the ionization parameter are considerered: those that would be produced by a star cluster of $M_\star$ = 1, 10³, 10⁶, and 10⁹ $M_\odot$, providing a range in ionization parameters of a factor 1000 at a given epoch. One should realize that our choice of density distribution is quite arbitrary. So far, little is known theoretically or observationally about the systematics of the evolution of the nebular geometry with time in giant H  II regions. Our model sequences are not necessarily meant to describe the true evolution of a giant H  II region with time. For example, it may well be that, due to the combined effects of expansion or stellar winds, the ionization parameter of giant H  II regions decreases with time more than by the sole effect of the decrease of the number of ionizing photons. This was suggested by SL96 from the comparison of a sample of young H  II galaxies with their grid of models. Furthermore, the time variation of the ionization parameter depends on the adopted evolution of the geometry. For example, the ionization parameter U in our models varies as $Q_{\rm H}^{1/3}$ ($Q_{\rm H}$ being the number of stellar photons able to ionize hydrogen per unit time) while in the modelsof García-Vargas & Díaz (1994) and García-Vargas et al. (1995), who constructed shells with a fixed outer nebular radius, Uvaries as $Q_{\rm H}$.

Figures 6, 7 and 8 correspond to our full sphere model sequences for instantaneous bursts with $M_{\rm up}$ = 120 $M_\odot$ and $M_\star$ = 10⁹, 10⁶, and 10³ $M_\odot$, respectively. Figure 9 corresponds to a $M_\star$ = 10⁶ $M_\odot$ burst uniformly extended over a period of 10 Myr. (In this case the time step is 2 Myr instead of 1 Myr.) Figure 10 is for a $M_\star$ = 10⁶ burst with $M_{\rm up}$ = 30 $M_\odot$. Figure 11 corresponds to our hollow sphere model sequences with $M_{\rm up}$ = 120 $M_\odot$ and $M_\star$ = 10⁹ $M_\odot$. Each model is represented by a symbol: circle for $Z/{Z_\odot } = 2$, square for $Z/{Z_\odot } = 1$, triangle for $Z/{Z_\odot } = 0.4$, diamond for $Z/{Z_\odot } = 0.2$ and plus sign for $Z/{Z_\odot } = 0.05$, and the successive models in a sequence are linked by a thin line.

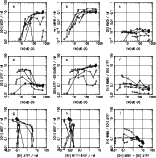Figure 6: Sequences of models for instantaneous bursts ( $M_{\rm up}$ = 120 $M_\odot$, $M_\star$ = 109 $M_\odot$), full sphere geometry, n = 10 cm-3, various metallicities. The metallicity is indicated by the following symbols: circle for $Z/{Z_\odot } = 2$, square for $Z/{Z_\odot } = 1$, triangle for $Z/{Z_\odot } = 0.4$, diamond for $Z/{Z_\odot } = 0.2$ and plus sign for $Z/{Z_\odot } = 0.05$. The symbols mark time steps of 1 Myr

Open with DEXTER

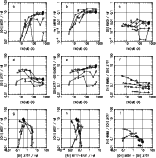	Figure 7: Same as Fig. 6 but for $M_{\rm up}$ = 120 $M_\odot$, $M_\star$ = 106 $M_\odot$
Open with DEXTER

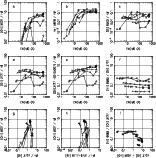	Figure 8: Same as Fig. 6 but for $M_{\rm up}$ = 120 $M_\odot$, $M_\star$ = 103 $M_\odot$
Open with DEXTER

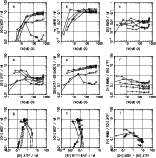	Figure 9: Same as Fig. 7, $M_{\rm up}$ = 120 $M_\odot$, $M_\star$ = 106 $M_\odot$, but for an extended burst (duration 10 Myr). Same symbols as in Fig. 7 but with time steps of 2 Myr
Open with DEXTER

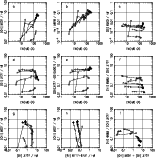	Figure 10: Same as Fig. 6 but for $M_{\rm up}$ = 30 $M_\odot$, $M_\star$ = 106 $M_\odot$
Open with DEXTER

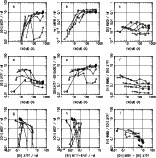	Figure 11: Sequences of models for instantaneous bursts ( $M_{\rm up}$ = 120 $M_\odot$, $M_\star$ = 109 $M_\odot$), hollow sphere geometry, n = 200 cm-3, various metallicities. These models have the same average ionization parameter as the models of Fig. 7. Same symbols as in Fig. 5
Open with DEXTER

It is important to realize that, while the model predictions for optical forbidden lines like [O  III] $\lambda$5007, [O  II] $\lambda$3727, [N  II] $\lambda$6584 are relatively robust and accurate for metallicities below solar, the situation worsens as one goes to higher metallicities. The reason is that, as metallicity increases, cooling by heavy elements becomes more and more important, and is gradually shifted from the optical forbidden lines to the fine structure, infrared lines, which have lower excitation potential. The emissivities of the infrared lines are little dependent on the electron temperature. As a consequence, the computed value of the electron temperature, obtained by equating the energy gains and losses of the electrons, strongly depends on the computed energy loss. Therefore, any small variation in the energy loss will induce an appreciable change in the emission of the optical forbidden lines. For example, since the infrared fine structure lines are easily collisionally de-excited, any gas clump of density above 500 cm^-3will induce collisional de-excitation of the infrared cooling lines, boosting the [O  III] $\lambda$5007 line. Another problem is that in many cases photoionized gas at temperatures below $\sim$5000 K is thermally unstable. Thus the temperatures computed in photoionization models do not reflect the whole range of temperatures that can be found in real objects. For these reasons the predicted intensities of the models with $Z/{Z_\odot} > 1$ (corresponding to O/H = 8.51 10^-4 as stated above) are less accurate than those of lower metallicity models. Another notorious problem of high metallicity models is that the intensities of optical forbidden lines, especially from the low ionization species, are very dependent on the amount of metals trapped in dust grains (Henry 1993; Shields & Kennicutt 1995). Our reference grids of models assume no depletion, although we have constructed additional models with only one tenth of the metals in the gas phase (see Sect. 4.3).

4 Observations versus models

We first analyze diagnostic diagrams involving the H$\beta$ equivalent width. The classical, pure emission line ratio diagnostic diagrams will be discussed subsequently.

4.1 Diagnostic diagrams with equivalent widths

The observed samples of H  II galaxies, and giant H  II regions in general, are characterized by a very narrow range in ionization parameters. This was already noted before from a comparison of observed diagrams with model grids (McCall et al. 1985; Dopita & Evans 1986; García-Vargas & Díaz 1994; García-Vargas et al. 1995; Stasinska & Leitherer 1996; Bresolin et al. 1999; Dopita et al. 2000). We show in Fig. 12 the values of [O  III]/[O  II] as a function of $EW({\rm H}\beta )$ for models with $M_\star$ = 1, 10³, 10⁶ and 10⁹ $M_\odot$ and metallicity 0.2 $Z_\odot$ (corresponding to a range of a factor 10 in U between each curve) superimposed on the Terlevich data. For $EW({\rm H}\beta )$ > 100 Å, the observed dispersion in [O  III]/[O  II] suggests a range in ionization parameters of about a factor 10. Most of the data are bracketed by the series with $M_\star$ = 10³ and 10⁶ $M_\odot$ (corresponding roughly U $\sim$ 1-2 10^-3 and to U $\sim$ 1-2 10^-2, for the first 5 Myr). At lower equivalent widths, the observations fall outside the predicted values, apparently indicating a much higher U. As we will show below, this would be a premature conclusion.

If H  II galaxies are powered by coeval star clusters, one expects the [O  III] $\lambda$5007/H$\beta$ ratio to decrease as time goes by and $EW({\rm H}\beta )$ decreases. Panels a in Figs. 6-11 show the predictions for [O  III] $\lambda$5007/H$\beta$ as a function of $EW({\rm H}\beta )$. All the sequences show a steep decline of [O  III] $\lambda$5007/H$\beta$ at an $EW({\rm H}\beta )$ around 20 Å, irrespective of metallicity. A similar effect was predicted by the models of SL96. This is due to the average effective temperature of the exciting stars (as roughly expressed by $Q_{\rm He^0}/Q_{\rm H}$) dropping much more rapidly than the total number of ionizing photons, once the most massive stars have disappeared. The rise in the curves in Figs. 6-11 prior to the final steep decline for the Z=2 $Z_\odot$ and $Z_\odot$ models is due to the appearance of Wolf-Rayet stars. The sequences of models with $M_{\rm up}$ = 30 $M_\odot$ show a strong accumulation of points at early ages since it takes stars with masses below 30 $M_\odot$ more than 4 Myr to evolve off the main-sequence. The drop in [O  III] $\lambda$5007/H$\beta$ at $EW({\rm H}\beta )$ smaller than 20 Å is of course the same as for the $M_{\rm up}$ = 120 $M_\odot$ sequences. The sample of H  II galaxies in the SL96 study had $EW({\rm H}\beta )$ too large to show this drop, as a consequence of the requirement on [O  III] $\lambda$4363, as stated in the introduction. Since no such restriction was applied here, the values of $EW({\rm H}\beta )$ go down to a few Angströms. The data in each sample have a tendency to a decrease of [O  III] $\lambda$5007/H$\beta$ with decreasing $EW({\rm H}\beta )$. This decrease, however, is rather mild and the scatter in [O  III] $\lambda$5007/H$\beta$ increases for lower $EW({\rm H}\beta )$. One might think that extending the star formation over a longer period would help to reconcile the predicted trends with the observations. However, Fig. 9 suggests that even considering a constant star formation during 10 Myr is not sufficient to produce the large [O  III]/H$\beta$ observed at $EW({\rm H}\beta )$ of 20 Å or smaller.

A similar effect is seen in the He  I $\lambda$5876/H$\beta$ versus $EW({\rm H}\beta )$ diagrams (panels b). In contrast to [O  III]/H$\beta$ which, for a given stellar radiation field depends on U and Z, He  I $\lambda$5876/H$\beta$ is independent of the ionization parameter and depends only weakly on metallicity (in the sense that at larger metallicities a lower electron temperature increases He  I $\lambda$5876/H$\beta$). Instantaneous starburst models predict a sharp drop in He  I $\lambda$5876/H$\beta$ at $EW({\rm H}\beta )$ around 20 Å. This is not seen in any of the observed samples. The observed He  I $\lambda$5876/H$\beta$ ratio in the Terlevich sample remains remarkably constant around a value of 0.1. The slight rise and the increasing dispersion at low $EW({\rm H}\beta )$ could be due to observational errors, He  I $\lambda$5876 being a weak line. Unfortunately, this line is measured in only 98 out of 305 objects, and one might argue that the remaining objects have a much lower He  I $\lambda$5876/H$\beta$ ratio. All the objects in the Izotov sample have the He  I $\lambda$5876 intensity measured with very good accuracy, and all except one are of the order of 0.1. Although the statistics are very poor, since only 10 objects in the Izotov sample have $EW({\rm H}\beta )$ of the order of 20 Å or smaller, there seems to be no drop of He  I $\lambda$5876/H$\beta$ at this $EW({\rm H}\beta )$. The Popescu & Hopp sample shows the same behavior as the Terlevich sample.

	Figure 12: Objects from the Terlevich sample superimposed on sequences of instantaneous burst models ( $M_{\rm up}$ = 120 $M_\odot$, $M_\star$ = 1, 103, 106 and 109 $M_\odot$), full sphere geometry, n = 10 cm-3 metallicity $Z/{Z_\odot } = 0.2$
Open with DEXTER

The presence of an older underlying stellar component in H  II galaxies, as supported by many studies based on infrared colors and stellar features, changes the interpretation of the diagrams. It would decrease the H$\beta$ equivalent width of the young, ionizing population ("dilution'' effect), and also lead to an underestimate of the nebular H$\beta$ luminosity due to underlying stellar absorption. Qualitatively, these effects work in the direction required to reconcile models and observations. Such an explanation is suggested by a recent study of Raimann et al. (2000a). These authors grouped 185 spectra from the Terlevich et al. (1991) paper into 19 templates in order to increase the signal-to-noise and to allow a population synthesis analysis from the absorption features. They found that H  II galaxies are age-composite stellar systems, and that they can contain a significant population of stars with ages larger than 10 Myr. In Fig. 13 we plotted the same quantities as in Figs. 1-3 for the spectral groups defined by Raiman et al. (2000a) (excluding the 3 groups corresponding to Seyferts which are not discussed in the present paper). Open circles represent the averaged observed spectra. Each open circle is linked by a straight line with a filled circle representing the data after correction for an underlying stellar population (line and continuum) and for internal reddening. The same trends with $EW({\rm H}\beta )$ are seen for the filled circles as for the data shown in Figs. 1-3, but with larger slopes. The drop in [O  III]/H$\beta$ starts at much higher values of $EW({\rm H}\beta )$. This is much more compatible with our models than the uncorrected data. The steep decline starts immediately, which seems to be in better agreement with our models with $M_{\rm up}$ = 30 $M_\odot$ (Fig. 10) than with 120 $M_\odot$. However, the distribution of the open circles in the [O  III]/H$\beta$ versus $EW({\rm H}\beta )$ diagram of Fig. 13 is quite different from the distribution of the individual galaxies from the Terlevich sample (Fig. 1); therefore this averaged sample is unsuitable for describing the general properties of H  II galaxies. The important point is that the work of Raimann et al. (2000a,b) demonstrates that signatures of older underlying stellar populations are present in the spectra of H  II galaxies and can explain the observed trend in the uncorrected [O  III]/H$\beta$ versus $EW({\rm H}\beta )$ diagrams of Figs. 1-3. The multiwavelength analysis of 17 H  II galaxies by Mas-Hesse & Kunth (1999) reached a similar conclusion. Using indicators of young stellar populations (the UV continuum, the stellar + interstellar W(Si  IV)/W(C  IV) ratio, the strength of the Wolf-Rayet bump), these authors conclude that the majority of these galaxies have experienced recent nearly instantaneous star formation dominating the ultraviolet light. Yet their synthetic spectra are often below the observed visible continuum, indicating the presence of an older stellar population.

Other causes may contribute to the behavior of [O  III]/H$\beta$ and He  I $\lambda$5876/H$\beta$ as a function of $EW({\rm H}\beta )$ as well. For example, H  II regions may become gradually density bounded or the covering factor may decrease with time. A lower covering factor decreases the H$\beta$ luminosity and thus $EW({\rm H}\beta )$. Allowing for leakage of ionizing photons from the outskirts of the emitting region maintains [O  III]/H$\beta$ and He  I $\lambda$5876/H$\beta$ at a high level. This is an attractive possibility, since as nebulae expand, they become less and less opaque to ionizing photons (for a homogeneous gas sphere, the mass that can be ionized changes as $Q_{\rm H}/n$). Alternatively, it is possible that most of the giant H  II regions in the samples are density bounded or have a covering factor smaller than 1, regardless of their evolutionary state. Another possibility is that the spectroscopic data encompass only part of the nebula (for simplicity, we will refer to these explanations as the "aperture effect''). Such "aperture effects'' are likely to occur in our H  II galaxy samples. A detailed study of the H  II galaxy I Zw 18 indicates that the brightest H  II region, which dominates the spectrum, is density bounded, at least in some directions (Stasinska & Schaerer 1999). This could be a general property since diffuse or filamentary ionized gas has been observed at large distances in a number of H  II galaxies (e.g., Hoopes et al. 1996; Martin 1997; Hunter & Gallagher 1997), implying that the data in this paper may be missing part of the distant low-ionization gas.

High values of [O  III]/H$\beta$ and He  I $\lambda$5876/H$\beta$ at low $EW({\rm H}\beta )$ could also result if the extinction of the ionized gas is systematically higher than that of the stellar light, as found in several studies of H  II galaxies and starbursts (e.g. Fanelli et al. 1988; Calzetti 1997; Mas-Hesse & Kunth 1999; Schaerer et al. 2000).

To summarize, simple photoionization models of H  II galaxies as pure evolving starbursts cannot entirely account for the observed diagrams involving $EW({\rm H}\beta )$ (panels a-d) of Figs. 1-3. One or more of these effects are likely explanations: (i) an older stellar population; (ii) starlight systematically suffering a smaller extinction than ionized gas; or (iii) an aperture effect where the observed spectra correspond to density bounded nebulae or nebulae with a covering factor smaller than 1. These interpretations explain in a natural way the absence of H  II galaxies with $EW({\rm H}\beta )$ larger than 400 Å in objective prism surveys, whereas starburst models for ionization bounded H  II regions predict values of up to 700 Å (see also discussion in SL96). This also implies that such surveys are biased against galaxies where the latest starbursting episode is older than about 5 Myr, as such objects would tend to have too weak H$\beta$ and H$\alpha$ emission lines to be detected.

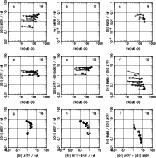	Figure 13: Groups of H  II galaxies as defined by Raimann et al. (2000a) from the Terlevich et al. (1991) catalogue. Open circles: the averaged spectra as used by Raiman et al. (2000a); filled circles: the same after correction for underlying stellar population and internal reddening
Open with DEXTER

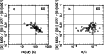	Figure 14: Comparison of the trends for [O  I]/([O  II]+[O  III]) as a function of $EW({\rm H}\beta )$ and O/H for the 60 objects with measured [O  III] $\lambda$4363 of the Izotov sample
Open with DEXTER

How can these explanations be reconciled with the increase of [O  I]/H$\beta$ as $EW({\rm H}\beta )$ decreases (panels c in Figs. 1-3)? This trend is also present in the corrected template spectra from Raimann et al. (Fig. 13), but the number of points is small and confirmation on a larger sample is required. One could argue that the old underlying population is stronger in higher metallicity objects, so that the increase in [O  I]/H$\beta$ with decreasing $EW({\rm H}\beta )$ could be attributed to a metallicity effect. We can test this idea by plotting [O  I]/([O  II]+[O  III]) as a function of O/H for the 60 objects with measured [O  III] $\lambda$4363 of the Izotov sample. This is done in panel b of Fig. 14. Panel a of this figure shows the same objects in the [O  I]/([O  II]+[O  III]) vs. $EW({\rm H}\beta )$ plane. Clearly, the metallicity effect is not a good explanation. Also, the behavior of [O  I] cannot be explained by the "aperture effect'' discussed above. Reducing the covering factor while keeping the nebulae ionization bounded does not change the [O  II]/H$\beta$ and [O  I]/H$\beta$ ratios. Making the nebulae density bounded reduces the ratios. Note that the observed behavior of [O  I]/H$\beta$ with $EW({\rm H}\beta )$ argues in favor of $EW({\rm H}\beta )$ remaining a statistical age indicator (although the age cannot be obtained by a direct comparison with photoionization models for pure starbursts). As pointed out by by Stasinska & Schaerer (1999) in the case of I Zw 18, strong [O  I] emission is easily produced by photoionization models in dense filaments which may contribute only marginally to the total emission in the other lines. Possibly, giant H  II regions are globally density bounded but contain high density filaments. Such filaments could be produced by shock-wave compression or instabilities, induced by stellar winds and supernovae whose effects are expected to increase with time.

4.2 On the strong line method to derive oxygen abundances

An important consequence of these observational selection effects in H  II galaxy samples is that the age of the ionizing population has little influence on the observed ([O  III]+[O  II])/H$\beta$ ratio (see panel e in Figs. 6-9). Combined with the narrow range of U in giant H  II galaxies (cf. panels a of Figs. 1-3 and  6-11), this explains a posteriori why strong line methods based on ([O  III]+[O  II])/H$\beta$ and methods utilizing the electron temperature lead to similar oxygen abundance estimates in these objects (Pilyugin 2000). A priori one would have expected large differences induced by the temporal variation of the ionizing radiation field during the evolution of a starburst.

Figure 15 shows how the [O  III]/[O  II] vs. ([O  III]+[O  II])/H$\beta$ diagram (introduced by McGaugh 1991, 1994 to derive O/H and U at the same time) changes over a period of 4 Myr. Continuous lines join models with equal metallicities (the thickest lines correspond to the most metal rich cases), dotted lines join models with equal M_*. Panels a, b, c correspond to starburst ages of .01, 2.01 and 4.01 Myr, respectively. The objects from the Terlevich sample are overlaid in the three panels. We see that the theoretical diagrams at metallicities lower than half solar evolve little over this period, demonstrating the applicability of the strong line method at these metallicities. In practice, it is however preferable to calibrate the method not on models but empirically with a sample of high signal-to-noise observations of H  II galaxies, as done by Pilyugin (2000).

Figure 15: Evolution of the McGaugh (1991) diagram over a period of 4 Myr for our instantaneous burst models ( $M_{\rm up}$ = 120 $M_\odot$), full sphere geometry, n = 10 cm-3. Models with equal metallicities are linked by full lines (whose thickness is proportional to the metallicity). Models with equal M* are linked with dotted lines. Panels a), b), c) correspond to starburst ages of .01, 2.01 and 4.01 Myr, respectively Superimposed are the objects from the Terlevich sample

Open with DEXTER

Interestingly, as already pointed out by Stasinska (1999), rapid evolution of the McGaugh (1991) diagram is, however, predicted at metallicities solar, due to important changes in the hardness of the stellar radiation field at such metallicities, and due to the strong impact on optical line ratios. This behavior of the stellar radiation field at large metallicity is due to the fact that the overall main sequence is shifted toward lower temperatures, and thus the temperature of the stars falls below 40 kK earlier, as the hardness measured by $Q_{\rm He}/Q_{\rm H}$ decreases rapidly. This explains the more rapid decrease of the hardness of the ionizing flux of stellar populations at high metallicity (cf. Schaerer & Vacca 1998; Leitherer et al. 1999). Therefore at metallicities around solar or above (where electron temperature based methods cannot be used), the results from strong line methods to derive the oxygen abundance are likely to be rather inaccurate.

We also emphasize that strong line methods are statistical, as compared to electron temperature methods. They should be used with caution in cases when a systematic variation in the starburst properties or the gas density distribution is expected. This applies to studies of environmental effects on metallicities, e.g., such as those of giant H  II regions seen in tidal tails of galaxies (Duc & Mirabel 1998) or H  II galaxies in the core of galaxy clusters (Vílchez 1995) as compared to isolated H  II galaxies.

4.3 Pure emission line ratio diagnostic diagrams

Next we consider classical diagnostic diagrams which exclusively rely on line ratios. To a first approximation, such diagrams depend only on the population of the most massive stars which produce the ionization. They have been extensively studied for giant H  II regions in spiral galaxies and, as mentioned in Sect. 2.4, it has been found that [O  III]/H$\beta$ versus [O  II]/H$\beta$, or [O  III]/H$\beta$ versus [O  II]/[O  III] define a very narrow sequence, called the H  II region sequence. This sequence was analyzed with the help of photoionization models and has been interpreted as a sequence in metallicity with effective temperature/ionization parameter varying in line with metallicity (McCall et al. 1985; Dopita & Evans 1986; Dopita et al. 2000).

Since H  II galaxy samples are believed to contain mostly low-metallicity objects, it is not surprising that the H  II galaxy sequences shown in Figs. 1-3 a are less populated at the low [O  III]/H$\beta$ end than the McCall et al. (1985) or van Zee et al. (1998) sequences, and that they extend to high [O  III]/H$\beta$.

Although some of the observed trends are met by the predictions, it is, nevertheless, apparent from Figs. 6-11 that our models do not reproduce the sequence very well. Compared to other classical diagnostic diagrams, the [O  III]/H$\beta$ vs. [O  II]/H$\beta$ diagram has the advantage of being independent of the abundances ratios of O/N or O/S. Therefore we will focus our discussion on this diagram, but the conclusions are similar for the [O  III]/H$\beta$ vs. [S  II]/H$\beta$ diagram. Diagrams involving [N  II] are discussed in Sect. 4.4.

Excluding the 2 $Z_\odot$ and $Z_\odot$ sequences (models represented by squares and circles), which are not representative of the bulk of the objects in our samples, the parameter space occupied by the models in the diagram does not exactly match the observations. First, our model sequences predict an almost vertical drop in the [O  III]/H$\beta$ vs. [O  II]/H$\beta$ diagram, and the maximum [O  II]/H$\beta$ is almost independent of the ionization parameter. This is due to oxygen mainly being in the form of O⁺when the most massive stars have disappeared. Since we have argued above that our H  II galaxies sample should contain few, if any, galaxies with the most recent starburst older than 5 Myr, our observational diagrams should be compared to the model sequences until 5 Myr only (roughly corresponding to $EW({\rm H}\beta )$ 50 Å in Figs. 6-11).

Even with that restriction, our photoionization models are unable to reproduce [O  II]/H$\beta$ ratios larger than 4 and the kink at [O  III]/H$\beta$ > 4 and [O  II]/H$\beta$ > 2. Moreover, the problem may become even worse if the model spectra used for the Wolf-Rayet phase were too hard (cf. Sect. 3.1). We have computed supplementary photoionization models especially for this purpose (including depletion of metals on grains or heating by X-rays), but without success. The disagreement becomes even larger if we assume that H  II galaxies are density bounded, as argued above. Whether additional heating sources (shocks, conduction, turbulence) may solve the problem is an open question.

Dopita et al. (2000) compared an observed sample of giant regions in spiral galaxies with photoionization models and found that their models could not reproduce the high [O  I]/H$\beta$ and [S  II]/H$\beta$ ratios seen in some objects, invoking shocks as an explanation. Our models use a different prescription for the density structure than those of Dopita et al. and differ also in other respects, such as numerical aspects and the N/O vs. O/H prescription. Still, we find that the problems exists not only for [O  I]/H$\beta$ and [S  II]/H$\beta$ but also for [O  II]/H$\beta$. Of course, the observed [O  II]/H$\beta$ ratio is largely affected by the dereddening procedure, while this is much less the case for the other two ratios. Since strong line diagnostics heavily rely on [O  II], and since this line is becoming increasingly important for the study of galaxies at high redshift, it would be useful to better constrain the problem by a detailed observational and theoretical study of those few H  II galaxies with a firm indication of shock excitation.

McCall et al. (1985) argued that giant H  II regions must be mostly ionization bounded, otherwise one would not observe such a tight sequence in emission line ratio diagrams. This is at variance with the fact that we now know that a fair portion of Lyman continuum radiation is leaking out of H  II regions (Martin 1997; Stasinska & Schaerer 1999; Beckman et al. 2000). However, if the density structure of giant H  II regions were driven by the mechanical action of winds and supernovae explosions from their embedded stellar populations, one could understand why there is so little dispersion among giant H  II regions in such diagrams, even if they are partially density bounded, since the driving parameter would boil down to the stellar population itself. In this respect, hydrodynamic modelling of the ionization structure of giant H  II regions (the follow-up of the single star H  II region modelling performed by Rodriguez-Gaspar & Tenorio-Tagle 1998) would be extremely important.

   
4.4 The N/O ratio

Among others, Kunth & Sargent (1986), Pagel et al. (1986, 1992), Olofsson (1995b) suggested that gas might be chemically enriched in, e.g., helium and nitrogen from the winds of Wolf-Rayet stars during the evolution of giant H  II regions. Traces of such a local pollution have been found in the irregular galaxy NGC 5253 from imaging spectroscopy (Walsh & Roy 1987, 1989; Kobulnicky et al. 1997), but other attempts to detect local N/O enhancement in Wolf-Rayet galaxies have failed (Kobulnicky & Skillman 1996, 1998; Kobulnicky 1999). Moreover, Izotov et al. (1997) and Kobulnicky & Skillman (1996) analyzed observational data on H  II galaxies in the literature and found that galaxies with strong Wolf-Rayet features in their integrated spectra exhibited the same N/O ratios as the remaining galaxies at identical O/H ratios, contrary to the claim of Pagel et al. (1986, 1992).

In the light of these previous studies, the [N  II]/[O  II] vs. $EW({\rm H}\beta )$ diagram is revealing. There is a definite trend of [N  II]/[O  II] strongly increasing as $EW({\rm H}\beta )$ decreases in all our H  II galaxy samples. If we take [N  II]/[O  II] as an indicator of N/O, it is tempting to attribute this trend to an increase in N/O as the ionizing starburst gets older. However, several biases must be examined first. Could the observed relation be the result of a selection effect? While the absence of low [N  II]/[O  II] ratios at small equivalent widths could be attributed to selection effects against the weakest lines, at large H$\beta$ equivalent widths, values of [N  II]/[O  II] larger than $\sim$0.2-2 should be observed if such objects exist. Moreover, there is no selection effect in the Izotov sample since all the objects appear in Fig. 2f, and the relation is seen there as well. The trend is less distinct than in the other samples, probably because the sample is weighted towards the most metal poor galaxies. Finally, as mentioned in Sect. 2.4, if a complete subsample is extracted from the Terlevich sample, the observed relation between [N  II]/[O  II] and $EW({\rm H}\beta )$ remains. Therefore, the observed relation cannot be attributed to a simple selection effect.

Turning to an interpretation, it is important bearing in mind that [N  II]/[O  II] does not only depend on N/O but also on the electron temperature. It is larger at lower electron temperatures and therefore at higher O/H for a given N/O. Second, at metallicities above solar, the [N  II] and [O  II] lines are produced by recombination rather than by collisional excitation (if the N⁺⁺/N⁺ and O⁺⁺/O⁺ratios in the nebula are not close to zero). Our models (panels f in Figs. 6-11) do account for that. We have already argued that models with ages 5 Myr may not be relevant to our samples of H  II galaxies, but that $EW({\rm H}\beta )$ is an indicator of the age of the ionizing starburst (in the sense that smaller $EW({\rm H}\beta )$ correspond to larger ages). We have also argued that one should perhaps consider density bounded rather than ionization bounded models. However, the [N  II]/[O  II] ratio would remain unchanged in a density bounded model. The large values of [N  II]/[O  II] ( 0.3) seen in some of the H  II regions of our samples therefore indicate a N/O ratio larger than the largest predicted by our models (0.1 at $Z = 2\ {Z_\odot}$).

If the metallicities (i.e., O/H ratios) in our samples have identical distributions in each age bin, the observed trend could be explained if the two following conditions hold at the same time: (i) the relation between N/O and O/H is steeper than the relation based on McGaugh (1991) adopted in our models and (ii) the most metal rich objects are those whose $EW({\rm H}\beta )$ values are the most affected by the contribution of an old stellar population. The first hypothesis might indeed be true. There are indirect indications, from studies of giant H  II regions in spiral galaxies, that at high metallicities N/O increases more rapidly than N/O $\alpha$ (O/H)^0.5 adopted in our models (cf. van Zee et al. 1998; Henry et al. 2000). The second hypothesis appears quite reasonable. Earlier generations of stars are necessary to produce the bulk of presently observed O/H in more metal rich H  II galaxies, and these earlier generations still contribute to the continuum. Qualitatively, the results of Raimann et al. (2000b) support this picture. We note however that the anticorrelation between [N  II]/[O  II] and $EW({\rm H}\beta )$ subsists in the Raimann et al. templates even after correction for the old stellar population (Fig. 13f). If this effect is real, it calls for an additional explanation.

N/O might be increasing with time. Such an explanation would be more compatible with the observed [N  II]/[O  II] versus ([O  II]+[O  III])/H$\beta$ diagram in Figs. 1-3i, in which the scatter in ([O  II]+[O  III])/H$\beta$ at a given [N  II]/[O  II] is extremely small. Models with ages smaller than 5 Myr (panels i in Figs. 6-11) show about the same scatter, but in order to compare with observations a convolution of the theoretical scatter with observational errors, and a correction for reddening and underlying H$\beta$ absorption is first required. With N/O increasing with time, the theoretical scatter at a given [N  II]/[O  II] becomes smaller. The hypothesis of N/O increasing with time can in principle be checked directly by plotting the N/O determined by electron temperature based methods as a function of $EW({\rm H}\beta )$. We performed this test. No obvious trend is seen, but none of the objects with large observed [N  II]/[O  II] in our samples has [O  III] $\lambda$4363 measured, so this test is not conclusive.

Deep spectroscopy for a detailed analysis of the stellar populations in the objects showing high [N  II]/[O  II] ratios should be obtained. High resolution emission line imaging and tailored photoionization modeling should also be undertaken, in order to put the strongest possible constraints on O/H and N/O in these objects.

5 Conclusions

We have reanalyzed the emission line properties of three large samples of H  II galaxies taken from the literature (Terlevich et al. 1991; Izotov and collaborators 1994-2000; Popescu & Hopp 2000) with the aim of studying the temporal evolution of these objects during the lifetime of the ionizing stars ( 10 Myr). We have constructed a series of diagrams using observed emission line ratios and equivalent widths, and found significant trends.

We interpreted these trends with photoionization models for integrated stellar populations. This study extends the work of Stasinska & Leitherer (1996), by including objects with no direct metallicity determination and using updated evolutionary tracks and atmospheric models.

The changes brought about by the inclusion of the latest non-rotating Geneva stellar evolution models and the CoStar non-LTE line blanketed atmosphere models including stellar winds for O stars have been summarized in Sect. 3.1. (cf. Fig. 5). These models have been successfully compared to observations in a large variety of studies related to massive stars (see e.g. Maeder & Meynet 1994; Stasinska & Schaerer 1997; Oey et al. 2000; Schaerer 2000). Despite this, the adopted models have also some known weaknesses, e.g. the neglect of stellar rotation leading to modifications of the stellar tracks (cf. Maeder & Meynet 2000), a possible overestimate of the hardness of the ionizing flux above $\sim$40 eV (Oey et al. 2000), or the lack of line blanketing in WR atmospheres (see Sect. 3.1). Essentially, the main dependence of the photoionization models on the stellar input physics enters through 1) the evolutionary timescales and the temperatures of main sequence O stars, and 2) the hardness of the He⁰/H ionizing spectrum. It is important to note that, while detailed outputs from photoionization models are sensitive to the exact stellar input physics, our main conclusions summarized below are quite robust.

The underlying principle of the comparison between models and observations is that the metallicity distribution is age-independent for sufficiently large and homogeneous samples, despite the fact that the metallicities of individual objects may be a priori unknown.

We have shown that H  II galaxies selected by objective-prism surveys do not correspond to the simplistic view of instantaneous starbursts surrounded by constant density, ionization bounded H  II regions. The observed relations between emission line ratios and H$\beta$ equivalent width can be understood if most H  II galaxies contain older stellar populations contributing, sometimes rather significantly, to the observed optical continuum. This is in line with the recent findings of Raimann et al. (2000a,b) who, from a spectroscopic analysis on the stellar features in very high signal-to-noise templates of H  II galaxies, showed that populations as old as 100 Myr and up to a few Gyr are detectable in the spectra and significantly affect the observed H$\beta$ equivalent widths. This is also consistent with the model of a long lasting low level of star formation in I Zw 18, as suggested by Legrand (1999). Two additional mechanisms may play a role. First, stars seem to suffer a smaller dust obscuration in the visible light than the ionized gas. Second, some Lyman continuum radiation is probably leaking out of most of the nebulae encompassed by the observing slits.

The combination of these effects reduces $EW({\rm H}\beta )$ with respect to the value predicted for an instantaneous starburst surrounded by an ionization bounded nebula. Therefore objective-prism selected samples of H  II galaxies are unlikely to contain significant numbers of starbursts older than about 5 Myr. Older stages in the evolution of starbursts must be selected from photometric surveys based on broad- or narrow-band colors.

An interesting consequence of this selection effect is that the strong line methods for deriving oxygen abundances work rather well in metal poor H  II galaxies because there is no large mean effective temperature spread. Under these conditions, a strong line method which is calibrated on objects with electron temperature based oxygen abundances determinations like that proposed by Pilyugin (2000), is the most valid approach to derive oxygen abundances in low signal-to-noise spectra of H  II galaxies. One must, however, keep in mind the statistical nature of this method and the fact that the unknown stellar absorption in H$\beta$ provides a further source of uncertainty.

We have shown that [O  I]/H$\beta$ uniformly increases with decreasing $EW({\rm H}\beta )$. This behavior suggests that this line ratio results from dynamical effects that shape the nebula and whose importance increases with time. These dynamical effects could also be responsible for the small range in ionization parameters that account for the observed emission line trends.

The classical emission line ratio diagnostic diagrams such as [O  III]/H$\beta$ vs. [O  II]/H$\beta$ imply a sequence in oxygen abundance and ionization parameter. This suggestion was made earlier on the basis of single-star photoionization models, but a physical interpretation remains elusive. Extra heating sources in addition to the Lyman continuum radiation from massive stars seem necessary in order to explain the largest observed [O  II]/H$\beta$ ratios.

The [N  II]/[O  II] ratio is shown to increase as $EW({\rm H}\beta )$ decreases. The observed trend is even stronger when considering the sample of high signal-to-noise H  II galaxy templates of Raimann et al. (2000a,b) after correction for the old stellar population. We conclude that either the relation between N/O and O/H is steeper than that adopted in our models (N/O $\propto$ O/H^0.5) and the underlying stellar population is stronger at higher metallicities, or the N/O ratio increases with time on a time scale of $\sim$5 Myr. This last option would support a scenario of self-pollution of giant H  II regions by nitrogen produced in situ. High signal-to-noise observations to directly uncover the old stellar populations and the H$\beta$ contamination in individual objects, especially those with the highest [N  II]/[O  II] ratios, are required to settle this important issue. The possible dependence of the above findings on the various main unknowns (underlying populations, escape of Lyman continuum photons, non stellar heating sources, etc.) affecting our analysis have been discussed in the respective sections. Luckily, not all the problems raised in this study are interconnected, and they may be attacked from various angles. E.g. our claim of underlying populations being responsible for an effective "age bias'' against burst events with ages 5 Myr and the puzzling behavior of [N  II]/[O  II] can be tested by additional and more detailed stellar population studies of H  II galaxies along the lines of Raimann et al. (2000a,b), using high signal-to-noise spectroscopy. A purely "stellar'' solution seems now clearly excluded for the problem of [O  III]/H$\beta$ vs. [O  II]/H$\beta$ as well as [S  II]/H$\beta$ (Sect. 4.3 and Stasinska & Schaerer 1999). Hydrodynamical models of the interaction of the interstellar medium with clusters of hot stars (in the vein of Cantó et al. 2000 or Franco et al. 2000) combined with photoionization calculations, should allow one to propose quantitative solutions. Such an approach may at the same time explain the behavior of [O  I]/H$\beta$ as a function of $EW({\rm H}\beta )$ and provide some quantitative estimate of the leakage of ionizing photons from giant H  II regions. Multi-wavelength high spectral resolution observations should provide important constraints to the models in this respect. The dust obscuration issue is perhaps trickier, since dust effects are extremely dependent on geometry. Here, systematic high resolution imaging of giant H  II regions, such as performed by Calzetti et al. (1997) or Johnson et al. (2000), should allow one to clarify the dust location and its effect on integrated H  II galaxies spectra. The insight gained from this study and the proposed directions for further theoretical and observational investigations will considerably increase our understanding of the physics of H  II regions and the complex interactions between its stellar and interstellar components.

Acknowledgements

We thank E. Telles for sending us the list of objects in the Terlevich sample that proved to be giant H  II regions in spiral galaxies. We thank D. Raimann for sending us unpublished data that were required to construct Fig. 13.

References

 

• Beckman, J. E., Rozas, M., Zurita, A., Watson, R. A., & Knapen, J. H. 2000, AJ, 119, 2728 In the text NASA ADS  
• Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 In the text NASA ADS  
• Bresolin, F., Kennicutt Jr., R. C., & Garnett, D. R. 1999, ApJ, 510, 104 In the text NASA ADS  
• Calzetti, D. 1997, in The Ultraviolet Universe at Low and High Redshift: Probing the Progress of Galaxy Evolution, ed. W. H. Waller et al., AIP Conf. Proc., 408, 403 In the text In the text  
• Calzetti, D., Meurer, G. R., Bohlin, R. C., et al. 1997, AJ, 114, 1834 NASA ADS  
• Cantó, J., Raga, A. C., & Rodriguez, L. F. 2000, ApJ, 536, 896 In the text NASA ADS  
• Crowther, P. A., Pasquali, A., de Marco, O., et al. 1999, A&A, 350, 1007 In the text NASA ADS  
• Davidson, K., & Kinman, T. D. 1985, ApJS, 58, 321 In the text NASA ADS  
• de Mello, D. F., Schaerer, D., Heldmann, J., & Leitherer, C. 1998, ApJ, 507, 199 In the text NASA ADS  
• Dopita, M. A., & Evans, I. N. 1986, ApJ, 307, 431 In the text NASA ADS  
• Dopita, M. A., Kewley, L. J., Heisler, C. A., & Sutherland, R. S. 2000, ApJ, 542, 224 In the text NASA ADS  
• Dottori, H. A. 1981, Ap&SS, 80, 267 In the text NASA ADS  
• Duc, P.-A., & Mirabel, I. F. 1998, A&A, 333, 813 In the text NASA ADS  
• Fanelli, M. N., O'Connell, R. W., & Thuan, T. X. 1988, ApJ, 334, 665 In the text NASA ADS  
• Franco, J., Garcia-Barreto,  J. A., & de  la  Fuente,  E. 2000, ApJ, 544, 277 In the text NASA ADS  
• García-Vargas, M. L., Bressan, A., & Díaz, A. I. 1995, A&AS, 112, 13 In the text NASA ADS  
• García-Vargas, M. L., & Díaz, A. I. 1994, ApJS, 91, 553 In the text NASA ADS  
• González Delgado, R. M., & Pérez, E. 2000, MNRAS, 317, 64 In the text In the text NASA ADS  
• González Delgado, R. M., Leitherer, C., & Heckman, T. M. 2000, ApJS, 125, 489 NASA ADS  
• Guseva, N., Izotov, Y. I., & Thuan, T. X. 2000, ApJ, 531, 776 In the text NASA ADS  
• Henry, R. B. C. 1993, MNRAS, 261, 306 In the text NASA ADS  
• Henry, R. B. C., Edmunds, M. G., & Köppen, J. 2000, ApJ, 541, 660 In the text NASA ADS  
• Hoopes, C. G., Walterbros, R. A., & Greenawalt, B. E. 1996, AJ, 112, 1429 In the text NASA ADS  
• Hunter, D. A., & Gallagher III, J. S. 1997, ApJ, 475, 65 In the text NASA ADS  
• Howarth, I. D. 1983, MNRAS, 203, 301 In the text NASA ADS  
• Izotov, Y. I., & Thuan, T. X. 1998, ApJ, 500, 188 In the text NASA ADS  
• Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1994, ApJ, 435, 647 In the text NASA ADS  
• Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1997, ApJS, 108, 1 In the text NASA ADS  
• Johnson,  K. E., Leitherer,  C., Vacca,  W. D., Conti,  P. S., AJ, 120, 1273  
• Kennicutt, R. C., & Garnett, D. R. 1996, ApJ, 456, 504 In the text NASA ADS  
• Kobulnicky, H. A., & Skillman, E. D. 1996, ApJ, 471, 211 In the text NASA ADS  
• Kobulnicky, H. A., & Skillman, E. D. 1998, ApJ, 497, 601 In the text NASA ADS  
• Kobulnicky, H. A. 1999, in Wolf-Rayet Phenomena in Massive Stars and Starbursts, ed. K. A. van der Hucht, G. Koenigsberger, & P. R. J. Eenens, IAU Symp., 193, 670 In the text  
• Kobulnicky, H. A., Skillman, E. D., Roy, J.-R., Walsh, J. R., & Rosa, M. R. 1997, ApJ, 477, 679 In the text NASA ADS  
• Kunth, D., & Sargent, W. L. W. 1986, ApJ, 300, 496 In the text NASA ADS  
• Kurucz, R. L. 1991, in Stellar Atmospheres: Beyond Classical Limits, ed. L. Crivellari, I. Hubeny, & D. G. Hummer (Dordrecht: Kluwer), 441 In the text  
• Legrand, F. 2000, A&A, 354, 504 NASA ADS  
• Leitherer, C., & Heckman, T. M. 1995, ApJS, 96, 9 In the text NASA ADS  
• Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 In the text NASA ADS  
• Luridiana, V., Peimbert, M., & Leitherer, C. 1999, ApJ, 572, 110 In the text  
• Maeder, A., & Meynet, G. 1994, A&A, 287, 803 In the text NASA ADS  
• Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 In the text NASA ADS  
• Martin, C. L. 1997, ApJ, 491, 561 In the text NASA ADS  
• Martin, P., & Friedli, D. 1999, A&A, 346, 769 In the text NASA ADS  
• Mas-Hesse, J. M., & Kunth, D. 1991, in Wolf-Rayet Stars and Interrelations with other Stars in Galaxies, ed. K. A. van der Hucht, & B. Hydayat, IAU Symp., 143, 613 In the text  
• Mas-Hesse, J. M., & Kunth, D. 1999, A&A, 349, 765 In the text NASA ADS  
• Mathis, J. S., & Cardelli, J. A. 1988, ApJ, 398, 610 In the text NASA ADS  
• McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 In the text NASA ADS  
• McGaugh, S. S. 1991, ApJ, 380, 140 In the text NASA ADS  
• McGaugh, S. S. 1994, ApJ, 426, 135 In the text NASA ADS  
• Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 In the text NASA ADS  
• Oey, M. S., Dopita, M. A., Shields, J. C., & Smith, R. C. 2000, ApJS, 128, 511 In the text NASA ADS  
• Olofsson, K. 1995a, A&AS, 111, 57 In the text NASA ADS  
• Olofsson, K. 1995b, A&A, 293, 652 In the text NASA ADS  
• Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 In the text NASA ADS  
• Pagel, B. E. J., Simonson, E. A., Terlevich, R. J., & Edmunds, M. G. 1992, MNRAS, 255, 325 In the text NASA ADS  
• Pagel, B. E. J., Terlevich, R. J., & Melnick, J. 1986, PASP, 98, 1005 In the text NASA ADS  
• Papaderos, P., Izotov, Y. I., Fricke, K. J., Thuan, T. X., & Guseva, N. G. 1998, A&A, 338, 43 In the text NASA ADS  
• Pilyugin, L. S. 2000, A&A, 362, 325 In the text NASA ADS  
• Popescu, C. C., & Hopp, U. 2000, A&AS, 142, 247 In the text NASA ADS  
• Raimann, D., Bica, E., Storchi-Bergmann, T., & Melnick, J. 2000a, MNRAS, 314, 295 In the text NASA ADS  
• Raimann, D., Storchi-Bergmann, T., Bica, E., Melnick, J., & Schmitt, H. 2000b, MNRAS, 316, 559 In the text NASA ADS  
• Rodriguez-Gaspar, J. A., & Tenorio-Tagle, G. 1998, A&A, 331, 347 In the text NASA ADS  
• Ryder, S. D. 1995, ApJ, 444, 610 In the text NASA ADS  
• Schaerer, D. 2000, in Stars, Gas and Dust in Galaxies: Exploring the Links, ed. D. Alloin, G. Galaz, & K. Olsen, ASP Conf. Ser., in press [astro-ph/0007307] In the text In the text  
• Schaerer, D., Contini, T., & Kunth, D. 1999, A&A, 341, 399 In the text NASA ADS  
• Schaerer, D., Guseva, N., Izotov, Y. I., & Thuan, T. X. 2000, , 362, 53 NASA ADS  
• Schaerer, D., & de Koter, A. 1997, A&A, 322, 598 In the text NASA ADS  
• Schaerer, D., & Vacca, W. D. 1998, ApJ, 497, 618 In the text NASA ADS  
• Schmutz, W., Leitherer, C., & Gruenwald, R. 1992, PASP, 104, 1164 In the text NASA ADS  
• Seaton, M. J. 1979, MNRAS, 187, 73P In the text  
• Shields, J. C., & Kennicutt, R. C. 1995, ApJ, 454, 807 In the text NASA ADS  
• Stasinska, G. 1999, in Dwarf Galaxies and Cosmology, ed. T. X. Thuan, C. Balkowski, V. Cayette, & J. Tran Than Van (Éditions Frontières, Gif-sur-Yvette, France), 259 In the text In the text  
• Stasinska, G. 1996, in The Impact of Stellar Physics on Galaxy Evolution, ed. C. Leitherer, U. Fritze-von-Alvensleben, & J. Huchra, ASP Conf. Ser., 98, 232 In the text In the text  
• Stasinska, G., & Leitherer, C. 1996, ApJS, 107, 661 (SL96) NASA ADS  
• Stasinska, G., & Schaerer, D. 1999, A&A, 351, 72 NASA ADS  
• Stasinska, G., & Schaerer, D. 1997, A&A, 322, 615 In the text NASA ADS  
• Stasinska, G., Tylenda, R., Acker, A., & Stenholm, B. 1992, A&A, 266, 486 In the text NASA ADS  
• Telles, E., & Terlevich, R. 1997, MNRAS, 286, 183 In the text NASA ADS  
• Terlevich, R., Melnick, J., Masegosa, J., Moles, M., & Copetti, M. V. F. 1991, A&AS, 91, 285 In the text NASA ADS  
• Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1995, ApJ, 445, 108 In the text NASA ADS  
• van Zee, L., Salzer, J. R., & Haynes, M. P. 1998, ApJ, 497, L1 In the text NASA ADS  
• Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 In the text NASA ADS  
• Vílchez, J. M. 1995, AJ, 110, 1090 In the text NASA ADS  
• Walsh, J. R., & Roy, J.-R. 1987, ApJ, 319, L57 In the text NASA ADS  
• Walsh, J. R., & Roy, J.-R. 1989, MNRAS, 239, 297 In the text NASA ADS  
• Whitford, A. E. 1958, AJ, 63, 201 In the text NASA ADS