A&A 370, 136-146 (2001)
DOI: 10.1051/0004-6361:20010212
R. Samadi1,2 - M.-J. Goupil3
1 -
Observatoire de Paris, DESPA, CNRS UMR 8632, 92195 Meudon, France
2 -
Astronomy Unit, Queen Mary, University of London, London E14NS, UK
3 -
Observatoire de Paris, DASGAL, CNRS UMR 8633, 92195 Meudon, France
Received 17 October 2000 / Accepted 19 January 2001
Abstract
Stochatic excitation of stellar oscillations by turbulent
convection is investigated and an expression for the power injected
into the oscillations by
the turbulent convection of the outer layers is derived which takes into
account excitation through turbulent Reynolds stresses
and turbulent entropy fluctuations.
This formulation generalizes results from previous works and
is built so as to enable investigations of various
possible spatial and temporal
spectra of stellar turbulent convection.
For the Reynolds stress contribution and assuming
the Kolmogorov spectrum we obtain a similar formulation
to those derived by previous authors.
The entropy contribution to excitation is found to originate from the advection
of the Eulerian entropy fluctuations by the turbulent velocity field. Numerical
computations in the solar case in a companion paper
indicate that the entropy source term
is dominant over the Reynold stress contribution to mode excitation,
except at high frequencies.
Key words: convection - turbulence - stars: oscillations - Sun: oscillations
Oscillation amplitudes and linewidths provide
information on excitation and damping processes of stellar
oscillation modes. In the solar case, the observed oscillation modes are believed to be
damped as a result of a competition between several non-adiabatic and turbulent
processes (Osaki 1990; Houdek et al. 1999). Excitation of solar oscillation modes is
attributed to turbulent convection at the surface of the Sun.
The first theoretical investigation of solar oscillation excitation
by turbulent convection was by Goldreich & Keeley (1977, hereafter GK).
These authors identified the turbulent term
of Reynolds stress as the main source term of stochastic excitation of
solar acoustic modes in the wave equation.
GK derived an approximate estimation for
the acoustic power injected into the oscillations by turbulent
convection which arises from an equipartition of energy between the
turbulent elements and the oscillations.
The result, however, underestimated the power
by a factor ![]() 103 compared to the solar observations
(Osaki 1990).
Amplitude estimations for solar-like oscillating stars have subsequently
been computed by Christensen-Dalsgaard & Frandsen (1983)
based on this simple picture of
equipartition of energy between turbulence and oscillation.
GK considered the adiabatic assumption for both the
oscillations and the turbulence.
A decade later, entropy
turbulent fluctuation
has been proposed as a possible additional excitation source
(Stein & Nordlund 1991; Balmforth 1992; Goldreich et al. 1994).
103 compared to the solar observations
(Osaki 1990).
Amplitude estimations for solar-like oscillating stars have subsequently
been computed by Christensen-Dalsgaard & Frandsen (1983)
based on this simple picture of
equipartition of energy between turbulence and oscillation.
GK considered the adiabatic assumption for both the
oscillations and the turbulence.
A decade later, entropy
turbulent fluctuation
has been proposed as a possible additional excitation source
(Stein & Nordlund 1991; Balmforth 1992; Goldreich et al. 1994).
The stochastic mechanism may be understood as follows: turbulent motions of the stellar material and turbulent fluctuations of thermodynamicals quantities, which occur in the convection zone, generate acoustic waves (Lighthill 1952; Stein 1967). The corresponding acoustic power then excites resonant modes of the stellar cavity (oscillations). This excitation of the oscillations results from a forcing by incoherent (turbulent) source terms due to the turbulent Reynolds stress and turbulent entropy fluctuations.
An alternative formulation for the power and amplitude oscillation is proposed by Balmforth (1992, hereafter B92) and is used by Houdek et al. (1999) to compute amplitude of oscillation for various solar-type stars. There is some disagreement between the conclusions of both formulations concerning the entropy contribution: it is found dominant in theoretical investigation (Goldreich et al. 1994, hereafter GMK) and as a result of numerical 3D simulations (Stein & Nordlund 1991), but negligible in some other cases (Balmforth 1992).
Both formulations are built following the method developed by GK and are based on a simplified description of the turbulent medium. The spectrum of turbulent energy in stellar conditions is, however, not well known. The best-known spectrum is, of course, the solar spectrum (Espagnet et al. 1993; Nesis et al. 1993) and observations tell us that a Kolmogorov spectrum does not represent the complete turbulent solar spectrum (Nesis et al. 1993).
The purpose of the present work therefore is to investigate the effect of several possible models of turbulence on the excitation of solar-like oscillation modes and to establish their signature in power spectra. To do so, a formulation must first be established which includes both (kinetic and entropic) contributions in a consistent and general way. The main goal is to allow the use of any form of the turbulent kinetic energy spectrum, of turbulent entropy fluctuations and the eddy temporal spectrum. Two free parameters are introduced to take into account uncertainties in the definitions of the coherence time of the turbulent eddies and in the magnitude of the wavenumber at which the inertial regime starts.
Once the general formulation is established, we study the specific case of a Gaussian time and Kolmogorov energy spectra, which enables us to compare our findings with results of previous works. In a companion paper, the present formulation is applied to the solar case and several turbulent models found in the literature are discussed. Both free parameters can be calibrated with solar observations and used to compute oscillation amplitudes for other potential solar-like oscillating stars (Samadi et al. 2001b, 2001c) in view of forthcoming space seismological experiments: COROT (Baglin & The Corot Team 1998), MONS (Kjeldsen & Bedding 1998), MOST (Matthews 1998), EDDINGTON (Favata et al. 2000).
Section 1 recalls how the stochastic excitation mechanism of stellar oscillations is modeled by source terms in the wave equation. We assume the modes are damped and find that they are excited through the turbulent Reynolds stresses (Goldreich & Keeley 1977) and the turbulent entropy fluctuations arising from the turbulent nature of the stellar convection region (Stein & Nordlund 1991; Balmforth 1992; Goldreich et al. 1994). We adopt the GK procedure and assume that the oscillation modes are decoupled from the turbulent medium. This description gives rise to an inhomogeneous wave equation for the oscillation modes. In this framework, the acoustic turbulent source acts as a forcing term for the oscillation normal modes. We consider adiabatic radial oscillations in the Cowling (1941) approximation. A homogeneous, isotropic, stationary turbulence is assumed. A formulation for the Reynolds stress contribution which can include any type of turbulent spectrum is established in Sect. 3. In Sect. 4, the contribution of turbulent fluctuations of entropy is worked out. We find that it is the advection of the entropy turbulent fluctuation by the turbulent velocity field which yields the entropy source. An appendix shows that cross terms between Reynolds and entropic sources do not contribute.
Section 5 finally establishes a general formulation which can be used to investigate any type of turbulent spectrum. Finally, Sect. 6 discusses the complete formulation, its limitations and advantages.
In the basic hydrodynamical equations, we use the symbols P, ![]() ,
,
![]() and
and ![]() to denote respectively pressure,
density, velocity and gravitational acceleration.
Equilibrium quantities are represented with a subscript 0.
Each variable f, except for the velocity
to denote respectively pressure,
density, velocity and gravitational acceleration.
Equilibrium quantities are represented with a subscript 0.
Each variable f, except for the velocity ![]() ,
is written as
the sum of the equilibrium quantity, f0 and a Eulerian fluctuation, f1,
f = f0 + f1 and
we retain terms which are linear and quadratic in the variables
P1 and
,
is written as
the sum of the equilibrium quantity, f0 and a Eulerian fluctuation, f1,
f = f0 + f1 and
we retain terms which are linear and quadratic in the variables
P1 and ![]() and neglect the gravitational perturbation.
Accordingly, one obtains for the perturbed momentum
and continuity equations:
and neglect the gravitational perturbation.
Accordingly, one obtains for the perturbed momentum
and continuity equations:
We assume adiabatic oscillations: the
Lagrangian entropy fluctuations are therefore only due to turbulence.
Lagrangian and Eulerian
entropy fluctuations are related to each other
by
Linearisation of Eqs. (1-3) yields for the velocity field,
in the absence of turbulence (
![]() ), the homogeneous wave equation
), the homogeneous wave equation
| (7) |
| (8) |
In the presence of turbulence, the pulsational displacement and velocity are
written in terms of the above adiabatic
solution
![]() and an instantaneous
amplitude A(t).
Accordingly
and an instantaneous
amplitude A(t).
Accordingly
Differentiating Eq. (1)
with respect to t, neglecting non-linear terms in
![]() ,
assuming an incompressible turbulence (
,
assuming an incompressible turbulence (
![]() )
and using Eqs. (2, 3, 5)
yields the inhomogeneous wave equation
)
and using Eqs. (2, 3, 5)
yields the inhomogeneous wave equation
The operator
![]() involves both the turbulent velocity field
(
involves both the turbulent velocity field
(![]() )
and the pulsational velocity and is defined as
)
and the pulsational velocity and is defined as
We assume a "free turbulence'', i.e. the turbulent medium evolves
freely and is not perturbed by the oscillations.
The continuity equation is verified by the turbulent medium such that
It can easily be shown that the
additional terms appearing in the RHS of Eq. (10)
are of order
![]() ,
where
,
where ![]() is the turbulent Mach number,
compared with the Reynolds source term (see also GK).
As
is the turbulent Mach number,
compared with the Reynolds source term (see also GK).
As ![]() is small in the solar convection zone (
is small in the solar convection zone (
![]() ), these additional terms have been neglected.
), these additional terms have been neglected.
The wave operator
![]() acting on the turbulent velocity field
acting on the turbulent velocity field ![]() in Eq. (10) gives rise to contributions
which are either negligible compared with
the Reynolds source term or of the same order. In this last case,
the associated source term does not contribute
to the wave excitation because it is linear in terms of
the turbulent fluctuations (see also Sect. 4.1).
Therefore, in the LHS of Eq. (10),
in Eq. (10) gives rise to contributions
which are either negligible compared with
the Reynolds source term or of the same order. In this last case,
the associated source term does not contribute
to the wave excitation because it is linear in terms of
the turbulent fluctuations (see also Sect. 4.1).
Therefore, in the LHS of Eq. (10), ![]() can be replaced by
can be replaced by
![]() .
.
In deriving Eq. (9), the time variation of the amplitude A is neglected
since we assume, as in the solar case, that the eddy time correlation is of the
order of a few minutes in the excitation region and
the associated angular frequency is comparable to
![]() (
(![]()
![]() ), which is much larger
than the oscillation damping rate
), which is much larger
than the oscillation damping rate ![]() (
(![]()
![]() .
.
Substituting Eq. (9) into
Eq. (10), gives, with the
help of Eq. (6),
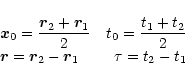 |
(20) |
In the excitation region the eddy lifetime is much smaller than the
oscillation lifetime (![]()
![]() )
such that the integration over
)
such that the integration over ![]() can be
extended to infinity.
We assume a stationary turbulence, therefore the source
term
can be
extended to infinity.
We assume a stationary turbulence, therefore the source
term ![]() is invariant over time t0.
Integration over t0 in Eq. (21) and using the definition of
is invariant over time t0.
Integration over t0 in Eq. (21) and using the definition of
![]() in Eq. (16) yields:
in Eq. (16) yields:
In the derivation of Eqs. (23) and (24)
integrations by parts have been performed in order for the gradient to
act on the eigenfunction instead of
turbulent quantities.
We next suppose that the terms
![]() and
and
![]() in Eq. (23)
do not change on the length scale of the eddies.
This implies that
in Eq. (23)
do not change on the length scale of the eddies.
This implies that
![]() .
Validity of this assumption will be justified a posteriori
below. Consequently, the Reynolds stress contribution can be expressed as:
.
Validity of this assumption will be justified a posteriori
below. Consequently, the Reynolds stress contribution can be expressed as:
| (26) |
We denote
![]() as the well known Fourier transform
of the second-order velocity correlations
as the well known Fourier transform
of the second-order velocity correlations
![]() (e.g. Stein 1967).
For a stationary, incompressible, homogeneous and isotropic turbulence, the
Fourier transform of the velocity correlation has the form (Batchelor 1970):
(e.g. Stein 1967).
For a stationary, incompressible, homogeneous and isotropic turbulence, the
Fourier transform of the velocity correlation has the form (Batchelor 1970):
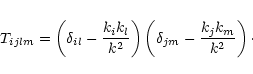
As in Sect. 3 we use
![]() in
Eq. (24) to obtain:
in
Eq. (24) to obtain:
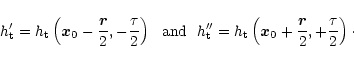 |
(37) |
We consider the contribution of the Lagrangian entropy fluctuations (i.e. the first term in the RHS of Eq. (40)).
In the Boussines approximation, the entropy fluctuation ![]() is related to the temperature fluctuation
is related to the temperature fluctuation ![]() as
as
Let
![]() be the Fourier transform of the correlation product of the
Eulerian entropy fluctuation.
For any passive scalar, one has the relation (Lesieur 1997, Chap. V-10)
be the Fourier transform of the correlation product of the
Eulerian entropy fluctuation.
For any passive scalar, one has the relation (Lesieur 1997, Chap. V-10)
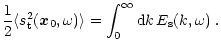 |
(43) |
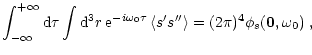 |
(44) |
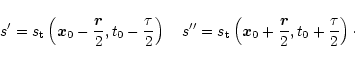 |
(45) |
This result may also be explained as follows: in term of mode excitation,
the linear entropy source term acts as a second-order correlation
product
![]() .
Turbulence and oscillation
are coupled through the phase term
.
Turbulence and oscillation
are coupled through the phase term
![]() and through the
turbulent time spectrum
and through the
turbulent time spectrum
![]() ,
which is the frequency-dependent
component of
,
which is the frequency-dependent
component of
![]() in the Fourier space.
Therefore coupling between turbulence and oscillation occurs at frequencies
close to the oscillation frequency
in the Fourier space.
Therefore coupling between turbulence and oscillation occurs at frequencies
close to the oscillation frequency ![]() and thus involves
eddies of wavenumber
and thus involves
eddies of wavenumber
![]() according to
Eq. (35).
On the other hand, the spatial component of
according to
Eq. (35).
On the other hand, the spatial component of
![]() in the Fourier space favors eddies with the
largest size (
in the Fourier space favors eddies with the
largest size (
![]() ).
These two opposite effects clearly are incompatible and lead to vanishing of
the entropy fluctuation contribution.
).
These two opposite effects clearly are incompatible and lead to vanishing of
the entropy fluctuation contribution.
This does not happen for the contribution of the Reynolds source term, which involves the fourth-order velocity correlation product. According to the QNA this term can be decomposed in terms of a product of two second-order velocity correlations. Coupling with the oscillation then becomes non-linear and leads to an effective non-zero contribution. Thus, only non-linear terms can contribute to mode excitation while linear terms do not. This may be considered as a general result and justifies neglect of several source terms in Sect. 2.2.
As the linear term does not contribute to the acoustic emission,
Eq. (40) becomes, with Eq. (39),
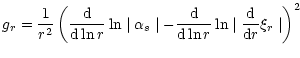 |
(51) |
The Mixing-Length Theory (hereafter MLT Böhm-Vitense 1958; Cox 1968; Gough 1977)
provides an estimate of the vertical velocity of the convective flow.
The corresponding kinetic energy is
transferred to smaller scales through the
turbulent cascade. The kinetic energy spectrum E(k) is normalized as
The MLT provides a relation between the temperature fluctuations and
the vertical convective velocity w (Gough 1977):
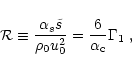 |
(56) |
The entropy contribution can then be written as:
With Eqs. (34) and (57), the oscillation
amplitude Eq. (22) is rewritten as
Results in Samadi et al. (2001a) for the solar case and in Samadi et al. (2001c) for Procyon are based on the above general expression for the mean square amplitude. In order to compare with results of previous works, we next consider specific temporal and energy spectra, namely the Gaussian time spectrum and the Kolmogorov spectrum.
Let consider the Gaussian time spectrum given by
Eq. (30). This time spectrum
corresponds in the time space to a Gaussian function
where linewidth is equal to ![]() and
and ![]() is
the characteristic time correlation length of an eddy of wavenumber k.
Hence
is
the characteristic time correlation length of an eddy of wavenumber k.
Hence ![]() and
and ![]() are related to each other as
are related to each other as
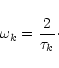 |
(60) |
Let us define the wavenumber k0 as the wavenumber of the largest eddy in
the inertial range. Thus we relate k0 to the mixing length as follows:
For convenience we define the following variables:
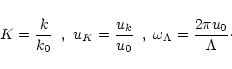 |
(64) |
The amplitude (Eq. (65)) is very sensitive to the
parameters ![]() and
and ![]() because it scales
as
because it scales
as
![]() and the quantity
and the quantity
![]() is
involved in the exponential function of Eq. (66) and
Eq. (67).
In Sect. 5.2
some physical arguments yield a crude estimate for the parameter
is
involved in the exponential function of Eq. (66) and
Eq. (67).
In Sect. 5.2
some physical arguments yield a crude estimate for the parameter ![]() .
Values of parameters
.
Values of parameters ![]() ,
,
![]() are discussed in some details in Samadi et al. (2001a) in connection with solar seismic observations.
are discussed in some details in Samadi et al. (2001a) in connection with solar seismic observations.
The normalization condition
Eq. (52) allows us
to express the Kolmogorov spectrum (Lesieur 1997, Chap. VI-4) as
We next turn to a specific case where
we assume that the entropy energy
spectrum lies in the inertial-convective range
i.e. the turbulent entropy spectrum scales as the kinetic spectrum.
According to the normalization conditions of Eq. (52)
and of Eq. (55),
this assumption provides the relation:
For sake of comparison with the GMK formulation,
we simplify
Eqs. (70) and (71)
by using the fact that most of the
stochastic emission occurs from eddies
with
![]() (i.e. with
(i.e. with
![]() ).
For
).
For
![]() integration over K leads then to the asymptotic forms
integration over K leads then to the asymptotic forms
We next turn to the parameter ![]() .
The time scale at which the convective energy
dissipates through the turbulent cascade is of order
.
The time scale at which the convective energy
dissipates through the turbulent cascade is of order ![]() .
Thus for stationary turbulence and using Eq. (52),
the rate of injection of kinetic energy
.
Thus for stationary turbulence and using Eq. (52),
the rate of injection of kinetic energy ![]() (Lesieur 1997, Chap. VI-3) can be crudely estimated as
(Lesieur 1997, Chap. VI-3) can be crudely estimated as
 |
(75) |
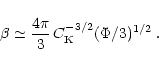 |
(76) |
The value suggested for ![]() is somewhat approximate.
Therefore, as in the case of the parameter
is somewhat approximate.
Therefore, as in the case of the parameter ![]() ,
we consider
,
we consider ![]() as a free parameter.
However, the value of
as a free parameter.
However, the value of
![]() is constrained by an upper limit. Indeed,
let
is constrained by an upper limit. Indeed,
let
![]() be the correlation time of the largest eddy in the inertial domain. The lifetime of the largest eddies in the inertial range cannot be longer than the characteristic time
be the correlation time of the largest eddy in the inertial domain. The lifetime of the largest eddies in the inertial range cannot be longer than the characteristic time
![]() at which the convective energy dissipates into the turbulent cascade.
Therefore we must have
at which the convective energy dissipates into the turbulent cascade.
Therefore we must have
![]() and according to Eqs. (61, 62) evaluated for k=k0 and Eqs. (63, 52) we obtain
and according to Eqs. (61, 62) evaluated for k=k0 and Eqs. (63, 52) we obtain
![]() .
.
In the present work, a formulation has been
established which yields the oscillation amplitude
of a stellar oscillation mode when it is stochastically excited by turbulent
convection. The main result of this paper is the expression for the mean square oscillation amplitude
![]() given by Eqs. (58) and (59).
The derivation is based on theoretical developments of previous
works (GK, GMK, B92) but an effort has been made
to obtain a sufficiently general expression which enables one to
implement any type of turbulent (kinetic and entropic) spectra
and any type of temporal spectra for the turbulent eddies.
given by Eqs. (58) and (59).
The derivation is based on theoretical developments of previous
works (GK, GMK, B92) but an effort has been made
to obtain a sufficiently general expression which enables one to
implement any type of turbulent (kinetic and entropic) spectra
and any type of temporal spectra for the turbulent eddies.
For comparison purpose, we next focused on a Gaussian temporal and Kolmogorov energy spectra; we then ended up with the same expression for the Reynolds stress contribution as obtained in GMK and B92. We must stress however that in order to use the same formulation for an energy spectrum other than the Kolmogorov one, such as for instance the Spiegel spectrum, a general expression such as Eq. (58) must be used.
As far as the entropy contribution is concerned, we found that the linear term due to the entropy fluctuation gives no contribution and that it is the advection of the Eulerian entropy fluctuations by the turbulent velocity field which produces a nonzero acoustic emission.
In the derivation of the expected mean-square amplitude (Eq. (58)),
several assumptions and approximations have been made. For instance, it has been assumed that the oscillations and the
stratification are decoupled for the eddies which
contribute to the stochastic power emission. This assumption was shown to
be valid and is in agreement with Goldreich & Kumar (1990).
In addition, we have used the plane-parallel approximation, which is valid in
the excitation region.
Other assumptions are based on results from Stein's work
(1967),
such as the separation of the kinetic energy spectrum
![]() in term
of a purely spatial energy spectrum E(k) and a time-dependent factor
in term
of a purely spatial energy spectrum E(k) and a time-dependent factor
![]() for an eddy of wavenumber k.
As in Stein (1967) the QNA has been used.
We have used crude approximations for estimations of the velocity
and the life-time of an eddy as proposed by Stein (1967).
This led us to introduce the free parameter
for an eddy of wavenumber k.
As in Stein (1967) the QNA has been used.
We have used crude approximations for estimations of the velocity
and the life-time of an eddy as proposed by Stein (1967).
This led us to introduce the free parameter ![]() in
the definition of the eddy lifetime.
in
the definition of the eddy lifetime.
The entropy fluctuation has been considered to act as a passive scalar and we have extended the separation of the kinetic energy spectrum in terms of a purely spatial energy spectrum E(k) and a time-dependent factor to the entropy energy spectrum.
The MLT was required in order to estimate the power injected in the velocity and entropy turbulent cascade (Eq. (65)). This theory, which assumes the Boussinesq approximation, is well known to be a crude approximation. For instance the MLT predicts that the characteristic size of the largest turbulent element is comparable with the scale height of the stratification. This is in contrast with the homogeneous hypothesis considered here for the description of the turbulent medium. However, it has already been stressed that the stochastic emission is not affected by the stratification. The use of an homogeneous turbulence is therefore valid.
The size of the largest eddy in the inertial range is estimated by the mixing length (![]() )
according to the MLT. We have related the wavenumber of the largest
eddy in the inertial range (k0) to the mixing length.
However, as for the eddy lifetime, this relation is rather arbitrary
and therefore involves uncertainties. We have therefore introduced an additional free
parameter
)
according to the MLT. We have related the wavenumber of the largest
eddy in the inertial range (k0) to the mixing length.
However, as for the eddy lifetime, this relation is rather arbitrary
and therefore involves uncertainties. We have therefore introduced an additional free
parameter ![]() .
.
We have considered an isotropic turbulence. However, effects of
anisotropy in the amplitude computaion have been partially taken into
account. In this way, two anisotropic factors
![]() and
and
![]() have been introduced for both contributions respectively.
These factors have been related to Gough (1977) anisotropic factor
have been introduced for both contributions respectively.
These factors have been related to Gough (1977) anisotropic factor ![]() .
.
It is possible to validate some of these approximations by comparing them with results of 3D simulations of the solar envelope (Samadi 2000, work in progress): for instance, the QNA is found to be reasonably valid.
To date, and in the solar case, several possible turbulent spectra can be investigated and compared with solar seismic observations (Samadi et al. 2001a). But we can anticipate that the entropy contribution will be dominant, as already pointed out by GMK. Comparison with solar data allows us to calibrate the free parameters which in turn can be used to compute oscillation power spectra for various solar-like oscillation stars. Indeed, unlike the Sun, it is not possible to determine the turbulent spectra of other stars from observations of the surface granulation. In the prospect of forthcoming space seismic projects (COROT, MONS, MOST, EDDINGTON) comparison of theoretical computations with seismic data of several solar-like oscillation stars will provide useful constraints on stellar turbulent spectra.
Acknowledgements
We are indebted to A. Mangeney for particularly useful suggestions and advice without which this work would not have been possible. We also thank J.-P. Zahn, M. Rieutord and A. Baglin for useful discussions.
The entropy and Reynolds source terms involve
three crossing terms arising from Eq. (21).
These terms are proportional to
| (A.1) | |||
| (A.2) |
The entropy source term introduces a crossing term
between the linear and the non-linear terms of
Eq. (39). This term is proportional to
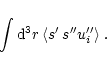 |
(A.4) |
As a conclusion, the crossing term
![]() and
the crossing terms between the linear and non-linear
terms of the entropy contribution do not
contribute to oscillation excitation.
and
the crossing terms between the linear and non-linear
terms of the entropy contribution do not
contribute to oscillation excitation.
The QNA provides the relation
| (B.1) |
We establish here the derivation of Eqs. (34) and (50)
where the anisotropy factors
![]() and
and
![]() have been
introduced. Thus we evaluate these factors for several
cases. Let (x,y,z) be the real (anisotropic) coordinates
and
have been
introduced. Thus we evaluate these factors for several
cases. Let (x,y,z) be the real (anisotropic) coordinates
and
![]() are isotropic coordinates.
We assume an isotropic turbulence in the horizontal layers
while the anisotropy occurs in the vertical direction only.
The two sets of coordinates are then
related to each other by the anisotropic factor
are isotropic coordinates.
We assume an isotropic turbulence in the horizontal layers
while the anisotropy occurs in the vertical direction only.
The two sets of coordinates are then
related to each other by the anisotropic factor
![]() as
as
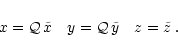 |
(C.1) |
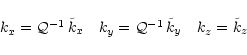 |
(C.2) |
Evaluation of Eq. (33) gives
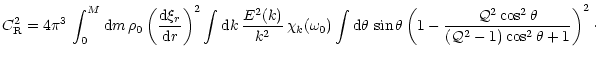 |
(C.3) |
As was done with the Reynolds stress contribution, it is
straightforward to obtain Eq. (50) from Eq. (B.6)
where the anisotropic factor
![]() is
is
| (C.8) |
![$\displaystyle \frac{1} { a^{5/2} }
\left [ \frac{2a^{3/2} - 3 \sqrt{a} } {a-1} - 3 \, \mathrm{atanh} ( \sqrt{a} ) \right ]$](/articles/aa/full/2001/16/aa10363/img258.gif) |
(C.9) |
| (C.10) |
| (C.11) |
|
|
a |
|
|
|
| 3 | 1 | 0 | 16/15 | 4/3 |
| 2 | 0.5 | 0.5 | 1.0 | 1.0 |
| 5/3 | 0.33 | 0.66 | 1.8 | 1.2 |
| 1.37 | 0.18 | 0.81 | 3.7 | 1.6 |