next previous
Up: High-resolution imaging of ultracompact

Subsections

3 Results

3.1 General morphology - Millimetre continuum and MSX data

First, we present the results of the 1.3mm continuum mapping of the two targets to give an overview of the regions where the UCH IIs are located. The resulting maps are shown in Figs. 1 and 2 together with contours of the 8.8 \ensuremath {\mu }m emission based on MSX images[*]. The coordinate systems in all figures relating to G11 are systems relative to the position of the UCH II given by Kurtz et al. (1994). Coordinates for G341 are centred on the OH maser position of Caswell (1998).

Note that the 1.3mm emission consists of the sum of free-free- and dust emission at that wavelength. The free-free contribution has been subtracted from the G11 map in Fig. 1. This was achieved by multiplying the 2cm map from KCW94 with a factor of (2/0.13)0.1 (assuming optically thin free-free emission) and convolving the resulting map with the SEST beam before subtracting it from the 1.3mm map. We note that the free-free contribution to the 1.3mm flux derived by this method is not really significant. At the maximum of the 2cm map we compute a relative contribution of 5% from free-free emission to the 1.3mm emission.

As for G341, no high-resolution continuum maps currently exist at centimetre wavelengths. The non-detection of Br \ensuremath {\gamma }-radiation from this source implies, however, that very little ionisation might be present in that source and thus no correction has to be made to the 1.3mm flux.

Both targets exhibit a rather irregular structure at 1.3mm. The diameters are of the order of 2 $.\mkern-4mu^\prime$5. However, G11 appears to be more concentrated towards a single core, while G341 comprises two major peaks with a clear gap in between, an indication for the presence of two dense cores. There seems to be an east-west elongation of the core of G11 while the 8.8 \ensuremath {\mu }m emission of this source is extended in north-south direction. This suggests that the heating sources are embedded in a filament or surrounded by a dust torus, similar to NGC6334A (Kraemer et al. 1999; Sandell 1999). The strongest 1.3mm peak of G341 lies immediately to the northeast of the reference position. The weaker secondary peak, more to the southeast, coincides roughly with the position of the infrared source IRAS 16487-4423 which Bronfman et al. (1996) listed as a source with colour characteristics typical of UCH IIs. We note that the 8.8 \ensuremath {\mu }m fluxes from the two cores of G341 behave in the opposite way to the behaviour of 1.3mm emission. Thus, it seems reasonable that the source associated with the maximum of the 1.3mm emission is less evolved compared to the UCH II-type object to the southeast. The offsets between the peaks of 8.8 \ensuremath {\mu }m and 1.3mm emission are presumably indicating that star formation started at the outskirts of these cores and is progressing towards their centres.

   
3.1.1 Dust masses


 

 
Table 3: Masses derived from the 1.3mm data

Region		 Ass. temp. [K] mm-flux [Jy] Mass [ \ensuremath{{M}_{\odot}}]

G11 Core		 40 2.2 620
G11 Halo 15 8.2 1.2 \ensuremath{~ 10^{4}}
G341 Core 1 40 2.8 400
G341 Core 2 40 2.6 370
G341 Halo 15 8.1 6.0 \ensuremath{~ 10^{3}}


The flux density emitted from an optically thin dust cloud with mass $M_{\rm dust}$ at frequency $\nu$ is given by:

 \begin{displaymath}F_{\nu} = \frac{2 M_{\rm dust} h \nu^3 \kappa_{\nu}}{d^2 c^2}\frac{1}{{\rm e}^{\frac{h\nu}{kT}}-1}\cdot \end{displaymath} (1)

In this expression, the dust mass absorption coefficient $\kappa_{\nu}$ is taken from Ossenkopf & Henning (1994) for the appropriate wavelength ( $\kappa=0.9$cm2g-1 for 1.3mm) assuming a gas density of 105 cm-3, a size distribution after MRN (Mathis et al. 1977), grains without ice mantles, and a coagulation time of 105 yr. The quantity T is the dust temperature, h the Planck constant, k the Boltzmann constant, and d the distance towards the source. In Table 3, the total masses obtained from $M_{\rm dust}$ with a gas-to-dust ratio of 150 are compiled.

G11 can be divided into a central region of $\sim$ $40\hbox{$^{\prime\prime}$ }$ diameter exhibiting an integrated flux density of 2.2 Jy and a halo region with $\sim$ $180\hbox{$^{\prime\prime}$ }$ diameter and a total flux density of 8.2 Jy. Assuming both regions to be concentric spheres and correcting for the halo contribution in the core aperture, we derive a cloud mass of 620 \ensuremath{{M}_{\odot}} in the core and 1.2 \ensuremath{~ 10^{4}} \ensuremath{{M}_{\odot}} in the halo. The temperatures used for this estimate were 40K in the core and 15K in the halo. When using such values, one should keep in mind that by a slight error of, e.g., 5K in the temperatures assumed above, the mass estimates can vary by a factor of up to 2 for the halo (assumed temperature of 15K) or 1.3 for the core (assumed temperature of 40K).

For a classification of the embedded stellar sources, it is crucial to de-redden their colours and thus to know the extinction towards these sources. This extinction can be measured in two ways, via the dust mass and via a comparison of radio free-free and NIR recombination emission. We will now derive K-band extinction values from the measured dust masses; a comparison to values derived from the second method will be given in the next section.

The complete dust mass seen in the core aperture (core plus contributing halo) corresponds to a mass column density of 6.7 \ensuremath{~ 10^{-3}}gcm-2. With a dust mass absorption coefficient of 2.15 \ensuremath{~ 10^{3}}cm-1g-1, again taken from Ossenkopf & Henning (1994) - this time for 2.2 \ensuremath {\mu }m, we derive a K-band extinction of 5.5mag. Assuming the UCH II to be embedded halfway into this cloud, we thus expect an extinction of AK=2.8mag. Note that when using Ryter's (1996) expression for the extinction,

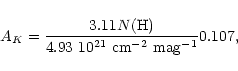\begin{displaymath}A_K=\frac{3.11 N({\rm H})}{4.93~10^{21}~\mbox{cm}^{-2}~\mbox{mag}^{-1}}0.107, \end{displaymath} (2)

where the last factor represents the conversion from AV to AKafter Mathis (1990), we get an extinction of 2.6mag halfway into the cloud. Ryter (1996) assumes the ratio of visual extinction to hydrogen column density, AV / N(H), to be that of the interstellar medium while the values of Ossenkopf & Henning (1994) are for dust grains that have been subject to coagulation for 105 years. Converting the derived extinctions to the V-band after Mathis (1990), we get AV=25.6mag for the coagulated case and AV= 24.2mag for the interstellar type case. We note that these estimates depend linearly on the mass and thus have the same uncertainty with respect to the chosen temperatures.

For G341, we find two core regions (see Fig. 2). The main peak has an integrated flux density of 2.8Jy, the secondary peak to the southeast of 2.6Jy. A flux density of 8.1Jy remains in the extended emission of the halo. Using the same temperatures as for G11, we find cloud masses of 400 \ensuremath{{M}_{\odot}} and 370 \ensuremath{{M}_{\odot}} in the primary and in the secondary cores, respectively, and 6000 \ensuremath{{M}_{\odot}} in the halo.

Applying the appropriate extinction estimation, we derive a K-band extinction of AK=2.1 mag (AV =19 mag) in the coagulation case or AK=1.7 mag (AV =16 mag) in the interstellar grain case. Both estimates assume the source to be embedded halfway into the halo.


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure1.ps} \end{figure} Figure 1: 1.3mm continuum map of G11 with 8.8 \ensuremath {\mu } m emission measured by the MSX satellite (contours). Free-free emission has been subtracted from this map (see text). The grayscale is given by the bar on the right. The contour levels are at 1, 1.6, 2.5, 4, 6.25, and 9.9 times 5 \ensuremath{~ 10^{-6}}Wm-2sr-1


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure2.ps}\end{figure} Figure 2: Same as Fig. 1 but for G341. The contour levels for the overlayed 8.8 \ensuremath {\mu } m map are at 1, 1.6, 2.5, 4, 6.25, and 9.9 times 6.3 \ensuremath{~ 10^{-6}}Wm-2sr-1


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure3_col.ps} \end{figure} Figure 3: Narrow-band emission from G11 (Strong contours). Underlayed is the narrow-band continuum image at 2.148 \ensuremath {\mu } m. (In the electronic version of the journal, a colour composite of the three narrow band images is underlayed. Here, blue denotes Br \ensuremath {\gamma }, green denotes continuum and red H2(1-0)S1 emission.) The strong contours show the remaining Br \ensuremath {\gamma } emission after subtraction of the continuum. Levels are 2, 4, and 8 times 0.04mJy/$\Box $ $^{\prime \prime }$ (solid strong contours) and -2, -4, and -8 times 0.04mJy/$\Box $ $^{\prime \prime }$ (dotted strong contours). Negative values close to bright stars indicate imperfect continuum subtraction. The light contours are from the 1.3mm map (Compare Fig. 1)

   
3.2 Narrow-band data - The ionized material

Figures 3 and 4 show the continuum-subtracted Br \ensuremath {\gamma } emission from G341 and G11, respectively.

All printed images taken in the infrared spectral range were filtered with the multi-scale maximum-entropy method described by Pantin & Starck (1995). This is to enhance the visibility of details in the printed version only.

No line emission is detected from G341. G11 does show Br \ensuremath {\gamma } emission, the integrated flux density is 0.019Jy. A comparison of the Br \ensuremath {\gamma }flux density distribution and the 2 and 3.6cm maps were used to derive the NIR extinction towards the source. For a thorough description of the technique used for this comparison, we refer the reader to an earlier paper (Feldt et al. 1998). As the spectral index between the 2cm and the 3.6cm emission measured by KCW94 is not exactly 0.1, as expected for optically thin free-free emission, we use only the 2cm map for the comparison with our Br \ensuremath {\gamma }data and assume this radiation to be optically thin. Assuming an electron temperature of 104K we derive a mean emission measure across G11 of 7.2 \ensuremath{~ 10^{5}} pccm-6 with a peak value of 2.8 \ensuremath{~ 10^{6}} pccm-6. Assuming the peak size to be of the order of the VLA resolution element, i.e. 0 $.\!\!^{\prime\prime}$5 or 0.01 pc, this implies a peak electron density of 1.6 \ensuremath{~ 10^{4}} \ensuremath{{\rm cm}^{-3}}. The mean electron density in G11 is about 4.3 \ensuremath{~ 10^{3}} \ensuremath{{\rm cm}^{-3}}. When predicting the Br \ensuremath {\gamma } flux density from these values and comparing them to those measured, we derive a mean extinction of 3.5mag at the wavelength of Br \ensuremath {\gamma }. The peak value is 4.3mag. Given the uncertainty of how deep the source actually is embedded in the cloud core, these values agree reasonably well with the extinction of 2.8 mag derived in Sect. 3.1.1.


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure4_col.ps} \end{figure} Figure 4: Narrow-band continuum image of the area around G341 at 2.148 \ensuremath {\mu } m. The logarithmic gray-scale ranges from 6.4mJy/$\Box $ $^{\prime \prime }$ to 256mJy/$\Box $ $^{\prime \prime }$. In the electronic version of the journal, this figure contains a colour composite which shows the H2(1-0)S1-emission in red , the continuum image in green and the Br \ensuremath {\gamma }-emission in blue. The contours are from the 1.3mm map (see Fig. 2)

  
3.3 $\mathsfsl N$-band data of G341

From our N-band map of G341, which is shown in Fig. 9 as a contour plot, we derive a total flux density of 1.4 Jy from the source. When we try to determine a mass of hot ($\sim$100K) dust from this flux using Eq. (1) with the proper values and an extinction coefficient of 2.4 \ensuremath{~ 10^{3}}cm2g-1, we derive a dust mass of 6 \ensuremath{~ 10^{-4}} \ensuremath{{M}_{\odot}}. This is of course an absolute lower limit, because G341 is situated near the core of the 1.3mm emission region and thus the dust emission is certainly far from being optically thin. Correcting for the extinction towards the core derived in Sect. 3.1.1 and converting it to a 10 \ensuremath {\mu }m extinction of 0.7mag, we can approximately double this value.

The size of the 10 \ensuremath {\mu }m emitting region is about 1 $^{\prime \prime }$ or 3700AU in radius. This gives a lower limit of 6.4 \ensuremath{~ 10^{-19}}g \ensuremath{{\rm cm}^{-3}} of total (gas + dust) density or a hydrogen number density of 2.8 \ensuremath{~ 10^{5}} \ensuremath{{\rm cm}^{-3}}.

   
3.4 MSX data of G11

G11 was detected as a point source by the MSX satellite. Flux densities in five bands were obtained from catalogue data and are given in Table 4. The data immediately imply a steep rise in the spectral energy distribution typical for deeply dust-embedded sources.


 

 
Table 4: MSX fluxes of G11
Band ID $\lambda$ [ \ensuremath {\mu } m] Flux [Jy] $\sigma $ [%]
A 8.8 9.13 5
B1 4.29 <16.3  
B2 4.25 < 8.8  
C 12.13 11.2 3
D 14.65 16.9 4
E 21.41 82.3 6


   
3.5 Polarimetry of G341


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure5.ps} \end{figure} Figure 5: Polarization map of G341. The greyscale image is the sum of our narrow-band observations made at the NTT. Polarization vectors are plotted in regions where the signal-to-noise ratio exceeds 3$\sigma $. The scale corresponding to 50% linear polarization is given at the bottom of the image. The ellipse denotes the 2$\sigma $ error of the most probable location of the light source

Imaging polarimetry at near-infrared wavelengths is a helpful tool to fix the position of the illuminating source when it his hidden from direct view and to find evidence for disk-like structures (see, e.g., Ageorges et al. 1996; Burkert et al. 2000).

Figure 5 shows the resulting polarization map of G341. It can be seen that the degree of polarization across the extended emission that marks G341 itself varies between a minimum of 2% and a peak value of 35%. The peak polarization occurs about 3 $^{\prime \prime }$ south of the intensity peak. At this location, the polarization vectors are aligned almost perfectly in an east-west direction.

Scattering theory implies that for single scattering, the polarization vector is perpendicular to the line connecting the light source and the scatterer. Thus, the location of the illuminator can be estimated by computing the centre of gravity of all intersection points of the normals to the polarization vectors. In the case of G341 this was done using vectors with polarization degrees exceeding 10%, i.e. arising from single scattering. The formal error of the position was derived from the scatter of the intersection points. The result of this procedure is shown in Fig. 5, where the ellipse represents the 2$\sigma $-error of the light source location derived from the polarization pattern. The primary illuminator is presumably situated slightly southeast of the peak of the K' emission. The shift may indicate an increase of the column density towards this direction, which is also evident from the comparison of the H and K' images (see Fig. 8). The near-infrared source geometry as inferred from the polarization map might be as follows. Light from a luminous source which is hidden from direct view by dust in the foreground emerges to the northeast and is scattered by dust lanes towards the observer. This causes the arc-like pattern of northern polarization vectors. A fraction of the light is also scattered towards the south, where it is reflected from dust in the foreground. Since the solid angle of the northern dust lanes as seen from the southern foreground cloud is much larger then the solid angle of the star as seen from the northern dust lanes, the alignment of the polarization vectors is no longer centrosymmetric but almost parallel.

  
3.6 AO data - the central sources

   
3.6.1 G11

Figures 6 and 7 show the results of our adaptive optics imaging of G11. To identify the ionizing source of the UCH II, we performed photometry on the 5 presumably stellar sources seen inside or close to the ionized region in Fig. 6. For photometry, an IDL adaption of DAOPHOT (Stetson 1987) was used. All five stars were used to derive a PSF. The results of the photometry are presented in Table 5. Offset positions in this table are given from the reference position in the figures. Columns 4 and 5 give the results of the photometric measurements. Columns 6 and 7 summarize the absolute magnitudes of the sources which have been derived by correcting for the distance modulus of 13.6mag and the mean extinction of 3.5mag in K determined in Sect. 3.2. It should be noted that all sources except the source No. 1, are outside the region where the extinction could be determined from the comparison of Br \ensuremath {\gamma } and radio emission, but at the location of No. 1 the extinction is indeed 3.5mag. Converting the absolute magnitudes into spectral types using a zero age main sequence (ZAMS) from Straizys (1995), we find an O5ZAMS star (source No. 1) and two stars around spectral type B1ZAMS. For two other sources, de-reddening with the standard extinction produces values far from the ZAMS.


 

 
Table 5: Photometry of stellar sources in G11

ID		 Offset RA [ $^{\prime \prime }$] Offset Dec. [ $^{\prime \prime }$] K [mag] H-K [mag] $K_{\rm d}$ [Mag] ( $H-K)_{\rm d}$ [Mag ] Spectral Type (ZAMS)
(1) (2) (3) (4) (5) (6) (7) (8)

1		 0.8 1.3 13.3 2.1 -3.8 -0.1 O5
2 2.8 -0.9 15.5 1.9 -1.6 -0.2 B0.5
3 4.1 -2.6 15.5 3.0 -1.6 0.8 -
4 -3.8 -1.4 14.9 1.1 -2.1 -1.1 -
5 -1.1 -1.8 16.6 2.3 -0.5 0.1 B1.5



  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure6.ps} \end{figure} Figure 6: K' image of G11. The logarithmic gray scale ranges from 0.22mJy/$\Box $ $^{\prime \prime }$ to 11.3mJy/$\Box $ $^{\prime \prime }$. The image was subject to a maximum entropy filtering algorithm (see text). The contours are from the 2cm VLA map by KCW94. The levels are 2, 4, 6, 15, and 30 times the $1\sigma $ level of 0.8mJy/beam


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure7_col.ps} \end{figure} Figure 7: H-band image of G11. The logarithmic gray scale ranges from 0.25mJy/$\Box $ $^{\prime \prime }$ to 17.5mJy/$\Box $ $^{\prime \prime }$. The contours are from the 3.6cm VLA map by KCW94. The levels are the same as for Fig. 6. In the electronic version of the Journal, a colour composite of the J, H, and K' frames is shown instead

   
3.6.2 G341

The results of the AO imaging of G341 are presented in Figs. 8 and 9. Similar to G11, the IDL adaption of DAOPHOT was used to perform photometry on the 9 point sources identifiable in both bands. Due to the lack of detectable Br \ensuremath {\gamma }and free-free emission, we cannot derive exact spectral types for G341. The results of the photometric measurements are presented as a colour-magnitude diagram in Fig. 10. The source magnitudes are corrected for the distance module of 12.8mag. For the brightest K'-band source, a de-reddening vector is given that represents the core extinction of AK = 2.5mag derived in Sect. 3.1.1. Regions of different grey-shades represent the reddening areas of several ZAMS spectral types. From these areas, we conclude that we have detected two late O-type stars and several stars of spectral type BZAMS. The bright K'-band source at the reference position with the extended feature attached to it is not shown in the diagram. Its distance, corrected K'-magnitude is -0.6 mag while it has a colour index of H-K' of 5.5mag. This source does not fall into the reddening area of the ZAMS. Such colour characteristics may arise from excess emission from large amounts of heated dust close to the star. The extended appearance of this object might favour such an explanation. As well as thermal emission of NIR radiation, such dust could scatter photons into the line of sight that would have otherwise escaped unnoticed by the observer. The moderate polarization level across the source of roughly 10% supports this hypothesis.

next previous
Up: High-resolution imaging of ultracompact

Copyright ESO 2001