A&A 370, 100-111 (2001)
DOI: 10.1051/0004-6361:20010227

High-resolution imaging of ultracompact HII regions

III. G11.11-0.40 and G341.21-0.21[*],[*]

Th. Henning1 - M. Feldt2 - B. Stecklum3 - R. Klein1


1 - Astrophysikalisches Institut und Universitäts-Sternwarte Jena, Schillergäßchen 3, 07745 Jena, Germany
2 - Max-Planck-Institut für Astronomie, Königsstuhl 17, 69117 Heidelberg, Germany
3 - Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg, Germany

Received 2 October 2000 / Accepted 7 February 2001

Abstract
We present the first near-infrared images of the two massive southern star-forming regions G11.11-0.40 and G341.21-0.21, obtained with adaptive optics at sub-arcsecond resolution. Together with conventional narrow-band near-infrared images and polarization maps, mid-infrared data, millimetre and radio data, we were able to determine the morphological structure and to constrain the stellar content of the regions. In both cases the molecular cloud cores have masses of about 500  \ensuremath{{M}_{\odot}} and contain clusters of OB stars. This supports the view that massive stars do not form in isolation. In the case of G11.11-0.40 we could identify the central O star responsible for the ionization of the ultracompact H II region. Our results for G341.21-0.21 indicate that this source is a precursor of an ultracompact H II region.

Key words: stars: formation - stars: early type - ISM: H II regions - methods: observational


1 Introduction

Very young massive stars are still deeply embedded in their parental molecular cloud cores and can only be observed at infrared and radio wavelengths (see, e.g., Garay & Lizano 1999; Henning et al. 2000a; Kurtz et al. 2000). Compact luminous infrared sources, hot molecular cores, and ultracompact H II regions (UCH IIs) are tracers of on-going massive star formation. How these stars form is largely unknown, because few observations with high spatial resolution at infrared, sub-millimetre, and radio wavelengths are available. Such observations are required in order to resolve the often complex and distant regions of massive star formation into individual sources and to characterize their local environment. We have started a comprehensive attempt to close this observational gap by near-infrared adaptive optics (AO) observations supplemented with multi-wavelength data (Feldt et al. 1998, 1999).

To continue our study, we selected the two UCH IIs G11.11-0.40 and G341.21-0.21 which were observed with the ALFA and ADONIS AO systems, respectively. Both objects are associated with IRAS sources (G11.11-0.40 with IRAS18085-1931 and G341.21-0.21 with IRAS16487-4423) which have colours typical of ultracompact H II regions (Wood & Churchwell 1989). The CS(2-1) survey performed by Bronfman et al. (1996) demonstrated that the sources are located in dense molecular cloud cores.

The object G11.11-0.40 was identified as an ultracompact radio source (Kurtz et al. 1994; Becker et al. 1994). The source velocity fits the kinematics of the 3 kpc arm. Kurtz et al. adopted a distance of 5.2 kpc which gives an IRAS luminosity of $\sim$ $7.6\ensuremath{~ 10^{4}} $ \ensuremath{{L}_{\odot}} (Walsh et al. 1997). G11.11-0.40 is also associated with high-velocity gas seen in the 12CO (J=1-0) line (Shepherd & Churchwell 1996).

The other object, G341.21-0.21, is associated with an H2O maser detected at the position of the IRAS source (Filho & Escalise 1990), which is generally taken as evidence for massive star formation. In addition, an OH maser was detected by Caswell (1998). In this paper, we adopt a kinematic distance towards this source of 3.7 kpc. Note that this distance corresponds to the near solution of the kinematic model, whereas Forster & Caswell (1999) prefer the far solution of 15.3 kpc. That far distance would, however, yield a total luminosity of more than 106 \ensuremath{{L}_{\odot}}, a value that seemed unrealistically large to us. For our chosen distance, the luminosity resulting from the IRAS fluxes is $\sim 6.1\ensuremath{~ 10^{4}} $ \ensuremath{{L}_{\odot}}.

2 Observations and data reduction


 

 
Table 1: Observations of G11.11-0.40

Date		 $\lambda$ Tel./Instr. FOV$^{\rm a}$ PSF Ref. Star$^{\rm b}$ Limiting
        FWHM   Mag.$^{\rm c}$

1999 Sep.		 J/H/K' CA3.5(ALFA/OMEGA) 40 $^{\prime \prime }$ 0 $.\!\!^{\prime\prime}$5/0 $.\!\!^{\prime\prime}$5/0 $.\!\!^{\prime\prime}$4$^{\rm d}$ FS28 (10.744/10.644/10.602) 19.5/19.8/19.1
1998 Jul. Br$\gamma$/Cont/H2(1-0)S1 ESO2.2m/IRAC2b 130 $^{\prime \prime }$ 1 $.\!\!^{\prime\prime}$5 HD 210427 (8.852) $\sim$17.5
1998 Mar. 1.3mm ESOSEST(Bolo) 4$^\prime$ 23 $^{\prime \prime }$ Uranus 50mJy/beam
$^{\rm a}$ Field of view for single frames.
$^{\rm b}$ Brightness given in magnitudes for the observed wavelength.
$^{\rm c}$ Derived from background noise for point sources with given PSF (1$\sigma $ detection).
$^{\rm d}$ Measured on target, the resolution on the WFS source is 0 $.\!\!^{\prime\prime}$19 (Strehl ratio 17%) in K'. The seeing was 0 $.\!\!^{\prime\prime}$8 in K'.



 

 
Table 2: Observations of G341.21-0.21

Date		 $\lambda$ Tel./Instr. FOV$^{\rm a}$ PSF Ref. Star$^{\rm b}$ Limiting
        FWHM   Mag.$^{\rm c}$

1999 Mar.		 K' Pol ESONTT / SOFI 4.9$^\prime$ 0 $.\!\!^{\prime\prime}$5 - -
1998 Jul. Br$\gamma$/Cont/H2(1-0)S1 ESO2.2m/IRAC2b 130 $^{\prime \prime }$ 1 $.\!\!^{\prime\prime}$5 HD 210427 (8.852) $\sim$17.5
1996 Oct. N ESO2.2(MANIAC) 43 $.\!\!^{\prime\prime}$5 1 $.\!\!^{\prime\prime}$1 $\alpha$Sco (-4.54) 6.3
1998 Mar. 1.3mm ESOSEST(Bolo) 4$^\prime$ 23 $^{\prime \prime }$ Uranus 50mJy/beam
1995 Aug. H/K' ESO3.6(ADONIS/SHARP2) 13 $^{\prime \prime }$ 0 $.\!\!^{\prime\prime}$39/0 $.\!\!^{\prime\prime}$25$^{\rm d}$ HD 97048/HD 2811 (6.19/7.067)  
$^{\rm a}$ Field of view for single frames.
$^{\rm b}$ Brightness given in magnitudes for the observed wavelength.
$^{\rm c}$ Derived from background noise for point sources with given PSF (1$\sigma $ detection).
$^{\rm d}$ The seeing was 0 $.\!\!^{\prime\prime}$7 in K'.


2.1 Adaptive optics NIR imaging

2.1.1 G11.11-0.40
G11.11 was observed as part of the ALFA science demonstration run in September 1999. This programme, designed to show the science capabilities of the new AO system ALFA (Hippler et al. 1998) on the 3.5m telescope on Calar Alto (Spain), allowed flexible scheduling of the observations to ensure optimal meteorological conditions. J, H, and K' images were taken in seeing conditions around 0 $.\!\!^{\prime\prime}$8 (K'). ALFA was locked on the mV=10.8mag star GSC 0627201030. 5$\times$5 subapertures on the wavefront sensor were used, allowing the correction of 18 modes at a speed of 100Hz. In spite of an airmass of 2.4 during the observations, a maximum Strehl ratio of 17% was reached in K', yielding a FWHM of 0 $.\!\!^{\prime\prime}$19 on the reference star. However, due to the target's distance of $\sim$20 $^{\prime \prime }$ from that star, this resolution degrades to 0 $.\!\!^{\prime\prime}$44 at the location of G11. In H and J these values are 0 $.\!\!^{\prime\prime}$52 and 0 $.\!\!^{\prime\prime}$55. In each band, a mosaic of five frames taken at slightly different positions were obtained. The total integration time amounted to one minute per band at each position. To achieve a photometric calibration and access the seeing value, open loop images of the UKIRT standard star FS28 were taken.

2.1.2 G341.21-0.21
For this object, near-infrared H and K' imaging was performed in August 1995 using ESO's AO system ADONIS (Beuzit et al. 1994) on the 3.6m telescope at La Silla/Chile. In both bands, data were taken at three positions to derive the sky background directly from the images. The total integration time was 6 min per band. The seeing during the observations was around 0 $.\!\!^{\prime\prime}$7 in K', the airmass was 1.06. The mV=12.7 mag star GSC0788001158, located at a distance of 12 $^{\prime \prime }$, served as the wavefront sensor star. The higher order AO corrections achieved a resolution of 0 $.\!\!^{\prime\prime}$3 in K' and 0 $.\!\!^{\prime\prime}$28 in H, respectively. In both bands, the Strehl number is approximately 6%. For photometric calibration, images of the standard star HD 2811 were taken.

2.1.3 Common reduction scheme
All frames were subject to the standard NIR reduction scheme for sky-subtraction, flat-fielding, bad pixel removal and photometric calibration. Sky frames were constructed by stacking the image frames taken at different mosaic positions directly and adjusting the mean background level through an additive constant. Then, for each pixel, the minimum (G341) or the next higher value (G11) was selected to efficiently remove all sources from the sky frame. Photometric calibration was achieved by a simple procedure of multiplying the frames with the known counts-(per unit time)-to-flux ratio of the standard frame. No corrections for colour terms or atmospheric extinction were introduced. This limits the accuracy of our photometry to about 0.1mag, which is sufficient for our purposes. Astrometric calibration was made by comparison to the corresponding images from the digitized sky survey (DSS). For G11, a set of five stars with their positions known from the DSS was fitted to produce the astrometric reference frame. For G341, 7 stars were fitted in the larger scale narrow-band continuum image (see below). The astrometric frame of that image was then transferred to the high-resolution images via comparison of 4 stars.

2.2 NIR narrow-band observations

Both targets were observed in June 1998 using the IRAC2b NIR-camera at ESO's 2.2m telescope on La Silla/Chile. Four filters were used with central wavelengths 2.105  \ensuremath {\mu }m (BP4), 2.121  \ensuremath {\mu }m (BP5, used as H2(1-0)S1 filter), 2.148  \ensuremath {\mu }m (BP7), and 2.164  \ensuremath {\mu }m (BP8, used as Br \ensuremath {\gamma } filter). The effective wavelengths were taken from the IRAC2b manual. The use of lens C resulted in a pixel scale of 0 $.\!\!^{\prime\prime}$507 per pixel. A mosaic of five frames was taken with the object once in the centre of the detector and once in the centre of each quadrant. The total integration time on source added up to 20 min. The same procedure was performed for the standard star HD 210427 with 10 min of total integration time. Sky subtraction, flat-fielding, bad pixel removal and photometric calibration were achieved in the same way as for the broad-band images. The procedure of subtracting the continuum for photometry of the Br$\gamma$ emission is described in Feldt et al. (1999). Astrometric calibration was achieved in the same way as for the broad-band images via a comparison with the DSS.

2.3 Polarimetric observations of G11.11-0.40

Polarimetry of G11 was carried out in March 1999 on ESO's NTT on La Silla/Chile. The images where taken using SOFI'S NB $2.195\,\ensuremath{\mu} {\rm m}$ filter ( $\Delta \lambda = 0.03$ \ensuremath {\mu }m) and a Wollaston prism as polarizer. Two perpendicular polarization orientations were mapped on the detector simultaneously. Two more orientations were obtained after offsetting the NTT's de-rotator by 45$^{\rm o}$. For each orientation of the de-rotator, 5 frames of 180s integration time with slight offsets in between were taken. The procedure was repeated using the NBBr \ensuremath {\gamma } filter of SOFI. Sky frames were constructed from the offset frames in the usual way. Flatfielding, sky subtraction, and bad-pixel removal followed standard IR techniques. No photometric calibration was done for these data. Polarization vectors were computed from the sum of the continuum and Br \ensuremath {\gamma } images using the light ratios in the four polarization orientations. Instrumental effects were calibrated out by declaring the polarization of 23 field stars to be zero, thereby computing an offset to the resulting Stokes vectors which yield the intrinsic instrumental polarization.

2.4 N-band observations of G341.21-0.21

G341 was subject to observations using the MANIAC (Böker et al. 1997) mid-infrared camera at ESO's 2.2m telescope on La Silla/Chile in March 1998. MANIAC's N-band filter ( $\lambda = 10.5\,\ensuremath{\mu} {\rm m}, \Delta\lambda=5.0\,\ensuremath{\mu} {\rm m}$) was used. The total integration time on source was 640s. This includes the combination of the two chopping beams. For photometric calibration, $\alpha$ Sco was observed as a standard star. As G341 is the only source visible in the N-band frame, the astrometric reference frame had to be established by identifying the maximum of the emission with the maximum of the broad-band K'-emission from the target.

2.5 1.3 mm continuum observations

The continuum radiation of both targets was mapped in March 1998 at the 15m SEST telescope at La Silla/Chile. The detector system was the $^{\rm 3}$He-cooled single-channel bolometer system (Kreysa 1990). The equivalent bandwidth of the bolometer is $\approx$50GHz centred on a frequency of $\nu_0 = 236\,$GHz ( ${\rm\lambda_0 = 1.27~mm}$). The effective beam size at this wavelength is $\theta_{\rm b} = 23$ $^{\prime \prime }$.

The source was mapped four times with the "double beam'' technique described first by Emerson et al. (1979). To generate the dual beams, a focal plane chopper with a chopping frequency of 6 Hz was used. Chopping was done in azimuth. The chopper throw was 67 $^{\prime \prime }$. The map rows were generated by moving the telescope continuously along the direction of the beam separation (i.e. in azimuth) with a scanning velocity of 8 $^{\prime \prime }$/s and an elevation separation between adjacent scans of 8 $^{\prime \prime }$.

Calibration maps of the planet Uranus (adopted brightness temperature 96K; Griffin & Orton 1993) were obtained with the same technique and parameters as used for the two science targets. The atmospheric transmission was measured by sky dips. The telescope pointing was found to be repeatable within $\pm$5 $^{\prime \prime }$.

Data reduction was performed with the SEST standard software and with the software package MOPSI (written by R. Zylka) which use the NOD2 and GAG libraries.

3 Results

3.1 General morphology - Millimetre continuum and MSX data

First, we present the results of the 1.3mm continuum mapping of the two targets to give an overview of the regions where the UCH IIs are located. The resulting maps are shown in Figs. 1 and 2 together with contours of the 8.8 \ensuremath {\mu }m emission based on MSX images[*]. The coordinate systems in all figures relating to G11 are systems relative to the position of the UCH II given by Kurtz et al. (1994). Coordinates for G341 are centred on the OH maser position of Caswell (1998).

Note that the 1.3mm emission consists of the sum of free-free- and dust emission at that wavelength. The free-free contribution has been subtracted from the G11 map in Fig. 1. This was achieved by multiplying the 2cm map from KCW94 with a factor of (2/0.13)0.1 (assuming optically thin free-free emission) and convolving the resulting map with the SEST beam before subtracting it from the 1.3mm map. We note that the free-free contribution to the 1.3mm flux derived by this method is not really significant. At the maximum of the 2cm map we compute a relative contribution of 5% from free-free emission to the 1.3mm emission.

As for G341, no high-resolution continuum maps currently exist at centimetre wavelengths. The non-detection of Br \ensuremath {\gamma }-radiation from this source implies, however, that very little ionisation might be present in that source and thus no correction has to be made to the 1.3mm flux.

Both targets exhibit a rather irregular structure at 1.3mm. The diameters are of the order of 2 $.\mkern-4mu^\prime$5. However, G11 appears to be more concentrated towards a single core, while G341 comprises two major peaks with a clear gap in between, an indication for the presence of two dense cores. There seems to be an east-west elongation of the core of G11 while the 8.8 \ensuremath {\mu }m emission of this source is extended in north-south direction. This suggests that the heating sources are embedded in a filament or surrounded by a dust torus, similar to NGC6334A (Kraemer et al. 1999; Sandell 1999). The strongest 1.3mm peak of G341 lies immediately to the northeast of the reference position. The weaker secondary peak, more to the southeast, coincides roughly with the position of the infrared source IRAS 16487-4423 which Bronfman et al. (1996) listed as a source with colour characteristics typical of UCH IIs. We note that the 8.8 \ensuremath {\mu }m fluxes from the two cores of G341 behave in the opposite way to the behaviour of 1.3mm emission. Thus, it seems reasonable that the source associated with the maximum of the 1.3mm emission is less evolved compared to the UCH II-type object to the southeast. The offsets between the peaks of 8.8 \ensuremath {\mu }m and 1.3mm emission are presumably indicating that star formation started at the outskirts of these cores and is progressing towards their centres.

   
3.1.1 Dust masses


 

 
Table 3: Masses derived from the 1.3mm data

Region		 Ass. temp. [K] mm-flux [Jy] Mass [ \ensuremath{{M}_{\odot}}]

G11 Core		 40 2.2 620
G11 Halo 15 8.2 1.2 \ensuremath{~ 10^{4}}
G341 Core 1 40 2.8 400
G341 Core 2 40 2.6 370
G341 Halo 15 8.1 6.0 \ensuremath{~ 10^{3}}


The flux density emitted from an optically thin dust cloud with mass $M_{\rm dust}$ at frequency $\nu$ is given by:

 \begin{displaymath}F_{\nu} = \frac{2 M_{\rm dust} h \nu^3 \kappa_{\nu}}{d^2 c^2}\frac{1}{{\rm e}^{\frac{h\nu}{kT}}-1}\cdot \end{displaymath} (1)

In this expression, the dust mass absorption coefficient $\kappa_{\nu}$ is taken from Ossenkopf & Henning (1994) for the appropriate wavelength ( $\kappa=0.9$cm2g-1 for 1.3mm) assuming a gas density of 105 cm-3, a size distribution after MRN (Mathis et al. 1977), grains without ice mantles, and a coagulation time of 105 yr. The quantity T is the dust temperature, h the Planck constant, k the Boltzmann constant, and d the distance towards the source. In Table 3, the total masses obtained from $M_{\rm dust}$ with a gas-to-dust ratio of 150 are compiled.

G11 can be divided into a central region of $\sim$ $40\hbox{$^{\prime\prime}$ }$ diameter exhibiting an integrated flux density of 2.2 Jy and a halo region with $\sim$ $180\hbox{$^{\prime\prime}$ }$ diameter and a total flux density of 8.2 Jy. Assuming both regions to be concentric spheres and correcting for the halo contribution in the core aperture, we derive a cloud mass of 620 \ensuremath{{M}_{\odot}} in the core and 1.2 \ensuremath{~ 10^{4}} \ensuremath{{M}_{\odot}} in the halo. The temperatures used for this estimate were 40K in the core and 15K in the halo. When using such values, one should keep in mind that by a slight error of, e.g., 5K in the temperatures assumed above, the mass estimates can vary by a factor of up to 2 for the halo (assumed temperature of 15K) or 1.3 for the core (assumed temperature of 40K).

For a classification of the embedded stellar sources, it is crucial to de-redden their colours and thus to know the extinction towards these sources. This extinction can be measured in two ways, via the dust mass and via a comparison of radio free-free and NIR recombination emission. We will now derive K-band extinction values from the measured dust masses; a comparison to values derived from the second method will be given in the next section.

The complete dust mass seen in the core aperture (core plus contributing halo) corresponds to a mass column density of 6.7 \ensuremath{~ 10^{-3}}gcm-2. With a dust mass absorption coefficient of 2.15 \ensuremath{~ 10^{3}}cm-1g-1, again taken from Ossenkopf & Henning (1994) - this time for 2.2 \ensuremath {\mu }m, we derive a K-band extinction of 5.5mag. Assuming the UCH II to be embedded halfway into this cloud, we thus expect an extinction of AK=2.8mag. Note that when using Ryter's (1996) expression for the extinction,

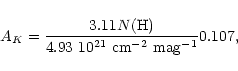\begin{displaymath}A_K=\frac{3.11 N({\rm H})}{4.93~10^{21}~\mbox{cm}^{-2}~\mbox{mag}^{-1}}0.107, \end{displaymath} (2)

where the last factor represents the conversion from AV to AKafter Mathis (1990), we get an extinction of 2.6mag halfway into the cloud. Ryter (1996) assumes the ratio of visual extinction to hydrogen column density, AV / N(H), to be that of the interstellar medium while the values of Ossenkopf & Henning (1994) are for dust grains that have been subject to coagulation for 105 years. Converting the derived extinctions to the V-band after Mathis (1990), we get AV=25.6mag for the coagulated case and AV= 24.2mag for the interstellar type case. We note that these estimates depend linearly on the mass and thus have the same uncertainty with respect to the chosen temperatures.

For G341, we find two core regions (see Fig. 2). The main peak has an integrated flux density of 2.8Jy, the secondary peak to the southeast of 2.6Jy. A flux density of 8.1Jy remains in the extended emission of the halo. Using the same temperatures as for G11, we find cloud masses of 400 \ensuremath{{M}_{\odot}} and 370 \ensuremath{{M}_{\odot}} in the primary and in the secondary cores, respectively, and 6000 \ensuremath{{M}_{\odot}} in the halo.

Applying the appropriate extinction estimation, we derive a K-band extinction of AK=2.1 mag (AV =19 mag) in the coagulation case or AK=1.7 mag (AV =16 mag) in the interstellar grain case. Both estimates assume the source to be embedded halfway into the halo.


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure1.ps} \end{figure} Figure 1: 1.3mm continuum map of G11 with 8.8 \ensuremath {\mu } m emission measured by the MSX satellite (contours). Free-free emission has been subtracted from this map (see text). The grayscale is given by the bar on the right. The contour levels are at 1, 1.6, 2.5, 4, 6.25, and 9.9 times 5 \ensuremath{~ 10^{-6}}Wm-2sr-1
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure2.ps}\end{figure} Figure 2: Same as Fig. 1 but for G341. The contour levels for the overlayed 8.8 \ensuremath {\mu } m map are at 1, 1.6, 2.5, 4, 6.25, and 9.9 times 6.3 \ensuremath{~ 10^{-6}}Wm-2sr-1
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure3_col.ps} \end{figure} Figure 3: Narrow-band emission from G11 (Strong contours). Underlayed is the narrow-band continuum image at 2.148 \ensuremath {\mu } m. (In the electronic version of the journal, a colour composite of the three narrow band images is underlayed. Here, blue denotes Br \ensuremath {\gamma }, green denotes continuum and red H2(1-0)S1 emission.) The strong contours show the remaining Br \ensuremath {\gamma } emission after subtraction of the continuum. Levels are 2, 4, and 8 times 0.04mJy/$\Box $ $^{\prime \prime }$ (solid strong contours) and -2, -4, and -8 times 0.04mJy/$\Box $ $^{\prime \prime }$ (dotted strong contours). Negative values close to bright stars indicate imperfect continuum subtraction. The light contours are from the 1.3mm map (Compare Fig. 1)
Open with DEXTER

   
3.2 Narrow-band data - The ionized material

Figures 3 and 4 show the continuum-subtracted Br \ensuremath {\gamma } emission from G341 and G11, respectively.

All printed images taken in the infrared spectral range were filtered with the multi-scale maximum-entropy method described by Pantin & Starck (1995). This is to enhance the visibility of details in the printed version only.

No line emission is detected from G341. G11 does show Br \ensuremath {\gamma } emission, the integrated flux density is 0.019Jy. A comparison of the Br \ensuremath {\gamma }flux density distribution and the 2 and 3.6cm maps were used to derive the NIR extinction towards the source. For a thorough description of the technique used for this comparison, we refer the reader to an earlier paper (Feldt et al. 1998). As the spectral index between the 2cm and the 3.6cm emission measured by KCW94 is not exactly 0.1, as expected for optically thin free-free emission, we use only the 2cm map for the comparison with our Br \ensuremath {\gamma }data and assume this radiation to be optically thin. Assuming an electron temperature of 104K we derive a mean emission measure across G11 of 7.2 \ensuremath{~ 10^{5}} pccm-6 with a peak value of 2.8 \ensuremath{~ 10^{6}} pccm-6. Assuming the peak size to be of the order of the VLA resolution element, i.e. 0 $.\!\!^{\prime\prime}$5 or 0.01 pc, this implies a peak electron density of 1.6 \ensuremath{~ 10^{4}} \ensuremath{{\rm cm}^{-3}}. The mean electron density in G11 is about 4.3 \ensuremath{~ 10^{3}} \ensuremath{{\rm cm}^{-3}}. When predicting the Br \ensuremath {\gamma } flux density from these values and comparing them to those measured, we derive a mean extinction of 3.5mag at the wavelength of Br \ensuremath {\gamma }. The peak value is 4.3mag. Given the uncertainty of how deep the source actually is embedded in the cloud core, these values agree reasonably well with the extinction of 2.8 mag derived in Sect. 3.1.1.


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure4_col.ps} \end{figure} Figure 4: Narrow-band continuum image of the area around G341 at 2.148 \ensuremath {\mu } m. The logarithmic gray-scale ranges from 6.4mJy/$\Box $ $^{\prime \prime }$ to 256mJy/$\Box $ $^{\prime \prime }$. In the electronic version of the journal, this figure contains a colour composite which shows the H2(1-0)S1-emission in red , the continuum image in green and the Br \ensuremath {\gamma }-emission in blue. The contours are from the 1.3mm map (see Fig. 2)
Open with DEXTER

  
3.3 $\mathsfsl N$-band data of G341

From our N-band map of G341, which is shown in Fig. 9 as a contour plot, we derive a total flux density of 1.4 Jy from the source. When we try to determine a mass of hot ($\sim$100K) dust from this flux using Eq. (1) with the proper values and an extinction coefficient of 2.4 \ensuremath{~ 10^{3}}cm2g-1, we derive a dust mass of 6 \ensuremath{~ 10^{-4}} \ensuremath{{M}_{\odot}}. This is of course an absolute lower limit, because G341 is situated near the core of the 1.3mm emission region and thus the dust emission is certainly far from being optically thin. Correcting for the extinction towards the core derived in Sect. 3.1.1 and converting it to a 10 \ensuremath {\mu }m extinction of 0.7mag, we can approximately double this value.

The size of the 10 \ensuremath {\mu }m emitting region is about 1 $^{\prime \prime }$ or 3700AU in radius. This gives a lower limit of 6.4 \ensuremath{~ 10^{-19}}g \ensuremath{{\rm cm}^{-3}} of total (gas + dust) density or a hydrogen number density of 2.8 \ensuremath{~ 10^{5}} \ensuremath{{\rm cm}^{-3}}.

   
3.4 MSX data of G11

G11 was detected as a point source by the MSX satellite. Flux densities in five bands were obtained from catalogue data and are given in Table 4. The data immediately imply a steep rise in the spectral energy distribution typical for deeply dust-embedded sources.


 

 
Table 4: MSX fluxes of G11
Band ID $\lambda$ [ \ensuremath {\mu } m] Flux [Jy] $\sigma $ [%]
A 8.8 9.13 5
B1 4.29 <16.3  
B2 4.25 < 8.8  
C 12.13 11.2 3
D 14.65 16.9 4
E 21.41 82.3 6


   
3.5 Polarimetry of G341


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure5.ps} \end{figure} Figure 5: Polarization map of G341. The greyscale image is the sum of our narrow-band observations made at the NTT. Polarization vectors are plotted in regions where the signal-to-noise ratio exceeds 3$\sigma $. The scale corresponding to 50% linear polarization is given at the bottom of the image. The ellipse denotes the 2$\sigma $ error of the most probable location of the light source
Open with DEXTER

Imaging polarimetry at near-infrared wavelengths is a helpful tool to fix the position of the illuminating source when it his hidden from direct view and to find evidence for disk-like structures (see, e.g., Ageorges et al. 1996; Burkert et al. 2000).

Figure 5 shows the resulting polarization map of G341. It can be seen that the degree of polarization across the extended emission that marks G341 itself varies between a minimum of 2% and a peak value of 35%. The peak polarization occurs about 3 $^{\prime \prime }$ south of the intensity peak. At this location, the polarization vectors are aligned almost perfectly in an east-west direction.

Scattering theory implies that for single scattering, the polarization vector is perpendicular to the line connecting the light source and the scatterer. Thus, the location of the illuminator can be estimated by computing the centre of gravity of all intersection points of the normals to the polarization vectors. In the case of G341 this was done using vectors with polarization degrees exceeding 10%, i.e. arising from single scattering. The formal error of the position was derived from the scatter of the intersection points. The result of this procedure is shown in Fig. 5, where the ellipse represents the 2$\sigma $-error of the light source location derived from the polarization pattern. The primary illuminator is presumably situated slightly southeast of the peak of the K' emission. The shift may indicate an increase of the column density towards this direction, which is also evident from the comparison of the H and K' images (see Fig. 8). The near-infrared source geometry as inferred from the polarization map might be as follows. Light from a luminous source which is hidden from direct view by dust in the foreground emerges to the northeast and is scattered by dust lanes towards the observer. This causes the arc-like pattern of northern polarization vectors. A fraction of the light is also scattered towards the south, where it is reflected from dust in the foreground. Since the solid angle of the northern dust lanes as seen from the southern foreground cloud is much larger then the solid angle of the star as seen from the northern dust lanes, the alignment of the polarization vectors is no longer centrosymmetric but almost parallel.

  
3.6 AO data - the central sources

   
3.6.1 G11

Figures 6 and 7 show the results of our adaptive optics imaging of G11. To identify the ionizing source of the UCH II, we performed photometry on the 5 presumably stellar sources seen inside or close to the ionized region in Fig. 6. For photometry, an IDL adaption of DAOPHOT (Stetson 1987) was used. All five stars were used to derive a PSF. The results of the photometry are presented in Table 5. Offset positions in this table are given from the reference position in the figures. Columns 4 and 5 give the results of the photometric measurements. Columns 6 and 7 summarize the absolute magnitudes of the sources which have been derived by correcting for the distance modulus of 13.6mag and the mean extinction of 3.5mag in K determined in Sect. 3.2. It should be noted that all sources except the source No. 1, are outside the region where the extinction could be determined from the comparison of Br \ensuremath {\gamma } and radio emission, but at the location of No. 1 the extinction is indeed 3.5mag. Converting the absolute magnitudes into spectral types using a zero age main sequence (ZAMS) from Straizys (1995), we find an O5ZAMS star (source No. 1) and two stars around spectral type B1ZAMS. For two other sources, de-reddening with the standard extinction produces values far from the ZAMS.


 

 
Table 5: Photometry of stellar sources in G11

ID		 Offset RA [ $^{\prime \prime }$] Offset Dec. [ $^{\prime \prime }$] K [mag] H-K [mag] $K_{\rm d}$ [Mag] ( $H-K)_{\rm d}$ [Mag ] Spectral Type (ZAMS)
(1) (2) (3) (4) (5) (6) (7) (8)

1		 0.8 1.3 13.3 2.1 -3.8 -0.1 O5
2 2.8 -0.9 15.5 1.9 -1.6 -0.2 B0.5
3 4.1 -2.6 15.5 3.0 -1.6 0.8 -
4 -3.8 -1.4 14.9 1.1 -2.1 -1.1 -
5 -1.1 -1.8 16.6 2.3 -0.5 0.1 B1.5



  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure6.ps} \end{figure} Figure 6: K' image of G11. The logarithmic gray scale ranges from 0.22mJy/$\Box $ $^{\prime \prime }$ to 11.3mJy/$\Box $ $^{\prime \prime }$. The image was subject to a maximum entropy filtering algorithm (see text). The contours are from the 2cm VLA map by KCW94. The levels are 2, 4, 6, 15, and 30 times the $1\sigma $ level of 0.8mJy/beam
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure7_col.ps} \end{figure} Figure 7: H-band image of G11. The logarithmic gray scale ranges from 0.25mJy/$\Box $ $^{\prime \prime }$ to 17.5mJy/$\Box $ $^{\prime \prime }$. The contours are from the 3.6cm VLA map by KCW94. The levels are the same as for Fig. 6. In the electronic version of the Journal, a colour composite of the J, H, and K' frames is shown instead
Open with DEXTER

   
3.6.2 G341

The results of the AO imaging of G341 are presented in Figs. 8 and 9. Similar to G11, the IDL adaption of DAOPHOT was used to perform photometry on the 9 point sources identifiable in both bands. Due to the lack of detectable Br \ensuremath {\gamma }and free-free emission, we cannot derive exact spectral types for G341. The results of the photometric measurements are presented as a colour-magnitude diagram in Fig. 10. The source magnitudes are corrected for the distance module of 12.8mag. For the brightest K'-band source, a de-reddening vector is given that represents the core extinction of AK = 2.5mag derived in Sect. 3.1.1. Regions of different grey-shades represent the reddening areas of several ZAMS spectral types. From these areas, we conclude that we have detected two late O-type stars and several stars of spectral type BZAMS. The bright K'-band source at the reference position with the extended feature attached to it is not shown in the diagram. Its distance, corrected K'-magnitude is -0.6 mag while it has a colour index of H-K' of 5.5mag. This source does not fall into the reddening area of the ZAMS. Such colour characteristics may arise from excess emission from large amounts of heated dust close to the star. The extended appearance of this object might favour such an explanation. As well as thermal emission of NIR radiation, such dust could scatter photons into the line of sight that would have otherwise escaped unnoticed by the observer. The moderate polarization level across the source of roughly 10% supports this hypothesis.

4 Discussion

4.1 The nature of G11

4.1.1 An embedded source

From Fig. 1 and the estimates regarding dust masses and resulting extinctions made in Sect. 3.1.1, it becomes clear that G11 is located close to the centre of a large molecular cloud. The K-band extinction, estimated in Sect. 3.1.1 under the assumption of G11 being located halfway into the observed cloud, amounts to 3.8mag. This matches fairly well with the mean extinction of 3.5mag measured by the comparison from free-free and Br \ensuremath {\gamma } radiation in Sect. 3.2. The peak value of 4.3mag derived by that comparison cannot be compared directly to the dust-based estimate because it appears on much smaller spatial scales than the resolution of the 1.3mm map can reproduce.

We find the density of the ionized gas of 4.3 \ensuremath{~ 10^{3}} \ensuremath{{\rm cm}^{-3}} derived in Sect. 3.2 to be slightly lower than the general hydrogen density of 3.6 \ensuremath{~ 10^{4}} \ensuremath{{\rm cm}^{-3}} based on the dust mass. For the outer regions, the millimetre-continuum measurements yield a lower value of 5.8 \ensuremath{~ 10^{3}} \ensuremath{{\rm cm}^{-3}}. This means that the electron density measured from the radio continuum at 2cm is of the same order as the measured halo density of the G11 molecular cloud, but falls short of the measured core density.

The coarse spatial resolution of the 1.3mm map would not reveal the presence of a potential cavity blown free of dust by the central O star. The density inside this cavity might be significantly lower than in the rest of the cloud core. Indeed, when judging from Figs. 6 and 7, the ionized region seems to be located at the rim of a region of much higher extinction immediately to the south (no fainter background sources south of G11 in Fig. 6). When judging the position from Fig. 1, the UCH II is located on the southern rim of the cloud core. This means that a small central cavity might indeed exist.

  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure8.ps} \end{figure} Figure 8: K' image of G341. The logarithmic gray scale ranges from 0.14mJy/$\Box $ $^{\prime \prime }$ to 33.8mJy/$\Box $ $^{\prime \prime }$. The image was subject to a maximum entropy filtering algorithm (see text). The position of the hydroxyl maser from Caswell (1998) is marked by a cross. The contours are from the H-band image, ranging from 0.007mJy/$\Box $ $^{\prime \prime }$ to 4.7mJy/$\Box $ $^{\prime \prime }$ in steps of 1.58 (0.5 mag)
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8cm]{figure9.ps} \end{figure} Figure 9: H-band image of G341. The logarithmic gray scale ranges from 0.23mJy/$\Box $ $^{\prime \prime }$ to 52.6mJy/$\Box $ $^{\prime \prime }$. The image was subject to a maximum entropy filtering algorithm (see text). The contours are from the N-band map. Contour levels are 84, 118, 151, 185, 218, and 252mJy/$\Box $ $^{\prime \prime }$. Again, the cross marks the position of the hydroxyl maser from Caswell (1998)
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=7.7cm]{figure10.ps} \end{figure} Figure 10: Colour-magnitude diagram of the point sources in G341
Open with DEXTER

4.1.2 The central engine
A major result of our observations is the identification of the ionizing source of G11. We should stress that G11 is one of the rare cases so far, where the central ionizing star of an UCH II could indeed be identified by NIR observations. In Sect. 3.6, we derived a spectral type of O5 for the central star of G11 from the colour-magnitude information. When estimating the necessary Lyman continuum photon flux to maintain the ionization of the nebula using expression (1) from KCW94,

 \begin{displaymath}N_{\rm c} \ge 8.04 ~ 10^{46} T_{\rm e}^{-0.85}U^3 , \end{displaymath} (3)

we end up with more than $N_{\rm c} \ge 10^{48.7}$ \ensuremath{{\rm s}^{-1}} Lyman continuum photons required. Here, we used an excitation parameter $U = r n_{\rm e}^{\frac{2}{3}} [\mbox{pc\,cm}^{-2}]$ computed from a linear size of G11 of r= 0.2 pc and the electron density of $n_{\rm e}=4.3\ensuremath{~ 10^{3}} $ \ensuremath{{\rm cm}^{-3}} from Sect. 3.2. According to Panagia (1973), this flux can be delivered by a star of spectral type O6.8ZAMS. This is of course only a lower limit for the spectral type. If some Lyman photons are absorbed by dust, a hotter star is needed to provide the ionizing flux.

Figure 11 shows the spectral energy distribution of G11. The data are taken from the IRAS point source catalogue (including the LRS spectrum), the MSX catalogue (see Sect. 3.4) and from our observations. Apart from the steeply rising shape of the SED up to 100 \ensuremath {\mu }m, which is typical for UCH IIs, we notice a strong emission feature around 7 \ensuremath {\mu }m. This feature is probably due to polycyclic aromatic hydrocarbons (PAHs). When we integrate the flux using a simple trapezoidal integration, we end up with a total luminosity of 7.2 \ensuremath{~ 10^{4}} \ensuremath{{L}_{\odot}}. This corresponds to a difference of 12.14mag from the bolometric absolute magnitude of a G2V star. According to Straizys (1995), the resulting bolometric absolute magnitude of -7.53mag points to a star of spectral type O7ZAMS. We note that although the error of the rough integration may be considerable, we expect it to be no larger than about 30%. This estimate comes from a comparison with an artificial SED for G11 that peaks at 200 \ensuremath {\mu }m at 400Jy and then stays constant out to 1.3mm.


  \begin{figure} \par\includegraphics[angle=90,width=8.1cm]{figure11.ps} \end{figure} Figure 11: Spectral energy distribution of G11
Open with DEXTER

Since both the SED and the ionization point to an O7ZAMS star, it appears that the determination of the spectral type from the colour magnitude diagram is contaminated by some additional flux in K and H. Since the de-reddening procedure described in Sect. 3.6.1 places the central star exactly on the ZAMS within the photometric errors of about 0.1mag, it seems unlikely that large errors arise from this step. Another error source might be the slope of NIR reddening vector, but the existing reddening laws differ little in this near-infrared region. Contamination of the Kmagnitude by Br \ensuremath {\gamma }-flux might be a reasonable cause, but our measurements show that the Br \ensuremath {\gamma }-flux contributes less than 0.1mag to the total K-magnitude, whereas the difference in brightness between an O7 and an O5ZAMS star is about 0.7mag. This brightness difference means that we measure about twice the flux in the NIR than expected from a star of spectral type O7.

Two possible explanations remain: first, the surrounding dust might scatter light into the line of sight that would not have reached the observer without this dust. The resulting anisotropic radiation distribution might resemble a source brighter in the NIR than is actually present. Future polarization measurements might clarify whether this is the case or not. Second, an unresolved binary system or even a very compact cluster might be contained in what we identify as the ionizing source. The most massive star allowed to contribute to the total luminosity of the system, besides an O7 star, would be of spectral type B0. An unresolved binary consisting of an O7 and a B0 star would have a combined K-band magnitude of 13.4mag, close to the measured 13.3mag and within the 0.1mag error limit. The colour index of the system would not be affected by the binary. The total luminosity of the system would be 30% above the result of the trapezoidal integration, only just within the limit of the above error estimate. A somewhat fainter star of spectral type B would be a better fit here. Several other stars of spectral type B have been identified inside G11 (see Table 5), so this might be asuggestive of an embedded cluster. However, our detection limit does not allow us to probe for more deeply embedded or lower mass members.

4.1.3 Star formation efficiency

The total mass of the G11 region is 1 \ensuremath{~ 10^{4}} \ensuremath{{M}_{\odot}}. As the central heating object appears to be of spectral type O7, its mass should be about 25 \ensuremath{{M}_{\odot}}. Two additional stars have been identified inside G11, both of spectral type around B1 and thus contributing a total mass of about 20 \ensuremath{{M}_{\odot}}. Assuming that these stars contain the most significant part of the total (young) stellar mass inside G11, we derive an absolute lower limit for the star formation efficiency of about 0.6% for G11. Together with the total luminosity of 7.2 \ensuremath{~ 10^{4}} \ensuremath{{L}_{\odot}}, we derive an L/M ratio of about 7 for the complete region while that of the central source is 2500 \ensuremath{{L}_{\odot}}/ \ensuremath{{M}_{\odot}}. The L/M value is often used as a measure for the star formation efficiency. The values obtained here compare well with the results discussed by Henning et al. (2000b) for other regions of massive star formation.

4.2 The nature of G341

4.2.1 Fragmented cloud cores

The millimetre continuum map (Fig. 2) shows the image of a filamentary and fragmented cloud. The region of G341 contains two clearly distinct cores. These cores are separated by a projected distance of about 1.6 pc. This distance points to two independently collapsing cores of an extended cloud rather than to a binary system of two massive young stars. The object G341 studied in this paper by AO and other observations is close to the northwestern core as can be seen from Figs. 8 and 4. The southeastern core is the known IRAS source 16487-4423, probably another region of massive star formation.

In the following discussion, we will concentrate on the northwestern core, which is also the location of the OH maser (Caswell 1998). The projected distances between the individual infrared sources visible in our AO image in Fig. 8 range from 2 $^{\prime \prime }$ to 4 $^{\prime \prime }$ (7000-14 000AU). These distances are comparable to those between the massive stars in the central area of the Orion nebula near the Trapezium region. A similar range of distances was found for the "pseudo Trapezium systems'' by Abt & Corbally (2000).

4.2.2 The central sources

From Fig. 10 we learn that most of the sources inside the region covered by our AO image are probably of spectral types O and B. The brightest source in the K'-band image (see Fig. 8) close to the OH maser position of Caswell (1998) is not plotted in the colour-magnitude diagram. Its H-K colour is 5.5mag. This might indicate that we are seeing extended emission from heated dust or scattered light. Scattering certainly does occur, as can be seen from the polarization map in Fig. 5.

The rather steep spectral index $a=\frac{{\rm d}(\log(\lambda F_{\lambda}))}{{\rm d}\log(\lambda)} \approx 2.3$ between 2.2 and 10.6$\mu$m would qualify this object as Lada class I, following Wilking et al. (1989). Dereddening can obviously not be applied to determine the spectral type of the embedded star. Using our four data points at 1.6, 2.2, 10.6, and 1300.0 \ensuremath {\mu }m for a simple trapezoidal integration, we derive a total luminosity of 195 \ensuremath{{L}_{\odot}}. Due to the lack of data points between 10.6 \ensuremath {\mu }m and the millimetre measurement, this should be seen as an absolute lower limit because we miss the peak emission at mid-infrared/far-infrared wavelengths. We note that the spectral properties of the central source are very similar to those of the luminous young stellar object MIR1 found by Feldt et al. (1998) slightly north of the cometary UCH II G45.45+0.06.

Evidence for an embedded massive star comes from the association of the source with an OH maser(Caswell 1998). OH masers in star-forming regions are generally associated with (compact) UCH IIs. It is mostly accepted that the OH masers are located in the compressed shell between the ionization and shock front (see, e.g., Elitzur 1987). The H II/OH masers are probably excited by a combination of collisions and far-infrared continuum radiation. Luminous sources with a low geometrical dilution factor are required to explain the high brightness temperatures of the OH masers (Pavlakis & Kylafis 1996).

Another hint towards a region of high-mass star formation is the mass of the cloud core of 400 \ensuremath{{M}_{\odot}}. This mass is comparable to the mass of G11's cloud core (620 \ensuremath{{M}_{\odot}}) and the core to the southeast, which is known to be associated with a luminous IRAS source and has a mass of 370 \ensuremath{{M}_{\odot}}.

4.2.3 No visible ionization

Starting from our hypothesis that there is indeed a young high-mass star embedded in G341, we need to find a reason why no detectable ionization occurs in its immediate surroundings.

Due to the probable combination of reddening and excess emission it is virtually impossible to determine the spectral type of the embedded star from photometry. If we rather arbitrarily assume a spectral type of O8, we end up with a factor of 40 fewer UV photons than for the central source of G11. Such a star would emit 1048.35 Lyman continuum photons per second (Panagia 1973). If we assume that this is also the number of recombinations in the nebula and that the ratio of recombinations to Br \ensuremath {\gamma } photons is about $N_{\rm c} / N_{\rm Br\ensuremath{\gamma} } \sim 70$(Hummer & Storey 1987), we can derive the expected Br \ensuremath {\gamma }flux in Wm-2 from

 \begin{displaymath}I_{\rm Br\ensuremath{\gamma} }=1.1~10^{-61}\left(\frac{N_{\rm... ...\mbox{s}^{-1}}\right) \left(\frac{D}{\mbox{kpc}}\right)^{-2} . \end{displaymath} (4)

Converting the result of 1.8 \ensuremath{~ 10^{-14}}Wm-2 to Jy via our known filter width of 0.034  \ensuremath {\mu }m and applying the extinction of 2.1mag derived in Sect. 3.1.1, we expect to find a flux density of 110mJy in our calibrated Br \ensuremath {\gamma } image. The detection limit in this image is about 0.5mJy for a point source of radius 3 pixels. To get a flux below the detection limit, we thus need to reduce the number of ionizing photons by a factor of 220 ending up with a star of spectral type B1 or later.

The above estimate holds for the assumption that the free-free emission from the ionized gas is optically thin. However, this may not be the case. The strong, extended K'-band emission indicates very dusty surroundings very close to the central source. UV photons might be absorbed before they can cause ionization of gas atoms. In such a scenario, the central star might be of earlier spectral type than derived above and still no detectable ionization would be expected. In Sect. 3.3, we derived a lower limit of 2.8 \ensuremath{~ 10^{5}} \ensuremath{{\rm cm}^{-3}} for the hydrogen density around the embedded source from the N-band flux. Computing the UV optical depth using Ryter (1996) and Mathis (1990), we find that such a density would lead to an optical depth of 1 for energetic UV photons after a line of sight of about 100AU in length. Should this density be present very close to the star, all of the ionizing radiation might be absorbed within a few hundred AU. Another possible cause for the lack of visible ionization might be the infall of material to be ionized (see also below).

Another complication is the second brightest star in Fig. 8 at position (+5 $^{\prime \prime }$, -1.5 $^{\prime \prime }$). This star appears in the colour-magnitude diagram about 0.7mag short of the ZAMS after de-reddening, as can be seen from Fig. 10. The rough determination of the extinction in Sect. 3.1.1, the uncertainty of the embedding depth plus additional circumstellar contributions can easily account for this shortfall. Hence, this second brightest source is almost certainly a star of spectral type O. Yet it doesn't produce a visible HII region. The source might be located at a much smaller distance and thus be not as bright in absolute magnitudes as it appears in Fig. 10, but this is unlikely because of the extinction which fits the one measured towards G341 very well. On the other hand, this source might be a fully evolved O star which has no detectable HII of its own any more. The projected distance towards G341 is about 22200AU. The linear size of G341 in Fig. 8 is about 11000AU. Thus the solid angle under which G341 is seen from the O star is about 0.16sr. Assuming the O star to be of spectral type O7, this means that 1046.72Lyman continuum photons per second should hit the dust shell of G341. Accordingly, gas atoms at the surface of this dust shell should be ionized. Again, we can convert this number into an expected Br \ensuremath {\gamma } flux using Eq. (4), and we end up with an expected flux density of $F_{\rm Br\ensuremath{\gamma} } \sim 18$mJy. This is still above our detection limit but only by a factor of about three. Intermediate absorption by dust or a slight error in the assumption of a spectral type can explain why we would not detect Br \ensuremath {\gamma } radiation from this type of ionization.

4.2.4 A UCHII precursor?

So far, we have been unable to determine exactly the type of the central source embedded in G341. However, we have argued that it might be a massive star and if it is, it must be so heavily enshrouded by dust that all of its ionizing radiation is absorbed before it can produce a detectable HII region or the HII region is suppressed by the accretion of matter (see, e.g., Yorke 1986; Henning 1990; Testi et al. 1997). The OH maser and the total mass of the cloud core are arguments in favour of a massive star-forming region. For a discussion of similar objects using radio continuum and OH maser data, we refer to Forster & Caswell (1999).

The strong excess emission in K' shows that large amounts of hot dust exist very close to the star. Its morphology would be governed both by local density variations and the temperature gradient. A very crude comparison to the model of Testi et al. (1997) shows that we should expect a colour index of K-H of about 5 mag on the central peak close to the star and about 1.5mag in outlying regions. We derived a colour index of 5.5mag for the central peak in K and measure a gradually decreasing colour index towards north/northeast which reaches 2.5mag at the northern end of the extended emission. Differences in foreground extinction and the density profiles can easily account for the differences. We should note however, that in contradiction to the model of Testi et al., in G341, intensity variations do not happen on scales of 1 \ensuremath{~ 10^{-4}} pc but on scales of 1 \ensuremath{~ 10^{-2}} pc.

5 Conclusions

Observations with high spatial resolution are necessary to assess the complicated structure of high-mass star-forming regions. Adaptive optics imaging at near-infrared wavelengths provides the resolution necessary to detect individual members of embedded clusters of early-type stars. A combination of Br$\gamma$ line observations with high-resolution radio maps provides extinction maps which allow the determination of spectral types of stars.

Our data demonstrate that both massive molecular clouds investigated by us contain clusters of OB stars, supporting the view that massive stars do not form in isolation. The object G11.11-0.40 is one of the rare cases where the central engine of an ultracompact H II region could be identified. This embedded O star is an excellent target for future near-infrared spectroscopy with very large telescopes in order to derive the exact spectral type of the object. There is some evidence that the ionizing source may even be a binary. The features of the object G341.21-0.21 suggest that it is in an early stage of massive star formation, presumably before the UCH II phase. Sensitive radio maps and molecular line data taken with interferometers are required to check this statement.

Acknowledgements
We would like to thank our referee, John Mathis, whose comments helped to improve the paper. B.St. acknowledges support from the DFG grant Ste 605/17-1.

References

 
Copyright ESO 2001