A&A 369, 1078-1087 (2001)
DOI: 10.1051/0004-6361:20010158

The X-ray nebula of the filled center supernova remnant 3C 58 and its interaction with the environment

F. Bocchino^1,2 - R. S. Warwick³ - P. Marty⁴ - D. Lumb¹ - W. Becker⁵ - C. Pigot⁶

1 - Astrophysics Division, Space Science Dept. of ESA, ESTEC, Postbus 299, 2200AG Noordwijk, The Netherlands
2 - Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
3 - Department of Physics and Astronomy, University of Leicester, Leicester LE1 7RH, UK
4 - Institut d'Astrophysique Spatiale, Campus Université Paris-Sud, 91405 Orsay Cedex, France
5 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstarsse 1, 85740 Garching, Germany
6 - DAPNIA/Service d'Astrophysique, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France

Received 5 December 2000 / Accepted 24 January 2001

Abstract
An XMM-Newton observation of the plerionic supernova remnant 3C 58 has allowed us to study the X-ray nebula with unprecedented detail. A spatially resolved spectral analysis with a resolution of 8 $^{\prime\prime}$ has yielded a precise determination of the relation between the spectral index and the distance from the center. We do not see any evidence for bright thermal emission from the central core. In contrast with previous ASCA and Einstein results, we derive an upper limit to the black-body 0.5-10 keV luminosity and emitting area of 1.8 10³² erg s^-1and 1.3 10¹⁰ cm², respectively, ruling out emission from the hot surface of the putative neutron star and also excluding the "outer-gap" model for hot polar caps. We have performed for the first time a spectral analysis of the outer regions of the X-ray nebula, where most of the emission is still non-thermal, but where the addition of a soft ( kT=0.2-0.3 keV) optically thin plasma component is required to fit the spectrum at E<1 keV. This component provides 6% of the whole remnant observed flux in the 0.5-10.0 keV band. We show that a Sedov interpretation is incompatible with the SN 1181-3C 58 association, unless there is a strong deviation from electron-ion energy equipartition, and that an origin of this thermal emission in terms of the expansion of the nebula into the ejecta core nicely fits all the radio and X-ray observations.

Key words: stars: neutron; supernovae: general; ISM: individual object: 3C 58; ISM: supernova remnants; X-rays: ISM

1 Introduction

3C 58 is a beautiful example of a filled-center (or plerionic) supernova remnant (SNR), probably associated with the historical supernova event in 1181 A.D. (Stephenson 1971). This object has always received much attention because, on the one hand, it shows some characteristics similar to the Crab SNR, while, on the other hand, it seems very different to the Crab itself. For instance, 3C 58 has a compact ( $10^\prime\times 6^\prime$) elliptical morphology with a very bright core (Reynolds & Aller 1988) and linear size similar to the Crab; Frail & Moffett (1993) have reported a wisp-like elongated structure at $2.6\hbox{$^{\prime\prime}$ }$ from the core, which has been observed also in the Crab and which is probably associated with the pulsar wind termination shock. However, unlike the Crab, there is no clear evidence of a pulsating point source located in the center, as would be expected, since the morphology strongly suggest that the nebula is powered by a spinning neutron star. Despite considerable effort, pulsations have not been detected so far in either radio (see e.g. Lorimer et al. 1998), nor in X-rays (Helfand et al. 1995, H95 hereafter). Moreover, the X-ray to radio flux ratio ( $f_{\rm X}/f_{\rm r}$) of 3C 58 is 100 times lower than that of the Crab (H95), its spectral break occurs at 50 GHz (300 times less than the break of the Crab, Green & Scheuer 1992) and its radio luminosity is increasing instead of decreasing as expected (Green 1987). These remarkable differences are also seen in other plerions, and Woltjer et al. (1997) have proposed the introduction of a new sub-class of plerions, the "non Crab-like plerions", of which 3C 58 can be considered the prototype. For these objects, a non-standard evolution of the pulsar can be invoked, but the details are not yet clear.

It is therefore very important to investigate the physical properties which render 3C 58 so peculiar, in order to put this object and its sub-class in the right perspective. In particular, the detection or non-detection of the central source is obviously a key point. Becker et al. (1982) reported the presence of a compact X-ray source in 3C 58 from their Einstein HRI observation, about 10 $^{\prime\prime}$ in extent, and contributing to 15% of the detected X-ray flux. Later, Helfand et al. (1995) revisited the X-ray emission of 3C 58 using ROSAT HRI data, confirming the compact source and favored a model in terms of hot polar caps to explain the emission. However, it has not been possible so far to take an X-ray spectrum of the source to study it, and to understand if it is really a point source or an enhancement of the pulsar nebula. Torii et al. (2000) have pointed out that the inclusion of a black-body component in the fit of the ASCA GIS+SIS data of 3C 58 yields an improvement of the $\chi ^2$. They claim that the best-fit black-body component is responsible for $\sim$7% of the unabsorbed flux in the 0.5-10 keV of the whole remnant, and that it is the spectral signature of the central source.

It is also very important to assess the presence of a shell around the pulsar nebula, for it may give compelling constraints on the age of the remnant, the shock velocity and the density of the environment. In the case of the $\sim$800 yr old 3C 58 (as other plerions as well), it is expected that the main shock will encounter the stellar ejecta and/or the interstellar medium (ISM) giving rise to a limb brightened shell. However, no sign of a shell has been detected at centimeter wavelengths at distances greater than $5\hbox{$^\prime$ }$ from the core (Reynolds & Aller 1985). However, Reynolds & Aller (1988) have imaged the faint outer emission of the nebula at a distance between 2$^\prime$ and $4\hbox{$^\prime$ }$and have noticed limb brightening at several locations. In this paper, we present a study of the XMM-Newton data of 3C 58 obtained during the Calibration and Performance Verification (Cal/PV) phase of the mission. We show that a stringent upper-limit can be imposed on the presence of thermal emission from a central point source, and we also find evidence for a thermal outer shell. The implications of these findings for current models of 3C 58 are also discussed.

2 Data analysis

2.1 Observations

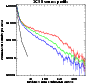	Figure 1: MOS1+2 source profile, centered at $2^{\rm h}05^{\rm m}38.0^{\rm s} +64^{\rm d}49^{\rm m}37^{\rm s}$ (J2000). Soft, medium and hard energy band as defined in Fig. 2 are represented as tick marked top, medium and bottom curves, respectively. The solid black line is the Point Spread Function (PSF) of the mirror module 3 at 1.5 keV (Aschenbach et al. 2000)
Open with DEXTER

Figure 2: MOS1+2 images binned at pixels of $2\hbox {$^{\prime \prime }$ }$ and smoothed using a Gaussian with $\sigma =3$ pixel to enhance the morphology of the faint nebula edge. Upper panel: soft image (0.1-1.0 keV). Center panel: medium energy image (1.0-2.0 keV). Lower panel: hard image (2.0-10.0 keV). Overlaid are contours representing the weakest ( $3\sigma =0.15$ Jy beam-1) 1446 MHz radio contour and the one corresponding to a flux density 4 times higher (both in white, from Reynolds & Aller 1988), and six X-ray contours (in yellow, from 1/100 of the peak to the peak value, logarithmically spaced)

Open with DEXTER

3C 58 has been observed as part of the Cal/PV phase of the XMM-Newton satellite (Jansen et al. 2000). In this paper, we focus on the 25 ks on-axis observation performed during orbit 47, on March 12th 2000. Data from the two MOS (Turner et al. 2000) cameras and the PN (Strueder et al. 2000) camera have been used. MOS and PN cameras are CCD arrays which collect X-ray photons between 0.1 and 15 keV and have a field of view of $30^\prime$. The pixel size is $1.1\hbox{$^{\prime\prime}$ }$ and $4.1\hbox{$^{\prime\prime}$ }$ for MOS and PN respectively, and this should be compared with the mirror PSF width of $6\hbox{$^{\prime\prime}$ }{-}15\hbox{$^{\prime\prime}$ }$ FWHM-HEW. The data have been acquired with the medium filter and in full image mode, and therefore the temporal resolution is low, 2.5 s and 73 ms for MOS and PN, respectively. The worse spatial resolution of the PN is compensated by its greater sensitivity, on the average 20-30% more than the combined two MOS.

The Standard Analysis System (SAS) software we have used (version 5.0 alpha, xmmsas-20001011-1559) takes care of most of the required events screening. However, we have further screened the data to eliminate some residual hot pixels and occasional background enhancement due to intense flux of soft protons in the magnetosphere. In particular, we have extracted the background light-curve from a region free of sources, and we have identified time intervals of unusually high count rates (more than twice the "quiescent" background rate) and removed them from subsequent analysis. Moreover we have also selected events with value of the PATTERN pipeline assigned keywords between 0 and 12. The exposure time of the screened observations is 16 ks for the MOS and 12 ks for the PN detectors.

2.2 X-ray morphology

In Fig. 1, we report the 3C 58 profile as seen by the MOS1+2 computed in 65 annuli with $\Delta r = 4\hbox{$^{\prime\prime}$ }$ up to a distance of $\sim$ $4\hbox{$^\prime$ }$ from the centroid, located at $2^{\rm h}05^{\rm m}38.0^{\rm s} +64^{\rm d}49^{\rm m}37^{\rm s}$ (J2000, $\pm 1\hbox{$^{\prime\prime}$ }$). The background was collected from a ring with $\Delta r = 30\hbox{$^{\prime\prime}$ }$located at $4.5\hbox{$^\prime$ }$ from the center, and has been chosen to fall entirely in the central MOS chip. The comparison with the expected mirror PSF, also shown in Fig. 1 indicates that the central source is extended. The bright core region can be defined up to $\sim$ $50\hbox{$^{\prime\prime}$ }$ from the center; Further out, the slope changes and the behavior of the soft curve and hard curve is different. The hard curve declines with the same slope down to the limit of the radio nebula at $\sim$ $200\hbox{$^{\prime\prime}$ }$, while the soft curve is clearly flatter than the hard one, with a sudden change of slope occurring at $140\hbox{$^{\prime\prime}$ }$.

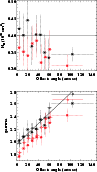Figure 3: Spatially resolved spectral analysis with a power-law model of the X-ray nebula associated with 3C 58. We show the results obtained on the 8 annuli and the "edge" regions (the last point) as defined in the text. Black is MOS, red is PN, dotted bars are fit with free $N_{\rm H}$, solid bars are fit with $N_{\rm H}$ fixed at 4 1021 cm-2. Regions are centered at $2^{\rm h}05^{\rm m}38.0^{\rm s}$ $+64^{\rm d}49^{\rm m}37^{\rm s}$ (J2000). A linear fit to the MOS points corresponding to fits with $N_{\rm H}$ fixed at 4 1021 cm-2 is shown in the lower panel

Open with DEXTER

The core is elongated in the N-S direction, with a FWHM of $13.5\pm 1.5\hbox{$^{\prime\prime}$ }$ in this direction ( $9.0\pm1.5\hbox{$^{\prime\prime}$ }$ in the E-W direction), in agreement with the ROSAT HRI results presented by H95. The centroid of the MOS1 emission is located 4 $^{\prime\prime}$ and 8 $^{\prime\prime}$ south of the ROSAT and Einstein positions. The data confirm that the radio wisp observed by Frail & Moffett (1993) is located to the East of the X-ray peak, at 5 $^{\prime\prime}$ from the the MOS1 centroid. However, the uncertainties in real attitude reconstruction, which is still not fully implemented, may give an uncertainty in absolute position determination as large as $\sim$ $5\hbox{$^{\prime\prime}$ }$.

Figure 2 shows the summed MOS1+2 images of 3C 58 in three different bands, namely 0.1-1 keV, 1-2 keV and 2-10 keV bands, along with the weakest 1446 MHz radio contour at 0.15 Jy beam^-1 and the contour at 0.6 Jy beam^-1 of Fig. 3 in Reynolds & Aller (1988) (both in white in Fig. 2). A small separation of the two contours (e.g. in the SW) indicates limb brightening and therefore confinement in the source. In addition, we also shown the X-ray contours (in yellow), and it is clear that there is correspondence between the radio contours and the X-ray emission of the soft image. In particular, the weakest radio contour matches the outer edge of the weak extended X-ray emission, especially at the north and south edges. Figure 2 also shows that the size of the nebula decreases as the energy increases, an effect also reported by Torii et al. (2000).

2.3 Spectral analysis

The high spatial and spectral resolution of the instrumentation aboard the XMM-Newton satellite allows us for the first time to perform spatially resolved spectral analysis of the X-ray nebula associated to 3C 58. To this end, we extracted spectra from 8 concentric annuli with $\Delta r = 8\hbox{$^{\prime\prime}$ }$ centered at the same position of the X-ray profiles of Fig. 1, covering the core emission up to 1.1$^\prime$ from the center. Given the uncertainties in present calibration of the MOS and PN cameras, and the energy dependence of the vignetting correction above 5 keV, we have restricted our spectral analysis to photons in the 0.5-5 keV energy band. The spectra have been background subtracted using the same background region introduced in the previous subsection, and have been rebinned to ensure that a minimum of 30 counts are present in each energy channel. As for response matrices and effective area files, we have used the latest version of standard MOS and PN matrices provided by the calibration team (mos1_medium_all_qe17_rmf3_tel5_15 and epn_fs20_sY9_medium). We have summed the spectra extracted with MOS1 and MOS2, and we have also rescaled the response matrix to reflect this operation. Besides the 8 annuli, we have also defined a region (the "edge'' region hereafter), represented by the union of two ellipses matching the outer X-ray edge of the nebula, minus a circle with same radius as the 8th annulus. This region is particularly suited for the study of the X-ray emission coming from the outermost fringes of the X-ray and radio nebula.

We have used three different emission models to fit the 3C 58 data, namely a power-law model, a power-law model plus the optically thin plasma model of Mewe et al. (1985) with Fe L calculation of Liedahl et al. (1995), pl+ MEKAL hereafter, and a power-law model plus a black-body spectrum, pl+bbody hereafter. These three models encompass what we could possibly expect from an X-ray nebula, the last two representing eventual contributions from a thermal shell (as in the case of known plerion-composite SNR), and from a compact source in the center as pointed out by Helfand et al. (1995). The temperature of the pl+ MEKAL model and of the pl+bbody models have been constrained in the 0.1-10 keV and in the 0.1-2.0 keV, respectively. Abundances are those of Anders & Grevesse (1989). All the models have been modified by the interstellar absorption according to cross-sections of Morrison & McCammon (1983), where we have let the equivalent hydrogen column density $N_{\rm H}$ vary. Since we have noted that the non-thermal component provides most of the flux in the XMM-Newton bandwidth, and that the residual thermal components of the model pl+ MEKAL and pl+bbody are correlated with the value of $N_{\rm H}$, we have also performed a set of fittings fixing the $N_{\rm H}$ value to 4 10²¹ cm^-2, which is compatible with previous estimates (Helfand et al. 1995; Torii et al. 2000) and it is also consistent with the result we obtained letting it vary.

 

 

Table 1: Goodness of MOS fits to the 8 annuli of 3C 58. The absorption is fixed to 4 10²¹ cm^-2. For each model, we report the value of $\chi ^2$, degrees of freedom (dof), null hypothesis probability. For the pl+ MEKAL and pl+bbody model, we also report the value of the best-fit temperature. The last column is the unabsorbed flux in the 0.5-10.0 keV in units of 10^-13 erg cm^-2 s^-1; its statistical error is $\pm 0.1$

Reg.	Power-law		Pow+ MEKAL			Pow+bbody
	$\chi^2/{\rm dof}$	Prob.	kT	$\chi^2/{\rm dof}$	Prob.	kT	$\chi^2/{\rm dof}$	Prob.	flux
1	74/73	46	1.0(>0.4)	71/71	48	0.2(>0.1)	73/71	40	15.3
2	69/65	35	6.0(>0.1)	67/63	35	0.9(>0.1)	68/63	30	13.0
3	65/63	41	0.6(>0.1)	65/61	34	$0.5\pm0.3$	62/61	44	11.4
4	52/59	71	0.1(>0.1)	51/57	70	0.1(>0.1)	51/57	69	12.3
5	54/61	72	0.7(>0.1)	52/59	72	0.2(>0.1)	53/59	69	12.0
6	52/59	74	0.1(>0.1)	50/57	72	0.6(>0.1)	50/57	72	10.9
7	96/60	0.2	0.2(<0.25)	91/58	0.4	0.8+0.2-0.1	91/58	0.4	10.7
8	79/58	3	0.3+0.2-0.1	71/56	8	0.8+0.3-0.1	73/56	7	10.6

2.3.1 The $\mathsfsl{\gamma}$ vs. radius relation

Figure 3 shows the best-fit value of the absorption and of the power-law photon index ($\gamma$) as a function of the distance from remnant center, obtained with a fit to a power-law emission model only. The data clearly show the effect of synchrotron burn-off of high energy electrons as the radius increases. This effect has also been observed in G21.5-0.9 both with Chandra (Slane et al. 2000) and XMM-Newton (Warwick et al. 2000) and it is related to inhomogeneity in the particle distribution inside the plerion nebula. The straight line in the lower panel of Fig. 3 represents the linear best-fit to the $\gamma - r$ relation, $\gamma=A+Br$ with $A=1.97\pm 0.03$ and $B=8.0\pm 0.6~10^{-3}$and r is in arcseconds. The MOS fits to the single power-law reported in Fig. 3 are statistically acceptable from ring 1 to ring 6, while not acceptable in rings 7-8 and in "the edge" region. This is true for both $N_{\rm H}$ free and $N_{\rm H}$ fixed fits, and Table 1 reports the $\chi^2/{\rm dof}$ values of the fits. It is interesting to note that the $N_{\rm H}$ value, when left free to vary, is significantly lower than the average value of 4 10²¹ cm^-2 for the outer nebula regions (Fig. 3). Moreover, the best-fit $\gamma$ of the shell is off the trend dictated by fit to the spectra of the rings when $N_{\rm H}$ is left free to vary, while it shows lower deviation in the fit with $N_{\rm H}$fixed. If the X-ray emission of the outer rings is dominated by the non-thermal component of the plerion, we do not expect significative variation of the absorption, and the data seem to confirm that a fixed $N_{\rm H}$ may be more appropriate. However, the fact that fits of the outer rings and "edge'' data are less acceptable than fits to inner rings data strongly suggests a contribution from other components.

2.3.2 Additional thermal components

Figure 4: A close up of MOS spectrum for the "edge'' region. Left panel: the fit with a simple power-law model does not well represent the spectrum below 1 keV. Center panel: the pl+ MEKAL model with kT=0.2 keV improves the description of the data. The spectral region near the oxygen edge (between 0.4 and 0.6) is know to have some residual calibration problem. Right panel: unfolded best-fit pl+ MEKAL model. Dot-dashed line represents the thermal component, which shows emission lines and falls off rapidly above 1 keV, where the power-law component dominates

Open with DEXTER

In order to assess the presence of any additional emission from a central compact source (as suggested by H95) and from any thermal shell, we now consider the results of fits with pl+ MEKAL and pl+bbody models. The inclusion of the additional component ( MEKAL or bbody) does not increase the null hypothesis probability above 5%, except for ring 8. This is also reported in Table 1, in which the reader finds the data needed to evaluate the goodness of the fits we have performed. However, it should be noted that the inclusion of the MEKAL component leads to a reduction of $\chi ^2$ (and therefore to a better fit in a relative way) for the outermost rings, and a dramatic reduction in case of the "edge" region, specially for MOS. This is also shown in Fig. 4, where we show the MOS "edge" spectrum along with its power-law only and pl+ MEKAL best-fit model and residuals, and in Table 2 where we summarize the results of spectral fitting to the "edge" spectrum. In Fig. 5, we report the ratio of the flux of the second component ( $f_{\rm mekal}$ from the pl+ MEKAL fit in the upper panel, and $f_{\rm bbody}$ from the pl+bbody fit in the lower panel) to the total flux of ring 1-8 and the "edge" region.

The fit with an additional black-body component to ring 1 places an upper limit to the unabsorbed flux due to this component of 20% of the total 0.5-2.0 keV flux in this region (i.e. 1.5 10^-13 erg cm^-2s^-1, or a luminosity $L_{\rm X}=1.8~10^{32}D^2_{3.2}$ ergs^-1, where D_3.2 is the distance in units of 3.2 kpc, which is the most reliable value according to Roberts et al. 1993) and 10% of the total 0.5-10.0 keV flux of this region (i.e. 1.6 10^-13 erg cm^-2s^-1, same $L_{\rm X}$ as before). Since the whole remnant 0.5-10 keV flux is 1.6 10^-11 erg cm^-2s^-1, the upper limit corresponds to 1% of the remnant flux, significantly below the 7% found by Torii et al. (2000). Figure 5 also shows that spectral fittings of rings 2-6 yields only upper-limits to the presence of an additional MEKAL or black-body thermal emission.

On the other hand, the situation is different for ring 8 and the "edge" region (Tables 1 and 2), where the addition of the thermal component yields a significant decrement of the $\chi ^2$ (according to an F-test) and the thermal flux contribution to the 0.5-2.0 total flux is between 5% and 30%. In particular, the pl+ MEKAL fit in the "edge" region suggests that between 10 and 20% of the 0.5-2.0 keV flux from this region ( 5-9 10^-13 erg cm^-2s^-1, or $L_{\rm X}=5.8-10.0~10^{32}D^2_{3.2}$ ergs^-1) is due to the thermal component (8-14% if we consider the 0.5-10 keV band). If compared to the whole remnant 0.5-10 keV flux, the thermal soft excess yields a contribution of 3%-6%. It is important to note that in this region the pl+ MEKAL model is to be preferred over the pl+bbody model (Table 2).

 

 

Table 2: PN and MOS fit results of the "edge" region of 3C 58. All the fits yield an absorbed flux of 6.1 10^-12 erg cm^-2s^-1 in the 0.5-10 keV band

Model	$N_{\rm H}$	$\gamma$	kT	$\chi^2/{\rm dof}$
	cm-2		keV
MOS1+2
pow-law	$3.5\pm 0.2$	$2.61\pm 0.06$	-	245/170
pl+ MEKAL	7.3+0.6-0.9	$2.89\pm 0.08$	$0.18\pm 0.01$	202/168
pl+bbody	5.5+0.5-0.8	$2.75\pm 0.06$	<0.11	231/168
pow-law	4.0	$2.75\pm 0.04$	-	261/171
pl+ MEKAL	4.0	$2.61\pm 0.05$	$0.25\pm 0.03$	226/169
pl+bbody	4.0	$3.07\pm 0.07$	$0.78\pm 0.08$	243/169
PN
pow-law	$3.1\pm 0.3$	$2.42\pm 0.11$	-	113/138
pl+ MEKAL	7.6+0.4-2.5	2.71+0.15-0.11	$0.18\pm 0.03$	107/136
pl+bbody	5.2+1.0-1.7	2.55+0.11-0.16	<0.13	109/136
pow-law	4.0	$2.66\pm 0.06$	-	130/139
pl+ MEKAL	4.0	$2.47\pm 0.10$	$0.24\pm 0.06$	110/137
pl+bbody	4.0	$2.46\pm0.10$	<0.13	110/136

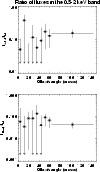	Figure 5: Same as in Fig. 3, but here we report the ratio between the 0.5-2.0 keV flux due to the additional component ( MEKAL in the upper panel, and bbody in the lower panel) to the total 0.5-2.0 keV flux versus the distance from the center. Arrows indicate upper limits. Goodness of fits are reported in Table 1
Open with DEXTER

2.3.3 PSF effects

We have also investigated whether our results are affected by any effect related to the Point Spread Function (PSF) of the XMM-Newton mirror. Since only 55% of the photons of a point source are contained within a circle of 8 $^{\prime\prime}$ radius, we expect a certain amount of scattering outside the rings. However, this effect is not likely to modify our conclusions. In the central ring, for instance, the strongly peaked morphology keeps the contamination from ring 2 low. Moreover, the scattering can only smooth the $\gamma - r$ relation in Fig. 3, so the observed slope is, strictly speaking, a lower limit to the real slope. Finally, in order to verify whether the soft component detected at large radii is an artifact of the PSF, we have followed this procedure: we have fitted the summed spectrum of rings 1-8 with a power-law model, and we have found $N_{\rm H}=3.9~10^{21}$ cm^-2 and $\gamma=2.21$; then, we have fitted the spectrum of the "edge" region with the best-fit model found for ring 1-8 with fixed $N_{\rm H}$ and $\gamma$, plus a second absorbed power-law model with free $N_{\rm H}$ and $\gamma$. The normalizations of the two models were left free to vary. We have found that the best-fit normalization of the "fixed" power-law is zero, suggesting that negligible contamination from the spectrum of the ring 1-8 is observed in the "edge" spectrum.

2.4 Timing analysis

In order to search pulsed X-ray emission from the central source which is powering 3C 58, we have calculated the power spectrum density of the time series of events of the central ring used for spectral analysis. Unfortunately, the time resolution of the EPIC cameras when operated in full image mode is low, and we were not able to sample frequencies above 1 Hz. For timing analysis, we have collected MOS1 and PN photons in ring 1 between 0.5 and 10 keV, and we have analyzed the two independently. Furthermore, we have also analyzed a more restricted energy range, 2-10 keV.

None of the power spectra show features significant at the 99% confidence level. The corresponding MOS1 upper limits to relative amplitude of a sinusoidal pulsed signal in the 5 10^-3-0.1 Hz is 6.2% and 10.0% for the 0.5-10 keV and 2-10 keV respectively, while the PN upper limits in the 10^-2-1 Hz are 2.0% and 3.1% in the broad and hard band, respectively.

3 Discussion

The good spatial and spectral resolution XMM-Newton data on 3C 58 has allowed us to perform a detailed spatially resolved spectral analysis of this remnant, and in particular, to address the topic of the spectra of the compact core at its center and the presence of an X-ray shell.

3.1 The compact core

The possible emission mechanisms for the compact core of 3C 58 have been reviewed by H95, and a preference has been given to a thermal model for the emission from hot polar caps, mostly on the basis of a review of ROSAT and Einstein HRI data. Torii et al. (2000) have confirmed the detection of an additional component in the remnant spectrum, which they have modeled with a black-body of kT=0.40-0.45 keV and a flux of 1.5 10³³D²_3.2 erg s^-1 in the 0.5-10 keV band. While the Torii et al. (2000) flux estimate is within 20% of the H95 one, we have found in ring 1 an upper limit to the flux of the kT=0.25 keV black-body component a factor of 10 less than the H95 estimate. The inferred upper limit on the emitting area is 1.3 10¹⁰ cm²(corresponding to a radius of $\sim$650 m), more or less the value found by Torii et al. (2000), and this is expected since our best-fit temperature is a factor of two less than the one derived by ASCA. By forcing the temperature at the value of Torii et al. (2000), the corresponding upper limits are 9.4 10^-14 erg cm^-2s^-1 ( $L_{\rm X}=1.1~10^{32}D^2_{3.2}$ erg s^-1) and 8 10⁸cm². While this large difference in the inferred black-body flux may seem puzzling, it may be explained by the dramatic improvement of the XMM-Newton spatial resolution compared with the ASCA one. In fact, if we compute the sum of our best-fit values for the flux of the black-body component of the pl+bbody fit over all the rings and the "edge" region, we obtain a 0.5-10 keV flux of 1.2 10^-12 erg cm^-2s^-1, or a luminosity of 1.3 10³³D²_3.2erg s^-1, in very good agreement with the value reported by H95 and Torii et al. (2000). More than 50% of this flux comes from ring 7-8 and the "edge" region: it is therefore probable that the ASCA data correctly detected a soft excess in the integrated spectrum of 3C 58, but this was incorrectly attributed to the thermal component of the central compact object, whereas Fig. 5 suggests that it comes from the external parts of the nebula. The more stringent XMM-Newton upper limit to the black-body component also heavily constrains its interpretation. Our value of the emission area is too low to assume that the whole surface of neutron star is loosing the residual heat of formation, and therefore would suggest the hot polar caps mechanisms. A review of the polar caps heating mechanisms can be found by Yancopoulos et al. (1994). H95 favors the "outer-gap" model, and in this case we expect $L_{\rm X}=10^{30}B_{12}P^{-2}$erg s^-1, where B₁₂ is the magnetic field in units of 10¹² G and P is the period in seconds. As shown in Fig. 6, our $L_{\rm X}$ upper limit yields a magnetic field higher than the highest value known for allowed B and P values of an 810 yr old pulsar. For this model to be compatible with the $L_{\rm X}$ upper limit, either an older pulsar must be present or, unlike the Crab, the pulsar has not suffered high energy losses, in which case all the points below the isochrone lines of Fig. 6 are allowed. Other mechanisms invoked to explain the hot polar caps yield estimates of $L_{\rm X}$ lower then the "outer-gap" model and in principle may be compatible with the observations. However, other observed pulsar nebulae-thermal pulsar pairs reported by Seward & Wang (1988) show a ratio between compact object luminosity and total (pulsar+nebula) luminosity $L_{\rm c}/L_{\rm tot}$ of $\sim$0.1-0.2 (the Crab has $L_{\rm c}/L_{\rm tot}=0.04$), while, using the observed total 3C 58 luminosity of 1.8 10³⁴ erg s^-1 and the upper limit we have derived, we derive a ratio <0.01. Figure 6 also shows that we expect a period less then 1 s for reasonable values of B, and therefore, to properly detect a pulsation, we would need a better time resolution than those of the EPIC camera in full image mode.

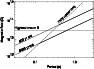Figure 6: The plot shows that allowed regions of the B-P plane according to the classical model for pulsars (e.g. Manchester & Taylor 1977) in solid lines (assuming the initial period was much less than the present period). We show the case for an 800 yr old pulsar (i.e. assuming that 3C 58 is related to SN 1181) and for a pulsar with an age a factor 10 larger. The dashed line represent the B-P values allowed by the "outer-gap" polar heated caps model of Cheng et al. (1986) and our derived upper limit to the black-body luminosity of the central source. The intersection of the observational and theoretical curves gives the allowed B-P values (thicker part of the isochrone lines). If 3C 58 is the remnant of SN 1181, the model would provide an unreasonably high B. Older pulsars and/or low rotational energy losses may yield more reasonable B values

Open with DEXTER

3.2 Thermal emission at the edge of the nebula

The interpretation of the additional component in terms of expansion of the main shock in the environment of the SNR cannot be excluded a priori: recently, there have been some cases of SNRs reclassified as composite (e.g. G11.2-0.3, Vasisht et al. 1996; G327.1-1.1, Sun et al. 1999). The observed temperature of the MEKAL component corresponds to a shock speed of $\sim$450 kms^-1, while the emissivity corresponds to a post-shock density of $(0.60\pm 0.15)D_{3.2}^{-1/2}$ cm^-3 and a pre-shock density four times smaller (assuming the emission comes from a thin shell at $r=2.5\hbox{$^\prime$ }$, where the soft profile in Fig. 1 drops rapidly, and $\Delta r=r/12$). The emitting mass is of the order of 0.1 $D^{5/2}_{3.2}~M_\odot$. The inferred density is very reasonable for typical low galactic latitude Sedov SNRs, but on the other hand it can hardly be reconciled with the association between SN 1181 and 3C 58. This is shown in Fig. 7, which reports the allowed values of the SNR age and of the distance according to a simple Sedov analysis following the outline given in Kassim et al. (1993). It is clear that from a pure geometrical point of view, the measured X-ray temperature may represent a Sedov shock of an $\sim$800 yr old SNR located at a distance of 3.2 kpc ("Geom." solid line in Fig. 7), but the measured emission measure of the MEKAL component yields a solution with a distance well above 10 kpc and and a remnant age well in excess of $\sim$10⁴ yr, if we assume that the explosion energy is of the order of the "canonical" value 10⁵¹erg ( $\log E_{51}=0$ in Fig. 7, where E₅₁ is in units of 10⁵¹ erg). Among the lowest values of the explosion energy quoted in the literature, we have E₅₁=0.1 for Vela (Bocchino et al. 1999) and 0.02-0.3 for G292.0+1.8 (Hughes & Singh 1994), and we note that, for E₅₁=0.01, Fig. 7 gives a solution of a remnant at 8-10 kpc and an age of 3000-6000 yr. The association 3C 58-SN 1181 suggests an explosion energy of the order of 10⁴⁸ erg, roughly ten times lower than the lowest inferred. We recall that the association have been questioned by Huang (1986), but recently Stephenson & Green (1999) have pointed out that, on the basis of an update of historical information, the association should be reliable. If so, the Sedov model does not provide a proper description of all the observational evidence.

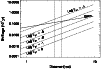Figure 7: Loci of allowed SNR age and distance according to a simple Sedov analysis of the thermal component of outer rim X-ray emission of 3C 58. The solid line labeled "Geom." gives the loci allowed by the simple geometrical relation between the real radius of the shell and the SNR age (Eq. (2) of Kassim et al. 1993). The radius is linked to the distance via the apparent shell radius, and we have used 2.5$^\prime$ to derive the relation. The dashed lines represent the loci of the solutions allowed by the Sedov relation R=14(E51/n0)1/5 t42/5, where n0 is derived from the emission measure of the MEKAL component assuming a spherical emitting volume with a radius of 2.5' and a filling factor of 25%. The intersection between the dashed lines and the solid line gives a solution. Vertical dashed lines mark the distance estimate of 2.6 and 3.2, due to Green & Gull (1982) and Roberts et al. (1993), respectively

Open with DEXTER

In order to understand the interaction between 3C 58 and its environment, and to understand the origin of the soft X-ray component, it is useful to compare its radio and X-ray emission. The soft X-ray maps of Fig. 2 show that the X-ray emission is in any case confined within 2$^\prime$-4$^\prime$ from the center, and therefore the presence of the shell is in agreement with the lack of detection of a radio shell at $r>~5\hbox{$^\prime$ }$ of Reynolds & Aller (1985). It is interesting to note that there is a close correspondence between the radio morphology of the outer regions of the nebula and the soft X-ray maps (Fig. 2, upper panel). This is also observed in other shell-like young SNR like Kepler (Matsui et al. 1984) and Cas A (Keohane et al. 1996), while, on the other hand, the radio emission of the Crab nebula is four times greater than its X-ray counterpart. Reynolds & Aller (1988) have pointed out that the radio image of the remnant at 1446 MHz shows confined-edge emission at some locations of the outer regions of the nebula, and some of these also show limb-brightening. According to them, this may be explained if the edge of the nebula is sweeping up moving material, e.g. ejecta, like in the "inhomogeneous" model of Reynolds & Chevalier (1984), or the shock model invoked by Sankrit & Hester (1997) to explain the [O III] emission seen at the boundary of the Crab. This may explain the small amount of limb brightening and is also in agreement with the relatively slow shock speed measured in X-rays. In fact, the expected shock speed in the moving ejecta material is $\sim$300 kms^-1(Reynolds & Chevalier 1984; 150-200 km s^-1 in the Crab according to Sankrit & Hester 1997), and we observe $v_{\rm s}=450$ kms^-1. Therefore, the thermal component we observe in the outer rim of 3C 58 may be associated with the expansion of the nebula in the inner ejecta core. Note that this is also in agreement with the discrepancy between the large speed measured in 3C 58 filaments ($\sim$900 kms^-1, Fesen 1983) and the X-ray derived speed. In fact, the filaments are composed of material ejected in the explosion itself, pushed on and accelerated by the synchrotron nebula, while the X-ray emission is due a shock expanding into moving ejecta. However, the low value of the X-ray emitting mass would imply that the interaction is only at its beginning.

Finally, it should be noted that the above conclusions rely on the hypothesis of fast electron-ion equipartition. Unfortunately, it is not possible to independently measure the proton temperature $T_{\rm p}$ of the 3C 58 shock. Bocchino et al. (1999) have shown that $T_{\rm e} < T_{\rm p} < 2T_{\rm e}$ for a shock region of the old Vela SNR, but Hughes et al. (2000) found evidence for $T_{\rm p}\sim 45 T_{\rm e}$ in the 1000 yr old SNR E0102.2-7219, suggesting that non-equipartition may be common among young SNRs. If also in case of 3C 58 $T_{\rm p}$ is $\sim$45 times higher than the X-ray derived electron temperature, than a Sedov solution with $E_0 \sim 3~10^{49}$ erg, would be compatible with a distance of 3.2 kpc and the association with SN 1181.

4 Summary and conclusions

The high spatial resolution of the EPIC camera on-board XMM-Newton has allowed us to look with unprecedented detail at the X-ray emission from the filled-center SNR 3C 58. We have presented soft (0.1-1 keV), medium (1-2 keV) and hard (2-10 keV) energy images, and we have found a close correlation of the soft image with radio emission at 1446 MHz. A quantitative study of the source profile shows the effect of synchrotron burn-off and indicates a different slope of the soft X-ray radial profile compared to that obtained in the hard band. Spatially resolved spectral analysis carried on in rings with $\Delta r = 8\hbox{$^{\prime\prime}$ }$ has allowed us to derive the relation between the spectral index and the distance from the core. In contrast with previous ASCA results, we have not found evidence for thermal black-body emission from a central source, and we have placed an upper limit to this component of $L_{\rm X}=1.8~10^{32}$ erg s^-1. This stringent upper-limit rules out thermal emission from the whole surface of the putative neutron star at the center of 3C 58, and also rules out the "outer-gap" model for hot polar caps of Cheng et al. (1986), unless the pulsar has very low rotational energy losses.

The large effective area of the XMM-Newton mirrors has allowed us to perform, for the first time, a spectral analysis of the outer edge of the 3C 58 X-ray nebula, excluding the inner and brighter regions. We have found that non-thermal emission is still responsible for most of the emission there, but a soft thermal component is required to better fit the spectrum below 1 keV. If represented with an optically thin emission model, this component gives kT=0.2-0.3 keV. If it is associated to the Sedov expansion of the 3C 58 shell, it is incompatible with the association between 3C 58 and SN 1181, unless there is strong deviation from electron-ion equipartition. If it is due to the expansion of the nebula into the inner core of moving ejecta, the X-ray spectra characteristics and the radio morphology of the outer nebula can be more easily reconciled.

Acknowledgements

We thank the whole XMM-Newton team for its effort in producing well-calibrated data at this early stage of the mission. We also thank the referee, R. Strom, for his useful suggestions. F. Bocchino acknowledges an ESA Research Fellowship and thanks R. Bandiera for helpful discussions.

References

 

• Anders, E., & Grevesse, N. 1989, Geocosmochim. Acta, 53, 197 In the text NASA ADS  
• Aschenbach, B., Briel, U., Haberl, F., et al. 2000 [astro-ph/0007256] In the text  
• Becker, R. H., Helfand, D. J., & Szymkowiak, A. E. 1982, ApJ, 255, 557 In the text NASA ADS  
• Bocchino, F., Maggio, A., & Sciortino, S. 1999, A&A, 342, 839 In the text NASA ADS  
• Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 In the text NASA ADS  
• Fesen, R. A. 1983, ApJ, 270, L53 In the text NASA ADS  
• Frail, D. A., & Moffett, D. A. 1993, ApJ, 408, 637 In the text NASA ADS  
• Green, D. A. 1987, MNRAS, 225, 11P In the text NASA ADS  
• Green, D. A., & Gull, S. F. 1982, Nature, 299, 606 In the text NASA ADS  
• Green, D. A., & Scheuer, P. A. G. 1992, MNRAS, 258, 833 In the text NASA ADS  
• Helfand, D. J., Becker, R. H., & White, R. L. 1995, ApJ, 453, 741 In the text NASA ADS  
• Huang, Y. L. 1986, Bull. Am. Astron. Soc., 18, 1043 In the text NASA ADS  
• Hughes, J. P., Rakowski, C. E., & Decourchelle, A. 2000, ApJ, 543, L61 In the text NASA ADS  
• Hughes, J. P., & Singh, K. P. 1994, ApJ, 422, 126 In the text NASA ADS  
• Jansen, F., Lumb, D., Altieri, B., et al. 2000, A&A, in press In the text  
• Kassim, N. E., Hertz, P., & Weiler, K. W. 1993, ApJ, 419, 733 In the text NASA ADS  
• Keohane, J. W., Rudnick, L., & Anderson, M. C. 1996, ApJ, 466, 309 In the text NASA ADS  
• Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 In the text NASA ADS  
• Lorimer, D. R., Lyne, A. G., & Camilo, F. 1998, A&A, 331, 1002 In the text NASA ADS  
• Manchester, R. N., & Taylor, J. H. 1977, Pulsars, San Francisco (W. H. Freeman), c1977 In the text  
• Matsui, Y., Long, K. S., Dickel, J. R., & Greisen, E. W. 1984, ApJ, 287, 295 In the text NASA ADS  
• Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 In the text NASA ADS  
• Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 In the text NASA ADS  
• Reynolds, S. P., & Aller, H. D. 1985, AJ, 90, 2312 In the text NASA ADS  
• Reynolds, S. P., & Aller, H. D. 1988, ApJ, 327, 845 In the text NASA ADS  
• Reynolds, S. P., & Chevalier, R. A. 1984, ApJ, 278, 630 In the text NASA ADS  
• Roberts, D. A., Goss, W. M., Kalberla, P. M. W., Herbstmeier, U., & Schwarz, U. J. 1993, A&A, 274, 427 In the text NASA ADS  
• Sankrit, R., & Hester, J. J. 1997, ApJ, 491, 796 In the text NASA ADS  
• Seward, F. D., & Wang, Z. 1988, ApJ, 332, 199 In the text NASA ADS  
• Slane, P., Chen, Y., Schulz, N. S., et al. 2000, ApJ, 533, L29 In the text NASA ADS  
• Stephenson, F. R. 1971, QJRAS, 12, 10 In the text NASA ADS  
• Stephenson, F. R., & Green, D. A. 1999, Astron. Geophys., 40, 27 In the text  
• Strueder, L., Briel, U., Dennerl, K., et al. 2000, A&A, in press In the text  
• Sun, M., Wang, Z., & Chen, Y. 1999, ApJ, 511, 274 In the text NASA ADS  
• Torii, K., Slane, P., Kinugasa, K., et al. 2000 [astro-ph/0006034] In the text  
• Turner, M., Abbey, A., Arnaud, M., et al. 2000, A&A, in press In the text  
• Vasisht, G., Aoki, T., Dotani, T., Kulkarni, S. R., & Nagase, F. 1996, ApJ, 456, L59 In the text NASA ADS  
• Warwick, R., Bernard, J.-P., Bocchino, F., et al. 2000, A&A, in press In the text  
• Woltjer, L., Salvati, M., Pacini, F., & Bandiera, R. 1997, A&A, 325, 295 In the text NASA ADS  
• Yancopoulos, S., Hamilton, T. T., & Helfand, D. J. 1994, ApJ, 429, 832 In the text NASA ADS