A&A 369, 915-924 (2001)
DOI: 10.1051/0004-6361:20010150

Results of a LMXB survey: Variation in the height
of the neutron star blackbody emission region

M. J. Church1,2 - M. Ba\lucinska-Church1,2


1 - School of Physics and Astronomy, University of Birmingham, Birmingham B15 2TT

2 - Institute of Astronomy, Jagiellonian University, ul. Orla 171, 30-244 Cracow, Poland

Received 5 October 2000 / Accepted 22 January 2001

Abstract
We present results of a survey of the spectra of Low Mass X-ray Binaries using ASCA. It is shown that all sources in the survey are well-fitted by the same two-component emission model that we have previously shown is able to describe both the non-dip and dip spectra of the dipping class of LMXB. This model consists of point-like blackbody emission from the neutron star plus Comptonized emission from a disk-like accretion disk corona of radius typically 50000 km. Additional data from results published elsewhere by us from BeppoSAX and ASCA are added to the survey. The large variation in blackbody luminosity of survey sources is shown to be due primarily to major changes in blackbody emitting area. Fitting a multi-temperature disk blackbody plus Comptonization model to the survey spectra requires values of inner disk radius substantially less than the neutron star radius in many cases, making disk origin of the blackbody highly unlikely. Assuming that the emission is from an equatorial strip on the neutron star, it is shown that the half-height of the strip h agrees well with the half-height H of the radiatively-supported inner accretion disk, this agreement spanning three orders of magnitude in each parameter. Possible mechanisms for the agreement are discussed, including radial accretion flow between inner disk and star, and accretion flow "creep'' on the surface of the neutron star.

Key words: X-rays: stars - stars: neutron - binaries: close - accretion: accretion disks


1 Introduction

Low mass X-ray binaries (LMXB) may be classified according to inclination angle and according to colour-colour properties. Frank et al. (1987) explained the markedly different light curves of LMXB in terms of a model of varying inclination. Sources having inclination angles between zero and $\sim$65$^\circ$ will show no orbital related variability, sources with inclination of 65- $\rm {80{^\circ}}$ will exhibit X-ray dipping, and sources with inclinations of 80- $\rm {90{^\circ}}$ will be Accretion Disk Corona (ADC) sources. Strong orbital-related variability is seen in the light curves of the dipping and ADC sources, but not in the other sources which are viewed from above the orbital plane. The second type of classification is based on examining the behaviour of LMXB on X-ray colour-colour diagrams. Hasinger et al. (1989) first used the term "Z-track'' to describe the evolution on a colour-colour diagram of bright LMXB such as Sco X-1 and Cyg X-2, the sources clearly undergoing marked spectral changes as they moved along the horizontal, normal and flaring branches. The Atoll sources were similarly recognised as having different colour-colour tracks (Hasinger & van der Klis 1989). Associated with tracks in the Z-track and Atoll sources was correlated timing behaviour, especially of QPOs (e.g. van der Klis 1995).

Clearly, strong spectral changes take place during track movement, but these are not understood. A number of surveys of the spectra of the Atoll and Z-track sources have been made, including that based on Exosat data (White et al. 1988). Schulz et al. (1989) classified a large number of sources in terms of colour-colour diagrams, and carried out spectral fitting using a blackbody plus cut-off power law model. A similar blackbody plus power law model was used by Schulz (1999) in a Rosat survey of LMXB. Christian & Swank (1997) produced a compilation of the properties of LMXB from the Einstein solid state and monitor proportional counter detectors.

There are considerable differences between the emission models that have been proposed for LMXB in general. A disk blackbody plus a Comptonized blackbody model was proposed by Mitsuda et al. (1989). A model also based on accretion disk blackbody emission was applied by Czerny et al. (1986) to Einstein data. The generalised thermal model (White et al. 1985) was used by White et al. (1988), with a blackbody added for high-luminosity sources which was not required for the lower luminosity burst sources, from which they concluded that spectral formation was dominated by Comptonizaton in the inner accretion disk. More recently, a two-component model proposed by Church & Ba\lucinska-Church (1995) has been shown to explain spectral evolution in the dipping LMXB sources, consisting of point-source blackbody emission identified with the neutron star plus Comptonized emission from an extended ADC modelled by a cut-off power law (Church & Ba\lucinska-Church 1993, 1995; Church et al. 1997, 1998a,b; Ba\lucinska-Church et al. 1999, 2000, 2001).

For the dipping LMXB sources, spectral analysis is more strongly constrained because of the requirement that a model fits not only the non-dip spectrum but also several levels of dipping. A major advantage of investigating spectral evolution in these sources is that dipping is characterised by the slow removal of Comptonized emission, and measurement of dip ingress times proves that the Comptonizing ADC has radial extent typically 50000 km (Church 2001), which is strongly inconsistent with Comptonization models involving a small region in the locality of the neutron star, allowing such models to be discounted.


 
Table 1: The observations

Source		 Type Date

GX 9+9		 Atoll 1994, Mar. 25
GX 13+1 Atoll 1994, Sep. 10
4U 1636-536 Atoll 1993, Aug. 9
Ser X-1 Prob Atoll 1994, Sep. 20
X 2127+119 Prob Atoll 1995, May. 16
Aql X-1   1994, Apr. 30
X 1746-371 Dipping 1995, Sep. 21
XB 1254-690 Dipping 1994, Mar. 18
GX 5-1 Z-track 1993, Oct. 9
Cyg X-2 Z-track 1993, Jun. 10


The success of this emission model with the dipping sources suggests that the model be tested with the other classes of LMXB, i.e. the Z-track and Atoll sources specifically. Other authors have successfully applied two-component blackbody + Comptonization models to Z-track and Atoll sources (above, and e.g. Hasinger et al. 1990; Barret et al. 2000). However, these often ascribe emission regions to the blackbody and Comptonized emission such as the accretion disk and a localised inner region respectively, e.g. Barret et al. (2000), and so physically, these models differ radically from ours and are also inconsistent with our measured ADC sizes. Recently, the comptt implementation of the Titarchuk (1994) Comptonization model has been used (together with a blackbody term) to fit BeppoSAX data on LMXB sources (e.g. in't Zand et al. 1999). It has been suggested that comptt is preferable to the cut-off power law which may overestimate the spectrum at low energies because of lack of soft seed photons. However, it is easy to calculate the spectrum of the disk (expressed as the photon number flux per keV) integrated to a radius equal to our measured ADC sizes, by combining the temperature gradient T(r) from standard thin disk theory with Planck's equation. This shows that for typical LMXB luminosities, the integrated spectrum forms a broad peak between 0.001 and 0.1 keV, thus producing a huge sea of soft photons, so that the cut-off power law is perfectly good above $\sim$0.1 keV. However, fitting the comptt model has produced high values of average kT for the seed photons, e.g. 1.0-2.0 keV (Guainazzi et al. 1998) which are >> than the above expected values and inconsistent with the assumption of Titarchuk (1994) that the seed photons are very soft: kT << $kT_{\rm {e}}$ (the electron temperature). This will lead to a substantial underestimation of the Comptonized spectrum at $\sim$1 keV as the Wien approximation (good for $h\nu >> kT$) is used in comptt to describe the seed photon spectrum.

In this paper, we apply the blackbody plus cut-off power law model to as many non-dipping Atoll and Z-track sources observed using ASCA as possible plus the non-dip spectra of two dipping sources. We show that the model provides a good description of the spectra of these sources.


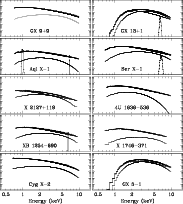  \begin{figure} \par\epsfxsize=160 mm \leavevmode \epsffile{f1a.eps} \vskip 1mm \... ....eps} \vskip 1 mm \epsfxsize=160 mm \leavevmode \epsffile{f1c.eps}\end{figure} Figure 1: Best fits to the ASCA spectra of 10 LMXB using the two-component continuum model discussed in the text, either in the form of blackbody + power law or blackbody + cut-off power law. Lines were added to the model in the 4 sources where definite line detections were made. In all cases the ordinate is in units of photon cm-2 s-1 keV-1
Open with DEXTER

2 Analysis and results

The observations of 10 LMXB with ASCA (Tanaka et al. 1994) were made between 1993, June and 1995, September as shown in Table 1. The designation "probably atoll'' was taken from van der Klis (1995) when the type is not well known. For each source, raw data files containing less than 100 counts were deleted, and the temperature-based gain correction was made. Screening was carried out after inspection of plots of the housekeeping parameters. Data were selected with the source less than $\rm {0.01{^\circ}}$ from the telescope pointing direction, elevation above the Earth's rim more than $\rm {5{^\circ}}$ and geomagnetic rigidity more than 6 GeV/c. Particle background was rejected for values of the background monitor rate of more than 200 count s-1 in most cases. Source data were selected from a 6$^\prime$ radius circular region in the image. Many of the sources were bright and so background subtraction was not important; when necessary, background data were extracted from an appropriate 6$^\prime$ region. Deadtime correction was performed on both light curves and spectra; this enabled high and medium bit rate data to be combined in a single light curve. In all cases except one, GIS2 data were used; in the case of X 1746-371, GIS3 data were used because of problems with the GIS2 raw data.

Light curves were extracted in the total GIS energy band and also in 3 standard bands: 0.7-4.0 keV, 4.0-7.0 keV and 7.0-10.0 keV. These were used to examine source variability and to construct colour-colour diagrams using the ratio of count rates 7.0-10.0 keV/4.0-7.0 keV and 4.0-7.0 keV/0.7-4.0 keV. Generally, there was little evidence for movement on the colour-colour diagrams during observations; some of the sources were constant, some showed slow drifts in intensity and some more rapid variability. To ensure that data could not be mixed from different intensity states, spectra were selected from appropriately narrow intensity bands for all sources, for example, in the band 75-80 count s-1 for GX 13+1. Response files were constructed appropriate to the position of each source in the image, and the latest corrections applied to the responses to correct for known differences between the detectors.

Spectra were grouped to a minimum of 100 counts per bin for strong sources and to 20 counts per bin for faint sources, and systematic errors of 2% added (Fukazawa et al. 1997). For each source, a range of models was tried including simple one-component models such as absorbed power law ( ABPL, where AB is the absorption term and PL the power law), absorbed

 

 
Table 2: Spectral fitting results. In most cases, the blackbody + cut-off power law model did not give any improvement over the blackbody + power law model, indicating a cut-off energy much higher than 10 keV. Only in cases where there was an improvement are results for both of these models given

Source		 Model $N_{\rm {H}}$ kT $\Gamma $ $E_{\rm {CO}}$ $\chi^{\rm {2}}$/dof
    $\rm {10^{22}}$ cm-2 kev   keV  

Atoll sources		            

GX 9+9		 Power law $0.55\pm 0.01$ ... $1.89\pm 0.07$ ... 4171/712
  Cut-off power law $0.19\pm 0.01$ ... $ 0.80\pm 0.03$ $4.1\pm 0.1 $ 507/711
  Blackbody + power law $0.37\pm 0.02$ $1.17\pm 0.02$ $1.95\pm 0.03$ ... 615/710
  Blackbody + cut-off power law $0.26\pm 0.01$ $1.27\pm 0.06$ $1.21\pm 0.03$ $\sim$6 514/710

GX 13+1

 Power law $4.4\pm 0.1$ ... $2.51\pm 0.02$ ... 1639/502
  Cut-off power law $2.4\pm 0.1$ ... $ -0.30\pm 0.13$ $1.9\pm 0.1 $ 459/501
  Blackbody + power law $3.5\pm 0.2$ $1.18\pm 0.02$ $2.88\pm 0.22$ ... 446/499

4U 1636-536

 Power law $0.55\pm 0.02$ ... $2.12\pm 0.02$ ... 423/396
  Cut-off power law $0.46\pm 0.03$ ... $ 1.83\pm 0.09$ 13.5+6.2-3.2 395/395
  Blackbody + power law $0.43\pm 0.05$ 0.65+0.08-0.05 $1.99\pm 0.07$ ... 391/394

Ser X-1

 Power law $0.71\pm 0.02$ ... $1.85\pm 0.02$ ... 1253/605
  Cut-off power law $0.43\pm 0.02$ ... $ 1.05\pm 0.05$ $5.4\pm 0.4 $ 513/604
  Blackbody + power law $0.62\pm 0.03$ $1.26\pm 0.08$ $2.00\pm 0.05$ ... 514/603

X 2127+119

 Power law $0.58\pm 0.04$ ... $2.04\pm 0.04$ ... 400/211
  Cut-off power law $0.14\pm 0.06$ ... $ 0.56\pm 0.19$ 2.7+0.4-0.3 218/210
  Blackbody + power law $0.24\pm 0.09$ $0.89\pm 0.06$ $1.85\pm 0.16$ ... 216/209

Aql X-1

 Power law $0.64\pm 0.03$ ... $1.75\pm 0.02$ ... 535/481
  Cut-off power law $0.48\pm 0.05$ ... $ 1.39\pm 0.10$ 12.4+4.2-2.6 497/480
  Blackbody + power law $0.49\pm 0.08$ 0.92+0.25-0.10 $1.66\pm 0.08$ ... 503/479

Dipping sources		            

XB 1746-371		 Power law $0.50\pm 0.05$ ... $1.83\pm 0.06$ ... 129/106
  Cut-off power law $0.31\pm 0.09$ ... $ 1.20\pm 0.27$ 6.4+4.9-2.0 115/105
  Blackbody + power law $0.50\pm 0.05$ 1.22+0.31-0.21 $1.91\pm 0.05$ ... 283/276

XB 1254-690

 Power law $0.48\pm 0.03$ ... $1.83\pm 0.03$ ... 389/281
  Cut-off power law $0.21\pm 0.05$ ... $ 0.93\pm 0.13$ 4.6+0.8-0.6 259/278
  Blackbody + power law $0.38\pm 0.06$ $1.17\pm 0.11$ $1.96\pm 0.13$ ... 264/277

Z-track sources		            

GX 5-1		 Power-law $4.8\pm 0.1$ ... $2.56\pm 0.03$ ... 952/438
  Cut-off power law $3.0\pm 0.1$ ... $ 0.20\pm 0.18$ $2.2\pm 0.2$ 476/437
  Blackbody + power law $3.4\pm 0.2$ $1.05\pm 0.04$ $2.29\pm 0.18$ ... 475/436

Cyg X-2

 Power-law $0.56\pm 0.01$ ... $2.11\pm 0.01$ ... 3186/541
  Cut-off power law $0.06\pm 0.02$ ... $ 0.45\pm 0.05$ $2.5\pm 0.1 $ 483/540
  Blackbody + power law $0.29\pm 0.02$ $1.01\pm 0.02$ $2.16\pm 0.05$ ... 559/539
  Blackbody + cut-off power law $0.10\pm 0.02$ $1.06\pm 0.12$ $0.75\pm 0.06$ $\sim$3 487/539


blackbody ( ABBB) and absorbed bremsstrahlung ( ABBR). The absorbed blackbody model always gave totally unacceptable fits with $\chi ^2$/degree of freedom (dof) typically 10; for the bremsstrahlung models the fits were also not acceptable with $\chi ^2$/dof varying between 1.2 and 2.0. Two-component models consisting of blackbody plus a Comptonized component were tried, in the forms AB(BB + PL) and AB(BB + CPL). The first form was used to approximate a cut-off power law at energies well below the Comptonization break. In several cases discussed below, it was necessary to add lines to the continuum model to obtain an acceptable fit. Results for the absorbed power law, absorbed cut-off power law and two-component models are given in Table 2 and these were obtained with lines added if appropriate.

In most sources, there was clear curvature, i.e. downcurving, in the spectrum between 1 and 10 keV (see Fig. 1), such that the ABPL model gave poor fits as can be seen from the $\chi ^2$ values in Table 2. The generalised thermal (model ABCPL, where CPL is a cut-off power law), provided good fits to all of the spectra. However, in the cases of several sources, particularly GX 13+1, X 2127+119, GX 5-1 and Cyg X-2, this was only achieved with very small and even negative values of the power law index $\Gamma $ which may be regarded as improbable. The values of cut-off energy $E_{\rm {CO}}$ are all very small ($\sim$few keV) which is typical of this model. However, we know from work on several dipping sources using BeppoSAX that the break energy is often much greater than 10 keV (Church et al. 1998b; Ba\lucinska-Church et al. 1999, 2000) and so the low values in most cases are unlikely to be real, but result from this model fitting the curvature between 1 and 10 keV actually due to the presence of a blackbody. Fitting a two-component model showed that in all cases, either the blackbody plus power law model or the blackbody plus cut-off power law model gave a fit as good or better than the ABCPL model, but without requiring any odd values. In most cases, the simpler AB(BB + PL) model gave a fit equally as good as the AB(BB + CPL) model showing that $E_{\rm {CO}}$ was >> 10 keV and so not possible to be determined using ASCA. In the case of GX 9+9 and Cyg X-2 this was not the case, showing that $E_{\rm {CO}}$ was less than 10 keV. Fitting for these sources, was carried out with $E_{\rm {CO}}$ fixed at a sequence of values as discussed below.


 

 
Table 3: Line detections

Source		 Energy Width $\sigma $ EW
  keV keV eV

GX 13+1		 $6.37\pm 0.23$ 0.1 44
Ser X-1 6.6 0.17 81
Aql X-1 $0.99\pm 0.04$ 0.01 53
  $6.81\pm 0.16$ 0.001 43
XB 1254-690 $6.40\pm 0.12$ 0.001 98


Lines were detected in the sources GX 13+1, Aql X-1, Ser X-1 and XB 1254-690, and the energies, widths and equivalent widths are shown in Table 3. These agree generally with the detections made in the extensive study of lines in LMXB using ASCA by Asai et al. (2000). There was also evidence for a weak line in XB 1746-371 at $\sim$6.4 keV also detected in SIS by Asai et al., and a possible weak detection of a line at $\sim$1.5 keV in GX 13+1. In Ser X-1, the iron feature detected was broad, and the width was not well-constrained using GIS data; consequently, to obtain the best continuum fit, the line energy and width $\sigma $ were set to the values determined by Asai et al. The best-fit two-component model for each source is shown in Fig. 1.


 

 
Table 4: Results of fitting a disk blackbody + cut-off power law model to ASCA and BeppoSAX data. The predominance of small or negative values of photon index $\Gamma $ can be seen, and the unphysical values of $r_{\rm {i}}$ less than the radius of the neutron star

Source		 Instrument $kT_{\rm {i}}$ $\Gamma $ $E_{\rm {CO}}$ $\chi^{\rm {2}}$/dof $r_{\rm {i}}$
    keV   keV   km

GX 9+9		 ASCA GIS $0.70\pm0.10$ -0.01+0.15-0.60 2.7 +0.2-0.4 490/709 10-17 +3-2
GX 13+1 ASCA GIS 1.14 +0.32-0.23 $-3.00\pm 0.01$ $1.17\pm0.01$ 435/499 11-19 +10-6
4U 1636-536 ASCA GIS $0.64\pm 0.07$ +0.50 +0.17-0.79 $4.0\pm 0.8$ 365/393 14-24 +7-4
Ser X-1 ASCA GIS 2.42 +0.13-0.08 +0.20+0.01-0.03 0.85 +0.80-0.34 489/601 2.7-4.7 +0.3-0.6
X 2127+119 ASCA GIS $3.22\pm 1.24$ -0.04+0.40-0.86 1.5 +0.2-0.8 213/208 0.79-1.1 +3.0-1.1
Aql X-1 ASCA GIS $1.00\pm 0.21$ $-1.05\pm 1.62$ 2.8 +3.3-0.8 482/480 2.8-4.8 +1.2-0.8
XB 1746-371 ASCA GIS 3.02 +3.06-0.83 -1.14+0.58-1.67 $0.85\pm 0.01$ 112/103 1.0-1.4 +1.5-1.1
XB 1254-690 ASCA GIS 2.51 +0.50-1.93 $+1.42\pm 0.63$ $3.98\pm 0.1$ 257/276 2.0- $2.9\pm 2.1$
GX 5-1 ASCA GIS 1.65 +0.06-0.13 $-1.36\pm 0.10$ 9.8 +3.0-2.0 473/435 15-26 +4-2
Cyg X-2 ASCA GIS $1.83\pm 0.17$ $-0.90\pm 0.04$ $0.74\pm 0.01$ 480/538 8.6-9.8 +1.0-3.0
XB 1916-053 SAX NFI $2.96\pm 0.24$ $+1.60\pm 0.04$ $200\pm 150$ 556/520 0.48- $0.67\pm 0.13$
XB 1323-619 SAX NFI 2.34 +0.56-0.25 +1.17 +0.24-0.39 $32\pm11$ 204/216 0.48- $0.67\pm 0.01$
X 1624-490 SAX NFI 5.1 +1.6-1.0 $-0.78\pm 0.58$ $1.7\pm 0.3$ 291/294 0.39-0.41 +0.38-0.21


2.1 X 1746-371, XB 1254-690

Spectral analysis results of the ASCA observations of these dipping sources have not previously been presented. These sources were well fitted by the two-component model. In XB 1746-371, the best-fit results were obtained by simultaneous fitting of the non-dip spectrum and the deepest dip spectrum. This technique has previously been used to constrain emission parameters better in dipping sources (e.g. Ba\lucinska-Church et al. 1999).

2.2 GX 9+9, Cyg X-2

In GX 9+9 and Cyg X-2 the blackbody plus power law model gave a substantially worse fit than the single component cut-off power law model showing that $E_{\rm {CO}}$ is not >>10 keV. The model AB(BB + CPL) gave improved qualities of fit. It was difficult to determine the cut-off energy because of the competition in modelling the 1-10 keV curvature between the blackbody and the Comptonization down-curving, and so $E_{\rm {CO}}$ was fixed at a series of values: 10, 8, 6, 4 and 2 keV. In GX 9+9, $\chi ^2$ became as good as for the cut-off power law model for $E_{\rm {CO}}$ $\sim$6 keV. For smaller cut-off energies, $\chi ^2$continued to improve, however the power law index decreased to <1 which is unlikely to be real. For Cyg X-2, stepping in $E_{\rm {CO}}$ gave acceptable $\chi ^2$ for $E_{\rm {CO}}\sim 3$ keV. This cut-off energy agrees well with the value of 3.32 keV obtained by Smale et al. (1993) from BBXRT. Thus, our preferred values of cut-off energy are $\sim$6 keV and $\sim$3 keV in GX 9+9 and Cyg X-2 respectively. Clearly, these should be re-measured in a wider band. However, test showed that the results presented below are not sensitive to the value of $E_{\rm {CO}}$.

2.3 Disk blackbody modelling

Finally, we tested the model consisting of disk blackbody emission plus a Comptonization term in the form of a cut-off power law, adding lines as before to the sources requiring lines. The 10 sources studied in the present ASCA survey were fitted, plus 3 sources recently studied using BeppoSAX (Ba\lucinska-Church et al. 1999, 2000; Church et al. 1998b). Results shown in Table 4 include values of inner disk radius $r_{\rm {i}}$ obtained from the normalization of the blackbody via: $r_{\rm {i}}$ = $({\rm norm}\, / {\rm cos}\, i)^{\rm {1/2}}\cdot d$, where i is the inclination angle of the binary system and d is the source distance. Inclination angles were assumed of $0 {-} {70{^\circ}}$ for Atoll and Z-track sources, $70 {-} \rm {80{^\circ}}$ for dipping sources, except for X 1624-490 where 60 - $\rm {65{^\circ}}$ was assumed, the upper limit being set by the absence of X-ray eclipses. For Cyg X-2, we use the range $58.5 {-} {66.5{^\circ}}$ (Orosz & Kuulkers 1999). Thus for each source a range of $r_{\rm {i}}$ values is shown, with 90% confidence uncertainties derived from the normalization uncertainties shown for the larger value in each case. Although good or acceptable fits were obtained, the results in many cases had improbably small or negative values of power law index. The values of $r_{\rm {i}}$ were in 8 out of 13 cases unphysical, i.e. < the radius of the neutron star $R_{\rm {*}}$, in 5 of these, $r_{\rm {i}}$ being 10 times smaller than $R_{\rm {*}}$. In 5 other cases, GX 9+9, GX 13+1, GX 5-1, Cyg X-2 and 4U 1636-536, $r_{\rm {i}}$ was not clearly unphysical, but the power law index was small or negative. We also note a tendency using ASCA to underestimate $kT_{\rm {i}}$and overestimate $r_{\rm {i}}$ compared with BeppoSAX as shown by restricting the BeppoSAX band to 1-10 keV, so in some cases, the $r_{\rm {i}}$ values in Table 4 may be too large. It is known that the multi-temperature disk blackbody model used can underestimate $r_{\rm {i}}$, however, maximum correction factors of $\sim$2-4 may be calculated based on the published work of Merloni et al. (2000) and Kubota et al. (2000). Allowing for this, the very small values of $r_{\rm {i}}$ in Table 4 make it unlikely that the blackbody emission is from the disk.

We have shown that the two-component model

  \begin{figure} \par\includegraphics[width=88mm,height=60mm,angle=0]{f2} \end{figure} Figure 2: Variation of blackbody luminosity in the band 1-30 keV with total luminosity in the same band; both luminosities are plotted in units of 1036 erg s-1. The dotted line shows the relationship expected from simple energy considerations that the blackbody luminosity of the neutron star should equal the luminosity of the accretion disk; i.e. 50% of the total luminosity
Open with DEXTER

(either as BB + PL or as BB + CPL) gives very good fits to all of the sources in our survey. In all cases, a blackbody component is required, and we next examine the properties of this component.

2.4 The blackbody-total luminosity relation

In Fig. 2 the variation of blackbody luminosity $L_{\rm {BB}}$ in the band 1-30 keV with the total luminosity $L_{\rm {Tot}}$ in the same band is shown. Also plotted in Fig. 2 are additional points from our analyses of the BeppoSAX observations of XB 1916-053 (Church et al. 1998b), XB 1323-619 (Ba\lucinska-Church et al. 1999) and X 1624-480 (Ba\lucinska-Church et al. 2000) and for XBT 0748-676 from ASCA data (Church et al. 1998a). These points are useful because the sources are weaker, and spectral parameters well-determined from the broadband BeppoSAX data. Source distances were taken from the Einstein Observatory survey of LMXB of Christian & Swank (1997). In the case of XB 1323-619, a distance of 10-20 kpc was derived by Parmar et al. (1989) based on the measured peak burst flux assumed to be Eddington-limited. As this may have underestimated the peak flux, we have assumed a value of 10 kpc. We also assumed 10 kpc for XBT 0748-676, the distance of which is not known. The sources in the present survey cover the luminosity range $\sim$5 1036 to $\rm {5~ 10^{38}}$ erg s-1. Errors in $L_{\rm {BB}}$ are derived from the 90% confidence limits in the blackbody normalization; similarly the errors in $L_{\rm {Tot}}$ were obtained from the 90% errors in power law normalization. Possible errors in source distance will move points equal amounts on both axes.

Additionally, a line is drawn showing the Newtonian value of 50% of $L_{\rm {Tot}}$ that should remain at the inner disk and be available for neutron star emission. In fact, the ratio of the energy available to the star to the energy in the disk depends on the spin of the neutron star (Sunyaev & Shakura 1986), varying from 2.2 for a slowly spinning star to small values for a star spinning rapidly, implying in the first case that the star can receive 69% of the energy. It can be seen that there is systematic behaviour in Fig. 2 such that the brighter sources approach the 50% line whereas the weaker sources fall increasingly below this line. Schulz et al. (1989) and Hasinger et al. (1990) found a similar variation of the blackbody luminosity with the total luminosity in Cyg X-2. It should be stressed that we do not claim a simple relationship between $L_{\rm {BB}}$ and $L_{\rm {Tot}}$, but rather a broad band in the figure where the sources lie. We next examine the reasons for the variation in blackbody luminosity over the sources investigated.

2.5 Blackbody properties

Table 5 lists the blackbody parameters derived from spectral fitting. Included here are the blackbody temperature $kT_{\rm {BB}}$, the blackbody luminosity in the band 1-30 keV and the blackbody radius $R_{\rm {BB}}$ defined by the relation $L_{\rm {BB}}$ = $4\,\pi\,R_{\rm {BB}}^{\rm {2}}\,\sigma\,T^{\rm {4}}$, where $\sigma $ is Stefan's constant. Also shown is the half-height h of the emission region assumed to be an equatorial strip on the neutron star. It can be seen that $L_{\rm {BB}}$ is reasonably well correlated with $R_{\rm {BB}}$. In Fig. 3 we show the variation of blackbody temperature with blackbody radius. It is striking that the major cause of variation is the emitting area. As the $L_{\rm {Tot}}$ increases as we move from the the extreme left of Fig. 3 (XB 1323-619) to the extreme right (GX 5-1), $kT_{\rm {BB}}$ falls by 40%, so that $T^{\rm {4}}$ decreases by a factor of 8. $R_{\rm {BB}}$ however, increases by a factor of $\sim$75 and emitting area by a factor of 5400 so that $L_{\rm {BB}}$ increases by a factor of $\sim$700, consistent with the change of $L_{\rm {BB}}$ between these sources in Fig. 2.


 

 
Table 5: Blackbody properties. h is the half-height of the emission region on the neutron star; the blackbody luminosity $L^{\rm {36}}_{\rm {BB}}$ (1-30 keV) is given in units of 1036 erg s-1

Source		 d $kT_{\rm {BB}}$ $L^{\rm {36}}_{\rm {BB}}$ $R_{\rm {BB}}$ h
  kpc keV   km km

GX 9+9		 5.0 1.27 1.66 3.2 1.03
GX 13+1 7.0 1.18 39.5 12.7 16.0
4U 1636-536 6.5 0.65 1.52 8.6 7.5
Ser X-1 8.4 1.26 15.7 7.0 4.9
X 2127+119 13.0 0.89 3.67 7.0 4.9
Aql X-1 4.8 0.92 0.29 1.81 0.33
XB 1746-371 9.0 1.22 0.58 1.4 0.21
XB 1254-690 12.0 1.17 4.74 4.5 2.0
GX 5-1 9.0 1.05 166.0 33.2 110.0
Cyg X-2 8.0 1.06 11.5 8.5 7.3
XB 1916-053 10.0 1.62 0.66 0.87 0.08
XB 1323-619 10.0 1.77 0.26 0.45 0.02
X 1624-490 15.0 1.31 25.5 8.3 6.8
XBT 0748-676 10.0 1.99 0.94 0.7 0.05


Thus, the large variation in emitting area is responsible for the large change in blackbody level. At low luminosity, the emission is from an equatorial strip on the star, which increases in height till at the higher luminosities, all of the star is emitting.


  \begin{figure} \epsfxsize=80 mm \par\leavevmode \epsffile{f3.eps}\end{figure} Figure 3: Variation of blackbody temperature $kT_{\rm {BB}}$ and radius $R_{\rm {BB}}$ for the survey sources plus additional sources discussed in the text. 90% confidence limits are shown
Open with DEXTER

2.6 Accretion disk properties

We next express the blackbody emitting area in terms of the half-height h of the emitting strip assumed to be an equatorial strip of varying height. The area is $4\,\pi\,h\,R_{\rm {*}}$ (for a sphere intersected by two parallel planes) equal to $4\,\pi\,R_{\rm {BB}}^{\rm {2}}$. Thus, the half-height h is related to $R_{\rm {BB}}$ by


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{f4a.ps}\hspace*{0.5mm} \includegraphics[angle=-90,width=8.8cm,clip]{f4b.ps} \end{figure} Figure 4: Left: variation of the height h of the blackbody emission region on the surface of the neutron star with the equilibrium height $H_{\rm {eq}}$ of the radiatively supported inner accretion disk. The triangles show the blackbody radius $R_{\rm {BB}}$ instead of h for the two bright sources GX 5-1 and GX 13+1. Right: h of the blackbody emission region versus the more accurate accretion disk height H (see text)
Open with DEXTER


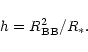\begin{displaymath}h = R_{\rm {BB}}^{\rm {2}}/R_{\rm {*}}. \end{displaymath} (1)

Values of h obtained in this way are included in Table 5.

Next, we compare h with the half-height of the inner radiatively-supported accretion disk. For a wide range of mass accretion rates, the inner disk is radiatively supported with half-height H given by


\begin{displaymath}H = {3\,\sigma_{\rm {T}}\,\dot M\over 8\, \pi\, m_{\rm {p}}\,... ...1\,-\,\biggl({R_{\rm {*}}\over r} \biggr)^{\rm {1/2}} \biggr] \end{displaymath} (2)

where $\sigma _{\rm {T}}$ is the Thomson cross section, $\dot M$ is the mass accretion rate and $m_{\rm {p}}$is the proton mass (Frank et al. 1992). The disk height H is zero at the surface of the star, but increases rapidly until it becomes independent of r having the equilibrium value $H_{\rm {eq}}$. Most of the increase takes place between r = 10 and r = 20 km, i.e. within 10 km of the stellar surface. In weak sources, with $L\sim 5~ 10^{\rm {36}}$ erg $\rm {s^{-1}}$, radiative support is over a limited radial extent so that $H_{\rm {eq}}$ is never achieved. In bright sources, $H_{\rm {eq}}$ is achieved, and radiative support continues typically to a radial distance of 400 km (for $L_{\rm {Tot}}$ = $\rm {10^{38}}$ erg $\rm {s^{-1}}$). Values of $H_{\rm {eq}}$ are, of course, much larger than the height of the gas-dominated thin disk calculated using the solution of Shakura & Sunyaev (1976) which for luminosities between 1036 and 1038 erg s-1, gives a half-height at a radius close to the neutron star ( $1.01\cdot R_{\rm {*}}$) varying between $\sim$25-50 m.

As a first approximation, in Fig. 4 (left), we show the variation of h with $H_{\rm {eq}}$, which was calculated using the total luminosity of each source to give $\dot M$ via $L_{\rm {Tot}}$ = $G M_{\rm {*}} \dot M /R_{\rm {*}}$. It can be seen that there is agreement between h and $H_{\rm {eq}}$; however, the lower luminosity points fall below the line h = $H_{\rm {eq}}$. This would be expected, since for lower luminosities $H_{\rm {eq}}$ is never achieved since the disk is radiatively-supported over an insufficient radial extent.

We calculate the actual maximum height of the disk in such cases as follows. The disk continues to be thick while the radiation pressure $p_{\rm {r}} >> p_{\rm {g}}$, the gas pressure. Czerny & Elvis (1987) discuss the transition from a thin disk to a thick disk. From their Eq. (19), it can be seen that the disk height becomes 90% of $H_{\rm {eq}}$ for $p_{\rm {r}}/(p_{\rm {r}}\,+\,p_{\rm {g}}) = 10$. For a calculation of disk height accurate to $\sim$10%, we have derived the radius $r_{\rm {10}}$ at which $p_{\rm {r}}=10$  $p_{\rm {g}}$, using the expressions for radiation pressure and gas pressure given by Shakura & Sunyaev (1976), to be $r_{\rm {10}}$ = $10.1\, M_{\rm {1}}^{\rm {-3/21}} \alpha ^{\rm {2/21}} \dot M_{\rm {16}}^{\rm {16/21}} f^{\rm {4/21}}$ km, where $M_{\rm {1}}$ is the mass of the neutron star in Solar masses, $\alpha $is the viscosity parameter, $\dot M_{\rm {16}}$ is in units of 1016 g s-1 and f = $[1 - (R_{\rm {*}}/r)^{\rm {1/2}}]^{\rm {1/4}}$. This equation can be solved numerically for $r_{\rm {10}}$ for particular values of $\dot M$. For example, using $\dot M$ values of $\rm {10^{17}}$ and $\rm {10^{18}}$ g s-1 equivalent to total luminosities of $\rm {2~ 10^{37}}$ and $\rm {2~ 10^{38}}$ erg s-1, and assuming $\alpha = 0.1$, $r_{\rm {10}}$ is $\sim$50 km and $\sim$300 km respectively, but for $\rm {3~ 10^{36}}$ ergs-1, $r_{\rm {10}} = 10.4$ km only. The actual maximum height of the disk will be $H(r_{\rm {10}})$. In Fig. 4 (right) we show the variation of h with $H(r_{\rm {10}})$, the more realistic calculation of disk height. It can be seen that there is remarkably good agreement between the height of the emission region and the height of the radiatively-supported disk, most points lying close to the line h = H.

In the case of GX 5-1, the agreement with h = H is poor, as h = 110 km and H = 43 km. However the blackbody radius in this case is 33 km showing that the emission is from a sphere three times larger than the star. There is a clear implication that the accretion flow is so strong that a spherical cloud of matter around the star has formed which is responsible for the blackbody emission. If we compare H with the height of this sphere, i.e. $R_{\rm {BB}}$ = 33 km, there is much better agreement between these quantities, again suggesting that the height of the disk determines the height of the emission region. In Fig. 4 we plot triangles for GX 5-1 and the other very bright source GX 13+1 to show their expected positions at h = $R_{\rm {BB}}$. Overall, there is good agreement between h and H in Fig. 4 (right) over about 3 orders of magnitude on each axis which is strong evidence for the significance of the agreement. Appropriate errors are shown for all points derived from 90% confidence limits in spectra parameters. Error in source distance will affect both h and H; adopting 10 km for the stellar radius will affect h, a value of 12 km reducing heights by 20%. It is also clear that we may introduce error by using the luminosity in the band 1-30 keV for calculating H, but this range was chosen to avoid extrapolating ASCA results too far above 10 keV. Using our work on XB 1916-053 from BeppoSAX (Church et al. 1998a) we have estimated possible errors. For this source, with $E_{\rm {CO}} = 80$ keV, and the total luminosity would have been underestimated by 28% using the band 1-30 keV. For $E_{\rm {CO}}$ = 20 keV, the error falls to 8% and for $E_{\rm {CO}}$ = 10 keV, the error is 1%. Thus there can be a further source of error in H requiring points to be moved to the right by up to 30%. Clearly, broadband spectral analysis is desirable for all sources in the survey. The implications of Fig. 4 will be discussed in the next section.

3 Discussion

We have shown that the two-component blackbody plus Comptonization model gives a good description of the ASCA spectra of the Atoll and Z-track sources analysed in this survey. We thus now propose that this model suggested by us as a unifying model for the dipping sources (Church & Ba\lucinska-Church 1995) gives a good description of LMXB in general. Fitting results for the disk blackbody plus Comptonization model were in 8 out of 13 cases unphysical having values of inner accretion disk radius substantially smaller than the neutron star radius making it unlikely that the blackbody emission originates in the disk. Our previous results for the dipping sources in particular (see Sect. 1), prove that the Comptonizing region is extended, indicating a flat, vertically shallow ADC above the inner accretion disk. Thus we do not expect significant Comptonization of blackbody emission from the neutron star in such an ADC since it is geometrically unlikely that blackbody photons will pass through this region. It is similarly unlikely that substantial Comptonization of the neutron star emission takes place in the inner radiatively-supported disk as this would require long path lengths of photons through the disk.

Next, we have shown that use of the two-component model reveals a broad dependence of the blackbody luminosity on the total luminosity not previously known for LMXB in general, the blackbody luminosity falling more rapidly than the total luminosity as the mass accretion rate decreases. The major change in blackbody emission has been shown to result primarily from changes in the emitting area, not the temperature. Assuming that the emission originates in an equatorial belt on the neutron star having radius $\sim$10 km, we have shown that its height agrees well with the height of the radiatively-supported inner accretion disk. This agreement extends to the less luminous sources where the radiatively-supported disk does not achieve its equilibrium height, and there is good agreement between h and H calculated at the position where $p_{\rm {r}}$ = $10\,p_{\rm {g}}$.

Possible explanations of the result that h = H are of two types; those in which the accretion disk height directly determines H, and those in which it does not. The direct mechanism requires radial (advective) flow of material between the inner disk edge and the star. Although there has been a very large amount of theoretical work on advective flow in black hole binaries (e.g. Abramowicz et al. 1996, and references therein), little work has been carried out for LMXB. It is not known whether the sonic point lies within the inner disk or within the star. However, Popham & Sunyaev (2000) show that the radial velocity increases by two orders of magnitude in the inner disk, but it is not known whether accretion flow can cross the gap between the inner disk edge and the star. Resolving this question will require detailed two- or three-dimensional hydrodynamic modelling.

Inogamov & Sunyaev (1999) have recently shown that accretion flow meeting the surface of the neutron star in the equatorial plane will spread over the surface of the star producing regions of enhanced X-ray brightness of vertical extent increasing with luminosity, as is the case in our observational result. The mechanism proposed is independent of the accretion disk height and so the h = H agreement would result from H being a measure of L. Preliminary work shows encouraging agreement between the emitting height on the neutron star predicted by Inogamov and Sunyaev. A detailed comparison between the present results and this theory will be made in a further paper.

The above results have a bearing on alternative models for LMXB. Our results are very inconsistent with models in which the blackbody originates in the accretion disk, and the agreement of h = H is positive evidence for neutron star blackbody emission. Additionally, we have used the timescales for dip ingress and egress in several observations of dipping sources (Church 2001) to obtain the radius of the extended Comptonizing ADC region: $r_{\rm {ADC}}$, typically $\rm {5~ 10^9}$ cm. These measurements are supported by the fact that the Comptonized emission component is gradually covered during dipping. Thus the ADC is 5000 times larger than the neutron star, and this rules out models in which Comptonization is supposed to take place in the neighbourhood of the neutron star.

We clearly need to improve our knowledge of the emission parameters of some of the sources studied by obtaining broadband spectra extending to $\sim$100 keV, allowing the cut-off energy to be measured, which has not in general been possible in the present work. Further investigation of both very bright sources and very weak sources will also be of interest. A complete description of the blackbody and Comptonized emission in LMXB must be more complicated than given here. For example, during flaring, major changes take place on the neutron star and inner disk and this is investigated in work currently taking place (Ba\lucinska-Church et al. 2001).

Acknowledgements
MJC and MBC thank the Royal Society and the British Council for financial support, and Andrew King, W\lodek Kluzniak, Nail Inogamov and Rashid Sunyaev for helpful discussions.

References

 
Copyright ESO 2001