We present evolutionary calculations for 74 close binaries systems with initial primary masses in the range 12...25
A&A 369, 939-959 (2001)
DOI: 10.1051/0004-6361:20010151
S. Wellstein1 - N. Langer1,2 - H. Braun3
1 -
Institut für Physik, Universität
Potsdam, 14415 Potsdam, Germany
2 -
Astronomical Institute, Utrecht University, Princetonplein 5,
3584 CC, Utrecht, The Netherlands
3 -
Max-Planck-Institut für Astrophysik, 85740 Garching, Germany
Received 7 September 2000 / Accepted 23 January 2001
Abstract
We present evolutionary calculations for 74 close binaries systems
with initial primary masses in the range 12...25![]() ,
and initial
secondary masses between 6 and 24
,
and initial
secondary masses between 6 and 24![]() .
The initial periods were
chosen such that mass overflow starts during the core hydrogen
burning phase of the primary (Case A), or shortly thereafter
(Case B). We use a newly developed binary code with up-to-date
physics input. Of particular relevance is the use of OPAL opacities,
and the time-dependent treatment of semiconvective and thermohaline
mixing. We assume conservative evolution for contact-free systems,
i.e., no mass or angular momentum loss from those system except due
to stellar winds.
We investigate the borderline between contact-free evolution and
contact, as a function of the initial system parameters. The
fraction of the parameter space where binaries may evolve while
avoiding contact - which we found already small for the least
massive systems considered - becomes even smaller for larger
initial primary masses. At the upper end of the considered mass
range, no contact-free Case B systems exist. While for primary
masses of 16
.
The initial periods were
chosen such that mass overflow starts during the core hydrogen
burning phase of the primary (Case A), or shortly thereafter
(Case B). We use a newly developed binary code with up-to-date
physics input. Of particular relevance is the use of OPAL opacities,
and the time-dependent treatment of semiconvective and thermohaline
mixing. We assume conservative evolution for contact-free systems,
i.e., no mass or angular momentum loss from those system except due
to stellar winds.
We investigate the borderline between contact-free evolution and
contact, as a function of the initial system parameters. The
fraction of the parameter space where binaries may evolve while
avoiding contact - which we found already small for the least
massive systems considered - becomes even smaller for larger
initial primary masses. At the upper end of the considered mass
range, no contact-free Case B systems exist. While for primary
masses of 16![]() and higher the Case A systems dominate the
contact-free range, at primary masses of 12
and higher the Case A systems dominate the
contact-free range, at primary masses of 12![]() contact-free
systems are more frequent for Case B. We identify the drop of the
exponent x in the main sequence mass-luminosity relation of the
form
contact-free
systems are more frequent for Case B. We identify the drop of the
exponent x in the main sequence mass-luminosity relation of the
form
![]() as the main cause for this behaviour.
For systems which evolve into contact, we find that this can occur
for distinctively different reasons. While Case A systems are prone
to contact due to reverse mass transfer during or after the
primary's main sequence phase, all systems obtain contact for
initial mass ratios below
as the main cause for this behaviour.
For systems which evolve into contact, we find that this can occur
for distinctively different reasons. While Case A systems are prone
to contact due to reverse mass transfer during or after the
primary's main sequence phase, all systems obtain contact for
initial mass ratios below ![]() 0.65, with a merger as the likely
outcome. We also investigate the effect of the treatment of
convection, and found it relevant for contact and supernova order in
Case A systems, particularly for the highest considered masses.
For Case B systems we find contact for initial periods above
0.65, with a merger as the likely
outcome. We also investigate the effect of the treatment of
convection, and found it relevant for contact and supernova order in
Case A systems, particularly for the highest considered masses.
For Case B systems we find contact for initial periods above ![]() 10 d. However, in that case (and for not too large periods)
contact occurs only after the mass ratio has been reversed, due to
the increased fraction of the donor's convective envelope. As most
of the mass transfer occurs conservatively before contact is
established, this delayed contact is estimated to yield to the
ejection of only a fraction of the donor star's envelope. Our
models yield the value of
10 d. However, in that case (and for not too large periods)
contact occurs only after the mass ratio has been reversed, due to
the increased fraction of the donor's convective envelope. As most
of the mass transfer occurs conservatively before contact is
established, this delayed contact is estimated to yield to the
ejection of only a fraction of the donor star's envelope. Our
models yield the value of ![]() ,
i.e., the fraction of the
primaries envelope which is accreted by the secondary.
We derive the observable properties of our systems after the major
mass transfer event, where the mass gainer is a main sequence or
supergiant O or early B type star, and the mass loser is a helium
star. We point out that the assumption of conservative evolution for
contact-free systems could be tested by finding helium star
companions to O stars. Those are also predicted by non-conservative
models, but with different periods and mass ratios. We describe
strategies for increasing the probability to find helium star
companions in observational search programs.
,
i.e., the fraction of the
primaries envelope which is accreted by the secondary.
We derive the observable properties of our systems after the major
mass transfer event, where the mass gainer is a main sequence or
supergiant O or early B type star, and the mass loser is a helium
star. We point out that the assumption of conservative evolution for
contact-free systems could be tested by finding helium star
companions to O stars. Those are also predicted by non-conservative
models, but with different periods and mass ratios. We describe
strategies for increasing the probability to find helium star
companions in observational search programs.
Key words: stars: evolution - stars: binaries - stars: blue stragglers - stars: circumstellar matter
To understand the evolution of massive close binary system is relevant
for many current astrophysical problems. Massive binaries provide the
unique means to obtain accurate fundamental stellar properties of
massive stars for various evolutionary stages. I.e., they have been
used to derive masses of Wolf-Rayet stars (van der Hucht 2000) and to
establish mass-luminosity relations for massive stars (Martin et al.
1998; Ostrov et al. 2000). They also lead to the existence of stellar
configurations which do not evolve from single stars and which have
highly exciting observational manifestations. Examples are the
peculiar supernova 1987A, which several authors attribute to binary
evolution (Podsiadlowski 1992; de Loore & Vanbeveren 1992; Braun &
Langer 1995), short-period Wolf-Rayet binaries (e.g., Harries &
Hilditch 1997), massive X-ray binaries (Chevalier & Ilovaisky 1998),
supernovae of types Ib and Ic (Podsiadlowski et al. 1992), and
![]() -ray burster (Fryer et al. 1999)
-ray burster (Fryer et al. 1999)
However, the evolutionary theory of massive close binaries still
suffers from fundamental uncertainties. The evolution of such systems
has been modelled by various authors, e.g., Paczynski (1967),
Kippenhahn (1969), de Loore & De Greve (1992), Pols (1994),
Vanbeveren et al. (1998a,b,c), Wellstein & Langer (1999). One
longstanding important question in binary models which include mass
transfer is: how much of the transfered matter can actually be
accreted by the secondary star? In most calculations so far, the
fraction ![]() of the accreted matter which is retained on the
accreting star is chosen as a constant, with
of the accreted matter which is retained on the
accreting star is chosen as a constant, with
![]() being a
frequent choice (e.g., Moers & van den Heuvel 1989; De Greve & De Loore 1992; De Loore & De Greve 1992; Vanbeveren et al. 1998a,b,c).
This means that half of the matter lost by the donor star is accreted
by the mass gainer; the other half supposed to leave the binary system
due to an undefined force, and carrying an amount of angular momentum
which needs to be described by a second parameter (cf. Huang & Taam
1990; Podsiadlowski et al. 1992). Also the assumption of a fully
conservative mass transfer where all matter is accreted by the
secondary, i.e.
being a
frequent choice (e.g., Moers & van den Heuvel 1989; De Greve & De Loore 1992; De Loore & De Greve 1992; Vanbeveren et al. 1998a,b,c).
This means that half of the matter lost by the donor star is accreted
by the mass gainer; the other half supposed to leave the binary system
due to an undefined force, and carrying an amount of angular momentum
which needs to be described by a second parameter (cf. Huang & Taam
1990; Podsiadlowski et al. 1992). Also the assumption of a fully
conservative mass transfer where all matter is accreted by the
secondary, i.e. ![]() ,
has been used. Physical models which
yield the parameter
,
has been used. Physical models which
yield the parameter ![]() as a function of the system parameters, or
even as a function of time for a give system, are lacking.
as a function of the system parameters, or
even as a function of time for a give system, are lacking.
Arguments of
![]() on average are being used in the
literature (De Greve & de Loore 1992; de Loore & De Greve 1992;
Vanbeveren et al. 1998a,b,c), and correspondingly massive close binary
models using
on average are being used in the
literature (De Greve & de Loore 1992; de Loore & De Greve 1992;
Vanbeveren et al. 1998a,b,c), and correspondingly massive close binary
models using
![]() have been computed (see above). Here, we
pursue a different approach. We adopt
have been computed (see above). Here, we
pursue a different approach. We adopt ![]() as long as the two
stars in the binary system do not evolve into contact. We want to
find out how many massive binaries actually avoid contact when
as long as the two
stars in the binary system do not evolve into contact. We want to
find out how many massive binaries actually avoid contact when ![]() is used, and whether the result can be compatible with an average
value of
is used, and whether the result can be compatible with an average
value of
![]() .
.
Mass transfer in systems with initial mass ratios very different from
unity is known to lead to the rapid expansion of the accreting star
and thus to a contact system (Benson 1970; Ulrich & Burger 1976).
Also systems with large initial periods are prone to develop contact,
as convective envelopes of the donor stars lead to very high mass
transfer rates (cf. Podsiadlowski et al. 1992). Pols (1994) found that
Case A![]() systems with primary masses in the range 8...16
systems with primary masses in the range 8...16![]() avoid contact
for initial mass ratios
avoid contact
for initial mass ratios
![]() and initial periods
and initial periods
![]() d. However, Pols used opacities from Cox &
Stewart (1970), the Schwarzschild criterion for convection, and
instantaneous thermohaline mixing. In the present work, we reconsider
the work done by Pols using updated physics input, and we extend the
considered parameters space towards higher masses and larger initial
periods.
We describe our computational method in Sect. 2, and illustrate our
binary model computation at the example of two representative cases in
Sect. 3. In Sect. 4, we present the results of 74 model systems
and discuss the formation of contact as a function of the main system
parameters and the applied stellar physics. We discuss our results in
Sect. 5, attempt a comparison with observations in Sect. 6, and
summarise our main conclusions in Sect. 7.
d. However, Pols used opacities from Cox &
Stewart (1970), the Schwarzschild criterion for convection, and
instantaneous thermohaline mixing. In the present work, we reconsider
the work done by Pols using updated physics input, and we extend the
considered parameters space towards higher masses and larger initial
periods.
We describe our computational method in Sect. 2, and illustrate our
binary model computation at the example of two representative cases in
Sect. 3. In Sect. 4, we present the results of 74 model systems
and discuss the formation of contact as a function of the main system
parameters and the applied stellar physics. We discuss our results in
Sect. 5, attempt a comparison with observations in Sect. 6, and
summarise our main conclusions in Sect. 7.
We computed the evolution of massive close binary systems using a computer code generated by Braun (1997) on the basis of an implicit hydrodynamic stellar evolution code for single stars (cf. Langer 1991, 1998). It invokes the simultaneous evolution of the two stellar components of a binary and computes mass transfer within the Roche approximation (Kopal 1978).
Mass loss from the Roche lobe filling component through the first
Lagrangian point is computed according to Ritter (1988) as
| (1) |
Due to the exponential dependence of the mass transfer rate on the stellar radius, an explicit scheme for computing the mass transfer rate can easily lead to numerical instabilities. Thus, we derive the mass transfer rate implicitly using an iterative scheme (combined Secant/Bisection-method; cf. Press et al. 1988), which is numerically more stable (Braun 1997). However, for each iteration a complete stellar model needs to be computed.
The change of the orbital period due to the mass transfer and stellar wind mass loss is computed according to Podsiadlowski et al. (1992), with the specific angular momentum of the stellar wind material being determined according to Brookshaw & Tavani (1993). The spin angular momentum of both stars is neglected. Mass transfer is treated quasi conservatively. The only mass loss from the system is due to the stellar winds of both components. The adopted stellar wind mass loss rates are described in Wellstein & Langer (1999).
We include time-dependent thermohaline mixing - i.e. mixing in radiatively stable regions which occurs due to an outwards increase of the mean molecular weight. This mixing process is important in stars which accrete helium-enriched material. A time-dependent treatment of thermohaline mixing is important for identifying the borderline between contact and contact-free close binary systems as it occurs on the thermal time scale of the accreting star, which - at the borderline of contact-free systems - is just equal to the mass transfer time scale. I.e., a time dependent treatment is required to reproduce the radius evolution of the accreting star during the mass transfer phase correctly as soon as helium-enriched material is being transferred (cf., Braun 1997).
Numerically, we treat thermohaline mixing through a diffusion scheme
(Braun 1997). The corresponding diffusion coefficient is based on the
work of Stern (1960), Ulrich (1972), and Kippenhahn et al. (1980); it reads
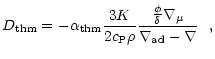 |
(2) |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{m12i4.hrd.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg40.gif) |
Figure 1:
Evolutionary tracks of the primary
(solid and dotted line) and secondary star (dashed line) of our
case A binary system No. 31 (initial masses are
|
| Open with DEXTER | |
The entropy of the accreted material is assumed to be equal to that of
the surface of the mass gainer and the gravitational energy release
due to mass transfer is treated as in Neo et al. (1977). Convection
and semiconvection are treated as described in Langer (1991) and Braun
& Langer (1995) (cf. also Langer et al. 1983). A semiconvective
efficiency parameter of
![]() is applied in most
models. We do not include so called convective core overshooting in
our models, as recent evidence implies that the physical effect of
increased convective core masses in massive main sequence stars may be
due to effects of rapid rotation rather than convection (Maeder 1987;
Langer 1992; Heger et al. 2000). As the rotation rates in close
binaries may be reduced due to orbit circularisation and spin-orbit
synchronisation (e.g., Savonije & Papaloizou 1997), it is unclear to
what extent any convective core mass increase would occur in those
objects. Opacities are taken from Iglesias & Rogers (1996). Changes
in the chemical composition are computed using a nuclear network
including the pp-chains, the CNO-tri-cycle, and the major helium-,
carbon, neon and oxygen burning reactions. Further details about the
computer program and input physics can be found in Langer (1998) and
Wellstein & Langer (1999). For all models, a metallicity of 2% is
adopted.
is applied in most
models. We do not include so called convective core overshooting in
our models, as recent evidence implies that the physical effect of
increased convective core masses in massive main sequence stars may be
due to effects of rapid rotation rather than convection (Maeder 1987;
Langer 1992; Heger et al. 2000). As the rotation rates in close
binaries may be reduced due to orbit circularisation and spin-orbit
synchronisation (e.g., Savonije & Papaloizou 1997), it is unclear to
what extent any convective core mass increase would occur in those
objects. Opacities are taken from Iglesias & Rogers (1996). Changes
in the chemical composition are computed using a nuclear network
including the pp-chains, the CNO-tri-cycle, and the major helium-,
carbon, neon and oxygen burning reactions. Further details about the
computer program and input physics can be found in Langer (1998) and
Wellstein & Langer (1999). For all models, a metallicity of 2% is
adopted.
We have computed 74 Case A and Case B systems to derive the
limits of contact free evolution for massive close binaries
within the assumptions made in Sect. 2.
Before we present the results of these models, we want to discuss
the evolution of one typical Case A system (No. 31; cf. Sect. 4 below),
and one Case B system (No. 37) in the following, to illustrate the
capabilities of our method and the type and quality of the derived
results. Those two systems are picked to show one detailed
example per considered
initial primary star mass - i.e., 12 ![]() and 16
and 16 ![]() ;
we have
discussed details of models with 25
;
we have
discussed details of models with 25 ![]() initial primary mass
in Wellstein & Langer (1999). Furthermore, the two examples
shown in detail below correspond to systems which evolve
contact-free. Therefore, we could follow the evolution
of both binary components until the end of carbon burning
(where we stopped the calculations).
initial primary mass
in Wellstein & Langer (1999). Furthermore, the two examples
shown in detail below correspond to systems which evolve
contact-free. Therefore, we could follow the evolution
of both binary components until the end of carbon burning
(where we stopped the calculations).
Table 1 and Fig. 1 describe the evolution of
our Case A system No. 31 (cf. Table 3 below), which
initially consists of a 12 ![]() primary
primary![]() and a 7.5
and a 7.5 ![]() secondary
star in a 2.5
secondary
star in a 2.5![]() d orbit. Mass transfer starts at a system age of
d orbit. Mass transfer starts at a system age of
![]()
![]() yr, at a core helium mass fraction
of the primary of 0.89. The mass transfer rate rises to some
yr, at a core helium mass fraction
of the primary of 0.89. The mass transfer rate rises to some
![]() during the so called
rapid Case A mass transfer phase (Fig. 2), i.e. to values of
the order of
during the so called
rapid Case A mass transfer phase (Fig. 2), i.e. to values of
the order of
![]() ,
M1 being the primary mass and
,
M1 being the primary mass and
![]() the thermal time scale of the primary. The reason is
that the orbital separation of both stars decreases until both
components have the same mass, here about 9.75
the thermal time scale of the primary. The reason is
that the orbital separation of both stars decreases until both
components have the same mass, here about 9.75![]() .
During the slow Case A mass transfer phase, the
mass transfer is driven by the nuclear evolution of the primary, and the
mass transfer rate drops to some
.
During the slow Case A mass transfer phase, the
mass transfer is driven by the nuclear evolution of the primary, and the
mass transfer rate drops to some
![]() ,
i.e. values of the
order of
,
i.e. values of the
order of
![]() .
.
It is remarkable that the mass transfer does not immediately relax at
the time of minimum orbital separation. In fact,
Fig. 2 shows that only a small amount of mass (![]()
![]() )
is transfered during that slow Case A mass transfer, i.e.
that its rapid phase does not stop until the primary mass is as small
as 4
)
is transfered during that slow Case A mass transfer, i.e.
that its rapid phase does not stop until the primary mass is as small
as 4![]() .
The reason is that, in contrast to the rule of thumb
that stars with radiative envelopes shrink upon mass loss,
the evolved core hydrogen burning 12
.
The reason is that, in contrast to the rule of thumb
that stars with radiative envelopes shrink upon mass loss,
the evolved core hydrogen burning 12![]() star has a negative
mass-radius exponent, i.e. its thermal equilibrium radius increases
for decreasing mass as a response to the increasing
core-mass/envelope-mass ratio. The thermally unstable mass transfer
during the rapid Case A is ended only when the mass ratio becomes
sufficiently small (cf. Ritter 1988).
star has a negative
mass-radius exponent, i.e. its thermal equilibrium radius increases
for decreasing mass as a response to the increasing
core-mass/envelope-mass ratio. The thermally unstable mass transfer
during the rapid Case A is ended only when the mass ratio becomes
sufficiently small (cf. Ritter 1988).
During the rapid phase of the Case A mass transfer the primary becomes
underluminous and the secondary becomes overluminous, due to the rapid
mass loss and gain, respectively. I.e., they deviate by up to a
factor of two from their thermal equilibrium luminosity (see the kinks
in the evolutionary tracks towards the end of the Case A mass transfer
in Fig. 1). During the slow phase of the Case A mass
transfer, primary and secondary relax to thermal equilibrium. Due to
the change in total mass, the secondary becomes more luminous than the
primary, even though the primary, after the mass transfer, is strongly
overluminous, i.e. its luminosity exceeds that of a 4![]() single
star by a factor of 10.
single
star by a factor of 10.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{aroche.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg50.gif) |
Figure 2:
Mass transfer rate as function of time for our
Case A system No. 31 (initial masses are
|
| Open with DEXTER | |
| time | M1 | M2 | P | |||
| Myr | d | kms-1 | kms-1 | |||
| ZAMS | 0 | 12.0 | 7.50 | 2.5 | 162 | 260 |
| begin Case A | 12.96 | 11.9 | 7.49 | 2.52 | 162 | 258 |
| end Case A | 14.93 | 3.92 | 15.5 | 7.99 | 228 | 57.8 |
| ECHB primary | 15.17 | 3.92 | 15.5 | 7.99 | 228 | 57.8 |
| begin Case AB | 15.17 | 3.92 | 15.5 | 7.99 | 228 | 57.8 |
| end Case AB | 15.46 | 1.45 | 17.8 | 102.6 | 113 | 9.2 |
| ECHB secondary | 18.94 | 1.45 | 17.7 | 104.2 | 112 | 9.2 |
| ECHeB primary | 20.55 | 1.45 | 17.4 | 108.0 | 110 | 9.2 |
| ECHeB secondary | 20.82 | 1.45 | 17.2 | 108.1 | 109 | 9.2 |
| ECCB secondary | 21.16 | 1.45 | 17.0 | 108.4 | 109 | 9.2 |
| ECCB primary | 22.14 | 1.45 | -- | -- | -- | -- |
At core hydrogen exhaustion, the primary mass is about 3.9![]() .
As
it still contains a hydrogen-rich envelope, a hydrogen burning shell
ignites and the star attempts to expand to red giant dimensions. This
initiates the so called Case AB mass transfer, which proceeds on the
thermal time scale of the primary and produces correspondingly high
mass transfer rates (cf. Fig. 2). It leads to the loss of almost all
remaining hydrogen and to the extinction of the hydrogen burning
shell. The Case AB mass transfer reduces the primary mass to about
.
As
it still contains a hydrogen-rich envelope, a hydrogen burning shell
ignites and the star attempts to expand to red giant dimensions. This
initiates the so called Case AB mass transfer, which proceeds on the
thermal time scale of the primary and produces correspondingly high
mass transfer rates (cf. Fig. 2). It leads to the loss of almost all
remaining hydrogen and to the extinction of the hydrogen burning
shell. The Case AB mass transfer reduces the primary mass to about
![]() ,
which corresponds to the mass of the convective hydrogen
burning core at central hydrogen exhaustion. Due to the extreme mass
ratio (cf. Table 1) the orbital period grows from 8 d to about 100 d
during the Case AB mass transfer. The primary spends about 5 Myr for
core helium burning, during which it remains on the helium-main
sequence in the HR diagram (cf. Fig. 1). The ensuing helium shell
burning expands the star to red giant dimensions, and a so called
Case ABB mass transfer would occur (Kippenhahn & Thomas 1979) - it
does occur in other systems of our sample - if the secondary star
would not have exploded in the meantime (see below). We follow the
primary's evolution until core carbon exhaustion. Due to its small
final mass, it is unlikely to produce a supernova explosion. Instead,
mass loss during its red giant stage at moderate rates would suffice
to substantially reduce the total mass before the core mass can grow
to ignite neon burning (Habets 1986a,b; Woosley et al. 1995). I.e., our
primary star of initially 12
,
which corresponds to the mass of the convective hydrogen
burning core at central hydrogen exhaustion. Due to the extreme mass
ratio (cf. Table 1) the orbital period grows from 8 d to about 100 d
during the Case AB mass transfer. The primary spends about 5 Myr for
core helium burning, during which it remains on the helium-main
sequence in the HR diagram (cf. Fig. 1). The ensuing helium shell
burning expands the star to red giant dimensions, and a so called
Case ABB mass transfer would occur (Kippenhahn & Thomas 1979) - it
does occur in other systems of our sample - if the secondary star
would not have exploded in the meantime (see below). We follow the
primary's evolution until core carbon exhaustion. Due to its small
final mass, it is unlikely to produce a supernova explosion. Instead,
mass loss during its red giant stage at moderate rates would suffice
to substantially reduce the total mass before the core mass can grow
to ignite neon burning (Habets 1986a,b; Woosley et al. 1995). I.e., our
primary star of initially 12![]() ends as an isolated ONeMg-white
dwarf.
ends as an isolated ONeMg-white
dwarf.
The secondary star grows to 17.81![]() and finishes core hydrogen
burning about 3.5 Myr after the end of the case AB mass transfer. At
this time it begins to expand to become a supergiant. However, due to
the presence of a strong mean molecular weight barrier above the
convective core at the onset of the mass transfer, it does not
rejuvenate during core hydrogen burning, i.e. it does not adapt its
convective core mass to its new total mass (cf. Hellings 1983, 1984;
Braun & Langer 1995). Therefore, the secondary star has, after the
mass transfer, a much smaller helium core to envelope mass ratio as a
single star of the same mass. For this reason, it remains in the blue
part of the HR diagram and does never become a red supergiant (Braun
& Langer 1995).
and finishes core hydrogen
burning about 3.5 Myr after the end of the case AB mass transfer. At
this time it begins to expand to become a supergiant. However, due to
the presence of a strong mean molecular weight barrier above the
convective core at the onset of the mass transfer, it does not
rejuvenate during core hydrogen burning, i.e. it does not adapt its
convective core mass to its new total mass (cf. Hellings 1983, 1984;
Braun & Langer 1995). Therefore, the secondary star has, after the
mass transfer, a much smaller helium core to envelope mass ratio as a
single star of the same mass. For this reason, it remains in the blue
part of the HR diagram and does never become a red supergiant (Braun
& Langer 1995).
Whether or not a secondary star rejuvenates depends strongly on the
- still poorly known - efficiency of semiconvection mixing (Langer
et al. 1983; Braun & Langer 1995). Were rejuvenation occurring in
our secondary, it would, after the mass transfer, evolve similar to a
single star of ![]()
![]() and attempt to become a red supergiant
after core hydrogen exhaustion. This would lead to a reverse Case B
mass transfer in this system, with the consequence of contact
evolution and a likely merging of both stars, due to the extreme mass
ratio (cf. System No. 25 below, and Sect. 5.2, for more details).
and attempt to become a red supergiant
after core hydrogen exhaustion. This would lead to a reverse Case B
mass transfer in this system, with the consequence of contact
evolution and a likely merging of both stars, due to the extreme mass
ratio (cf. System No. 25 below, and Sect. 5.2, for more details).
Because the secondary star has a small helium core mass, its fuel
supply for core helium burning is small. However, due to its
comparatively large total mass, its luminosity is large. Both factors
together imply a very short core helium burning life time of only
2 Myr. As a consequence, the secondary overtakes the primary in the
evolutionary status and ends its evolution first. It explodes as a
nitrogen-rich blue supergiant with properties similar to those of the
progenitor of SN 1987A. It is helium- and nitrogen enriched due to
the accretion, by factors 1.26 and 5.4, respectively, while carbon and
oxygen are depleted by factors of 0.23 and 0.81 (cf. Wellstein &
Langer 2001). Its core still has a memory of the lower initial mass:
the helium core mass is only ![]()
![]() at core carbon exhaustion.
This model applied to SN 1987A would predict the
existence of a
at core carbon exhaustion.
This model applied to SN 1987A would predict the
existence of a
![]() helium star with a luminosity of
helium star with a luminosity of ![]()
![]() and a temperature of
and a temperature of ![]()
![]() K in the supernova
remnant.
K in the supernova
remnant.
In many of our Case A systems - always for those with a 12![]() primary - the secondary is the first star which reaches the
supernova stage. This supernova reversal is discussed in more detail
in Sect. 5.2.
primary - the secondary is the first star which reaches the
supernova stage. This supernova reversal is discussed in more detail
in Sect. 5.2.
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{m16b8.hrd.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg58.gif) |
Figure 3:
Evolutionary tracks of the primary
(solid and dotted line) and secondary star (dashed line) of our
case B binary system No. 37 (initial masses are
|
| Open with DEXTER | |
Table 2 and Fig. 3 describe the evolution
of our case B system No. 37 (cf. Table 3), starting
with a 16![]() primary and a 15
primary and a 15![]() secondary in an 8 d orbit. As
the primary expands on a thermal time scale after core hydrogen
exhaustion, the Case B mass transfer occurs on the thermal time scale
of the primary, with mass transfer rates of the order of
secondary in an 8 d orbit. As
the primary expands on a thermal time scale after core hydrogen
exhaustion, the Case B mass transfer occurs on the thermal time scale
of the primary, with mass transfer rates of the order of
![]() (cf. Sect. 3.1). Both stars are far from thermal
equilibrium during the whole mass transfer phase. However, also in
this case, a fast and a somewhat slower Case B mass transfer phase can
be distinguished (Fig. 4), since the orbit shrinks at
first and expands after the mass ratio is reversed.
(cf. Sect. 3.1). Both stars are far from thermal
equilibrium during the whole mass transfer phase. However, also in
this case, a fast and a somewhat slower Case B mass transfer phase can
be distinguished (Fig. 4), since the orbit shrinks at
first and expands after the mass ratio is reversed.
In the considered system, the mass transfer achieves about
![]() during the Case B mass overflow. This implies an
accretion time scale of the secondary of the same order as its
Kelvin-Helmholtz time scale. Consequently, the secondary swells
considerably during the Case B mass transfer.
While here, contact is not quite achieved, for an initial
period of 9 d instead of 8 d the primary's radius at the onset of mass
transfer is slightly larger, the mass transfer rate as well, and the
system does evolve into contact at this stage (cf. system No. 39 in
Sect. 4 below).
during the Case B mass overflow. This implies an
accretion time scale of the secondary of the same order as its
Kelvin-Helmholtz time scale. Consequently, the secondary swells
considerably during the Case B mass transfer.
While here, contact is not quite achieved, for an initial
period of 9 d instead of 8 d the primary's radius at the onset of mass
transfer is slightly larger, the mass transfer rate as well, and the
system does evolve into contact at this stage (cf. system No. 39 in
Sect. 4 below).
| time | M1 | M2 | P | |||
| Myr | d | kms-1 | kms-1 | |||
| ZAMS | 0 | 16.0 | 15.0 | 8 | 162 | 173 |
| ECHB primary | 9.472 | 15.8 | 14.8 | 8.19 | 160 | 170 |
| begin Case B | 9.490 | 15.8 | 14.8 | 8.19 | 160 | 170 |
| end Case B | 9.513 | 3.83 | 26.7 | 94.9 | 128 | 18.3 |
| ECHeB primary | 10.46 | 3.61 | 26.5 | 99.1 | 126 | 17.1 |
| begin Case BB | 10.68 | 2.81 | 26.5 | 102.9 | 126 | 13.4 |
| ECCB primary | 10.68 | 2.33 | 26.8 | 170.7 | 109 | 9.4 |
| end Case BB | 10.68 | 2.32 | 26.8 | 172.1 | 108 | 9.4 |
| ECHB secondary | 10.95 | -- | 26.7 | -- | -- | -- |
| ECHeB secondary | 11.71 | -- | 26.0 | -- | -- | -- |
| ECCB secondary | 11.83 | -- | 25.9 | -- | -- | -- |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{broche.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg60.gif) |
Figure 4:
Mass transfer rate as function of time for our Case B system No. 37
(initial masses are
|
| Open with DEXTER | |
After the Case B mass transfer, very little hydrogen is left in the
primary star. It evolves quickly into a hot and compact helium star of
![]()
![]() ,
as which it burns helium in its core for about 1 Myr.
Thereafter, it expands again (cf. Sect. 3.1) and fills its Roche lobe
a second time, which initiates the so called case BB mass transfer.
During this phase, it loses the major fraction of its helium envelope
- 0.49
,
as which it burns helium in its core for about 1 Myr.
Thereafter, it expands again (cf. Sect. 3.1) and fills its Roche lobe
a second time, which initiates the so called case BB mass transfer.
During this phase, it loses the major fraction of its helium envelope
- 0.49 ![]() - to the secondary. This mass transfer occurs
again on the thermal time scale of the primary (cf.
Fig. 4). Between core carbon exhaustion and neon
ignition, the mass transfer ends. During the further evolution the
binary system remains detached, but the primary remains an extended
supergiant and nearly fills its Roche lobe. In the final state, the
once 16
- to the secondary. This mass transfer occurs
again on the thermal time scale of the primary (cf.
Fig. 4). Between core carbon exhaustion and neon
ignition, the mass transfer ends. During the further evolution the
binary system remains detached, but the primary remains an extended
supergiant and nearly fills its Roche lobe. In the final state, the
once 16![]() primary is a 2.3
primary is a 2.3![]() helium giant with a remaining
helium mass of 0.74
helium giant with a remaining
helium mass of 0.74 ![]() .
The core of the primary will collapse and
produce a supernova explosion. The explosion characteristics may
resemble those of types Ib or Ic supernovae (Shigeyama et al. 1990;
Woosley et al. 1995). However, the helium envelope of our model star
is very extended; its radius is
.
The core of the primary will collapse and
produce a supernova explosion. The explosion characteristics may
resemble those of types Ib or Ic supernovae (Shigeyama et al. 1990;
Woosley et al. 1995). However, the helium envelope of our model star
is very extended; its radius is ![]()
![]() .
Theoretical models for
the explosions for such cool helium giants are still missing in the
literature. Due to the large final mass ratio of 27/2.3, this system
has a good chance to remain bound after the explosion of the primary
component.
.
Theoretical models for
the explosions for such cool helium giants are still missing in the
literature. Due to the large final mass ratio of 27/2.3, this system
has a good chance to remain bound after the explosion of the primary
component.
The secondary star grows to almost 27![]() during the Case B mass
transfer. It continues its main sequence evolution thereafter and is
still burning hydrogen in its core when the primary
explodes. During the Case BB mass transfer, it accretes 0.49
during the Case B mass
transfer. It continues its main sequence evolution thereafter and is
still burning hydrogen in its core when the primary
explodes. During the Case BB mass transfer, it accretes 0.49![]() of
almost pure helium from the primary. During this phase, it becomes
very helium and nitrogen rich at the surface. Even though during and
after the Case BB mass transfer this enrichment is strongly diluted by
thermohaline mixing, the final helium and nitrogen enrichment factors
are 1.25 and 4, i.e. the final surface mass fractions are 0.35 and 0.0041
for helium and nitrogen, respectively.
of
almost pure helium from the primary. During this phase, it becomes
very helium and nitrogen rich at the surface. Even though during and
after the Case BB mass transfer this enrichment is strongly diluted by
thermohaline mixing, the final helium and nitrogen enrichment factors
are 1.25 and 4, i.e. the final surface mass fractions are 0.35 and 0.0041
for helium and nitrogen, respectively.
After core hydrogen exhaustion, the secondary expands, but it remains a blue supergiant up to its supernova explosion (Fig. 3) due to the lack of rejuvenation (cf. Sect. 3.1). The explosion of the secondary disrupts the binary system with a high probability.
In this section, we present results for 74 computed systems. Rather than providing a detailed description of the evolution of each system, we focus on the general trends of key properties as function of the major initial parameters. Table 3 provides the most important quantities for all computed systems. We focus on the various mechanisms which can drive massive close binary systems into contact.
| No. | M1 | M2 | Pi | case | Y</I>1 |
|
|
|
|
|
|
|
||||
| d | % | log( |
d |
|
||||||||||||
| 1 | 12 | 11.5 | 2.5 | A | - | 87 | 1.42 | 21.5 | 2.98 | 4.99 | 0.3 | 16.5 | 218 | 0.71 | 1.8 | 1.00 |
| 2 | 12 | 11 | 3 | B | - | 98 | 2.44 | 20.4 | 3.93 | 4.74 | 0.8 | 7.2 | 54 | 4.0 | 7.3 | 1.00 |
| 3 | 12 | 11 | 6 | B | - | 98 | 2.38 | 20.4 | 3.82 | 4.79 | 0.6 | 6.8 | 115 | 10 | 7.3 | 1.00 |
| 4 | 12 | 11 | 10 | B | - | 98 | -- | -- | -- | -- | -- | -- | -- | 17 | 7.5 | 1.00 |
| 5 | 12 | 11 | 16 | B | - | 98 | -- | -- | -- | -- | -- | -- | -- | 25 | 7.5 | 1.00 |
| 6 | 12 | 11 | 22 | B | - | 98 | -- | -- | -- | -- | -- | -- | -- | 28 | 7.6 | 1.00 |
| 7 | 12 | 11 | 30 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | >33 | 6.5 | 0.68 |
| 8 | 12 | 11 | 40 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | >33 | 5.7 | 0.60 |
| 9 | 12 | 10.5 | 2 | A | M | 75 | -- | -- | -- | -- | -- | -- | -- | 0.67 | 1.5 | 0.70 |
| 10 | 12 | 10.5 | 2.5 | A | - | 87 | 1.42 | 20.7 | 2.97 | 4.87 | 0.3 | 7.9 | 190 | 0.93 | 2.0 | 1.00 |
| 11 | 12 | 10 | 2 | A | M | 76 | -- | -- | -- | -- | -- | -- | -- | 0.82 | 1.6 | 0.68 |
| 12 | 12 | 10 | 16 | B | - | 98 | 2.43 | 19.4 | 3.81 | 4.71 | 0.6 | 6.6 | 255 | 22 | 7.0 | 1.00 |
| 13 | 12 | 10 | 22 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | >28 | 6.9 | 0.73 |
| 14 | 12 | 9.5 | 2 | A | - | 76 | 1.29 | 19.4 | 2.93 | 5.00 | 0.4 | 32.3e | 171 | 1.8 | 2.0 | 1.00 |
| 15 | 12 | 9.5 | 2.5 | A | - | 88 | 1.41 | 19.7 | 2.96 | 4.79 | 0.3 | 7.5 | 166 | 1.2 | 2.0 | 1.00 |
| 16 | 12 | 9.5 | 3.5 | B | - | 98 | 2.45 | 18.9 | 3.94 | 4.63 | 0.8 | 6.3 | 50 | 4.0 | 2.9 | 1.00 |
| 17a | 12 | 9 | 2 | A | R | 76 | 1.15 | 19.4 | 2.67 | 4.87 | 0.3 | 9.0 | 214 | 1.2 | 1.7 | 1.00 |
| 18 | 12 | 9 | 3.5 | B | - | 98 | 2.32 | 18.5 | 3.74 | 4.63 | 0.6 | 6.5 | 53 | 6.5 | 3.4 | 1.00 |
| 19 | 12 | 9 | 6 | B | - | 98 | 2.36 | 18.5 | 3.81 | 4.63 | 0.6 | 6.2 | 87 | 9.9 | 7.4 | 1.00 |
| 20 | 12 | 9 | 10 | B | - | 98 | -- | -- | -- | -- | -- | -- | -- | 15 | 7.0 | 1.00 |
| 21 | 12 | 9 | 16 | B | d | 98 | -- | -- | -- | -- | -- | -- | -- | 28 | 7.0 | 1.00 |
| 22 | 12 | 9 | 22 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | >29 | 5.9 | 0.62 |
| 23 | 12 | 8.5 | 2.5 | A | - | 88 | 1.43 | 18.8 | 2.97 | 4.72 | 0.3 | 6.8 | 135 | 1.6 | 2.1 | 1.00 |
| 24 | 12 | 8 | 2 | A | - | 77 | 1.12 | 18.5 | 2.64 | 4.84 | 0.3 | 8.5 | 189 | 3.0 | 2.3 | 1.00 |
| 25c | 12 | 8 | 2.5 | A | R | 87 | 1.66 | 17.9 | 3.18 | 4.68 | 0.4 | 6.5 | 81.5 | 3.6 | 2.5 | 1.00 |
| 26 | 12 | 8 | 3.5 | B | q | 98 | -- | -- | -- | -- | -- | -- | -- | 7.3 | 3.0 | 1.00 |
| 27 | 12 | 8 | 6 | B | - | 98 | 2.37 | 17.5 | 3.79 | 4.55 | 0.6 | 5.8 | 72 | 8.9 | 3.5 | 1.00 |
| 28 | 12 | 8 | 10 | B | - | 98 | -- | -- | -- | -- | -- | -- | -- | 15 | 6.8 | 1.00 |
| 29 | 12 | 8 | 16 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | >24 | 6.0 | 0.63 |
| 30 | 12 | 7.5 | 2 | A | q | 78 | -- | -- | -- | -- | -- | -- | -- | 2.1 | 2.0 | 1.00 |
| 31 | 12 | 7.5 | 2.5 | A | - | 89 | 1.45 | 17.8 | 2.99 | 4.64 | 0.3 | 6.3 | 104 | 2.5 | 2.0 | 1.00 |
| 32 | 12 | 7.5 | 3.5 | B | Q | 98 | -- | -- | -- | -- | -- | -- | -- | >8.1 | 2.8 | 0.27 |
| 33 | 12 | 6.5 | 2 | A | Q | 78 | -- | -- | -- | -- | -- | -- | -- | >4.6 | 1.4 | 0.13 |
| 34 | 16 | 15.7 | 3.2 | A | - | 91 | 2.79 | 27.8 | 3.88 | 5.14 | 0.5 | 9.3 | 75 | 3.5 | 3.6 | 1.00 |
| 35 | 16 | 15.7 | 6 | B | - | 98 | 3.49 | 27.5 | 4.17 | 5.14 | 0.6 | 8.3 | 86 | 22 | 7.7 | 1.00 |
| 36 | 16 | 15 | 2.5 | A | M | 80 | -- | -- | -- | -- | -- | -- | -- | 2.5 | 2.6 | 0.70 |
| 37 | 16 | 15 | 8 | B | - | 98 | 3.63 | 26.7 | 4.20 | 5.10 | 0.7 | 8.9 | 96 | 29 | 8.0 | 1.00 |
| No. | M1 | M2 | P</I>i | case | Y</I>1 |
|
|
|
|
|
|
|
||||
| d | % | log( |
d |
|
||||||||||||
| 38 | 16 | 15 | 9 | B | d | 98 | 3.64 | 26.7 | 4.22 | 5.10 | 0.7 | 8.1 | 107 | 32 | 8.1 | 1.00 |
| 39 | 16 | 15 | 15 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | >37 | 6.7 | 0.48 |
| 40 | 16 | 14 | 2 | A | M | 69 | -- | -- | -- | -- | -- | -- | -- | 2.2 | 2.2 | 0.86 |
| 41a | 16 | 14 | 2 | A | - | 68 | 2.12 | 27.0 | 3.68 | 5.21 | 0.6 | 11.0 | 110 | 1.2 | 2.1 | 1.00 |
| 42 | 16 | 14 | 2.5 | A | - | 80 | 2.39 | 26.5 | 3.78 | 5.17 | 0.6 | 11.0 | 97.5 | 3.1 | 2.9 | 1.00 |
| 43 | 16 | 14 | 3 | A | - | 87 | 2.52 | 26.6 | 3.75 | 5.10 | 0.5 | 9.0 | 101 | 2.0 | 2.8 | 1.00 |
| 44 | 16 | 14 | 6 | B | - | 98 | 3.60 | 25.8 | 4.19 | 5.04 | 0.6 | 7.8 | 67 | 24 | 7.9 | 1.00 |
| 45 | 16 | 14 | 9 | B | D | 98 | 3.64 | 25.7 | 4.21 | 5.04 | 0.7 | 7.6 | 98 | 31 | 8.2 | 0.64f |
| 46 | 16 | 13 | 2 | A | M | 69 | -- | -- | -- | -- | -- | -- | -- | 3.0 | 2.5 | 0.68 |
| 47 | 16 | 13 | 2.5 | A | - | 80 | 2.28 | 26.1 | 3.65 | 5.11 | 0.5 | 9.1 | 99 | 2.1 | 2.4 | 1.00 |
| 48c | 16 | 13 | 2.5 | A | - | 79 | 2.47 | 25.6 | 3.77 | 5.10 | 0.6 | 7.6 | 78 | 4.3 | 3.0 | 1.00 |
| 49 | 16 | 13 | 3 | A | - | 88 | 2.64 | 25.3 | 3.84 | 5.07 | 0.5 | 9.1 | 64 | 5.2 | 3.5 | 1.00 |
| 50c | 16 | 13 | 3 | A | - | 87 | 2.66 | 25.2 | 3.81 | 5.08 | 0.5 | 7.8 | 62,5 | 5.1 | 3.2 | 1.00 |
| 51 | 16 | 13 | 4 | B | d | 98 | 3.55 | 24.8 | 4.19 | 4.99 | 0.7 | 8.2 | 41 | 18 | 6.9 | 1.00 |
| 52 | 16 | 13 | 6 | B | D | 98 | 3.70 | 24.7 | 4.24 | 4.95 | 0.7 | 6.8 | 57 | 27 | 7.8 | 0.62f |
| 53 | 16 | 12 | 1.5 | A | M | 54 | -- | -- | -- | -- | -- | -- | -- | 3.5 | 2.4 | 0.71 |
| 54 | 16 | 12 | 1.7 | A | M | 61 | -- | -- | -- | -- | -- | -- | -- | 3.7 | 2.5 | 0.75 |
| 55 | 16 | 12 | 2 | A | - | 70 | 2.07 | 24.8 | 3.57 | 5.17 | 0.5 | 11.8 | 93 | 4.2 | 2.8 | 1.00 |
| 56 | 16 | 12 | 4 | B | d | 98 | 3.55 | 23.9 | 4.17 | 4.93 | 0.6 | 7.0 | 37 | 18 | 6.3 | 1.00 |
| 57 | 16 | 12 | 6.5 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | 26 | 7.7 | 0.38f |
| 58 | 16 | 11 | 2 | A | - | 71 | 2.00 | 24.1 | 3.56 | 5.10 | 0.5 | 10.8 | 89 | 5.7 | 3.1 | 1.00 |
| 59c | 16 | 11 | 2 | A | qR | 69 | 2.10 | 24.0 | 3.54 | 5.13 | 0.5 | 8.4 | 77 | 5.9 | 3.1 | 1.00 |
| 60 | 16 | 11 | 3 | A | - | 89 | 2.52 | 23.8 | 3.74 | 4.95 | 0.5 | 7.3 | 61 | 3.8 | 2.8 | 1.00 |
| 61 | 16 | 11 | 3.2 | A | - | 92 | 2.81 | 23.3 | 3.87 | 4.93 | 0.5 | 7.4 | 42 | 8.2 | 4.0 | 1.00 |
| 62 | 16 | 10 | 2.5 | A | q | 81 | 2.28 | 23.1 | 3.77 | 4.97 | 0.6 | 7.8 | 65 | 8.7 | 3.5 | 1.00 |
| 63 | 16 | 10 | 3 | B | q | 89 | -- | -- | -- | -- | -- | -- | -- | 9.9 | 3.9 | 1.00 |
| 64 | 16 | 9 | 2.5 | A | Q | 82 | -- | -- | -- | -- | -- | -- | -- | 12 | 3.4 | 0.16f |
| 65 | 25 | 24 | 3.5 | A | - | 83 | 5.15 | 40.6 | 4.53 | 5.54 | 0.6 | 13.7 | 41 | 3.0 | 4.6 | 1.00 |
| 66a | 25 | 24 | 3.5 | A | - | 83 | 5.21 | 40.6 | 4.54 | 5.54 | 0.6 | 12.4 | 40 | 3.0 | 4.2 | 1.00 |
| 67b | 25 | 24 | 3.5 | A | - | 82 | --d | 40.5 | --d | 5.54 | --d | 11.2 | -- | 3.0 | 4.6 | 1.00 |
| 68 | 25 | 24 | 5 | B | d | 98 | 7.28 | 39.2 | 4.85 | 5.45 | 0.8 | 11.9 | 31 | 30 | 8.2 | 1.00 |
| 69 | 25 | 24 | 9 | B | D | 98 | -- | -- | -- | -- | -- | -- | -- | >37 | 7.4 | 0.43 |
| 70 | 25 | 23 | 4 | A | - | 87 | 5.31 | 39.4 | 4.56 | 5.49 | 0.6 | 12.4 | 39 | 4.0 | 5.2 | 1.00 |
| 71 | 25 | 22 | 2.5 | A | - | 70 | 4.80 | 39.6 | 4.45 | 5.55 | 0.7 | 14.2 | 39 | 2.7 | 2.9 | 1.00 |
| 72c | 25 | 22 | 2.5 | A | - | 68 | 4.68 | 38.9 | 4.44 | 5.62 | 0.7 | 10.5 | 39 | 5.3 | 3.6 | 1.00 |
| 73 | 25 | 19 | 4 | A | - | 88 | 5.26 | 35.9 | 4.55 | 5.38 | 0.7 | 8.7 | 30 | 6.3 | 4.9 | 1.00 |
| 74 | 25 | 16 | 4 | A | - | 89 | 5.22 | 33.3 | 4.54 | 5.29 | 0.6 | 8.8 | 24 | 8.8 | 5.0 | 1.00 |
| a
b c Schwarzschild criterion instead of Ledoux criterion used. d Only secondary is computed but primary should not be very different from Nos. 65 and 66. e Secondary at ECHeB. f Treated as if |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{m12bxx.roche1.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg74.gif) |
Figure 5:
Mass transfer rates as a function of secondary mass
for Case B systems initially consisting of a 12 |
| Open with DEXTER | |
Case B systems with an initial mass ratio close to 1 and a rather
short initial period (early Case B) are known to have a good
chance to avoid contact during the Case B mass transfer (cf. Pols
1994). Our Table 3 contains 15 examples, i.e. systems Nos. 2...6, 12,
16, 18...20, 27, 28 (initial primary mass of
![]() ), and Nos. 35, 37
and 44 (initial primary mass of
), and Nos. 35, 37
and 44 (initial primary mass of
![]() ). The fact that no such
system with an initial primary mass of
). The fact that no such
system with an initial primary mass of
![]() could be found is
discussed in Sect. 5.1. It is often assumed that late Case B
systems, i.e. such with a relatively large initial period, evolve
through a common envelope stage (Podsiadlowski et al. 1992; Vanbeveren
1998a,b,c). In the following, we will have a closer look to the
transition region in between both extremes.
could be found is
discussed in Sect. 5.1. It is often assumed that late Case B
systems, i.e. such with a relatively large initial period, evolve
through a common envelope stage (Podsiadlowski et al. 1992; Vanbeveren
1998a,b,c). In the following, we will have a closer look to the
transition region in between both extremes.
Figure 5 shows the mass transfer rates as a function
of the secondary mass for Case B binaries with initial primary and
secondary masses of 12![]() and 11
and 11![]() ,
respectively, but different
initial periods in the range 6...40
,
respectively, but different
initial periods in the range 6...40![]() d (Systems Nos. 3 to 8).
Generally, initially wider systems develop larger mass transfer rates.
However, it is interesting to consider the time dependence of the mass
transfer rate of these systems in some detail. The first maximum in
the mass transfer rate is related to the end of decrease of the
orbital separation at mass ratio one. I.e., when the primary has
become the less massive component in the system, the period and the
Roche lobe of the primary begin to grow, and the increase of the mass
transfer rate flattens. This happens with some time delay due to the
finite thermal response time of the primary.
d (Systems Nos. 3 to 8).
Generally, initially wider systems develop larger mass transfer rates.
However, it is interesting to consider the time dependence of the mass
transfer rate of these systems in some detail. The first maximum in
the mass transfer rate is related to the end of decrease of the
orbital separation at mass ratio one. I.e., when the primary has
become the less massive component in the system, the period and the
Roche lobe of the primary begin to grow, and the increase of the mass
transfer rate flattens. This happens with some time delay due to the
finite thermal response time of the primary.
Later during the mass transfer, the orbit widens significantly.
Therefore, the primary becomes more extended and its surface
temperature decreases. In the wider systems considered in
Fig. 5, the outer envelope of the primary becomes
even convectively unstable. It is the drop of the adiabatic
mass-radius exponent
![]() (cf. Ritter 1988) which leads to
another rise of the mass transfer rate even though the orbit widens.
We designate this feature as delayed contact. Table 3 shows nine
systems which evolve delayed contact. It is restricted to the Case B
and has no counterpart in our Case A systems (cf. Sect. 4.1.2).
(cf. Ritter 1988) which leads to
another rise of the mass transfer rate even though the orbit widens.
We designate this feature as delayed contact. Table 3 shows nine
systems which evolve delayed contact. It is restricted to the Case B
and has no counterpart in our Case A systems (cf. Sect. 4.1.2).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{m12bxx.roche2.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg77.gif) |
Figure 6: Radius of the secondary during mass transfer as a function of its mass, for the same systems as in Fig. 5. In the systems with 30 and 40 days initial period the large increase in radius leads to contact, at which time we stop the calculation |
| Open with DEXTER | |
Figure 6 displays the radius evolution of the
secondary stars of the systems considered in Fig. 5.
Initially, the radii do not grow significantly, although it can be
seen seen that larger radii are obtained for larger initial periods,
i.e. for larger mass transfer rates. Later on, mass transfer rates in
excess of ![]()
![]() make the secondary swell enormously.
This mass transfer rate corresponds roughly to
make the secondary swell enormously.
This mass transfer rate corresponds roughly to
![]() ,
i.e. to the condition
,
i.e. to the condition
![]() for the secondary.
In the two systems with initial periods of 30 and 40 days, the radius
increases until the secondary also fills its Roche lobe and a contact
system is formed. This effect marks the limit of contact free systems
towards larger periods.
for the secondary.
In the two systems with initial periods of 30 and 40 days, the radius
increases until the secondary also fills its Roche lobe and a contact
system is formed. This effect marks the limit of contact free systems
towards larger periods.
It is remarkable that approximately 5 ![]() for the 40 d binary
(system No. 8) and 6
for the 40 d binary
(system No. 8) and 6 ![]() for the 30 d binary (system No. 7) are
transfered before the contact occurs (cf. Fig. 6). From
Fig. 6 we see that contact occurs the earlier (in
terms of already transfered mass) the larger the initial system period
is. I.e., there is a continuous transition towards very wide binaries
with convective primaries, which evolve into contact at the very
beginning of the mass transfer process (Podsiadlowski et al. 1992).
for the 30 d binary (system No. 7) are
transfered before the contact occurs (cf. Fig. 6). From
Fig. 6 we see that contact occurs the earlier (in
terms of already transfered mass) the larger the initial system period
is. I.e., there is a continuous transition towards very wide binaries
with convective primaries, which evolve into contact at the very
beginning of the mass transfer process (Podsiadlowski et al. 1992).
According to the estimate of Webbink (1984), which compares the
orbital energy of the binary with the binding energy of the envelope,
our System No. 7 does not merge during the Case B mass transfer.
Instead, with an efficiency parameter of
![]() ,
it
obtains a period of about 7.5 d in a common envelope evolution by
expelling the remaining envelope of the primary of
,
it
obtains a period of about 7.5 d in a common envelope evolution by
expelling the remaining envelope of the primary of ![]()
![]() from
the system.
from
the system.
In summary, in delayed contact systems a conservative part of Case B
mass transfer is followed by a non-conservative one, leading to an
oscillation of the orbit: it first shrinks until the mass ratio is 1,
then widens up to the end of the conservative part, and then shrinks
again due to mass and angular momentum loss from the system. For our
System No. 7, the parameter ![]() for the complete Case B mass
transfer, i.e., the ratio of the amount of mass accreted by the
secondary to the amount lost by the primary, is about
for the complete Case B mass
transfer, i.e., the ratio of the amount of mass accreted by the
secondary to the amount lost by the primary, is about
![]() .
.
After the delayed contact and common envelope evolution, System No. 7
consists of a ![]()
![]() main sequence star - the secondary -
and a
main sequence star - the secondary -
and a ![]()
![]() helium star in a 7.5 d orbit. The further
evolution (which we have not computed) depends on the
post-common envelope period. For 7.5 d,
the primary fills its Roche lobe as it expands to a helium giant, and transfers
part of its helium envelope to the secondary in a Case BB mass
transfer, similar to that discussed in Sect. 3.2 for system No. 37.
helium star in a 7.5 d orbit. The further
evolution (which we have not computed) depends on the
post-common envelope period. For 7.5 d,
the primary fills its Roche lobe as it expands to a helium giant, and transfers
part of its helium envelope to the secondary in a Case BB mass
transfer, similar to that discussed in Sect. 3.2 for system No. 37.
In contrast, the systems which avoid contact during the Case B mass
transfer all together can often, even if the secondary evolves faster,
avoid the reverse Case B mass transfer if the secondary star does not
rejuvenate (cf. values of
![]() in Table 3). After
the Case B mass transfer, their periods are typically larger than
50 d.
in Table 3). After
the Case B mass transfer, their periods are typically larger than
50 d.
We find that in our most massive systems, with a primary mass of
25![]() ,
even early Case B mass transfer leads into contact,
even for an initial mass ratios very close to 1 (cf. systems Nos. 68
and 69 in Table 3). In the two considered systems, large amounts of
mass are transferred conservatively before contact occurs (8.2
,
even early Case B mass transfer leads into contact,
even for an initial mass ratios very close to 1 (cf. systems Nos. 68
and 69 in Table 3). In the two considered systems, large amounts of
mass are transferred conservatively before contact occurs (8.2![]() and 7.4
and 7.4![]() ;
cf. Table 3), i.e., we have a delayed contact situation.
In system No. 68, the contact is marginal, in system No. 69 it is not.
;
cf. Table 3), i.e., we have a delayed contact situation.
In system No. 68, the contact is marginal, in system No. 69 it is not.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{m16+12.R.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg87.gif) |
Figure 7:
Secondary radius as a function of its mass during Case A mass
transfer, for three systems starting out with a 16 |
| Open with DEXTER | |
Figure 7 demonstrates a completely different mechanism
of contact formation operating in Case A systems, which occurs for
short periods (cf. also Pols 1994). It shows the radius
evolution of three secondaries in Case A systems which have identical
initial parameters except the period (systems Nos. 53...55 in
Table 3). All three secondaries evolve through the
rapid part of the Case A mass transfer (cf. Sect. 3.1) without
expanding significantly (which is different for initial mass ratios
![]() ;
cf. Sect. 5.1). However, in the two closer systems, the
mass transfer appears so early in the evolution of the primary that
the now more massive secondary finishes core hydrogen burning first.
It then starts to expand, but soon fills its Roche lobe and attempts a
reverse Case B mass transfer (in systems Nos. 53 and 54). Thus, both
stars now fill their Roche lobes and come into contact while the
primary is still burning hydrogen in its core; we designate this as
premature contact. The likely outcome of premature contact is a
merger because the corresponding periods are too small for a
successful common envelope ejection. This effect marks the lower
period limit for contact free binaries.
;
cf. Sect. 5.1). However, in the two closer systems, the
mass transfer appears so early in the evolution of the primary that
the now more massive secondary finishes core hydrogen burning first.
It then starts to expand, but soon fills its Roche lobe and attempts a
reverse Case B mass transfer (in systems Nos. 53 and 54). Thus, both
stars now fill their Roche lobes and come into contact while the
primary is still burning hydrogen in its core; we designate this as
premature contact. The likely outcome of premature contact is a
merger because the corresponding periods are too small for a
successful common envelope ejection. This effect marks the lower
period limit for contact free binaries.
In model No. 55, the primary ends core H-burning first. Therefore, Case AB mass transfer (cf. Sect. 3.1) sets in before the secondary expands strongly. This has two effects: it drives the two stars further apart - the period increases from 5.24 d at the beginning to 93 d at the end of Case AB mass transfer -, and it enhances the mixing of hydrogen into the core (cf. Braun & Langer 1995) and thus delays the evolution of the secondary. I.e., if the initial period exceeds a critical value, Case AB mass transfer starts before the secondary expands and premature contact can be avoided. If the secondary star does not rejuvenate, reverse Case B mass transfer is avoided as well. Curiously, the secondary star in our Case A system No. 1 finishes core hydrogen burning just after the end of the Case A mass transfer and before the beginning of the Case AB mass transfer. However, the accretion due to the Case AB mass overflow leads to a shrinkage of its radius, and contact is avoided (see also Fig. 11 below).
The lower period limit for contact free binaries depends sensitively
on the convection criterion. As mentioned in Sect. 2, we compute
stellar models using the Ledoux criterion for convection and
semiconvection with an efficiency parameter of
![]() .
The semiconvective mixing efficiency - which is infinite in
the case of the Schwarzschild criterion for convection - determines
to a large extent whether an accreting core hydrogen burning star
rejuvenates or not (Braun & Langer 1995). If it fails, which is the
more likely for less efficient semiconvection and the more advanced
the star is in its evolution when it starts to accrete, it retains an
unusual structure, with a smaller helium core mass and a larger
hydrogen envelope mass compared to single stars. As such a structure
keeps the star relatively compact during all the advanced burning
stages - i.e., it avoids the red supergiant stage (Braun & Langer
1995) - it will not fill its Roche lobe after core hydrogen burning.
This is the situation in all our Case A systems which avoid premature
contact and have initial mass ratios of
.
The semiconvective mixing efficiency - which is infinite in
the case of the Schwarzschild criterion for convection - determines
to a large extent whether an accreting core hydrogen burning star
rejuvenates or not (Braun & Langer 1995). If it fails, which is the
more likely for less efficient semiconvection and the more advanced
the star is in its evolution when it starts to accrete, it retains an
unusual structure, with a smaller helium core mass and a larger
hydrogen envelope mass compared to single stars. As such a structure
keeps the star relatively compact during all the advanced burning
stages - i.e., it avoids the red supergiant stage (Braun & Langer
1995) - it will not fill its Roche lobe after core hydrogen burning.
This is the situation in all our Case A systems which avoid premature
contact and have initial mass ratios of
![]() .
.
For models computed with the Schwarzschild criterion, the secondaries in Case A systems rejuvenate during or shortly after the rapid Case A mass transfer. This results in longer main sequence life times for the secondaries, and thus leads to less premature contact situations. I.e., the critical initial period for premature contact is shifted to smaller values. In this case, the secondaries all expand to red supergiants. Assuming the primary star is still present at that time, this is likely to initiate reverse Case B mass transfer. As the life time of a rejuvenating star is extended, the primaries have often finished their evolution by that time and the binary may even be disrupted (cf. Pols 1994). However, as the life time of a low mass helium star (i.e. the primary of such a system) can be comparable to the remaining hydrogen burning life time of the very massive secondary, reverse Case B mass transfer onto the low mass helium star may also occur. In this case, the helium star builds up a hydrogen envelope and swells to red giant dimensions. We designate the ensuing contact situation in Table 3 as reverse contact.
This scenario is illustrated by five of our Case A systems (Nos. 25,
48, 50, 59, and 72) which are computed using the Schwarzschild instead
of the Ledoux criterion (marked "c'' in Table 3). Nos. 25 and
59, initially having a 12![]() and a 16
and a 16![]() primary, a mass ratio
of 0.67 and 0.69, and a period of 2.5 d and 2.0 d, respectively, avoid
premature contact. However, they encounter reverse contact when the
primaries have burnt 91% and 80% of their helium in the core. Both
systems avoid contact altogether when they are computed with our
standard convection physics, and evolve a reverse supernova order.
I.e., an increase of the semiconvective mixing efficiency may reduce
the number of systems with premature contact but increase the number
with reverse contact. From system Nos. 25 we conclude that, were the
Schwarzschild criterion correct, the majority of Case A binaries with
12
primary, a mass ratio
of 0.67 and 0.69, and a period of 2.5 d and 2.0 d, respectively, avoid
premature contact. However, they encounter reverse contact when the
primaries have burnt 91% and 80% of their helium in the core. Both
systems avoid contact altogether when they are computed with our
standard convection physics, and evolve a reverse supernova order.
I.e., an increase of the semiconvective mixing efficiency may reduce
the number of systems with premature contact but increase the number
with reverse contact. From system Nos. 25 we conclude that, were the
Schwarzschild criterion correct, the majority of Case A binaries with
12 ![]() primaries would evolve into reverse contact.
Comparing our models Nos. 58 and 59, which have identical initial
conditions but vary in the treatment of convection, shows that also in
systems with 16
primaries would evolve into reverse contact.
Comparing our models Nos. 58 and 59, which have identical initial
conditions but vary in the treatment of convection, shows that also in
systems with 16 ![]() primaries the lower period limit for contact
free systems increases.
primaries the lower period limit for contact
free systems increases.
In the three other systems computed with the Schwarzschild criterion, systems Nos. 48, 50, and 72, the primaries explode as supernovae before the reverse mass transfer can occur. Two of these (Nos. 48 and 72), when computed with our standard convection physics, have a reverse supernova order (see systems Nos. 47 and 71 in Table 3), the other (No. 50) does not (cf. system No. 49 in Table 3).
Thus, the lower period limit for contact free evolution with the
Schwarzschild criterion is expected between the lower period limit and
the limit for reverse supernova order for Ledoux criterion and
![]() .
The one early case A system containing a
25
.
The one early case A system containing a
25 ![]() primary (No. 72) also shows no reverse mass transfer before
the supernova explosion of the primary, despite being a system with
reverse supernova order when computed with our standard convection
physics. We conclude that for large masses, the amount of contact free
case A systems does not change very much for different convection
physics. On the contrary, at 12
primary (No. 72) also shows no reverse mass transfer before
the supernova explosion of the primary, despite being a system with
reverse supernova order when computed with our standard convection
physics. We conclude that for large masses, the amount of contact free
case A systems does not change very much for different convection
physics. On the contrary, at 12 ![]() primary mass and below no
contact free case A system are expected at all if the Schwarzschild
criterion is used.
primary mass and below no
contact free case A system are expected at all if the Schwarzschild
criterion is used.
While the previous two subsections concerned contact formation due to large (delayed contact) or small (premature and reverse contact) initial periods, we investigate here contact formation due to large or small initial mass ratios.
Figure 8 shows the mass transfer rate as function of
the transferred amount of mass for three Case B systems with identical
initial primary mass (12![]() )
and period (6 d), but different
initial secondary masses. For smaller initial mass ratios
)
and period (6 d), but different
initial secondary masses. For smaller initial mass ratios
![]() ,
the mass transfer rates are
somewhat larger in the early part of the mass transfer, since the
orbit shrinks more rapidly for smaller
,
the mass transfer rates are
somewhat larger in the early part of the mass transfer, since the
orbit shrinks more rapidly for smaller ![]() .
For conservative
evolution (also ignoring stellar winds), the minimum separation
depends on initial separation
.
For conservative
evolution (also ignoring stellar winds), the minimum separation
depends on initial separation ![]() and mass ratio
and mass ratio ![]() as
as
![]() .
As, in a given system, period and orbital separation
scale as
.
As, in a given system, period and orbital separation
scale as
![]() ,
this means that in systems with the same
initial period, the primary star is, at the time when
,
this means that in systems with the same
initial period, the primary star is, at the time when
![]() ,
squeezed into a smaller volume for smaller
,
squeezed into a smaller volume for smaller ![]() .
This makes the
mass transfer rate during the first phase of Case B mass transfer
larger for smaller
.
This makes the
mass transfer rate during the first phase of Case B mass transfer
larger for smaller ![]() .
.
However, the maximum mass transfer rate, which is achieved after mass
ratio reversal (cf. Sect. 4.1), is very similar in all three systems,
even though the post-mass transfer periods (115 d, 87 d, and 72 d for
secondary initial masses of 11![]() ,
9
,
9![]() ,
and 8
,
and 8![]() ,
respectively) are not the same. Also the amount of mass which is
transferred is independent of the secondary mass - it consists of
the whole hydrogen-rich envelope of the primary.
,
respectively) are not the same. Also the amount of mass which is
transferred is independent of the secondary mass - it consists of
the whole hydrogen-rich envelope of the primary.
Whether or not contact is reached is here mostly determined by the
reaction of the secondary star to the accretion.
Figure 9 shows that the primary with the lowest
initial mass swells most during the mass transfer. The smallest
initial mass ratio for which contact is avoided corresponds roughly to
the condition that the mass accretion time scale of the secondary
![]() remains smaller than its thermal time scale
remains smaller than its thermal time scale
![]() .
We designate contact due to
this reason as q-contact.
.
We designate contact due to
this reason as q-contact.
As q-contact is established during the first phase of Case B mass transfer, it is quite distinct from delayed contact (Sect. 4.1). As q-contact evolves early during Case B mass transfer, it does not allow a major amount of mass to be accreted by the secondary. I.e., either the major part of the primary's hydrogen-rich envelope can be ejected from the system, or both stars merge. The situation that the secondary star can accrete significant amounts after a non-conservative early q-contact phase is unlikely since it would bring both stars even closer together.
In principle, there is also a maximum initial mass ratio for
contact-free evolution of Case B systems: for
![]() ,
both
stars age at the same rate and attempt to expand to red giants
simultaneously. However, since the limiting value is very close to
,
both
stars age at the same rate and attempt to expand to red giants
simultaneously. However, since the limiting value is very close to
![]() ,
we ignore this effect here as statistically
insignificant.
,
we ignore this effect here as statistically
insignificant.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{m12X9.mdot2.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg99.gif) |
Figure 8:
Mass transfer rates as function of the transfered amount of
mass for three Case B systems with 12 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{m12X9.mdot1.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg100.gif) |
Figure 9: Radii of the secondary stars as function of their mass for the same systems as shown in Fig. 8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{m12X4.mdot2.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg101.gif) |
Figure 10:
Mass transfer rate as a function of transfered amount of mass,
for five Case A systems with the same initial primary mass
(
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{m12X4.mdot1.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg102.gif) |
Figure 11: Radii of the secondary stars as function of their mass for the same systems shown in Fig. 10. The first maximum is achieved during rapid Case A mass transfer. The second maximum is achieved during slow Case A mass transfer due to the nuclear evolution of the secondary. The radius decrease after the second maximum is due to the Case AB mass transfer |
| Open with DEXTER | |
The maximum mass transfer rate in Case A systems is achieved during
the rapid mass transfer phase while the orbit is shrinking.
Figure 10 shows the mass transfer rates of five Case A
systems with identical initial conditions except for the initial
secondary mass and thus the initial mass ratio ![]() .
As shown
in Sect. 4.2.1, the smaller
.
As shown
in Sect. 4.2.1, the smaller ![]() the larger is the maximum mass
transfer rate since the primary is squeezed into a smaller volume.
Also, more mass is transfered during the rapid Case A mass transfer
for smaller
the larger is the maximum mass
transfer rate since the primary is squeezed into a smaller volume.
Also, more mass is transfered during the rapid Case A mass transfer
for smaller ![]() .
As for Case B, q-contact may occur for small
.
As for Case B, q-contact may occur for small
![]() due to higher maximum mass transfer rates and due to
larger thermal time scales of the secondary, the latter effect being
the more important one. In Fig. 11, all systems shown
avoid q-contact, but the relative radius increase during the rapid
Case A mass transfer is clearly larger for the systems with smaller
initial secondary masses.
due to higher maximum mass transfer rates and due to
larger thermal time scales of the secondary, the latter effect being
the more important one. In Fig. 11, all systems shown
avoid q-contact, but the relative radius increase during the rapid
Case A mass transfer is clearly larger for the systems with smaller
initial secondary masses.
The second expansion of the secondaries during the Case A mass transfer (Fig. 11) is due to their nuclear evolution during the slow mass transfer phase. It is ended by the onset of Case AB mass transfer. The secondary star in system No. 1 has already ended core hydrogen burning and expanded appreciably before the onset of Case AB mass transfer. The onset of Case AB mass transfer stops its expansion and prevents the system from evolving into premature contact. However, Figs. 10 and 11 demonstrate, that for too large mass ratios, massive Case A binaries evolve into premature contact as in the case of too small initial periods (cf. Sect. 4.1.2). I.e., while Case B systems evolve into contact only when their initial mass ratio is too large, Case A binaries can do so for too large or too small initial mass ratio.
Figure 10 shows also, that the total amount of mass
which is transfered during case A and AB is nearly independent of
![]() .
This can not be expected in general, as we shall see
below that the primary mass after Case A and AB mass transfer depends
on the core hydrogen abundance at the onset of mass transfer and on
the initial mass ratio (cf. Fig. 14 below). While
smaller initial mass ratios lead to smaller primary masses, the larger
Roche lobe due to the lower secondary mass (for the same period) leads
to mass transfer only later in the evolution of the primary and thus
to larger post-mass transfer primary masses. Both effects cancel each
other in the models shown in Fig. 10.
.
This can not be expected in general, as we shall see
below that the primary mass after Case A and AB mass transfer depends
on the core hydrogen abundance at the onset of mass transfer and on
the initial mass ratio (cf. Fig. 14 below). While
smaller initial mass ratios lead to smaller primary masses, the larger
Roche lobe due to the lower secondary mass (for the same period) leads
to mass transfer only later in the evolution of the primary and thus
to larger post-mass transfer primary masses. Both effects cancel each
other in the models shown in Fig. 10.
Figures 12 and 13 summarise the range of
contact-free evolution for systems with 12![]() and 16
and 16![]() primaries, respectively. For all mass transfer cases and primary
masses, there is a rather well defined critical initial mass ratio
primaries, respectively. For all mass transfer cases and primary
masses, there is a rather well defined critical initial mass ratio
![]() such that only systems with larger
such that only systems with larger ![]() avoid
contact. For
avoid
contact. For
![]() ,
they evolve into q-contact.
Likely, most of the systems undergoing q-contact merge, since
contact occurs early during the mass transfer, at a small orbital
separation. We find
,
they evolve into q-contact.
Likely, most of the systems undergoing q-contact merge, since
contact occurs early during the mass transfer, at a small orbital
separation. We find
![]() for all Case A systems
with primaries in the initial mass range 12...25
for all Case A systems
with primaries in the initial mass range 12...25![]() .
For Case B
systems,
.
For Case B
systems, ![]() decreases from
decreases from
![]() at 12
at 12![]() to
to
![]() at 16
at 16![]() and
and
![]() at
25
at
25![]() initial primary mass.
initial primary mass.
The range of contact-free Case A systems is further limited by the possibility of premature contact, which occurs for initial periods below a certain threshold, but also for initial mass ratios above a critical value, i.e. too close to one. We should note that for even smaller initial periods than investigated here, premature contact may occur already before the secondary has finished core hydrogen burning (cf. Pols 1994). In any case, the outcome of premature contact is most likely the merging of both stars. The possibility of reverse contact and of a reverse supernova order for the Case A systems, and their dependence on the semiconvective mixing time scale are discussed in the next section.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{per-q12.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg109.gif) |
Figure 12:
Distribution of all computed binaries with 12 |
| Open with DEXTER | |
As described in Sect. 4.1.2, the uncertain efficiency of semiconvective mixing introduces a considerable uncertainty to the evolution of Case A systems. Semiconvective mixing affects the rejuvenation process in an essential way, as it is this process which transports hydrogen into the convective core of the accretion stars. While for infinitely fast semiconvective mixing - which corresponds to the use of the Schwarzschild criterion for convection - all accretion stars rejuvenate (Hellings 1983), this is not the case for finite semiconvective mixing time scales (Braun & Langer 1995). Longer mixing time scales lead to shorter core hydrogen burning life times of the secondaries. Therefore, slow semiconvection - as assumed here - leads to earlier contact. Nevertheless, slow semiconvection leads perhaps not to a smaller total number of contact systems, since for those systems which avoid premature contact, the chance of reverse contact during core helium burning of the secondary is much smaller than in the case of fast semiconvective mixing (cf. Sect. 4.1.2).
We note that although semiconvection can be important for the upper
end of the mass spectrum of our study (cf. also Wellstein & Langer
1999), another effect dominates for the less massive Case A systems.
In our systems with an initial primary mass of 12![]() ,
the
luminosity ratio after the mass transfer is very large, of the order
of 100, while it is only of the order of 10 for our most massive
systems (see Table 3). The reason for the drop of the luminosity
ratio for higher primary masses is simply the flattening of the
stellar mass-luminosity relation for increasing mass. As the
luminosity ratio reflects the ratio of the evolutionary speeds of both
components, it is clear that with a post-mass transfer value of 100,
only very late Case A systems can avoid contact - independent of
whether the secondary rejuvenates or not. The large luminosity ratio
for lower primary initial masses is also the main reason why the
initial parameter space for contact-free evolution becomes smaller for
lower mass systems.
,
the
luminosity ratio after the mass transfer is very large, of the order
of 100, while it is only of the order of 10 for our most massive
systems (see Table 3). The reason for the drop of the luminosity
ratio for higher primary masses is simply the flattening of the
stellar mass-luminosity relation for increasing mass. As the
luminosity ratio reflects the ratio of the evolutionary speeds of both
components, it is clear that with a post-mass transfer value of 100,
only very late Case A systems can avoid contact - independent of
whether the secondary rejuvenates or not. The large luminosity ratio
for lower primary initial masses is also the main reason why the
initial parameter space for contact-free evolution becomes smaller for
lower mass systems.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{per-q16.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg110.gif) |
Figure 13:
The same as in Fig. 12 but for systems
with initial primary masses of
|
| Open with DEXTER | |
Finally, there is an upper period which limits the contact-free regime of the Case B systems. Our calculations have shown that systems close to this limit may experience delayed contact, with the consequence of considerable accretion on the secondary, and a high chance to avoid the merging of both stars. Initially even wider systems may correspond more to the standard common envelope scenario, again with the possibility to avoid a merger, but likely without significant accretion of the secondary.
By comparing Figs. 12 and 13, and including
our results for even more massive systems (see Table 3, and Wellstein
& Langer 1999), it becomes clear that the range of contact-free
Case A systems becomes smaller for smaller initial primary masses,
while that for contact-free Case B systems becomes smaller for larger
ones. E.g., there are no contact-free Case B systems for initial
primary masses of 25![]() .
We conclude that at lower masses,
conservative evolution is to be expected mainly from close Case B
systems, while at larger masses Case A systems dominate the
conservative evolution. Considering that massive binaries with
initial periods of up to some thousand days may interact, and adopting
an equal number of binaries per
.
We conclude that at lower masses,
conservative evolution is to be expected mainly from close Case B
systems, while at larger masses Case A systems dominate the
conservative evolution. Considering that massive binaries with
initial periods of up to some thousand days may interact, and adopting
an equal number of binaries per ![]() bin, up to one third of all
interacting systems in the considered mass range and with
bin, up to one third of all
interacting systems in the considered mass range and with
![]() may evolve conservatively.
may evolve conservatively.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{eala.ps}
\end{figure}](/articles/aa/full/2001/15/aah2433/Timg113.gif) |
Figure 14:
Masses after Case AB mass transfer for
primaries with an initial mass of
|
| Open with DEXTER | |
Those of our systems which avoid merging evolve into OB+He star systems. We discuss in the following the further evolution of the primaries, the secondaries, and of merger stars.
Table 3 shows that the helium star masses after the Case AB/B mass
transfer in our systems fall into the range 1...7![]() .
The helium
star masses in the Case B systems correspond simply to the helium core
mass of the primary at core hydrogen exhaustion, with a very small
scatter (
.
The helium
star masses in the Case B systems correspond simply to the helium core
mass of the primary at core hydrogen exhaustion, with a very small
scatter (
![]() ). Figure 14 shows that the situation
is more complex for the Case A systems. We find a strong dependence
of the helium star mass on the initial period, i.e. on the central
hydrogen abundance of the primary when the mass transfer begins. We
also find a weaker dependence on the initial mass ratio (cf., systems
Nos. 41, 55, 58). Figure 14 demonstrates that our 16
). Figure 14 shows that the situation
is more complex for the Case A systems. We find a strong dependence
of the helium star mass on the initial period, i.e. on the central
hydrogen abundance of the primary when the mass transfer begins. We
also find a weaker dependence on the initial mass ratio (cf., systems
Nos. 41, 55, 58). Figure 14 demonstrates that our 16![]() Case A primaries become 2...3
Case A primaries become 2...3![]() helium stars - compared to a
Case B post-mass transfer mass of
helium stars - compared to a
Case B post-mass transfer mass of ![]()
![]() ,
which is independent
of other parameters. We point out that these strongly reduced Case A
primary masses are often ignored in simplified binary studies which
rely on single star evolutionary models.
,
which is independent
of other parameters. We point out that these strongly reduced Case A
primary masses are often ignored in simplified binary studies which
rely on single star evolutionary models.
The further evolution of the helium stars depends strongly on their
mass, and partly on the evolution of their companion stars. The more
massive helium stars in our mass range correspond to Wolf-Rayet stars,
and will undergo wind mass loss before they explode as types Ib/Ic
supernova. Those helium stars with masses below ![]()
![]() expand to
giant dimensions after core helium exhaustion. Depending on whether
the companion star is still present at that time, this may lead to
Case ABB/BB mass transfer, and a further reduction of the mass of the
helium star by
expand to
giant dimensions after core helium exhaustion. Depending on whether
the companion star is still present at that time, this may lead to
Case ABB/BB mass transfer, and a further reduction of the mass of the
helium star by ![]()
![]() or so (cf. system No. 37 in Sect. 3.2).
Independent of this, the helium stars with final masses in the range
2...4
or so (cf. system No. 37 in Sect. 3.2).
Independent of this, the helium stars with final masses in the range
2...4![]() are likely to explode as helium giants. The
effect of the large radii of these stars on the supernova light curve
is still unexplored. Helium stars in the mass range 1.4...2
are likely to explode as helium giants. The
effect of the large radii of these stars on the supernova light curve
is still unexplored. Helium stars in the mass range 1.4...2![]() could, in principle, also make it to core collapse, but as their
post-core helium burning life time is rather large it may be more
likely that stellar winds will reduce their mass below the
Chandrasekhar mass and they end up as white dwarfs, like their
counterparts with masses between 1...1.4
could, in principle, also make it to core collapse, but as their
post-core helium burning life time is rather large it may be more
likely that stellar winds will reduce their mass below the
Chandrasekhar mass and they end up as white dwarfs, like their
counterparts with masses between 1...1.4![]() .
.
We point out that all 12![]() primaries in our contact-free Case A
systems end up as white dwarfs, and even some 16
primaries in our contact-free Case A
systems end up as white dwarfs, and even some 16![]() primaries may
do so (e.g., system No. 55). I.e., the limiting initial mass
separating white dwarf formation from core collapse is largely
increased in Case A binaries, compared to single stars. We note that
this effect exists also for Case B binaries, strongly so for primaries
which undergo a Case BB mass transfer, but at a moderate level even
otherwise. The same effect for the limiting initial mass between
neutron star and black hole formation has been discussed by Wellstein
& Langer (1999).
primaries may
do so (e.g., system No. 55). I.e., the limiting initial mass
separating white dwarf formation from core collapse is largely
increased in Case A binaries, compared to single stars. We note that
this effect exists also for Case B binaries, strongly so for primaries
which undergo a Case BB mass transfer, but at a moderate level even
otherwise. The same effect for the limiting initial mass between
neutron star and black hole formation has been discussed by Wellstein
& Langer (1999).
Finally, we can not exclude that some of the helium stars with masses
close to but above the Chandrasekhar mass develop a degenerate
C/O-core and ignite carbon explosively. In that case, they would
produce a type Ia supernova. However, in the 1.45![]() helium star of
system No. 31 (cf. Sect. 3.1), a luminosity of
helium star of
system No. 31 (cf. Sect. 3.1), a luminosity of ![]()
![]() during
shell helium burning implies a growth rate of the C/O-core mass of
during
shell helium burning implies a growth rate of the C/O-core mass of
![]()
![]() ,
which is fast enough to allow carbon to ignite
non-explosively.
,
which is fast enough to allow carbon to ignite
non-explosively.
All our secondary stars evolve to core collapse. In Case A systems,
about half of the secondaries does so before the primary has ended its
evolution (cf. Table 3). As most of our primaries did not rejuvenate,
they remain blue supergiants throughout their post-main sequence
evolution (cf. Figs. 1 and 3). When they explode as type II
supernova, they will thus resemble SN 1987A. We noted in Sect. 3.1
that the secondary of system No. 31 provides a viable progenitor model
for SN 1987A. In this case, there should be a ![]()
![]() helium
star left in the supernova remnant.
In similar systems, however, the supernova order
is not reversed and no such helium star would be expected (cf. Table 3).
helium
star left in the supernova remnant.
In similar systems, however, the supernova order
is not reversed and no such helium star would be expected (cf. Table 3).
Several of our systems evolve into contact and are likely to lead to a merger. While it is beyond our scope to predict the properties of the merged stars, we can distinguish two types of events. If the merging occurs during Case A mass transfer and before the secondary has terminated core hydrogen burning, the merged object will still be a core hydrogen burning star. Its surface may be enriched in hydrogen burning products, but otherwise it might resemble a normal main sequence star in many respects.
However, a merger during a Case B or reverse Case B mass transfer (cf. Sect. 4.1.1; note that the latter may even occur during a Case A mass transfer; cf. Fig. 7) has a different result. Since the original primary has already developed a compact hydrogen-free core, the merger star will have a hydrogen-free core with a mass close to that of the primary. It is uncertain how much of the hydrogen-rich material is lost during the merging process, and whether some hydrogen-rich matter can penetrate into the helium core. However, if the mass of the merger star exceeds the mass of the primary star, which appears likely, then the helium core mass of the merger star is much smaller than the helium core mass of a single star of comparable mass. I.e., its structure is similar to that of our non-rejuvenating accretion stars during core helium burning. As a consequence of their small helium core mass, these stars may avoid to evolve into red supergiants (Podsiadlowski et al. 1990, 1992).
In our Case A binaries, a reversal of the supernova order appears in
all systems containing a 12 ![]() primary (cf.
Fig. 12) and in some systems containing a 16
primary (cf.
Fig. 12) and in some systems containing a 16 ![]() primary (cf. Fig. 13). At 12
primary (cf. Fig. 13). At 12![]() ,
supernova order
reversal depends not so much on whether or not the secondary star
rejuvenates. Instead, the mass ratio after the rapid phase of the
Case A transfer, and thereby the luminosity ratio, is essential. Due
to the strong decrease of the primaries mass, it becomes a factor of
about 100 less luminous than the secondary. Therefore, independent of
how much fresh hydrogen is mixed into the secondaries core, it
finishes its evolution first as long as no reverse mass transfer
occurs.
,
supernova order
reversal depends not so much on whether or not the secondary star
rejuvenates. Instead, the mass ratio after the rapid phase of the
Case A transfer, and thereby the luminosity ratio, is essential. Due
to the strong decrease of the primaries mass, it becomes a factor of
about 100 less luminous than the secondary. Therefore, independent of
how much fresh hydrogen is mixed into the secondaries core, it
finishes its evolution first as long as no reverse mass transfer
occurs.
However, in case of rapid semiconvective mixing, the secondary may
rejuvenate, with the consequence of reverse mass transfer before
it can evolve into a supernova. Due to the extreme mass ratio, the
reverse mass transfer is expected to be non-conservative. Its outcome
is either a merger or a short period double helium star binary.
Assuming the latter, we can estimate whether or not the supernova
order would be reversed. In system No. 17 - computed with
![]() - the secondary is more evolved at time
of reverse mass transfer, i.e. both stars burn helium in their cores,
with central helium mass fractions of 0.5/0.3 for the
primary/secondary. Thus the supernova order is expected to be
reversed. For system No. 25 computed with Schwarzschild criterion, it
is less clear what happens. The primary has already spent about
6 106 yr at central helium burning and has reached a core helium
mass fraction of 0.09. The secondary has reached a core helium mass
fraction of 0.63 after only 3 105 years of central helium burning.
Because the primary's helium shell burning phase is expected to last
more than 1 106 years (cf. system No. 31 in Table 1)
it appears possible that also in this system the supernova order is
reversed, if the system does not merge.
- the secondary is more evolved at time
of reverse mass transfer, i.e. both stars burn helium in their cores,
with central helium mass fractions of 0.5/0.3 for the
primary/secondary. Thus the supernova order is expected to be
reversed. For system No. 25 computed with Schwarzschild criterion, it
is less clear what happens. The primary has already spent about
6 106 yr at central helium burning and has reached a core helium
mass fraction of 0.09. The secondary has reached a core helium mass
fraction of 0.63 after only 3 105 years of central helium burning.
Because the primary's helium shell burning phase is expected to last
more than 1 106 years (cf. system No. 31 in Table 1)
it appears possible that also in this system the supernova order is
reversed, if the system does not merge.
For systems with an initial primary mass of 25 ![]() the convection
physic dominates the question whether the supernova order is reversed.
This can be seen in systems Nos. 65, 66 and 67, where the value for the
efficiency parameter for semiconvective mixing
the convection
physic dominates the question whether the supernova order is reversed.
This can be seen in systems Nos. 65, 66 and 67, where the value for the
efficiency parameter for semiconvective mixing
![]() is
the only difference. Only in system No. 65 with
is
the only difference. Only in system No. 65 with
![]() the supernova oder is reversed. With
the supernova oder is reversed. With
![]() no reversal appears. Also the case B system 68 reverses its
supernova order with
no reversal appears. Also the case B system 68 reverses its
supernova order with
![]() .
This shows that the
mass of the primary after mass transfer in this systems is not very
important because the nuclear time scales of the stars in this mass
range vary less with mass than for lower mass stars. Also the early
case A binary No. 71 has a reverse supernova order in contrast to
system No. 72, which has the same parameters, but is calculated with
the Schwarzschild criterion. The systems with 16
.
This shows that the
mass of the primary after mass transfer in this systems is not very
important because the nuclear time scales of the stars in this mass
range vary less with mass than for lower mass stars. Also the early
case A binary No. 71 has a reverse supernova order in contrast to
system No. 72, which has the same parameters, but is calculated with
the Schwarzschild criterion. The systems with 16 ![]() primary are
an intermediate case, but seems to behave more like the systems
containing a 25
primary are
an intermediate case, but seems to behave more like the systems
containing a 25 ![]() primary (cf. systems Nos. 47 and 48).
primary (cf. systems Nos. 47 and 48).
Whether or not a reverse mass transfer occurs before the primary becomes a compact object depends strongly on the semiconvective mixing speed. For fast semiconvective mixing, the secondaries become red supergiants. Then, the crucial question is not if reverse mass transfer occurs but when it occurs. A shorter semiconvective mixing time scale has two effects. First, the maximum radius of the secondary after core hydrogen exhaustion increases (cf. Wellstein & Langer 1999). This makes it more likely for the secondary to fill its Roche lobe and transfer matter back to the primary. Second, the time the secondary spends on the main sequence increases, as more hydrogen is mixed into the convective core during central hydrogen burning. Thus it is less likely that the reverse mass transfer occurs before the primary has finished its evolution and has become a compact object.
Although in general, systems which have a normal supernova order would
be able to avoid reverse mass transfer and vice versa, some systems
which show a reverse supernova order for slow semiconvective mixing
(
![]() )
avoid reverse mass transfer during the
lifetime of the primary when the Schwarzschild criterion is used, as
shown by systems Nos. 48 and 72.
)
avoid reverse mass transfer during the
lifetime of the primary when the Schwarzschild criterion is used, as
shown by systems Nos. 48 and 72.
Pols (1994) presented 24 binary models for initial primary masses in
the range 8...16![]() ,
mostly for Case A systems. Since he used the
Schwarzschild criterion for convection, the secondary components
rejuvenated in all computed cases. As a consequence, contact phases
during slow case A mass transfer occurred for shorter periods than in
our models. Furthermore, due to the rejuvenation, a supernova
explosion of the secondary as the first star could only appear after a
reverse mass transfer phase. This mass transfer appears at very large
mass ratios and must therefore be non-conservative. As discussed by
Pols, it is an open question whether or not such a binary merges or is
able to expel the secondary's hydrogen-rich envelope to form a close
binary consisting of two helium stars. As the helium star resulting
from the secondary is then the more massive component, a supernova
order reversal is possible if the merging of both stars can be
avoided.
,
mostly for Case A systems. Since he used the
Schwarzschild criterion for convection, the secondary components
rejuvenated in all computed cases. As a consequence, contact phases
during slow case A mass transfer occurred for shorter periods than in
our models. Furthermore, due to the rejuvenation, a supernova
explosion of the secondary as the first star could only appear after a
reverse mass transfer phase. This mass transfer appears at very large
mass ratios and must therefore be non-conservative. As discussed by
Pols, it is an open question whether or not such a binary merges or is
able to expel the secondary's hydrogen-rich envelope to form a close
binary consisting of two helium stars. As the helium star resulting
from the secondary is then the more massive component, a supernova
order reversal is possible if the merging of both stars can be
avoided.
Sybesma (1985) computed 5 binary sequences starting with a primary
mass of 20 ![]() ,
a secondary mass of 10
,
a secondary mass of 10 ![]() ,
and periods
ranging from 1.5 up to 10 days. His results differ from ours mainly
due his assumption of huge convective core overshooting. This leads
to much more massive helium-rich cores in the main sequence models.
Consequently, he obtains Case A mass transfer for initial periods
which fall in our Case B regime. As Case A mass transfer is more
likely conservative in this mass range, Sybesma obtains conservative
evolution for larger periods than we (e.g. 10 days), and for smaller
initial mass ratio (q=0.5).
,
and periods
ranging from 1.5 up to 10 days. His results differ from ours mainly
due his assumption of huge convective core overshooting. This leads
to much more massive helium-rich cores in the main sequence models.
Consequently, he obtains Case A mass transfer for initial periods
which fall in our Case B regime. As Case A mass transfer is more
likely conservative in this mass range, Sybesma obtains conservative
evolution for larger periods than we (e.g. 10 days), and for smaller
initial mass ratio (q=0.5).
Several authors specify the fraction ![]() of the primary's envelope
which is accreted by the secondary in advance. E.g., based on
observations, De Greve & de Loore (1992) and de Loore & De Greve
(1992) use
of the primary's envelope
which is accreted by the secondary in advance. E.g., based on
observations, De Greve & de Loore (1992) and de Loore & De Greve
(1992) use
![]() ,
which means half of the primary's envelope
mass leaves the system, together with an amount of angular momentum
which needs to be specified additionally. While an average value of
,
which means half of the primary's envelope
mass leaves the system, together with an amount of angular momentum
which needs to be specified additionally. While an average value of
![]() appears in fact possible, our models favour the idea that
appears in fact possible, our models favour the idea that
![]() decreases continuously for larger initial periods, with
decreases continuously for larger initial periods, with ![]() for systems which avoid contact and
for systems which avoid contact and ![]() for large initial
periods. E.g., we obtained
for large initial
periods. E.g., we obtained
![]() and
and
![]() for our
systems Nos. 7 and 8 (cf. Table 3). By comparison with De Greve &
de Loore (1992) and de Loore & De Greve (1992), we note that the
contact-free regime is expanded somewhat if
for our
systems Nos. 7 and 8 (cf. Table 3). By comparison with De Greve &
de Loore (1992) and de Loore & De Greve (1992), we note that the
contact-free regime is expanded somewhat if
![]() is used ab
initio.
is used ab
initio.
| No. | M1 | M2 | Pi |
|
|
|
|
|
|
|
|
|
|
|
|||
| d | log( |
103 K |
|
d | kms-1 | ||||||||||||
| 1 | 12 | 11.5 | 2.5 | 1.42 | 21.5 | 15.1 | 2.98 | 4.99 | 56 | 25 | 0.3 | 16.5 | 0.06 | 433 | 218 | 94 | 6.2 |
| 2 | 12 | 11 | 3 | 2.44 | 20.4 | 8.4 | 3.93 | 4.74 | 63 | 33 | 0.8 | 7.2 | 0.07 | 170 | 54 | 143 | 17.1 |
| 3 | 12 | 11 | 6 | 2.38 | 20.4 | 8.6 | 3.82 | 4.79 | 65 | 35 | 0.6 | 6.8 | 0.04 | 282 | 115 | 111 | 13.0 |
| 10 | 12 | 10.5 | 2.5 | 1.42 | 20.7 | 14.6 | 2.97 | 4.87 | 56 | 34 | 0.3 | 7.9 | 0.03 | 390 | 190 | 97 | 6.7 |
| 12 | 12 | 10 | 16 | 2.43 | 19.4 | 8.0 | 3.81 | 4.71 | 64 | 34 | 0.6 | 6.6 | 0.02 | 472 | 255 | 83 | 10.4 |
| 15 | 12 | 9.5 | 2.5 | 1.41 | 19.7 | 14.0 | 2.96 | 4.79 | 56 | 33 | 0.3 | 7.5 | 0.03 | 351 | 166 | 100 | 7.1 |
| 16 | 12 | 9.5 | 3.5 | 2.45 | 18.9 | 7.7 | 3.94 | 4.63 | 62 | 33 | 0.8 | 6.3 | 0.07 | 158 | 50 | 142 | 18.4 |
| 18 | 12 | 9 | 3.5 | 2.32 | 18.5 | 8.0 | 3.74 | 4.63 | 66 | 33 | 0.6 | 6.5 | 0.07 | 163 | 53 | 138 | 17.4 |
| 19 | 12 | 9 | 6 | 2.36 | 18.5 | 7.8 | 3.81 | 4.63 | 65 | 33 | 0.6 | 6.2 | 0.04 | 227 | 87 | 117 | 15.0 |
| 23 | 12 | 8.5 | 2.5 | 1.43 | 18.8 | 13.1 | 2.97 | 4.72 | 57 | 33 | 0.3 | 6.8 | 0.04 | 301 | 135 | 105 | 8.0 |
| 24 | 12 | 8 | 2 | 1.12 | 18.5 | 16.5 | 2.64 | 4.84 | 48 | 32 | 0.3 | 8.5 | 0.04 | 373 | 189 | 94 | 5.7 |
| 27 | 12 | 8 | 6 | 2.37 | 17.5 | 7.4 | 3.79 | 4.55 | 65 | 33 | 0.6 | 5.8 | 0.05 | 197 | 72 | 122 | 16.5 |
| 31 | 12 | 7.5 | 2.5 | 1.45 | 17.8 | 12.3 | 2.99 | 4.64 | 57 | 33 | 0.3 | 6.3 | 0.04 | 249 | 104 | 112 | 9.1 |
| 34 | 16 | 15.7 | 3.2 | 2.79 | 27.8 | 10.0 | 3.88 | 5.14 | 76 | 37 | 0.5 | 9.3 | 0.07 | 234 | 75 | 143 | 14.4 |
| 35 | 16 | 15.7 | 6 | 3.49 | 27.5 | 7.9 | 4.17 | 5.14 | 80 | 39 | 0.6 | 8.3 | 0.06 | 257 | 86 | 134 | 17.0 |
| 37 | 16 | 15 | 8 | 3.63 | 26.7 | 7.4 | 4.20 | 5.10 | 80 | 36 | 0.7 | 8.9 | 0.06 | 275 | 96 | 128 | 17.3 |
| 38 | 16 | 15 | 9 | 3.64 | 26.7 | 7.3 | 4.22 | 5.10 | 80 | 38 | 0.7 | 8.1 | 0.05 | 295 | 107 | 123 | 16.8 |
| 42 | 16 | 14 | 2.5 | 2.39 | 26.5 | 11.1 | 3.78 | 5.17 | 68 | 34 | 0.6 | 11.0 | 0.07 | 274 | 98 | 130 | 11.7 |
| 43 | 16 | 14 | 3 | 2.52 | 26.6 | 10.6 | 3.75 | 5.10 | 72 | 36 | 0.5 | 9.0 | 0.06 | 280 | 101 | 128 | 12.2 |
| 44 | 16 | 14 | 6 | 3.60 | 25.8 | 7.2 | 4.19 | 5.04 | 80 | 38 | 0.6 | 7.8 | 0.07 | 214 | 67 | 142 | 19.8 |
| 47 | 16 | 13 | 2.5 | 2.28 | 26.1 | 11.4 | 3.65 | 5.11 | 66 | 36 | 0.5 | 9.1 | 0.06 | 274 | 99 | 129 | 11.3 |
| 49 | 16 | 13 | 3 | 2.64 | 25.3 | 9.6 | 3.84 | 5.07 | 74 | 35 | 0.5 | 9.1 | 0.08 | 204 | 64 | 146 | 15.2 |
| 51 | 16 | 13 | 4 | 3.55 | 24.8 | 7.0 | 4.19 | 4.99 | 80 | 36 | 0.7 | 8.2 | 0.10 | 152 | 41 | 164 | 23.6 |
| 55 | 16 | 12 | 2 | 2.07 | 24.8 | 12.0 | 3.57 | 5.17 | 62 | 33 | 0.5 | 11.8 | 0.08 | 258 | 93 | 130 | 10.8 |
| 56 | 16 | 12 | 4 | 3.55 | 23.9 | 6.7 | 4.17 | 4.93 | 80 | 37 | 0.6 | 7.0 | 0.09 | 141 | 37 | 168 | 24.9 |
| 58 | 16 | 11 | 2 | 2.00 | 24.1 | 12.1 | 3.56 | 5.10 | 62 | 33 | 0.5 | 10.8 | 0.07 | 249 | 89 | 131 | 10.8 |
| 60 | 16 | 11 | 3 | 2.52 | 23.8 | 9.4 | 3.74 | 4.95 | 73 | 37 | 0.5 | 7.3 | 0.07 | 194 | 61 | 145 | 15.4 |
| 61 | 16 | 11 | 3.2 | 2.81 | 23.3 | 8.3 | 3.87 | 4.93 | 77 | 36 | 0.5 | 7.4 | 0.09 | 151 | 42 | 162 | 19.5 |
| 62 | 16 | 10 | 2.5 | 2.28 | 23.1 | 10.1 | 3.77 | 4.97 | 67 | 36 | 0.6 | 7.8 | 0.06 | 200 | 65 | 142 | 14.0 |
| 65 | 25 | 24 | 3.5 | 5.15 | 40.6 | 7.9 | 4.53 | 5.54 | 98 | 38 | 0.6 | 13.7 | 0.14 | 179 | 41 | 196 | 24.8 |
| 68 | 25 | 24 | 5 | 7.28 | 39.2 | 5.4 | 4.85 | 5.45 | 106 | 39 | 0.8 | 11.9 | 0.15 | 149 | 31 | 205 | 38.1 |
| 70 | 25 | 23 | 4 | 5.31 | 39.4 | 7.4 | 4.56 | 5.49 | 99 | 39 | 0.6 | 12.4 | 0.13 | 172 | 39 | 196 | 26.4 |
| 71 | 25 | 22 | 2.5 | 4.80 | 39.6 | 8.3 | 4.45 | 5.55 | 91 | 37 | 0.7 | 14.2 | 0.15 | 171 | 39 | 198 | 24.0 |
| 73 | 25 | 19 | 4 | 5.26 | 35.9 | 6.8 | 4.55 | 5.38 | 99 | 43 | 0.7 | 8.7 | 0.11 | 140 | 30 | 206 | 30.2 |
| 74 | 25 | 16 | 4 | 5.22 | 33.3 | 6.4 | 4.54 | 5.29 | 99 | 41 | 0.6 | 8.8 | 0.14 | 118 | 24 | 215 | 33.8 |
While it is unlikely that any of the binary systems considered here
has an observable counterpart during the mass transfer - with the
exception of the slow phase of the Case A mass transfer - they have
a relatively long-lived post-mass transfer stage. We emphasise that
this is true for those binary which survive the mass transfer, but
also for those which lead to mergers. Therefore, we characterise the
typical properties of systems after the first mass transfer phase in
Table 4. At this stage, the systems consist of a main sequence or
supergiant O or early B star of 18...40![]() ,
and a helium star in
the mass range 1...7
,
and a helium star in
the mass range 1...7![]() .
The orbital periods range from 24 d to
255 d.
.
The orbital periods range from 24 d to
255 d.
An inspection of Table 4 indicates that it may be a challenging task to try to detect systems like these observationally. A photometric investigation will have limited success due to three factors. First, the luminosity ratio of both stars is large, mostly of the order of 10, with the worst case of 160 (system No. 24) and the best of 4 (system No. 68). Second, the less luminous star has a much smaller radius than the brighter star, which minimises the brightness amplitude in case of an eclipse. Third, both stars underfill their Roche volumes by a large factor, which means that they are likely to radiate isotropically, and that eclipses are not likely.
We note that after core helium burning, all the helium stars below
![]()
![]() expand to giant dimensions and - if the OB star has not
yet turned into a supernova - may even fill their Roche volumes (cf.
Sect. 3.2). As also their luminosities increase by up to a factor 10,
a photometric detection may indeed be more likely in this stage.
However, for the more massive helium stars (
expand to giant dimensions and - if the OB star has not
yet turned into a supernova - may even fill their Roche volumes (cf.
Sect. 3.2). As also their luminosities increase by up to a factor 10,
a photometric detection may indeed be more likely in this stage.
However, for the more massive helium stars (
![]() ), this stage is very short lived (
), this stage is very short lived (
![]()
![]() Myr) compared
to their core helium burning life times (
Myr) compared
to their core helium burning life times (![]()
![]() Myr; cf. Table 2).
In systems with lower mass helium stars, the time scales are more
favourable: the 1.45
Myr; cf. Table 2).
In systems with lower mass helium stars, the time scales are more
favourable: the 1.45![]() helium star of system No. 31 burns helium
in its core for about 5 Myr, and its ensuing shell burning stage lasts
at least 1 Myr, possibly more depending on the mass loss rate during
this stage (cf. Sect. 3.1 and Table 1).
helium star of system No. 31 burns helium
in its core for about 5 Myr, and its ensuing shell burning stage lasts
at least 1 Myr, possibly more depending on the mass loss rate during
this stage (cf. Sect. 3.1 and Table 1).
Table 4 also shows the orbital velocities of both components after the mass transfer. While the helium stars have favourably large velocities of the order of 100...200 kms-1, they might be unobservable against the glare of their OB companion. The latter moves with only 5...35 kms-1. While these velocities are small, it may not be hopeless to try to detect these motions in OB stars.
It is interesting to note that the assumption of conservative
evolution leads, in all respects, to system properties which are less
favourable for an observational detection of such systems, compared to
the assumption of mass- and angular momentum loss from the system.
This is demonstrated by the estimated outcome of our delayed contact
system No. 7 in Sect. 4.1.1, which results in a shorter orbital period
(7 d), correspondingly larger orbital velocities, and a mass- and
luminosity ratio closer to 1, compared to similar conservative
systems. This tendency can also be verified in the results obtained by
de Loore & De Greve (1992) obtained with
![]() ,
i.e. assuming
that half of the transferred mass leaves the system.
,
i.e. assuming
that half of the transferred mass leaves the system.
The best chances to find post-mass transfer systems like those of
Table 4 seems to be at the upper end of the considered mass range. Our
systems with initial primary masses of 25![]() obtain the smallest
luminosity ratio
obtain the smallest
luminosity ratio
![]() /
/
![]() ,
the shortest
periods, and the largest orbital velocities. The helium star masses in
these systems are in the range 5...7
,
the shortest
periods, and the largest orbital velocities. The helium star masses in
these systems are in the range 5...7![]() ,
which makes the stars
comparable to Wolf-Rayet stars, or, more specifically, WN stars.
However, although we know 12 OB+WN systems with established mass
ratios and orbital periods (van der Hucht 2000), none of them fits to
our models. While 8 out of these 12 binaries have clearly much higher
initial system masses than those systems considered here, the
remaining four (WR3, WR31, WR97, and WR139; cf. van der Hucht 2000)
all have mass ratios of
,
which makes the stars
comparable to Wolf-Rayet stars, or, more specifically, WN stars.
However, although we know 12 OB+WN systems with established mass
ratios and orbital periods (van der Hucht 2000), none of them fits to
our models. While 8 out of these 12 binaries have clearly much higher
initial system masses than those systems considered here, the
remaining four (WR3, WR31, WR97, and WR139; cf. van der Hucht 2000)
all have mass ratios of
![]() /
/
![]() ,
and mostly
much shorter periods than our models.
,
and mostly
much shorter periods than our models.
There are two possible ways to interpret the disagreement between our
models and the observed OB+WN binaries. One possibility is that our
assumption of conservative evolution does not hold for systems with
primaries of initially ![]()
![]() .
This can be motivated by the
increasing role of radiation pressure in higher mass systems (cf.,
Schuerman 1972; Vanbeveren 1978). On the other hand, strong
non-conservative effects in massive systems may result in an
uncomfortably large upper critical ZAMS mass for neutron star
formation of
.
This can be motivated by the
increasing role of radiation pressure in higher mass systems (cf.,
Schuerman 1972; Vanbeveren 1978). On the other hand, strong
non-conservative effects in massive systems may result in an
uncomfortably large upper critical ZAMS mass for neutron star
formation of ![]()
![]() ,
as imposed by the massive X-ray binary
Wray 977 (Kaper et al. 1995; Ergma & van den Heuvel 1998; Vanbeveren
1998b).
,
as imposed by the massive X-ray binary
Wray 977 (Kaper et al. 1995; Ergma & van den Heuvel 1998; Vanbeveren
1998b).
The other possibility involves to estimate the probability of finding
one system of the kind computed here among four OB+WR binaries. As
outlined in Sect. 5.1, the parameter range for conservative evolution
becomes narrower for higher masses. For our systems with 25![]() primaries, contact is avoided for an initial period of 4 d, while 5 d
resulted already in contact (cf. systems Nos. 65...74 in
Table 3). Assuming initially an equal number of binaries per
log P-interval, and an upper period limit for interaction of 2000 d,
results in a ratio of contact-free versus contact surviving binary
systems of 1/3.7 if all Systems with initial mass ratios
primaries, contact is avoided for an initial period of 4 d, while 5 d
resulted already in contact (cf. systems Nos. 65...74 in
Table 3). Assuming initially an equal number of binaries per
log P-interval, and an upper period limit for interaction of 2000 d,
results in a ratio of contact-free versus contact surviving binary
systems of 1/3.7 if all Systems with initial mass ratios
![]() merge. If only the systems with initial mass ratios
merge. If only the systems with initial mass ratios
![]() and initial periods
and initial periods
![]() d merge this ratio becomes
1:6.6. Because it is not well known how much systems really merge -
also an unknown fraction of the large period contact systems might
actually lead to a merger rather than to a OB+WR binary - we assume
that the ratio is between 1:4 and 1:7. Thus the probability of finding
one suitable binary among four may be of the order of 1/2 or lower.
However, the survivors of the non-conservative contact evolution end
up as shorter period systems with a mass and luminosity ratio closer
to one
d merge this ratio becomes
1:6.6. Because it is not well known how much systems really merge -
also an unknown fraction of the large period contact systems might
actually lead to a merger rather than to a OB+WR binary - we assume
that the ratio is between 1:4 and 1:7. Thus the probability of finding
one suitable binary among four may be of the order of 1/2 or lower.
However, the survivors of the non-conservative contact evolution end
up as shorter period systems with a mass and luminosity ratio closer
to one![]() than the contact-free systems, and are thus detected
much easier.
than the contact-free systems, and are thus detected
much easier.
In summary, the failure to detect counterparts of our more massive
post-mass transfer systems is inconclusive. For our lower mass
systems, i.e. such with initial primary masses of 12![]() and
16
and
16![]() ,
the chance to detect counterparts may even be lower than for
our higher mass systems (cf. Table 4). In fact, we do not know of any suitable OB star with a 1...3.6
,
the chance to detect counterparts may even be lower than for
our higher mass systems (cf. Table 4). In fact, we do not know of any suitable OB star with a 1...3.6![]() helium star companion.
The object which comes closest to our models may be
helium star companion.
The object which comes closest to our models may be ![]() Persei, a
Persei, a
![]()
![]() B star with a 53
B star with a 53![]() 000
000![]() K hot 1.1
K hot 1.1![]() companion in a
127 d orbit (Gies et al. 1998). Its properties, and the fact that the
B star is spinning rapidly, support actually the possibility of a
close-to-conservative evolution at least in this system. A more
puzzling system which may be relevant in the context is
companion in a
127 d orbit (Gies et al. 1998). Its properties, and the fact that the
B star is spinning rapidly, support actually the possibility of a
close-to-conservative evolution at least in this system. A more
puzzling system which may be relevant in the context is
![]() Sco, a
Sco, a ![]()
![]() B dwarf with a massive white dwarf
companion in a
B dwarf with a massive white dwarf
companion in a ![]()
![]() d orbit (Berghöfer et al. 2000). Waters
et al. (1989) speculate that unseen companions in a number of Be stars
may actually be helium stars, in accordance with Pols et al. (1991)
and Portegies Zwart (1995).
d orbit (Berghöfer et al. 2000). Waters
et al. (1989) speculate that unseen companions in a number of Be stars
may actually be helium stars, in accordance with Pols et al. (1991)
and Portegies Zwart (1995).
The lack of OB+He star systems which are more massive than ![]() Per
but less massive than OB+WR systems is, anyhow, very remarkable. I.e.,
if the evolution of binaries with 12...16
Per
but less massive than OB+WR systems is, anyhow, very remarkable. I.e.,
if the evolution of binaries with 12...16![]() primaries would, for a
big fraction of the possible period range, proceed non-conservatively
and without leading to mergers, we would expect short period OB+He
star systems which are easier detectable, with a smaller mass- and
luminosity ratio compared to our models. Therefore, a non-detection of
such systems may be easiest understood if the conservative evolution
makes up for a large fraction of the non-merging interacting binaries
in the considered mass range.
primaries would, for a
big fraction of the possible period range, proceed non-conservatively
and without leading to mergers, we would expect short period OB+He
star systems which are easier detectable, with a smaller mass- and
luminosity ratio compared to our models. Therefore, a non-detection of
such systems may be easiest understood if the conservative evolution
makes up for a large fraction of the non-merging interacting binaries
in the considered mass range.
Whichever way it is, there are two kinds of observations hinting for a
large number of OB+He star binaries waiting to be discovered. One is
the existence of massive X-ray binaries, which are likely evolving
from an OB+He star stage (e.g., Moers & van den Heuvel 1989). The
second is the relatively large number of types Ib/Ic supernovae, which
are mostly attributed to exploding helium stars with masses above
2![]() (Podsiadlowski et al. 1992). I.e., it might be a rewarding
project to attempt an observational search for helium star components
to OB stars. In that respect, Table 4 can give indications of the
expected parameters, with the remark that if mass transfer is partly
non-conservative, then mass ratio, luminosity ratio, period and
orbital velocities become more favourable for a detection.
(Podsiadlowski et al. 1992). I.e., it might be a rewarding
project to attempt an observational search for helium star components
to OB stars. In that respect, Table 4 can give indications of the
expected parameters, with the remark that if mass transfer is partly
non-conservative, then mass ratio, luminosity ratio, period and
orbital velocities become more favourable for a detection.
Assuming a ratio of interacting binaries to single stars of 0.3, and ignoring the unknown fraction of mergers among the binaries, implies that 1 out of 3 OB stars in the considered mass range would, during its life time, obtain a He star companion. Depending of the rejuvenation of the secondary, this phase may last a considerable fraction, say one third, of the secondary's life time. This optimistic estimate indicates that only one out of ten OB stars in the considered mass range may have a helium star companion. However, these OB stars have a surface composition which is typically enriched in helium by 10...20%, and which has a N/C-ratio of about one order of magnitude above solar (cf. Sect. 3, and Wellstein & Langer 2001). I.e., even though also single stars may become helium- and nitrogen-rich during their main sequence evolution due to rotational mixing (Heger & Langer 2000), a pre-selection of chemically enriched OB stars may lead to a large detection probability of helium star companions.
Another way to pre-select OB stars with potential helium star
companions is to identify OB type blue stragglers in young clusters or
associations. The accretion of substantial amounts of matter by the
primary may lead it to achieve a mass which is already above the
turn-off mass of the cluster or associations. E.g., the 7.5![]() Case A secondary shown in Fig. 1 grows to about 18
Case A secondary shown in Fig. 1 grows to about 18![]() at an age of
13 Myr, which is the turn-off age for 13...14
at an age of
13 Myr, which is the turn-off age for 13...14![]() .
The 15
.
The 15![]() Case B primary, upon turn-off of its 16
Case B primary, upon turn-off of its 16![]() companion, even grows to
27
companion, even grows to
27![]() .
The remaining main sequence life time of the secondaries
after accretion is of the order of 1 Myr, which may be long enough to
catch them during this stage. Furthermore, the accretion of angular
momentum may spin up the star, and lead to internal mixing processes
and thereby to an overluminosity of the star with respect to its mass.
.
The remaining main sequence life time of the secondaries
after accretion is of the order of 1 Myr, which may be long enough to
catch them during this stage. Furthermore, the accretion of angular
momentum may spin up the star, and lead to internal mixing processes
and thereby to an overluminosity of the star with respect to its mass.
In summary, enriched surface abundances, blue straggler nature, overluminosity for the actual mass, and rapid rotation in an O or early B star may be hints to a helium star companion.
In this paper, we have, on the basis of evolutionary models with
up-to-date input physics, investigated the regime of contact-free
evolution in close binaries with initial primary masses in the range
12...25![]() ,
under the assumption that contact-free systems evolve
conservatively, i.e., that no matter except stellar winds leaves these
systems. Our results confirm earlier obtained ones qualitatively
(e.g., Pols 1994), but differ quantitatively and extend over a wider
parameter range.
,
under the assumption that contact-free systems evolve
conservatively, i.e., that no matter except stellar winds leaves these
systems. Our results confirm earlier obtained ones qualitatively
(e.g., Pols 1994), but differ quantitatively and extend over a wider
parameter range.
We demonstrate that the number ratio of contact free Case A-to-Case B
systems is a strong function of the system mass. At the high mass end
(25![]() initial primary mass), the contact-free Case B channel is
closed completely, while contact-free Case A systems exist for a wide
parameter range (cf. Table 3), although we find this range to depend
strongly on the semiconvective mixing efficiency (cf. Sect. 5, and
Wellstein & Langer 1999). In contrast, the contact-free Case A
channel becomes narrow at 12
initial primary mass), the contact-free Case B channel is
closed completely, while contact-free Case A systems exist for a wide
parameter range (cf. Table 3), although we find this range to depend
strongly on the semiconvective mixing efficiency (cf. Sect. 5, and
Wellstein & Langer 1999). In contrast, the contact-free Case A
channel becomes narrow at 12![]() initial primary mass, whatever the
assumptions on semiconvective mixing are, while the contact-free
Case B range becomes large (Fig. 12). At an initial primary mass of
16
initial primary mass, whatever the
assumptions on semiconvective mixing are, while the contact-free
Case B range becomes large (Fig. 12). At an initial primary mass of
16![]() ,
the situation is intermediate (Fig. 13).
,
the situation is intermediate (Fig. 13).
We investigate the vastly different types of contact situations of
systems in the considered mass range, and determine the critical
periods and mass ratios to avoid contact (Sect. 5.1). We also estimate
the consequences of the various kinds of contact. As a new phenomenon,
we find that in what we call delayed contact, Case B systems can
transfer the majority of the primary's envelope conservatively before
- towards the end of the Case B mass transfer - contact and
possibly a common envelope evolution occur. We find the delayed
contact regime may lead, with increasing initial period, to a smooth
transition from conservative contact-free evolution to the classical
common envelope evolution, with the parameter ![]() ,
which describes
which fraction of the primary's envelope is accreted by the secondary,
varying smoothly from
,
which describes
which fraction of the primary's envelope is accreted by the secondary,
varying smoothly from ![]() to
to ![]() .
We are able to compute
values of
.
We are able to compute
values of ![]() for our delayed contact systems, which we find in
the range
for our delayed contact systems, which we find in
the range ![]() = 0.4...0.7.
= 0.4...0.7.
How far or close our model sequences actually are to the evolution of
binary systems in nature depends to a large extent on the question
whether contact-free systems do indeed evolve conservatively. I.e.,
the accreting star is likely to be rapidly spun-up to close to
critical rotation (e.g., Packet 1981), and it depends on unknown
viscous time scales whether or not it will be able to continue to grow
in mass (Paczynski 1991). This question can in principle be answered
by comparing our post-mass transfer models with corresponding observed
binaries. However, as outlined in Sect. 6, even though virtually no
observed counterparts to our post-mass transfer models - i.e., no
OB+He star systems with large mass ratios and orbital periods - are
known, we could not conclude that conservative evolution in massive
binaries is not realised in nature, for two reasons. First,
identifying rather far and faint helium star companions to bright OB
stars may be too difficult. Second, non-conservative evolution
predicts even easier detectable OB+He star systems but, again, no such
systems are known, at least not corresponding to primary masses
between 12 and 20![]() - while three known OB+WN binaries might
indeed be the result of non-conservative binary evolution with
primaries above 20
- while three known OB+WN binaries might
indeed be the result of non-conservative binary evolution with
primaries above 20![]() .
.
We want to emphasise that an answer to the question whether massive
binaries can evolve conservatively is important to understand the late
evolutionary stages: e.g., types Ib/Ic supernovae, massive X-ray and
black hole binaries, and ![]() -ray bursts due to massive binaries.
In principle one may constrain the conservativity of massive binaries
by observations of the advanced stages. However, assumptions on even
more uncertain processes have to be made in such attempts - e.g., on
common envelope evolution, neutron star birth kicks, etc. - which
strongly limits the success of such approaches. Furthermore, often,
e.g. in population synthesis studies, only statistical information is
obtained. For example, Dalton & Sarazin (1995) find the period
distribution of massive X-ray binaries consistent with an average loss
of
-ray bursts due to massive binaries.
In principle one may constrain the conservativity of massive binaries
by observations of the advanced stages. However, assumptions on even
more uncertain processes have to be made in such attempts - e.g., on
common envelope evolution, neutron star birth kicks, etc. - which
strongly limits the success of such approaches. Furthermore, often,
e.g. in population synthesis studies, only statistical information is
obtained. For example, Dalton & Sarazin (1995) find the period
distribution of massive X-ray binaries consistent with an average loss
of ![]() 70% of the transferred envelope mass. However, this can
neither support nor defeat the existence of conservative evolution for
contact-free massive binaries.
70% of the transferred envelope mass. However, this can
neither support nor defeat the existence of conservative evolution for
contact-free massive binaries.
The very best way to constrain the first major mass transfer phase in massive close binaries would indeed be to identify a sample of helium star companions to OB stars. We repeat that those are predicted by conservative and by non-conservative binary evolution models, but with different periods and mass ratios. They are also indirectly proven to exist abundantly by the relatively large number of types Ib/Ic supernovae and massive X-ray binaries. In Sect. 6, we identify several ways to pre-select OB star candidates with an improved probability for a helium star companion.
Acknowledgements
We are grateful to Doug Gies, Lex Kaper, Jerry Orosz, and Philipp Podsiadlowski for many helpful discussions and suggestions and to Karel van der Hucht for providing us with results prior to publication. This work has been supported by the Deutsche Forschungsgemeinschaft through grants La 587/15 and La 587/16.