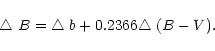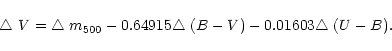A&A 369, 1140-1142 (2001)
DOI: 10.1051/0004-6361:20010205
Useful transformations between photometric systems
P. Harmanec1,2 - H. Bozic2,3
1 -
Astronomical Institute of the Charles University,
V Holesovickách 2, 180 00 Praha 8, Czech Republic
2 -
Astronomical Institute, Academy of Sciences,
251 65 Ondrejov, Czech Republic
3 -
Hvar Observatory, Faculty of Geodesy, Zagreb University,
Kaciceva 26, 10000 Zagreb, Croatia
Received 15 August 2000 / Accepted 31 January 2001
Abstract
In the course of detailed studies of the long-term variations of particular
Be stars, we have practically verified that the non-linear transformations,
needed for a reliable transformation between a standard and an instrumental
photometric system can also be successfully used to the transformations
between two particular standard photometric systems.
To demonstrate the importance and power of non-linear transformations
and to provide pieces of information useful for a broader astronomical
community, we summarize the transformation formulæ already published
(but hidden from the general community in papers dealing with particular
Be stars) and present several other useful transformations derived
by us. All transformation formulæ presented here are transformations
from various photometric systems to Johnson's UBV system. However,
the general procedures applied here would allow construction of
similar transformations between other photometric systems, too.
Key words: methods: observational - techniques: photometric
Prime reductions of photoelectric observations, i.e. transformations of
observed instrumental magnitudes to instrumental magnitudes outside
the Earth atmosphere, and transformations of instrumental magnitudes
to a standard system, are considered well-established
procedures. The principal steps of these reductions were described in
the influential paper by Hardie (1962) and many photometrists still
continue to follow his advice. This is unfortunate since it was shown
several times - cf., e.g. Cousins & Jones (1976),Harmanec et al. (1994),Young (1992) among others -
that the linear transformation formulæ given by Hardie (1962) do not
ensure accurate enough reductions. The most comprehensive accounts of
why the very nature of the problem dictates the use of non-linear
tranformation formulæ even for narrow-band photometric systems
were given by Young (1992) and Harmanec et al. (1994) where also references to previous
work can be found. The studies that followed had demonstrated that the
consistent application of non-linear transformation formulæ and
determination of accurate UBV magnitudes of many non-variable
stars by Harmanec et al. (1994) led in a sense to a "rehabilitation" of the
UBV system since all three UBV magnitudes can now be derived
from different stations and instrumentations (even from stations
near the sea level and high-mountain stations) with an accuracy of about
0
 01 from all-sky observations. This was convincingly demonstrated
by Harmanec (1998). He was able to define a very accurate transformation
between the broad-band Hipparcos
01 from all-sky observations. This was convincingly demonstrated
by Harmanec (1998). He was able to define a very accurate transformation
between the broad-band Hipparcos  magnitude published by Perryman et al. (1997) and
mean UBV magnitudes from Hvar and Skalnaté Pleso derived by Harmanec et al. (1994).
Such an accurate transformation would not be possible if any of the
two data sets were not reduced properly.
magnitude published by Perryman et al. (1997) and
mean UBV magnitudes from Hvar and Skalnaté Pleso derived by Harmanec et al. (1994).
Such an accurate transformation would not be possible if any of the
two data sets were not reduced properly.
For convenience of the astronomical community we summarize here
several useful transformation formulæ which allow reliable
transformations of various photometries to passbands of the standard
Johnson system.
First, we give the transformations between two well-established
photometric systems:
In their study of the Be binary V360 Lac, Hill et al. (1997) derived
the following transformation from the DAO system - see, e.g.,
Hill et al. (1976) - to the UBV system:
| V |
= |
[55], |
(1) |
| (B-V) |
= |
1.1348 X + 0.02368 Y, |
(2) |
| (U-B) |
= |
0.24453X+0.74611Y |
|
| |
|
-0.37301X2+0.50754X3, |
(3) |
where
X=[44]-[55] a
Y=[35]-[44].
In a study of the Be star OT Gem, In the text
Bozic et al. (1999) published a transformation
between the 13-colour photometry by Johnson & Mitchell (1975) and the UBV system
but gave incomplete information on the meaning of the symbols used. Here,
we reproduce this transformation in the proper, directly usable form:
| V |
= |
m55+0.01930bv+0.01830ub |
|
| |
|
-0.06538bv2+0.02411bv3+0.01434 |
(4) |
| B |
= |
m43-0.03528bv+0.01464ub |
|
| |
|
-0.02837bv2-0.03429bv3+0.00006 |
(5) |
| U |
= |
m35+0.10478bv-0.15289ub |
|
| |
|
+0.11294bv2-0.06538bv3+0.01686, |
(6) |
where
| m35 |
= |
m52+[(33-52)+(35-52)+(37-52)]/3, |
(7) |
| m43 |
= |
m52+[(45-52)+(40-52)]/2, |
(8) |
| m55 |
= |
m52+(52-58)/2, |
(9) |
| bv |
= |
m43-m55, |
(10) |
| ub |
= |
m35-m43. |
(11) |
The symbols m52, (33-52), etc. denote the reference
magnitudes and colour indices of the Johnson 13-C system.
For the first time we present here a transformation from the Geneva
7-colour photometry to the Johnson system. To obtain it, we used,
as in other cases, all constant stars with good UBVvalues from Harmanec et al. (1994) for which we could also find Geneva photometry
in the compilation by Burki et al. (1998). It turned out that a bilinear
transformation is sufficient for the V magnitude and the transformation
reads as follows:
| V |
= |
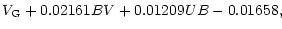 |
(12) |
| B |
= |
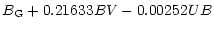 |
|
| |
|
-0.01643BV2+0.00120BV3+0.78412, |
(13) |
| U |
= |
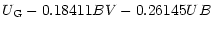 |
|
| |
|
+0.01763BV2+0.06330BV3-0.02095, |
(14) |
where
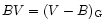 and
and
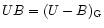 (i.e. colours
B and U in the usual Geneva group tabulation). The rms errors of the fits
per 1 observation amount to 0
(i.e. colours
B and U in the usual Geneva group tabulation). The rms errors of the fits
per 1 observation amount to 0
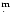 0102, 0
0102, 0
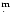 0100, and 0
0100, and 0
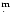 0254 for
V, B and U, respectively.
0254 for
V, B and U, respectively.
Finally, we also derived new transformations between Strömgren
and Johnson colours, using the weighted mean Strömgren colours from the
catalogue of Hauck & Mermilliod (1998). They read as follows:
| (B-V) |
= |
1.41694bv+0.07010ub |
|
| |
|
+0.57145bv2-0.60399bv3-0.10118, |
(15) |
| (U-B) |
= |
0.66567ub-0.09718bv |
|
| |
|
+0.24407bv2+0.29340bv3-0.91958, |
(16) |
where bv=(b-y) and ub=(u-b) are the Strömgren colours.
The rms errors of the fits per 1 observation are 0
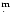 0170 and 0
0170 and 0
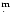 0165
for the B-V and U-B, respectively.
0165
for the B-V and U-B, respectively.
Since in many catalogues, values V, (b-y), m1 and c1 are
tabulated for Strömgren photometry, we remind that
| b |
= |
V+(b-y), |
(17) |
| v |
= |
b+(b-y)+m1=V+2(b-y)+m1, |
(18) |
| u |
= |
v+(b-y)+m1+c1 |
|
| |
= |
V+3(b-y)+2m1+c1, |
(19) |
| (u-b) |
= |
2(b-y)+2m1+c1. |
(20) |
It is interesting to compare our transformation to that published by
Turner (1990). He derived his transformation formulæ in the form
| (B-V) |
= |
1.584(b-y)+0.681m1-0.116, |
(21) |
| (U-B) |
= |
0.675(u-b)-0.938, |
(22) |
valid only for hot stars with
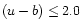 .
He obtained rms errors
of 0
.
He obtained rms errors
of 0
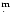 016 and 0
016 and 0
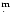 022 for B-V and U-B, respectively. As a matter
of curiosity, we reproduced his second relation, also for hot stars only,
in the form
022 for B-V and U-B, respectively. As a matter
of curiosity, we reproduced his second relation, also for hot stars only,
in the form
| (U-B) |
= |
0.659(u-b)-0.912, |
(23) |
the rms error per 1 observation being 0
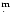 0174 only. Note that our
relations (20) and (21) hold over the whole range of stellar colours.
0174 only. Note that our
relations (20) and (21) hold over the whole range of stellar colours.
Since the (B-V) and (U-B) colour indices are often known for
the stars in question, it is possible to define transformations
to either V or B Johnson magnitude from some photometries
based on observations in one passband only.
Investigating 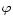 Per, Bozic et al. (1995) found that the magnitude
differences based on the old photoelectric observations with a Rb diode,
which were secured by Guthnick & Prager (1918), can be reliably transformed into
Johnson's B magnitude differences with the help of the following
relation:
Per, Bozic et al. (1995) found that the magnitude
differences based on the old photoelectric observations with a Rb diode,
which were secured by Guthnick & Prager (1918), can be reliably transformed into
Johnson's B magnitude differences with the help of the following
relation:
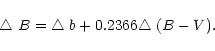 |
(24) |
A similar transformation for early photoelectric photometry from the Lick
Observatory, secured by Stebbins (1916) and Stebbins (1921), was derived
by Holmgren et al. (1999):
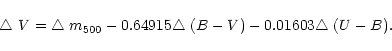 |
(25) |
Recently, Harmanec (1998) published the following useful transformation
which allows an accurate determination of the Johnson V magnitude from
the broad-band 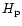 magnitude from the Hipparcos satellite:
magnitude from the Hipparcos satellite:
V=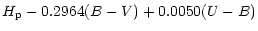 +0.1110(B-V)2+0.0157(B-V)3+0.0072. +0.1110(B-V)2+0.0157(B-V)3+0.0072. |
(26) |
A package of FORTRAN programs which allow reliable photometric reductions
has been published with detailed documentation by Harmanec & Horn (1998) and
is also available on request from the first author of this note.
Acknowledgements
We gratefully acknowledge useful comments on the first version of
this note provided by Drs. D. H. Holmgren, J. R. Percy, E. Poretti,
R. R. Shobbrook, C. Sterken and G. A. H. Walker and by an anonymous
referee. This study was supported by grant 30304 of the Granting Agency of
the Czechoslovak Academy of Sciences and its finishing was made possible
through the support via research plan J13/98: 113200004 Investigation of
the Earth and the Universe.
- Bozic, H., Ruzdjak, D.,
& Sudar, D. 1999, A&A, 350, 566
In the text
NASA ADS
- Bozic, H., Harmanec, P.,
Horn, J., et al. 1995, A&A, 304, 235
In the text
NASA ADS
- Burki, G., et al. 1998,
In the text
http://obswww.unige.ch/gcpd/cgi-bin/photoSys.cgi
- Cousins, A. W. J., & Jones, D. H. P. 1976, Mem. R. Astron. Soc., 81, 1
In the text
NASA ADS
- Guthnick, P., & Prager, R. 1918,
Veröff. Berlin Babelsberg 2, 3, 113
In the text
- Hardie, R. H. 1962, in Stars and Stellar
Systems, vol. II: Astronomical Techniques, ed. G. P. Kuiper, & B. M. Middlehurst (Univ. of Chicago Press, Chicago, USA), 178
In the text
- Harmanec, P. 1998, A&A, 335, 173
In the text
NASA ADS
- Harmanec, P., & Horn, J. 1998,
Journal Astron. Data No. 4 CD-ROM file 5
In the text
- Harmanec, P., Horn, J., & Juza, K. 1994, A&AS, 104, 121
In the text
NASA ADS
- Hauck, B., & Mermilliod, M. 1998,
A&AS, 129, 431
In the text
NASA ADS
- Hill, G., Hilditch, R. W., & Pfannenschmidt, E. L. 1976, Publ. Dom. Astrophys. Obs., 15, 1
NASA ADS
- Hill, G., Harmanec, P., Pavlovski, K.,
et al. 1997, A&A, 324, 965
In the text
NASA ADS
- Holmgren, D. E., Hadrava, P.,
Harmanec, P., et al. 1999, A&A, 345, 855
In the text
NASA ADS
- Johnson, H. L., & Mitchell, R. I. 1975, Rev. Mex. Astron. Astrofís., 1, 299
In the text
NASA ADS
- Perryman, M. A. C, Høg, E., Kovalevsky, J., Lindegren, L., & Turon, C. 1997, ESA SP-1200,
The Hipparcos and Tycho Catalogues
In the text
- Stebbins, J. 1916, Lick Obs. Bull., 8,
No. 277, 186 & 192
In the text
- Stebbins, J. 1921, ApJ, 54, 81
In the text
NASA ADS
- Turner, D. G. 1990, PASP, 102, 1331
In the text
NASA ADS
- Young, A. T. 1992, A&A, 257, 366
In the text
NASA ADS
Copyright ESO 2001
![]() Per, Bozic et al. (1995) found that the magnitude
differences based on the old photoelectric observations with a Rb diode,
which were secured by Guthnick & Prager (1918), can be reliably transformed into
Johnson's B magnitude differences with the help of the following
relation:
Per, Bozic et al. (1995) found that the magnitude
differences based on the old photoelectric observations with a Rb diode,
which were secured by Guthnick & Prager (1918), can be reliably transformed into
Johnson's B magnitude differences with the help of the following
relation: