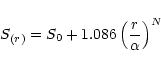2 The art of profile fitting

Suitable fitting of radial profiles in low surface brightness galaxies is a delicate task which, like an art, requires good skills and the knowledge of the appropriate technique. Every error sources, from seeing and photon noise, as well as any uncertainty in the sky cleaning must be accounted for, and we have to pay attention at the same time also to preserve astrophysical self-consistency of our output.

In a fit of digitized plots of the NGC5044 galaxy sample from Fig. 1 in C99, Young & Currie (2001) obtained, for each galaxy, a new set of Sérsic parameters. Like C99, they worked in the surface brightness domain, that is by using Eq. (1) in the form

$$S_{(r)} = S_0 + 1.086 \left( r \over \alpha \right) ^N$$ (2)

with S_(r) in mag arcsec^-2. In particular, they obtained very different N (i.e., shape) values for galaxies N42, N51, and N95A, with respect to C99's results. According to their results, YC00 claim that "none of the three relatively bright galaxies cited as possessing convex profiles actually has a convex profile'', meaning the three "outliers'' N42, N49, and N50.

One of the questioned objects in the C99 sample is galaxy N42, for which C99 indicates N=1.43 to be compared with N=0.60in the YC00 fit. At least two evident weak points emerge, in our opinion, from the YC00 analysis. Contrary to the C99 fitting procedure, that only relied on the S/N>1 portion of galaxy surface brightness profile (i.e. with $I(r) > \sigma_{\rm SKY}$), the new fit extends much farther from galaxy centre. In the outermost regions, photon noise and statistical uncertainty in the sky subtraction begin to dominate causing the output profile to artificially level off at large radii. By itself, this effect works in inducing nominally "concave'' (i.e., N<1) surface brightness profiles throughout in the YC00 fit (see Andredakis et al. 1995 for similar conclusions dealing with bulge deconvolution in spiral galaxies).

Figure 1: V band surface brightness profiles of galaxies N42 (top) and N29 (bottom). Sérsic law fits are shown as solid lines. Small ticks show the inner and the two outer ( $1\sigma _{\rm SKY}$and $\sigma /2_{\rm SKY}$) radius cutoffs in C99 model fitting. Crosses show the bulge component of N42 after model subtraction. The fitting shape parameter N results 1.43 for N42 and 0.54 for N29

In addition, even at first glance (cf. Fig. 1) the N42 surface brightness profile reveals at least two distinct components: an inner bulge and a main body extending out to $\sim$ $50\hbox{$^{\prime\prime}$ }$. This galaxy would therefore need a multi-component scheme (e.g.: Papaderos et al. 1996) to properly decompose its profile. Cellone's (1999) model for the N42 main component provided an integrated magnitude $V_{\rm T}=15.3$ mag. After subtraction, this leaves the inner bulge component, with $V_{\rm bulge}=16.4$, and extending out to $r \simeq 17\hbox{$^{\prime\prime}$ }$, as evident from Fig. 1. Although this decomposition scheme might probably be not unique, it shows however that the main morphological component of the galaxy, providing about 3/4 of the total V luminosity, is in fact suitably fitted by the original "convex'' profile. Our choice is also supported by a $\chi^2$ test on the fitting residuals confirming that a simple Sérsic fit can be ruled out at a $95\%$ confidence level.

As a comparison, Fig. 1 (lower panel) also shows the profile of the bright dwarf N29. In this case, no change in slope is evident, and a single Sérsic law (with N=0.54) fits nicely this profile all along its useful range, as confirmed again by the $\chi^2$ statistics.

The case of N51 (the second galaxy disputed by YC00) is similar to that of N42, although not so extreme, while for the third object, the previously uncatalogued galaxy N95A, C99 reported an exceedingly low surface brightness ( $S_0 \sim 24$ mag arcsec^-2) that definitely prevented any reliable fit. For this reason this galaxy was not included in any subsequent analysis.

While statistical tests support in our case both the choice of a two-component fit for N42, and a simple Sérsic law for N29, more generally any suitable correction for the bulge contribution in dwarf galaxies may be a non-univocal task. Seeing conditions and other internal bias sources (e.g. ongoing star formation) act in facts in the sense of disturbing galaxy morphology making any fitting procedure somewhat dependent on galaxy apparent size and on environment conditions as well.

In spite of any standard criterion to single out the bulge component, it is clear however that by simply neglecting the problem one would more likely tend to predict too "spiked'' galaxy profiles preferring lower values of N (Andredakis et al. 1995). We will turn back on this point and its impact on the L-N relationship in Sect. 4.

Figure 2: Top: $1\hbox {$^\prime $ }\times 1\hbox {$^\prime $ }$ contour plot (gband) of N50. The faintest and brightest contours displayed are 25 and 20 mag arcsec-1, respectively, with 0.25 mag arcsec-1separation between concentric contour levels. North is up and East to the left. Bottom left: greyscale plot after subtraction of a Sérsic model. Orientation and scale are the same as in the upper panel. Bottom right: enlarged view ( $15\hbox {$^{\prime \prime }$ }\times 15\hbox {$^{\prime \prime }$ }$) of the central region with identification for the knots (see Table 1)