Th. Rivinius^1,4 - D. Baade¹ - S. Stefl² - R. H. D. Townsend ³ - O. Stahl⁴ - B. Wolf⁴ - A. Kaufer^5,4

1 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
2 - Astronomical Institute, Academy of Sciences, 251 65 Ondrejov, Czech Republic
3 - Department of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
4 - Landessternwarte Königstuhl, 69117 Heidelberg, Germany
5 - European Southern Observatory, Casilla 19001, Santiago 19, Chile

Abstract
After the description and time series analysis of the variability of the circumstellar and stellar lines, respectively, in Papers I and II of this series, this paper sets out to model the stellar variability in terms of multi-mode nonradial pulsation (nrp), but also adds another 109 echelle spectra to the database, obtained in 1999. While the near-circumstellar emission has faded further, the six periods and the associated line profile variabilities (lpv) have remained unchanged. For the modeling, ${\cal P}_1$ of the periods ${\cal P}_1$ - ${\cal P}_4$ close to 0.5 day, and ${\cal P}_5$ of the two periods ${\cal P}_5$ and ${\cal P}_6$ near 0.28 day were selected, because they have the largest amplitude in their respective groups, which are characterized by their own distinct phase-propagation pattern. Permissable ranges of mass, radius, effective temperature, projected equatorial rotation velocity, and inclination angle were derived from calibrations and observations available in the literature. A total of 648 different combinations of these parameters were used to compute a number of trial series of line profiles for comparison with the observations. Next to reproducing the observed variability, the primary constraint on all models was that the two finally adopted solutions for ${\cal P}_1$ and ${\cal P}_5$ had to be based on only one common set of values of these quantities. This was, in fact, accomplished. Townsend's (1997b) code BRUCE was deployed to model the pulsational perturbations of the rotationally distorted stellar surface. With the help of KYLIE, from the same author, these perturbations were converted into observable quantities. The local flux and the atmosphere structure were obtained from a grid of ATLAS9 models with solar metallicity, while the formation of 5967 spectral lines was calculated with the LTE code of (1966). An initial coarse grid of models using all these ingredients was computed for all 12 nrp modes with $\ell$ $\leq$ 3 and m $\neq$ 0. Comparison with the observed variability of C II4267, which is the best compromise between contamination by circumstellar emission and significance of the variability, yielded ( $\ell$ =2, m=+2) for ${\cal P}_1$ (and, by implication, ${\cal P}_2$ - ${\cal P}_4$ ) and ( $\ell$ =3, m=+3) for ${\cal P}_5$ (and ${\cal P}_6$ ) as the best matching nrp modes. At $9~M_{\odot}$ / $3.4~R_{\odot}$ and 440 kms^-1, respectively, the mass-to-radius ratio and the equatorial velocity are on the high side, but not in fundamental conflict with established knowledge. The photometric variations of all six modes combine at most to a maximal peak-to-peak amplitude of 0.015 mag, consistent with the non-detection of any of the spectroscopic periods by photometry. Without inclusion of additional physical processes, present-day linear nrp models are fundamentally unable to explain major red-blue asymmetries in the power distribution, which however seem to be limited to only some lines and the modes with the highest amplitudes. Nevertheless, the model reproduces very well a wide range of observed details. Most notable among them are: (i) Although all modeling was done on the residuals from the mean profiles only, the mean spectrum predicted by the model closely fits the observed one. (ii) Dense series of high-quality spectra obtained as early as 1987 and as recently as 1999, published independently but not included in the modeling efforts of this paper, are matched in great detail by the multiperiodic nrp model. As in $\omega$ CMa, the inferred modes are retrograde in the corotating frame and in the observer's frame appear prograde only because of the rapid rotation. This has implications for models of the ejection of matter during line emission outbursts, which in $\mu$ Cen are correlated with the beating of modes in the 0.5-d group of periods. The length of the corotating periods as well as the horizontal-to-vertical velocity amplitude ratios suggest a g-mode character.

Key words: line: profiles - line: formation - stars: oscillation - stars: Be - stars: individual: $\mu$ Cen

1 Introduction

Non-radial pulsation (nrp) in the upper main sequence is a widely-seen phenomenon. There are hardly any regions of the Hertzsprung-Russell Diagram left in which no instability resides (Gautschy & Saio 1995,1996). For non-supergiant B stars these instabilities include the $\beta$ Cephei strip and the SPB-region (the Slowly Pulsating B stars). Both mechanisms are based on the metal-opacity bump at $T \approx 1.5~10^5$ K. But while the $\beta$ Cephei mechanism excites short-period p-modes in early B-type stars, the SPB-mechanism excites long-period g-modes in mid to late B-type stars. The available theoretical calculations for instability regions are, however, restricted to non- or slowly rotating models (Dziembowski & Pamyatnykh 1993; Dziembowski et al. 1993; Balona & Dziembowski 1999).

Since the periods for such g-modes are of the same order of magnitude as the rotational period for a rapid rotator (Balona 1995), the instability will not remain unaltered in the rotating case (Ushomirsky & Bildsten 1998). Therefore, it would not be fully unexpected if rapidly rotating g-mode pulsators were found well outside the calculated g-mode instability strip for non-rotating stars.

For some time, Be stars have been suspected to be such objects. Early observational evidence was given e.g. by Baade (1982, $\omega$ CMa). $\omega$ CMa shows strong periodic line profile variability (lpv) with a period of 1.37 day, and the typical appearance of low order g-modes. However, just the proximity of the observed periods to the expected rotational periods posed the question of whether the observed periods are not merely due to rotation and the variability due to stellar spots or corotating clouds. In principle, such mechanisms could also be able to explain some of the characteristics of the lpv (Baade & Balona 1994; Smith et al. 2000). More recently, it was again $\omega$ CMa for which these hypotheses have been tested by modeling. Balona et al. (1999) found it impossible to model the lpv as non-radial pulsation with a period of 1.37 day and physically acceptable parameters. Instead, a model that assumed different intrinsic line-widths inside and outside a spot-region could explain the lpv, although only crudely. Such a behaviour could have been understood best as a region of low turbulence, and was interpreted as a co-rotating cloud by Balona (1999).

Maintz et al. (2000) showed, however, that the parameter space explored by Balona et al. (1999) in their nrp modeling was not complete, but that they had missed a parameter combination consisting of a retrograde pulsation mode, that due to the rapid rotation of the star appears to the terrestrial observer as prograde. Assuming this, Maintz et al. (2000) were able to model the variability with acceptable parameters in great detail. In particular, the lpv manifesting as so-called spikes and ramps was modeled for the first time, which Balona et al. (1999) were not able to reproduce when assuming a corotating structure. However, $\omega$ CMa is, so far, the only star for which such a successful detailed modeling has been achieved. The ubiquity of nonradial pulsation in the upper left corner of the Hertzsprung-Russell diagram provides a strong motivation for exploring this explanation further.

1.1 $\mu$ Cen

Observational efforts over the last decade have resulted in one of the most extensive spectroscopic databases of a single Be star, $\mu$ Cen (= HR5193 = HD120324; B2IV-Ve) (Baade 1991; Rivinius et al. 1998a, hereafter Paper I). In Paper I the long- and medium-term evolution of the circumstellar emission lines was investigated.

The analysis of the data with respect to lines formed in the stellar photosphere revealed multiperiodicity, with at least six stable periods that can be sorted into two groups around 0.5 and 0.28day, respectively (Rivinius et al. 1998b), hereafter Paper II. A distinct type of profile variability, namely sharply-defined absorption spikes, morphologically similar to the ones in $\omega$ CMa, seems to occur preferentially during the early phases of an outburst.

Not only was a causal connection between stellar and circumstellar activity shown on the base of already existing data, but a prediction of the times of outburst activity was verified in early 1997 (Rivinius et al. 1997; Rivinius et al. 1998c,d.

**Table 1:** The $\mu$ Cen observing campaigns 1999
Observing		No. of spectra/		Typical	Typical	Resolving	Spectral
season	Telescope	No. of Nights	Instrument	exposure time	S/N	power	range
1999 Jan.	ESO 1.5 m	4/7	FEROS	2min	300	48000	3650-9200 Å
1999 May/June	ESO 0.5 m	62/71	HEROS	30 min	125	20000	3450-8620 Å
1999 July	ESO 1.5 m	43/21	FEROS	2 min	250	48000	3650-9200 Å

While Paper II concentrated on accurate time series analyses, with the intent of making the detection of multiperiodicity most reliable, the individual properties of the period groups were addressed only in brief. In this paper, therefore, we concentrate on the physical interpretation of the observed multiperiodic variability. While preliminary results were presented by Rivinius (2000), this paper represents the final modeling result and overrides the previously published parameter set.

Contrary to $\omega$ CMa, in which so far only one stable period has been found, the six-fold multiperiodicity of $\mu$ Cen provides a compelling argument for the adoption of an nrp model, which is independent of the quality of the lpv modeling. However, the match between the observations and the nrp model calculations presented below appears very satisfactory in many details.

Additional high quality data have been obtained meanwhile, and are described in Sect. 2 and included in the further analysis. While Sect. 3 describes the observed properties of the periodic variability, Sect. 4 introduces the modeling technique, which is applied in Sect. 5. The derived parameters and modeled variations are presented and discussed in Sects. 6 and 7, respectively. Section 8 concentrates on possible relations of $\mu$ Cen to other pulsating stars as well as to the Be stars, and the conclusions are given in Sect. 9.

2 Observations

2.1 Spectroscopy

$\mu$ Cen was included in the target list for a further Be star campaign in 1999. After a few reconnaissance spectra in January, it was observed once per night in May and June from La Silla with the HEROS instrument as already described in Paper I. In July, a few minutes per night of the guaranteed time of the FEROS Consortium (Kaufer et al. 1997,1999) were dedicated to $\mu$ Cen. The observing runs since those covered by Paper I are outlined in Table 1.

2.2 Published photometry

By now, three independent photometric studies have investigated $\mu$ Cen. Cuypers et al. (1989) found a double wave period of $2\hbox{$.\!\!^{\rm d}$ }10$ with a peak-to-peak amplitude decreasing from 0.08 mag in 1987 to 0.04 mag in 1988. The photometric single-wave period of 1.06 day reported by Dachs & Lemmer (1991) for 1986-1989, with an amplitude of 0.06 mag, is obviously the same, depending on whether or not even cycles are more similar to each other than to odd cycles. Only the data of Cuypers et al. are published. Our re-analysis, using the methods described in Paper II, suggests a period near 1.05 day but cannot distinguish between it and its 1c/d alias near 23 days, although formally the longer period has even a slightly higher significance.

Finally, the HIPPARCOS and TYCHO photometry (Perryman et al. 1997) is dominated by strong incoherent variability on longer timescales, which is conceivably related to long- and medium-term processes in the circumstellar environment (Paper I). However, the sampling of these data is not dense enough to follow events such as the observed line-emission outbursts (see Paper I). For the same reason, it is not realistically possible to subtract this long-term variability from the light curve, and in this data none of the 6 short periods could be recovered. Nevertheless, a careful analysis by Aerts (2000) revealed a period of 1.779 day (f=0.5621c/d), with A=0.027 mag, which is possibly related to the two strongest spectroscopic frequencies by $f_5-f_1-1 = 0.5652\,$ c/d. Of the second, longer period reported by Aerts, 9.14 day, no spectroscopic evidence was found.

The 1.05 day period is about twice the ${\cal P}_1\approx 0.5$ day period, but since the photometry does not resolve the group nature of this period, an exact match would not be expected, even if the periods would be due to the same phenomenon. However, a relation between both is not yet established, and given the problems of period searching in one-dimensional datasets (see Paper II) in $\mu$ Cen, we assume for this analysis that the 1.05 day period is not related to the spectroscopic variability. For instance, in a similar case, $\omega$ CMa, the photometric period of 1.47 day (Balona et al. 1987) is not related to the photospheric period of 1.37 day (Baade 1982), but rather to circumstellar effects (Stefl et al. 1999).

Taking into account the various sources of incoherent variability that could hamper the detection, we conclude that any photometric variability with the spectroscopic periods is below a detection threshold of about 0.02 mag for peak-to-peak amplitude.

3 Periodic variability properties

The variability analysis of a single scalar quantity derived from the entire profile, as radial velocity or equivalent width, has the advantage that the information content is focused in a single number and the effects of noise are reduced. However, especially for asymmetric variations, physical information is lost. To exploit this information, two techniques have been developed in recent years, the moment method (Aerts et al. 1992), and the full-profile 2D method (Gies & Kullavanijaya 1988; Telting & Schrijvers 1997, also called intensity period search, IPS).

However, it is not clear how the presence of circumstellar emission in the line wings influences the moment method, since it relies on absolute values of the moments for mode identification. Even the period detection may be seriously hampered by the presence of variable circumstellar contributions and transient periods occuring in the line wings (Stefl et al. 1999, Paper I).

$\mu$ Cen shows obvious emission components in the Hei 5876, 6678, and 7065 lines, and trace emission cannot be excluded for even the weakest lines. When the emission was strong in Hei lines, as in 1997, the residuals of these data after subtraction of spectra from a low Hei emission state, as in 1999, exhibit clear signatures of double peaked disk emission. Figure 1 shows this for a selection of lines, but the same holds in principle for all Hei lines which were re-observed.

The full-profile 2D method is preferred for the following analysis. This is because i) a constant emission contribution would play no rôle at all, ii) irregularly variable emission would just increase the frequency noise, and iii) a (transient) periodically variable part of the emission is well distinguishable in Fourier-space when present, and was already discussed in Paper I. Therefore, circumstellar emission may make the full-profile 2D period detection and analysis noisier, but does not introduce systematic effects.

In addition, experience, supported by simple physical conjectures, shows that high-frequency variations in emission components are largely confined to velocities around $\pm v_{\rm rot} \sin i$ or more. Since, contrary to the moment method, there is no crosstalk between the single time series analysis at sufficiently different velocities, the results of the 2D-method are the least likely to be globally affected by localized phenomena.

In Paper II it was shown that the periods in each of the two period groups have a common variability pattern, which is, however, clearly different between the groups. This analysis therefore concentrates on the strongest variability in either group, i.e. ${\cal P}_1 = 0\hbox{$.\!\!^{\rm d}$ }502925\pm6$ out of the ${\cal P}_1$ - ${\cal P}_4$ group and ${\cal P}_5=0\hbox{$.\!\!^{\rm d}$ }281405\pm5$ out of ${\cal P}_5$ and ${\cal P}_6$ . More details about the other periods and their exact values can be found in Paper II.

Before deriving details from the combined dataset, reported in the next subsections, it was ascertained that all periods given in Paper II were still present after inclusion of the observations of Table 1, and that no further periods became apparent.

3.1 The longer period group, i.e. $\mathsfsl{{\cal P}_1}$

This variability consists of a pronounced blue-to-red propagation of subfeatures in the residuals (Fig. 7 of Paper II). This blue-to-red propagation is of the order of $1.5\pi$ (Note that this is a circular phase difference. As the phased plots show linear phases, this corresponds to 0.75 in the figures). In other words, the feature takes about $\frac{3}{4}$ cycles to travel from $-v_{\rm rot} \sin i$ (blue wing) to $+v_{\rm rot} \sin i$ (red wing). Figure 3 illustrates the results of the 2D-analysis done for 20 spectral lines for ${\cal P}_1$ , together with the phase-binned profiles. The variation is evidently concentrated in the line wings. As a consequence, the power distribution across the profile has a minimum at zero velocity.

$\begin{figure} \par\includegraphics[angle=270,width=7.8cm,clip]{10561_1a.ps} % \par\includegraphics[angle=270,width=8.2cm,clip]{10561_1b.ps} \end{figure}$

Figure 1: Circumstellar emission in Hei4009, 4026, 4471, and Mgii4481 and other lines. In July 1999 the emission from the close circumstellar environment was hardly present. Therefore the averaged spectrum from this FEROS run was used as a non-emission template to derive the emission contribution to different lines (the residuals) at times of high emission, as in the average 1997 data. The disk emission is clearly seen in Hei4026, 4471, and Mgii4481, but also two weak Feii emission lines at $\approx$ 4490 Å are detected, as well as some indication of emission in Hei4009. Note that the strength of emission from the close circumstellar environment is not indicative of the strength of the H $\alpha$ emission, which was still fairly strong in 1999 ( $E/C \approx 2.7, W_\lambda \approx 5$ Å), and probably originates from gas at much greater distances from the star

Open with DEXTER

$\begin{figure} \parbox{4.4cm}{ \psfig{figure=10561_2a.ps,width=4.3cm,angle=0,cli... ...ox{4.4cm}{ \psfig{figure=10561_2b.ps,width=4.3cm,angle=0,clip=t} }\end{figure}$

Figure 2: The unprocessed power spectra (no CLEAN or other mechanisms applied) of the Hei4713 (left) and 6678 (right) lines of all HEROS data (1995 to 1999). The high amount of noise caused by the circumstellar emission in the wings of Hei6678 is clearly seen, while there is no enhanced frequency noise for Hei4713. Therefore the high signal beyond $v_{\rm rot} \sin i\approx140$ kms^-1 in Hei6678 cannot be trusted. But, as the example of Hei4713 shows, at least part of this variability is due to true periodicity. The frequencies of the photospheric variabilities are f₁ = 2c/d and f₅ = 3.5c/d

Open with DEXTER

3.1.1 Asymmetric power distribution

In Fig. 3 an asymmetry in the power distribution, and partly also the phase propagation, is visible across the line profiles. In particular, the Hei lines show an increasing power asymmetry with line strength. The most symmetric lines are Hei4009, 4121, and 4713. The asymmetry strengthens in Hei4144 and 4922, reaching a maximum in Hei4026, 4388, and 4471, while the three red Hei lines, 5876, 6678, and 7065, typically formed in the upper atmosphere, vary symmetrically again. Connected to the asymmetry is a slight change in the phase propagation of the variability across the line profile. The stronger the blue variability, the less constant is the phase velocity of the variation, with the phase velocity being lower on the blue side (Fig. 3). A similar asymmetry was observed in $\eta$ Cen by Stefl et al. (1995).

The lines affected least by these effects, but still strong enough to exhibit lpv at good S/N, are Hei4009, 4121, 4713 and Cii4267. These lines were considered for the initial modeling (Sect. 4). However, Hei4121 is located too close to H $\delta$ for comfortable modeling, and for Hei4009 the input grid of modeled line profiles was not applicable for reasons described in Sect. 4.2.2. Since we believed that Cii4267 would more likely be free of emission at any given time, this line was chosen for the computations of the grid of line profile variability. Although our final results show that Hei4713 would have given a better match of the mean profile (Fig. 7), the modeling of the residuals should not be affected to any degree above the observational noise.

Table 2: Characteristics of the analyzed Hei lines and the magnitude of the power asymmetry observed in ${\cal P}_1$

Wave- transition type lower upper blue/

length level level red

[Å] [eV] [eV] power

4713.200 $2^3{\rm P}-4^3{\rm S}$ tripl. 20.87 23.49 B > R

4120.993 $2^3{\rm P}-5^3{\rm S}$ tripl. 20.87 23.87 $B\approx R$

4009.270 $2^1{\rm P}-7^1{\rm D}$ singl. 21.13 24.21 $B\approx R$

4921.929 $2^1{\rm P}-4^1{\rm D}$ singl. 21.13 23.63 B > R

4143.759 $2^1{\rm P}-6^1{\rm D}$ singl. 21.13 24.11 $B\gg R$

4026.200 $2^3{\rm P}-5^3{\rm D}$ tripl. 20.87 23.94 $B\gg R$

4471.477 $2^3{\rm P}-4^3{\rm D}$ tripl. 20.87 23.63 $B\gg R$

4387.928 $2^1{\rm P}-5^1{\rm D}$ singl. 21.13 23.94 $B\gg R$

5875.700 $2^3{\rm P}-3^3{\rm D}$ tripl. 20.87 22.97 B > R

6678.150 $2^1{\rm P}-3^1{\rm D}$ singl. 21.13 22.97 $B\approx R$

7065.190 $2^3{\rm P}-3^3{\rm S}$ tripl. 20.87 22.62 $B\approx R$

**Table 2:** Characteristics of the analyzed Hei lines and the magnitude of the power asymmetry observed in ${\cal P}_1$
Wave-	transition	type	lower	upper	blue/
length			level	level	red
[Å]			[eV]	[eV]	power
4713.200	$2^3{\rm P}-4^3{\rm S}$	tripl.	20.87	23.49	B > R
4120.993	$2^3{\rm P}-5^3{\rm S}$	tripl.	20.87	23.87	$B\approx R$
4009.270	$2^1{\rm P}-7^1{\rm D}$	singl.	21.13	24.21	$B\approx R$
4921.929	$2^1{\rm P}-4^1{\rm D}$	singl.	21.13	23.63	B > R
4143.759	$2^1{\rm P}-6^1{\rm D}$	singl.	21.13	24.11	$B\gg R$
4026.200	$2^3{\rm P}-5^3{\rm D}$	tripl.	20.87	23.94	$B\gg R$
4471.477	$2^3{\rm P}-4^3{\rm D}$	tripl.	20.87	23.63	$B\gg R$
4387.928	$2^1{\rm P}-5^1{\rm D}$	singl.	21.13	23.94	$B\gg R$
5875.700	$2^3{\rm P}-3^3{\rm D}$	tripl.	20.87	22.97	B > R
6678.150	$2^1{\rm P}-3^1{\rm D}$	singl.	21.13	22.97	$B\approx R$
7065.190	$2^3{\rm P}-3^3{\rm S}$	tripl.	20.87	22.62	$B\approx R$

3.1.2 Periodic variability at $\mathsfsl{\vert v\vert > v_{\mathsf {rot}}\,sin\,i}$

In Hei5876, 6678, and 7065 there is considerable variability power outside the $\pm v_{\rm rot} \sin i$ range. For these three lines, however, this might be noise due to the circumstellar variability, with some coincidental signal at the frequency of ${\cal P}_1$ (Fig. 2, right).

Most other lines also show some weak variability outside $v_{\rm rot} \sin i$ ; however, the circumstellar noise in these lines is much weaker (Fig. 2, left). For this reason, the power beyond $v_{\rm rot} \sin i$ cannot, as for lines with significant emission, be attributed predominantly to the stochastic variability of the circumstellar environment. Periodic variations in the circumstellar environment itself seem unlikely, as the variation power is not connected to the strength of the residual emission at different times as shown in Fig. 1. It is important to note that the variability seen is not just an extension, but, in all lines where it can be detected, forms a local maximum of variability, separated from the main peaks by a minimum at about $\pm v_{\rm rot} \sin i$ .

3.1.3 Other periods in this group

There are three other periods belonging to the 0.5 day period group with the same behaviour in phase propagation and the double-peaked power distribution. However, they do not exhibit a pronounced asymmetry, such as that shown in Sect. 3.1.1. The variability is strong enough that such an asymmetry would certainly have been detected. I.e. co-adding the power distributions of ${\cal P}_1$ to ${\cal P}_4$ will not result in a symmetric distribution. It is not clear whether the variability outside $v_{\rm rot} \sin i$ described in Sect. 3.1.2 is present for these periods. Due to the weaker variability power of ${\cal P}_2$ , ${\cal P}_3$ , and ${\cal P}_4$ compared to ${\cal P}_1$ , it may well be present below the detection threshold, as there is some, albeit very weak (non-significant), indication.

3.2 The shorter period group, i.e. $\mathsfsl{{\cal P}_5}$

The phase-locked variability connected to ${\cal P}_5$ shows a feature propagating by about $2\dots2.5\pi$ over the profile width, depending somewhat on whether $v_{\rm rot}\sin i =130$ kms^-1 or 155 kms^-1 is adopted (see Sects. 4.1 and 6.1 for a discussion of the stellar parameters).

In Paper II, the shorter periods could not be found in Siiii4553 with sufficient significance. The inclusion of the new datasets now makes this possible (Fig. 4, rightmost panel). The non-detection in the previous datasets was due to the weakness of the variability in the Siiii lines, that was overcome now only by including the 1999 HEROS and, especially, FEROS datasets.

The power distribution of ${\cal P}_5$ is triple peaked. While for some lines the central peak is of equal strength to the outer peaks, for others it is considerably weaker (Fig. 4). The most extreme example is Siiii4553, for which the central power peak is almost suppressed. Similar to ${\cal P}_1$ , the phase propagation tends to be flatter at positions with higher variation power, leading to some curvature of the propagation. As for the longer period group, the phase propagation with ${\cal P}_5$ and ${\cal P}_6$ is very nearly identical in all lines (Paper II).

$\begin{figure} \par\includegraphics[angle=-90,width=17.6cm,clip]{10561_3.ps} \end{figure}$

Figure 3: Spectral variability patterns of ${\cal P}_1$ for some of the observed spectral lines. In the respective upper panels, sixteen phase-binned profiles are overplotted to give an idea of the variability in the profiles and the strengths of the individual lines. In the other panels, the power distribution (middle) and the phase propagation across the line profile (lower) are shown for the same lines with either open circles (for the spectral line plotted in the uppermost panel) or crosses. The power excess on the blue side for some lines is discussed in Sect. 3.1.1, the additional power outside $v_{\rm rot} \sin i$ for lines showing emission in Sect. 3.1.2. All data have been shifted by $-14.5~{\rm km\,s^{-1}}$ , to allow for the systemic velocity (Paper II). The dotted lines indicate the zero and $\pm v \sin i=130~{\rm km\,s^{-1}}$ velocities, respectively

Open with DEXTER

3.3 Consequences for interpretation and modeling

These variation properties, together with those shown in Paper II, give important clues for the interpretation of the variability. Although already the number and distribution of periods is a strong argument in favour of nrp, there is independent evidence, such as that the absolute variation power in a given line scales well with the line strength. This is not only the case for different lines of a given ion, such as Hei, but even for lines from different species. Because different species usually have different temperature-/gravity-dependencies, in terms of non-radial pulsation, the latter indicates that the pulsational velocity fields are dominant over the temperature variations in perturbing the line profile (except possibly for a line like Siiii, due to gravity darkening, as will be shown below). On the other hand, if the variability were due to co-rotating circumstellar clouds, such a model would have to explain that the spectral signature imposed by the clouds is extremely similar to the mean photospheric spectrum. For the shorter period of 0.28 day, the rotational hypothesis is immediately ruled out, unless an implausible number of clouds is assumed.

In a rapid rotator, the shape of the power distribution of ${\cal P}_1$ is a clear indication that the variability is dominated by horizontal velocity fields, because they are projected best at the stellar limbs, forming the wings (in a slow rotator it would instead be indicative of radial pulsation). Pulsational p-modes are therefore excluded, a stance supported by the relatively long period. Under special circumstances, non-radial pulsation in g-modes is able to explain even variability exceeding the limits of $\pm v \sin i$ in terms of photospheric velocity fields. Whether this is an acceptable hypothesis in the case of $\mu$ Cen is investigated in the following section.

The shorter period and the steeper phase propagation of ${\cal P}_5$ compared to ${\cal P}_1$ can be well understood as pulsation in a different mode with $\ell_1 < \ell_5$ and |m₁| < |m₅|, while m₅and m₆ as well as $\ell_5$ and $\ell_6$ should be equal.

4 Nonradial pulsation modeling technique

As shown in the previous section, the data properties leave little room for interpretations other than nonradial pulsation (nrp), yet a positive mode identification in terms of accurate physical modeling is required. For reference to various methods for nrp analysis, a thorough discussion was given e.g. by Aerts & Eyer (2000).

We used Townsend's (1997b modeling codes BRUCE and KYLIE (Version 2.71) to investigate the variability observed in $\mu$ Cen. BRUCE calculates the pulsational perturbations to a rotating stellar surface. The technique, used to calculate the rotational modifications to the pulsational eigenmodes following Lee & Saio (1990b), is especially suitable for long-period pulsators, and thus for g-modes (as noted in Sect. 3.3, p-modes are largely excluded, so that g-modes must be considered). It completely accounts for the Coriolis forces, but neglects the centrifugal forces. Therefore, for extremely rapid rotation, the model may not be completely correct. The inputs for BRUCE are the stellar parameters, the angular pulsational mode indices ( $\ell$ and m) and their respective amplitudes.

The code is able to take into account gravity darkening of a rotating star. $\beta = 0.25$ was chosen for von Zeipel's (1924 gravity darkening parameterization, which is appropriate for early type stars (Townsend 1997b, cf. his Eq. (35)) in the case of a geometrically thin atmosphere (Hadrava 1992).

The computed pulsational pertubations, superimposed on the equilibrium configuration of the rotating star (Townsend 1997b, his Sect. 4.1), include pulsational velocity fields in all three directions ( $r, \phi, \theta$ ), temperature fluctuations, variations in the visible surface area and finally the variations in the viewing angle of a given surface element. Because of limb darkening, the latter is especially useful when modeling photometric variability and should allow for estimates more accurate than previously calculated.

KYLIE computes observable quantities from the pertubation fields given by BRUCE by computing and integrating the observables, e.g. the observer-directed spectrum or flux, of each surface element individually from an input grid of stationary atmosphere models. KYLIE can be used not only to calculate spectral line profiles, but also to estimate the photometric variability, if an absolute flux grid is used as input instead of synthetic line profiles.

The parameter space to be explored is huge. The example of $\omega$ CMa demonstrates that it can be fatal to omit even at-first-sight unlikely regions. Given that BRUCE is a rather new tool, we decided to approach the problem in a "brute force'' way, namely to include every imaginable parameter set. This was done also to gain experience for future work on other objects. The grid including these parameter sets is hereafter called the coarse grid (Sect. 4.1 and Table 3). Based on this coarse grid, most parameter sets and modes could be excluded. A fine grid was subsequently computed to obtain the parameters giving the best approximation to the observed variability.

The full modeling procedure starts with guessing plausible stellar parameters (Sect. 4.1), then the set of model profiles is computed (Sects. 4.3 and 4.4), and finally these model profiles are compared to the observations (Sect. 5).

4.1 Grid of stellar parameters computed

Physical parameters for $\mu$ Cen have been computed using Walraven photometry by de Geus et al. (1989). They obtained $T_{\rm eff}=20\,500$ K, $\log g = 3.94$ , $\log L_{\star}/L_{\odot}= 3.6$ , and a distance of 145 pc. The HIPPARCOS distance is a little greater, $162\pm^{21}_{17}$ pc. Brown & Verschueren (1997) derived $v_{\rm rot}\sin i =130$ kms^-1 from high resolution echelle spectroscopy, while Slettebak (1982) gave $v_{\rm rot} \sin i = 155$ kms^-1. This relatively low value and the shape of emission line profiles point towards a low-to-intermediate inclination (Hanuschik et al. 1996). For a rapidly rotating star, however, the values for $T_{\rm eff}$ , $\log g$ , and $\log L_{\star}$ cannot be translated directly into parameters like radius and mass using standard calibrations. Due to the rotational deformation, the observationally derived radii, luminosities, and temperatures depend on the inclination angle due to gravity darkening and rotational deformation. Therefore, from these observations, only the boundaries of the parameter grid, for which we performed pulsational model calculations, can be derived.

The input stellar parameters required by the model are polar radius $R_{\star, {\rm polar}}$ , polar temperature $T_{\rm eff, polar}$ , mass $M_{\star}$ , the rotational velocity $v_{\rm rot}$ , and the inclination i. Since the latter two, for modeling a given star, are not independent but connected via the measured $v_{\rm rot} \sin i$ , only certain combinations $<v_{\rm rot}, i>$ are acceptable. Thus a complete set of parameters is given by $R_{\star,{\rm polar}}, T_{\rm eff, polar}, M_{\star}$ and $<v_{\rm rot}, i>$ .

Due to gravity darkening in a rapid rotator, the polar temperature will be higher than the one inferred from observations. On the other hand, the gravity darkening gives extremely low temperatures only in a small equatorial band. Since the models do not depend greatly on the polar temperature, only three values with a 2000 K step size were tested. Similarly, the main influence of the mass is that it will alter the critical velocity of the star and, therefore, the rotational deformation. As the dependency is not sensitive, however, only three values were computed, so that any main sequence B1 to B2 star has a mass within the used limits (e.g. calibration by (Balona 1995).

The limits for the radius were chosen similarly to the mass, but as the model is more sensitive to radius, six steps were computed to ensure smooth variations between two neighbouring parameter sets. Also, while for $v_{\rm rot} \sin i$ good estimates exist, the value of $v_{\rm rot}$ has the second most important effect on the resulting calculations. Therefore, six steps were calculated for $v_{\rm rot}$ from the lowest believable value ( $\mu$ Cen is certainly not viewed edge-on or close to edge-on, i.e. $i< 50^\circ$ ) up to the critical velocity. For each $v_{\rm rot}$ , two inclinations were computed, so that the observationally derived values of $v_{\rm rot} \sin i$ are bracketed. Table 3 lists the grid of parameters chosen.

This leads to a total of 648 different stellar parameter sets to be calculated for each mode. Parameter sets yielding physical impossibilities, such as super-critical equatorial velocities, or for which the computed local surface parameters would exceed the limits of the synthetical atmosphere grid (Sect. 4.2), were not computed.

Table 3: Adopted stellar parameter ranges for the coarse grid. Note that i is calcutaled for each $v_{\rm rot}$ assuming either of the two considered values of $v_{\rm rot} \sin i = 130, 160$ kms^-1
Parameter Range

Radius, $R_{\star, {\rm polar}}$ [ $R_{\odot}$ ] 4.0 $\dots$ 6.0, step 0.4

Temperature, $T_{\rm eff, polar}$ [kK] 20, 22, 24

Mass, $M_{\star}$ [ $M_{\odot}$ ] 7, 8.5, 10

Equ. rotation, $v_{\rm rot}$ [kms^-1] 200 $\dots$ 400, step 40

$v_{\rm rot} \sin i$ to compute i [kms^-1] 130, 160

**Table 3:** Adopted stellar parameter ranges for the coarse grid. Note that i is calcutaled for each $v_{\rm rot}$ assuming either of the two considered values of $v_{\rm rot} \sin i = 130, 160$ kms^-1
Parameter		Range
Radius, $R_{\star, {\rm polar}}$	[ $R_{\odot}$ ]	4.0 $\dots$ 6.0, step 0.4
Temperature, $T_{\rm eff, polar}$	[kK]	20, 22, 24
Mass, $M_{\star}$	[ $M_{\odot}$ ]	7, 8.5, 10
Equ. rotation, $v_{\rm rot}$	[kms^-1]	200 $\dots$ 400, step 40
$v_{\rm rot} \sin i$ to compute i	[kms^-1]	130, 160

4.2 Grid of stellar atmosphere models

For the computation of the observable stellar variability from the perturbations of the stellar surface, the intrinsic observables for each surface element are needed. The NLTE model grid of intensity spectra used by Townsend (1997a), and a similar NLTE flux spectra grid by Gummersbach et al. (1998), unfortunately were too limited both in the $\log g$ - $T_{\rm eff}$ plane and in the number of ions computed to be used for this work. Therefore, in calculating the flux variations to estimate the photometric amplitudes, we used a theoretical absolute flux grid described in Sect. 4.2.1, while for the line profile variability the intrinsic profiles were interpolated from the models introduced in Sect. 4.2.2.

4.2.1 Stellar atmosphere structure and continua

Gummersbach et al. (1998) have calculated a grid of ATLAS9 atmospheric models for different metallicities. Since publication, their grid has been extended, now reaching from $T_{\rm eff} = 9000$ K to 50000 K in steps of 1000 K, and from the lowest numerically converging $\log g$ to an upper limit of $\log g = 5.0$ in steps of 0.1 dex. From these we have selected a subset of solar metallicity models in the range of 10000 K $\le T_{\rm eff} \le$ 31000 K, and $\log g \le 4.3$ . The lower boundary was chosen to be able to model also very rapid rotation, which causes an equatorial temperature significantly lower than $T_{\rm eff}$ . The stellar fluxes computed from this grid were used as input data for KYLIE to model the photometric variability.

Table 4: The formally best matching modes ( $\chi ^2$ test on the residuals from the observed Cii4267 profiles) and the corresponding parameter sets found in the coarse grid for ${\cal P}_1$ . The first two columns give the mode indices, the next five the stellar input parameters radius, temperature, mass, rotation and inclination. The following four show the equilibrium (i.e. non-pulsating) configuration of the rotating model star, while the last three list the corotating period, the $\chi ^2$ , and the peak-to-peak photometric amplitude of the pulsating model. The lpv of these Cii4267 and the six modes listed here are shown in Fig. 5
$\ell$ m $R_{\star, {\rm polar}}$ $T_{\rm eff, polar}$ $M_{\star}$ $v_{\rm rot}$ i ${\cal P}_{\rm rot}$ ${\cal P}_{\it nrp,\rm corot}$ $\chi ^2$ $\Delta b$

[ $R_{\odot}$ ] [K] [ $M_{\odot}$ ] [kms^-1] $^\circ$ [1.5ex] $\frac{\textstyle{\cal P}_{\rm rot}}{{\textstyle\cal P}_{\rm crit}}$ [1.5ex] $\frac{\textstyle R_{\rm equ}}{{\textstyle R_{\rm pol}}}$ [1.5ex] $\frac{\textstyle T_{\rm eff,equ}}{{\textstyle T_{\rm eff,pol}}}$ [hours] [hours] [mag]

1 1 4.4 20000 8.5 320 24.0 0.65 1.16 0.84 19.40 7.43 3.06 0.025

1 -1 5.6 20000 8.5 400 19.0 0.91 1.38 0.59 23.51 24.64 3.12 0.003

2 2 4.0 20000 8.5 400 19.0 0.77 1.25 0.76 15.14 20.41 3.13 0.013

2 -1 4.8 20000 7.0 400 19.0 0.93 1.40 0.56 20.47 29.18 3.20 0.055

3 2 4.0 24000 8.5 400 19.0 0.77 1.25 0.76 15.14 20.41 3.36 0.004

3 -1 6.0 20000 10.0 400 19.0 0.87 1.34 0.65 24.35 23.77 3.91 0.028

**Table 4:** The formally best matching modes ( $\chi ^2$ test on the residuals from the observed Cii4267 profiles) and the corresponding parameter sets found in the coarse grid for ${\cal P}_1$ . The first two columns give the mode indices, the next five the stellar input parameters radius, temperature, mass, rotation and inclination. The following four show the equilibrium (i.e. non-pulsating) configuration of the rotating model star, while the last three list the corotating period, the $\chi ^2$ , and the peak-to-peak photometric amplitude of the pulsating model. The *lpv* of these Cii4267 and the six modes listed here are shown in Fig. 5
$\ell$	m	$R_{\star, {\rm polar}}$	$T_{\rm eff, polar}$	$M_{\star}$	$v_{\rm rot}$	i				${\cal P}_{\rm rot}$	${\cal P}_{\it nrp,\rm corot}$	$\chi ^2$	$\Delta b$
		[ $R_{\odot}$ ]	[K]	[ $M_{\odot}$ ]	[kms^-1]	$^\circ$	[1.5ex] $\frac{\textstyle{\cal P}_{\rm rot}}{{\textstyle\cal P}_{\rm crit}}$	[1.5ex] $\frac{\textstyle R_{\rm equ}}{{\textstyle R_{\rm pol}}}$	[1.5ex] $\frac{\textstyle T_{\rm eff,equ}}{{\textstyle T_{\rm eff,pol}}}$	[hours]	[hours]		[mag]
1	1	4.4	20000	8.5	320	24.0	0.65	1.16	0.84	19.40	7.43	3.06	0.025
1	-1	5.6	20000	8.5	400	19.0	0.91	1.38	0.59	23.51	24.64	3.12	0.003
2	2	4.0	20000	8.5	400	19.0	0.77	1.25	0.76	15.14	20.41	3.13	0.013
2	-1	4.8	20000	7.0	400	19.0	0.93	1.40	0.56	20.47	29.18	3.20	0.055
3	2	4.0	24000	8.5	400	19.0	0.77	1.25	0.76	15.14	20.41	3.36	0.004
3	-1	6.0	20000	10.0	400	19.0	0.87	1.34	0.65	24.35	23.77	3.91	0.028

4.2.2 Intrinsic line profiles

Besides the absolute flux, ATLAS9 also gives the atmospheric structure needed as an input to model the intrinsic line profiles. For spectral synthesis the BHT LTE code by Baschek et al. (1966) was used. This code is able to use approaches different for Hei lines than for metal lines, as it computes the Hei profiles following specialized theories (Barnard et al. 1974; Gieske & Griem 1969). Because of the spectral peculiarities, especially of the Hei triplet lines, their intrinsic profile can differ significantly from a Gaussian or Lorentzian. Due to an accidental omission, this special treatment was not included in the computations for Hei4009, although the shape of this line also differs strongly from a Gaussian, like, e.g. Hei4026. The effect of this inaccurate treatment is displayed in Fig. 7. Unfortunately this was discovered only after the, extremely time-consuming, grid computations were completed.

For each of the selected atmosphere models above, a synthetic spectrum was calculated that included in total 5967 spectral lines of Hi, Hei, Cii, Nii, Oi, Oii, Nei, Mgii, Aliii, Siii, Siiii, Sii, Caii Feii, and Feiii from 3900 Å to 6700 Å. The microturbulence for the BHT calculations was set to 2 kms^-1. These synthetical spectra form the grid of input profiles, on which the spectroscopic modeling was based. This model grid is available from TR on request.

$\begin{figure} \includegraphics[width=18cm,clip]{10561f5.eps} \end{figure}$

Figure 5: Comparison of Cii4267 data to the best matching modes taken from the coarse grid (Table 4). We show the residuals only, as the variations are at a level of $\approx$ 1%, while the line itself has a depth of the order of $\approx$ 10%, which does not give enough contrast of the variations compared to the profiles to be displayed as a grayscale image. Given that sufficient data are available for constructing the mean spectrum, however (in our case more than 400 spectra taken over a number of years), the residuals are defined unambiguously. Although the Cii4267 line was chosen with special regard to symmetry, the stellar variability seen in the data is still not completely symmetric. At the moment, no solid explanation can be given for this

Open with DEXTER

4.3 Photometric modeling

The photometric variations at a given wavelength are computed from the physical properties of the perturbed stellar surface as calculated by BRUCE.

First, the local emerging fluxes are interpolated linearly from the ATLAS9 grid introduced in Sect. 4.2.1 using the local $T_{\rm eff}$ and $\log g$ . Then geometrical projection effects are taken into account, including the perturbations to the projected area due to pulsation, and the individual limb darkening for each surface element is applied. It appears that for g-modes the latter may alter the amplitude of the integrated light variations significantly up to even a total cancellation (Townsend 1997a).

Therefore, the treatment of limb darkening is crucial for obtaining photometric amplitudes. Parameterized linear limb darkening coefficients obtained by least square fits to the values computed by Díaz-Cordovés et al. (1995) for ATLAS9 atmospheres were used. Finally, the contributions from all flux elements are integrated to derive the total flux.

The flux variability was calculated at sixteen phase steps per pulsation cycle and converted into magnitude differences. This was done for the central wavelengths of the standard photometric bands of the Johnson (UBV) and Strömgren (uvby) systems.

4.4 Line profile modeling

The procedure to obtain line profiles is similar, but includes an additional step. For photometry the velocity field is not important, since the photometric passbands are broad compared to the typical velocity offsets and selected to contain no major lines at their limits.

For the lpv on the other hand, the velocity field is the most important. Therefore, after interpolating the intrinsic profile for an individual surface element from the grid described in Sect. 4.2.2, the resulting profile is shifted by the projected velocity in the observer's frame, before continuing as above. The limb darkening coefficient can be strongly variable across a spectral line, reaching even negative values. However, Townsend (1997a) showed that this is of little importance for lpv modeling. Rather than using the approach suitable for the continuum (see Sect. 4.3) the limb darkening was adopted to be constant for line profile synthesis. According to Townsend (1997a) this is an acceptable simplification.

5 Pulsational models vs. observations

5.1 Test method

For each period ( ${\cal P}_1$ and ${\cal P}_5$ ) several pulsation modes were tested (Table 4). For each mode, then, hundreds of different parameter sets were calculated. Therefore, the first evaluation of how the models compare to the data had to be performed automatically. To do so, the observed profiles were phased in eight bins ( $\Delta\phi = 0.125$ ) and the residuals from the averaged line profile were calculated. For the model, which calculates sixteen equally-spaced phase steps ( $\Delta\phi = 0.0625$ ), profiles from odd and even phase steps were merged, and then treated similarly for comparison with the data.

Then, the model residuals were cross-correlated against a fixed reference, namely the extreme blueshifted phase (chosen for the sake of unambiguity) of the observed phase-binned profiles, to derive the phase shift of the model compared to the data. Because this coarse grid, as a first step, was only computed with a fixed amplitude (see also Sect. 5.2), the residuals were normalized to reduce the impact of such an approach, since the $\chi ^2$ technique is very sensitive to amplitude differences. In the following step, the $\chi ^2$ of the model residuals from the observations was calculated for each bin according to the derived phase. The individual $\chi ^2$ values were averaged over all eight bins and the full profile width.

5.2 Coarse modeling grid

The amplitude for this initial modeling was fixed to $A_1=15~{\rm km\,s^{-1}}$ for ${\cal P}_1$ and $A_5=7~{\rm km\,s^{-1}}$ for ${\cal P}_5$ as the maximal physical particle velocity on the stellar surface. This resulted in the variation power of the model differing from the observed one by up to about $\pm50\%$ . However, the characteristics of the variability are relatively stable against amplitude variations. Except for a few special cases discussed below, changing the model amplitude only scales the model variation power. The normalization of the residuals (Sect. 5.1) is therefore justified and leads to reliable results.

For the parameter range given in Table 3, all twelve modes with $\ell\le3$ and $m\ne0$ were calculated for ${\cal P}_1$ . The zonal modes (m=0) were excluded, since their variability pattern would not show phase propagation, due to their axisymmetry. Modes with $\ell\ge4$ are not expected to have corotating periods within the possible range, giving an observed period of twelve hours.

Of the modes calculated, most retrograde modes could safely be excluded after brief inspection. This is because the stellar rotation is not fast enough in these cases to make the variability look prograde to the observer. The ( $\ell=1, m=+1$ ) mode, however, is an exception, as it was formally the best candidate mode (Table 4), and the ( $\ell =2,m=+2$ ) mode was found to actually appear prograde to an observer, due to rotation. The ( $\ell=3, m=-3$ ) mode resulted in either a single or a triple-peaked power distribution, while the observed variability of ${\cal P}_1$ appears as double-peaked, so this mode was excluded. Similarly, the ( $\ell=2, m=-2$ ) mode showed significant mis-matches in the power distribution.

All parameter sets with slow rotation ( $v_{\rm rot} < 320$ kms^-1) were significantly poorer at reproducing the observations than the fast ones. Also, in all cases, the lower inclination for a given $v_{\rm rot}$ had a lower $\chi ^2$ , indicating that the $v_{\rm rot} \sin i$ is closer to 130 kms^-1 than to 160 kms^-1. This is supported by visual inspection of the data, since the profiles modeled with $v_{\rm rot}\sin i =130$ kms^-1 are only slightly narrower than the observed ones, while for the ones with $v_{\rm rot}\sin i=160$ kms^-1the difference is larger.

Modeling of the variability attributed to ${\cal P}_5$ leads to very similar constraints, i.e. that the lower $v \sin i$ gives better agreement between models and observations, and that a very high rotational velocity in connection with mostly small radii will result in a better model reproduction of the variability. Therefore, at this stage, modeling ${\cal P}_5$ is not useful in constraining further the best parameter set. On the other hand, the best models found for ${\cal P}_1$ are in the same region of the parameter space as the best models for ${\cal P}_5$ . This can be understood as an indication that the stellar model parameters are sound.

5.3 Determining the pulsation mode

One parameter set takes on average nine minutes on a PIII 500 MHz processor running LINUX. This time includes an automated initial analysis to obtain figures like Figs. 3 and 5 that can be compared to the data. For the coarse grid, about 16000 models were computed for ${\cal P}_1$ and ${\cal P}_5$ on a double processor system, taking about $1\frac{1}{2}$ months of pure computing time (the "impossible'' parameter sets as defined in the last paragraph of Sect. 4.1 were excluded beforehand). Given the time-expensive computations, we attempted to narrow down further the number of possible modes from Table 4.

As Fig. 5 shows, the $\chi ^2$ method is a good measure for judging the general quality of a model. However, it misses significant details, that are as important in the modeling as the overall quality of fits, e.g. points 4 to 6 at the end of Sect. 5.1.

5.3.1 Modes with $\mathsf{{\mathsfsl m}=-1}$

The ( $\ell=1,m=-1$ ) mode does not show as pronounced blue-to-red propagation across the whole line profile as the observational data. Instead there is almost no variability in the center of the line. It turned out that modes with the same m, but different l, spectroscopically do not appear different from each other in principle, but do in the details. The ( $\ell=2,m=-1$ ) and ( $\ell=3,m=-1$ ) modes show increasing differences in the behaviour of the line wings. The ( $\ell=2,m=-1$ ) mode, which spectroscopically looks like the most acceptable candidate among the m=-1 modes, has an associated photometric peak-to-peak amplitude of 0.05mag (Table 4), which is unacceptably high. In general, the m=-1 modes reproduce the data at a gross level, but not in detail (Fig. 5).

5.3.2 The ( $\mathsf{\ell=1,{\mathsfsl m}=+1}$ ) mode

5.3.3 Modes with $\mathsf{{\mathsfsl m}=+2}$

The two modes with m=+2 look quite similar, except that the variability is generally concentrated more towards the outer line wings for $\ell=3$ .

The variability outside the limits of the projected rotational velocity is clearly reproduced by these modes. Also, both modes show a retrograde feature. Finally, if the amplitude of the m=+2 modes are increased, they start forming spikes and ramps, just as in the observed profiles, during times of beating of ${\cal P}_1$ to ${\cal P}_4$ , i.e. high constructive amplitude. The formation of these features is due to the same effect as in $\omega$ CMa, where also an ( $\ell =2,m=+2$ ) mode is thought to be present (Maintz et al. 2000, their Fig. 2).

The pulsational properties of both modes differ in so far as an $\ell=3$ mode with the same co-rotationg period requires higher temperature perturbations than an $\ell=2$ mode. Although the photometric variability is small in both cases, this is mostly due to the low inclination. Already the ( $\ell =2,m=+2$ ) mode requires several thousand Kelvin variability at the equator with the parameters derived from the coarse grid. Even though these extreme variations are concentrated to a very small region around the equator only, we prefer the mode requiring the less extreme values, ( $\ell =2,m=+2$ ), mainly because the resulting non-linearity for ( $\ell=3,m=+2$ ) would be too strong to be readily believed. The final solution given below needs less extreme variations, but the argument in favour of ( $\ell =2,m=+2$ ) remains unchanged.

5.4 Fine modeling grid

For this latter mode, models for about a thousand additional stellar parameter sets were computed with a finer mesh in parameter space to obtain the most accurate match and an estimate of the errors. Since the best matching model for the ( $\ell =2,m=+2$ ) mode was located at the edge of the coarse grid, the explored parameter space was extended to smaller radii and higher rotational velocities. On the other hand, the temperature, which was found to play a minor rôle only, was fixed at 23000 K. For the pulsational amplitude, three values were allowed. All parameter values are compiled in Table 5.

Table 5: Adopted stellar parameter ranges for the fine grid to model the ( $\ell =2,m=+2$ ) mode
Parameter Range

Radius, $R_{\star, {\rm polar}}$ [ $R_{\odot}$ ] 3.0 $\dots$ 4.6, step 0.2

Temperature, $T_{\rm eff, polar}$ [kK] 23

Mass, $M_{\star}$ [ $M_{\odot}$ ] 8.5, 9.0, 9.5

Equ. rotation, $v_{\rm rot}$ [kms^-1] 340 $\dots$ 500, step 20

$v_{\rm rot} \sin i$ to compute i [kms^-1] 134, 138, 142

Amplitude A [kms^-1] 10, 13, 16

**Table 5:** Adopted stellar parameter ranges for the fine grid to model the ( $\ell =2,m=+2$ ) mode
Parameter		Range
Radius, $R_{\star, {\rm polar}}$	[ $R_{\odot}$ ]	3.0 $\dots$ 4.6, step 0.2
Temperature, $T_{\rm eff, polar}$	[kK]	23
Mass, $M_{\star}$	[ $M_{\odot}$ ]	8.5, 9.0, 9.5
Equ. rotation, $v_{\rm rot}$	[kms^-1]	340 $\dots$ 500, step 20
$v_{\rm rot} \sin i$ to compute i	[kms^-1]	134, 138, 142
Amplitude A	[kms^-1]	10, 13, 16

It turned out that the parameters are not independent. The model properties are somewhat degenerated in the critical rotation fraction $w = v_{\rm rot}/v_{\rm crit}$ . All models with $w\approx0.77$ are similarly good. Therefore increasing $v_{\rm rot}$ while lowering the inclination i will give a comparable match if also a lower radius and/or a higher mass is adopted. Because the degeneracy is not complete, this works only to within some limits, however.

In Fig. 6 the $\chi ^2$ for all models computed for the fine grid is plotted against the different stellar parameters varied. The final parameter set is given in Table 6. The minimum obtained $\chi ^2$ was 2.73, while the overall minimum for the coarse grid was only 3.13 for this mode ( $\ell=2,m=2$ ), and 3.06 for ( $\ell=1,m=1$ ).

Since the models for ${\cal P}_5$ are not decisive in terms of stellar parameters, one model was calculated for each mode with the stellar parameters found by modeling ${\cal P}_1$ . The ( $\ell =3,m=+3$ ) mode was found to match the observations better than any other mode for ${\cal P}_5$ .

Figures 8 and 9 show the model calculations for ${\cal P}_1$ and ${\cal P}_5$ and five different spectral lines, respectively.

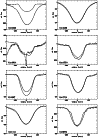$\begin{figure} \par\parbox{4.4cm}{ \psfig{figure=10561_7a.ps,width=4.35cm,angle... ...4cm}{ \psfig{figure=10561_7h.ps,width=4.35cm,angle=270,clip=t} }\end{figure}$

Figure 7: Comparison of the observed average line profiles in the low emission state of 1999 (cf. Fig. 1) to the average profiles derived from the final model for ${\cal P}_1$ shown in Fig. 8. To give an impression of the degree of inaccuracy introduced by using Gaussians, we show also the Hei4009 line, which was computed with this approximation and standard LTE techniques instead of a specialized theory (Sect. 4.2.2). The Caii3934 line is disturbed by a sharp interstellar component and an unmodeled line on the blue side, while the blend on the red side due to Hei3936 is modeled. The discrepancy in strength for Cii4267 is a well known problem of LTE modeling. The additional circumstellar emission in Hei5876 is clearly visible. In addition, but not shown, the lines of Mgii4481 and Hei 4121, 4388, 4471, 4922, and 6678 were modeled with similar agreement. While the profiles are reproduced reasonably well with the stellar parameters in Table 6, the systemic velocity of the star is inconsistent for a few lines. While the models for most lines have not been shifted at all, for Hei4144 and Hei5876 a shift by +20 kms^-1 is needed to match the observations. After ensuring that this is not a systematic effect of data reduction (it is present in all seasons and different instruments) or synthetic modeling (checking the rest wavelengths in the model input file), there is currently no explanation for this shift

Open with DEXTER

$\begin{figure} \includegraphics[width=18cm,clip]{10561f8.eps} \end{figure}$

Figure 8: Comparison of the observational data for five spectral lines to the final model for ${\cal P}_1$ ( $\ell =2,m=+2$ ). The grayscales are the same for the data and model of each line (but may differ from line to line) to allow an estimate of the accuracy of the model amplitude. It suits the data well, with the exception of Hei5876. This line can be strongly affected by photospheric NLTE effects, but also by circumstellar emission. The asymmetric variability, like in Hei4144 could not be reproduced by the model

Open with DEXTER

Table 6: Characteristics of the final multiperiodic model. For the input parameters the estimated uncertainties are given. The circular phases refer to ${\rm MJD}=50\,000$ . For a discussion of the table see Sect. 8
Stellar model

$R_{\rm pole}$ $(3.4\pm.3)$ $R_{\odot}$ $R_{\rm equ}$ 4.21 $R_{\odot}$

$\log g_{\rm pole}$ 4.33 $\log g_{\rm equ}$ 3.86

$T_{\rm pole}$ $(23\pm2)$ kK $T_{\rm equ}$ 17.6kK

M $(9.0\pm1.0)$ $M_{\odot}$ $v_{\rm rot}$ $(440\pm40)$ kms^-1

i $(19\pm3)^\circ$ $v_{\rm rot} \sin i$ 143 kms^-1

${\cal P}_{\rm rot}$ $11\hbox{$.\!\!^{\rm h}$ }615$ $v_{\rm rot}/v_{\rm crit}$ 0.759

$R_{\rm eq}/R_{\rm crit}$ 0.825

$T_{\rm eff, spherical}$ 19.77kK $\log L_{\rm true}$ 3.32 $L_\odot$

$T_{\rm eff, app}$ 20.76kK $\log L_{\rm app}$ 3.46 $L_\odot$

**Table 6:** Characteristics of the final multiperiodic model. For the input parameters the estimated uncertainties are given. The circular phases refer to ${\rm MJD}=50\,000$ . For a discussion of the table see Sect. 8
Stellar model
$R_{\rm pole}$	$(3.4\pm.3)$ $R_{\odot}$	$R_{\rm equ}$	4.21 $R_{\odot}$
$\log g_{\rm pole}$	4.33	$\log g_{\rm equ}$	3.86
$T_{\rm pole}$	$(23\pm2)$ kK	$T_{\rm equ}$	17.6kK
M	$(9.0\pm1.0)$ $M_{\odot}$	$v_{\rm rot}$	$(440\pm40)$ kms^-1
i	$(19\pm3)^\circ$	$v_{\rm rot} \sin i$	143 kms^-1
${\cal P}_{\rm rot}$	$11\hbox{$.\!\!^{\rm h}$ }615$	$v_{\rm rot}/v_{\rm crit}$	0.759
$R_{\rm eq}/R_{\rm crit}$	0.825
$T_{\rm eff, spherical}$	19.77kK	$\log L_{\rm true}$	3.32 $L_\odot$
$T_{\rm eff, app}$	20.76kK	$\log L_{\rm app}$	3.46 $L_\odot$

${\cal P}_1$ parameters ${\cal P}_2$ parameters

$\ell=2\hspace{10mm} m=+2$ $\ell=2\hspace{10mm} m=+2$

${\cal P}_{\rm obs}$ $-12\hbox{$.\!\!^{\rm h}$ }0702\pm1$ ${\cal P}_{\rm obs}$ $-12\hbox{$.\!\!^{\rm h}$ }1804\pm2$

${\cal P}_{\rm corot}$ $11\hbox{$.\!\!^{\rm h}$ }193$ ${\cal P}_{\rm corot}$ $11\hbox{$.\!\!^{\rm h}$ }099$

$\phi_0$ $323^\circ$ $\phi_0$ $54^\circ$

A $15\pm2$ kms^-1 A $6\pm2$ kms^-1

k 3.706 k 3.664

${\cal P}_3$ parameters ${\cal P}_4$ parameters

$\ell=2\hspace{10mm} m=+2$ $\ell=2\hspace{10mm} m=+2$

${\cal P}_{\rm obs}$ $-11\hbox{$.\!\!^{\rm h}$ }8686\pm3$ ${\cal P}_{\rm obs}$ $-12\hbox{$.\!\!^{\rm h}$ }3926\pm4$

${\cal P}_{\rm corot}$ $11\hbox{$.\!\!^{\rm h}$ }372$ ${\cal P}_{\rm corot}$ $10\hbox{$.\!\!^{\rm h}$ }929$

$\phi_0$ $233^\circ$ $\phi_0$ $332^\circ$

A $3\pm2$ kms^-1 A $3\pm2$ kms^-1

k 3.825 k 3.533

${\cal P}_5$ parameters ${\cal P}_6$ parameters

$\ell=3\hspace{10mm} m=+3$ $\ell=3\hspace{10mm} m=+3$

${\cal P}_{\rm obs}$ $-6\hbox{$.\!\!^{\rm h}$ }7537\pm1$ ${\cal P}_{\rm obs}$ $-6\hbox{$.\!\!^{\rm h}$ }9920\pm2$

${\cal P}_{\rm corot}$ $9\hbox{$.\!\!^{\rm h}$ }072$ ${\cal P}_{\rm corot}$ $9\hbox{$.\!\!^{\rm h}$ }173$

$\phi_0$ $306^\circ$ $\phi_0$ $153^\circ$

A $6\pm2$ kms^-1 A $3\pm2$ kms^-1

k 2.435 k 2.489

6 Derived stellar and pulsational parameters

6.1 Model parameters

In Sect. 5.1 six conditions were listed which should be fulfilled by a good model. The details of the line profile variability that should be modeled have already been discussed above. In addition, the mean modeled line profiles match the observed ones well (Fig. 7). Considering that the underlying parameters were chosen to model the line profile variations rather than the profiles themselves, the agreement is in fact remarkable.

But are the derived stellar parameters plausible? In particular the radius of $3.4\,R_\odot$ for a $9\,M_\odot$ star, and the rotational velocity of 440 kms^-1, do not seem to be. It is true that 440 kms^-1 is rapid, and even among the equatorially-viewed shell stars it is unusual. For comparison, 48Lib is believed to rotate at 400 kms^-1(Slettebak 1982). However, in terms of the critical fraction $w = v_{\rm rot}/v_{\rm crit}$ , $\mu$ Cen is still an average Be star with w=0.76 (Table 6).

Another interesting effect to take into account is what is understood as luminosity and effective temperature. In Sect. 4.1 the observed luminosity $\log L_{\rm obs} = 3.6$ and effective temperature $T_{\rm eff, obs} = 20\,500$ K are given. Despite the polar temperature of 23000 K, the model of $\mu$ Cen (Table 6) would appear as a star with $\log L_{\rm app} = 3.46$ and $T_{\rm eff, app} = 20\,760$ K, because the observer sees large parts of the hot polar caps face-on and the equatorial regions limb-darkened by bolometric limb-darkening. The stellar disk area seen would correspond to a stellar radius of $R_{\star, {\rm app}} = 4.17\,R_\odot$ due to the flattening, where again a rotational flattened ellipsoid basically is seen from above. The high polar model temperature of 23000 K is, therefore, in full agreement with an observed effective temperature of 20500 K.

The true luminosity in the sense of energy emitted over $4\pi$ steradian is, however, $\log L_{\rm true}= 3.32$ only. This radiation is emitted through a total stellar surface corresponding to a sphere with $3.89\,R_\odot$ , which would then have $T_{\rm eff, spherical} = 19\,770$ K.

The rather small radius is more of a concern. Calibrations, such as that of Balona (1995), give 4.75 to $6.55\,R_\odot$ for a B2IV-V star. The calibration by Harmanec (1988) lists $4.28\,R_\odot$ , $8.62\,M_\odot$ , and 23120 K for a B2V star. The rotational flattening not only increases the equatorial radius, but also shrinks the polar radius by up to 7% (Moujtahid et al. 1999, for critical rotation $R_{\rm equ}/R_{\rm pol} = 1.5$ , but $R_{\rm equ}/R_{\rm norot} = 1.44$ and, therefore, $R_{\rm pol}/R_{\rm norot} = 0.93$ ). This has to be compared to the polar radius of the model $3.4\pm.3\,R_\odot$ . The difference between the calibration values for B2 stars and the model polar radius of $\mu$ Cen is then 15 to 20%. This makes the radius undoubtedly low, but certainly not unbelievable. Theoretical calculations of stellar evolution typically yield smaller radii than calibrations, in a range similar to the one derived here. For instance the models of Claret (1995) give a ZAMS radius of $3.68\,R_\odot$ for a $9\,M_\odot$ star. On the other hand, observational determinations of the radius of $\mu$ Cen as an individual star have to be compared to the apparent radius of $4.17\,R_\odot$ (see above paragraphs), which is larger because we see the rotationally flattened star almost pole-on. This is still smaller than what e.g. Harmanec (2000) derived, namely $5.28\pm.07\,R_\odot$ . However, such deteminations face a number of problems. $\mu$ Cen is a member of the Sco OB2_2 OB association (Upper Cen Lup, UCL). Nevertheless, since UCL is very extended, the mean cluster parallax is not a good approximation of the distance to $\mu$ Cen. Additionally, recent results by de Bruijne (1999) indicate that $\mu$ Cen is closer to the Earth than indicated by HIPPARCOS ( $\pi=7.10\pm0.38$ mas instead of $6.19\pm0.71$ mas). Finally, the assumption that the bolometric correction (B.C.) is a function of $T_{\rm eff}$ only, is not valid for rapidly rotating stars (e.g. Pérez Hernández et al. 1999). Instead, not only the temperature (see above), but also the B.C. is a function of $T_{\rm pole}$ , w, and inclination. While we do not attempt to derive a final conclusion here, the above discussion shows that our model of $\mu$ Cen cannot be rejected on the basis of existing stellar parameter studies.

6.2 Phase propagation vs. $\mathsf{\ell}$ and m

Telting & Schrijvers (1997) found that modes with the same $\ell$ look similar, while in our study this is the case for the same m (Fig. 5). However, the study by Telting et al. gave this result with greater confidence for modes with higher $\ell$ than studied here, and while the present models are for g-modes, they investigated p-modes. Following their Figs. 3 to 8, the relation between $\ell$ and $\Delta\phi$ becomes less tight with low inclination and high k, both of which is the case for the present models. Moreover, with decreasing inclination they find that the phase propagation of a feature across the full profile $\Delta\phi\propto m$ rather than $\Delta\phi\propto\ell$ as for higher inclination. Therefore, our results are not contradictory with their findings.

7 Testing the results

The final criterion is if the actually observed line profiles and line profile variability can be reproduced by the model. A variety of tests were performed to compare the model to our own data, but also to results published by other investigators.

7.1 Parameters derived from observations and model

We started with the observed radial velocity amplitude as a guess for the maximum physical velocities of each mode. However, these quantities lack physical meaning, and a cross-check against the corresponding quantities predicted by the model is required.

To do this, the expected line profiles for more than 400 HEROS observations were computed and re-analyzed in the same way as the originally observed data. The periods and phases derived from all HEROS data (Table 6; Paper II) were used, the circular phases are given for ${\rm MJD}=50\,000.0$ , which is ${\rm JD}-\,2\,450\,000.5$ . Within the limits of the time-series analysis discussed in Paper II, the analysis of the model-reconstructed dataset gave the same results as the orginal data for periods and phases. However, it proved that the variability is better reproduced with somewhat different amplitudes than derived from the radial velocity variations.

Model parameters of all modes and of the star are given in Table 6. The amplitude given is the maximum physical velocity due to that mode, $\vert v\vert _{\rm max}$ , regardless of direction.

Another result was that the huge asymmetries in the power distribution are not a sampling effect or otherwise an artifact of the analysis method. The analysis results for any mode in the multimode model are somewhat different from the corresponding single-mode model, but only at the level of a few percent. The main reason is probably that the sampling for the multimode model was the same as for the data, while for the single mode check-models only one cycle each was calculated with 16 model profiles.

7.2 Re-analysis of Si III4553 using the enlarged observational database

An interesting point in the re-analysis is the behaviour of the Siiii4553 line. The low observed variation power in this line, especially in its center, is reproduced by the model (Figs. 8 and 9, leftmost panels). Since the velocity field is the same, affecting all spectral lines equally, all differences produced by the model are consequences of the properties of individual spectral lines, such as the intrinsic line profiles and the dependence on $\log g$ and $T_{\rm eff}$ .

Since, in the investigated sample of species, Siiii4553 is the line with the steepest gradient in equivalent width towards higher temperatures, the suppressed power is probably to be attributed to gravity darkening. This line is formed at more polar latitudes than the other lines investigated.

The modeled pulsational modes, g-modes, have comparably high horizontal velocity components. As $\mu$ Cen is seen at high inclination, the radial velocity field and the longitudinal ( $\phi$ )-component of the horizontal velocity field, both being highest in equatorial regions, are projected with $\sin i \approx 0.3$ on the observer's line of sight.

On the other hand, the latitudinal ( $\theta$ )-component of the horizontal velocity field, being high at intermediate to high latitudes, is projected with $\cos i \approx 0.9$ . This will cause the Siiii line, formed at higher latitudes, to show variability caused by the $\theta$ -component of the velocity field enhanced compared to the two other components. The $\theta$ -component affects strongest the line wings. This may sound surprising, but Maintz et al. (2000) have already presented arguments why this is so for pole-on geometries and high horizontal velocity fields. Therefore the variation in appearance of the Siiii lines, at first sight not compatible with an nrp interpretation, actually confirms nrp in a detailed modeling.

$\begin{figure} \includegraphics[width=18cm,clip]{10561f10.eps} \end{figure}$

Figure 10: CAT data of Hei6678 taken during five nights in April 1987 (left) and the modeled lpv (right). Additionally, the modeled pattern is computed with a time shift of -0.15 day (middle left), which was found to give a better match than the unshifted model. Given that the major part of the data for the period analysis dates from 1995 to 1997, however, this is within the uncertainties of the six contributing periods and phases. The relative strengths of the ridges and valleys in the flux residuals differ somewhat between observation and model (see the traveling narrow features observed on MJD46898 and 46899, or the differing strength of the observed features on MJD46895 and 46902), but in principle observed features are reproduced by the multiperiodic nrp-model. The variations at velocities higher than $\pm v \sin i\approx140$ kms^-1 and the presence of backward (right-to-left) traveling bumps in both observations and model are the most striking features reproduced. The middle right panel shows also the shifted model computations, but performed with the most recent version of BRUCE to demonstrate the robustness of our results against the improvements and bug-fixes in the model code (Sect. 7.7)

Open with DEXTER

7.3 Detailed modeling

7.3.1 Baade's 1987 spectra

A more demanding task than to reproduce the observations used for the analysis was to model the Hei6678 variability observed by Baade with the CAT/CES (cf. Paper I). This is so mainly because the data was taken in 1987, almost ten years before the main campaign on $\mu$ Cen started. In Fig. 10 the data are compared to the model. Obviously, the time elapsed had an influence on the accuracy of the phasing. However, the pattern still can be recognized with some shift. The shift is about 0.15 day. The uncertainties of ${\cal P}_1$ over this time can add up to about 0.05 day only, but, however, since this is the best constrained of all six periods, the others will introduce larger shifts. The individual contribution of a single period uncertainty to the overall effect of all six periods cannot be estimated, however, and therefore cannot be used to improve the periods.

A difference that cannot be explained this way is that the retrograde feature apparent in the third panel (above) and the prograde feature in the second panel are much stronger than modeled. However, in the other panels the features are of comparable strength.

Since $\mu$ Cen also shows aperiodic processes in this line, the visibility of these two individual features could have been enhanced by stochastic variability.

7.3.2 The 1999 observation of Balona et al.

Balona et al. (2000) recently cast doubt on the period analysis presented in Paper II. This was already answered by Baade et al. (2000) from the point of view of period analysis. But whether the observations published by Balona et al. (2000), their Fig. 2) can be reproduced by a multimode nrp model still seems a conclusive check. To do so, the dates of observations were extracted from their Fig. 2. Then, the five lines they show were modeled with the parameter values of Table 6, and the variability was co-added. With exactly the same periods and phases as derived from the HEROS data obtained between 1992 and 1997, Balona et al.'s (2000 figures, showing spectra taken in 1999, could be very satisfactorily reproduced. Especially the nightly alternating appearance, used as a major argument against the ${\cal P}_1$ period, is well explained by interference effects (Fig. 11).

Therefore, the nrp model for $\mu$ Cen is complete in the sense that, apart from the already identified asymmetries, the model is able to reproduce the periodic part of the spectroscopic variability for any epoch within the limits imposed by uncertainties of the periods and phases.

7.4 Extreme conditions

In the modeled multimode pulsations, we have looked up the most extreme conditions to have an estimate of the minimum and maximum net variability that occurs at times of low and high constructive interference of all modes, respectively. For instance, in modeling the observations by Balona et al. (2000), carried out at the minimum combined amplitude (Baade et al. 2000, their Fig. 1), a maximal true velocity amplitude on the star of $\vert v\vert _{\rm max}\approx 12$ kms^-1, maximal radial displacement $\vert\Delta R\vert/R\approx 0.002$ , and maximal temperature variation $\vert\Delta T\vert/T\approx 0.08$ is found. This results in a combined photometric peak-to-peak amplitude of about 0.003 mag.

At the other extreme, the modeling of the CAT/CES data taken in 1987 during times of high constructive interference gave $\vert v\vert _{\rm max}\approx 33$ kms^-1, maximal radial displacement $\vert\Delta R\vert/R\approx 0.015$ , and maximal temperature variation $\vert\Delta T\vert/T\approx 0.24$ with 0.015 mag combined photometric peak-to-peak amplitude (still below the assumed detection threshold of 0.02 mag).

However, the latter pulsational configuration exceeds the linearity limits, especially in $v_{\rm rot}$ and T. One may say this is unphysical. But as this is not a stationary configuration that had developed by itself, but rather has been forced by the beating of otherwise linear pulsations, this might in turn even be the instability leading to the bursting ejection of material.

Additionally, although v=33 kms^-1 is greater than the speed of sound (typically $\approx$ 20 kms^-1), this does not necessarily mean that shocks will develop. This is strictly valid only for fully stochastic motions. For ordered motions, it is rather the local velocity shear over some kind of coherency length, that is limited by $v_{\rm sonic}$ . For pulsation, this velocity shear depends strongly on the mode characteristics. The importance of this coherency length becomes clear if one recalls that ordered motions like rotation increase from 0 kms^-1 at the pole to about $20\times v_{\rm sonic}$ at the equator without shocks.

7.5 Periodic high velocity spikes

In Paper II, the presence of phase-locked high velocity spikes, resembling those in $\omega$ CMa was discussed. They seem to be present at times of high combined velocity amplitude only. Results by Maintz et al. (2000) show that the spikes in $\omega$ CMa are a high amplitude phenomenon, occuring because the star is viewed pole on and the pulsation is dominated by horizontal velocities. Since both also hold for $\mu$ Cen, a series of model calculations, taking into account all six modes, was computed for an epoch of high combined amplitude. We have chosen the time of the 1987 CAT observations, shown in Fig. 10 and discussed in Sect. 7.2. The HEROS data are not of sufficient temporal sampling to discuss the spikes in enough detail for modeling (see also Paper II, Sect. 4). However, taking into account also previous observations by Baade (1984), it becomes clear that spikes appear preferrably in lines like Siiii4553 and Mgii4481, but less in Hei6678 and hardly in Hei4471. This is also supported by the 1999 FEROS data, which, like the HEROS data, however, lacks sufficient sampling to follow the spikes. The model reproduces the positions and relative strengths of the spikes well, in addition to the preferred occurence at times of combined high amplitudes (Fig. 12). It does not reproduce, however, the total strength of the spikes. In the actual data, spikes can be much stronger than modeled.

One may argue that since spikes are seen preferrably at times of high amplitude, which are also the times of outbursts, this discrepancy could hold the key to the outburst process. Without additional information, namely a dense series of observations during an outburst, however, this remains speculative.

$\begin{figure} \includegraphics[width=3.5cm,clip]{1056111a.ps}\includegraphics... ...,clip]{1056111c.ps}\includegraphics[width=3.5cm,clip]{1056111d.ps} \end{figure}$

Figure 11: Model of the nrp variability for the observations published by Balona et al. (2000). The same spectral lines as in Balona et al. (2000, Hei4144, 4388, 4471, 4922, 5016) have been co-added for the greyscales. The weak variability seen on the blue side of the greysacles is a consequence of blended lines in the model atmosphere. In the data this variability is probably hidden by the noise. Note that besides the observing date, and which spectral lines were used, no information from the observations was used for the modeling. Different from our other figures time runs downwards to ensure comparability with the plots of Balona et al. (2000)

Open with DEXTER

$\begin{figure} \parbox{18cm}{ \parbox{4.4cm}{% {\ion{He}{i}4471}} \parbox{4.4c... ... \psfig{figure=1056112d.ps,width=4.35cm,angle=270,clip=t} } } \end{figure}$	Figure 12: Modelling of spikes at times of high pulsation amplitude in $\mu$ Cen. The spikes are reproduced at the observed positions, about $\pm 90\dots 100$ kms^-1, and with the observed relative strengths between individual lines, strengthening from Hei4471 to Siiii4553 and Mgii4481, but too weak in general
Open with DEXTER

7.6 Asymmetric power distributions

As the list of Hei lines in Table 2 shows, the asymmetric power distribution for ${\cal P}_1$ is not sensitive to the singlet/triplet nature of individual transitions. For both types, the same asymmetry sequence exists with similar strength. Therefore most NLTE radiation effects can be excluded, as they would produce distinct differences between singlet and triplet lines (Smith et al. 1994,1997, show example mechanisms how NLTE effects change the variability of Hei lines). Similarly, the relatively symmetric appearance of the red Hei lines formed in the outermost regions of the photosphere does not support a circumstellar origin. Another possibility which may lead to asymmetry is non-adiabaticity of the pulsation. This causes a phase shift between velocity and temperature perturbations which could account for such an asymmetry as well. The maximal phase shift found in model calculations by one of us (RT), however, is by far too small to explain such a large asymmetry.

Even if the asymmetry itself is seated in the photosphere, it might be related to the circumstellar material. One hypothesis concerning asymmetries in pulsational line profile variability is based on wave leakage (Townsend 2000a,b,c). In this case the relatively symmetric appearance of the Hei lines at 5876, 6678, and 7065 Å would not be easy to understand. However, since the contributions from photosphere and disk are nearly impossible to disentangle in these lines, it would be premature to exclude wave-leakage for only this reason. A more severe obstacle is that Townsend (2000c), studying low-order modes with radial node numbers n less than $\approx$ 50, found wave-leakage to be negligible for the modes in question here. But if n were increased to higher numbers, wave leakage will become important again (Townsend 2000c).

7.7 Modeling code improvements and bug fixes

After the completion of the main computations for this work, the BRUCE code was improved and a few errors, affecting the computations of the horizontal velocity field, were corrected. In detail, the horizontal velcity fields of modes with $\ell-\vert m\vert>2$ were put to zero instead of the correct values. Due to rotational mixing this also affected modes with $\ell-\vert m\vert\leq2$ .

To ensure the validity of the results obtained with BRUCEv2.71, spot checks were performed by recalculating models with BRUCEv2.84-1 for several parameter sets from the coarse grid. The evidence in favour of an $\ell=2,m=2$ pulsation mode proved to be highly robust, as only details of the lpv changed, but none of the overall characteristics of the resulting model variability.

To check the derived stellar parameters against the model code changes and estimate the effect of the incomplete horizontal velocity field the entire fine grid (Sect. 5.4) was recomputed, which took about another two weeks of CPU time, and the $\chi ^2$ test was repeated. The position of the $\chi ^2$ minimum did not change by more than the parameter step width, i.e. the same parameters as before had the lowest $\chi ^2$ value. The absolute $\chi ^2$ value differs only slightly from the first ones, now being 2.74 instead of 2.73 with version 2.71 of BRUCE.

Finally, the multiperiodic model was recomputed for the CAT/CES run in April 1987 (Sect. 7.2). The results presented in Fig. 10 show that the improvements of the code only result in marginal differences, lower than the noise in the observational data, for the nrp model of $\mu$ Cen.

A significant difference occurred in the temperature and radius variation and, therefore, the photometric amplitude. The amplitudes of all three quantities are lower when computed with v2.84-1 than with v2.71 for the best model of $\mu$ Cen. The new values computed for the CAT/CES 1987 observations are for the maximal radial displacement $\vert\Delta R\vert/R\approx 0.005$ instead of 0.015, for the maximal temperature variation $\vert\Delta T\vert/T\approx 0.20$ instead of 0.24, and the combined photometric peak-to-peak amplitude is 0.010 mag instead of 0.015 mag. None of these changes, however, affect the arguments and reasoning presented in this work.

8 Related objects and phenomena

8.1 Other pulsating stars

As discussed in Sect. 3.1, the pulsations of $\mu$ Cen are likely to be g-modes. Multiperiodic pulsational g-modes are generally accepted to be present in slower rotators, the so-called slowly pulsating B-stars (SPB) (Waelkens 1991; Aerts et al. 1999). Dziembowski et al. (1993) derived as a specific feature of g-mode pulsating B stars that such stars should have more than one mode excited with identical angular indices $\ell$ and m, differing only in radial order n, n being a large ( $\sim$ 20) integer number. Such modes should exhibit periods with a spacing ${\cal P}^{n+1} \approx {\cal P}^{n}/(1-n^{-1})$ .

Comparing $\mu$ Cen to the g-mode instability region, it is a bordercase. Using the parameter values for total luminosity and spherical temperature (Table 6), $\mu$ Cen will pulsate in $\ell=2$ g-modes if the computations are carried out with OP opacities, but remains stable, or may pulsate in p-modes, if OPAL opacities are used (Pamyatnykh 1999, Figs. 3 and 4). However, the co-rotating periods for $\ell=2$ modes are expected to be $1.2\dots2.6$ day for a $9\,M_\odot$ star, while the present modeling gave about 0.5 day.

It is worth recalling that the differences between the four periods of the longer group in $\mu$ Cen are 1.6%-0.8%-1.6% in the corotating frame. This may be explained if they are caused by g-mode pulsation of high radial orders In such a case a mode selection mechanism would have to act to leave at least two modes unexcited, or drive them much more weakly than the near neighbouring ones, which otherwise would be located in the gaps of the double difference.

This might be compared to the SPBs, where Waelkens (1991) found five modes differing by as little as 0.1% and beat periods of several years in HD160124, being the most extreme, but not the only, example. Other SPBs have periods separated by about 1%. It must, however, be kept in mind that most SPB are believed to be slow rotators. It is unclear in what way the excited modes in slow rotators are related to the unstable modes in rapid rotators (Soufi et al. 1998; Lee & Saio 1997,1990a,1987). Especially it is not straightforward that rotation generally stabilizes (or destabilizes) the stellar pulsation, but this seems to depend strongly on the radial structure of the mode under consideration. Ushomirsky & Bildsten (1998) found, that while rotation may stabilize some modes, it destabilizes other ones. This may happen even for modes with the same $\ell$ but different m.

In so far, the lack of long-period instability among early B type stars found by Balona & Dziembowski (1999) for non-rotating models is not conclusive to generally exclude pulsation in the rapidly rotating Be stars.

8.2 Outbursts

The beat-phenomenon within the ${\cal P}_1$ group of periods determines the times of circumstellar outbursts in $\mu$ Cen (Rivinius et al. 1998c,d). Whether this is a direct observation of the Be-phenomenon or merely a triggering effect, without the proper mechanism being exposed, however, remains to be established.

Several mechanisms based on non-radial pulsation have been proposed for mass ejection of Be stars. One of the more appealing, the directed wave breaking suggested by Osaki and rephrased recently (Osaki 1998), relies on angular momentum transfer from inside the star to the surface. This is possible only for prograde modes. However, both in $\mu$ Cen and $\omega$ CMa (Maintz et al. 2000) the nrp modeling strongly favours retrograde modes. Therefore Osaki's (1998) mechanism will not work in these cases.

9 Conclusions and outlook

The nrp model presented for $\mu$ Cen is quantitatively linked to a dense network of inferred parameters entirely unrelated to the nrp hypothesis. This spans a wide range including atmospheric structure, rotational distortion and surface temperature distribution, inclination angle, and global stellar parameters. Therefore, this model is precise and vulnerable to change from new observations - as any good (in this context not to be confused with: correct) model should be.

In spite of the above, even if future work reveals a necessity for some adjustments, key credit to the nrp model comes from the detailed explanation of particular lpv patterns. This includes the well-reproduced level of prominence of such patterns as a function of the predominant range in stellar latitude, at which specific spectral lines are formed, but also spikes and ramps as a result of the interplay between nrp velocity fields and aspect angle.

Since the aspect angle plays such a critical role, a stringent test will it be to "observe'' the present model for $\mu$ Cen (stripped down to the highest-amplitude mode but otherwise entirely unchanged) at different inclination angles and to compare it at each of them with actual observations of a number of other Be stars. This will be the subject of a forthcoming study.

Once stability analyses of stellar pulsations have been sufficiently extended to rapidly rotating B stars, a comparison with the results of empirical nrp modeling should permit a first identification of the pulsational modes. In a next step, involving inferred parameters of the stellar interior, an observational check on stellar evolution calculations might become possible. Also, the evolutionary relation between Be and equally rapidly rotating non-Be stars could be revealed.

With such quantitatively constrained models, the rôle of nonradial pulsation in triggering discrete mass loss events, for which the case of $\mu$ Cen provides strong evidence (Rivinius et al. 1998d), should become clearer. Also the asymmetric power distribution, which seems to be particularly noticeable in high-amplitude modes, calls for continued efforts to better understand the atmopsheric response to the nrp velocity field.

This study has not identified any basic peculiarities that would distinguish $\mu$ Cen from other Be stars. However, its spectral type is B2, and short-periodic spectroscopic and photometric variability are much less commonly observed in later spectral sub-types. Accordingly, $\mu$ Cen cannot be proto-typical of all Be stars. Conversely, general models for the Be phenomenon should not ignore the nonradial pulsator nature of at least some Be stars.

$\begin{figure} \par\includegraphics[angle=-90,width=17.5cm,clip]{10561_4.ps} \end{figure}$	Figure 4: Same as Fig. 3, but for ${\cal P}_5$ . The appearance of the variability is discussed in Sect. 3.2
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=8.1cm,clip]{10561_6.ps} \end{figure}$	Figure 6: The distribution of $\chi ^2$ values computed from the fine model grid against the model parameters varied
Open with DEXTER

$\begin{figure} \includegraphics[width=18cm,clip]{10561f9.eps} % \end{figure}$	Figure 9: Like Fig. 8, but for ${\cal P}_5$ ( $\ell =3,m=+3$ ). For Hei5876 the amplitude difference between observation and model is less pronounced. The observed triple peaked power distribution apparent in Fig. 4 is well seen in the models
Open with DEXTER

${\cal P}_1$ parameters		${\cal P}_2$ parameters
$\ell=2\hspace{10mm} m=+2$		$\ell=2\hspace{10mm} m=+2$
${\cal P}_{\rm obs}$	$-12\hbox{$.\!\!^{\rm h}$ }0702\pm1$	${\cal P}_{\rm obs}$	$-12\hbox{$.\!\!^{\rm h}$ }1804\pm2$
${\cal P}_{\rm corot}$	$11\hbox{$.\!\!^{\rm h}$ }193$	${\cal P}_{\rm corot}$	$11\hbox{$.\!\!^{\rm h}$ }099$
$\phi_0$	$323^\circ$	$\phi_0$	$54^\circ$
A	$15\pm2$ kms^-1	A	$6\pm2$ kms^-1
k	3.706	k	3.664
${\cal P}_3$ parameters		${\cal P}_4$ parameters
$\ell=2\hspace{10mm} m=+2$		$\ell=2\hspace{10mm} m=+2$
${\cal P}_{\rm obs}$	$-11\hbox{$.\!\!^{\rm h}$ }8686\pm3$	${\cal P}_{\rm obs}$	$-12\hbox{$.\!\!^{\rm h}$ }3926\pm4$
${\cal P}_{\rm corot}$	$11\hbox{$.\!\!^{\rm h}$ }372$	${\cal P}_{\rm corot}$	$10\hbox{$.\!\!^{\rm h}$ }929$
$\phi_0$	$233^\circ$	$\phi_0$	$332^\circ$
A	$3\pm2$ kms^-1	A	$3\pm2$ kms^-1
k	3.825	k	3.533
${\cal P}_5$ parameters		${\cal P}_6$ parameters
$\ell=3\hspace{10mm} m=+3$		$\ell=3\hspace{10mm} m=+3$
${\cal P}_{\rm obs}$	$-6\hbox{$.\!\!^{\rm h}$ }7537\pm1$	${\cal P}_{\rm obs}$	$-6\hbox{$.\!\!^{\rm h}$ }9920\pm2$
${\cal P}_{\rm corot}$	$9\hbox{$.\!\!^{\rm h}$ }072$	${\cal P}_{\rm corot}$	$9\hbox{$.\!\!^{\rm h}$ }173$
$\phi_0$	$306^\circ$	$\phi_0$	$153^\circ$
A	$6\pm2$ kms^-1	A	$3\pm2$ kms^-1
k	2.435	k	2.489

Stellar and circumstellar activity of the Be star Centauri

III. Multiline nonradial pulsation modeling

2 Observations

2.2 Published photometry

3 Periodic variability properties

3.1 The longer period group, i.e.

3.1.1 Asymmetric power distribution

3.1.2 Periodic variability at

3.2 The shorter period group, i.e.

3.3 Consequences for interpretation and modeling

4 Nonradial pulsation modeling technique

4.1 Grid of stellar parameters computed

4.2 Grid of stellar atmosphere models

4.2.1 Stellar atmosphere structure and continua

4.2.2 Intrinsic line profiles

4.3 Photometric modeling

4.4 Line profile modeling

5 Pulsational models vs. observations

5.1 Test method

5.2 Coarse modeling grid

5.3 Determining the pulsation mode

5.4 Fine modeling grid

6 Derived stellar and pulsational parameters

6.1 Model parameters

7 Testing the results

7.2 Re-analysis of Si III4553 using the enlarged observational database

7.7 Modeling code improvements and bug fixes

8 Related objects and phenomena

9 Conclusions and outlook

Stellar and circumstellar activity of the Be star $\mathsf{\mu}$ Centauri

3.1 The longer period group, i.e. $\mathsfsl{{\cal P}_1}$

3.1.2 Periodic variability at $\mathsfsl{\vert v\vert > v_{\mathsf {rot}}\,sin\,i}$

3.2 The shorter period group, i.e. $\mathsfsl{{\cal P}_5}$