A&A 369, 812-825 (2001)
DOI: 10.1051/0004-6361:20010180

Deep VLT search for globular clusters in NGC 5128: Color-magnitude diagrams and globular cluster luminosity function[*]

M. Rejkuba1,2


1 - European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
2 - Department of Astronomy, P. Universidad Católica, Casilla 306, Santiago 22, Chile

Received 8 November 2000 / Accepted 31 January 2001

Abstract
At the distance of NGC 5128 ( $3.6\pm 0.2$ Mpc) it is possible to resolve globular clusters with high resolution imaging from the ground, thus allowing the globular cluster candidate selection primarily through their morphological properties. I report the discovery of 71 globular clusters in NGC 5128 on VLT UT1+FORS1 images, including the faintest members ($M_V\sim-5$) known to date in this galaxy as well as in 5 previously-known clusters. U- and V-band photometry has been measured for all the candidates and the luminosity function, spanning -10.1<MV<-4.9 and -9.3<MU<-3.3, constructed. These are the deepest globular cluster luminosity functions in an elliptical galaxy determined so far. The Kolmogorov-Smirnov statistics show that the difference between the globular cluster luminosity functions of NGC 5128 and the MW is not larger than the difference between the ones of M 31 and the MW. The (U-V)0 color histogram shows a bimodal distribution. For 23 globular clusters I obtained K-band images with SOFI at the NTT in La Silla. Their positions in the (U-V) vs. (V-K) color-color diagram indicate that they are indeed old globular clusters. Assuming that the globular clusters in NGC 5128 span a similar age range as the ones in the Milky Way and adopting a linear fit between the metallicity and (U-V)0 color, the metal-rich clusters peak at ${\rm [Fe/H]}=-0.6$ dex and the metal-poor ones peak at ${\rm [Fe/H]}=-1.7$ dex.

Key words: galaxies: star clusters - galaxies: formation - galaxies: individual: NGC 5128


1 Introduction

Globular Clusters are among the oldest objects in the Universe. Moreover, they are intrinsically luminous and found around almost all galaxies in which searches have been made. There is growing evidence for globular cluster formation during major star-formation episodes (Schweizer 1997; Larsen & Richtler 1999). This makes them useful tracers of the formation and the evolution of galaxies (Harris 1991,2000; Kissler-Patig et al. 1998; van den Bergh 2000).

The globular cluster luminosity function (GCLF) of a galaxy is the relative number of its globular clusters per luminosity (or magnitude) interval. It is usually unimodal and nearly symmetric with a peak at a characteristic (turn-over) magnitude. Empirically, it was found that turn-over magnitudes for galaxies at the same distance (e.g. in the same galaxy cluster) differ by <0.1, which makes the GCLF a good standard candle (Harris 1991; Jacoby et al.  1992). However, the full calibration of the GCLF is incomplete. The essential problem is that the galaxies at large distances, for which the GCLF method is mostly used, are giant ellipticals in which globular clusters are found in largest numbers and in which there are usually fewer problems with extinction, whilst the primary calibration of the standard candle MV0 rests on the MW and M 31, which are spiral galaxies. In fact, evidence that GCLFs depend on Hubble type and environment has been proposed (Fleming et al. 1995), but the former is probably due to differences in mean metallicity of the globular clusters and the latter was never reliably demonstrated (Kissler-Patig 2000).

There is strong observational evidence that most luminous giant ellipticals have a bimodal globular cluster metallicity distribution (Gebhardt & Kissler-Patig 1999; Kundu 1999). The globular cluster specific frequencies (the number of clusters normalized to the galaxy luminosity; Harris & van den Bergh 1981) are typically higher in ellipticals than in spirals (Harris 1991,2000). To explain the high number of globular clusters and the presence of several populations indicated by the bimodal metallicity distributions, different globular cluster formation mechanisms have been proposed (e.g. Ashman & Zepf 1992; Côté et al. 1998; Forbes et al. 1997). The number, chemical abundance and spatial distribution of a globular cluster system (GCS) put strong constraints on the formation of its parent galaxy.

At the distance of 3.6 Mpc (Soria et al. 1996; Harris et al. 1999) NGC 5128 is the closest giant elliptical galaxy. The first globular cluster in NGC 5128 was discovered by Graham & Phillips (1980). Its brightness was high, with $V=17.2\pm0.1$ mag, which corresponds to MV=-10.6 mag. Subsequent investigation of photographic plates (van den Bergh et al.  1981; Hesser et al.  1984, 1986) revealed a rich GCS in this galaxy. The estimated number of globular clusters in NGC 5128 is $N\sim 1700$ (Harris et al. 1984) compared with $N\sim 150$ for the MW.


 

 
Table 1: Journal of observations
Field $\alpha_{(2000)}$ $\delta_{(2000)}$ Date Telescope & Exposure FILTER Airmass Seeing
# (h min s) ($^\circ$ $\hbox{$^\prime$ }$ $\hbox{$^{\prime\prime}$ }$) dd/mm/yy Instrument (s)     $\hbox{$^{\prime\prime}$ }$

1

 13 26 23.5 -42 52 00 12/Jul./1999 Antu+FORS1 $2\times 900$ U 1.536 0.52
1 13 26 23.5 -42 52 00 12/Jul./1999 Antu+FORS1 $2\times 900$ V 1.768 0.54
2 13 25 24.0 -43 10 00 11/Jul./1999 Antu+FORS1 $2\times 900$ U 1.283 0.53
2 13 25 24.0 -43 10 00 11/Jul./1999 Antu+FORS1 $2\times 900$ V 1.196 0.44
2 13 25 24.0 -43 09 04 20/Feb./2000 NTT+SOFI $45\times 6\times10$ K$_{\rm s}$ 1.055 0.56
1 13 26 48.1 -42 46 00 28/Feb./2000 2.2 m+WFI $3\times 210$ V 1.117 1.00
2 13 26 48.1 -43 16 01 28/Feb./2000 2.2 m+WFI $3\times 210$ V 1.037 0.81
2 13 24 07.6 -43 15 58 29/Feb./2000 2.2 m+WFI $3\times 210$ V 1.057 1.12


On the basis of the near IR colors for a magnitude-limited sample of 12 globular clusters, Frogel (1980,1984) found one third of the sample to be super metal rich (above solar metallicity) and luminous. However, the Washington photometry of 62 spectroscopically confirmed clusters (Harris et al. 1992) as well as a spectrophotometry for 5 clusters (Jablonka et al. 1996) showed less extreme metallicity. Harris et al. (1992) found a large spread in metallicities with a mean of [Fe/H] $_{C-T_1}=-0.8\pm0.2$ dex. They also found evidence for a weak spatial metallicity gradient, but state that the same could be produced by unknown reddening effects. Zepf & Ashman (1993), using the same photometric data, suggest that the metallicity distribution of globular clusters in NGC 5128 is bimodal, with the higher metallicity peak at ${\rm [Fe/H]}=+0.25$ dex, and proposed that this was due to the formation of a second population of globular clusters in a previous merger which created NGC 5128.

Several photometric studies in the inner regions of NGC 5128 have been conducted, with the aim of constraining the dependence of globular cluster metallicity on galactocentric radius and of finding super-metal-rich clusters (Minniti et al. 1996; Holland et al. 1999). These studies suggest the existence of radial gradients and bimodal distribution in globular cluster metallicity. However, their conclusions are limited due to the restricted samples, possible reddening within NGC 5128 that is especially severe in the central parts around the prominent dust lane, and possible contamination by stars within NGC 5128 as well as background galaxies.

In this paper, I present a sample of globular clusters from two fields in the halo of NGC 5128. Deep images combined with the high resolving power of the VLT and the proximity of NGC 5128 allow the identification of globular clusters primarily on the basis of their non-stellar PSF. Constructing the GCLF for a statistically significant number of clusters that span the whole range of magnitudes, I pursue the question of the uniqueness of GCLF in elliptical galaxies.

This paper is organized as follows. The data, the photometric calibrations and completeness tests are described in Sect. 2. In Sect. 3 the color-magnitude diagram for the NGC 5128 globular clusters is compared to the ones of the MW and M 31. The luminosity function is presented in Sect. 4 and the color distribution in Sect. 5. In the latter, the mean abundances are determined for the metal-poor and metal-rich populations. The results are summarized in Sect. 6.

   
2 The data

2.1 Observations and data reduction

I used the VLT Antu (UT1)+FORS1 (FOcal Reducer/low dispersion Spectrograph) to obtain the Bessel U- and V-band photometry of globular clusters and stars in two different fields in NGC 5128. The field of view was $6\hbox{$.\mkern-4mu^\prime$ }8 \times 6\hbox{$.\mkern-4mu^\prime$ }8$ and the pixel scale $0\hbox{$.\!\!^{\prime\prime}$ }2/$pixel. The FORS1 detector is a $2048\times 2048$ CCD with 24 $\mu$m pixels.

Field 1 was centered on the prominent N-E shell $\sim$14$^\prime$ away from the center of the galaxy, while Field 2 was chosen to overlap with Soria et al. (1996) HST observations at a distance of $\sim$9$^\prime$ from the center of the galaxy. Observations were carried out on the 11th and 12th of July 1999 in service mode. Pairs of images of 15 min exposure time were taken per field in each filter. The journal of observations is given in Table 1.

In addition to VLT data, I obtained a 45 min long exposure of Field 2 in $K_{\rm s}$ using SOFI at the New Technology Telescope (NTT) at the ESO/La Silla Observatory. The field of view of SOFI is $4\hbox{$.\mkern-4mu^\prime$ }94 \times 4\hbox{$.\mkern-4mu^\prime$ }94$ and the pixel scale $0\hbox{$.\!\!^{\prime\prime}$ }292/$pixel. This field is smaller than the one of FORS1 and so only about 40% of objects in one field have $K_{\rm s}$-band magnitudes.

Both fields were also observed with the Wide Field Imager (WFI) at the 2.2 m telescope on La Silla. The data from WFI observations are used here to assess the V-band magnitude of some of the brightest cluster candidates that were saturated on V-band FORS1 images. I calibrated the WFI photometry by comparing magnitudes of globular clusters well exposed (but not saturated) on VLT and WFI images in order to determine the zero point of WFI observations.

For optical data (VLT and 2.2 m images), the standard image processing, including the overscan and bias subtraction and the flat-field correction, was performed within the IRAF[*] environment. The pairs of exposures in each filter were registered using the imalign task and averaged to obtain the final images. Cosmic rays were rejected in this process using the crreject algorithm within the imcombine task in IRAF. Bad pixels were masked out.

The standard procedure in reducing infrared (IR) data consists of sky subtraction, flat-field correction, registering and combining the images. Good sky subtraction in a crowded field like that of a galactic halo is particularly important. For that step I used the DIMSUM package (Stanford et al. 1995) within IRAF. In DIMSUM the sky subtraction is made in two passes. In the first one a median sky is computed for each image from 6 temporarily closest frames. The shifts between the sky subtracted frames are then computed and all the images stacked together using a rejection algorithm to remove cosmic rays. An object mask is computed for the coadded image and then shifted back in order to create object masks for the individual frames. In the second pass, the sky subtraction is made using the object masks to avoid overestimation of the sky level. These masks are also used to check that the bright object cores were not removed as cosmic rays in the previous pass. After the mask-pass sky subtraction, the frames are registered with imalign and combined with imcombine task in IRAF.


  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics{10447f1.eps}} } \end{figure} Figure 1: Residual image of a $51\hbox {$^{\prime \prime }$ }\times 51\hbox {$^{\prime \prime }$ }$portion of Field 2. On the left panels the V-band image (top) and its residual image (bottom) and on the right panels the corresponding U-band images are shown. Three globular cluster candidates are circled. The left-most globular cluster is slightly overexposed in the V-band image. Its classification as a globular cluster follows from the U-band residuals
Open with DEXTER

2.2 Cluster identification and photometry

NGC 5128 is close enough that its globular clusters can be distinguished from stars on the basis of their slightly non-stellar appearance on high resolution ground-based images taken in excellent seeing conditions. At the distance of NGC 5128 (3.6 Mpc) a typical MW globular cluster with a mean King core radius of $r_{\rm c}=2.3$ pc had, on the best seeing VLT images, a FWHM of 2.6 pix, which is $\sim$0.4 pix bigger than the stellar FWHM. The excellent seeing, especially on the V-band images of Field 2, allowed me to identify globular cluster candidates with $r_{\rm c}$ as small as 1.7 pc, corresponding to observed FWHM of 2.4 pix (see f2.GC-6 in Table 4), purely on the basis of their non-stellar appearance through the following procedure within IRAF: (i) first the daofind algorithm was run in order to detect all the stars and clusters in the image; (ii) photometry through a 3 pixels aperture was performed on all the objects; (iii) relatively bright, isolated, stellar objects were used to create the PSF, which was then fitted to all the objects, subtracted and the residual images created. DAOPHOT II (Stetson 1987) permits creation of the variable PSF, which was necessary for the U-band images that showed fixed pattern residuals upon subtraction of the non-variable PSF. In order to create a variable PSF I used 35 stars per image.

Because of their slightly larger FWHM and non-stellar PSF, globular clusters were easily detected on residual images created by subtracting the objects fitted with a stellar PSF. This subtraction was performed using the allstar task. Globular cluster residuals were oversubtracted in the center and undersubtracted in the wings (Fig. 1). Images were visually inspected and the residuals in the U- and V-band images compared. This was necessary to discard obvious galaxies from the candidate list.

After visual inspection of the residual images, 50 and 81 objects in Field 1 and 2, respectively, were retained as candidates for globular clusters. Good globular cluster candidates, the ones that have round ring-like residuals, are listed in Table 3. Other extended objects for which the visual distinction was not very clear, some of them being blended stars or round galaxies, but some of which might be globular clusters as well, are listed in Table 4. The Sextractor programme (Bertin & Arnouts 1996) was used to measure precise coordinates, FWHM (fU and fV columns in Tables 3 and  4) and ellipticities ( $\epsilon _V$ and $\epsilon _U$ columns) for these objects.

I performed aperture photometry within IRAF for all the objects. Since the fields were quite crowded, stellar objects had to be removed in order to obtain more precise photometry of globular clusters. To do so, I first subtracted all the stars (this time excluding the globular cluster candidates from the aperture photometry list) from the original images using the allstar task. Aperture photometry of globular cluster candidates was then measured through circular apertures of 16, 20 and 25 pixel radii. In some cases a bright saturated star or another globular cluster candidate was found near the cluster, or the latter was located near the edge of the image and thus only a 3 pix aperture magnitude was used. The 3 pix magnitudes were later extrapolated to 25 pix magnitude values using an aperture correction calculated as a median correction for more isolated globular clusters. The error in magnitude for these clusters is larger and hard to quantify, since the aperture correction depends on the concentration and compactness of the cluster. The positions and magnitudes of globular clusters are presented in Tables 3 and 4. The clusters with magnitudes measured through a smaller aperture and later corrected are flagged with "b'' (near the bright star or another globular cluster) or "e'' (near the edge of the image).


  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics[angle=270]{10447f2.eps}} } \end{figure} Figure 2: Photometric calibration of Landolt (1992) stars during the nights of observations in U and V filters. Left panels: the scatter for the calibration without the color term; right panels: the scatter for the calibration with the color term
Open with DEXTER


  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics[angle=270]{10447f3.eps}} } \end{figure} Figure 3: Photometric calibration of Persson et al. (1998) stars in $K_{\rm s}$ filter
Open with DEXTER

2.3 Photometric calibration

For the photometric calibration of the VLT images, a total of 14 stars in 4 different Landolt (1992) fields, spanning the color range -1.321<(U-V)< 4.162, were observed during the two nights. The following transformations were calculated:

 
$\displaystyle u_{\rm inst}$ = $\displaystyle U - 24.262(\pm0.089 ) + 0.379 (\pm0.068 )*X$  
    $\displaystyle -0.042(\pm0.007)*(U-V)$ (1)


 \begin{displaymath}v_{\rm inst} = V - 27.348 (\pm 0.042) + 0.213 (\pm 0.034)*X \end{displaymath} (2)

where X is the mean airmass of the observations, $u_{\rm inst}$ and $v_{\rm inst}$ are the instrumental magnitudes and U and V magnitudes from the Landolt (1992) catalogue. The one sigma scatter around the mean was 0.031 mag for the U band and 0.023 mag for the V band (Fig. 2 left panel). Adding the color term (U-V) in the transformations slightly reduces the scatter in the V-band to 0.017 mag (Fig. 2 right panel). However, the calibration equation without the color term for the V-band was prefered, since the data in that filter go much deeper and Umagnitudes for some objects could not be measured accurately enough.

SOFI images were calibrated using 6 standards from the Persson et al. (1998) list observed during the night and spanning an airmass range from 1.1 to 3.4. Each standard star was observed at 5 different positions on the IR-array. In this way, a total of 30 independent measurements was obtained. The least square fit (Fig. 3) yielded the following calibration equation:

 \begin{displaymath}k_{\rm s,inst} = K_{\rm s} - 22.34 (\pm 0.01) + 0.058 (\pm 0.007) * X. \end{displaymath} (3)

   
2.4 Completeness

I made completeness tests for detection of stars on the U- and V-band images. Using the IRAF task addstar within the DAOPHOT package I added 400 stars each time to each of the U- and V-band images, all with the same magnitude and uniformly distributed over the whole field, and re-computed the photometry. The completeness and the accuracy of photometry were measured at 0.5 mag bins. The 90% completeness for stellar sources is reached at magnitude 25 in the V-band and 23.5 in U-band. The completeness drops to 50% at $V\sim26$ and $U\sim24.5$. More detailed results of completeness tests will be presented in the forthcoming paper where the stellar photometry of NGC 5128 is analyzed (Rejkuba et al. 2001b).

Globular clusters have larger PSFs than stars, their selection is based mainly on the recognition of a "globular-like'' residual on a subtracted image and thus their identification as such is more subjective. In order to check the completeness level of globular cluster detections, I made similar simulations as for the stars. The fainter globular clusters, that are of interest in simulation, are not resolved and thus I just treat them as stars. To add a correct, typical globular cluster PSF, the best cluster candidates' PSFs were used to create simulated images. In order to investigate the dependence of detection on core radius, simulations with different typical PSFs were made. Two sets of simulations were done using the PSFs of clusters with small core radii, f1.GC-17 and f2.GC-4, to add objects, while in the other two sets much less concentrated clusters f1.GC-10 and f2.GC-36 were used. At each pass 100 clusters were added, distributed uniformly, all with the same magnitude. The completeness of the globular cluster detection was measured for each half magnitude.

The detection depends quite significantly on core radius in the sense that more small $r_{\rm c}$ clusters are lost at the faint end. The incompleteness magnitude is defined as magnitude where more than 50% of the added clusters are not detected as such (they are actually all detected, but their residuals are not recognized as globular cluster-like, because they are lost in noise). It begins in at $V\sim22.7$ mag for clusters like f1.GC-17 and f2.GC-4, but most of the larger clusters, like f1.GC-10 and f2.GC-36, can still be detected at the 90% level at magnitude V=23. The incompleteness for clusters with large $r_{\rm c}$ begins in at magnitude V=23.5. In the simulations, clusters could be detected with magnitudes as faint as V=24. However, at those magnitude limits it is almost impossible to distinguish globular cluster residuals from galaxies.

From the simulations I conclude that clusters fainter than $V\sim23$ mag would probably not be detected. MW clusters corresponding to these magnitudes are Pal 1, Pal 13, Terzan 1, E 3 and AM 4. However, at magnitude V=22.0 ($\sim$2 magnitudes past the GCLF peak) more than 90% of the clusters are detected.


 

 
Table 2: Comparison with the data from literature
ID1 ID2 $B_{\rm pg}$ $V_{\rm pg}$ $V_{\rm Wash}$ $V_{\rm WFI}$ (U-V)
f1.GC-13 C36 19.04 18.24 18.27 18.39 0.91
f1.GC-16 C37 19.24 18.17 18.46 18.47 1.33
f1.GC-23 C38 19.00  $\cdots$   $\cdots$  18.40 1.16
f2.GC-26 C15 19.76 18.62  $\cdots$  18.58 1.40
f2.GC-81 C12 18.82 17.74 17.79 18.01 1.47


   
2.5 Comparison with published data

The most recent studies of the GCS in NGC 5128 (Holland et al. 1999; Alonso & Minniti 1997) have investigated the central regions of the galaxy away from the fields studied here. The only photometry of globular clusters found in common with the data presented here is the photographic plate measurements of five clusters in Hesser et al. (1986, 1984) and the Washington photometry of the three of these 5 clusters in Harris et al. (1992). The clusters in common are C36, C37, C38, C12 and C15 (numbering from Hesser et al. 1984, 1986). While in the Hesser et al. papers only the $\langle B \rangle$ magnitude is given, Harris et al. (1992) report also photographic V-band magnitudes as well as Washington photometry for C12, C36 and C37. In order to compare the Washington photometry with Bessell V magnitudes, I used the transformation equation (Harris et al. 1992): V = T1 + 0.66 (M-T1).

The clusters in common are among the brightest ones and in this study their magnitudes were measured on 2.2 m+WFI images. The comparison between the data from the literature and my measurements is given in Table 2. In Cols. 1 and 2 the identification of the objects in common is given, $B_{\rm pg}$ magnitudes are from Hesser et al. (1984, 1986), $V_{\rm pg}$ and $V_{\rm Wash}$ are photographic magnitudes and the V-band brightness derived from Washington photometry. The last two columns present my measurements. There is a good agreement between the V-band magnitude derived from the Washington photometry and my measurements. The largest difference is for cluster C12 (f2.GC-81), which I measured 0.2 magnitudes fainter, probably due to the vicinity of a bad column on the WFI chip.

 

 
Table 3: Coordinates, photometry, FWHM (fV and fU), ellipticities ( $\epsilon _V$ and $\epsilon _U$) and projected galactocentric distance of globular cluster candidates
name alpha delta V $\sigma_V$ U $\sigma_U$ $K_{\rm s}$ $\sigma_{K{\rm s}}$ fV fU $\epsilon _V$ $\epsilon _U$ R c
  (2000) (2000) mag mag mag mag mag mag pix pix     kpc  
f1.GC-1 13:26:26.32 -42:48:55.8 19.58 0.00 20.49 0.04  $\cdots$   $\cdots$  8.70 7.40 0.21 0.24 17.07  
f1.GC-2 13:26:29.01 -42:49:44.7 20.77 0.03 23.26 0.30  $\cdots$   $\cdots$  4.11 4.34 0.05 0.3 16.79  
f1.GC-3 13:26:26.99 -42:49:50.4 22.41 0.04 24.5: 0.4  $\cdots$   $\cdots$  5.17  $\cdots$  0.11  $\cdots$  16.45 u
f1.GC-4 13:26:28.13 -42:51:29.5 21.02 0.03 24.17 0.31  $\cdots$   $\cdots$  4.09 3.49: 0.04 0.4: 15.41 u, n
f1.GC-5 13:26:33.52 -42:51:00.6 19.52 0.05 21.11 0.03  $\cdots$   $\cdots$  3.32 3.46 0.05 0.04 16.53 b
f1.GC-6 13:26:40.76 -42:50:18.2 21.10 0.10 24.1: 0.4  $\cdots$   $\cdots$  4.23  $\cdots$  0.11  $\cdots$  18.07 u, b, n
f1.GC-7 13:26:21.10 -42:48:41.4 19.59 0.00 21.32 0.04  $\cdots$   $\cdots$  4.61 4.77 0.06 0.09 16.62  
f1.GC-8 13:26:19.88 -42:49:11.5 20.27 0.10 19.44 0.05  $\cdots$   $\cdots$  3.80 3.84 0.15 0.27 16.06 b, n
f1.GC-9 13:26:21.36 -42:49:59.6 20.79 0.01 21.69 0.05  $\cdots$   $\cdots$  3.45 3.63 0.07 0.09 15.60  
f1.GC-10 13:26:14.80 -42:50:09.1 20.80 0.01 21.74 0.09  $\cdots$   $\cdots$  5.07 5.33 0.23 0.32 14.67  
f1.GC-11 13:26:09.76 -42:50:29.9 20.30 0.09 21.47 0.07  $\cdots$   $\cdots$  4.33 4.66 0.03 0.20 13.80 b
f1.GC-12 13:26:08.77 -42:51:28.5 19.70 0.05 21.15 0.07  $\cdots$   $\cdots$  4.30 4.86 0.16 0.14 12.87  
f1.GC-13 13:26:07.80 -42:52:00.3 18.39 0.10 19.30 0.01  $\cdots$   $\cdots$   $\cdots$  3.45  $\cdots$  0.19 12.31 v
f1.GC-14 13:26:09.45 -42:53:17.4 19.93 0.05 20.85 0.02  $\cdots$   $\cdots$  4.01 4.22 0.05 0.21 11.52 b
f1.GC-15 13:26:08.96 -42:53:42.4 19.44 0.01 20.93 0.06  $\cdots$   $\cdots$  4.49 5.32 0.09 0.08 11.14  
f1.GC-16 13:26:10.65 -42:53:42.4 18.47 0.10 19.80 0.02  $\cdots$   $\cdots$   $\cdots$  3.58  $\cdots$  0.19 11.37 v
f1.GC-17 13:26:22.03 -42:53:45.0 19.58 0.01 20.36 0.03  $\cdots$   $\cdots$  3.42 3.49 0.08 0.15 13.02  
f1.GC-18 13:26:22.04 -42:54:25.9 19.67 0.01 20.45 0.04  $\cdots$   $\cdots$  3.44 3.58 0.07 0.15 12.61  
f1.GC-19 13:26:05.27 -42:54:58.1 18.75 0.10 19.52 0.01  $\cdots$   $\cdots$   $\cdots$  3.29  $\cdots$  0.12 9.72 v
f1.GC-20 13:26:05.45 -42:55:22.4 21.51 0.05 23.33 0.10  $\cdots$   $\cdots$  5.52 4.29: 0.06 0.5: 9.47 u, e
f1.GC-21 13:26:10.60 -42:55:00.0 21.65 0.03 23.72 0.28  $\cdots$   $\cdots$  4.16 3.89: 0.07 0.4: 10.48 u
f1.GC-22 13:26:15.95 -42:55:00.5 18.09 0.10 18.95 0.01  $\cdots$   $\cdots$   $\cdots$  3.34  $\cdots$  0.17 11.30 v
f1.GC-23 13:26:23.81 -42:54:00.5 18.40 0.10 19.56 0.01  $\cdots$   $\cdots$   $\cdots$  3.32  $\cdots$  0.17 13.14 v
f1.GC-24 13:26:28.87 -42:52:35.9 19.33 0.00 20.17 0.02  $\cdots$   $\cdots$  3.73 3.84 0.12 0.11 14.8  
f1.GC-34 13:26:09.76 -42:53:16.8 21.27 0.10 23.22 0.30  $\cdots$   $\cdots$  4.45 5.63 0.09 0.32 11.57 b
f1.GC-38 13:26:20.06 -42:55:22.8 21.84 0.10 23.54 0.30  $\cdots$   $\cdots$  5.29 4.49: 0.13 0.46: 11.75 u, e
f2.GC-1 13:25:42.07 -43:12:44.2 23.10 0.07 24.9: 0.4  $\cdots$   $\cdots$  3.79  $\cdots$  0.03  $\cdots$  12.43 u
f2.GC-2 13:25:41.92 -43:10:40.7 19.52 0.10 20.40 0.03  $\cdots$   $\cdots$   $\cdots$  3.61  $\cdots$  0.14 10.33 v
f2.GC-3 13:25:40.82 -43:08:15.1 20.10 0.10 20.62 0.03  $\cdots$   $\cdots$   $\cdots$  3.56  $\cdots$  0.13 7.84 v
f2.GC-4 13:25:40.46 -43:07:16.9 19.77 0.01 21.13 0.06  $\cdots$   $\cdots$  2.81 3.59 0.05 0.08 6.87  
f2.GC-7 13:25:39.04 -43:12:56.7 22.41 0.05 25.8: 0.4  $\cdots$   $\cdots$  3.45  $\cdots$  0.13  $\cdots$  12.53 u, n
f2.GC-8 13:25:38.97 -43:10:40.9 21.55 0.02 23.27 0.14  $\cdots$   $\cdots$  3.62 5.95 0.07 0.08 10.20  
f2.GC-9 13:25:38.10 -43:13:01.2 20.59 0.01 21.66 0.07  $\cdots$   $\cdots$  3.07 4.00 0.06 0.13 12.57  
f2.GC-10 13:25:37.58 -43:12:32.3 23.16 0.10 23.90 0.20  $\cdots$   $\cdots$  3.15 3.68 0.15 0.38 12.06 u
f2.GC-11 13:25:36.65 -43:12:49.9 22.30 0.04 26.0: 0.4  $\cdots$   $\cdots$  3.49  $\cdots$  0.05  $\cdots$  12.34 u, n
f2.GC-13 13:25:35.84 -43:07:27.2 20.96 0.02 22.60 0.10  $\cdots$   $\cdots$  2.66 3.32 0.07 0.13 6.77  
f2.GC-14 13:25:35.82 -43:07:15.3 22.08 0.02 22.70 0.10  $\cdots$   $\cdots$  2.85 4.17 0.06 0.16 6.57  
f2.GC-15 13:25:35.55 -43:08:36.1 20.83 0.01 21.99 0.07 18.29 0.10 2.88 3.72 0.06 0.05 7.94  
f2.GC-17 13:25:34.01 -43:10:44.6 20.48 0.10 21.43 0.05 17.60 0.10 2.73 3.50 0.08 0.05 10.10 b
f2.GC-18 13:25:33.58 -43:07:18.5 21.44 0.04 22.41 0.09 17.96 0.19 2.85 4.02 0.05 0.12 6.54  
f2.GC-20 13:25:33.07 -43:07:00.6 21.26 0.04 22.84 0.04 17.68 0.09 3.18 4.62 0.07 0.18 6.21 b
f2.GC-21 13:25:33.03 -43:09:20.8 20.84 0.01 21.54 0.05 18.18 0.11 2.86 3.70 0.04 0.09 8.63  
f2.GC-22 13:25:32.76 -43:11:51.1 21.13 0.04 25.4: 0.5  $\cdots$   $\cdots$  3.26  $\cdots$  0.05  $\cdots$  11.23 u, n
f2.GC-23 13:25:32.71 -43:07:01.6 18.80 0.10 20.03 0.02 15.60 0.03  $\cdots$  3.50  $\cdots$  0.16 6.22 v, b
f2.GC-24 13:25:32.25 -43:07:16.5 20.12 0.01 20.95 0.04 17.71 0.08 2.83 3.56 0.05 0.08 6.46  
f2.GC-26 13:25:30.35 -43:11:48.4 18.58 0.10 19.98 0.02  $\cdots$   $\cdots$   $\cdots$  3.88  $\cdots$  0.19 11.15 v
f2.GC-28 13:25:30.10 -43:06:54.0 21.49 0.03 22.56 0.16 17.05 0.08 3.49 4.35 0.13 0.08 6.02  
f2.GC-29 13:25:29.68 -43:11:41.7 19.76 0.10 20.62 0.04  $\cdots$   $\cdots$   $\cdots$  3.61  $\cdots$  0.15 11.03 v
f2.GC-31 13:25:29.38 -43:07:41.1 20.66 0.02 21.47 0.08 18.24 0.12 2.97 3.74 0.09 0.13 6.84  
f2.GC-34 13:25:28.06 -43:06:46.3 22.40 0.09 23.12 0.17  $\cdots$   $\cdots$  3.17 3.68 0.02 0.15 5.87  
f2.GC-35 13:25:26.75 -43:09:39.7 19.54 0.00 20.44 0.03 17.00 0.05 3.40 4.01 0.10 0.12 8.90  
f2.GC-36 13:25:26.68 -43:08:52.7 19.72 0.01 20.57 0.03 17.12 0.06 4.50 5.13 0.09 0.08 8.08  
f2.GC-40 13:25:24.32 -43:07:58.5 19.59 0.10 20.58 0.04 16.72 0.04  $\cdots$  3.75  $\cdots$  0.16 7.15 v
f2.GC-41 13:25:22.61 -43:07:37.6 21.43 0.04 23.29 0.19 17.65 0.09 3.85 5.36 0.08 0.16 6.83  
f2.GC-43 13:25:21.26 -43:10:03.0 21.41 0.02 21.78 0.10 17.62 0.12 4.91 5.48 0.12 0.13 9.38  
f2.GC-46 13:25:20.63 -43:06:35.6 20.27 0.20 21.50 0.20  $\cdots$   $\cdots$  3.11 3.73 0.07 0.07 5.83 e
f2.GC-47 13:25:19.90 -43:07:43.5 20.22 0.01 21.78 0.05 16.75 0.04 3.25 4.04 0.05 0.15 7.02  



 
Table 3: continued
name alpha delta V $\sigma_V$ U $\sigma_U$ $K_{\rm s}$ $\sigma_{K{\rm s}}$ fV fU $\epsilon _V$ $\epsilon _U$ R c
  (2000) (2000) mag mag mag mag mag mag pix pix     kpc  
f2.GC-48 13:25:19.42 -43:11:51.0 21.09 0.02 21.63 0.09  $\cdots$   $\cdots$  3.99 4.89 0.21 0.13 11.29  
f2.GC-49 13:25:18.79 -43:07:11.1 22.21 0.23 23.59 0.15 18.88 0.28 5.07  $\cdots$  0.16  $\cdots$  6,52 b, u
f2.GC-50 13:25:18.79 -43:10:53.7 22.61 0.08 24.4: 0.3 18.39 0.11 3.31  $\cdots$  0.06  $\cdots$  10.32 u
f2.GC-52 13:25:17.84 -43:13:21.4 21.94 0.12 22.44 0.08  $\cdots$   $\cdots$  4.45 6.57 0.19 0.31 12.90  
f2.GC-53 13:25:17.28 -43:08:38.6 19.87 0.10 20.69 0.03 16.61 0.08 3.11 3.50 0.07 0.12 8.07 b
f2.GC-54 13:25:16.91 -43:09:27.4 19.48 0.10 20.41 0.03 16.55 0.05  $\cdots$  3.67  $\cdots$  0.10 8.91 v
f2.GC-57 13:25:15.19 -43:08:38.8 20.86 0.02 22.10 0.05 17.58 0.08 2.86 3.72 0.07 0.14 8.18  
f2.GC-59 13:25:13.82 -43:07:32.3 20.61 0.02 22.04 0.11 17.43 0.07 3.09 4.01 0.05 0.08 7.17 b
f2.GC-60 13:25:12.90 -43:06:39.2 20.50 0.05 23.52 0.16  $\cdots$   $\cdots$  2.51 4.30 0.04 0.01 6.39 n
f2.GC-61 13:25:12.85 -43:07:58.9 18.23 0.10 19.64 0.01 15.12 0.02  $\cdots$  3.46  $\cdots$  0.14 7.67 v
f2.GC-63 13:25:12.76 -43:10:42.7 20.75 0.02 22.39 0.19 17.77 0.08 4.45 5.95 0.09 0.19 10.38  
f2.GC-65 13:25:10.39 -43:08:11.1 22.74 0.09 23.73 0.25  $\cdots$   $\cdots$  3.00 5.23: 0.07 0.43: 8.04 u
f2.GC-66 13:25:10.11 -43:06:41.7 21.05 0.02 23.43 0.15  $\cdots$   $\cdots$  2.50 4.79: 0.01 0.20 6.68  
f2.GC-69 13:25:09.07 -43:10:01.4 19.87 0.01 21.23 0.04  $\cdots$   $\cdots$  2.78 3.64 0.10 0.07 9.92  
f2.GC-70 13:25:08.92 -43:08:53.3 20.30 0.01 21.33 0.05  $\cdots$   $\cdots$  3.67 4.51 0.06 0.06 8.83  
f2.GC-71 13:25:08.78 -43:09:09.1 19.42 0.10 20.43 0.03  $\cdots$   $\cdots$   $\cdots$  3.88  $\cdots$  0.12 9.09 v
f2.GC-74 13:25:07.48 -43:12:28.6 20.43 0.01 21.40 0.07  $\cdots$   $\cdots$  2.89 4.18 0.12 0.19 12.44  
f2.GC-75 13:25:07.41 -43:07:34.8 21.83 0.04 23.36 0.17  $\cdots$   $\cdots$  4.10 5.80 0.13 0.40 7.74 u
f2.GC-76 13:25:07.31 -43:08:29.3 20.67 0.01 21.80 0.07  $\cdots$   $\cdots$  3.78 4.28 0.02 0.15 8.58  
f2.GC-79 13:25:05.88 -43:12:02.2 22.70 0.07 23.97 0.37  $\cdots$   $\cdots$  3.19 5.25: 0.11 0.46: 12.11 u
f2.GC-81 13:25:05.70 -43:10:30.2 18.01 0.20 19.48 0.01  $\cdots$   $\cdots$   $\cdots$  3.83  $\cdots$  0.11 10.63 v


comment: b = near bright (saturated) star.
  e = near edge of the field.
  u = marginal or no detection.
  v = object saturated in V; V mag from WFI data.
  n = object does not satisfy all the criteria for globular cluster classification.



   
Table 4: Same as Table 3, but for other extended objects, some of which might well be globular clusters
name alpha delta V $\sigma_V$ U $\sigma_U$ $K_{\rm s}$ $\sigma_{K{\rm s}}$ fV fU $\epsilon _V$ $\epsilon _U$ R c
  (2000) (2000) mag mag mag mag mag mag pix pix     kpc  
f1.GC-25 13:26:28.27 -42:50:03.9 20.43 0.10 19.68 0.10  $\cdots$   $\cdots$  4.65 4.42 0.29 0.32 16.45  
f1.GC-26 13:26:25.48 -42:51:07.5 21.15 0.11 21.23 0.04  $\cdots$   $\cdots$  7.63 9.06 0.39 0.33 15.3  
f1.GC-27 13:26:30.45 -42:52:10.8 18.33 0.10 19.19 0.01  $\cdots$   $\cdots$   $\cdots$  3.62  $\cdots$  0.31 15.3 v
f1.GC-28 13:26:14.46 -42:49:34.1 20.20 0.05 24.13 0.30  $\cdots$   $\cdots$  4.85  $\cdots$  0.18  $\cdots$  15.12 u
f1.GC-29 13:26:07.23 -42:51:38.1 17.09 0.10 18.92 0.01  $\cdots$   $\cdots$   $\cdots$  2.84  $\cdots$  0.11 12.55 v
f1.GC-30 13:26:16.36 -42:54:28.5 21.37 0.02 21.84 0.10  $\cdots$   $\cdots$  6.05 7.33 0.38 0.55 11.69  
f1.GC-31 13:26:17.40 -42:54:14.5 19.24 0.10 19.76 0.02  $\cdots$   $\cdots$   $\cdots$  2.99 0.10  $\cdots$  12.00 v
f1.GC-32 13:26:06.37 -42:53:54.4 20.74 0.04 21.20 0.03  $\cdots$   $\cdots$  2.83 3.26 0.08 0.23 10.64  
f1.GC-33 13:26:04.74 -42:54:00.6 22.90 0.10 22.91 0.20  $\cdots$   $\cdots$  4.53 5.51 0.14 0.38 10.35 u, e
f1.GC-35 13:26:07.81 -42:55:05.6 19.95 0.00 21.19 0.04  $\cdots$   $\cdots$  2.80 3.15 0.08 0.18 10.00  
f1.GC-36 13:26:11.89 -42:54:51.8 16.95 0.10 19.35 0.01  $\cdots$   $\cdots$   $\cdots$  3.10  $\cdots$  0.21 10.76 v
f1.GC-37 13:26:14.14 -42:54:37.6 20.91 0.02 21.09 0.04  $\cdots$   $\cdots$  5.41 6.56 0.25 0.32 11.26  
f1.GC-39 13:26:26.66 -42:55:19.3 17.01 0.10 19.49 0.01  $\cdots$   $\cdots$   $\cdots$  2.93  $\cdots$  0.21 12.88 v
f1.GC-40 13:26:09.63 -42:54:26.2 22.32 0.05 23.22 0.23  $\cdots$   $\cdots$  4.15 4.11 0.11 0.09 10.71  
f1.GC-41 13:26:07.05 -42:52:37.5 17.14 0.10 18.07 0.01  $\cdots$   $\cdots$   $\cdots$  2.98  $\cdots$  0.17 11.72 v
f1.GC-42 13:26:05.18 -42:52:34.0 16.59 0.10 17.94 0.00  $\cdots$   $\cdots$   $\cdots$  3.10  $\cdots$  0.18 11.55 v
f1.GC-43 13:26:06.78 -42:52:43.2 17.62 0.10 18.30 0.01  $\cdots$   $\cdots$   $\cdots$  2.97  $\cdots$  0.15 11.61 v
f1.GC-44 13:26:11.93 -42:53:02.9 18.65 0.10 19.25 0.01  $\cdots$   $\cdots$   $\cdots$  2.94  $\cdots$  0.14 12.03 v
f1.GC-45 13:26:07.65 -42:54:28.3 17.76 0.10 19.16 0.01  $\cdots$   $\cdots$   $\cdots$  3.04  $\cdots$  0.20 10.41 v
f1.GC-46 13:26:07.22 -42:54:20.7 17.43 0.10 18.24 0.00  $\cdots$   $\cdots$   $\cdots$  3.16  $\cdots$  0.22 10.43 v
f1.GC-47 13:26:06.43 -42:54:21.3 18.88 0.10 20.26 0.02  $\cdots$   $\cdots$   $\cdots$  3.10  $\cdots$  0.22 10.32 v
f1.GC-48 13:26:06.19 -42:54:30.3 18.54 0.10 19.25 0.01  $\cdots$   $\cdots$   $\cdots$  3.08  $\cdots$  0.20 10.18 v
f1.GC-49 13:26:10.13 -42:54:56.4 19.89 0.10 21.16 0.05  $\cdots$   $\cdots$   $\cdots$  3.27  $\cdots$  0.22 10.45 v
f1.GC-50 13:26:14.97 -42:55:21.4 17.57 0.10 18.26 0.15  $\cdots$   $\cdots$   $\cdots$  3.08  $\cdots$  0.23 10.94 v
f2.GC-5 13:25:40.13 -43:10:13.3 21.96 0.03 26.3: 0.5  $\cdots$   $\cdots$  4.12  $\cdots$  0.23  $\cdots$  9.78 u
f2.GC-6 13:25:39.11 -43:12:11.6 21.34 0.02 23.11 0.11  $\cdots$   $\cdots$  2.40 3.78 0.04 0.14 11.76  
f2.GC-12 13:25:36.39 -43:08:02.7 21.47 0.07 22.35 0.16  $\cdots$   $\cdots$  4.98 5.32 0.29 0.32 7.40  
f2.GC-16 13:25:34.40 -43:12:04.2 23.58 0.13 23.58 0.21  $\cdots$   $\cdots$  3.95 5.24 0.16 0.46 11.49 u
f2.GC-19 13:25:33.25 -43:10:19.6 22.67 0.06 24.6: 0.5 17.75 0.11 4.01  $\cdots$  0.17  $\cdots$  9.65 u
f2.GC-25 13:25:31.09 -43:10:27.6 21.13 0.02 24.34 0.24 17.00 0.10 3.54 4.01 0.10 0.09 9.75 u
f2.GC-27 13:25:30.30 -43:11:26.6 21.90 0.03 24.04 0.30  $\cdots$   $\cdots$  4.84  $\cdots$  0.09  $\cdots$  10.77 u
f2.GC-30 13:25:29.42 -43:09:21.9 22.36 0.06 24.60 0.26 20.03 0.47 3.58  $\cdots$  0.03  $\cdots$  8.59 u
f2.GC-32 13:25:29.00 -43:12:50.9 22.44 0.05 23.67 0.19  $\cdots$   $\cdots$  6.74 3.40: 0.43 0.39 12.23  
f2.GC-33 13:25:28.26 -43:06:40.0 22.31 0.06 24.71 0.27  $\cdots$   $\cdots$  4.26  $\cdots$  0.04  $\cdots$  5.76 u
f2.GC-37 13:25:24.77 -43:06:54.8 22.36 0.09 24.07 0.26 17.84 0.18 4.36  $\cdots$  0.17  $\cdots$  6.04 u
f2.GC-38 13:25:24.66 -43:11:50.6 21.95 0.03 23.48 0.38  $\cdots$   $\cdots$  4.06 6.91: 0.10 0.49 11.19 u
f2.GC-39 13:25:24.61 -43:08:15.2 22.97 0.11 26.1: 0.6 16.90 0.07 4.16  $\cdots$  0.26  $\cdots$  7.44 u
f2.GC-42 13:25:21.46 -43:11:43.8 20.80 0.20 21.80 0.08  $\cdots$   $\cdots$  6.46 7.17 0.42 0.45 11.12  
f2.GC-44 13:25:21.24 -43:06:57.0 20.70 0.01 24.66 0.32 16.92 0.08 2.42 4.31 0.03 0.21 6.17  
f2.GC-45 13:25:21.03 -43:08:31.9 21.83 0.04 21.98 0.07 18.14 0.08 5.72 5.57 0.29 0.25 7.81  
f2.GC-51 13:25:18.00 -43:06:57.6 22.09 0.05 23.07 0.11 17.86 0.10 4.23 5.19 0.39 0.31 6.33  
f2.GC-55 13:25:16.76 -43:13:13.5 19.38 0.00 21.16 0.05  $\cdots$   $\cdots$  3.65 4.98 0.08 0.26 12.79  
f2.GC-56 13:25:16.72 -43:13:18.4 20.63 0.20 22.19 0.10  $\cdots$   $\cdots$  3.98 5.62 0.26 0.14 12.88  
f2.GC-58 13:25:14.84 -43:11:00.3 22.81 0.09 22.95 0.16 18.22 0.10 4.58 6.75 0.33 0.41 10.58  
f2.GC-62 13:25:12.81 -43:12:00.7 21.51 0.05 25.8: 0.5:  $\cdots$   $\cdots$  5.55  $\cdots$  0.35  $\cdots$  11.70 u
f2.GC-64 13:25:12.17 -43:08:48.7 21.31 0.10 23.43 0.20 17.30 0.09 6.31  $\cdots$  0.15  $\cdots$  8.52 u
f2.GC-67 13:25:09.32 -43:09:58.4 22.88 0.10 23.99 0.12  $\cdots$   $\cdots$  5.15  $\cdots$  0.15  $\cdots$  9.85 u
f2.GC-68 13:25:09.06 -43:13:18.4 20.44 0.01 22.00 0.09  $\cdots$   $\cdots$  7.25 8.77 0.46 0.27 13.19  
f2.GC-72 13:25:08.11 -43:10:37.4 21.00 0.03 21.51 0.07  $\cdots$   $\cdots$  6.21 6.69 0.36 0.19 10.57  
f2.GC-73 13:25:08.03 -43:09:51.8 22.99 0.12 23.88 0.17  $\cdots$   $\cdots$  5.32  $\cdots$  0.16  $\cdots$  9.84 u
f2.GC-77 13:25:06.66 -43:08:57.9 21.16 0.03 23.41 0.19  $\cdots$   $\cdots$  5.73 4.25 0.18 0.29 9.09 u
f2.GC-78 13:25:06.11 -43:06:51.9 22.06 0.05 24.4: 0.5  $\cdots$   $\cdots$  3.39  $\cdots$  0.08  $\cdots$  7.23 u
f2.GC-80 13:25:05.72 -43:06:50.9 20.96 0.02 23.91 0.40  $\cdots$   $\cdots$  2.52 4.51 0.08 0.18 7.26  


comment: b = near bright (saturated) star.
  e = near edge of the field.
  u = marginal or no detection.
  v = object saturated in V; V mag is from WFI data.


   
2.6 Selection of globular clusters

Typical Galactic globular clusters have mean King core radii $r_{\rm c}=2.3\pm3.6$ pc, mean tidal radii $r_{\rm t}=45.1 \pm 32.4$ pc and mean ellipticities $\epsilon = 0.07 \pm 0.01$ (June 1999 update of the Harris 1996 catalogue; White & Shawl 1987).

Holland et al. (1999) used HST WFPC2 data to find globular clusters in the central parts of NGC 5128 and measured their structural parameters. They did not find any significant difference between the MW and NGC 5128 globular clusters' King core radii ($r_{\rm c}$), tidal radii ($r_{\rm t}$) and half-mass radii ($r_{\rm h}$). They also found no trend in $r_{\rm c}$, $r_{\rm t}$ or $r_{\rm h}$ with galactocentric distance, contrary to what one may expect due to stronger tidal forces closer to the galactic center. However, they measured higher mean ellipticities for their globular cluster candidates with respect to the MW globular clusters. Their samples are restricted only to the brighter clusters in NGC 5128, corresponding to the absolute magnitude MV=-6.4. For comparison, the present sample reaches almost 2 magnitudes deeper.

I measured the FWHM and ellipticity for all the objects in Tables 3 and 4 using the Sextractor programme (Bertin & Arnouts 1996). U-band images had variable PSF across the frame and the objects were, in some places, elongated, thus showing higher ellipticity than in the V-band images.

The FWHM vs. ellipticity for all the objects in Fields 1 and 2 is plotted in Fig. 4. The upper panel shows the results obtained from the V-band, the lower panel the ones obtained from the U-band. The vertical line indicates the mean FWHM for stars. The objects from Table 4, some of which might as well be blended stars or galaxies, are plotted as open symbols, while the filled dots were used for objects from Table 3 (i.e. good candidates). Objects that were slightly saturated on the V-band VLT images are shown only in the U-band diagram (lower panel). Due to the poorer seeing conditions during the observations with the 2.2 m telescope, their profiles are more similar to the stellar profiles on the WFI images.


  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics[angle=270]{10447f4.eps}} } \end{figure} Figure 4: FWHM vs. ellipticity: objects retained as good globular cluster candidates after the visual inspection of the residual images of Field 1 and 2 are plotted with filled circles. Empty circles are used for other extended objects
Open with DEXTER

In order to classify an object as a globular cluster all of the following criteria were imposed:

1.
non-stellar PSF that leaves ring-like residuals on subtracted images (Fig. 1);
2.
FWHM> mean stellar FWHM and ellipticity (V)<0.4 (Fig. 4)
3.
0<(U-V)0 < 2.5 (Fig. 6).
The selection of objects with ellipticity measured on the V-band images smaller than 0.4 excludes galaxies from the sample. The color range in the last criterion corresponds to the observed range of the (U-V)0 colors for the MW and M 31 globular clusters. This range does not include the reddest M 31 clusters (Fig. 6) because they were corrected only for the foreground average extinction towards M 31 and thus might still be reddened. The cutoff at (U-V)0=2.5 takes into account the bulk of M 31 clusters around $V_0\sim21$. The objects that did not pass all of the above criteria were flagged with "n'' in Table 3.

   
3 Color-magnitude and color-color diagrams


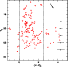  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics{10447f5.eps}} } \end{figure} Figure 5: Color-magnitude diagram for all objects found in Field 1 (diamonds) and in Field 2 (triangles). Objects retained as good globular cluster candidates after the visual inspection of images are plotted as filled symbols and the rest as open ones
Open with DEXTER

The UV color-magnitude diagram (CMD) for all the objects is presented in Fig. 5. As before, the objects retained as good candidates after visual inspection of the images are plotted as filled symbols and the rest as open symbols. The objects from Field 1 are plotted as diamonds, the ones from Field 2 as triangles. Vertical lines indicate the color range within which the MW and majority of M 31 globular clusters are located. Note that several open symbols are found in the same area of the CMD as globular clusters. Spectroscopic observations are necessary to assess the real nature of these objects.

The object at (U-V)0=-0.99 and V0=19.96 (f1.GC-8) is located very close to the area where a large number of bright young blue stars were found (Rejkuba et al. 2001a). It might be a young object, precursor of a globular cluster, similar to the ones found in other merging galaxies (e.g. Whitmore et al. 1999), as well as to some clusters found in the central regions of NGC 5128 (Holland et al. 1999).

There is a number of objects brighter than V<17.5 that were all identified in Field 1. Probably these are bright stars blended with some faint companions. They all appear saturated in the V-band VLT images and were found in the lower right corner (south-west) of Field 1 on U-band images. Their FWHM, that was larger than stellar, is probably an artifact due to the distortion of the PSF in that part of the chip.


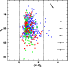  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics{10447f6.eps}} } \end{figure} Figure 6: Color-magnitude diagram for globular clusters in NGC 5128 (filled circles) compared to the MW (stars) and M 31 globular clusters (open squares)
Open with DEXTER

Figure 6 shows the CMD for all NGC 5128 globular clusters (filled circles) that satisfy all the selection criteria. This CMD is compared with the ones of the MW (stars) and M 31 (squares) globular clusters. Globular clusters populate a similar region of the CMD in the three galaxies. Data for the MW clusters were taken from the web page of W. Harris (1996). M 31 clusters are from the catalogue of Barmby et al. (2000). I did not take into account globular clusters with colors bluer than B-V=0.55, as they might be younger objects (Barmby et al. 2000). The magnitudes were corrected for the mean reddening towards M 31 ( E(B-V)=0.08). For the globular cluster candidates in NGC 5128, a mean foreground reddening of E(B-V)=0.1 (Burstein & Heiles 1982; Schlegel et al. 1998) was used. The reddening vector plotted in the upper right corner corresponds to E(B-V)=0.2.

By constraining the colors to be within the range of the reddest MW and bluest M 31 globular cluster colors (cf. the third selection criterion) I exclude distant compact galaxies (Barrientos 2000). The total number of bona fide globular cluster candidates is 71, with 23 in Field 1 and 48 in Field 2. Only those are taken into account in the further analysis.


  \begin{figure} \par\includegraphics[angle=270,width=17.5cm]{10447f7.eps} \end{figure} Figure 7: Color-color diagram for globular clusters in NGC 5128 (filled circles). The lines are the isochrones of SSP models. The number next to each isochrone indicate the age in Gyr. Each isochrone is plotted for a range of metallicities and for a Salpeter IMF. The four different models are from: a) Kurth et al. (1999) for Z=0.0001, 0.0004, 0.008, 0.004, 0.02 and 0.05; b) Bruzual & Charlot (2001) for the same range of age and Zas the previous model; c) Maraston (2001) for ${\rm [Fe/H]}=-2.25$ (only 14 Gyr isochrone), -1.35, -0.55, -0.33, 0.00 and 0.35 dex; and d) Worthey (1994) for Z=0.0002, 0.0004, 0.008, 0.004, 0.02 and 0.05
Open with DEXTER

$K_{\rm s}$ band magnitudes were measured on SOFI images for 23 of the bona fide globular cluster candidates and 10 of the extended objects, some of which might also be globular clusters. The U-V color is strongly dependent on both metallicity and age (Buzzoni 1995; Kurth et al. 1999; Maraston 1998). Adding the K-band magnitude information it is possible to disentangle the young from the old objects. The color-color plot is shown in Fig. 7. Filled dots are used to denote globular cluster candidates that satisfied all of the classification criteria. The lines are isochrones of evolutionary synthesis models of simple stellar populations (SSP) calculated for a Salpeter IMF and a range of metallicities from Z=0.0001 to 0.05 (see caption for the exact metallicities plotted for each model). The four different models displayed on panels (a), (b), (c) and (d) are from Kurth et al. (1999), Bruzual & Charlot (2001), Maraston (2001) and Worthey (1994), respectively. The ages are indicated with numbers denoting Gyr next to the lines. Unfortunately the models do not allow one to discriminate between ages in the range of 5-20 Gyr. However, it is comforting to see that almost all the objects are concentrated towards the isochrones in excess of 1 Gyr. This is additional evidence that they are indeed globular clusters. A spread of metallicities of more than 1.5 dex is also evident.

In Fig. 7 most of the clusters lie slightly to the right and below the model lines. There are two possible explanations. First, a difference with the SSP models, particularly significant in U-V and B-V colors, has already been pointed out by Barmby & Huchra (2000). They suggested U fluxes from the stellar libraries, systematic problems with modeling HB color and observational errors as possible causes of this offset. Second, in the data presented here additional offset may arise from the difference between the Bessel and Johnson U-band transmission curves (Bessel 1995).

   
4 Luminosity function

The V-band GCLF for NGC 5128 is compared to the ones of the MW and M 31 in Fig. 8. The actual shape of the luminosity function depends on the size of the bins and on the bin-centers. Statistically it is possible to compare them independently of binning using the Kolmogorov-Smirnov (KS) test. In Fig. 9 the cumulative distribution functions for the three GCLFs are shown. The thick line is used for NGC 5128, thin line for the MW and dotted line for M 31. Absolute magnitudes for NGC 5128 globular clusters were calculated using the distance modulus value of ( m-M)0=27.8 (Soria et al.  1996) and reddening value of E(B-V)=0.1.

The KS statistic measures the maximum value of the absolute difference between two cumulative distribution functions from which a probability that the two distributions are drawn from a common distribution can be calculated. The probability that the GCLF of NGC 5128 matches the one of the MW is 89%, comparable to the probability that M 31 GCLF matches the MW one (85%). The difference is slightly bigger in the U-band distributions (Fig. 9 right panel), but it is also probable that the three luminosity functions are essentially similar for the three galaxies. I conclude that the NGC 5128 GCLF is as similar (or as different) to the MW GCLF as the M 31 one.


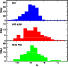  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics{10447f8.eps}} } \end{figure} Figure 8: From top to bottom: V-band GCLF for M 31, NGC 5128 and MW
Open with DEXTER

Usually the GCLF is fitted with a Gaussian or t5 distribution function in order to determine its peak magnitude. It should be noted, however, that the reasonably complete luminosity functions are known only for the two spiral galaxies, the MW and M 31. Both of these GCLFs appear to depart from the Gaussian distribution (Ashman et al. 1995), while there is no complete GCLF for any elliptical galaxy. The dependence of the turn-over magnitude on the detection of the faint end of GCLF is discussed in Ashman et al. (1995). The determination of the turn-over magnitude for NGC 5128 is left for a subsequent paper where the complete analysis of WFI data will to be presented.

The detection of the faint end of the GCLF in an elliptical galaxy is also important from the dynamical point of view. The faint globular clusters are typically also the less massive ones and their presence in the deep potential of a giant elliptical puts strong constraints on the potential itself, as well as on the effects of tidal forces in the halo. Unfortunately, the faintest globular clusters, corresponding to the MW Pal 1, AM 4, Terzan 1 and Pal 13 are probably not detectable on FORS1 images (see Sect. 2.4).

The processes that destroy globular clusters can be divided into internal, such as two-body relaxation and mass loss during stellar evolution, and external. The external processes depend greatly on environment and therefore on the position of the clusters in the galaxy. While tidal shocks preferentially destroy less dense clusters, dynamical friction brings more massive clusters very close to the galactic centre. Both of these external processes are much stronger in the inner part of the galaxy. According to theoretical simulations (Vesperini 2000; Ostriker & Gnedin 1997) in a galaxy like NGC 5128, with the total mass of $\sim$4 1011 $M_\odot$ (Israel 1998) and $R_{\rm e}=5.24$ kpc (Dufour et al. 1979), a strong disruption and mass loss are efficient only within a galactocentric distance of 1-2 $R_{\rm e}$, while at larger radii most of the mass loss is due to effects of stellar evolution. Field 1 is located at 2-3.5 $R_{\rm e}$ and Field 2 at 1.2-2.3 $R_{\rm e}$. While the dynamical effects may still be important for Field 2 clusters, they are probably completely negligible for clusters in the outer field. It is not possible to quantify these effects by simple comparison of the two subsamples, because of the small number statistics.


  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics[angle=270]{10447f9.eps}} } \end{figure} Figure 9: Kolmogorov-Smirnov statistic: the cumulative distribution function for NGC 5128 (thick line) is constructed from the V-band GCLF (left panel) and U-band GCLF (right panel) and compared with the ones of the MW (thin line) and M 31 (dotted line)
Open with DEXTER


  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics[angle=270]{10447f10.eps}} } \end{figure} Figure 10: The color distribution for M 31, NGC 5128 and the MW. The line overplotted on the NGC 5128 histogram is the best nonparametric kernel estimate (Silverman 1986) of the color distribution
Open with DEXTER

   
5 Color and metallicity distributions

The (U-V)0 color histogram for 71 globular clusters in NGC 5128 indicates a bimodal distribution (Fig. 10). Note that the (U-V)0 color distribution of the MW globular clusters does not show bimodality, while the one of M 31 does. The (U-V)0color distribution of the MW globular clusters is in fact biased due to lack of U-magnitude and higher reddening values (only clusters with E(B-V)<0.5 are plotted) of a bulge (more metal-rich and redder) cluster. The blue peaks of the MW, M 31 and NGC 5128 globular cluster color distributions coincide. The blue cutoff in the three galaxies is quite sharp and is driven principally by the colors of blue horizontal branch stars. The red side of the color distribution is much broader. In M 31 it can be partially driven by differential reddening inside the host spiral galaxy, because the colors for M 31 clusters presented here were corrected only for the mean foreground reddening of E(B-V)=0.08. Examination of the stellar (U-V) vs. (V-K) diagram in the two fields in NGC 5128 indicates that the amount of reddening does not vary much in the halo of this giant elliptical (Rejkuba et al. 2001b). Harris et al. (1992) and Holland et al. (1999) also found more red (metal-rich) clusters in their NGC 5128 data.

The color distribution of the MW globular clusters in Fig. 10, being dominated by halo clusters, is representative of the GCS of our Galaxy as if observed from outside. The NGC 5128 clusters in Harris et al. (1992) and in this work belong as well to the halo population. The differences in the color (metallicity) distribution of clusters and stars in the halo of a spiral, like MW and a gE like NGC 5128, are reflected in Fig. 10 with a much larger metallicity spread in the gE galaxy.

The line overplotted on the color distribution of NGC 5128 is the best nonparametric kernel estimate (Silverman 1986) of the color distribution used to measure accurately the blue and the red peaks of the distribution. The blue and red peaks are measured at ( $U-V)_0=0.73\pm0.01$ and $1.28\pm0.01$, respectively.


  \begin{figure} { \resizebox{\hsize}{!}{\includegraphics[angle=270]{10447f11.eps}} } \end{figure} Figure 11: The (U-V)0 vs. [Fe/H] color-metallicity linear relation (full line) derived from the MW globular clusters with E(B-V)<0.5 (stars). The M 31 clusters with spectroscopic metallicities and accurate (U-V) colors plotted for comparison (squares) were not used for the fit. Typical errors in measured metallicities are plotted on in the box. Short dashed lines are the SSP models from Kurth et al. (1999) for ages of 5, 10 and 15 Gyrs, from blue to left, respectively. Each model spans metallicities from Z=0.0001 to 0.05
Open with DEXTER

From the color-color diagram (Fig. 7) it is obvious that the globular clusters in NGC 5128 are older than 1 Gyr. Unfortunately, the models do not allow one to better constrain the ages (Fig. 7; see also Barmby & Huchra 2000). Assuming that the globular clusters in NGC 5128 have similar ages as the MW ones, one can use the Galactic globular clusters to calibrate the metallicity scale. It is known that for the very low and very high metallicities the color-metallicity relation cannot be expressed by a simple linear function, but extrapolation from lower metallicities towards the higher ones by using the higher polynomial fit might lead to unphysical results. Thus I prefered to make a linear fit with Gaussian errors in $\sigma{\rm (Fe/H)}=0.1$ in order to calibrate the metallicity as a function of intrinsic (U-V)0 color. Only MW globular clusters from the W. Harris (1996) web list with E(B-V)<0.5 (equivalent to E(U-V)<0.82; Rieke & Lebofsky 1985) were used in the fit. The following color-metallicity relation is based on the Zinn & West (1984) scale and is valid only for the range of metallicities observed in the MW globular clusters (Fig. 11):

 \begin{displaymath}{\rm [Fe/H]} = -2.93 (\pm 0.07) + 1.79 (\pm 0.07) \times (U-V)_0. \end{displaymath} (4)

In Fig. 11 the linear (U-V)0 vs. [Fe/H] color-metallicity relation (Eq. (4); full line) is plotted along with the evolutionary synthesis models of simple stellar populations (short dashed lines) from Kurth et al. (1999). Using the empirical linear calibration and the SSP models I calculate the metallicity of the two peaks in the color-distribution. The blue and the red peak correspond to ${\rm [Fe/H]}=-1.7$ dex and ${\rm [Fe/H]}=-0.6$ dex using the linear relation (Eq. (4)) and to ${\rm [Fe/H]}=-1.7$ dex and ${\rm [Fe/H]}=-0.5$ dex using the models.

Although it is not obvious from the (U-V)0 color distribution, but rather from the spectroscopically measured [Fe/H] distribution, the metallicity distribution of MW globular clusters is bimodal with the metal-poor and metal-rich peaks at -1.6 and -0.6 dex respectively (Harris 2000). These values are practically the same as the ones derived here for globular clusters in NGC 5128 from the (U-V)0 colors. On the other hand, on the basis of Washington photometry of 62 globular clusters in NGC 5128, Harris et al. (1992) conclude that "in both the range and distribution of abundance, the NGC 5128 GCS is clearly different from the Galactic GCS and quite similar to that of the large elliptical NGC 1399''. They measured a mean metallicity of $\langle{\rm [Fe/H]}_{C-T_1}\rangle=-0.8\pm0.2$ dex, substantially more metal-rich than the mean value for the MW GCS. They, however, mention that the values exceeding ${\rm [Fe/H]}\sim -0.25$ are extrapolated, a fact that is also true in the metallicity calibration from (U-V)0 color distribution. The extrapolation leads to large errors and a possible overestimation of abundances of the metal-rich clusters. Because of this I do not report here the metallicities of individual clusters.

Note also that I restricted the (U-V)0 color to be within the range observed in MW and bulk of the M 31 globular clusters. In this way the sample was selected to be as clean as possible from the very compact and red galaxies. It is not surprising that the clusters with supra-solar abundances are not present, reducing the mean abundance of the sample. However, relaxing the red color cut and adding the 6 "good'' globular cluster candidates redder than ( U-V)0=2.5 (filled symbols in Fig. 5) the mean of the color distribution shifts from $\langle(U-V)_0\rangle=1.05\pm0.45$ to $\langle(U-V)_0\rangle=1.22\pm0.75$, corresponding to mean metallicities of $\langle{\rm [Fe/H]}\rangle=-1.1\pm0.1$ dex and $\langle{\rm [Fe/H]}\rangle=-0.7\pm0.2$ dex, respectively. The latter value is very similar to the mean metallicity derived from Washington photometry by Harris et al. (1992). In order to assess the real nature of the objects redder than ( U-V)0=2.5spectroscopic observations are necessary.

   
6 Conclusions

The main results and their implications presented in this work are the following:

1.
On the basis of high resolution ground-based images, taken with VLT and FORS1, I identified 71 bona fide globular clusters in the halo of the nearest giant elliptical galaxy NGC 5128. Only 5 of these clusters were previously known;

2.
In a UV color-magnitude diagram for the complete sample of 71 clusters and a UVK color-color diagram for a subsample of 23 clusters, the objects span a similar magnitude and color range as the globular clusters in the MW and M 31. Note, however, that there is no cluster corresponding to $\omega$ Cen, the brightest MW cluster, in these two fields. The position of 23 objects in the (U-V)0 vs. (V-K)0color-color diagram is consistent with their classification as old globular clusters;

3.
The GCLFs spanning -10.1<MV<-4.9and -9.3<MU<-3.3 have been constructed. These are the deepest GCLFs of an elliptical galaxy made so far. Kolmogorov-Smirnov statistics show that the difference between the GCLFs of NGC 5128 and MW is not larger than the difference between the GCLFs of M 31 and MW. Similarity of the GCLFs of an elliptical with respect to the spiral galaxy had never before been tested at the faint end;

4.
The presence of faint globular clusters in the halo of NGC 5128 puts constraints on the effectiveness of the tidal forces in the deep elliptical galaxy potential. The dynamical effects may be important for clusters that are found within $\sim$2 $R_{\rm e}$ from the galactic center. Unfortunately, the selection of globular clusters from VLT images is not sensitive to the most compact and the faintest clusters, similar to ones like Pal 1, Pal 13, AM 4 and Terzan 1 in our Galaxy, while the less dense ones start to be confused with background galaxies at faint magnitudes;

5.
The (U-V)0 color histogram of 71 clusters indicates a bimodal distribution, supporting the Zepf & Ashman  (1993) suggestion. Assuming that the clusters in NGC 5128 and in the MW span a similar age interval, and adopting the linear fit between the (U-V)0color and metallicity, I derived the [Fe/H] of the red and blue peaks of the bimodal distribution to be -1.7 dex and -0.6 dex, respectively. Using the SSP models from Kurth et al. (1999), instead of the linear fit, the results do not change significantly, giving values of -1.7 dex and -0.5 dex for the metal-poor and metal-rich peaks, respectively. This is different from the Harris et al. (1992) and Zepf & Ashman (1993) result, but is partially due to the adopted color cut of ( U-V)0<2.5 in selecting globular clusters and to small number statistics, since both samples have <10% of the total cluster population. Relaxing the red color cut, the mean color of the distribution corresponds to a mean metallicity of [Fe/H]=-0.7 dex, very similar to the Harris et al. (1992) result. The true nature of the redder objects has to be assessed through spectroscopy.

Acknowledgements
I am grateful to Dante Minniti for his guidance and help with this project. I thank Andres Meza for providing the code that calculates the kernel estimator. I would like to acknowledge the referee for valuable comments which led to improvements in the paper and useful discussions with Markus Kissler-Patig, Thomas Puzia and Steve Zepf. Thanks also go to Tim Bedding, Dave Silva and Elena Pancino. This research was partially supported by FONDECYT grant No. 1990440.

References

 
Copyright ESO 2001