A&A 369, 1009-1026 (2001)
DOI: 10.1051/0004-6361:20010164
N. Przybilla1,2 - K. Butler1 - S. R. Becker1 - R. P. Kudritzki1,2![]()
1 - Universitäts-Sternwarte München,
Scheinerstraße 1, 81679 München, Germany
2 -
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1,
85740 Garching bei München, Germany
Received 19 September 2000 / Accepted 11 January 2001
Abstract
An extensive model atom for non-LTE line-formation calculations for
neutral and singly-ionized magnesium is presented, taking into account
recent improvements in the atomic data.
As a test and first application of the model, stellar parameters
and magnesium abundances are determined on the basis of
line-blanketed LTE model atmospheres for three stars:
Vega (A0V), ![]() Leo (A0Ib) and HD92207
(A0Iae) using high S/N and high resolution spectra at visual and near-IR
wavelengths. The ionization equilibrium of Mg I/II
proves to be a sensible temperature indicator for early A-type
stars at all luminosities. Evidence is given that in late
A and early F-type supergiants (
Leo (A0Ib) and HD92207
(A0Iae) using high S/N and high resolution spectra at visual and near-IR
wavelengths. The ionization equilibrium of Mg I/II
proves to be a sensible temperature indicator for early A-type
stars at all luminosities. Evidence is given that in late
A and early F-type supergiants (
![]() K) the
determination of accurate
stellar parameters is hampered by the presence of a pressure inversion region
in the model atmospheres at line-formation depths.
The Mg I/II lines in the observations
are reproduced simultaneously by the calculated line profiles with high
accuracy. For Vega spectral synthesis in the UV region of the Mg I/II
resonance lines also proves excellent consistency with the results from the
visual.
The dependence of the non-LTE effects on the atmospheric
parameters is discussed with special emphasis on the supergiants
where a strong radiation field at low particle densities favours
deviations from LTE, especially in the minor ionic species of neutral magnesium.
Non-LTE corrections turn out to be small in Mg I - typically
K) the
determination of accurate
stellar parameters is hampered by the presence of a pressure inversion region
in the model atmospheres at line-formation depths.
The Mg I/II lines in the observations
are reproduced simultaneously by the calculated line profiles with high
accuracy. For Vega spectral synthesis in the UV region of the Mg I/II
resonance lines also proves excellent consistency with the results from the
visual.
The dependence of the non-LTE effects on the atmospheric
parameters is discussed with special emphasis on the supergiants
where a strong radiation field at low particle densities favours
deviations from LTE, especially in the minor ionic species of neutral magnesium.
Non-LTE corrections turn out to be small in Mg I - typically
![]() 0.3 dex - even in supergiants, but are essential for an accurate
effective temperature determination. From the Mg II spectrum, only the
features at
0.3 dex - even in supergiants, but are essential for an accurate
effective temperature determination. From the Mg II spectrum, only the
features at
![]() 4481 and 7877-96 Å react sensitively to
non-LTE effects. Furthermore, the influence of microturbulence on the
statistical-equilibrium calculations is investigated. The line strengths are
found to be systematically affected.
4481 and 7877-96 Å react sensitively to
non-LTE effects. Furthermore, the influence of microturbulence on the
statistical-equilibrium calculations is investigated. The line strengths are
found to be systematically affected.
Key words: atomic data - line: formation - stars: abundances, fundamental parameters, supergiants
In combination with abundances of the
iron peak elements, this offers the opportunity to study the cosmochemical
evolution of a large number of galaxies. The primary source for the
enrichment of ![]() -elements in the interstellar medium are
supernova type II events, while iron peak elements are released
in supernovae of high and low mass stars. Thus, knowledge of abundance
ratios also helps to constrain
the star-formation history. Direct observational evidence for this is
given by the
-elements in the interstellar medium are
supernova type II events, while iron peak elements are released
in supernovae of high and low mass stars. Thus, knowledge of abundance
ratios also helps to constrain
the star-formation history. Direct observational evidence for this is
given by the ![]() -enhancement found in galactic Population II stars
(e.g. Fuhrmann 1998).
-enhancement found in galactic Population II stars
(e.g. Fuhrmann 1998).
The simultaneous presence of magnesium lines of the neutral and singly-ionized species in A and F-type stars also offers the opportunity to determine their effective temperatures from the ionization equilibrium as an alternative to purely photometric or spectrophotometric methods. In combination with the fitting of the line wings of the higher members of the Balmer series, the slight dependence of the ionization equilibrium on surface gravity can be overcome. This purely spectroscopic approach was recently used by Venn (1995, 1999) and Venn et al. (2000,2001) to derive the stellar parameters for galactic and extragalactic (SMC, M 31, NGC6822) supergiants. Here, non-LTE effects influence the ionization balance by overionization of the minor ionic species, Mg I, again an effect most pronounced in supergiants. The studies are based on the non-LTE model atom from Gigas (1988), extensively tested on the main sequence star Vega. Meanwhile, improved line-blanketed model atmospheres have become available (Kurucz 1991) and the accuracy of atomic data has been enhanced enormously due to the efforts of e.g. the Opacity Project (OP; see Seaton et al. 1994, for a general overview). The wealth of available atomic data has been facilitated by the simplicity of the atomic structure, which allows good theoretical modeling. A critical reinvestigation therefore seems appropriate in order to determine the possibilities for improving the accuracy of abundance and stellar parameter determinations.
Several other interesting topics can be investigated by using strong magnesium lines. In the early-type stars, the UV lines are tracers for stellar outflow, with velocity fields altering the line profiles dramatically (e.g. Talavera & Gomez de Castro 1987; Verdugo et al. 1999). Terminal wind velocities for A-type supergiants are preferentially derived from the violet extent of the black absorption troughs of the Mg II resonance lines (Lamers et al. 1995). At later spectral types than studied here, the Mgb lines become a sensitive diagnostic tool for surface gravity determination (e.g. Deeming 1960). Sophisticated model atoms for Mg I find only quite small deviations from LTE in the sun, but these are essential for the interpretation of the infrared Mg I emission features (Carlsson et al. 1992; Zhao et al. 1998). By analogy, Sigut & Lester (1996) predict similar features for Mg II Rydberg transitions in B-type stars.
This paper concentrates on the accurate abundance and stellar temperature determination from observed Mg I/II lines in A-type stars with special emphasis on supergiants. A comprehensive model atom for Mg I/II is presented in the next section, together with a critical examination of the expected uncertainties. The results from our LTE and non-LTE line-formation computations are discussed in Sect. 3. In the following section, the atmospheric parameters and magnesium abundances for a test sample of three stars are determined from high S/N and high resolution spectra. Finally, a short summary is given in Sect. 5.
The application of the model to the determination of stellar parameters and magnesium abundances in extragalactic supergiants (see Herrero et al. 2000, for first results) will be the subject of further investigation. An implementation of the model atom for the hydrodynamic radiative transfer code of Santolaya-Rey et al. (1997) is also intended for a quantitative analysis of the stellar wind dominated Mg II resonance lines of supergiants.
The calculations are performed using the standard assumptions of plane-parallel, homogeneous and stationary stellar atmospheres in hydrostatic and radiative equilibrium. Magnesium is a trace element; in the A star regime its contribution to the overall opacity is negligible. Thus we obtain statistical-equilibrium populations for Mg I/II while keeping the atmospheric parameters fixed.
The non-LTE Mg I/II line profiles are computed on the basis of ATLAS9 (Kurucz 1979, 1991) LTE line-blanketed model atmospheres using LTE Opacity Distribution Functions (ODFs, Kurucz 1992) to account for line blocking in the spectrum synthesis. For the calculation of model atmospheres for the most extreme supergiants close to the Eddington limit, modifications in the treatment of opacities and the radiative pressure in the outermost depth points within ATLAS9 were made in order to achieve convergence. Comparisons at stellar parameters for which standard ATLAS9 converges have shown that the stratification deeper in the atmosphere is only marginally affected by these modifications.
With the assumptions cited above, reliable analyses can be performed in the
given temperature range from main sequence stars through to bright giants, as
indicated by Kudritzki (1988). At spectral types later than
![]() A7V, an outer convection zone becomes increasingly important for the
energy transport through the atmosphere, as the
observation of chromospheres in these stars indicates; see e.g.
Simon & Landsman
(1997) for recent results. Convection is therefore taken into
account in the standard way for ATLAS9
atmospheric models with
A7V, an outer convection zone becomes increasingly important for the
energy transport through the atmosphere, as the
observation of chromospheres in these stars indicates; see e.g.
Simon & Landsman
(1997) for recent results. Convection is therefore taken into
account in the standard way for ATLAS9
atmospheric models with
![]() ,
applying a value
,
applying a value
![]() (mixing length to scale height).
(mixing length to scale height).
At slightly lower temperatures (
![]() K),
hydrostatic model atmospheres for supergiants develop a
pressure inversion layer which eventually extends into the line-formation
region. Here our line-formation calculations are expected to be hampered by
systematic effects on the stellar parameter determination, see Sect.
3.3 for details.
K),
hydrostatic model atmospheres for supergiants develop a
pressure inversion layer which eventually extends into the line-formation
region. Here our line-formation calculations are expected to be hampered by
systematic effects on the stellar parameter determination, see Sect.
3.3 for details.
A thorough discussion of the possible deviations from the standard assumptions on the model atmosphere structure of supergiants is given by Venn (1995). Additionally, non-LTE effects are often less significant for the model structure than is line blanketing, as demonstrated by Przybilla (1997). However, close to the Eddington limit (luminosity classes Iae and Ia+) further studies on this topic are desireable; however, appropriate theoretical models are still unavailable.
The line-formation calculations are performed using the programs
DETAIL and
SURFACE (Giddings 1981; Butler & Giddings 1985),
with the former solving the radiative transfer and the
statistical-equilibrium equations and the latter computing the emergent flux.
Recent
improvements by inclusion of an ALI scheme (using the treatment of Rybicki &
Hummer 1991) allow the utilisation of
quite elaborate model atoms while the necessary computational resources
remain low (typically ![]() 30min CPU time for model convergence
on a PC).
30min CPU time for model convergence
on a PC).
 |
Figure 1: Grotrian diagram for the Mg I singlet system. Displayed are the radiative transitions treated explicitly in the non-LTE calculations |
| Open with DEXTER | |
 |
Figure 2: Grotrian diagram for the Mg I triplet system |
| Open with DEXTER | |
Energy levels up to ![]() 0.2/0.5 eV below the ionization threshold are therefore
explicitly included in our Mg I/II model as listed by Martin &
Zalubas (1980). Missing states at high orbital angular
momentum number
0.2/0.5 eV below the ionization threshold are therefore
explicitly included in our Mg I/II model as listed by Martin &
Zalubas (1980). Missing states at high orbital angular
momentum number ![]() are calculated using a polarization theory (Chang
& Noyes 1983). This includes all energy levels with principal
quantum number
are calculated using a polarization theory (Chang
& Noyes 1983). This includes all energy levels with principal
quantum number ![]() and the 10s and 10p states in Mg I and all levels with
and the 10s and 10p states in Mg I and all levels with ![]() and
and
![]() in Mg II. Only the ground state of Mg III is
considered, as excited levels of Mg III are separated by a large
energy gap of
in Mg II. Only the ground state of Mg III is
considered, as excited levels of Mg III are separated by a large
energy gap of ![]() 53 eV. Fine structure splitting is not taken into account:
sub-levels belonging to the same term are combined into a single level.
53 eV. Fine structure splitting is not taken into account:
sub-levels belonging to the same term are combined into a single level.
Additionally, the remaining level populations of Mg I and Mg II up to n=12 and n=10, respectively, are computed in LTE relative to the ground state of the higher ionization stage with energies derived from their quantum defects. They are considered only in the number conservation equation.
All optically allowed bound-bound transitions between energy levels with non-LTE populations are considered. The required LS-coupling oscillator strengths are adopted from OP data (Butler et al. 1990, 1991, 1993) for Mg I and K.T. Taylor (available only from the TOPBASE database, Cunto & Mendoza 1992) for Mg II. Missing data are calculated in the Coulomb approximation (Bates & Damgaard 1949). In order to improve the computational efficiency, the individual lines of a multiplet are reduced to a single effective "multiplet line''.
Grotrian diagrams for the singlet and triplet spin systems of Mg I and
for Mg II are displayed in Figs. 1-3. The non-LTE
calculations are performed simultaneously for Mg I/II. Additional
radiative coupling between both spin systems of Mg I is provided by
the intercombination transitions
![]() -
-
![]() ,
,
![]() -
-
![]() ,
-
,
-
![]() ,
-
,
-
![]() ,
-
,
-
![]() and
and
![]() -
-
![]() with
a mean gf-value from Wiese et al. (1969) and Moccia & Spizzo
(1988) for the first transition and from Kurucz & Peytremann
(1975) for the latter transitions.
A detailed comparison of the adopted oscillator strengths with
theoretical work by other authors is performed by Butler et al.
(1993); the majority of the data is expected to be accurate to
within 10%,
superseding most of the older data used in previous studies of non-LTE effects
on Mg I. A similar accuracy in the radiative data has to be expected for
the Mg II ion.
with
a mean gf-value from Wiese et al. (1969) and Moccia & Spizzo
(1988) for the first transition and from Kurucz & Peytremann
(1975) for the latter transitions.
A detailed comparison of the adopted oscillator strengths with
theoretical work by other authors is performed by Butler et al.
(1993); the majority of the data is expected to be accurate to
within 10%,
superseding most of the older data used in previous studies of non-LTE effects
on Mg I. A similar accuracy in the radiative data has to be expected for
the Mg II ion.
Photoionizations from all energy levels with non-LTE populations are
treated using detailed
cross-sections from the Opacity Project (Butler et
al. 1993) for
Mg I and K.T. Taylor (available only from the
TOPBASE database, Cunto & Mendoza 1992) for Mg II.
A carefully chosen frequency grid ensures a thorough representation of the
numerous resonances present in the results of the R-matrix calculations for
Mg I.
Butler et al. (1993) discuss the reliability of the
cross-sections for the first three states of Mg I in the context of
the available experimental data and theoretical results from the literature;
fairly good agreement is found. A new theoretical study of the
photoionization from the ground state of Mg I (Kim & Tayal
2000) confirms the reliability of the OP data.
Butler et al. (1993) expect the accuracy of the rest of the
Mg I photoionization cross-sections to be high. For test purposes we
assume an accuracy of ![]() 10%. This accuracy we also expect for the
photoionization data for Mg II. Cross sections for energy levels missing
in the OP data (at high
10%. This accuracy we also expect for the
photoionization data for Mg II. Cross sections for energy levels missing
in the OP data (at high ![]() )
are calculated in the hydrogenic
approximation (Mihalas 1978, p. 99).
In summary, the use of the detailed OP
data significantly improves the description of the photoionization processes
compared to previous Mg I/II non-LTE studies.
)
are calculated in the hydrogenic
approximation (Mihalas 1978, p. 99).
In summary, the use of the detailed OP
data significantly improves the description of the photoionization processes
compared to previous Mg I/II non-LTE studies.
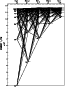 |
Figure 3: Grotrian diagram for Mg II |
| Open with DEXTER | |
In the first step of the computations, i.e. in DETAIL, the level
populations are
calculated using depth-dependent Doppler profiles assuming LS coupling;
microturbulence is explicitly included as an additional
term in the Doppler width (
![]() ):
):
These LS-coupling populations are then split according to the
statistical weights
of the individual sub-levels in order to calculate line profiles via
the program SURFACE. In this step of the calculation,
Voigt profile functions are adopted and the same
microturbulent velocity as in DETAIL is applied.
Wavelengths are taken from Kaufman & Martin (1991) and transition
probabilities from several sources, as indicated in Table 3.
The damping parameters are calculated from OP radiative lifetimes
(Butler et al. 1991) for the radiative widths and
adopted from Dimitrijevic & Sahal-Bréchot (1996)
and Griem (1964, 1974) for electron impact and ion
broadening in Mg I/II. Missing collisional damping data are computed
from the approximation of Cowley (1971). Van der Waals damping
can be neglected in the parameter range considered here, as tests at the lower
![]() boundary of
boundary of ![]() 8000 K have shown.
8000 K have shown.
Experimental cross sections from Freund et al. (1990) and
Crandall et al. (1982) are adopted for the collisional
ionization of the ground states of Mg I and Mg II, respectively.
These authors expect an accuracy of ![]() 10% for the measurements. All the
remaining collisional ionization data are computed using the Seaton formula
(Seaton 1962) with threshold photoionization cross sections from
the OP data where available or from the hydrogenic approximation.
10% for the measurements. All the
remaining collisional ionization data are computed using the Seaton formula
(Seaton 1962) with threshold photoionization cross sections from
the OP data where available or from the hydrogenic approximation.
The stellar radiation field is strongly affected by continuous and line opacities which must be correctly accounted for in the statistical-equilibrium calculations. We explicitly include bound-free opacities for the following atoms: H, He, C, N and O with abundances determined from lines in the visual and near-IR. Level populations for the first two elements are calculated in non-LTE using updated versions of the model atoms of Husfeld et al. (1989). Besides hydrogen (Lyman edge), C I is the most important continuous opacity source in the far-UV. Its sensitivity to non-LTE has a notable impact on the stellar flux at these wavelengths (see Lemke & Venn 1996). Non-LTE populations for C I are therefore determined from a comprehensive model atom (Przybilla et al. 2001a). Where necessary an additional iteration step in the determination of the stellar parameters is introduced. Neutral oxygen and nitrogen populations are determined using the model atoms of Przybilla et al. (2000, 2001b).
Line opacities are represented by LTE ODFs (Kurucz 1992) for the
appropriate metallicity and microturbulence. The original sawtooth pattern is
transformed into a step function by averaging over the 10Å-wide
intervals. This procedure meets the requirements for calculating the
radiation field as a whole. However, at certain important wavelengths a more
detailed description is desirable. In particular, the line opacity between the
Balmer jump and ![]() 3800Å is poorly reproduced as the higher Balmer
lines gradually merge into the continuum. The photoionizations from
the Mg I
3800Å is poorly reproduced as the higher Balmer
lines gradually merge into the continuum. The photoionizations from
the Mg I
![]() state (at a threshold wavelength of
3756.6Å) might be affected by this, explaining some of the problems with
fitting the spectral lines originating from this level. Except for this,
no other photoionization edges or important lines of Mg I/II are
situated at wavelengths with uncertain background opacities.
state (at a threshold wavelength of
3756.6Å) might be affected by this, explaining some of the problems with
fitting the spectral lines originating from this level. Except for this,
no other photoionization edges or important lines of Mg I/II are
situated at wavelengths with uncertain background opacities.
Despite our success in reproducing the observations, our calculations might be affected by a systematic effect neglected in the atmosphere modeling. Non-LTE effects will cause an overionization of the relevant elements in the opacity determination. The backwarming introduced by line blanketing might therefore be overestimated in LTE, as well as the magnitude of line blocking. First calculations of non-LTE line-blanketed model atmospheres for main sequence A-types (Hubeny & Lanz 1993) indicate some changes in the expected direction but adequate models for the more interesting case of supergiants are still lacking. Also, the line-blocking effects will change in non-LTE.
To assess the importance of various parameters entering the non-LTE
computations and to estimate systematic errors on the effective temperature
determination and abundance analysis, test calculations were performed
for typical atmospheric parameters of early A-type stars: a
main sequence model with 9500K/4.0 at
![]() and
a supergiant model with 9500K/1.5 at
and
a supergiant model with 9500K/1.5 at
![]() assuming
solar metallicity.
Below
assuming
solar metallicity.
Below
![]() K the hydrostatical
model atmospheres for supergiants develop pressure inversion and should
therefore - as well as for other reasons - be viewed with caution as a
reliable description of the physical conditions, see Sect. 3.3.
For a given synthetic spectrum of magnesium,
the abundance is adjusted in the model with modified parameters to reproduce
the original line strengths. The results of the tests (mean values from
several lines used in abundance analyses) are summarised in Table 1.
K the hydrostatical
model atmospheres for supergiants develop pressure inversion and should
therefore - as well as for other reasons - be viewed with caution as a
reliable description of the physical conditions, see Sect. 3.3.
For a given synthetic spectrum of magnesium,
the abundance is adjusted in the model with modified parameters to reproduce
the original line strengths. The results of the tests (mean values from
several lines used in abundance analyses) are summarised in Table 1.
| changes in
|
||||||
| 9500/4.0 | 9500/1.5 | |||||
| Mg I | Mg II | Mg I | Mg II | |||
| Atmospheric parameters: | ||||||
|
|
|
-0.11 | -0.01 | -0.18 | -0.03 | |
|
|
|
-0.06 | -0.01 | -0.16 | -0.05 | |
|
|
-0.10 | -0.03 | -0.02 | -0.07 | ||
| [M/H]-0.2dex |
|
-0.01 | -0.01 | +0.02 | ||
| Line transitions: | ||||||
| Oscillator strengths +10% |
|
-0.04 | -0.04 | -0.02 | ||
| Damping constant *2 |
|
-0.05 | -0.05 | |||
| Photoionizations: | ||||||
| Cross-sections +10% |
|
|||||
| Cross-sections *5 | +0.03 | +0.03 | -0.01 | |||
| Collisional transitions: | ||||||
| Cross-sections *0.1 | +0.02 | -0.02 | +0.01 | +0.01 | ||
| Cross-sections *0.5 |
|
+0.01 | -0.01 | +0.01 | +0.01 | |
| Cross-sections *2 |
|
+0.01 | -0.02 | -0.01 | ||
| Cross-sections *10 | +0.01 | +0.03 | -0.01 | -0.01 | ||
| Collisional ionization: | ||||||
| Cross-sections *0.1 |
|
+0.01 | +0.01 | |||
| Cross-sections *10 |
|
-0.04 | -0.02 | |||
| Continuum placement |
|
|||||
| Estimated total uncertainty |
|
|||||
Two important conclusions can be drawn from this. First, for the given model atom, uncertainties in the atomic data are not a critical issue. Uncertainties in the oscillator strengths have the greatest impact and our model certainly benefits from the highly accurate OP data. In the main sequence model, the line-broadening parameters also become important due to the higher particle densities in its atmosphere. Quite accurate data are available in this case. This relative insensitivity of our magnesium model to the atomic parameters corresponds to the small non-LTE corrections found from the comparison with observations.
The second conclusion is the strong dependence of the ionization equilibrium of
Mg I/II on the atmospheric parameters. As the major ionization stage
of Mg II turns out to be quite insensitive to variations in
![]() and
and ![]() - and therefore should be viewed as the
preferable abundance indicator - the Mg I populations react
differently. Even small changes are reflected.
Hence, this delicate ionization balance is an ideal tool for stellar
parameter determination. The temperature sensitivity is highest but for
supergiants the dependence on surface gravity becomes comparable.
In either case, one can profit from this sensitivity only so long as the
atmospheric
models reliably reflect the local conditions in the star. For models close
to the Eddington limit, this will need further investigation.
- and therefore should be viewed as the
preferable abundance indicator - the Mg I populations react
differently. Even small changes are reflected.
Hence, this delicate ionization balance is an ideal tool for stellar
parameter determination. The temperature sensitivity is highest but for
supergiants the dependence on surface gravity becomes comparable.
In either case, one can profit from this sensitivity only so long as the
atmospheric
models reliably reflect the local conditions in the star. For models close
to the Eddington limit, this will need further investigation.
Lines of intermediate strength are most affected by microturbulence. Weak lines
with equivalent widths
![]() 100 mÅ should be preferred for the
analyses. For further discussion concerning this parameter, see Sect. 3.2.
100 mÅ should be preferred for the
analyses. For further discussion concerning this parameter, see Sect. 3.2.
Metallicity has only small effects on the magnesium populations. We achieved the appropriate changes in the background opacities by choosing ODFs for elemental abundances reduced by typical uncertainties. On the other hand, line blocking is an important ingredient for the statistical-equilibrium calculations and must not be neglected.
Another source of systematic error is the continuum placement in the
observed spectra. This strongly depends on the S/N ratio obtained. Our
estimate in Table 1 should be applicable to high quality data with
![]() only. In general, equivalent widths studies are more
susceptible to
this systematic error than the spectrum synthesis technique, which also
accounts for the continuum regions explicitly.
only. In general, equivalent widths studies are more
susceptible to
this systematic error than the spectrum synthesis technique, which also
accounts for the continuum regions explicitly.
The total uncertainties are computed from the sum of the squares of the
appropriate uncertainties listed above, assuming them to be independent:
![\begin{eqnarray*}%
\sigma_{\rm sys}^2 & = & \sigma_{T_{\rm eff}}^2+\sigma_{\log
...
...}^2+\sigma_{\rm [M/H]}^2+\sigma_{\log gf}^2+
\sigma_{\rm damp}^2
\end{eqnarray*}](/articles/aa/full/2001/15/aa10287/img65.gif)
|
(2) |
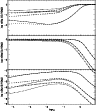 |
Figure 4:
Non-LTE and LTE ionization balance of magnesium for the sample
stars of Sect. 4: Vega (solid lines/filled circles), |
| Open with DEXTER | |
Departure coefficients bi=
![]() (the ni denoting the level populations)
for energy levels i are displayed in Fig. 5 as a function of the
Rosseland optical depth
(the ni denoting the level populations)
for energy levels i are displayed in Fig. 5 as a function of the
Rosseland optical depth
![]() for our models of the objects
discussed in Sect. 4.
The lower levels involved in the transitions giving rise to
all the observed Mg I lines in the
visual/near-IR have rather low excitation energies of
2.71 eV (
for our models of the objects
discussed in Sect. 4.
The lower levels involved in the transitions giving rise to
all the observed Mg I lines in the
visual/near-IR have rather low excitation energies of
2.71 eV (
![]() )
and 4.35 eV
(
)
and 4.35 eV
(
![]() ).
The corresponding Mg II lines
originate from the 3d and the n=4 levels (
).
The corresponding Mg II lines
originate from the 3d and the n=4 levels (
![]() 8.8 eV
above the ground state).
Additional features in the UV also give information about the ground states
of both ionization stages. In particular, the whole sequence
8.8 eV
above the ground state).
Additional features in the UV also give information about the ground states
of both ionization stages. In particular, the whole sequence
![]() -
-
![]() -
-
![]() -
-
![]() of Mg II is sampled, giving rise to prominent absorption features.
of Mg II is sampled, giving rise to prominent absorption features.
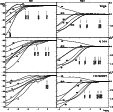 |
Figure 5:
Departure coefficients bi for Mg I (left) and
Mg II (right) as a function of Rosseland optical
depth
|
Deep in the atmosphere, the departure coefficients approach unity as the
density increases and collisional processes dominate, enforcing LTE (inner
boundary condition). Farther out, marked deviations from
LTE occur, setting in at larger
![]() and being more pronounced
in supergiants. Non-LTE corrections are expected to be small for Mg I
as the departure coefficients deviate only slightly from unity at
line-formation depths. In addition, the line formation is progressively
shifted to deeper layers with decreasing surface gravity at comparable effective
temperatures, thus compensating for the
stronger deviations of the bi. The energetically low-lying
Mg I levels are systematically depopulated by photoionizations,
resulting in bi<1. We test this by replacing the mean intensity
with the Planck function,
and being more pronounced
in supergiants. Non-LTE corrections are expected to be small for Mg I
as the departure coefficients deviate only slightly from unity at
line-formation depths. In addition, the line formation is progressively
shifted to deeper layers with decreasing surface gravity at comparable effective
temperatures, thus compensating for the
stronger deviations of the bi. The energetically low-lying
Mg I levels are systematically depopulated by photoionizations,
resulting in bi<1. We test this by replacing the mean intensity
with the Planck function, ![]() =
=![]() ,
for the photoionization
continua in our
,
for the photoionization
continua in our ![]() Leo model, thus eliminating the non-LTE radiation
field for these transitions: the bi then show much smaller deviations from
unity, typically <0.2 dex even close to the outer boundary of our models.
The more excited levels are also affected by photoionizations but
also show a stronger collisional coupling to the ground state
of Mg II, resulting in smaller departures.
Leo model, thus eliminating the non-LTE radiation
field for these transitions: the bi then show much smaller deviations from
unity, typically <0.2 dex even close to the outer boundary of our models.
The more excited levels are also affected by photoionizations but
also show a stronger collisional coupling to the ground state
of Mg II, resulting in smaller departures.
The lowest two energy levels of Mg II are essentially in LTE
throughout the atmosphere, even for the supergiant models.
Practically all radiative transitions from the ground state occur at
optically thick conditions (at wavelengths shortward of the Lyman jump or
coinciding with Lyman lines), thus reducing the non-LTE effects.
In addition, collisions couple the first excited level
to the ground state (with the collisional rates exceeding the radiative
rates typically by several orders of magnitude).
The optically thick resonance lines
in the UV (Mg II
![]() 2795, 2802) are therefore in
detailed balance throughout the depth range of our models (but see also
Sect. 4.4).
2795, 2802) are therefore in
detailed balance throughout the depth range of our models (but see also
Sect. 4.4).
Photoionizations help to depopulate the lower excited Mg II levels
(mostly the 3d and the n=4 levels) and facilitate the overpopulation
of the Mg III ground state. Adopting ![]() for the
photoionization continua of the Mg II levels in the case of our
for the
photoionization continua of the Mg II levels in the case of our
![]() Leo model (see above) results in a slight underpopulation of
Mg III instead. In addition, the 3d and 4s levels are kept close
to LTE populations throughout the line formation region due to their
(optically thick) radiative coupling with the thermalised 3p level.
Then, the depopulation of the other Mg II levels
results from the complex interaction of photoionizations, collisional
ionizations and excitation processes.
Modifications in the ionizations via photon
or electron impact (by setting
Leo model (see above) results in a slight underpopulation of
Mg III instead. In addition, the 3d and 4s levels are kept close
to LTE populations throughout the line formation region due to their
(optically thick) radiative coupling with the thermalised 3p level.
Then, the depopulation of the other Mg II levels
results from the complex interaction of photoionizations, collisional
ionizations and excitation processes.
Modifications in the ionizations via photon
or electron impact (by setting ![]() =
=![]() or increasing the b-f
collision rates of the highly excited Mg II levels
(n
or increasing the b-f
collision rates of the highly excited Mg II levels
(n![]() 8) by a factor of
thousand) alone do not remove these strong depopulations; they are
only weakened. Again, the highly excited levels of Mg II
approach the departure of the ground state of the higher
ionization stage.
8) by a factor of
thousand) alone do not remove these strong depopulations; they are
only weakened. Again, the highly excited levels of Mg II
approach the departure of the ground state of the higher
ionization stage.
| |
Figure 6:
Ratio of line source function |
| Open with DEXTER | |
The non-LTE abundance corrections for our sample stars as derived in
Table 3 are
explained in view of the run of the departure coefficients and the
corresponding line source function
![]() for a given transition.
Figure 6 shows the ratio of the line source function
to the Planck function
for a given transition.
Figure 6 shows the ratio of the line source function
to the Planck function
| |
Figure 7:
Theoretical line profiles for the |
| Open with DEXTER | |
A non-LTE strengthening of lines will occur in cases where
bi>bj;
otherwise a weakening is seen, as is inferred from Eq. (3).
Thus, the entirely positive non-LTE corrections for Mg I transitions
in the supergiants result from the relative overpopulation of the upper
levels, leading to shallower line profiles (
![]() ).
The triplet lines in Vega, on the other hand, experience a strengthening
as the line cores are formed farther out in the atmosphere where
the ratio of
).
The triplet lines in Vega, on the other hand, experience a strengthening
as the line cores are formed farther out in the atmosphere where
the ratio of ![]() to
to ![]() drops below unity. For the singlet
lines the conditions are similar to those of the supergiant case.
In Mg II only the features
drops below unity. For the singlet
lines the conditions are similar to those of the supergiant case.
In Mg II only the features
![]() 4481 and 7877-96 are affected by stronger non-LTE
corrections, as can be inferred from the formation depths (
4481 and 7877-96 are affected by stronger non-LTE
corrections, as can be inferred from the formation depths (
![]() )
of the corresponding line cores as marked in Figs. 5 and 6.
Photon escape most probably reduces the line centre intensities of these
lines, an effect
strongest in the extended atmospheres of supergiants. For the other
Mg II lines the ratio
)
of the corresponding line cores as marked in Figs. 5 and 6.
Photon escape most probably reduces the line centre intensities of these
lines, an effect
strongest in the extended atmospheres of supergiants. For the other
Mg II lines the ratio
![]() remains close to unity.
remains close to unity.
Recently, McErlean et al. (1998) explicitly included microturbulence in the statistical-equilibrium calculations (with DETAIL, Eq. (1)) for helium in OB stars and find significantly different profiles as compared to the standard procedure of including microturbulence only in the final step of the spectrum synthesis (with SURFACE) for microturbulent velocities in excess of 10 kms-1.
This rather subtle effect depends on the details of the ionization balance and the departure coefficients for a given element as shown by Przybilla et al. (2000). Lines from both species, Mg I and Mg II, are expected to show some sensitivity to a non-zero microturbulence in the statistical-equilibrium calculations as the occupation numbers of the levels involved vary significantly over the line-formation depths. Thus the radiative transitions occur under slightly different conditions as the formation depths of the line centres are pushed deeper into the atmosphere but simultaneously the frequency bandwidths for absorption are broadened by an increased microturbulent velocity. Changes in the non-LTE level populations and the line source functions vary in magnitude for different lines. Even lines too weak to react sensitively to microturbulence in the classical sense might therefore be affected.
In Fig. 7, test calculations for our model of ![]() Leo with
an increased microturbulence are displayed. For the weak Mg I
Leo with
an increased microturbulence are displayed. For the weak Mg I
![]() 8806 feature, the equivalent width decreases by
8806 feature, the equivalent width decreases by ![]() 20% as
20% as ![]() is
increased from 0 to 10 km s-1 in the statistical-equilibrium
computations with DETAIL. The line formation is then performed
with SURFACE on the basis of the resulting population numbers for
is
increased from 0 to 10 km s-1 in the statistical-equilibrium
computations with DETAIL. The line formation is then performed
with SURFACE on the basis of the resulting population numbers for
![]() =10 km s-1, as in the classical approach.
Equivalent widths for all other Mg I lines are also decreased with
variations of typically several percent. On the other hand, Mg II
lines are strengthened by several percent (
=10 km s-1, as in the classical approach.
Equivalent widths for all other Mg I lines are also decreased with
variations of typically several percent. On the other hand, Mg II
lines are strengthened by several percent (![]() 12% at maximum).
12% at maximum).
For typical microturbulence values (<10 kms-1) found in our sample stars, the magnitude of this effect is reduced but nevertheless has to be accounted for in high S/N observations such as ours. Moreover, the systematical weakening of Mg I and strengthening of Mg II lines mimics a change in effective temperature - impacting all other derived quantities. We therefore use a consistent microturbulence in all our statistical-equilibrium and line-formation calculations in order to reduce the systematic error in the stellar parameter and abundance determination.
Pressure inversion is an uncommon phenomenon encountered in atmospheric
modeling. It develops in hydrostatic equilibrium models for cases
where the stellar luminosity locally exceeds the Eddington luminosity,
resulting in
A pressure inversion layer can also be present in hydrodynamical models where Eq. (4) has to be replaced by the momentum equation as Achmad et al. (1997) and Asplund (1998) have shown. It is not removed by mass outflow except for very high mass loss rates not supported by the observations. Moreover, this local super-Eddington luminosity does not initiate the stellar wind. In a stability analysis for late-type stars close to the Eddington limit, Asplund (1998) finds no conclusive evidence for the suppression or the realization of pressure inversion in real stellar atmospheres. Further efforts with more sophisticated methods are needed.
Nevertheless, assuming that the pressure inversion is an artefact of
inappropriate assumptions in the model atmosphere calculations, the
determination of stellar parameters on the basis of these models
becomes subject to systematic uncertainties which are hard to quantify.
In particular, supergiant models with
![]() between
7000 K and 8000K (corresponding to late A-type and early F-type)
will be affected as the pressure inversion layer extends
into the line-forming region (see Table 1 in Achmad et al.
1997). At cooler temperatures, the hydrogen ionization zone
progressively shifts to deeper atmospheric layers and the modeling of spectral
features will be only influenced indirectly.
between
7000 K and 8000K (corresponding to late A-type and early F-type)
will be affected as the pressure inversion layer extends
into the line-forming region (see Table 1 in Achmad et al.
1997). At cooler temperatures, the hydrogen ionization zone
progressively shifts to deeper atmospheric layers and the modeling of spectral
features will be only influenced indirectly.
In our approach the surface gravity is determined by Balmer line fitting.
The shape of the hydrogen lines is determined by (linear) Stark broadening
which reacts sensitively to the local electron density
(![]()
![]() ). Within a pressure
inversion layer this density is increased by up to an order of magnitude in some
cases. The derived surface gravities will therefore be systematically
underestimated. Also, the temperature indicator - the Mg I/II
ionization equilibrium - is affected, even if to a lesser extent.
In the simplified case of LTE
the local electron density influences the ionization balance through the
Saha equation. Higher electron densities result in a strengthening of the
calculated Mg I line strengths. An overestimation of
). Within a pressure
inversion layer this density is increased by up to an order of magnitude in some
cases. The derived surface gravities will therefore be systematically
underestimated. Also, the temperature indicator - the Mg I/II
ionization equilibrium - is affected, even if to a lesser extent.
In the simplified case of LTE
the local electron density influences the ionization balance through the
Saha equation. Higher electron densities result in a strengthening of the
calculated Mg I line strengths. An overestimation of
![]() will follow from a comparison with the observations. This situation
also arises in non-LTE, at least qualitatively.
will follow from a comparison with the observations. This situation
also arises in non-LTE, at least qualitatively.
The suspected higher ![]() values help to resolve discrepancies
in the mass determination for these objects. Spectroscopic masses are
in better
agreement with the masses determined from evolutionary tracks for higher
surface gravities at a given luminosity.
values help to resolve discrepancies
in the mass determination for these objects. Spectroscopic masses are
in better
agreement with the masses determined from evolutionary tracks for higher
surface gravities at a given luminosity.
On the other hand, it should be noted that the
determination of elemental abundances seems not to be severely affected
by these systematics on the parameter analysis and the enhanced (metal) line
broadening (quadratic Stark and van der Waals damping) due to higher
particle densities. Objects for "critical''
combinations of
![]() /
/![]() show similar abundances as objects
well outside the pressure inversion regime (see e.g. Venn 1995).
The question of whether this is a coincidence or evidence for realization of
pressure inversion in real stellar atmospheres can be settled by an analysis of
an appropriate (visual) binary system with one component in the pressure
inversion regime and the other outside, which would act as the abundance
reference. This test still has to be performed.
show similar abundances as objects
well outside the pressure inversion regime (see e.g. Venn 1995).
The question of whether this is a coincidence or evidence for realization of
pressure inversion in real stellar atmospheres can be settled by an analysis of
an appropriate (visual) binary system with one component in the pressure
inversion regime and the other outside, which would act as the abundance
reference. This test still has to be performed.
From these considerations, some doubt in the reliability of present modeling techniques for late A-type and F-type supergiants seems appropriate. We therefore refrain from including such stars in our sample in Sect. 4 which would otherwise extend the variety of diagnostic lines for Mg I/II. A quantitative analysis of the problem is far beyond the scope of this work but we hope to have given further motivation to study this sparsely-populated region of the Hertzsprung-Russell diagram (e.g. Blaha & Humphreys 1989).
So far, the only Mg I/II non-LTE model atom comparable to ours in complexity is that of Gigas (1988). A comparison of both is desireable in order to check the validity of the non-LTE calculations.
Gigas himself performs non-LTE calculations for magnesium only for Vega.
The departure coefficients found by him (Figs. 3 and 4 in Gigas 1988)
show qualitatively and quantitatively similar behaviour to ours
(Fig. 5). Consequently, as the atmospheric parameters and gf values do
not differ drastically, his LTE and non-LTE abundances match well with ours
within the uncertainties (see Table 5). Nevertheless, some
trend seems to be indicated: the Mgb lines and the Mg II
![]() 4481 feature are subject to stronger non-LTE corrections in our
approach.
4481 feature are subject to stronger non-LTE corrections in our
approach.
The systematic differences are expected to be amplified in supergiants at
conditions more suitable for non-LTE. Venn (1995) analyses the
supergiant ![]() Leo using the Gigas model to determine the magnesium
ionization equilibrium. Indeed, our abundance corrections for the Mg I
lines are more pronounced, by over 0.1 dex, whereas those for
the weak Mg II lines show no significant differences.
Accounting for her higher
Leo using the Gigas model to determine the magnesium
ionization equilibrium. Indeed, our abundance corrections for the Mg I
lines are more pronounced, by over 0.1 dex, whereas those for
the weak Mg II lines show no significant differences.
Accounting for her higher
![]() value for this star even
worsens the situation, as the difference in the non-LTE abundance corrections
increases.
value for this star even
worsens the situation, as the difference in the non-LTE abundance corrections
increases.
Our consistent modeling of the observations for Vega and
![]() Leo with reduced random errors (cf. Table 5)
clearly indicates the improvement achieved in the description of the real
processes, applying our model atom instead of that of Gigas (1988).
The recent efforts of various groups in
providing accurate atomic data play an important part in this.
Leo with reduced random errors (cf. Table 5)
clearly indicates the improvement achieved in the description of the real
processes, applying our model atom instead of that of Gigas (1988).
The recent efforts of various groups in
providing accurate atomic data play an important part in this.
For both supergiants, Echelle spectra using FEROS
(Kaufer et al. 1999) at the ESO 1.52 m
telescope in La Silla were taken in January 1999. Nearly complete wavelength
coverage between 3600 and 9100Å was achieved with a resolving power
R=
![]()
![]() 48000 (with 2.2 pixels per
48000 (with 2.2 pixels per
![]() resolution element) yielding a S/N of several hundred in V.
The exposure times were 2min (
resolution element) yielding a S/N of several hundred in V.
The exposure times were 2min (![]() Leo) and 5min (HD92207).
Data reduction was performed using the MIDAS package, as described in the
FEROS documentation (http://www.ls.eso.org/lasilla/Telescopes/2p2T/E1p5M/FEROS/docu/Ferosdocu.html).
The spectra were normalized by fitting a spline function to continuum points
and finally shifted in wavelength to the rest frame using the radial
velocity
Leo) and 5min (HD92207).
Data reduction was performed using the MIDAS package, as described in the
FEROS documentation (http://www.ls.eso.org/lasilla/Telescopes/2p2T/E1p5M/FEROS/docu/Ferosdocu.html).
The spectra were normalized by fitting a spline function to continuum points
and finally shifted in wavelength to the rest frame using the radial
velocity
![]() determined from cross-correlation with an appropriate
synthetic spectrum.
determined from cross-correlation with an appropriate
synthetic spectrum.
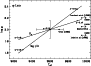 |
Figure 8:
H |
| Open with DEXTER | |
An Echelle spectrum of Vega was kindly made available by A. Korn with almost
complete wavelength coverage between 3900 and 9400Å. FOCES
(Pfeiffer et al. 1998) at the Calar Alto 2.2 m telescope was
used in June 1999 to obtain three exposures of 4s and 2![]() 10s,
respectively.
The spectra were reduced in the standard way using the routines described by
Pfeiffer et al. (1998). After merging of the single spectra and
rectification, a S/N of
10s,
respectively.
The spectra were reduced in the standard way using the routines described by
Pfeiffer et al. (1998). After merging of the single spectra and
rectification, a S/N of ![]() 750 near
750 near
![]() was measured at
was measured at
![]() (2 pixels per
(2 pixels per
![]() resolution element).
resolution element).
A second spectrum of Vega taken with HEROS was provided by A. Kaufer,
extending the wavelength range for the analysis from 3900Å down to
the Balmer jump. A S/N>200 at
![]() was achieved
(cf. Kaufer et al. 1996a, 1996b, for details on the
observations and the data reduction procedures).
was achieved
(cf. Kaufer et al. 1996a, 1996b, for details on the
observations and the data reduction procedures).
In general, the observations are of high quality with few spectral regions corrupted by CCD defects or cosmic ray impacts. As the data were obtained only as a supplement to the main observing program, no additional spectra of a fast rotator are available at the correct airmass to remove the telluric features.
| HD | Name | Sp.Type | V(mag) |
|
|
|
|
y |
|
|||
|
|
|
(K) | (cgs) |
|
|
|||||||
| 172167 | A0V | 0.03 | 67.44 | +19.24 | -14 | 22 | 9550 | 3.95 | 0.09 | 2 | 0 | |
| +2 | ||||||||||||
| 87737 | A0Ib | 3.52 | 219.53 | +50.75 | +3 | 9 | 9600 | 2.00 | 0.13 | 4 | 12 | |
| 92207 | ... | A0Iae | 5.45 | 286.29 | -0.26 | -9 | 28 | 9100 | 0.98 | 0.23 | 6 | 18 |
| +400
-150 |
+0.30
-0.15 |
+0.03
-0.10 |
Prior to an abundance analysis, atmospheric parameters have to be determined
accurately. A purely spectroscopic approach is chosen.
![]() and
and ![]() are derived simultaneously by finding the
ionization equilibrium of Mg I/ II and by fitting the wings
of the higher Balmer lines (typically from
are derived simultaneously by finding the
ionization equilibrium of Mg I/ II and by fitting the wings
of the higher Balmer lines (typically from
![]() upwards) which
are still formed in photospheric regions, in contrast to the
upwards) which
are still formed in photospheric regions, in contrast to the
![]() and
and
![]() features which are affected by the stellar wind
in supergiants. The profiles are calculated using the Stark broadening tables
of Vidal et al. (1973). He I lines are used to assess the
stellar helium abundance
features which are affected by the stellar wind
in supergiants. The profiles are calculated using the Stark broadening tables
of Vidal et al. (1973). He I lines are used to assess the
stellar helium abundance
![]() .
The stellar density structure responds to
changes in the helium abundance because of its higher mean molecular weight
(see e.g. Kudritzki 1973).
.
The stellar density structure responds to
changes in the helium abundance because of its higher mean molecular weight
(see e.g. Kudritzki 1973).
![]() and
and ![]() have to be appropriately adjusted at this point in some cases, see Fig.
8. The microturbulent velocity
have to be appropriately adjusted at this point in some cases, see Fig.
8. The microturbulent velocity ![]() is determined from LTE
spectrum synthesis for a large ensemble of Fe II and Cr II lines
by demanding that there is no relation between abundance and line strength.
From this, the metallicity of the object is also fixed by assuming
is determined from LTE
spectrum synthesis for a large ensemble of Fe II and Cr II lines
by demanding that there is no relation between abundance and line strength.
From this, the metallicity of the object is also fixed by assuming
![]() .
Elemental abundances for the important
background-opacity species are obtained by detailed non-LTE calculations (see
Sect. 2.3). Rotational velocities
.
Elemental abundances for the important
background-opacity species are obtained by detailed non-LTE calculations (see
Sect. 2.3). Rotational velocities ![]() and macroturbulence
and macroturbulence
![]() in the radial-tangential model are derived
from spectrum synthesis as both broadening mechanisms alter the line profile
in different ways (Gray 1992). Usually, several iteration steps are
necessary to obtain the final set of parameters.
in the radial-tangential model are derived
from spectrum synthesis as both broadening mechanisms alter the line profile
in different ways (Gray 1992). Usually, several iteration steps are
necessary to obtain the final set of parameters.
The basic properties and atmospheric parameters of the test stars are summarised in Table 2, as are the error estimates. Information on the basic properties are taken from the Bright Star Catalogue (Hoffleit 1982).
The atmospheric model for our spectrum synthesis calculations on Vega is adopted from Castelli & Kurucz (1994). Excellent agreement between observations and our spectrum synthesis is found on the basis of this model, thus confirming the reliability of the atmospheric parameters derived in that work.
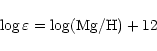 |
(5) |
| (6) |
In Fig. 9, theoretical line profiles for the
derived mean non-LTE magnesium abundance are compared with the observations;
excellent agreement is found with few exceptions
(Mg I
![]() 4702 and 5528).
For comparison, profiles from the mean LTE
abundance (Mg II) are also shown. Other
elements are included for the spectrum synthesis in LTE in order to
disentangle line blends. As some of the magnesium lines are formed in the wings
of H I lines, profiles for hydrogen are calculated on the basis
of non-LTE level populations. He I is also treated in non-LTE due to
its importance for the atmospheric structure. The magnesium
abundances for the test stars are:
4702 and 5528).
For comparison, profiles from the mean LTE
abundance (Mg II) are also shown. Other
elements are included for the spectrum synthesis in LTE in order to
disentangle line blends. As some of the magnesium lines are formed in the wings
of H I lines, profiles for hydrogen are calculated on the basis
of non-LTE level populations. He I is also treated in non-LTE due to
its importance for the atmospheric structure. The magnesium
abundances for the test stars are:
| Vega |
|
|
|
|
| HD92207 |
|
Vega shows a magnesium deficiency of 0.56 dex. This is comparable to the
general underabundance of the heavier elements by typically
![]() 0.5 dex (solar abundances adopted from Grevesse et al.
1996) which leads to the conclusion that Vega is a mild
0.5 dex (solar abundances adopted from Grevesse et al.
1996) which leads to the conclusion that Vega is a mild
![]() Bootis star (Venn & Lambert 1990). We find only small
non-LTE corrections for this main sequence star.
In the case of
Bootis star (Venn & Lambert 1990). We find only small
non-LTE corrections for this main sequence star.
In the case of ![]() Leo the magnesium abundance is consistent with the
solar value, as are the abundances of other
Leo the magnesium abundance is consistent with the
solar value, as are the abundances of other ![]() and iron peak elements.
Non-LTE corrections are <0.2 dex for most of the lines.
These corrections slightly increase at still higher luminosity, as for
HD92207. For this star we derive
and iron peak elements.
Non-LTE corrections are <0.2 dex for most of the lines.
These corrections slightly increase at still higher luminosity, as for
HD92207. For this star we derive
![]() dex which matches well
with its elemental underabundance of
dex which matches well
with its elemental underabundance of ![]() 0.4 dex. As discussed earlier,
non-LTE effects on the atmospheric structure of this extreme object are
expected which would bring its metal abundance into better agreement with
typical abundances derived for galactic objects.
0.4 dex. As discussed earlier,
non-LTE effects on the atmospheric structure of this extreme object are
expected which would bring its metal abundance into better agreement with
typical abundances derived for galactic objects.
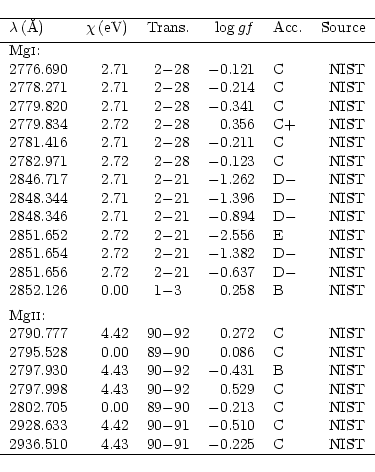
See Table 3 for accuracy indicators and gf value sources.
|
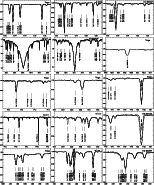 |
Figure 9:
Spectral synthesis for selected Mg I/II lines in the test
stars. Abscissa units are wavelengths in Å, ordinate is relative flux.
Observed (thin solid) and computed (thick solid) non-LTE profiles for
the magnesium abundances in Table 3 are displayed with line
identifiers. Profiles for the appropriate Mg II LTE abundances are
marked by a dotted line. Line formation for species other than H I,
He I and Mg I/II is performed assuming LTE level populations.
Note that in the case of Mg I |
| Open with DEXTER | |
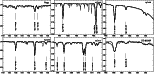 |
Figure 9:
continued. Numerous sharp telluric lines contaminate the red
part of the spectrum. Note that the local continuum in the wing of H |
| Open with DEXTER | |
| |
Figure 10:
Spectral synthesis of the UV region in Vega. Observed (thin
solid) and computed (thick solid) non-LTE profiles (for
|
| Open with DEXTER | |
Spectrum synthesis is mandatory for the interpretation of the UV lines in Vega.
In addition to magnesium we include the iron peak elements in our
line-formation calculation which account for the overwhelming majority of lines
in the spectral region of interest. The gf values are adopted
from Kurucz & Bell (1995) or from Martin et al. (1988) and
Fuhr et al. (1988) where available. Elemental abundances are adopted
from previous determinations from lines in the visual. The atomic data for
the magnesium lines are summarised in Table 4. Fitting of the
observed resonance line profiles is best accomplished by using collisional
damping data calculated from the approximation of Cowley (1971).
| Source |
|
|
|
|
| This work |
|
|
|
|
| Castelli (1993) | 7.04 | 7.04 | ... | ... |
| Venn & Lambert (1990) | ... |
|
... | ... |
| Adelman & Gulliver (1990) | 6.93(1) |
|
... | ... |
| Gigas (1988) |
|
|
|
|
| Freire Ferrero et al. (1983) | ... | ... | ... | 7.00(2) |
| Sadakane & Nishimura (1981) | 7.53(1) | ... | ... | ... |
| Sadakane & Nishimura (1979) |
|
7.04(1) | ... | ... |
| This Work |
|
|
|
|
| Venn (1995) |
|
|
7.58(4) | 7.46(5) |
| Lambert et al. (1988) | ... | 7.78 | ... | ... |
| Wolf (1971) | 7.76(1) |
|
... | ... |
Listed are the abundances with 1![]() errors from the line-to-line scatter
(number of lines analysed in parenthesis).
errors from the line-to-line scatter
(number of lines analysed in parenthesis).
There is generally good accordance between observations and our model
calculations; see Fig. 10. The discrepancies are expected to
arise from observational noise, inaccurate atomic data, unaccounted line
blends by other
elements and neglected non-LTE effects for the iron group elements.
In particular, the majority of the
magnesium lines are correctly predicted except for the centres of the
resonance lines. Here interstellar absorption is likely to contribute to the
observed line profiles. The extra absorption slightly blueward of the line
centres of Mg I ![]() 2852 and Mg II
2852 and Mg II
![]() 2795-2802 is well correlated with the interstellar
Fe II components identified by Lallement et al. (1995).
In addition the Mg II resonance lines remain optically thick even at the
outer boundary of our model atmosphere, at
2795-2802 is well correlated with the interstellar
Fe II components identified by Lallement et al. (1995).
In addition the Mg II resonance lines remain optically thick even at the
outer boundary of our model atmosphere, at
![]() =-8.
The centres of these lines are therefore artifically truncated,
introducing a small inaccuracy.
In general, deviations from LTE are small for the UV magnesium lines.
=-8.
The centres of these lines are therefore artifically truncated,
introducing a small inaccuracy.
In general, deviations from LTE are small for the UV magnesium lines.
In the following, our results for the sample stars are compared with those of other recent analyses.
Venn & Lambert (1990) find a magnesium abundance 0.35 dex lower
than our value from an LTE analysis of Mg II ![]() 4481 and two
IR lines not included in our study. Atmospheric parameters of
4481 and two
IR lines not included in our study. Atmospheric parameters of
![]() K and
K and
![]() have been used
with ATLAS6 (Kurucz 1979) and gf
values identical with ours (in the case of Mg II
have been used
with ATLAS6 (Kurucz 1979) and gf
values identical with ours (in the case of Mg II ![]() 4481).
The discrepancy most likely results from the broadening data used in the
line-formation calculations as the measured equivalent widths only differ by
several percent.
4481).
The discrepancy most likely results from the broadening data used in the
line-formation calculations as the measured equivalent widths only differ by
several percent.
Adelman & Gulliver (1990) derive a slightly lower LTE magnesium abundance from almost identical equivalent widths and gf values as used in our work. A systematic shift results from their choice of atmospheric parameters (9400/3.95). Considering this, both LTE results match well.
A LTE and non-LTE study of Gigas (1988) finds Mg I/II
abundances similar to ours. The small differences can be attibuted to
an interplay of model parameters (9500/3.90), small variations in the
measured
![]() and the choice of gf values.
Our results also agree well with those of the non-LTE study by Freire
Ferrero et al. (1983) of the Mg II UV resonance lines,
which nevertheless are poor abundance indicators due to their saturation.
and the choice of gf values.
Our results also agree well with those of the non-LTE study by Freire
Ferrero et al. (1983) of the Mg II UV resonance lines,
which nevertheless are poor abundance indicators due to their saturation.
Sadakane & Nishimura (1979, 1981) find a large scatter in magnesium abundances from lines in the visible and near UV, respectively. The quality of atomic data has significantly improved in the past twenty years and their relatively high magnesium abundance (from Mg I) can, for the most part, be attributed to the inaccuracies in their gf values. Their atmospheric parameters (9660/3.94) and equivalent widths are comparable with the "modern'' values.
Lambert et al. (1988) find a magnesium abundance of
+0.2 dex above solar. They do not give enough details to reconstruct their
work, but the higher abundance should result from a rather high
![]() of 10500 K.
of 10500 K.
Finally the early work of Wolf (1971) found a similarly high
abundance to that of Lambert et al. (1988). This results from
similar stellar
parameters (10400/2.05, no line blanketing) and slightly larger
![]() than those measured in the present study.
than those measured in the present study.
| Vega |
|
|
|
|
| HD92207 |
|
Our results support the findings of a general metal underabundance of
![]() 0.5 dex for Vega in previous studies. For
0.5 dex for Vega in previous studies. For ![]() Leo the magnesium
abundance is consistent with the solar value while in HD92207 magnesium seems
to be slightly underabundant but consideration of non-LTE effects on the
atmospheric structure are likely to bring it into better concordance.
Our model calculations generally match the observed profiles well.
For Vega, the study of the UV spectral region containing the resonance lines
further confirmes the results obtained at visual and near-IR wavelengths.
Leo the magnesium
abundance is consistent with the solar value while in HD92207 magnesium seems
to be slightly underabundant but consideration of non-LTE effects on the
atmospheric structure are likely to bring it into better concordance.
Our model calculations generally match the observed profiles well.
For Vega, the study of the UV spectral region containing the resonance lines
further confirmes the results obtained at visual and near-IR wavelengths.
In general, non-LTE abundance corrections are small (
![]() 0.3 dex)
in Mg I and negligible in Mg II, except for the
0.3 dex)
in Mg I and negligible in Mg II, except for the
![]() 4481 and 7877-96 features which show marked deviations from
LTE. The nature of the non-LTE effects is well understood.
4481 and 7877-96 features which show marked deviations from
LTE. The nature of the non-LTE effects is well understood.
Subtle effects are evoked by the inclusion of the microturbulence parameter in the statistical-equilibrium calculations for Mg I/II. In contrast to the standard approach - accounting for microturbulence only in the line formation - even weak lines might be affected by modified level populations. Mg I line strengths are systematicaly weakened while Mg II lines are strengthened, which mimics a change in the stellar effective temperature. The effect is small but cannot be neglected for high quality observations.
Finally, evidence is given that accurate analyses of late A- and early F-type supergiants are hampered by systematics originating in the pressure inversion region present in common model atmospheres. Enhanced local particle densities in the line-formation region of model atmospheres affect all broadening mechanisms and especially lead to underestimated surface gravities. No conclusive statement can be given on this topic as the question of how nature deals with this problem can only be deduced from sophisticated hydrodynamical stability analyses that still have to be performed.
Acknowledgements
We are grateful to A. Kaufer for his help with obtaining some of the spectra at La Silla and for providing observations of Vega and to S. Tubbesing for his help with the data reduction. We further express our thanks to A. Korn for providing a beautiful spectrum of Vega. We are also grateful to our referee, Dr. D. Kiselman, who helped to improve the paper by his suggestions. Funding through the MPIA, Garching, is gratefully acknowledged (NP).